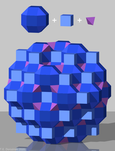
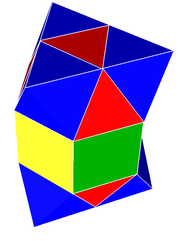
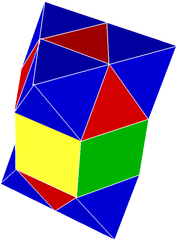
Тетраэдрально-октаэдрические соты

Переменные кубические соты

Тип	Равномерные соты
Семья	Альтернативные гиперкубические соты Симплектические соты
Индексирование ^[1]	Дж _21,31,51 , А ₂ В ₉ , Г ₁
Символы Шлефли	ч{4,3,4} {3 ^[4]} хт _0.3 {4,3,4} ч{4,4}ч{∞} ht _0,2 {4,4}h{∞} ч{∞}ч{∞}ч{∞} с{∞}с{∞}с{∞}
Диаграммы Кокстера	= = = =
Клетки	{3,3} {3,4}
Лица	треугольник {3}
Краевая фигура	[{3,3}.{3,4}] ² ( прямоугольник )
Вершинная фигура	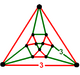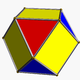( кубооктаэдр )
Группа симметрии	Фм 3 м (225)
Группа Коксетера	${\tilde {B}}_{3}$ , [4,3 ^1,1]
Двойной	Додекаэдрилл ромбические додекаэдрические соты Клетка:
Характеристики	вершинно-транзитивные , реберно-транзитивные , квазирегулярные соты

Тетраэдрально -октаэдрические соты , чередующиеся кубические соты представляют собой квазирегулярную, заполняющую пространство мозаику (или соты ) в евклидовом 3-мерном пространстве . Он состоит из чередующихся правильных октаэдров и тетраэдров в соотношении 1:2.

Другие названия включают полукубические соты , полукубические ячейки или тетрагональные дисфеноидальные ячейки . Джон Хортон Конвей называет эту соту тетраоктаэдрилом , а ее двойник — додекаэдрилом .

Р. Бакминстер Фуллер объединяет два слова октаэдр и тетраэдр в октетную ферму, ромбоэдр, состоящий из одного октаэдра (или двух квадратных пирамид) и двух противоположных тетраэдров.

Он вершинно-транзитивен и имеет 8 тетраэдров и 6 октаэдров вокруг каждой вершины . Он транзитивен по ребрам , на каждом ребре чередуются 2 тетраэдра и 2 октаэдра.

Геометрические соты — это заполнение пространства многогранными ячейками более высокой размерности или ячейками , чтобы не было пробелов. Это пример более общего математического разбиения или мозаики в любом количестве измерений.

Соты обычно строятся в обычном евклидовом («плоском») пространстве, как и выпуклые однородные соты . Они также могут быть построены в неевклидовых пространствах , таких как гиперболические однородные соты . Любой конечный однородный многогранник можно спроецировать на его описанную сферу, чтобы сформировать однородную соту в сферическом пространстве.

Это часть бесконечного семейства однородных сот, называемых чередующимися гиперкубическими сотами , образованных как чередование гиперкубических сот и состоящих из полугиперкуба и перекрестных многогранных граней. Он также является частью другого бесконечного семейства однородных сот, называемых симплексическими сотами .

В этом случае трехмерного пространства кубические соты чередуются, сводя кубические ячейки к тетраэдрам, а удаленные вершины создают октаэдрические пустоты. По существу, его можно представить расширенным символом Шлефли h{4,3,4}, содержащим половину вершин кубических сот {4,3,4}.

Существуют похожие соты, называемые спиральными тетраэдрально-октаэдрическими сотами , слои которых повернуты на 60 градусов, поэтому половина ребер имеет соседние, а не чередующиеся тетраэдры и октаэдры.

Симметрию тетраэдрально-октаэдрических сот можно удвоить, разместив тетраэдры на октаэдрических ячейках, создав неоднородную соту, состоящую из тетраэдров и октаэдров (как треугольные антипризмы). Его вершинная фигура представляет собой усеченный триакис-тетраэдр третьего порядка . Эти соты представляют собой двойные соты триакиса с усеченными тетраэдрическими ячейками.

Декартовы координаты

Для чередующихся кубических сот с краями, параллельными осям, и с длиной ребра, равной 1, декартовы координаты вершин таковы: (Для всех целых значений: i , j , k с i + j + k четным )

(я, дж, к)

На этой диаграмме показано в разобранном виде ячейки, окружающие каждую вершину.

Симметрия

Имеются две светоотражающие конструкции и множество чередующихся кубических сот ; примеры:

Симметрия	${\tilde {B}}_{3}$ , [4,3 ^1,1] = ½ ${\tilde {C}}_{3}$ , [1 ⁺,4,3,4]	${\tilde {A}}_{3}$ , [3 ^[4]] = ½ ${\tilde {B}}_{3}$ , [1 ⁺,4,3 ^1,1]	[[(4,3,4,2 ⁺)]]	[(4,3,4,2 ⁺)]
Космическая группа	Фм 3 м (225)	Ф 4 3м (216)	Я 4 3м (217)	П 4 3м (215)
Изображение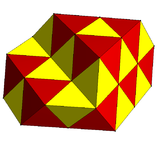
Виды тетраэдров	1	2	3	4
Коксетер диаграмма	=	= =

Чередованные кусочки кубических сот

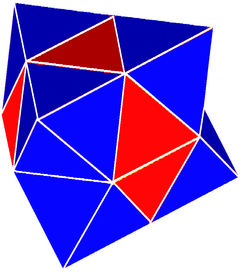
Перемежающиеся кубические соты можно разрезать на секции, где внутри октаэдра создаются новые квадратные грани. Каждый срез будет содержать квадратные пирамиды, обращенные вверх и вниз, и тетраэдры, расположенные на их ребрах. Второе направление среза не требует новых граней и включает чередование тетраэдра и октаэдра. Эти плитные соты представляют собой чешуйчатые соты, а не однородные, поскольку имеют неоднородные ячейки.

Проекция путем складывания

Перемежающиеся кубические соты можно ортогонально спроецировать на плоские квадратные плитки с помощью операции геометрического сгиба , которая отображает одну пару зеркал друг в друга. Проекция чередующихся кубических сот квадратной мозаики создает две смещенные копии расположения вершин на плоскости:

Коксетер группа	${\tilde {A}}_{3}$	${\tilde {C}}_{2}$
Коксетер диаграмма
Изображение
Имя	чередующиеся кубические соты	квадратная плитка

Решетка A3/D3

Его расположение вершин представляет собой A ₃ решетку или D ₃ решетку . ^[2]^[3] Эта решетка известна в кристаллографии как гранецентрированная кубическая решетка , а также кубическая плотноупакованная решетка , поскольку ее вершины являются центрами плотной упаковки с равными сферами, которая достигает максимально возможной средней плотности. Тетраэдрально-октаэдрические соты представляют собой трехмерный случай симплектических сот . Его ячейка Вороного представляет собой ромбический додекаэдр , двойственный вершинной фигуре кубооктаэдра для сот октаэдра.

Д ⁺
_{Упаковка 3} может быть построена объединением двух решеток D ₃ (или A ₃ ). Д ⁺
_n упаковка представляет собой лишь решетку четных размеров. Число поцелуев — 2. ²=4, (2 ^n-1 для n<8, 240 для n=8 и 2n(n-1) для n>8). ^[4]

∪

А ^*
₃ или Д ^*
₃ решетка (также называемая A ⁴
₃ или Д ⁴
₃ ) может быть построено объединением всех четырех решеток А ₃ и идентично расположению вершин дисфеноидных тетраэдрических сот , двойных сот однородных кубических сотов с надрезанием : ^[5] Это также телоцентрированный куб , объединение двух кубических сот в двойных положениях.

∪

= двойственное

=

∪

.

Поцелуйное число D ^*
₃ решетка это 8 ^[6] а его мозаика Вороного представляет собой усеченные кубические соты , , содержащий все усеченные октаэдрические ячейки Вороного , . ^[7]

Связанные соты

Соты C3

[4,3,4], генерирует Группа Кокстера 15 комбинаций однородных сот, 9 из которых имеют четкую геометрию, включая чередующиеся кубические соты. Расширенные кубические соты (также известные как сморщенные тессерактические соты) геометрически идентичны кубическим сотам.

Соты C3
Space group	Fibrifold	Extended symmetry	Extended diagram	Order	Honeycombs
Pm3m (221)	4⁻:2	[4,3,4]		×1	₁, ₂, ₃, ₄, ₅, ₆
Fm3m (225)	2⁻:2	[1⁺,4,3,4] ↔ [4,3^1,1]	↔	Half	₇, ₁₁, ₁₂, ₁₃
I43m (217)	4^o:2	[[(4,3,4,2⁺)]]		Half × 2	₍₇₎,
Fd3m (227)	2⁺:2	[[1⁺,4,3,4,1⁺]] ↔ [[3^[4]]]	↔	Quarter × 2	₁₀,
Im3m (229)	8^o:2	[[4,3,4]]		×2	₍₁₎, ₈, ₉

Соты B3

[4,3 ^1,1], генерирует Группа Кокстера 9 комбинаций однородных сот, 4 из которых имеют четкую геометрию, включая чередующиеся кубические соты.

Соты B3
Space group	Fibrifold	Extended symmetry	Extended diagram	Order	Honeycombs
Fm3m (225)	2⁻:2	[4,3^1,1] ↔ [4,3,4,1⁺]	↔	×1	₁, ₂, ₃, ₄
Fm3m (225)	2⁻:2	<[1⁺,4,3^1,1]> ↔ <[3^[4]]>	↔	×2	₍₁₎, ₍₃₎
Pm3m (221)	4⁻:2	<[4,3^1,1]>		×2	₅, ₆, ₇, ₍₆₎, ₉, ₁₀, ₁₁

Соты А3

Эти соты являются одними из пяти различных однородных сот. ^[8] построенный ${\tilde {A}}_{3}$ Группа Кокстера . Симметрию можно умножить на симметрию колец в диаграммах Кокстера – Дынкина :

Соты А3
Space group	Fibrifold	Square symmetry	Extended symmetry	Extended diagram	Extended group	Honeycomb diagrams
F43m (216)	1^o:2	a1	[3^[4]]		${\tilde {A}}_{3}$	(None)
Fm3m (225)	2⁻:2	d2	<[3^[4]]> ↔ [4,3^1,1]	↔	${\tilde {A}}_{3}$ ×2₁ ↔ ${\tilde {B}}_{3}$	₁, ₂
Fd3m (227)	2⁺:2	g2	[[3^[4]]] or [2⁺[3^[4]]]	↔	${\tilde {A}}_{3}$ ×2₂	₃
Pm3m (221)	4⁻:2	d4	<2[3^[4]]> ↔ [4,3,4]	↔	${\tilde {A}}_{3}$ ×4₁ ↔ ${\tilde {C}}_{3}$	₄
I3 (204)	8^−o	r8	[4[3^[4]]]⁺ ↔ [[4,3⁺,4]]	↔	½ ${\tilde {A}}_{3}$ ×8 ↔ ½ ${\tilde {C}}_{3}$ ×2	_(*)
Im3m (229)	8^o:2	r8	[4[3^[4]]] ↔ [[4,3,4]]	↔	${\tilde {A}}_{3}$ ×8 ↔ ${\tilde {C}}_{3}$ ×2	₅

Квазирегулярные соты

Квазирегулярная полихора и соты: h{4,p,q}
Space	Finite	Affine	Compact	Paracompact
Schläfli symbol	h{4,3,3}	h{4,3,4}	h{4,3,5}	h{4,3,6}	h{4,4,3}	h{4,4,4}
Schläfli symbol	$\left\{3,{3 \atop 3}\right\}$	$\left\{3,{4 \atop 3}\right\}$	$\left\{3,{5 \atop 3}\right\}$	$\left\{3,{6 \atop 3}\right\}$	$\left\{4,{4 \atop 3}\right\}$	$\left\{4,{4 \atop 4}\right\}$
Coxeter diagram	↔	↔	↔	↔	↔	↔
Coxeter diagram	↔					↔
Image
Vertex figure r{p,3}

Кантические кубические соты

Кантические кубические соты
Тип	Равномерные соты
Символ Шлефли	ч ₂ {4,3,4}
Диаграммы Кокстера	= =
Клетки	т{3,4} г{4,3} т{3,3}
Лица	треугольник {3} квадрат {4} шестигранник {6}
Вершинная фигура	прямоугольная пирамида
Группы Кокстера	[4,3 ^1,1], ${\tilde {B}}_{3}$ [3 ^[4]], ${\tilde {A}}_{3}$
Группа симметрии	Фм 3 м (225)
Двойной	полусплюснутый октаэдрилл Клетка:
Характеристики	вершинно-транзитивный

Кантические кубические соты , кантические кубические соты или усеченные полукубические соты представляют собой однородную мозаику , заполняющую пространство (или соты ) в евклидовом трехмерном пространстве. Он состоит из усеченных октаэдров , кубооктаэдров и усеченных тетраэдров в соотношении 1:1:2. Его вершинная фигура представляет собой прямоугольную пирамиду .

Джон Хортон Конвей называет эти соты усеченным тетраоктаэдрилом , а его двойной полусплюснутый октаэдрилл .

Симметрия

Он имеет две разные однородные конструкции. ${\tilde {A}}_{3}$ Построение можно увидеть с поочередно окрашенными усеченными тетраэдрами .

Симметрия	[4,3 ^1,1], ${\tilde {B}}_{3}$ =<[3 ^[4]]>	[3 ^[4]], ${\tilde {A}}_{3}$
Космическая группа	Фм 3 м (225)	Ф 4 3м (216)
Раскраска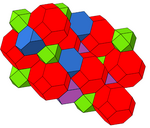
Коксетер	=	=
Вершинная фигура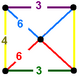

Связанные соты

Это связано с зубчатыми кубическими сотами . Ромбокубооктаэдры редуцируются до усеченных октаэдров, а кубы — до усеченных тетраэдров.

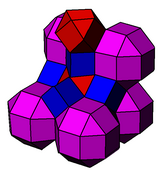зубчатый кубический	Кантик кубический
, , рр{4,3} , р{4,3} , {4,3}	, , т{3,4} , г{4,3} , т{3,3}

Рунические кубические соты

Рунические кубические соты
Тип	Равномерные соты
Символ Шлефли	ч ₃ {4,3,4}
Диаграммы Кокстера	=
Клетки	рр{4,3} {4,3} {3,3}
Лица	треугольник {3} квадрат {4}
Вершинная фигура	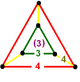треугольная деталь
Группа Коксетера	${\tilde {B}}_{4}$ , [4,3 ^1,1]
Группа симметрии	Фм 3 м (225)
Двойной	четверть кубиля Клетка:
Характеристики	вершинно-транзитивный

Рунические кубические соты или рунические кубические ячейки — это однородная, заполняющая пространство мозаика (или соты ) в евклидовом трехмерном пространстве. Он состоит из ромбокубооктаэдров , кубов и тетраэдров в соотношении 1:1:2. Его вершинная фигура представляет собой усеченный треугольник с тетраэдром на одном конце, кубом на противоположном конце и тремя ромбокубооктаэдрами вокруг трапециевидных сторон.

Джон Хортон Конвей называет эти соты 3-RCO-трилью , а ее двойную четверть кубилью .

Четверть кубиль

Двойник рунических кубических сот называется четвертью кубиля с диаграммой Коксетера. , с гранями в 2 из 4 гиперплоскостей ${\tilde {B}}_{4}$ , [4,3 ^1,1] фундаментальная область симметрии.

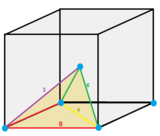
Ячейки можно рассматривать как 1/4 рассеченного куба, используя 4 вершины и центр. Вокруг 6 ребер существуют четыре клетки, а вокруг 3 ребер — 3 клетки.

Связанные соты

Он похож на сужающиеся кубические соты , в которых четверть кубов чередуются с тетраэдрами, а половина расширяется в ромбокубооктаэдры.

Ранцинированный кубический	Руничский кубический =
{4,3} , {4,3} , {4,3} , {4,3} , , ,	ч{4,3} , рр{4,3} , {4,3} , ,

Эти соты можно разделить на усеченные квадратные плиточные плоскости, используя центры восьмиугольников ромбокубооктаэдров, создавая квадратные купола . Эти чешуйчатые соты представлены диаграммой Кокстера. и символ s ₃ {2,4,4} с симметрией обозначений Кокстера [2 ⁺,4,4].

.

Рансикантические кубические соты

Рансикантические кубические соты
Тип	Равномерные соты
Символ Шлефли	ч _2,3 {4,3,4}
Диаграммы Кокстера	=
Клетки	тр{4,3} т{4,3} т{3,3}
Лица	треугольник {3} квадрат {4} шестигранник {6} восьмиугольник {8}
Вершинная фигура	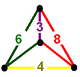зеркальная клиновидная кость
Группа Коксетера	${\tilde {B}}_{4}$ , [4,3 ^1,1]
Группа симметрии	Фм 3 м (225)
Двойной	половина пирамидиллы Клетка:
Характеристики	вершинно-транзитивный

Рунцикантические кубические соты или рункикантические кубические ячейки представляют собой однородную, заполняющую пространство мозаику (или соты ) в евклидовом трехмерном пространстве. Он составлен из усеченных кубооктаэдров , усеченных кубов и усеченных тетраэдров в соотношении 1:1:2, с зеркальной клиновидной вершинной фигурой . Это связано с кубическими сотами с ранцикантелляцией .

Джон Хортон Конвей называет эти соты f-tCO-trill , а их двойную полупирамидиллю .

Половина пирамидиллы

Двойник кубических сот с усеченными краями называется полупирамидиллей с диаграммой Кокстера . . Грани существуют в 3 из 4 гиперплоскостей [4,3 ^1,1], ${\tilde {B}}_{3}$ Группа Кокстера.

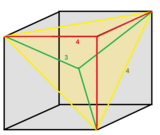
Ячейки представляют собой неправильные пирамиды и могут рассматриваться как 1/12 куба или 1/24 ромбододекаэдра , каждая из которых имеет три угла и центр куба.

Родственные косые апейроэдры

Существует родственный однородный косой апейроэдр с таким же расположением вершин , но удалены треугольники и квадраты. Его можно рассматривать как усеченные тетраэдры и усеченные кубы, сложенные вместе.

Связанные соты

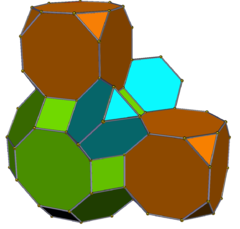Рансикантический куб	Ранцикантеллярный кубический

Закручивающиеся тетраэдрически-октаэдрические соты

Закручивающиеся тетраэдрически-октаэдрические соты
Тип	выпуклые однородные соты
Диаграммы Кокстера
Символы Шлефли	ч{4,3,4}:г ч{6,3}ч{∞} с{3,6}ч{∞} с{3 ^[3]}ч{∞}
Клетки	{3,3} {3,4}
Лица	треугольник {3}
Вершинная фигура	треугольный ортобикупол G3.4.3.4
Космическая группа	Р6 ₃ /ммц (194) [3,6,2 ⁺,∞]
Двойной	трапезо-ромбические додекаэдрические соты
Характеристики	вершинно-транзитивный

Вращающиеся тетраэдрально-октаэдрические соты или вращающиеся чередующиеся кубические соты представляют собой заполняющую пространство мозаику (или соты ) в евклидовом трехмерном пространстве, состоящую из октаэдров и тетраэдров в соотношении 1:2.

Он вершинно-однороден , вокруг каждой вершины находится 8 тетраэдров и 6 октаэдров.

Он не является однородным по краям . Все ребра имеют по 2 тетраэдра и 2 октаэдра, но некоторые чередуются, а некоторые парные.

Это можно увидеть как отражающие слои этого сотового слоя:

Строительство путем вращения

Это менее симметричная версия другой соты, тетраэдро-октаэдрической соты, в которой каждое ребро окружено чередующимися тетраэдрами и октаэдрами. Оба можно рассматривать как состоящие из слоев толщиной в одну клетку, внутри которых строго чередуются два типа клеток. Поскольку грани на плоскостях, разделяющих эти слои, образуют правильный узор из треугольников , соседние слои можно расположить так, чтобы каждый октаэдр в одном слое встречался с тетраэдром в следующем слое, или так, чтобы каждая ячейка встречалась с ячейкой своего вида ( граница слоя, таким образом, становится плоскостью отражения ). Последняя форма называется циркулярной .

Вершинная фигура называется треугольным ортобикуполом по сравнению с тетраэдрально-октаэдрическими сотами, вершинная фигура которого кубооктаэдр в более низкой симметрии называется треугольным гиробикуполом , поэтому префикс гиро- используется наоборот.

Вершинные фигуры
Соты	Вращающийся тет-окт	Светоотражающий тет-окт
Изображение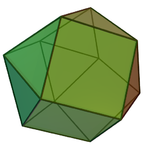
Имя	треугольный ортобикупол	треугольный гирокупол
Вершинная фигура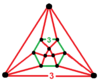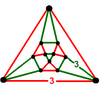
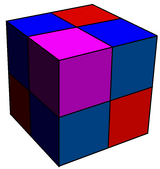
Симметрия	Д _3ч , заказ 12	Д _3д , заказать 12 (Ох _, заказ 48)

Строительство попеременно

Геометрию также можно построить с помощью операции чередования , примененной к шестиугольным призматическим сотам . Ячейки шестиугольной призмы превращаются в октаэдры , а пустоты образуют треугольные бипирамиды , которые можно разделить на пары тетраэдров этой соты. Такие соты с бипирамидами называются дитетраэдрически-октаэдрическими сотами . Существует 3 диаграммы Кокстера-Динкина , которые можно рассматривать как октаэдры 1, 2 или 3 цветов:

Гироудлиненные чередующиеся кубические соты

Гироудлиненные чередующиеся кубические соты
Тип	Равномерные соты
Символ Шлефли	ч{4,3,4}:ge {3,6}ч ₁ {∞}
Диаграмма Кокстера
Клетки	{3,3} {3,4} (3.4.4)
Лица	треугольник {3} квадрат {4}
Вершинная фигура
Космическая группа	Р6 ₃ /ммц (194) [3,6,2 ⁺,∞]
Характеристики	вершинно-транзитивный

Гироудлиненные чередующиеся кубические соты или удлиненные треугольные антипризматические ячейки ) , заполняющую пространство, представляют собой мозаику (или соты в евклидовом трехмерном пространстве . Он состоит из октаэдров , треугольных призм и тетраэдров в соотношении 1:2:2.

Он вершинно-транзитивен, вокруг каждой вершины расположены 3 октаэдра, 4 тетраэдра и 6 треугольных призм.

Это один из 28 выпуклых однородных сот .

Удлиненные чередующиеся кубические соты имеют одинаковое расположение ячеек в каждой вершине, но общее расположение различается. В вытянутой форме каждая призма встречается с тетраэдром на одной из треугольных граней и октаэдром на другой; в гировытянутой форме призма встречает такой же вид дельтаэдра на каждом конце .

Удлиненные чередующиеся кубические соты

Удлиненные чередующиеся кубические соты
Тип	Равномерные соты
Символ Шлефли	ч{4,3,4}:е {3,6}г ₁ {∞}
Клетки	{3,3} {3,4} (3.4.4)
Лица	треугольник {3} квадрат {4}
Вершинная фигура	треугольный купол, соединенный с равнобедренной шестиугольной пирамидой
Группа симметрии	[6,(3,2 ⁺,∞,2 ⁺)] ?
Характеристики	вершинно-транзитивный

Удлиненные чередующиеся кубические соты или удлиненные треугольные гиропризматические ячейки представляют собой заполняющую пространство мозаику (или соты ) в евклидовом трехмерном пространстве . Он состоит из октаэдров , треугольных призм и тетраэдров в соотношении 1:2:2.

Он вершинно-транзитивен, вокруг каждой вершины расположены 3 октаэдра, 4 тетраэдра и 6 треугольных призм. Каждая призма на одном конце пересекается с октаэдром, а на другом — с тетраэдром.

Это один из 28 выпуклых однородных сот .

Он имеет закрученную форму, называемую гироудлиненными чередующимися кубическими сотами , с одинаковым расположением ячеек в каждой вершине.

См. также

Примечания

^ Для перекрестных ссылок им даны списочные индексы Андреини (1-22), Уильямса (1-2,9-19), Джонсона (11-19, 21-25, 31-34, 41-49, 51). -52, 61-65) и Грюнбаум (1-28).
^ «Решетка Д3» .
^ «Решетка А3» .
^ Конвей (1998), с. 119
^ «Решетка Д3» .
^ Конвей (1998), с. 120
^ Конвей (1998), с. 466
^ [1] , OEIS последовательность A000029 6-1 случаев, пропуск одного с нулевыми отметками

Ссылки

Джон Х. Конвей , Хайди Бургель, Хаим Гудман-Штраус , (2008) Симметрии вещей , ISBN 978-1-56881-220-5 (Глава 21, Наименование архимедовых и каталонских многогранников и мозаик, Архитектурные и катоптрические мозаики, стр. 292–298, включает все непризматические формы)
Георгий Ольшевский, Равномерные паноплоидные тетракомбы , Рукопись (2006) (Полный список из 11 выпуклых однородных мозаик, 28 выпуклых однородных сот и 143 выпуклых однородных тетракомб)
Бранко Грюнбаум , Равномерные разбиения трехмерного пространства. Геомбинаторика 4 (1994), 49–56.
Нормана Джонсона Равномерные многогранники , Рукопись (1991)
Уильямс, Роберт (1979). Геометрическая основа естественной структуры: справочник по дизайну . Dover Publications, Inc. ISBN 0-486-23729-Х .
Кричлоу, Кейт (1970). Порядок в космосе: справочник по дизайну . Викинг Пресс. ISBN 0-500-34033-1 .
Калейдоскопы: Избранные сочинения HSM Коксетера , под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони К. Томпсона, Азии Ивик Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [2]
- (Документ 22) HSM Коксетер, Правильные и полуправильные многогранники I , [Math. Зейт. 46 (1940) 380–407, МР 2,10] (1.9 Равномерные заполнения пробелов)
- (Документ 24) HSM Коксетер, Правильные и полуправильные многогранники III , [Math. Зейт. 200 (1988) 3-45]
А. Андреини , О правильных и полуправильных сетях многогранников и о соответствующих корреляционных сетях , Mem. Società Italiana della Scienze, Ser.3, 14 (1905) 75–129.
ДМИ Соммервилль , Введение в геометрию n измерений. Нью-Йорк, EP Dutton, 1930. 196 стр. (издание Dover Publications, 1958). Глава X: Правильные многогранники.
Конвей Дж. Х., Слоан Нью-Джерси (1998). Сферические упаковки, решетки и группы (3-е изд.). Спрингер. ISBN 0-387-98585-9 .

Внешние ссылки

v т и Основные выпуклые правильные и однородные соты размеров 2–9.
Космос	Семья	${\tilde {A}}_{n-1}$	${\tilde {C}}_{n-1}$	${\tilde {B}}_{n-1}$	${\tilde {D}}_{n-1}$	${\tilde {G}}_{2}$ / ${\tilde {F}}_{4}$ / ${\tilde {E}}_{n-1}$
И ²	Равномерная укладка плитки	{3 ^[3]}	д ₃	HD ₃	квартал ₃	Шестиугольный
И ³	Равномерные выпуклые соты	{3 ^[4]}	д ₄	HD ₄	4 _{квартала}
И ⁴	Униформа 4-сотовая	{3 ^[5]}	д ₅	hδ ₅	qδ ₅	24-ячеистые соты
И ⁵	Униформа 5-сотовая	{3 ^[6]}	д ₆	HD ₆	qδ ₆
И ⁶	Униформа 6-сотовая	{3 ^[7]}	д ₇	hδ ₇	qδ ₇	2 ₂₂
И ⁷	Униформа 7-сотовая	{3 ^[8]}	д ₈	hδ ₈	8 _{кварталов}	1 ₃₃ • 3 ₃₁
И ⁸	Униформа 8-сотовая	{3 ^[9]}	д ₉	HD ₉	qδ ₉	1 ₅₂ • 2 ₅₁ • 5 ₂₁
И ⁹	Униформа 9-сотовая	{3 ^[10]}	д ₁₀	HD ₁₀	10 _{кварталов}
И ¹⁰	Униформа 10-сотовая	{3 ^[11]}	д ₁₁	HD ₁₁	qδ ₁₁
И ^{п -1}	Равномерный ( n -1)- сотовый	{3 ^[н]}	δ _н	hδ _н	qδ _н	1 _{лиц 2} • 2 _{лиц 1} • лиц ₂₁

[1] Для перекрестных ссылок им даны списочные индексы Андреини (1-22), Уильямса (1-2,9-19), Джонсона (11-19, 21-25, 31-34, 41-49, 51). -52, 61-65) и Грюнбаум (1-28).

[2] «Решетка Д3» .

[3] «Решетка А3» .

[4] Конвей (1998), с. 119

[5] «Решетка Д3» .

[6] Конвей (1998), с. 120

[7] Конвей (1998), с. 466

[8] [1] , OEIS последовательность A000029 6-1 случаев, пропуск одного с нулевыми отметками

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]