Связывающий номер

«Номер ссылки» перенаправляется сюда. Чтобы узнать о логической задаче, см. Numberlink .

Две кривые этого (2, 8) -звена тора имеют зацепление номер четыре.

В математике число сцепления — это числовой инвариант , описывающий соединение двух замкнутых кривых в трехмерном пространстве . Интуитивно понятно, что число связей представляет собой количество раз, когда каждая кривая обвивает другую. В евклидовом пространстве связующее число всегда является целым числом , но может быть положительным или отрицательным в зависимости от ориентации двух кривых (это неверно для кривых в большинстве трехмерных многообразий , где связующие числа также могут быть дробными или просто не существовать). совсем).

Число зацепления было введено Гауссом в виде интеграла зацепления . Это важный объект исследования в теории узлов , алгебраической топологии и дифференциальной геометрии , и он имеет многочисленные приложения в математике и науке , включая квантовую механику , электромагнетизм и изучение суперспирализации ДНК .

Определение

Любые две замкнутые кривые в пространстве, если им разрешено проходить через себя, но не друг через друга, могут быть перемещены ровно в одно из следующих стандартных положений. Это определяет связывающий номер:

⋯
	связующее число −2	связующее число −1	связующий номер 0
					⋯
		связующий номер 1	связующее номер 2	связующий номер 3

Каждая кривая может проходить через себя во время этого движения, но обе кривые должны оставаться разделенными. Это формализуется как регулярная гомотопия , которая дополнительно требует, чтобы каждая кривая была погружением , а не просто любым отображением. Однако это добавленное условие не меняет определение числа зацепления (не имеет значения, должны ли кривые всегда быть погружениями или нет), что является примером h -принципа (принципа гомотопии), означающего, что геометрия сводит к топологии.

Доказательство

Этот факт (то, что связующее число является единственным инвариантом) легче всего доказать, поместив один круг в стандартное положение, а затем показав, что связующее число является единственным инвариантом другого круга. Подробно:

• Отдельная кривая является регулярной гомотопной стандартной окружности (любой узел можно развязать, если позволить кривой пройти через себя). Тот факт, что оно гомотопно, очевиден, поскольку 3-пространство стягиваемо и, следовательно, все отображения в него гомотопны, хотя тот факт, что это можно сделать посредством погружений, требует некоторых геометрических аргументов.
• Дополнение к стандартной окружности гомеоморфно полноторию с удаленной точкой (в этом можно убедиться, интерпретируя 3-пространство как 3-сферу с удаленной бесконечной точкой, а 3-сферу как два полнотория, склеенных вдоль граница), или дополнение может быть проанализировано напрямую.
• Фундаментальная группа трехмерного пространства минус круг — это целые числа, соответствующие числу зацеплений. Это можно увидеть с помощью теоремы Зейферта – Ван Кампена (либо добавление точки на бесконечности, чтобы получить полноторие, либо добавление круга, чтобы получить трехмерное пространство, позволяет вычислить фундаментальную группу желаемого пространства).
• Таким образом, гомотопические классы кривой в 3-мерном пространстве без круга определяются числом зацепления.
• Верно также и то, что регулярные гомотопические классы определяются числом зацепления, что требует дополнительных геометрических аргументов.

Вычисление связующего числа

Имея шесть положительных пересечений и два отрицательных пересечения, эти кривые имеют соединение номер два.

Существует алгоритм расчета числа связей двух кривых по диаграмме связей . Обозначьте каждое пересечение как положительное или отрицательное в соответствии со следующим правилом:

Общее количество положительных пересечений минус общее количество отрицательных пересечений равно удвоенному числу сшивок. То есть:

${\text{linking number}}={\frac {n_{1}+n_{2}-n_{3}-n_{4}}{2}}$

где n ₁ , n ₂ , n ₃ , n ₄ представляют собой количество пересечений каждого из четырех типов. Две суммы $n_{1}+n_{3}\,\!$ и $n_{2}+n_{4}\,\!$ всегда равны, что приводит к следующей альтернативной формуле

${\text{linking number}}\,=\,n_{1}-n_{4}\,=\,n_{2}-n_{3}.$

Формула $n_{1}-n_{4}$ включает только пересечение синей кривой красной, тогда как $n_{2}-n_{3}$ включает в себя только перекрёстки.

Свойства и примеры

Две кривые связи Уайтхеда имеют нулевой номер связи.

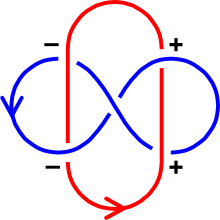
• Любые две несвязанные кривые имеют связующий номер ноль. Однако две кривые с нулевым номером связи все же могут быть связаны (например, связь Уайтхеда ).
• Изменение ориентации любой из кривых на противоположное отменяет число связи, а изменение ориентации обеих кривых оставляет его неизменным.
• Число связи является хиральным : зеркальное отображение ссылки отменяет число связи. Соглашение о положительном числе связей основано на правиле правой руки .
• Число витков ориентированной кривой в плоскости x - y равно числу ее связей с осью z (представляя ось z как замкнутую кривую в трехмерной сфере ).
• либо из кривых проста , то первая группа гомологии ее дополнения изоморфна Z. смысле, если какая - В более общем В этом случае число зацепления определяется классом гомологии другой кривой.
• В физике число связи является примером топологического квантового числа .

Интегральное определение Гаусса

Даны две непересекающиеся дифференцируемые кривые. $\gamma _{1},\gamma _{2}\colon S^{1}\rightarrow \mathbb {R} ^{3}$, определим Гаусса отображение $\Gamma$ от тора к сфере ​

$\Gamma (s,t)={\frac {\gamma _{1}(s)-\gamma _{2}(t)}{|\gamma _{1}(s)-\gamma _{2}(t)|}}$

Выберите точку на единичной сфере v так, чтобы ортогональная проекция звена на плоскость, перпендикулярную v , давала диаграмму звеньев. Обратите внимание, что точка ( s , t ), которая переходит в v при отображении Гаусса, соответствует пересечению на диаграмме связей, где $\gamma _{1}$ закончилось $\gamma _{2}$. Кроме того, окрестность ( s , t ) отображается при отображении Гаусса в окрестность v, сохраняя или меняя ориентацию в зависимости от знака пересечения. Таким образом, чтобы вычислить число зацеплений диаграммы, соответствующей v, достаточно подсчитать знаковое количество раз, когда карта Гаусса покрывает v . Поскольку v является регулярной величиной , это в точности степень отображения Гаусса (т. е. количество раз, когда образ Γ покрывает сферу). Изотопическая инвариантность числа зацепления получается автоматически, поскольку степень инвариантна относительно гомотопических отображений. Любое другое обычное значение даст то же число, поэтому номер связи не зависит от какой-либо конкретной диаграммы связей.

Эта формулировка числа связи γ ₁ и γ ₂ позволяет получить явную формулу в виде интеграла двойной линии , интеграла связи Гаусса :

${\begin{aligned}\operatorname {link} (\gamma _{1},\gamma _{2})&={\frac {1}{4\pi }}\oint _{\gamma _{1}}\oint _{\gamma _{2}}{\frac {\mathbf {r} _{1}-\mathbf {r} _{2}}{|\mathbf {r} _{1}-\mathbf {r} _{2}|^{3}}}\cdot (d\mathbf {r} _{1}\times d\mathbf {r} _{2})\\[4pt]&={\frac {1}{4\pi }}\int _{S^{1}\times S^{1}}{\frac {\det \left({\dot {\gamma }}_{1}(s),{\dot {\gamma }}_{2}(t),\gamma _{1}(s)-\gamma _{2}(t)\right)}{\left|\gamma _{1}(s)-\gamma _{2}(t)\right|^{3}}}\,ds\,dt\end{aligned}}$

Этот интеграл вычисляет общую площадь изображения карты Гаусса со знаком (подынтегральная функция является якобианом Γ ), а затем делится на площадь сферы (которая равна 4 π ).

В квантовой теории поля

В квантовой теории поля определение интеграла Гаусса возникает при вычислении среднего значения петли Вильсона, наблюдаемой в $U(1)$ Черна–Саймонса Калибровочная теория . Явно абелево действие Черна–Саймонса для калибровочного потенциала одной формы $A$ на трёхмногообразии $M$ дается

$S_{CS}={\frac {k}{4\pi }}\int _{M}A\wedge dA$

Нас интересует получение интеграла по траекториям Фейнмана для Черна–Саймонса в $M=\mathbb {R} ^{3}$:

$Z[\gamma _{1},\gamma _{2}]=\int {\mathcal {D}}A_{\mu }\exp \left({\frac {ik}{4\pi }}\int d^{3}x\varepsilon ^{\lambda \mu \nu }A_{\lambda }\partial _{\mu }A_{\nu }+i\int _{\gamma _{1}}dx^{\mu }\,A_{\mu }+i\int _{\gamma _{2}}dx^{\mu }\,A_{\mu }\right)$

Здесь, $\epsilon$ является антисимметричным символом. Поскольку теория является просто гауссовой, ультрафиолетовая регуляризация или перенормировка не требуются. Следовательно, топологическая инвариантность правой части гарантирует, что результат интеграла по путям будет топологическим инвариантом. Единственное, что осталось сделать, — это обеспечить общий коэффициент нормализации, и тогда появится естественный выбор. Поскольку теория является гауссовой и абелевой, интеграл по путям можно получить, просто решив теорию классически и заменив $A$.

Классические уравнения движения:

$\varepsilon ^{\lambda \mu \nu }\partial _{\mu }A_{\nu }={\frac {2\pi }{k}}J^{\lambda }$

Здесь мы связали поле Черна – Саймонса с источником с членом $-J_{\mu }A^{\mu }$ в лагранжиане. Очевидно, заменив соответствующие $J$, мы можем вернуть петли Вильсона. Поскольку мы находимся в трёх измерениях, мы можем переписать уравнения движения в более привычных обозначениях:

${\vec {\nabla }}\times {\vec {A}}={\frac {2\pi }{k}}{\vec {J}}$

Берем завиток обеих сторон и выбираем калибровку Лоренца. $\partial ^{\mu }A_{\mu }=0$, уравнения принимают вид

$\nabla ^{2}{\vec {A}}=-{\frac {2\pi }{k}}{\vec {\nabla }}\times {\vec {J}}$

Решение из электростатики:

$A_{\lambda }({\vec {x}})={\frac {1}{2k}}\int d^{3}{\vec {y}}\,{\frac {\varepsilon _{\lambda \mu \nu }\partial ^{\mu }J^{\nu }({\vec {y}})}{|{\vec {x}}-{\vec {y}}|}}$

Интеграл по путям для произвольного $J$ теперь легко сделать, подставив это в действие Черна – Саймонса, чтобы получить эффективное действие для $J$ поле. Чтобы получить интеграл по траекториям для петель Вильсона, мы заменим источник, описывающий две частицы, движущиеся по замкнутым петлям, т.е. $J=J_{1}+J_{2}$, с

$J_{i}^{\mu }(x)=\int _{\gamma _{i}}dx_{i}^{\mu }\delta ^{3}(x-x_{i}(t))$

Поскольку эффективное действие квадратично по $J$, ясно, что будут члены, описывающие самодействие частиц, и они неинтересны, поскольку они были бы там даже при наличии всего лишь одной петли. Поэтому мы нормируем интеграл по путям на множитель, точно сокращающий эти члены. Проходя алгебру, получаем

$Z[\gamma _{1},\gamma _{2}]=\exp {\left({\frac {2\pi i}{k}}\Phi [\gamma _{1},\gamma _{2}]\right)},$

где

$\Phi [\gamma _{1},\gamma _{2}]={\frac {1}{4\pi }}\int _{\gamma _{1}}dx^{\lambda }\int _{\gamma _{2}}dy^{\mu }\,{\frac {(x-y)^{\nu }}{|x-y|^{3}}}\varepsilon _{\lambda \mu \nu },$

который представляет собой просто интеграл связи Гаусса. Это простейший пример топологической квантовой теории поля , где интеграл по путям вычисляет топологические инварианты. явно показал Это также послужило намеком на то, что неабелев вариант теории Черна – Саймонса вычисляет другие инварианты узлов, и Эдвард Виттен , что неабелева теория дает инвариант, известный как полином Джонса.

Калибровочная теория Черна-Саймонса существует в трех измерениях пространства-времени. В более общем смысле, существуют топологические квантовые теории поля более высоких размерностей. Существуют более сложные многопетлевые/струнные статистики четырехмерных калибровочных теорий, захватываемые инвариантами зацепления экзотических топологических квантовых теорий поля в четырех измерениях пространства-времени.

Обобщения

обобщают Инварианты Милнора число зацепления на связи с тремя или более компонентами, позволяя доказать, что кольца Борромео связаны, хотя любые два компонента имеют число зацепления 0.

• Подобно тому, как замкнутые кривые могут быть связаны в трех измерениях, любые два замкнутых многообразия размерностей m и n могут быть связаны в евклидовом пространстве размерности $m+n+1$. Любая такая связь имеет связанное с ней отображение Гаусса, степень которого является обобщением числа связи.
• Любой оснащенный узел имеет число самосвязывания , полученное путем вычисления числа зацепления узла С с новой кривой, полученной путем небольшого перемещения точек С вдоль векторов оснащения. Число самосвязывания, полученное при перемещении по вертикали (вдоль каркаса доски), известно как число самосвязывания Кауфмана .
• Связующий номер определяется для двух связанных кругов; учитывая три или более кругов, можно определить инварианты Милнора , которые представляют собой числовой инвариант, обобщающий число зацеплений.
• В алгебраической топологии произведение чашки представляет собой далеко идущее алгебраическое обобщение числа зацепления, при этом произведения Мэсси являются алгебраическими аналогами инвариантов Милнора .
• Бесзвенное вложение неориентированного графа — это такое вложение в трехмерное пространство, при котором каждые два цикла имеют нулевое число зацеплений. Графы с вложением без связей имеют запрещенную минорную характеристику как графы без семейства Петерсена минора .

См. также

• Дифференцируемая кривая - Исследование кривых с дифференциальной точки зрения.
• Инвариант Хопфа - гомотопический инвариант отображений между n-сферами.
• Число поцелуев – геометрическая концепция
• Врит — инвариант диаграммы узлов.

Ссылки

• А. В. Чернавский (2001) [1994], «Коэффициент связи» , Энциклопедия Математики , EMS Press
• А. В. Чернавский (2001) [1994], «Корчащееся число» , Энциклопедия Математики , EMS Press