Лунное расстояние (навигация)
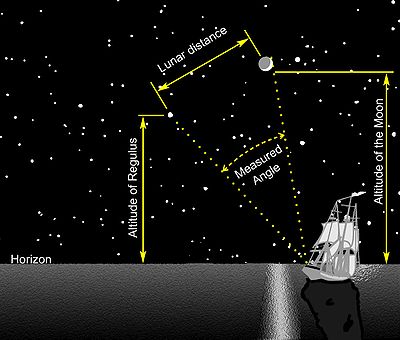
В астрономической навигации лунное расстояние , также называемое лунным , представляет собой угловое расстояние между Луной и другим небесным телом . Метод лунных расстояний использует этот угол и морской альманах для расчета времени по Гринвичу, если это необходимо, или, как следствие, любого другого времени. Это рассчитанное время можно использовать при решении сферического треугольника . Теория была впервые опубликована Иоганном Вернером в 1524 году, до того, как были опубликованы необходимые альманахи. Более полный метод был опубликован в 1763 году и использовался примерно до 1850 года, когда его заменил морской хронометр . использует положения галилеевых спутников Юпитера Подобный метод .
Цель
[ редактировать ]В астронавигации знание времени в Гринвиче (или другом известном месте) и измеренных положениях одного или нескольких небесных объектов позволяет навигатору рассчитать широту и долготу . [1] Надежные морские хронометры были недоступны до конца 18 века и недоступны до 19 века. [2] [3] [4] После того как метод был впервые опубликован в 1763 году британским астрономом Ройалом Невилом Маскелином , основанным на новаторских работах Тобиаса Майера , в течение примерно ста лет (примерно до 1850 года) [5] моряки, у которых не было хронометра, использовали метод лунных расстояний для определения времени по Гринвичу как ключевой шаг в определении долготы. И наоборот, моряк с хронометром мог проверить его точность, используя лунное определение времени по Гринвичу. [2] Этот метод использовался вплоть до начала 20-го века на небольших судах, которые не могли позволить себе хронометр или были вынуждены полагаться на этот метод для коррекции хронометра. [6]
Метод
[ редактировать ]Краткое содержание
[ редактировать ]Метод основан на относительно быстром движении Луны по фоновому небу, совершая оборот на 360 градусов за 27,3 дня ( сидерический месяц), или 13,2 градуса в день. За час он сдвинется примерно на полградуса. [1] примерно его собственный угловой диаметр по отношению к фоновым звездам и Солнцу.
С помощью секстанта навигатор точно измеряет угол между Луной и другим телом . [1] Это может быть Солнце или одна из избранной группы ярких звезд, лежащих недалеко от пути Луны, недалеко от эклиптики . В этот момент любой на поверхности Земли, кто может видеть одни и те же два тела, после поправки на параллакс будет наблюдать тот же угол. Затем навигатор сверяется с подготовленной таблицей лунных расстояний и времени, в которое они произойдут. [1] [7] Сравнивая исправленное расстояние до Луны с табличными значениями, навигатор определяет время по Гринвичу для этого наблюдения. Зная время по Гринвичу и местное время, навигатор может определить долготу. [1]
Местное время можно определить по секстанту, наблюдающему за высотой Солнца или звезды. [8] [9] Тогда долгота (относительно Гринвича) легко вычисляется по разнице между местным временем и временем по Гринвичу с разницей в 15 градусов в час.
На практике
[ редактировать ]Измерив лунное расстояние и высоты двух тел, навигатор может найти время по Гринвичу в три этапа:
- Предварительные сведения : таблицы Альманаха предсказывают лунные расстояния между центром Луны и другим телом (опубликовано между 1767 и 1906 годами в Великобритании). [10] [11] Однако наблюдатель не может точно найти центр Луны (или Солнца, которое было наиболее часто используемым вторым объектом). Вместо этого лунные расстояния всегда измеряются до ярко освещенного внешнего края (лимба, а не терминатора ) Луны (или Солнца). Первая поправка к лунному расстоянию — это расстояние между лимбом Луны и ее центром. Поскольку видимый размер Луны меняется в зависимости от ее расстояния от Земли, в альманахах указываются полудиаметры Луны и Солнца на каждый день. [12] Дополнительно наблюдаемые высоты очищаются от полудиаметра.
- Очистка : расстояние до Луны корректируется с учетом влияния параллакса и атмосферной рефракции на наблюдение. В альманахе указаны лунные расстояния такими, какими они выглядели бы, если бы наблюдатель находился в центре прозрачной Земли. Поскольку Луна находится намного ближе к Земле, чем звезды, положение наблюдателя на поверхности Земли смещает относительное положение Луны на целый градус. [13] [14] Поправка на просветление параллакса и рефракции является тригонометрической функцией наблюдаемого лунного расстояния и высот двух тел. [15] Навигаторы использовали наборы математических таблиц для выполнения этих вычислений любым из десятков различных методов очистки. Для практического применения сегодня используются таблицы Брюса Старка. [16] может использоваться для преодоления лунного расстояния. Они построены таким образом, что вместо тригонометрических оценок требуются только сложения и вычитания табличных чисел.
- Определение времени : Навигатор, очистив лунное расстояние, теперь сверяется с подготовленной таблицей лунных расстояний и времени, в которое они произойдут, чтобы определить гринвичское время наблюдения. [1] [7] Чтобы предсказать положение Луны на годы вперед, необходимо решить задачу трех тел , поскольку в ней участвовали все Земля, Луна и Солнце. Эйлер разработал использованный ими численный метод, названный методом Эйлера , и получил грант от Совета по долготе на проведение вычислений.
Найдя (абсолютное) гринвичское время, штурман либо сравнивает его с наблюдаемым местным видимым временем (отдельное наблюдение), чтобы найти свою долготу, либо сравнивает его с гринвичским временем на хронометре (если он имеется), если он хочет проверить хронометр. [1]
Ошибки
[ редактировать ]Ошибка альманаха
[ редактировать ]К 1810 году ошибки в предсказаниях альманаха сократились примерно до четверти угловой минуты. Примерно к 1860 году (после того как наблюдения за расстоянием до Луны практически ушли в прошлое) ошибки альманаха наконец сократились до уровня, меньшего, чем погрешность секстанта в идеальных условиях (одна десятая угловой минуты).
Наблюдение за лунным расстоянием
[ редактировать ]Более поздние секстанты (около г. 1800 ) могли указывать угол до 0,1 угловой минуты после того, как использование нониуса было популяризировано благодаря его описанию на английском языке в книге Navigatio Britannica, опубликованной в 1750 году Джоном Барроу математиком и историком . На практике на море реальные ошибки были несколько больше. Если небо облачное или Луна новая (спрятана близко к бликам Солнца), наблюдения за расстоянием до Луны не могут быть выполнены.
Общая ошибка
[ редактировать ]Расстояние до Луны меняется со временем со скоростью примерно полградуса, или 30 угловых минут, в час. [1] Два источника ошибок вместе взятые обычно составляют около половины угловой минуты на лунном расстоянии, что эквивалентно одной минуте по гринвичскому времени, что соответствует ошибке в одну четверть градуса долготы, или около 15 морских миль (28 км) по экватору.
В литературе
[ редактировать ]Капитан Джошуа Слокам , совершая первое одиночное кругосветное плавание вокруг Земли в 1895–1898 годах, несколько анахронично использовал лунный метод наряду с точным счислением в своей навигации . он комментирует В книге «Sailing Alone Round the World» снимок, сделанный в южной части Тихого океана . После исправления ошибки, которую он обнаружил в своих таблицах журналов , результат оказался на удивление точным: [17]
В результате трех наблюдений, после долгой борьбы с лунными таблицами, я обнаружил, что ее долгота совпадала с точностью в пяти милях от этой долготы по счислению пути.Это было чудесно; оба, однако, могли быть ошибочными, но почему-то я чувствовал уверенность, что оба почти верны и что еще через несколько часов я увижу землю; Так и произошло, потому что тогда я увидел остров Нукахива , самый южный из группы Маркизских островов , четко очерченный и высокий. Подтвержденная долгота при сближении находилась где-то между двумя значениями; это было необычно. Все мореплаватели скажут вам, что изо дня в день корабль может потерять или набрать более пяти миль в своем плавательном счете, и опять же, что касается лун, даже опытные лунники считаются проделавшими умную работу, если их среднее значение находится в пределах восьми мили правды...
Результат этих наблюдений, естественно, пощекотал мое тщеславие, поскольку я знал, что это нечто — стоять на палубе огромного корабля и с двумя помощниками проводить наблюдения Луны, приблизительно близкие к истине. Как один из беднейших американских моряков, я гордился своим маленьким достижением на шлюпе, даже если это было случайно...
Работа лунатика, хотя и редко практикуемая в наши дни хронометров, прекрасно поучительна, и нет ничего в области навигации, что вызывало бы большее восхищение в сердце.
В своей книге 1777 года «Вокруг света» натуралист Георг Форстер описал свои впечатления от плавания с капитаном Джеймсом Куком на борту корабля HMS «Резольюшн» в южной части Тихого океана. Кук имел на борту два новых хронометра: один изготовлен Ларкамом Кендаллом, другой — Джоном Арнольдом , по образцу знаменитых часов Джона Харрисона . 12 марта 1774 года, приближаясь к острову Пасхи , Форстер счёл похвальным метод лунных расстояний как лучший и наиболее точный метод определения долготы по сравнению с часами, которые могли выйти из строя из-за механических проблем.
См. также
[ редактировать ]- Королевская обсерватория, Гринвич
- Йозеф де Мендоса-и-Риос
- Джон Харрисон
- История долготы
- Приз за долготу
- Генри Рэпер
- Американский практический навигатор Боудича
- Натаниэль Боудич
Ссылки
[ редактировать ]- ^ Jump up to: а б с д и ж г час Нори, JW (1828 г.). Новое и полное воплощение практической навигации . Лондон. п. 222. Архивировано из оригинала 27 сентября 2007 г. Проверено 2 августа 2007 г.
- ^ Jump up to: а б Нори, JW (1828 г.). Новое и полное воплощение практической навигации . Лондон. п. 221. Архивировано из оригинала 27 сентября 2007 г. Проверено 2 августа 2007 г.
- ^ Тейлор, Джанет (1851). Воплощение навигации и морской астрономии (девятое изд.). Тейлор. п. 295ф . Проверено 2 августа 2007 г.
Морской альманах 1849-1851 гг.
- ^ Бриттен, Фредерик Джеймс (1894). Бывшие часовщики и их работа . Нью-Йорк: Спон и Чемберлен. п. 230 . Проверено 8 августа 2007 г.
Хронометры регулярно не поставлялись в Королевский флот примерно до 1825 года.
- ^ Леки, Сквайр, Морщины в практической навигации
- ^ Боудич, Натаниэль (2002). . . США: Национальное агентство изображений и картографии . п. – через Wikisource .
- ^ Jump up to: а б Королевская Гринвичская обсерватория. «РАСТОЯНИЯ центра Луны от Солнца и от звезд к востоку от нее» . В Гранате (ред.). Морской альманах и астрономические эфемериды за 1804 год (изд. «Второе американское впечатление»). Нью-Джерси: Блаувельт. п. 92. Архивировано из оригинала 27 сентября 2007 г. Проверено 2 августа 2007 г. ;
Вепстер, Стивен. «Предварительно рассчитанные лунные расстояния» . Архивировано из оригинала 15 декабря 2007 г. Проверено 2 августа 2007 г. - ^ Нори, JW (1828 г.). Новое и полное воплощение практической навигации . Лондон. п. 226. Архивировано из оригинала 27 сентября 2007 г. Проверено 2 августа 2007 г.
- ^ Нори, JW (1828 г.). Новое и полное воплощение практической навигации . Лондон. п. 230. Архивировано из оригинала 27 сентября 2007 г. Проверено 2 августа 2007 г.
- ^ Морской альманах и астрономические эфемериды за 1767 год , Лондон: В. Ричардсон и С. Кларк, 1766 г.
- ^ Морской альманах, сокращенный для моряков, 1924 г.
- ^ Данлоп, Джорджия; Шуфельдт, Х.Х. (1972). Навигация и пилотирование Даттона . Аннаполис, Мэриленд, США: Издательство Военно-морского института . п. 409. Авторы показывают пример поправки на полудиаметр Луны.
- ^ Даффет-Смит, Питер (1988). Практическая астрономия с калькулятором, третье издание . Издательство Кембриджского университета. п. 66. ИСБН 9780521356992 .
- ^ Монтенбрук и Пфлегер (1994). Астрономия на персональном компьютере, второе издание . Спрингер. стр. 45–46. ISBN 9783540672210 .
- ^ Шлайтер, Пол. «Топоцентрическое положение Луны» .
- ^ Старк, Брюс (2010). Таблицы Старка для преодоления лунного расстояния, третье издание . Публикации Звездного пути. ISBN 9780914025214 .
- ^ Капитан Джошуа Слокам, Одиночное плавание вокруг света, Глава 11 , 1900 г.
- Новое и полное воплощение практического мореплавания, содержащее все необходимые инструкции по ведению судового счисления в море... к которому добавлен новый и правильный набор таблиц - Дж. В. Нори, 1828 г.
- Эндрюс, Уильям Дж. Х. (Ред.): В поисках долготы . Кембридж, Массачусетс, 1996 г.
- Форбс, Эрик Г.: Рождение навигационной науки . Лондон 1974 г.
- Жюльен, Винсент (ред.): Вычисление долгот: проблема математики, астрономии, измерения времени и навигации . Ренн 2002
- Хауз, Дерек: Время по Гринвичу и долгота . Лондон 1997 г.
- Хауз, Дерек: Невил Маскелин. Морской астроном. Кембридж, 1989 г.
- Национальный морской музей (ред.): 4 шага к долготе . Лондон 1962 г.
Внешние ссылки
[ редактировать ]- О лунах... Джорджа Хакстейбла. (Бесплатный учебник)
- Навигационные таблицы: Лунное расстояние
- Навигационные алгоритмы - бесплатное программное обеспечение для Лунаров
- Долгота по Лунарсу онлайн
- Время и положение по C-программе LUNARS-V13
- Очерк метода лунного расстояния, автор Ричард Данн. Архивировано 6 ноября 2015 г. в Wayback Machine.


