Идеальное равновесие в подигре
| Подигра «Идеальное равновесие» | |
|---|---|
| Концепция решения в теории игр | |
| Отношение | |
| Подмножество | Равновесие Нэша |
| Пересекается с | Эволюционно стабильная стратегия |
| Значение | |
| Предложено | Райнхард Зельтен |
| Используется для | Обширная форма игры |
| Пример | Ультиматум игра |
В теории игр ( идеальное равновесие подигры или идеальное равновесие Нэша подигры ) является уточнением равновесия Нэша, используемого в динамических играх . Профиль стратегии является идеальным равновесием подигры, если он представляет равновесие Нэша каждой подигры исходной игры. Неформально это означает, что в любой момент игры поведение игроков с этого момента должно представлять собой равновесие Нэша продолжения игры (т. е. подигры), независимо от того, что произошло раньше. Каждая конечная обширная игра с идеальным отзывом имеет идеальное равновесие подигры. [1] Совершенное припоминание — это термин, введенный Гарольдом В. Куном в 1953 году и «эквивалентный утверждению, что правила игры позволяют каждому игроку помнить все, что он знал на предыдущих ходах, и все свои решения на этих ходах» . [2]
Распространенным методом определения идеального равновесия в подыграх в случае конечной игры является обратная индукция . Здесь сначала рассматриваются последние действия игры и определяются, какие действия последний игрок должен предпринять в каждом возможном случае, чтобы максимизировать свою полезность . Затем предполагается, что эти действия выполнит последний актор, и рассматривают предпоследние действия, снова выбирая те, которые максимизируют полезность этого актора. Этот процесс продолжается до тех пор, пока не будет достигнут первый ход игры. Оставшиеся стратегии представляют собой набор всех совершенных равновесий подигр для обширных игр с конечной информацией и конечным интервалом. [1] Однако обратную индукцию нельзя применять к играм с несовершенной или неполной информацией неодноэлементной , поскольку это влечет за собой прорезание наборов информации .
Идеальное равновесие в подыгре обязательно удовлетворяет принципу одноразового отклонения .
Набор идеальных равновесий подыгры для данной игры всегда является подмножеством множества равновесий Нэша для этой игры. В некоторых случаях наборы могут быть идентичными.
Игра «Ультиматум» представляет собой интуитивный пример игры с меньшим количеством идеальных равновесий в подыграх, чем равновесия Нэша.
Пример
[ редактировать ]Определение идеального равновесия подигры с помощью обратной индукции показано ниже на рисунке 1. Стратегии для игрока 1 задаются как {Up, Uq, Dp, Dq}, тогда как у игрока 2 есть стратегии среди {TL, TR, BL, BR}. В этом примере есть 4 подигры с 3 собственными подиграми.
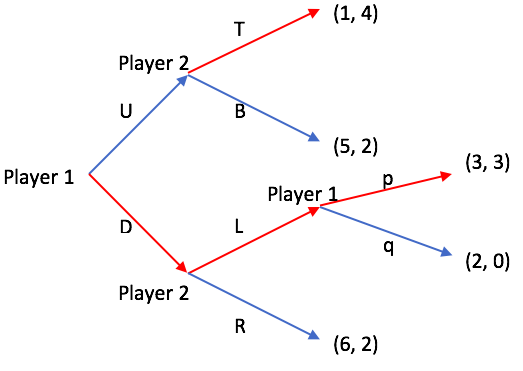
Используя обратную индукцию, игроки будут предпринимать следующие действия для каждой подигры:
- Подигра для действий p и q: Игрок 1 предпримет действие p с выигрышем (3, 3), чтобы максимизировать выигрыш Игрока 1, поэтому выигрыш для действия L станет (3,3).
- Подигра для действий L и R: Игрок 2 выполнит действие L при 3 > 2, поэтому выигрыш за действие D составит (3, 3).
- Подигра для действий T и B: Игрок 2 предпримет действие T, чтобы максимизировать выигрыш Игрока 2, поэтому выигрыш за действие U станет (1, 4).
- Подигра для действий U и D: Игрок 1 предпримет действие D, чтобы максимизировать выигрыш Игрока 1.
Таким образом, идеальным равновесием в подыгре является {Dp, TL} с выигрышем (3, 3).
Игра развернутой формы с неполной информацией представлена ниже на рисунке 2. Обратите внимание, что узел для Игрока 1 с действиями A и B, а также всеми последующими действиями является подигрой. Узлы игрока 2 не являются подигрой, поскольку они являются частью одного и того же набора информации.

Первая игра в нормальной форме — это представление в нормальной форме всей игры в развернутой форме. На основании предоставленной информации (UA, X), (DA, Y) и (DB, Y) являются равновесиями Нэша для всей игры.
Вторая игра в нормальной форме представляет собой представление подигры в нормальной форме, начиная со второго узла Игрока 1 с действиями A и B. Для второй игры в нормальной форме равновесие по Нэшу в подигре равно (A, X).
Для всей игры равновесия Нэша (DA, Y) и (DB, Y) не являются идеальными равновесиями подыгры, поскольку ход Игрока 2 не представляет собой равновесие Нэша. Равновесие Нэша (UA, X) является совершенным подигрой, поскольку оно включает равновесие Нэша подигры (A, X) как часть своей стратегии. [3]
Чтобы решить эту игру, сначала найдите равновесия Нэша по взаимному наилучшему ответу в подигре 1. Затем используйте обратную индукцию и подставьте (A,X) → (3,4) так, чтобы (3,4) стали выигрышами в подигре 2. [3]
Пунктирная линия показывает, что игрок 2 не знает, будет ли игрок 1 играть в A или B в одновременной игре.

Игрок 1 выбирает U, а не D, потому что 3 > 2 для выигрыша Игрока 1. В результате равновесие будет (A, X) → (3,4).

Таким образом, идеальным равновесием подигры посредством обратной индукции является (UA, X) с выигрышем (3, 4).
Повторные игры
[ редактировать ]Для конечно повторяющихся игр, если этапная игра имеет только одно уникальное равновесие Нэша, идеальное равновесие подигры состоит в том, чтобы играть без учета прошлых действий, рассматривая текущую подигру как игру с одним выстрелом. Примером этого является конечно повторяющаяся игра «Дилемма Узника» . Дилемма Узника получила свое название от ситуации, в которой есть два виновных. Когда их допрашивают, у них есть возможность промолчать или сбежать. Если оба преступника промолчат, они оба отсидят короткий срок. Если оба дезертируют, они оба отбывают умеренное наказание. Если они выберут противоположные варианты, то виновный в отступничестве освобождается, а виновный, который молчит, получает длительный срок. В конечном счете, используя обратную индукцию, последняя подигра в конечно повторяющейся дилемме Узника требует, чтобы игроки играли в уникальное равновесие Нэша (оба игрока отступают). По этой причине во всех играх, предшествующих последней подигре, также будет использоваться равновесие Нэша, чтобы максимизировать свои выигрыши за один период. [4] Если сценическая игра в конечно повторяющейся игре имеет несколько равновесий Нэша, идеальные равновесия подигры могут быть построены для выполнения действий равновесия Нэша, не относящихся к сценической игре, с помощью структуры «кнута и пряника». Один игрок может использовать равновесие Нэша на одном этапе игры, чтобы стимулировать выполнение действия, не относящегося к равновесию Нэша, при этом используя равновесие Нэша на этапе игры с более низким выигрышем для другого игрока, если он решит отказаться. [5]
Нахождение идеального равновесия для подыгры
[ редактировать ]
Рейнхард Зельтен доказал, что любая игра, которую можно разбить на «подигры», содержащие подмножество всех доступных вариантов выбора в основной игре, будет иметь подыгру, идеальную стратегию равновесия Нэша (возможно, как смешанную стратегию, дающую недетерминированные подыгры). игровые решения). Совершенство подигр используется только в играх с полной информацией . Совершенство подигры можно использовать в играх развернутой формы с полной, но несовершенной информацией .
Идеальное для подигры равновесие Нэша обычно выводится путем « обратной индукции » из различных конечных результатов игры, исключая ветки, которые предполагают, что любой игрок сделает ход, который не заслуживает доверия (потому что он неоптимален) из этого узла . Одна игра, в которой хорошо известно решение обратной индукции, — это «крестики-нолики» , но теоретически даже в го есть такая оптимальная стратегия для всех игроков. Проблема взаимосвязи между совершенством подигр и обратной индукцией была решена Камински (2019), который доказал, что обобщенная процедура обратной индукции создает все идеальные равновесия подигр в играх, которые могут иметь бесконечную длину, бесконечные действия в качестве каждого набора информации и несовершенные информацию, если условие окончательной поддержки выполнено.
Интересный аспект слова «достоверный» в предыдущем абзаце заключается в том, что в целом (не обращая внимания на необратимость достижения подигр) существуют стратегии, которые превосходят идеальные подыгровые стратегии, но которые не являются заслуживающими доверия в том смысле, что угроза их выполнение нанесет вред игроку, создающему угрозу, и предотвратит эту комбинацию стратегий. Например, в игре « цыпленок », если у одного игрока есть возможность оторвать руль от своей машины, он всегда должен ею воспользоваться, потому что это приводит к «дополнительной игре», в которой его разумный противник не может сделать то же самое ( и убить их обоих). Колесо-рыхлитель всегда выиграет игру (заставив своего противника отклониться), и угроза противника последовать его примеру неправдоподобна.
См. также
[ редактировать ]- игра многоножка
- Динамическая несогласованность
- Глоссарий теории игр
- Теорема о минимаксе
- Ретроградный анализ
- Концепция решения
- Принцип оптимальности Беллмана
Ссылки
[ редактировать ]- ^ Jump up to: а б Осборн, MJ (2004). Введение в теорию игр . Издательство Оксфордского университета.
- ^ Кун, Гарольд Уильям; Такер, Альберт Уильям (2 марта 2016 г.). Вклад в теорию игр (AM-28), том II . Издательство Принстонского университета. ISBN 978-1-4008-8197-0 .
- ^ Jump up to: а б Джоэл., Ватсон (9 мая 2013 г.). Стратегия: введение в теорию игр (Третье изд.). Нью-Йорк. ISBN 9780393918380 . OCLC 842323069 .
{{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка ) - ^ Йылдыз, Мухамет (2012). «12 повторяющихся игр» . 14.12. Экономические приложения теории игр . Массачусетский технологический институт: MIT OpenCourseWare . Проверено 27 апреля 2021 г.
- ^ Такако, Фудзивара-Греве (27 июня 2015 г.). Теория некооперативных игр . Токио. ISBN 9784431556442 . OCLC 911616270 .
{{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка )
Внешние ссылки
[ редактировать ]- Зельтен, Р. (1965). Теория игр трактует модель олигополии с инерцией спроса. Журнал всей политической науки/Журнал институциональной и теоретической экономики , (H. 2), 301–324, 667–689. [на немецком языке — часть 1 , часть 2 ]
- Пример игры с расширенной формой и несовершенной информацией
- Java-апплет для поиска идеального решения равновесия Нэша для подигры обширной игры с сайта gametheory.net.
- Java-апплет для поиска идеального решения равновесия Нэша для подигры обширной игры с сайта gametheory.net.
- Каминский, М. М. Обобщенная обратная индукция: обоснование народного алгоритма . Игры 2019, 10, 34.