Выпуклые однородные соты

В геометрии выпуклые однородные соты представляют собой однородную мозаику , которая заполняет трехмерное евклидово пространство непересекающимися выпуклыми однородными многогранными ячейками.

Известно двадцать восемь таких сот:

знакомые кубические соты и 7 их усечений;
чередующиеся кубические соты и 4 их усечения;
10 призматических форм на основе однородных плоских мозаик (11 с учетом кубических сот);
5 модификаций некоторых из вышеперечисленных за счет удлинения и/или вращения.

Их можно считать трехмерным аналогом однородных мозаик плоскости .

Диаграмма Вороного любой решетки образует выпуклые однородные соты, ячейками которых являются зоноэдры .

История

1900 : Торольд Госсет перечислил список полуправильных выпуклых многогранников с правильными ячейками ( платоновых тел ) в своей публикации «О правильных и полуправильных фигурах в пространстве n измерений» , включая одну правильную кубическую соту и две полуправильные формы с тетраэдрами и октаэдрами.
1905 : Альфредо Андреини перечислил 25 таких мозаик.
1991 : Нормана Джонсона В рукописи «Унифицированные многогранники» указан список из 28. ^[1]
1994 : Бранко Грюнбаум в своей статье «Равномерные мозаики трехмерного пространства » также независимо перечислил все 28, после обнаружения ошибок в публикации Андреини. Он обнаружил, что в статье 1905 года, в которой было перечислено 25, 1 ошибка, а 4 отсутствуют . Грюнбаум заявляет в этой статье, что Норман Джонсон заслуживает приоритета для достижения такого же подсчета в 1991 году. Он также упоминает, что И. Алексеев из России связался с ним по поводу предполагаемого перечисления этих форм, но Грюнбаум не смог проверить это в то время.
2006 : Георгий Ольшевский в своей рукописи Uniform Panoploid Tetracombs , наряду с повторением полученного списка из 11 выпуклых однородных мозаик и 28 выпуклых однородных сот, расширяет дальнейший производный список из 143 выпуклых однородных тетракомб (соты однородных 4-многогранников в 4- космос). ^[2]^[1]

В этих узорах встречаются только 14 выпуклых однородных многогранников:

три из пяти платоновых тел ( тетраэдр , куб и октаэдр ),
шесть из тринадцати архимедовых тел (обладающих отражающей тетраэдрической или октаэдрической симметрией) и
пять из бесконечного семейства призм (3-, 4-, 6-, 8- и 12-угольные; 4-угольная призма дублирует куб).

Икосаэдр . , курносый куб и квадратная антипризма появляются в некоторых чередованиях, но эти соты не могут быть реализованы со всеми ребрами, имеющими единичную длину

Имена

Этот набор можно назвать регулярными и полуправильными сотами . Его назвали архимедовыми сотами по аналогии с выпуклыми однородными (неправильными) многогранниками, обычно называемыми архимедовыми телами . Недавно Конвей предложил назвать этот набор архитектоническими мозаиками , а двойные соты — катоптрическими мозаиками .

Отдельные соты перечислены с именами, данными им Норманом Джонсоном . (Некоторые из терминов, используемых ниже, определены в разделе « Равномерный 4-многогранник # Геометрические выводы для 46 непризматических однородных 4-многогранников Витоффа» )

Для перекрестных ссылок им даны списочные индексы Андрейни (1–22), Уильямса (1–2,9–19), Джонсона (11–19, 21–25, 31–34, 41–49). , 51–52, 61–65) и Грюнбаум (1–28). Коксетер использует δ ₄ для кубических сот , hδ ₄ для чередующихся кубических сот , qδ ₄ для четвертькубических сот , с индексами для других форм, основанных на кольцевых узорах диаграммы Коксетера.

Компактные евклидовы равномерные мозаики (по их бесконечным семействам групп Кокстера)

Фундаментальными бесконечными группами Кокстера для трехмерного пространства являются:

The ${\tilde {C}}_{3}$ , [4,3,4], кубический, (8 уникальных форм плюс одна альтернатива)
The ${\tilde {B}}_{3}$ , [4,3 ^1,1], чередующаяся кубическая, (11 форм, 3 новых)
The ${\tilde {A}}_{3}$ циклическая группа, [(3,3,3,3)] или [3 ^[4]], (5 форм, одна новая)

Между всеми тремя семьями существует переписка. Снятие одного зеркала с ${\tilde {C}}_{3}$ производит ${\tilde {B}}_{3}$ , и сняв одно зеркало с ${\tilde {B}}_{3}$ производит ${\tilde {A}}_{3}$ . Это позволяет создавать несколько конструкций из одних и тех же сот. Если ячейки раскрашены в зависимости от уникальных положений в каждой конструкции Витхоффа, можно показать эти разные симметрии.

Кроме того, есть 5 специальных сот, которые не имеют чистой отражательной симметрии и построены из отражательных форм с помощью операций удлинения и вращения .

Всего уникальных сот, указанных выше, — 18.

Призматические стопки из бесконечных групп Кокстера для трехмерного пространства:

The ${\tilde {C}}_{2}$ × ${\tilde {I}}_{1}$ , [4,4,2,∞] призматическая группа, (2 новые формы)
The ${\tilde {G}}_{2}$ × ${\tilde {I}}_{1}$ , [6,3,2,∞] призматическая группа, (7 уникальных форм)
The ${\tilde {A}}_{2}$ × ${\tilde {I}}_{1}$ , [(3,3,3),2,∞] призматическая группа, (Нет новых форм)
The ${\tilde {I}}_{1}$ × ${\tilde {I}}_{1}$ × ${\tilde {I}}_{1}$ , [∞,2,∞,2,∞] призматическая группа, (Все это становится кубическими сотами )

Кроме того, существует особая вытянутая форма треугольных призматических сот.

Общее количество уникальных призматических сот, указанных выше (исключая кубические, подсчитанные ранее), составляет 10.

Объединив эти числа, 18 и 10 дают нам всего 28 однородных сот.

Группа C̃ ₃ , [4,3,4] (кубическая)

Обычные кубические соты, представленные символом Шлефли {4,3,4}, предлагают семь уникальных производных однородных сот посредством операций усечения. (Одна избыточная форма, продолговатые кубические соты , включена для полноты картины, хотя и идентична кубическим сотам.) Отражательная симметрия — это аффинная группа Коксетера [4,3,4]. Есть четыре подгруппы индекса 2, которые генерируют чередования: [1 ⁺,4,3,4], [(4,3,4,2 ⁺)], [4,3 ⁺,4] и [4,3,4] ⁺, причем первые две порождают повторяющиеся формы, а последние две являются неоднородными.

Соты C3
Space group	Fibrifold	Extended symmetry	Extended diagram	Order	Honeycombs
Pm3m (221)	4⁻:2	[4,3,4]		×1	₁, ₂, ₃, ₄, ₅, ₆
Fm3m (225)	2⁻:2	[1⁺,4,3,4] ↔ [4,3^1,1]	↔	Half	₇, ₁₁, ₁₂, ₁₃
I43m (217)	4^o:2	[[(4,3,4,2⁺)]]		Half × 2	₍₇₎,
Fd3m (227)	2⁺:2	[[1⁺,4,3,4,1⁺]] ↔ [[3^[4]]]	↔	Quarter × 2	₁₀,
Im3m (229)	8^o:2	[[4,3,4]]		×2	₍₁₎, ₈, ₉

[4,3,4], пр. группа Pm 3 м (221)
Ссылка Индексы	Сотовое имя Диаграмма Кокстера и символ Шлефли	Количество ячеек/вершина и позиции в кубических сотах						Рамки (Перспектива)	Вершинная фигура	Двойная ячейка
Ссылка Индексы	Сотовое имя Диаграмма Кокстера и символ Шлефли	(0)	(1)	(2)	(3)	Все	Твердые вещества (Частичное)	Рамки (Перспектива)	Вершинная фигура	Двойная ячейка
Дж _11,15 А ₁ Вт ₁ Г ₂₂ д ₄	кубический (чон) т ₀ {4,3,4} {4,3,4}				(8) (4.4.4)				октаэдр	Куб ,
Дж _12.32 В ₁₅ Вт ₁₄ G ₇ О ₁	ректификованный кубический (богатый) т ₁ {4,3,4} г {4,3,4}	(2) (3.3.3.3)			(4) (3.4.3.4)		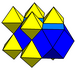		кубовидный	Квадратная бипирамида
Дж ₁₃ A ₁₄ Вт ₁₅ Г ₈ т ₁ δ ₄ О ₁₅	усеченный кубический (тич) т _0,1 {4,3,4} т{4,3,4}	(1) (3.3.3.3)			(4) (3.8.8)				квадратная пирамида	Равнобедренная квадратная пирамида
Дж ₁₄ А ₁₇ Вт ₁₂ G_G9 т _0,2 д ₄ О ₁₄	согнутый кубический (срич) т _0,2 {4,3,4} рр{4,3,4}	(1) (3.4.3.4)	(2) (4.4.4)		(2) (3.4.4.4)				косая треугольная призма	Треугольная бипирамида
Дж ₁₇ В _{18 лет} Вт ₁₃ Г ₂₅ т _0,1,2 д ₄ О ₁₇	кантиусеченный кубический (грич) т _0,1,2 {4,3,4} тр{4,3,4}	(1) (4.6.6)	(1) (4.4.4)		(2) (4.6.8)				неправильный тетраэдр	Треугольная пирамидиль
Дж ₁₈ А ₁₉ Вт ₁₉ G_G20 т _0,1,3 д ₄ О ₁₉	неусеченный кубический (прич) т _0,1,3 {4,3,4}	(1) (3.4.4.4)	(1) (4.4.4)	(2) (4.4.8)	(1) (3.8.8)				косая трапециевидная пирамида	Квадратная четверть пирамидиллы
Дж _21,31,51 A_А2 W_W9 Г ₁ HD ₄ О ₂₁	чередующаяся кубическая (октет) ч{4,3,4}				(8) (3.3.3)	(6) (3.3.3.3)			кубооктаэдр	Додекаэдрилл
Дж _22,34 А ₂₁ Вт ₁₇ Г ₁₀ ч ₂ д ₄ О ₂₅	Кантическая кубика (тато) ↔	(1) (3.4.3.4)			(2) (3.6.6)	(2) (4.6.6)			прямоугольная пирамида	Полусплюснутый октаэдрилл
Дж ₂₃ А ₁₆ Вт ₁₁ Г ₅ ч ₃ δ ₄ О ₂₆	Руничский куб (срато) ↔	(1) (4.4.4)			(1) (3.3.3)	(3) (3.4.4.4)			коническая треугольная призма	Четверть кубиль
Дж ₂₄ 20 Вт ₁₆ Г ₂₁ ч _2,3 δ ₄ О ₂₈	Рунцикантический куб (грато) ↔	(1) (3.8.8)			(1) (3.6.6)	(2) (4.6.8)			Неправильный тетраэдр	Половина пирамидиллы
Неравномерная _б	курносый выпрямленный кубический (поиск) ср{4,3,4}	(1) (3.3.3.3.3)	(1) (3.3.3)		(2) (3.3.3.3.4)	(4) (3.3.3)			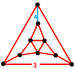Ирр. трехмерный икосаэдр
Неоднородный	Кантик курносый кубический (кэш) 2с ₀ {4,3,4}	(1) (3.3.3.3.3)			(2) (3.4.4.4)	(3) (3.4.4)
Неоднородный	Рансикантический курносый кубический (руш)	(1) (3.4.3.4)	(2) (4.4.4)	(1) (3.3.3)	(1) (3.6.6)	(3) Трикуп
Неоднородный	Рунчич кантитусеченный кубический (эш) ср ₃ {4,3,4}	(1) (3.3.3.3.4)	(1) (4.4.4)	(1) (4.4.4)	(1) (3.4.4.4)	(3) (3.4.4)

[[4,3,4]] соты, пространственная группа Im 3 м (229)
Ссылка Индексы	Сотовое имя Диаграмма Кокстера и символ Шлефли	Количество ячеек/вершина и позиции в кубических сотах			Твердые вещества (Частичное)	Рамки (Перспектива)	Вершинная фигура	Двойная ячейка
Ссылка Индексы	Сотовое имя Диаграмма Кокстера и символ Шлефли	(0,3)	(1,2)	Все	Твердые вещества (Частичное)	Рамки (Перспектива)	Вершинная фигура	Двойная ячейка
Дж _11,15 А ₁ Вт ₁ Г ₂₂ д ₄ О ₁	сморщенный кубический (то же самое, что и обычный кубический ) (чон) т _0,3 {4,3,4}	(2) (4.4.4)	(6) (4.4.4)				октаэдр	Куб
Д ₁₆ A_А3 Вт ₂ Г ₂₈ т _1,2 δ ₄ Ему ₁₆	битусеченный кубический (пакетный) т _1,2 {4,3,4} 2т{4,3,4}	(4) (4.6.6)		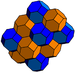			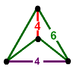( дисфеноид )	Сплюснутый тетраэдрилл
Дж ₁₉ А ₂₂ Вт ₁₈ Г ₂₇ т _0,1,2,3 д ₄ О ₂₀	всеусеченный куб (гиппич) т _0,1,2,3 {4,3,4}	(2) (4.6.8)	(2) (4.4.8)				неправильный тетраэдр	Восьмая пирамидиль
Дж _21,31,51 A_А2 W_W9 Г ₁ HD ₄ О ₂₇	Четвертькубические соты (батато) хт ₀ хт ₃ {4,3,4}	(2) (3.3.3)	(6) (3.6.6)				вытянутая треугольная антипризма	Сплюснутая кабинка
Дж _21,31,51 A_А2 W_W9 Г ₁ HD ₄ О ₂₁	Чередованная промежуточная кубическая (октет) (то же, что и альтернативная кубическая) хт _0.3 {4,3,4}	(2) (3.3.3)	(6) (3.3.3)	(6) (3.3.3.3)			кубооктаэдр
Неоднородный	Биортоснуб кубический сот (габрета) 2с _0,3 {(4,2,4,3)}	(2) (4.6.6)	(2) (4.4.4)	(2) (4.4.6)
Неравномерная _а	Попеременная битусеченная куба (биш) h2t{4,3,4}	(4) (3.3.3.3.3)		(4) (3.3.3)
Неоднородный	Кантическая двустворчатая кубическая (cabisch) 2с _0,3 {4,3,4}	(2) (3.4.4.4)	(2) (4.4.4)	(2) (4.4.4)
Неравномерное _с	Чередованная всеусеченная куба (снич) чт _0,1,2,3 {4,3,4}	(2) (3.3.3.3.4)	(2) (3.3.3.4)	(4) (3.3.3)

B̃ ₃ , [4,3 ^1,1] группа

The ${\tilde {B}}_{3}$ , [4,3] группа предлагает 11 производных форм посредством операций усечения, четыре из которых представляют собой уникальные однородные соты. Выделяют 3 подгруппы индекса 2, которые порождают чередования: [1 ⁺,4,3 ^1,1], [4,(3 ^1,1) ⁺] и [4,3 ^1,1] ⁺. Первый генерирует повторяющиеся соты, а два последних являются неоднородными, но включены для полноты.

Соты из этой группы называются чередующимися кубическими, потому что первую форму можно рассматривать как кубические соты с удаленными чередующимися вершинами, сводящими кубические ячейки к тетраэдрам и образующими в промежутках ячейки октаэдра.

Узлы индексируются слева направо как 0,1,0',3 , где 0' находится ниже и взаимозаменяем с 0 . Указанные альтернативные кубические имена основаны на этом порядке.

Соты B3
Space group	Fibrifold	Extended symmetry	Extended diagram	Order	Honeycombs
Fm3m (225)	2⁻:2	[4,3^1,1] ↔ [4,3,4,1⁺]	↔	×1	₁, ₂, ₃, ₄
Fm3m (225)	2⁻:2	<[1⁺,4,3^1,1]> ↔ <[3^[4]]>	↔	×2	₍₁₎, ₍₃₎
Pm3m (221)	4⁻:2	<[4,3^1,1]>		×2	₅, ₆, ₇, ₍₆₎, ₉, ₁₀, ₁₁

[4,3 ^1,1] соты однородные, пространственная группа Fm 3 м (225)
Ссылка индексы	Сотовое имя Диаграммы Кокстера	Ячейки по местоположению (и посчитаем вокруг каждой вершины)				Твердые вещества (Частичное)	Рамки (Перспектива)	вершина фигуры
Ссылка индексы	Сотовое имя Диаграммы Кокстера	(0)	(1)	(0')	(3)	Твердые вещества (Частичное)	Рамки (Перспектива)	вершина фигуры
Дж _21,31,51 A_А2 W_W9 Г ₁ HD ₄ О ₂₁	Альтернативная кубическая (октет) ↔			(6) (3.3.3.3)	(8) (3.3.3)			кубооктаэдр
Дж _22,34 А ₂₁ Вт ₁₇ Г ₁₀ ч ₂ д ₄ О ₂₅	Кантическая кубика (тато) ↔	(1) (3.4.3.4)		(2) (4.6.6)	(2) (3.6.6)			прямоугольная пирамида
Дж ₂₃ А ₁₆ Вт ₁₁ Г ₅ ч ₃ δ ₄ О ₂₆	Руничский куб (срато) ↔	(1) куб		(3) (3.4.4.4)	(1) (3.3.3)			коническая треугольная призма
Дж ₂₄ 20 Вт ₁₆ Г ₂₁ ч _2,3 δ ₄ О ₂₈	Рунцикантический куб (грато) ↔	(1) (3.8.8)		(2) (4.6.8)	(1) (3.6.6)			Неправильный тетраэдр

<[4,3 ^1,1]> соты однородные, пространственная группа Pm 3 м (221)
Ссылка индексы	Сотовое имя Диаграммы Кокстера ↔	Ячейки по местоположению (и посчитаем вокруг каждой вершины)				Твердые вещества (Частичное)	Рамки (Перспектива)	вершина фигуры
Ссылка индексы	Сотовое имя Диаграммы Кокстера ↔	(0,0')	(1)	(3)	Все	Твердые вещества (Частичное)	Рамки (Перспектива)	вершина фигуры
Дж _11,15 А ₁ Вт ₁ Г ₂₂ д ₄ О ₁	Кубический (чон) ↔	(8) (4.4.4)						октаэдр
Дж _12.32 В ₁₅ Вт ₁₄ G ₇ т ₁ δ ₄ О ₁₅	Ректифицированный кубический (богатый) ↔	(4) (3.4.3.4)		(2) (3.3.3.3)				кубовидный
Дж _12.32 В ₁₅ Вт ₁₄ G ₇ т ₁ δ ₄ О ₁₅	Ректифицированный кубический (богатый) ↔	(2) (3.3.3.3)		(4) (3.4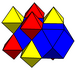.3.4)				кубовидный
Дж ₁₃ A ₁₄ Вт ₁₅ Г ₈ т _0,1 д ₄ О ₁₄	Усеченный кубический (тич) ↔	(4) (3.8.8)		(1) (3.3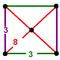.3.3)				квадратная пирамида
Дж ₁₄ А ₁₇ Вт ₁₂ G_G9 т _0,2 д ₄ О ₁₇	Согнутый кубический (срич) ↔	(2) (3.4.4.4)	(2) (4.4.4)	(1) (3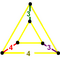.4.3.4)				наклонная треугольная призма
Д ₁₆ A_А3 Вт ₂ Г ₂₈ т _0,2 д ₄ Ему ₁₆	Битусеченный кубический (пакетный) ↔	(2) (4.6.6)		(2) (4.6.6)				равнобедренный тетраэдр
Дж ₁₇ В _{18 лет} Вт ₁₃ Г ₂₅ т _0,1,2 д ₄ И ₁₈	Кантитусеченный кубический (грич) ↔	(2) (4.6.8)	(1) (4.4.4)	(1) (4.6.6)				неправильный тетраэдр
Дж _21,31,51 A_А2 W_W9 Г ₁ HD ₄ О ₂₁	Альтернативная кубическая (октет) ↔	(8) (3.3.3)			(6) (3.3.3.3)			кубооктаэдр
Дж _22,34 А ₂₁ Вт ₁₇ Г ₁₀ ч ₂ д ₄ О ₂₅	Кантическая кубика (тато) ↔	(2) (3.6.6)		(1) (3.4.3.4)	(2) (4.6.6)			прямоугольная пирамида
Неравномерная _а	Попеременная битусеченная куба (биш) ↔	(2) (3.3.3.3.3)		(2) (3.3.3.3.3)	(4) (3.3.3)
Неравномерная _б	Чередованная кантитусеченная куба (поиск) ↔	(2) (3.3.3.3.4)	(1) (3.3.3)	(1) (3.3.3.3.3)	(4) (3.3.3)			Ирр. трехмерный икосаэдр

Ã ₃ , [3 ^[4]] группа

Есть 5 форм ^[3] построенный из ${\tilde {A}}_{3}$ , [3 ^[4]] Группа Кокстера , из которой только соты в четверть куба уникальны . Существует одна подгруппа индекса 2 [3 ^[4]] ⁺ что порождает курносую форму, которая не является единообразной, но включена для полноты.

Соты А3
Space group	Fibrifold	Square symmetry	Extended symmetry	Extended diagram	Extended group	Honeycomb diagrams
F43m (216)	1^o:2	a1	[3^[4]]		${\tilde {A}}_{3}$	(None)
Fm3m (225)	2⁻:2	d2	<[3^[4]]> ↔ [4,3^1,1]	↔	${\tilde {A}}_{3}$ ×2₁ ↔ ${\tilde {B}}_{3}$	₁, ₂
Fd3m (227)	2⁺:2	g2	[[3^[4]]] or [2⁺[3^[4]]]	↔	${\tilde {A}}_{3}$ ×2₂	₃
Pm3m (221)	4⁻:2	d4	<2[3^[4]]> ↔ [4,3,4]	↔	${\tilde {A}}_{3}$ ×4₁ ↔ ${\tilde {C}}_{3}$	₄
I3 (204)	8^−o	r8	[4[3^[4]]]⁺ ↔ [[4,3⁺,4]]	↔	½ ${\tilde {A}}_{3}$ ×8 ↔ ½ ${\tilde {C}}_{3}$ ×2	_(*)
Im3m (229)	8^o:2	r8	[4[3^[4]]] ↔ [[4,3,4]]	↔	${\tilde {A}}_{3}$ ×8 ↔ ${\tilde {C}}_{3}$ ×2	₅

[[3 ^[4]]] соты однородные, пространственная группа Fd 3 м (227)
Ссылка индексы	Сотовое имя Диаграммы Кокстера	Ячейки по местоположению (и посчитаем вокруг каждой вершины)		Твердые вещества (Частичное)	Рамки (Перспектива)	вершина фигуры
Ссылка индексы	Сотовое имя Диаграммы Кокстера	(0,1)	(2,3)	Твердые вещества (Частичное)	Рамки (Перспектива)	вершина фигуры
Дж _25,33 А ₁₃ Вт ₁₀ Г ₆ 4 _{квартала} О ₂₇	четверть куба (батато) ↔ д{4,3,4}	(2) (3.3.3)	(6) (3.6.6)			треугольная антипризма

<[3 ^[4]]> ↔ [4,3 ^1,1] соты однородные, пространственная группа Fm 3 м (225)
Ссылка индексы	Сотовое имя Диаграммы Кокстера ↔	Ячейки по местоположению (и посчитаем вокруг каждой вершины)			Твердые вещества (Частичное)	Рамки (Перспектива)	вершина фигуры
Ссылка индексы	Сотовое имя Диаграммы Кокстера ↔	0	(1,3)	2	Твердые вещества (Частичное)	Рамки (Перспектива)	вершина фигуры
Дж _21,31,51 A_А2 W_W9 Г ₁ HD ₄ О ₂₁	чередующаяся кубическая (октет) ↔ ↔ ч{4,3,4}		(8) (3.3.3)	(6) (3.3.3.3)			кубооктаэдр
Дж _22,34 А ₂₁ Вт ₁₇ Г ₁₀ ч ₂ д ₄ О ₂₅	кантик кубический (татох) ↔ ↔ ч ₂ {4,3,4}	(2) (3.6.6)	(1) (3.4.3.4)	(2) (4.6.6)			Прямоугольная пирамида

[2[3 ^[4]]] ↔ [4,3,4] однородные соты, пространственная группа Pm 3 м (221)
Ссылка индексы	Сотовое имя Диаграммы Кокстера ↔	Ячейки по местоположению (и посчитаем вокруг каждой вершины)		Твердые вещества (Частичное)	Рамки (Перспектива)	вершина фигуры
Ссылка индексы	Сотовое имя Диаграммы Кокстера ↔	(0,2)	(1,3)	Твердые вещества (Частичное)	Рамки (Перспектива)	вершина фигуры
Дж _12.32 В ₁₅ Вт ₁₄ G ₇ т ₁ δ ₄ О ₁	ректификованный кубический (богатый) ↔ ↔ ↔ г {4,3,4}	(2) (3.4.3.4)	(1) (3.3.3.3)			кубовидный

[4[3 ^[4]]] ↔ [[4,3,4]] однородные соты, пространственная группа Im 3 м (229)
Ссылка индексы	Сотовое имя Диаграммы Кокстера ↔ ↔	Ячейки по местоположению (и посчитаем вокруг каждой вершины)		Твердые вещества (Частичное)	Рамки (Перспектива)	вершина фигуры
Ссылка индексы	Сотовое имя Диаграммы Кокстера ↔ ↔	(0,1,2,3)	Все	Твердые вещества (Частичное)	Рамки (Перспектива)	вершина фигуры
Д ₁₆ A_А3 Вт ₂ Г ₂₈ т _1,2 δ ₄ Ему ₁₆	битусеченный кубический (пакетный) ↔ ↔ 2т{4,3,4}	(4) (4.6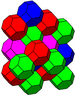.6)				равнобедренный тетраэдр
Неравномерная _а	Чередованная кантиусеченная куба (биш) ↔ ↔ h2t{4,3,4}	(4) (3.3.3.3.3)	(4) (3.3.3)

Нонвитоффовы формы (закрученные и удлиненные)

Еще три однородные соты создаются путем разрушения одной или другой из вышеуказанных сот, где ее грани образуют непрерывную плоскость, затем вращения чередующихся слоев на 60 или 90 градусов ( вращение ) и/или вставки слоя призм ( удлинение ).

Вытянутые и гировытянутые чередующиеся кубические мозаики имеют одинаковую фигуру вершин, но не похожи друг на друга. В вытянутой форме каждая призма встречается с тетраэдром на одном треугольном конце и октаэдром на другом. В гировытянутой форме призмы, соприкасающиеся с тетраэдрами на обоих концах, чередуются с призмами, соприкасающимися с октаэдрами с обоих концов.

Гироудлиненная треугольная призматическая мозаика имеет ту же фигуру вершин, что и одна из простых призматических мозаик; оба могут быть получены из спиральных и плоских треугольных призматических мозаик соответственно путем вставки слоев кубов.

Ссылка индексы	символ	Сотовое имя	типы ячеек (# в каждой вершине)	вершина фигуры
Дж ₅₂ А _2' Г ₂ О ₂₂	ч{4,3,4}:г	вращающийся чередующийся кубический (gytoh)	тетраэдр (8) октаэдр (6)	треугольный ортобикупол
Дж ₆₁ А _? Г ₃ О ₂₄	ч{4,3,4}:ge	гироудлиненный, чередующийся кубический (гето)	треугольная призма (6) тетраэдр (4) октаэдр (3)
Дж ₆₂ А _? Г ₄ О ₂₃	ч{4,3,4}:е	удлиненный чередующийся кубический (это)	треугольная призма (6) тетраэдр (4) октаэдр (3)
Дж ₆₃ А _? Г ₁₂ О ₁₂	{3,6}:g × {∞}	вращающийся треугольный призматический (гитоф)	треугольная призма (12)
Дж ₆₄ А _? Г ₁₅ О ₁₃	{3,6}:ge × {∞}	гироудлиненная треугольная призматика (гетаф)	треугольная призма (6) куб (4)

Призматические стопки

Одиннадцать призматических плиток получаются путем укладки одиннадцати однородных плоских плиток , показанных ниже, в параллельные слои. (Одна из этих сот — кубическая, показанная выше.) Вершинная фигура каждой представляет собой неправильную бипирамиду , грани которой представляют собой равнобедренные треугольники .

C̃ ₂ ×Ĩ ₁ (∞), [4,4,2,∞], призматическая группа

В квадратной мозаике есть только 3 уникальные соты, но все 6 усечений мозаики перечислены ниже для полноты, а изображения мозаики показаны цветами, соответствующими каждой форме.

Индексы	Коксетер-Дынкин и Шлефли символы	Сотовое имя	Самолет плитка
Дж _11,15 А ₁ Г ₂₂	{4,4}×{∞}	Кубический (Квадратно-призматический) (чон)	(4.4.4.4)
	г{4,4}×{∞}
	рр{4,4}×{∞}
Дж ₄₅ А ₆ Г ₂₄	т{4,4}×{∞}	Усеченная/двуусеченная квадратная призматика (тассиф)	(4.8.8)
Дж ₄₅ А ₆ Г ₂₄	тр{4,4}×{∞}	Усеченная/двуусеченная квадратная призматика (тассиф)	(4.8.8)
Дж ₄₄ И ₁₁ Г ₁₄	ср{4,4}×{∞}	Курносый квадратный призматический (сассиф)	(3.3.4.3.4)
Неоднородный	ht _0,1,2,3 {4,4,2,∞}

Призматическая группа G̃ ₂ xĨ ₁ (∞), [6,3,2,∞]

Индексы	Коксетер-Дынкин и Шлефли символы	Сотовое имя	Самолет плитка
Дж ₄₁ A ₄ Г ₁₁	{3,6} × {∞}	Треугольно-призматический (тиф)	(3 ⁶)
Дж ₄₂ A_А5 Г ₂₆	{6,3} × {∞}	Шестиугольный призматический (хифт)	(6 ³)
Дж ₄₂ A_А5 Г ₂₆	т{3,6} × {∞}	Шестиугольный призматический (хифт)	(6 ³)
День ₄₃ А ₈ Г ₁₈	г{6,3} × {∞}	Тришестиугольная призматическая (тиф)	(3.6.3.6)
Дж ₄₆ A ₇ Г ₁₉	т{6,3} × {∞}	Усеченная шестиугольная призматика (таф)	(3.12.12)
Дж ₄₇ A_А9 Г ₁₆	rr{6,3} × {∞}	Ромбо-тригексагональная призматическая (сротафия)	(3.4.6.4)
Дж ₄₈ А ₁₂ Г ₁₇	ср{6,3} × {∞}	Курносый шестиугольный призматический (снатаф)	(3.3.3.3.6)
Дж ₄₉ A ₁₀ Г ₂₃	tr{6,3} × {∞}	усеченная тригексагональная призматика (гротаф)	(4.6.12)
Д ₆₅ А _11' Г ₁₃	{3,6}:e × {∞}	удлиненно-треугольно-призматический (этоф)	(3.3.3.4.4)
Дж ₅₂ А _2' Г ₂	h3t{3,6,2,∞}	вращающийся тетраэдр-октаэдр (гитох)	(3 ⁶)
Дж ₅₂ А _2' Г ₂	с2р{3,6,2,∞}	вращающийся тетраэдр-октаэдр (гитох)	(3 ⁶)
Неоднородный	ht _0,1,2,3 {3,6,2,∞}

Перечисление форм Витгофа

все непризматические конструкции Витгофа Ниже приведены по группам Кокстера вместе с их вариациями . Унифицированные решения включены в Бранко Грюнбаума список . Зеленый фон показан на повторяющихся сотах, а отношения выражены в расширенных диаграммах симметрии.

Группа Коксетера	Расширенный симметрия	Соты		Хиральный расширенный симметрия	Чередование сот
[4,3,4]	[4,3,4]	6	₂₂ \| ₇ \| ₈ ₉ \| ₂₅ \| ₂₀	[1 ⁺,4,3 ⁺,4,1 ⁺]	(2)	₁ \| _б
	[2 ⁺[4,3,4]] =	(1)	₂₂	[2 ⁺[(4,3 ⁺,4,2 ⁺)]]	(1)	₁ \| ₆
	[2 ⁺[4,3,4]]	1	₂₈	[2 ⁺[(4,3 ⁺,4,2 ⁺)]]	(1)	_а
	[2 ⁺[4,3,4]]	2	₂₇	[2 ⁺[4,3,4]] ⁺	(1)	_с
[4,3 ^1,1]	[4,3 ^1,1]	4	₁ \| ₇ \| ₁₀ \| ₂₈
	[1[4,3 ^1,1]]=[4,3,4] =	(7)	₂₂ \| ₇ \| ₂₂ \| ₇ \| ₉ \| ₂₈ \| ₂₅	[1[1 ⁺,4,3 ^1,1]] ⁺	(2)	₁ \| ₆ \| _а
	[1[4,3 ^1,1]]=[4,3,4] =	(7)	₂₂ \| ₇ \| ₂₂ \| ₇ \| ₉ \| ₂₈ \| ₂₅	[1[4,3 ^1,1]] ⁺ =[4,3,4] ⁺	(1)	_б
[3 ^[4]]	[3 ^[4]]	(никто)
	[2 ⁺[3 ^[4]]]	1	₆
	[1[3 ^[4]]]=[4,3 ^1,1] =	(2)	₁ \| ₁₀
	[2[3 ^[4]]]=[4,3,4] =	(1)	₇
	[(2 ⁺,4)[3 ^[4]]]=[2 ⁺[4,3,4]] =	(1)	₂₈	[(2 ⁺,4)[3 ^[4]]] ⁺ = [2 ⁺[4,3,4]] ⁺	(1)	_а

Примеры

Перемежающиеся кубические соты имеют особое значение, поскольку их вершины образуют кубическую плотную упаковку сфер. Заполняющая пространство ферма из упакованных октаэдров и тетраэдров, по-видимому, была впервые обнаружена Александром Грэмом Беллом и независимо повторно открыта Бакминстером Фуллером (который назвал ее октетной фермой и запатентовал ее в 1940-х годах). [3] [4] [5] [6] . Фермы Octet в настоящее время являются одними из наиболее распространенных типов ферм, используемых в строительстве.

Формы фриза

Если ячейкам разрешено быть однородными мозаиками , можно определить более однородные соты:

Семьи:

${\tilde {C}}_{2}$ × $A_{1}$ : [4,4,2] Кубические плитные соты (3 формы)
${\tilde {G}}_{2}$ × $A_{1}$ : [6,3,2] Три-шестиугольные плиты-соты (8 форм)
${\tilde {A}}_{2}$ × $A_{1}$ : [(3,3,3),2] Треугольные соты плиты (новых форм нет)
${\tilde {I}}_{1}$ × $A_{1}$ × $A_{1}$ : [∞,2,2] = Кубические столбчатые соты (1 форма)
$I_{2}(p)$ × ${\tilde {I}}_{1}$ : [p,2,∞] Соты многоугольных колонн (аналог дуопризм : они выглядят как единая бесконечная башня из p-угольных призм, а оставшееся пространство заполнено апейрогональными призмами )
${\tilde {I}}_{1}$ × ${\tilde {I}}_{1}$ × $A_{1}$ : [∞,2,∞,2] = [4,4,2] - = (То же, что и семейство сотовых кубических плит)

Примеры (частично нарисованы)
Кубическая ячеистая плита	Перемежающиеся соты из шестиугольных плит	Трехгексагональная плита сотовая

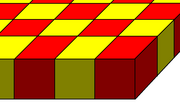(4) 4 ³: куб (1) 4 ⁴: квадратная плитка	(4) 3 ³: тетраэдр (3) 3 ⁴: октаэдр (1) 3 ⁶: треугольная плитка	(2) 3.4.4: треугольная призма (2) 4.4.6: шестиугольная призма (1) (3.6) ²: трехгексагональная мозаика

Первые две формы, показанные выше, являются полуправильными (однородными только с правильными гранями) и были перечислены Торольдом Госсетом в 1900 году соответственно как трехмерная полупроверка и тетраоктаэдрическая полупроверка . ^[4]

Чешуйчатые соты

Чешуйчатые . соты являются вершинно-транзитивными , как и однородные соты , с правильными многоугольными гранями, в то время как ячейки и более высокие элементы должны быть только орбиформными , равносторонними, с их вершинами, лежащими на гиперсферах Для 3D-сот это позволяет использовать подмножество тел Джонсона наряду с однородными многогранниками. Некоторые чешуйчатые формы могут образовываться путем чередования, оставляя, например, пирамид и куполов . промежутки ^[5]

Евклидовы соты чешуйчатых форм
Фризовые плиты			Призматические стопки
с ₃ {2,6,3},	с ₃ {2,4,4},	с{2,4,4},	3с ₄ {4,4,2,∞},


(1) 3.4.3.4: треугольный купол (2) 3.4.6: треугольный купол (1) 3.3.3.3: октаэдр (1) 3.6.3.6: тригексагональная мозаика	(1) 3.4.4.4: квадратный купол (2) 3.4.8: квадратный купол (1) 3.3.3: тетраэдр (1) 4.8.8: усеченная квадратная мозаика	(1) 3.3.3.3: квадратная пирамида (4) 3.3.4: квадратная пирамида (4) 3.3.3: тетраэдр (1) 4.4.4.4: квадратная мозаика	(1) 3.3.3.3: квадратная пирамида (4) 3.3.4: квадратная пирамида (4) 3.3.3: тетраэдр (4) 4.4.4: куб

Гиперболические формы

Существует 9 семейств групп Кокстера компактных однородных сот в гиперболическом трехмерном пространстве , порожденных как конструкции Витхоффа и представленных кольцевыми перестановками диаграмм Кокстера-Динкина для каждого семейства.

Из этих 9 семейств всего создано 76 уникальных сот:

[3,5,3] : - 9 форм
[5,3,4] : - 15 форм
[5,3,5] : - 9 форм
[5,3 ^1,1] : - 11 форм (7 пересекаются с семейством [5,3,4], 4 уникальны)
[(4,3,3,3)] : - 9 форм
[(4,3,4,3)] : - 6 форм
[(5,3,3,3)] : - 9 форм
[(5,3,4,3)] : - 9 форм
[(5,3,5,3)] : - 6 форм

Известны несколько невитоффовых форм, не входящих в список 76; неизвестно, сколько их.

Паракомпактные гиперболические формы

Существует также 23 паракомпактных группы Кокстера ранга 4. Эти семейства могут создавать однородные соты с неограниченными гранями или фигурами вершин, включая идеальные вершины на бесконечности:

Краткое описание симплектической гиперболической паракомпактной группы
Тип	Группы Кокстера	Уникальное количество сот
Линейные графики	\| \| \| \| \| \|	4×15+6+8+8 = 82
Трезубцы графы	\| \|	4+4+0 = 8
Циклические графики	\| \| \| \| \| \| \| \|	4×9+5+1+4+1+0 = 47
Петлевые графики	\| \| \|	4+4+4+2 = 14

Ссылки

^ Jump up to: Перейти обратно: ^а ^б Слоан, Нью-Джерси (ред.). «Последовательность A242941 (Выпуклые однородные мозаики в размерности n )» . Электронная энциклопедия целочисленных последовательностей . Фонд ОЭИС.
^ Георгий Ольшевский, (2006, Равномерные паноплоидные тетракомбы , Рукопись (Полный список из 11 выпуклых однородных мозаик, 28 выпуклых однородных сот и 143 выпуклых однородных тетракомб) [1]
^ [2] , A000029 6-1 случаев, пропуск одного с нулевыми оценками
^ Госсет, Торольд (1900). «О правильных и полуправильных фигурах в пространстве n измерений». Вестник математики . 29 : 43–48.
^ «Многогранник-дерево» .

Джон Х. Конвей , Хайди Бургель, Хаим Гудман-Штраус , (2008) Симметрии вещей , ISBN 978-1-56881-220-5 (Глава 21, Наименование архимедовых и каталонских многогранников и мозаик, Архитектурные и катоптрические мозаики, стр. 292–298, включает все непризматические формы)
Бранко Грюнбаум , (1994) Равномерные замощения трехмерного пространства. Геомбинаторика 4, 49 – 56.
Норман Джонсон (1991) Равномерные многогранники , рукопись
Уильямс, Роберт (1979). Геометрическая основа естественной структуры: справочник по дизайну . Dover Publications, Inc. ISBN 0-486-23729-Х . (Глава 5: Упаковка многогранников и заполнение пространства)
Кричлоу, Кейт (1970). Порядок в космосе: справочник по дизайну . Викинг Пресс. ISBN 0-500-34033-1 .
Калейдоскопы: Избранные сочинения HSM Коксетера , под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони К. Томпсона, Азии Ивик Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [7]
- (Документ 22) HSM Коксетер, Правильные и полуправильные многогранники I , [Math. Зейт. 46 (1940) 380–407, МР 2,10] (1.9 Равномерные заполнения пробелов)
А. Андреини , (1905) О сетях правильных и полуправильных многогранников и о соответствующих корреляционных сетях (О правильных и полуправильных сетях многогранников и о соответствующих корреляционных сетях), Mem. Società Italiana della Scienze, Сер.3, 14. 75– 129. PDF [8]
ДМИ Соммервилль , (1930) Введение в геометрию n измерений. Нью-Йорк, EP Dutton, . 196 стр. (издание Dover Publications, 1958 г.) Глава X: Правильные многогранники
Энтони Пью (1976). Многогранники: визуальный подход . Калифорния: Издательство Калифорнийского университета в Беркли. ISBN 0-520-03056-7 . Глава 5. Соединение многогранников
Кристаллография квазикристаллов: концепции, методы и структуры , Уолтер Стирер, София Делуди (2009), с. 54-55. 12 упаковок из 2 и более однородных многогранников кубической симметрии.

Внешние ссылки

Вайсштейн, Эрик В. «Соты» . Математический мир .
Однородные соты в трехмерных моделях VRML
Элементарные соты Вершинное переходное пространство, заполняющее соты неоднородными ячейками.
Равномерные разбиения трехмерного пространства, их родственники и вложения , 1999 г.
Однородные многогранники
Многогранники виртуальной реальности Энциклопедия многогранников
анимация октетной фермы
Обзор: А. Ф. Уэллс, Трехмерные сети и многогранники, HSM Coxeter (Источник: Bull. Amer. Math. Soc. Volume 84, Number 3 (1978), 466-470.)
Клитцинг, Ричард. «3D евклидовы мозаики» .
(последовательность A242941 в OEIS )

v т и Основные выпуклые правильные и однородные соты размеров 2–9.
Космос	Семья	${\tilde {A}}_{n-1}$	${\tilde {C}}_{n-1}$	${\tilde {B}}_{n-1}$	${\tilde {D}}_{n-1}$	${\tilde {G}}_{2}$ / ${\tilde {F}}_{4}$ / ${\tilde {E}}_{n-1}$
И ²	Равномерная укладка плитки	{3 ^[3]}	д ₃	HD ₃	квартал ₃	Шестиугольный
И ³	Равномерные выпуклые соты	{3 ^[4]}	д ₄	HD ₄	4 _{квартала}
И ⁴	Униформа 4-сотовая	{3 ^[5]}	д ₅	hδ ₅	qδ ₅	24-ячеистые соты
И ⁵	Униформа 5-сотовая	{3 ^[6]}	д ₆	HD ₆	qδ ₆
И ⁶	Униформа 6-сотовая	{3 ^[7]}	д ₇	hδ ₇	qδ ₇	2 ₂₂
И ⁷	Униформа 7-сотовая	{3 ^[8]}	д ₈	hδ ₈	8 _{кварталов}	1 ₃₃ • 3 ₃₁
И ⁸	Униформа 8-сотовая	{3 ^[9]}	д ₉	HD ₉	qδ ₉	1 ₅₂ • 2 ₅₁ • 5 ₂₁
И ⁹	Униформа 9-сотовая	{3 ^[10]}	д ₁₀	HD ₁₀	10 _{кварталов}
И ¹⁰	Униформа 10-сотовая	{3 ^[11]}	д ₁₁	HD ₁₁	qδ ₁₁
И ^{п -1}	Равномерный ( n -1)- сотовый	{3 ^[н]}	δ _н	hδ _н	qδ _н	1 _{лиц 2} • 2 _{лиц 1} • лиц ₂₁

[OEIS-1] Jump up to: Перейти обратно: ^а ^б Слоан, Нью-Джерси (ред.). «Последовательность A242941 (Выпуклые однородные мозаики в размерности n )» . Электронная энциклопедия целочисленных последовательностей . Фонд ОЭИС.

[2] Георгий Ольшевский, (2006, Равномерные паноплоидные тетракомбы , Рукопись (Полный список из 11 выпуклых однородных мозаик, 28 выпуклых однородных сот и 143 выпуклых однородных тетракомб) [1]

[3] [2] , A000029 6-1 случаев, пропуск одного с нулевыми оценками

[4] Госсет, Торольд (1900). «О правильных и полуправильных фигурах в пространстве n измерений». Вестник математики . 29 : 43–48.

[5] «Многогранник-дерево» .

[1]

[2]

[3]

[4]

[5]