конкурс Штакельберга

Модель лидерства Штакельберга — это стратегическая игра в экономике , в которой сначала движется фирма-лидер, а затем последовательно движутся фирмы-последователи (поэтому ее иногда называют «игрой лидер-последователь»). Она названа в честь немецкого экономиста Генриха Фрайхера фон Штакельберга, опубликовавшего в 1934 году «Marktform und Gleichgewicht» («Структура рынка и равновесие») , в котором была описана модель. С точки зрения теории игр , игроки в этой игре являются лидером и последователем и соревнуются в количестве. Лидера Штакельберга иногда называют лидером рынка.

Существуют и другие ограничения на поддержание равновесия Штакельберга. Лидер должен заранее знать , что ведомый наблюдает за его действиями. У последователя не должно быть средств принять на себя обязательство совершить действие будущего лидера, не являющегося Штакельбергом, и лидер должен это знать. Действительно, если бы «последователь» мог совершить действие лидера Штакельберга и «лидер» знал об этом, лучшим ответом лидера было бы разыграть действие последователя Штакельберга.

Фирмы могут участвовать в конкуренции по Штакельбергу, если у одной из них есть какое-то преимущество, позволяющее ей двигаться первым. В более общем плане лидер должен обладать властью брать на себя обязательства . Движение в первую очередь является наиболее очевидным средством обязательства: как только лидер сделал свой ход, он не может его отменить — он привержен этому действию. Движение первым может быть возможным, если лидером является действующая монополия отрасли, а последователем является новый участник отрасли. Удержание избыточных мощностей является еще одним средством принятия обязательств.

Идеальное равновесие Нэша в подыграх

Модель Штакельберга можно решить, чтобы найти идеальное равновесие или равновесие Нэша в подигре (SPNE), то есть профиль стратегии, который лучше всего служит каждому игроку с учетом стратегий другого игрока и который влечет за собой, что каждый игрок играет в равновесии Нэша в каждой подигре .

В самых общих чертах, пусть функция цены для отрасли (дуополии) будет равна $P$; Цена — это просто функция общего (отраслевого) выпуска, поэтому $P(q_{1}+q_{2})$ где индекс $_{1}$ представляет лидера и $_{2}$ представляет последователя. Предположим, фирма $i$ имеет структуру затрат $C_{i}(q_{i})$. Модель решается методом обратной индукции . Лидер думает, какова будет лучшая реакция последователя, т.е. как он отреагирует , когда увидит количество лидера. Затем лидер выбирает величину, которая максимизирует его выигрыш, предвидя прогнозируемую реакцию последователя. Последователь фактически наблюдает это и в состоянии равновесия выбирает ожидаемое количество в качестве ответа.

Чтобы рассчитать SPNE, сначала необходимо рассчитать лучшие функции отклика ведомого (расчет перемещается «назад» из-за обратной индукции).

Прибыль фирмы $2$ (последователь) — это доход минус затраты. Выручка — это произведение цены и количества, а себестоимость определяется структурой затрат фирмы, поэтому прибыль равна: $\Pi _{2}=P(q_{1}+q_{2})\cdot q_{2}-C_{2}(q_{2})$. Лучший ответ – найти значение $q_{2}$ это максимизирует $\Pi _{2}$ данный $q_{1}$, т.е. с учетом выпуска лидера (фирмы $1$), находится объем выпуска, который максимизирует прибыль ведомого. Следовательно, максимум $\Pi _{2}$ относительно $q_{2}$ предстоит найти. Сначала дифференцируйте $\Pi _{2}$ относительно $q_{2}$:

${\frac {\partial \Pi _{2}}{\partial q_{2}}}={\frac {\partial P(q_{1}+q_{2})}{\partial q_{2}}}\cdot q_{2}+P(q_{1}+q_{2})-{\frac {\partial C_{2}(q_{2})}{\partial q_{2}}}.$

Установка этого значения на ноль для максимизации:

${\frac {\partial \Pi _{2}}{\partial q_{2}}}={\frac {\partial P(q_{1}+q_{2})}{\partial q_{2}}}\cdot q_{2}+P(q_{1}+q_{2})-{\frac {\partial C_{2}(q_{2})}{\partial q_{2}}}=0.$

Значения $q_{2}$ которые удовлетворяют этому уравнению, являются лучшими ответами. Теперь рассматривается лучшая функция отклика лидера. Эта функция рассчитывается путем рассмотрения результатов ведомого как функции результатов лидера, как только что было вычислено.

Прибыль фирмы $1$ (лидер) является $\Pi _{1}=P(q_{1}+q_{2}(q_{1})).q_{1}-C_{1}(q_{1})$, где $q_{2}(q_{1})$ — количество последователей как функция количества лидера, а именно функция, рассчитанная выше. Лучший ответ – найти значение $q_{1}$ это максимизирует $\Pi _{1}$ данный $q_{2}(q_{1})$, т.е. при условии наилучшей функции отклика ведомого (фирмы) $2$), находится объем выпуска, максимизирующий прибыль лидера. Следовательно, максимум $\Pi _{1}$ относительно $q_{1}$ предстоит найти. Во-первых, дифференцируйте $\Pi _{1}$ относительно $q_{1}$:

${\frac {\partial \Pi _{1}}{\partial q_{1}}}={\frac {\partial P(q_{1}+q_{2})}{\partial q_{2}}}\cdot {\frac {\partial q_{2}(q_{1})}{\partial q_{1}}}\cdot q_{1}+{\frac {\partial P(q_{1}+q_{2})}{\partial q_{1}}}\cdot q_{1}+P(q_{1}+q_{2}(q_{1}))-{\frac {\partial C_{1}(q_{1})}{\partial q_{1}}}.$

Установка этого значения на ноль для максимизации:

${\frac {\partial \Pi _{1}}{\partial q_{1}}}={\frac {\partial P(q_{1}+q_{2})}{\partial q_{2}}}\cdot {\frac {\partial q_{2}(q_{1})}{\partial q_{1}}}\cdot q_{1}+{\frac {\partial P(q_{1}+q_{2})}{\partial q_{1}}}\cdot q_{1}+P(q_{1}+q_{2}(q_{1}))-{\frac {\partial C_{1}(q_{1})}{\partial q_{1}}}=0.$

Примеры

Следующий пример является очень общим. Он предполагает обобщенную линейную структуру спроса.

$p(q_{1}+q_{2})={\bigg (}a-b(q_{1}+q_{2}){\bigg )}$

и для простоты накладывает некоторые ограничения на структуру затрат, чтобы проблему можно было решить.

${\frac {\partial ^{2}C_{i}(q_{i})}{\partial q_{i}\cdot \partial q_{j}}}=0,\forall j$ и ${\frac {\partial C_{i}(q_{i})}{\partial q_{j}}}=0,j\neq \ i$

для удобства вычислений.

Прибыль подписчика составляет:

$\pi _{2}={\bigg (}a-b(q_{1}+q_{2}){\bigg )}\cdot q_{2}-C_{2}(q_{2}).$

Задача максимизации решается (из общего случая):

${\frac {\partial {\bigg (}a-b(q_{1}+q_{2}){\bigg )}}{\partial q_{2}}}\cdot q_{2}+a-b(q_{1}+q_{2})-{\frac {\partial C_{2}(q_{2})}{\partial q_{2}}}=0,$

$\Rightarrow \ -bq_{2}+a-b(q_{1}+q_{2})-{\frac {\partial C_{2}(q_{2})}{\partial q_{2}}}=0,$

$\Rightarrow \ q_{2}={\frac {a-bq_{1}-{\frac {\partial C_{2}(q_{2})}{\partial q_{2}}}}{2b}}.$

Рассмотрим проблему лидера:

$\Pi _{1}={\bigg (}a-b(q_{1}+q_{2}(q_{1})){\bigg )}\cdot q_{1}-C_{1}(q_{1}).$

Замена на $q_{2}(q_{1})$ из проблемы подписчика:

$\Pi _{1}={\bigg (}a-b{\bigg (}q_{1}+{\frac {a-bq_{1}-{\frac {\partial C_{2}(q_{2})}{\partial q_{2}}}}{2b}}{\bigg )}{\bigg )}\cdot q_{1}-C_{1}(q_{1}),$

$\Rightarrow \Pi _{1}={\bigg (}{\frac {a-b.q_{1}+{\frac {\partial C_{2}(q_{2})}{\partial q_{2}}}}{2}}){\bigg )}\cdot q_{1}-C_{1}(q_{1}).$

Задача максимизации решается (из общего случая):

${\frac {\partial \pi _{1}}{\partial q_{1}}}={\bigg (}{\frac {a-2bq_{1}+{\frac {\partial C_{2}(q_{2})}{\partial q_{2}}}}{2}}{\bigg )}-{\frac {\partial C_{1}(q_{1})}{\partial q_{1}}}=0.$

Теперь решаем для $q_{1}$ урожайность $q_{1}^{*}$, оптимальное действие лидера:

$q_{1}^{*}={\frac {a+{\frac {\partial C_{2}(q_{2})}{\partial q_{2}}}-2\cdot {\frac {\partial C_{1}(q_{1})}{\partial q_{1}}}}{2b}}.$

Это лучший ответ лидера на реакцию последователя в равновесии. Фактическое значение последователя теперь можно найти, введя это значение в его функцию реакции, рассчитанную ранее:

$q_{2}^{*}={\frac {a-b\cdot {\frac {a+{\frac {\partial C_{2}(q_{2})}{\partial q_{2}}}-2\cdot {\frac {\partial C_{1}(q_{1})}{\partial q_{1}}}}{2b}}-{\frac {\partial C_{2}(q_{2})}{\partial q_{2}}}}{2b}},$

$\Rightarrow q_{2}^{*}={\frac {a-3\cdot {\frac {\partial C_{2}(q_{2})}{\partial q_{2}}}+2\cdot {\frac {\partial C_{1}(q_{1})}{\partial q_{1}}}}{4b}}.$

Все равновесия Нэша $(q_{1}^{*},q_{2}^{*})$. Очевидно (если предположить, что предельные издержки равны нулю – т.е. затраты по существу игнорируются), что лидер имеет значительное преимущество. Интуитивно понятно, что если бы положение лидера было не лучше, чем у его последователя, он просто принял бы стратегию конкуренции Курно .

Подключение количества последователей $q_{2}$, обратно в функцию лучшего ответа лидера не даст $q_{1}$. Это связано с тем, что, как только лидер взял на себя обязательства по достижению результата и наблюдал за последователями, он всегда хочет сократить свой результат постфактум. Однако неспособность сделать это позволяет ей получать более высокие прибыли, чем при Курно.

Экономический анализ

Представление в развернутой форме часто используется для анализа модели «лидер-последователь» Штакельберга. Модель , также называемая « деревом решений », показывает комбинацию результатов и выигрышей обеих фирм в игре Штакельберга.

Игра Штакельберга, представленная в развернутой форме.

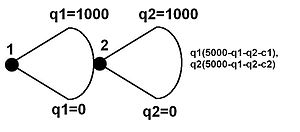
На изображении слева в развернутом виде изображена игра Штакельберга. Выплаты показаны справа. Этот пример довольно прост. Существует базовая структура затрат, включающая только предельные затраты отсутствуют ( постоянные затраты ). Функция спроса линейна, а ценовая эластичность спроса равна 1. Однако она иллюстрирует преимущество лидера.

Последователь хочет выбрать $q_{2}$ максимизировать свою отдачу $q_{2}\times (5000-q_{1}-q_{2}-c_{2})$. Взяв производную первого порядка и приравняв ее нулю (для максимизации), получим $q_{2}={\frac {5000-q_{1}-c_{2}}{2}}$ как максимальное значение $q_{2}$.

Лидер хочет выбрать $q_{1}$ максимизировать свою отдачу $q_{1}\times (5000-q_{1}-q_{2}-c_{1})$. Однако в равновесии он знает, что последователь выберет $q_{2}$ как указано выше. Таким образом, на самом деле лидер хочет максимизировать свой выигрыш. $q_{1}\times (5000-q_{1}-{\frac {5000-q_{1}-c_{2}}{2}}-c_{1})$ (заменив $q_{2}$ для функции наилучшего отклика ведомого). В результате дифференцирования максимальный выигрыш определяется выражением $q_{1}={\frac {5000-2c_{1}+c_{2}}{2}}$. Включение этого в функцию наилучшего ответа последователя дает $q_{2}={\frac {5000+2c_{1}-3c_{2}}{4}}$. Предположим, что предельные издержки для фирм равны (поэтому у лидера нет другого рыночного преимущества, кроме первого шага) и, в частности, $c_{1}=c_{2}=1000$. Лидер произведет 2000, а последователь — 1000. Это принесет лидеру прибыль (выплату) в два миллиона, а последователю — один миллион. Просто двигаясь первым, лидер получает вдвое большую прибыль, чем его последователь. Однако прибыль Курно здесь составляет 1,78 миллиона на штуку (строго, $(16/9)10^{6}$ за штуку), так что лидер мало что выиграл, а ведомый потерял. Однако это зависит от примера. Могут быть случаи, когда лидер Штакельберга имеет огромную прибыль сверх прибыли Курно, приближающуюся к монопольной прибыли (например, если лидер также имел большое преимущество в структуре затрат, возможно, из-за лучшей производственной функции ). Также могут быть случаи, когда последователь действительно получает более высокую прибыль, чем лидер, но только потому, что у него, скажем, гораздо меньшие затраты. Такое поведение последовательно работает на рынках дуополии, даже если фирмы асимметричны.

Правдоподобные и недостоверные угрозы со стороны последователя

Если бы после того, как лидер выбрал равновесное количество, последователь отклонился от равновесия и выбрал какое-то неоптимальное количество, это не только навредило бы самому себе, но и могло бы навредить лидеру. Если последователь выберет гораздо большее количество, чем его лучший ответ, рыночная цена снизится, и прибыль лидера упадет, возможно, ниже прибыли уровня Курно. В этом случае ведомый может объявить лидеру до начала игры, что, если лидер не выберет равновесное количество по Курно, ведомый выберет отклоняющееся количество, которое ударит по прибыли лидера. В конце концов, количество, выбранное лидером в равновесии, является оптимальным только в том случае, если ведомый также играет в равновесии. Однако лидеру ничего не угрожает. Как только лидер выбрал равновесное количество, для последователя было бы иррационально отклоняться, потому что это тоже повредит. Как только лидер сделал выбор, последователю будет выгоднее играть по равновесному пути. Следовательно, такая угроза со стороны последователя не будет заслуживать доверия.

Однако в (бесконечно) повторяющейся игре Штакельберга последователь может принять стратегию наказания, при которой он угрожает наказать лидера в следующем периоде, если он не выберет неоптимальную стратегию в текущем периоде. Эта угроза может быть правдоподобной, поскольку для последователя может быть разумным наказать в следующем периоде, чтобы лидер после этого выбрал количества Курно.

Штакельберг по сравнению с Курно

Модели Штакельберга и Курно схожи, поскольку в обеих конкуренция ведется по количеству. Однако, как видно, первый ход дает лидеру Штакельберга решающее преимущество. В игре Штакельберга также имеется важное предположение о совершенной информации : ведомый должен соблюдать количество, выбранное лидером, иначе игра сводится к Курно. При несовершенстве информации описанные выше угрозы могут быть правдоподобными. Если ведомый не может наблюдать за ходом лидера, для ведомого уже не является иррациональным выбор, скажем, уровня количества Курно (фактически это и есть равновесное действие). Однако должно быть так, что информация несовершенна , и ведомый не может наблюдать за движением лидера, потому что для ведомого нерационально не наблюдать, если он может, после того, как лидер переместился. Если он может наблюдать, он будет это делать, чтобы принять оптимальное решение. Любая угроза со стороны последователя, утверждающего, что он не будет наблюдать, даже если сможет, столь же неправдоподобна, как и приведенные выше. Это пример того, как слишком много информации вредит игроку. В соревновании Курно именно одновременность игры (несовершенство знаний) не приводит к тому, что ни один из игроков ( при прочих равных условиях ) находится в невыгодном положении.

Теоретико-игровые соображения

Как уже упоминалось, несовершенство информации в игре на лидерство сводится к конкуренции по Курно. Однако некоторые профили стратегии Курно поддерживаются как равновесия Нэша , но могут быть устранены как невероятные угрозы (как описано выше), применяя концепцию решения подыгрового совершенства . Действительно, именно это делает профиль стратегии Курно равновесием Нэша в игре Штакельберга и не позволяет ему быть идеальным на подыграх.

Рассмотрим игру Штакельберга (т. е. такую, которая удовлетворяет описанным выше требованиям для поддержания равновесия Штакельберга), в которой по какой-то причине лидер считает, что какое бы действие он ни предпринял, ведомый выберет величину Курно (возможно, лидер считает, что ведомый иррационально). Если лидер разыграл действие Штакельберга, то (он полагает), что последователь сыграет Курно. Следовательно, для лидера играть по Штакельбергу неоптимально. Фактически, его лучший ответ (по определению равновесия Курно) — это сыграть в количество Курно. Как только он это сделает, лучшим ответом ведомого будет сыграть по Курно.

Рассмотрим следующие профили стратегий: лидер играет по Курно; последователь играет по Курно, если лидер играет по Курно, а последователь играет по Штакельбергу, если лидер играет по Штакельбергу, и если лидер играет во что-то еще, последователь играет произвольную стратегию (следовательно, это фактически описывает несколько профилей). Этот профиль представляет собой равновесие Нэша. Как утверждалось выше, на пути равновесия игра является лучшим ответом на лучший ответ. Однако игра по Курно не была бы лучшим ответом лидера, если бы последователь играл бы Штакельберга, если бы он (лидер) играл Штакельберга. В этом случае лучшим ответом лидера будет игра Штакельберга. Следовательно, что делает этот профиль (или, скорее, эти профили) равновесием Нэша (или, скорее, равновесием Нэша), так это тот факт, что последователь будет играть не по Штакельбергу, если лидер будет играть по Штакельбергу.

Однако сам этот факт (то, что последователь будет играть не по Штакельбергу, если лидер будет играть по Штакельбергу) означает, что этот профиль не является равновесием Нэша в подигре, начиная с того момента, когда лидер уже сыграл в Штакельберга (подыгра вне пути равновесия). . Если лидер уже сыграл в Штакельберга, лучший ответ для последователя — сыграть в Штакельберга (и, следовательно, это единственное действие, которое приводит к равновесию Нэша в этой подигре). Следовательно, профиль стратегии Курно не является идеальным для подыгры.

Сравнение с другими моделями олигополии

По сравнению с другими моделями олигополии,

• Совокупный выпуск Штакельберга больше, чем совокупный выпуск Курно, но меньше, чем совокупный выпуск Бертрана .
• Цена Штакельберга ниже цены Курно, но выше цены Бертрана.
• Потребительский излишек Штакельберга больше потребительского излишка Курно, но ниже потребительского излишка Бертрана.
• Совокупный выпуск Штакельберга превышает выпуск чистой монополии или картеля , но меньше выпуска совершенной конкуренции .
• Цена Штакельберга ниже цены чистой монополии или картеля, но выше цены совершенной конкуренции.

Приложения

Концепция Штакельберга была распространена на динамические игры Штакельберга. С добавлением времени в качестве измерения были обнаружены явления, отсутствующие в статических играх, такие как нарушение лидером принципа оптимальности.

В последние годы игры Штакельберга нашли применение в области безопасности. В этом контексте защитник (лидер) разрабатывает стратегию защиты ресурса, при которой ресурс остается в безопасности независимо от стратегии, принятой злоумышленником (последователем). Дифференциальные игры Штакельберга также используются для моделирования цепочек поставок и каналов сбыта . Другие приложения игр Штакельберга включают гетерогенные сети , генетическая конфиденциальность , робототехника , автономное вождение , электрические сети , и интегрированные энергетические системы .

См. также

• Экономическая теория
• Конкурс Курно
• Бертран конкурс
• Игра с расширенной формой
• Промышленная организация
• Математическое программирование с равновесными ограничениями

Ссылки

• Х. фон Штакельберг, Структура рынка и равновесие: перевод 1-го издания на английский язык, Bazin, Urch & Hill, Springer 2011, XIV, 134 стр., ISBN   978-3-642-12585-0
• Фуденберг Д. и Тироль Дж. (1993) Теория игр , MIT Press. (см. главу 3, раздел 1)
• Гиббонс, Р. (1992) Учебник по теории игр , Harvester-Wheatsheaf. (см. главу 2, раздел 1Б)
• Осборн, М.Дж. и Рубинштейн, А. (1994) Курс теории игр , MIT Press (см. стр. 97–98).
• Теория олигоплии стала простой , глава 6 книги Экономика серфинга» « Хью Диксона .