Функция делителя


В математике , и особенно в теории чисел , функция делителя — это арифметическая функция, связанная с делителями целого числа . Когда ее называют функцией делителя, она подсчитывает количество делителей целого числа (включая 1 и само число). Оно проявляется в ряде замечательных тождеств, включая соотношения дзета-функции Римана и Эйзенштейна ряда модулярных форм . Функции делителей изучал Рамануджан , который дал ряд важных сравнений и тождеств ; они рассматриваются отдельно в статье « Сумма Рамануджана» .
Родственной функцией является функция суммирования делителей , которая, как следует из названия, представляет собой сумму по функции делителя.
Определение
[ редактировать ]Сумма положительных делителей функции σ z ( n ) для действительного или комплексного числа z определяется как сумма z х - степеней положительных делителей числа n . Это можно выразить в сигма-нотации как
где является сокращением от « d делит n ».Обозначения d ( n ), ν ( n ) и τ ( n ) (для немецкого Teiler = делители) также используются для обозначения σ 0 ( n ) или функции числа делителей [1] [2] ( ОЭИС : A000005 ). Когда z равно 1, функция называется сигма-функцией или функцией суммы делителей . [1] [3] а нижний индекс часто опускается, поэтому σ( n ) совпадает с σ1 ( n ) ( OEIS : A000203 ).
Аликвотная сумма s ( n ) числа n представляет собой сумму собственных делителей (то есть делителей, исключающих сам n , OEIS : A001065 ), и равна σ 1 ( n ) − n ; последовательность аликвот n . формируется путем многократного применения функции суммы аликвот
Пример
[ редактировать ]Например, σ 0 (12) — количество делителей числа 12:
а σ 1 (12) — сумма всех делителей:
а аликвотная сумма s(12) собственных делителей равна:
σ -1 ( n ) иногда называют индексом изобилия n : , и мы имеем
Таблица значений
[ редактировать ]Случаи x = 2–5 перечислены в OEIS : A001157 – OEIS : A001160 , x = 6–24 перечислены в OEIS : A013954 – OEIS : A013972 .
| н | факторизация | 𝜎 0 ( п ) | 𝜎 1 ( п ) | 𝜎 2 ( п ) | 𝜎 3 ( п ) | 𝜎 4 ( п ) |
|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 2 | 2 | 3 | 5 | 9 | 17 |
| 3 | 3 | 2 | 4 | 10 | 28 | 82 |
| 4 | 2 2 | 3 | 7 | 21 | 73 | 273 |
| 5 | 5 | 2 | 6 | 26 | 126 | 626 |
| 6 | 2×3 | 4 | 12 | 50 | 252 | 1394 |
| 7 | 7 | 2 | 8 | 50 | 344 | 2402 |
| 8 | 2 3 | 4 | 15 | 85 | 585 | 4369 |
| 9 | 3 2 | 3 | 13 | 91 | 757 | 6643 |
| 10 | 2×5 | 4 | 18 | 130 | 1134 | 10642 |
| 11 | 11 | 2 | 12 | 122 | 1332 | 14642 |
| 12 | 2 2 ×3 | 6 | 28 | 210 | 2044 | 22386 |
| 13 | 13 | 2 | 14 | 170 | 2198 | 28562 |
| 14 | 2×7 | 4 | 24 | 250 | 3096 | 40834 |
| 15 | 3×5 | 4 | 24 | 260 | 3528 | 51332 |
| 16 | 2 4 | 5 | 31 | 341 | 4681 | 69905 |
| 17 | 17 | 2 | 18 | 290 | 4914 | 83522 |
| 18 | 2×3 2 | 6 | 39 | 455 | 6813 | 112931 |
| 19 | 19 | 2 | 20 | 362 | 6860 | 130322 |
| 20 | 2 2 ×5 | 6 | 42 | 546 | 9198 | 170898 |
| 21 | 3×7 | 4 | 32 | 500 | 9632 | 196964 |
| 22 | 2×11 | 4 | 36 | 610 | 11988 | 248914 |
| 23 | 23 | 2 | 24 | 530 | 12168 | 279842 |
| 24 | 2 3 ×3 | 8 | 60 | 850 | 16380 | 358258 |
| 25 | 5 2 | 3 | 31 | 651 | 15751 | 391251 |
| 26 | 2×13 | 4 | 42 | 850 | 19782 | 485554 |
| 27 | 3 3 | 4 | 40 | 820 | 20440 | 538084 |
| 28 | 2 2 ×7 | 6 | 56 | 1050 | 25112 | 655746 |
| 29 | 29 | 2 | 30 | 842 | 24390 | 707282 |
| 30 | 2×3×5 | 8 | 72 | 1300 | 31752 | 872644 |
| 31 | 31 | 2 | 32 | 962 | 29792 | 923522 |
| 32 | 2 5 | 6 | 63 | 1365 | 37449 | 1118481 |
| 33 | 3×11 | 4 | 48 | 1220 | 37296 | 1200644 |
| 34 | 2×17 | 4 | 54 | 1450 | 44226 | 1419874 |
| 35 | 5×7 | 4 | 48 | 1300 | 43344 | 1503652 |
| 36 | 2 2 ×3 2 | 9 | 91 | 1911 | 55261 | 1813539 |
| 37 | 37 | 2 | 38 | 1370 | 50654 | 1874162 |
| 38 | 2×19 | 4 | 60 | 1810 | 61740 | 2215474 |
| 39 | 3×13 | 4 | 56 | 1700 | 61544 | 2342084 |
| 40 | 2 3 ×5 | 8 | 90 | 2210 | 73710 | 2734994 |
| 41 | 41 | 2 | 42 | 1682 | 68922 | 2825762 |
| 42 | 2×3×7 | 8 | 96 | 2500 | 86688 | 3348388 |
| 43 | 43 | 2 | 44 | 1850 | 79508 | 3418802 |
| 44 | 2 2 ×11 | 6 | 84 | 2562 | 97236 | 3997266 |
| 45 | 3 2 ×5 | 6 | 78 | 2366 | 95382 | 4158518 |
| 46 | 2×23 | 4 | 72 | 2650 | 109512 | 4757314 |
| 47 | 47 | 2 | 48 | 2210 | 103824 | 4879682 |
| 48 | 2 4 ×3 | 10 | 124 | 3410 | 131068 | 5732210 |
| 49 | 7 2 | 3 | 57 | 2451 | 117993 | 5767203 |
| 50 | 2×5 2 | 6 | 93 | 3255 | 141759 | 6651267 |
Характеристики
[ редактировать ]Формулы в простых степенях
[ редактировать ]Для простого p числа
потому что по определению делители простого числа равны 1 и самому себе. Кроме того, где p n # обозначает первоначальный ,
поскольку n простых множителей допускают последовательность двоичного выбора ( или 1) из n слагаемых для каждого образовавшегося собственного делителя. Однако это, как правило, не самые маленькие числа, число делителей которых равно степени двойки ; вместо этого наименьшее такое число может быть получено путем умножения первых n простых чисел Ферми – Дирака , степеней простых чисел, показатель степени которых равен степени двойки. [4]
Четко, для всех , и для всех , .
Функция делителя мультипликативна (поскольку каждый делитель c произведения mn с отчетливо соответствуют делителю a числа m и делителю b числа n ), но не полностью мультипликативны :
Следствием этого является то, что если мы напишем
где r = ω ( n ) — количество различных простых делителей числа , n pi — й i- простой делитель, а ai — максимальная степень числа pi , которую n делится на , тогда мы имеем: [5]
что, когда x ≠ 0, эквивалентно полезной формуле: [5]
Когда х = 0, является: [5]
Этот результат можно непосредственно вывести из того факта, что все делители однозначно определяются отдельными кортежами целых чисел с (т.е. независимый выбор для каждого ).
Например, если n равно 24, существует два простых делителя ( p 1 равно 2; p 2 равно 3); отметив, что 24 является произведением 2 3 ×3 1 , a 1 равно 3, a 2 равно 1. Таким образом, мы можем вычислить вот так:
Восемь делителей, подсчитываемых по этой формуле, — это 1, 2, 4, 8, 3, 6, 12 и 24.
Другие свойства и личности
[ редактировать ]Эйлер доказал замечательную повторяемость: [6] [7] [8]
где если это произойдет и для , и представляют собой последовательные пары обобщенных пятиугольных чисел ( OEIS : A001318 , начиная со смещения 1). Действительно, Эйлер доказал это посредством логарифмического дифференцирования тождества в своей теореме о пятиугольных числах .
Для неквадратного целого числа n каждый делитель d числа n соединяется с делителем n / d числа n и четный; для квадратного целого числа один делитель (а именно ) не сопряжен с отдельным делителем и странно. Аналогично, число нечетно тогда и только тогда, когда n — квадрат или дважды квадрат. [9]
Также отметим s ( n ) знак равно σ ( n ) - n . Здесь s ( n ) обозначает сумму собственных делителей числа n , то есть делителей числа n , исключая само число n . Эта функция используется для распознавания совершенных чисел , которые представляют собой n такие, что s ( n ) = n . Если s ( n )> n , то n — обильное число , а если s ( n )< n , то n — дефицитное число .
Если n является степенью 2, , затем и , что делает n почти идеальным .
Например, для двух простых чисел , позволять
- .
Затем
и
где — это полная функция Эйлера .
Тогда корни
выражайте p и q только через σ ( n ) и φ ( n ), не требуя знания n или , как
Также, зная n и либо или или, альтернативно, и либо или позволяет легко восстановить p и q .
В 1984 году Роджер Хит-Браун доказал, что равенство
верно для бесконечного числа значений n , см. OEIS : A005237 .
Серийные отношения
[ редактировать ]Два ряда Дирихле, включающие функцию делителя: [10]
где — дзета-функция Римана . Ряд для d ( n ) = σ 0 ( n ) дает: [10]
и Рамануджана личность [11]
что является частным случаем свертки Рэнкина – Сельберга .
Ряд Ламберта, включающий функцию делителя: [12]
для произвольного комплекса | д | ≤ 1 и а . Это суммирование также появляется как ряд Фурье ряда Эйзенштейна и инварианты эллиптических функций Вейерштрасса .
Для существует явное представление в виде ряда с суммами Рамануджана как : [13]
Вычисление первых членов показывает его колебания вокруг «среднего значения» :
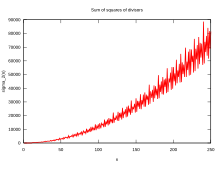
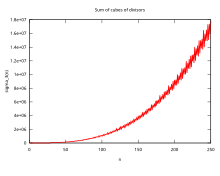
Темпы роста
[ редактировать ]В обозначениях «маленькое о» функция делителя удовлетворяет неравенству: [14] [15]
Точнее, Северин Вигерт показал, что: [15]
С другой стороны, поскольку простых чисел бесконечно много , [15]
В Big-O обозначениях Питер Густав Лежен Дирихле показал, что средний порядок функции делителя удовлетворяет следующему неравенству: [16] [17]
где — гамма-константа Эйлера . Улучшение границы в этой формуле известна как проблема делителей Дирихле .
Поведение сигма-функции нерегулярно. Асимптотическую скорость роста сигма-функции можно выразить следующим образом: [18]
где lim sup — верхний предел . Этот результат представляет собой Грёнвалля теорему , опубликованную в 1913 году ( Grönwall 1913 ). Его доказательство использует третью теорему Мертенса , которая гласит, что:
где p обозначает простое число.
В 1915 году Рамануджан доказал, что в предположении гипотезы Римана неравенство Робина
- (где γ — постоянная Эйлера–Машерони )
справедливо для всех достаточно больших n ( Ramanujan 1997 ). Наибольшее известное значение, которое нарушает неравенство, — n = 5040 . В 1984 году Гай Робин доказал, что неравенство верно для всех n > 5040 тогда и только тогда, когда верна гипотеза Римана ( Robin 1984 ). Это теорема Робина , и после него это неравенство стало известно. Робин, кроме того, показал, что если гипотеза Римана неверна, то существует бесконечное количество значений n , нарушающих неравенство, и известно, что наименьшее такое n > 5040 должно быть избыточным ( Akbary & Friggstad 2009 ). Было показано, что неравенство справедливо для больших нечетных целых чисел и чисел без квадратов и что гипотеза Римана эквивалентна неравенству только для n , делящегося на пятую степень простого числа ( Choi et al. 2007 ).
Робин также безоговорочно доказал, что неравенство:
справедливо для всех n ≥ 3.
Соответствующая оценка была дана Джеффри Лагариасом в 2002 году, который доказал, что гипотеза Римана эквивалентна утверждению, что:
для любого натурального числа n > 1, где — номер n- й гармоники ( Lagarias 2002 ).
См. также
[ редактировать ]- Свертки суммы делителей , перечисляет несколько тождеств, включающих функции делителя.
- Функция тотента Эйлера , фи-функция Эйлера
- Рефакторизуемый номер
- Таблица делителей
- Унитарный делитель
Примечания
[ редактировать ]- ^ Jump up to: Перейти обратно: а б Лонг (1972 , стр. 46)
- ^ Петтофреззо и Биркит (1970 , стр. 63)
- ^ Петтофреззо и Биркит (1970 , стр. 58)
- ^ Рамануджан, С. (1915), «Высокосоставные числа» , Труды Лондонского математического общества , s2-14 (1): 347–409, doi : 10.1112/plms/s2_14.1.347 ; см. раздел 47, стр. 405–406, воспроизведено в Сборнике статей Шринивасы Рамануджана , Cambridge Univ. Пресс, 2015, стр. 124–125.
- ^ Jump up to: Перейти обратно: а б с Харди и Райт (2008) , стр. 310 f, §16.7.
- ^ Эйлер, Леонард; Белл, Джордан (2004). «Наблюдение о суммах делителей». arXiv : math/0411587 .
- ^ https://scholarlycommons.pacific.edu/euler-works/175/ , Открытие совершенно необычного закона чисел по отношению к сумме их делителей.
- ^ https://scholarlycommons.pacific.edu/euler-works/542/ , О чудесных свойствах пятиугольных чисел.
- ^ Джой и Вайдья (1967) .
- ^ Jump up to: Перейти обратно: а б Харди и Райт (2008) , стр. 326–328, §17.5.
- ^ Харди и Райт (2008) , стр. 334–337, §17.8.
- ^ Харди и Райт (2008) , стр. 338–341, §17.10.
- ^ Э. Кретцель (1981). Теория чисел . Берлин: Немецкое научное издательство VEB. п. 130. (Английский)
- ^ Апостол (1976) , с. 296.
- ^ Jump up to: Перейти обратно: а б с Харди и Райт (2008) , стр. 342–347, §18.1.
- ^ Апостол (1976) , Теорема 3.3.
- ^ Харди и Райт (2008) , стр. 347–350, §18.2.
- ^ Харди и Райт (2008) , стр. 469–471, §22.9.
Ссылки
[ редактировать ]- Акбари, Амир; Фриггстад, Закари (2009), «Сверхизбыточные числа и гипотеза Римана» (PDF) , American Mathematical Monthly , 116 (3): 273–275, doi : 10.4169/193009709X470128 , заархивировано из оригинала (PDF) 04.2014 г. 11 .
- Апостол, Том М. (1976), Введение в аналитическую теорию чисел , Тексты для студентов по математике, Нью-Йорк-Гейдельберг: Springer-Verlag, ISBN 978-0-387-90163-3 , МР 0434929 , Збл 0335.10001
- Бах, Эрик ; Шалит, Джеффри , Алгоритмическая теория чисел , том 1, 1996, MIT Press. ISBN 0-262-02405-5 , см. стр. 234 в разделе 8.8.
- Кавени, Джеффри; Николя, Жан-Луи ; Сондоу, Джонатан (2011), «Теорема Робина, простые числа и новая элементарная переформулировка гипотезы Римана» (PDF) , ЦЕЛЫЕ ЧИСЛА: Электронный журнал комбинаторной теории чисел , 11 : A33, arXiv : 1110.5078 , Bibcode : 2011arXiv1110.5078C
- Чой, ЁнгДжу ; Личиардополь, Николай; Мори, Питер ; Соле, Патрик (2007), «О критерии Робина для гипотезы Римана», Journal of Number Theory of Bordeaux , 19 (2): 357–372, arXiv : math.NT/0604314 , doi : 10.5802/jtnb.5914 , . ISSN 1246-7405 , MR 2394891 , S2CID 3207238 , Збл 1163.11059
- Джоя, А.А.; Вайдья, AM (1967), «Дружественные числа с противоположной четностью», The American Mathematical Monthly , 74 (8): 969–973, doi : 10.2307/2315280 , JSTOR 2315280 , MR 0220659
- Грёнвалль, Томас Хакон (1913), «Некоторые асимптотические выражения в теории чисел», Труды Американского математического общества , 14 : 113–122, doi : 10.1090/S0002-9947-1913-1500940-6
- Харди, штат Джорджия ; Райт, Э.М. (2008) [1938], Введение в теорию чисел , отредактированное Д. Р. Хит-Брауном и Дж. Х. Сильверманом . Предисловие Эндрю Уайлса . (6-е изд.), Оксфорд: Oxford University Press , ISBN 978-0-19-921986-5 , МР 2445243 , Збл 1159.11001
- Ивич, Александр (1985), Дзета-функция Римана. Теория дзета-функции Римана с приложениями , Публикация Wiley-Interscience, Нью-Йорк и т. д.: John Wiley & Sons, стр. 385–440, ISBN. 0-471-80634-Х , Збл 0556.10026
- Лагариас, Джеффри К. (2002), «Элементарная проблема, эквивалентная гипотезе Римана», The American Mathematical Monthly , 109 (6): 534–543, arXiv : math/0008177 , doi : 10.2307/2695443 , ISSN 0002-9890 , JSTOR 2695443 , MR 1908008 , S2CID 15884740
- Лонг, Кэлвин Т. (1972), Элементарное введение в теорию чисел (2-е изд.), Лексингтон: DC Heath and Company , LCCN 77171950
- Петтофреззо, Энтони Дж.; Биркит, Дональд Р. (1970), Элементы теории чисел , Энглвуд Клиффс: Прентис Холл , LCCN 77081766
- Рамануджан, Шриниваса (1997), «Высокосложные числа, с аннотациями Жана-Луи Николя и Гая Робина», The Ramanujan Journal , 1 (2): 119–153, doi : 10.1023/A:1009764017495 , ISSN 1382-4090 , MR 1606180 , S2CID 115619659
- Робин, Гай (1984), «Большие значения функции суммы делителей и гипотеза Римана», Журнал чистой и прикладной математики , девятая серия, 63 (2): 187–213, ISSN 0021-7824 , MR 0774171
- Уильямс, Кеннет С. (2011), Теория чисел в духе Лиувилля , Тексты для студентов Лондонского математического общества, том. 76, Кембридж: Издательство Кембриджского университета , ISBN 978-0-521-17562-3 , Збл 1227.11002
Внешние ссылки
[ редактировать ]- Вайсштейн, Эрик В. «Функция делителя» . Математический мир .
- Вайсштейн, Эрик В. «Теорема Робина» . Математический мир .
- Элементарная оценка некоторых сумм свертки с участием функций делителей PDF статьи Хуарда, Оу, Спирмана и Уильямса. Содержит элементарные (т.е. не опирающиеся на теорию модулярных форм) доказательства сверток суммы делителей, формулы количества способов представления числа в виде суммы треугольных чисел и связанные с ними результаты.




























![{\displaystyle {\begin{aligned}\sigma _{1}(n)&=\sigma _{1}(n-1)+\sigma _{1}(n-2)-\sigma _{1} (n-5)-\sigma _{1}(n-7)+\sigma _{1}(n-12)+\sigma _{1}(n-15)+\cdots \\[12mu]& =\sum _{i\in \mathbb {N} }(-1)^{i+1}\left(\sigma _{1}\left(n-{\frac {1}{2}}\left (3i^{2}-i\right)\right)+\sigma _{1}\left(n-{\frac {1}{2}}\left(3i^{2}+i\right)\ вправо)\вправо),\end{выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57edf7ce8b5ba7cd703d6696d6272fc4bce20ffc)
















![{\displaystyle (xp)(xq)=x^{2}-(p+q)x+n=x^{2}-[(\sigma (n)-\varphi (n))/2]x+[ (\sigma (n)+\varphi (n))/2-1]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ad1713c0c16dad5582f05ac235d6f6a116b598a)

![{\displaystyle p=(\sigma (n)-\varphi (n))/4-{\sqrt {[(\sigma (n)-\varphi (n))/4]^{2}-[(\ сигма (n)+\varphi (n))/2-1]}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4451d4e5cba4e47140fd055650c0cc07739186a2)
![{\displaystyle q=(\sigma (n)-\varphi (n))/4+ {\sqrt {[(\sigma (n)-\varphi (n))/4]^{2}-[(\ сигма (n)+\varphi (n))/2-1]}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec0c03afb9b83137b596f0c857be23fa65b66806)











![{\displaystyle \sigma _{k}(n)=\zeta (k+1)n^{k}\left[1+{\frac {(-1)^{n}}{2^{k+1 }}}+{\frac {2\cos {\frac {2\pi n}{3}}}{3^{k+1}}}+{\frac {2\cos {\frac {\pi n }{2}}}{4^{k+1}}}+\cdots \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf656d9d28eb4e6b5948ea58d577e6f17bf3fbdd)












