Теорема Гёделя о полноте

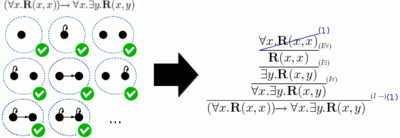
Теорема Гёделя о полноте — фундаментальная теорема математической логики , устанавливающая соответствие между семантической истиной и синтаксической доказуемостью в логике первого порядка .

Теорема о полноте применима к любой теории первого порядка : если T — такая теория, а φ — предложение (на том же языке), и каждая модель T является моделью φ, то существует доказательство (первого порядка). φ, используя утверждения T как аксиомы. Иногда говорят, что «все истинное во всех моделях доказуемо». (Это не противоречит теореме Гёделя о неполноте , которая касается формулы φ _u , которая недоказуема в некоторой теории Т , но верна в «стандартной» модели натуральных чисел: φ _u ложна в какой-то другой, «нестандартной» модели. модели Т. ^[1])

Теорема о полноте устанавливает тесную связь между теорией моделей , которая занимается тем, что истинно в различных моделях, и теорией доказательств , которая изучает то, что может быть формально доказано в конкретных формальных системах .

Впервые это было доказано Куртом Гёделем в 1929 году. Затем оно было упрощено, когда Леон Хенкин заметил в своей докторской диссертации. тезис о том, что сложную часть доказательства можно представить в виде теоремы существования модели (опубликовано в 1949 г.). ^[2] Доказательство Хенкина было упрощено Гисбертом Хасеньягером в 1953 году. ^[3]

Предварительные сведения [ править ]

Существует множество дедуктивных систем логики первого порядка, включая системы естественной дедукции и системы в стиле Гильберта . Общим для всех дедуктивных систем является понятие формальной дедукции . Это последовательность (или, в некоторых случаях, конечное дерево ) формул со специально обозначенным выводом . Определение вывода таково, что оно конечно и что можно алгоритмически (например, с помощью компьютера или вручную) проверить, что данная последовательность (или дерево) формул действительно является выводом.

Формула первого порядка называется логически корректной, если она истинна в каждой структуре языка формулы (т. е. при любом присвоении значений переменным формулы). Чтобы формально сформулировать, а затем доказать теорему о полноте, необходимо также определить дедуктивную систему. Дедуктивная система называется полной, если каждая логически обоснованная формула является заключением некоторого формального вывода, а теоремой о полноте конкретной дедуктивной системы является теорема о ее полноте в этом смысле. Таким образом, в некотором смысле для каждой дедуктивной системы существует своя теорема о полноте. Обратной стороной полноты является правильность , то есть только логически обоснованные формулы доказуемы в дедуктивной системе.

Если некоторая конкретная дедуктивная система логики первого порядка является правильной и полной, то она «совершенна» (формула доказуема тогда и только тогда, когда она логически верна), таким образом, эквивалентна любой другой дедуктивной системе того же качества (любое доказательство в одной системе могут быть преобразованы в другую).

Заявление [ править ]

Сначала зафиксируем дедуктивную систему исчисления предикатов первого порядка, выбрав любую из известных эквивалентных систем. Первоначальное доказательство Гёделя предполагало систему доказательств Гильберта-Акермана.

Гёделя формулировка Оригинальная

Теорема о полноте гласит, что если формула логически верна, то существует конечный вывод (формальное доказательство) формулы.

Таким образом, дедуктивная система является «полной» в том смысле, что для доказательства всех логически обоснованных формул не требуется никаких дополнительных правил вывода. Обратной стороной полноты является правильность , то есть только логически обоснованные формулы доказуемы в дедуктивной системе. Вместе с корректностью (которую легко проверить) из этой теоремы следует, что формула логически верна тогда и только тогда, когда она является результатом формального вывода.

Более общая форма [ править ]

Теорема может быть выражена в более общем смысле в терминах логического следствия . Мы говорим, что предложение s является синтаксическим следствием теории T , обозначаемым $T\vdash s$ , если s доказуемо из T в нашей дедуктивной системе. Мы говорим, что s является семантическим следствием T , обозначаемым $T\models s$ , если s в каждой модели T выполняется . Теорема о полноте тогда гласит, что для любой теории T первого порядка с хорошо упорядочиваемым языком и любого предложения s на языке T ,

если

T\models s

, затем

T\vdash s

.

Поскольку справедливо и обратное (корректность), то $T\models s$ если и только если $T\vdash s$ , и, таким образом, это синтаксическое и семантическое следствие эквивалентно для логики первого порядка.

Эта более общая теорема используется неявно, например, когда доказывается доказуемость предложения на основе аксиом теории групп путем рассмотрения произвольной группы и показа, что эта группа удовлетворяет этому предложению.

Исходная формулировка Гёделя выведена на основе рассмотрения частного случая теории без каких-либо аксиом.

существования Теорема модели

Теорему о полноте можно также понимать с точки зрения непротиворечивости , как следствие теоремы существования модели Хенкина . Мы говорим, что теория T если синтаксически непротиворечива, не существует предложения s такого, что и s , и его отрицание ¬ s доказуемы из T в нашей дедуктивной системе. первого порядка Теорема существования модели гласит, что для любой теории T с хорошо упорядочиваемым языком

если

T

синтаксически непротиворечив, то

T

есть модель.

Другая версия, связанная с теоремой Левенхайма – Скулема , гласит:

Каждая синтаксически непротиворечивая счетная теория первого порядка имеет конечную или счетную модель.

Учитывая теорему Хенкина, теорему о полноте можно доказать следующим образом: если $T\models s$ , затем $T\cup \lnot s$ не имеет моделей. По противоположности теоремы Хенкина тогда $T\cup \lnot s$ является синтаксически противоречивым. Итак противоречие( $\bot$ ) доказуемо из $T\cup \lnot s$ в дедуктивной системе. Следовательно $(T\cup \lnot s)\vdash \bot$ , и тогда по свойствам дедуктивной системы $T\vdash s$ .

Как теорема арифметики [ править ]

Теорема существования модели и ее доказательство могут быть формализованы в рамках арифметики Пеано . Точнее, мы можем систематически определить модель любой непротиворечивой эффективной теории T первого порядка в арифметике Пеано, интерпретируя каждый символ T арифметической формулой, свободные переменные которой являются аргументами символа. (Во многих случаях нам придется предполагать в качестве гипотезы конструкции, что T непротиворечиво, поскольку арифметика Пеано не может доказать этот факт.) Однако определение, выраженное этой формулой, не является рекурсивным (но, вообще говоря, является , Δ ₂ ).

Последствия [ править ]

Важным следствием теоремы о полноте является то, что можно рекурсивно перечислить семантические следствия любой эффективной теории первого порядка, перечислив все возможные формальные выводы из аксиом теории, и использовать это для перечисления их выводов. .

Это контрастирует с прямым значением понятия семантической последовательности, которая количественно оценивает все структуры в конкретном языке, что явно не является рекурсивным определением.

Кроме того, это делает концепцию «доказуемости» и, следовательно, «теоремы» ясной концепцией, которая зависит только от выбранной системы аксиом теории, а не от выбора системы доказательства.

с теоремами о Связь неполноте

Теоремы Гёделя о неполноте показывают, что существуют внутренние ограничения того, что можно доказать в рамках любой данной теории первого порядка в математике. «Неполнота» в их названии относится к другому значению слова « полный» (см. Теорию моделей – Использование теорем о компактности и полноте ): Теория $T$ является полным (или разрешимым), если каждое предложение $S$ на языке $T$ либо доказуемо ( $T\vdash S$ ) или опровергаемый ( $T\vdash \neg S$ ).

Первая теорема о неполноте утверждает, что любой $T$ которое является непротиворечивым , эффективным и содержит арифметику Робинсона (« Q »), должно быть неполным в этом смысле, за счет явного построения предложения $S_{T}$ которое явно не является ни доказуемым, ни опровергнутым в рамках $T$ . Вторая теорема о неполноте расширяет этот результат, показывая, что $S_{T}$ может быть выбран так, чтобы он выражал последовательность $T$ сам.

С $S_{T}$ не может быть доказано в $T$ , из теоремы о полноте следует существование модели $T$ в котором $S_{T}$ является ложным. Фактически, $S_{T}$ является Π ₁ предложением , т. е. оно утверждает, что некоторое финитистское свойство справедливо для всех натуральных чисел; поэтому, если это ложь, то какое-то натуральное число является контрпримером. Если бы этот контрпример существовал в рамках стандартных натуральных чисел, его существование опровергло бы $S_{T}$ в пределах $T$ ; но теорема о неполноте показала, что это невозможно, поэтому контрпример не должен быть стандартным числом и, следовательно, любой моделью $T$ в котором $S_{T}$ значение false должно включать нестандартные числа .

В действительности модель любой теории, содержащей Q , полученная систематическим построением теоремы существования арифметической модели, всегда является нестандартной с неэквивалентным предикатом доказуемости и неэквивалентным способом интерпретации собственной конструкции, так что эта конструкция нерекурсивно (поскольку рекурсивные определения были бы однозначными).

Кроме того, если $T$ хотя бы немного сильнее Q (например, если он включает индукцию для ограниченных экзистенциальных формул), то теорема Тенненбаума показывает, что он не имеет рекурсивных нестандартных моделей.

теоремой компактности Связь с

Теорема полноты и теорема компактности — два краеугольных камня логики первого порядка. Хотя ни одну из этих теорем невозможно доказать полностью эффективно , каждую можно эффективно получить из другой.

Теорема о компактности гласит, что если формула φ является логическим следствием (возможно, бесконечного) набора формул Γ, то она является логическим следствием конечного подмножества Γ. Это является непосредственным следствием теоремы о полноте, поскольку только конечное число аксиом из Γ может быть упомянуто при формальном выводе φ, и тогда из корректности дедуктивной системы следует, что φ является логическим следствием этого конечного множества. Это доказательство теоремы о компактности первоначально принадлежит Гёделю.

И наоборот, для многих дедуктивных систем можно доказать теорему полноты как эффективное следствие теоремы о компактности.

Неэффективность теоремы о полноте можно измерить методами обратной математики . При рассмотрении счетного языка теоремы о полноте и компактности эквивалентны друг другу и эквивалентны слабой форме выбора, известной как слабая лемма Кенига , с эквивалентностью, доказуемой в RCA ₀ второго порядка, (вариант арифметики Пеано ограниченный индукцией над Σ ⁰₁ формулы). Слабая лемма Кенига доказуема в ZF, системе теории множеств Цермело–Френкеля без аксиомы выбора, и, таким образом, теоремы полноты и компактности для счетных языков доказуемы в ZF. Однако ситуация меняется, когда язык имеет сколь угодно большую мощность, поскольку тогда, хотя теоремы о полноте и компактности остаются доказуемо эквивалентными друг другу в ZF, они также доказуемо эквивалентны слабой форме аксиомы выбора , известной как лемма об ультрафильтре. . В частности, ни одна теория, расширяющая ZF, не может доказать теоремы о полноте или компактности над произвольными (возможно, несчетными) языками, не доказав также лемму об ультрафильтре на множестве той же мощности.

Полнота в других логиках [ править ]

Теорема о полноте — центральное свойство логики первого порядка , которое справедливо не для всех логик. Логика второго порядка , например, не имеет теоремы о полноте для своей стандартной семантики (хотя имеет свойство полноты для семантики Хенкина ), а набор логически допустимых формул в логике второго порядка не является рекурсивно перечислимым. То же самое относится и ко всем логикам высшего порядка. Можно создать надежные дедуктивные системы для логики высшего порядка, но ни одна такая система не может быть полной.

Теорема Линдстрема утверждает, что логика первого порядка является самой сильной (с учетом определенных ограничений) логикой, удовлетворяющей как компактности, так и полноте.

Теорема о полноте может быть доказана для модальной логики или интуиционистской логики относительно семантики Крипке .

Доказательства [ править ]

Гёделя Первоначальное доказательство теоремы основывалось на сведении проблемы к частному случаю для формул в определенной синтаксической форме, а затем на обработке этой формы с помощью специального аргумента.

В современных текстах по логике теорема Гёделя о полноте обычно доказывается с помощью доказательства Хенкина , а не с помощью оригинального доказательства Гёделя. Доказательство Хенкина напрямую строит термомодель для любой непротиворечивой теории первого порядка. Джеймс Маргетсон (2004) разработал компьютеризированное формальное доказательство, используя средство доказательства теоремы Изабель . ^[4] Известны и другие доказательства.

См. также [ править ]

Дальнейшее чтение [ править ]

Гёдель, К. (1929). О полноте логического исчисления (тезис). Докторская диссертация. Венский университет. Первое доказательство теоремы о полноте.
Гёдель, К. (1930). «Полнота аксиом исчисления логических функций». Ежемесячные журналы по математике (на немецком языке). 37 (1): 349–360. дои : 10.1007/BF01696781 . ЯФМ 56.0046.04 . S2CID 123343522 . Тот же материал, что и диссертация, за исключением более кратких доказательств, более сжатых объяснений и отсутствия длинного введения.
Ганс Гермес (1973). Введение в математическую логику . Hochschultext (Springer-Verlag). Лондон: Спрингер. ISBN 3540058192 . ISSN 1431-4657 . Глава 5: «Теорема Гёделя о полноте» .

^ Бацоглу, Серафим (2021). «Теорема Гёделя о неполноте». arXiv : 2112.06641 [ math.HO ]. (стр. 17). Доступ осуществлен 1 декабря 2022 г.
^ Леон Хенкин (сентябрь 1949 г.). «Полнота функционального исчисления первого порядка». Журнал символической логики . 14 (3): 159–166. дои : 10.2307/2267044 . JSTOR 2267044 . S2CID 28935946 .
^ Гисберт Ф.Р. Хасеньягер (март 1953 г.). «Заметка о доказательстве Хенкина полноты исчисления предикатов первого порядка». Журнал символической логики . 18 (1): 42–48. дои : 10.2307/2266326 . JSTOR 2266326 . S2CID 45705695 .
^ Джеймс Маргетсон (сентябрь 2004 г.). Доказательство теоремы о полноте в Isabelle/HOL (PDF) (технический отчет). Архивировано (PDF) из оригинала 22 февраля 2006 г.

Внешние ссылки [ править ]

Стэнфордская энциклопедия философии : « Курт Гёдель » — Джульетты Кеннеди .
Биография МакТьютора: Курт Гёдель. Архивировано 13 октября 2005 г. в Wayback Machine.
Детловс Вилнис и Подниекс Карлис « Введение в математическую логику » .

[1] Бацоглу, Серафим (2021). «Теорема Гёделя о неполноте». arXiv : 2112.06641 [ math.HO ]. (стр. 17). Доступ осуществлен 1 декабря 2022 г.

[2] Леон Хенкин (сентябрь 1949 г.). «Полнота функционального исчисления первого порядка». Журнал символической логики . 14 (3): 159–166. дои : 10.2307/2267044 . JSTOR 2267044 . S2CID 28935946 .

[3] Гисберт Ф.Р. Хасеньягер (март 1953 г.). «Заметка о доказательстве Хенкина полноты исчисления предикатов первого порядка». Журнал символической логики . 18 (1): 42–48. дои : 10.2307/2266326 . JSTOR 2266326 . S2CID 45705695 .

[4] Джеймс Маргетсон (сентябрь 2004 г.). Доказательство теоремы о полноте в Isabelle/HOL (PDF) (технический отчет). Архивировано (PDF) из оригинала 22 февраля 2006 г.

[1]

[2]

[3]

[4]