Счетные стержни
| Часть серии о |
| Системы счисления |
|---|
| Список систем счисления |

| Счетные стержни | |||
|---|---|---|---|
| Китайское имя | |||
| Традиционный китайский | Рассчитать | ||
| Упрощенный китайский | Рассчитать | ||
| |||
| Альтернативное китайское название | |||
| китайский | оператор | ||
| |||
| Вьетнамское имя | |||
| Вьетнамский алфавит | калькулятор расчет | ||
| Хан-Ном | 𣠗комбинированный Рассчитать | ||
| Корейское имя | |||
| хангыль | жетон лес | ||
| Ханджа | Рассчитать- Арифметическое дерево | ||
| |||
| Японское имя | |||
| Кандзи | Арифметическое дерево Рассчитать | ||
| Хирагана | Санги Санчу | ||
| |||
Счетные стержни (筭) представляют собой небольшие бруски, обычно длиной 3–14 см (от 1 до 6 дюймов), которые использовались математиками для вычислений в древней Восточной Азии . Они размещаются горизонтально или вертикально для обозначения любого целого или рационального числа .
Письменные формы, основанные на них, называются стержневыми числительными . Это настоящая позиционная система счисления с цифрами от 1 до 9 и пробелом для 0, относящаяся к периоду Воюющих государств (около 475 г. до н.э.). [1] до 16 века.
История [ править ]
Китайские арифметики использовали счетные палочки более двух тысяч лет назад.
В 1954 году сорок с лишним счетных стержней периода Воюющих царств (5 век до н. э. – 221 г. до н. э.) были найдены в могиле № 15 Цзуцзягуншань (左家公山) Чу в Чанше , провинция Хунань . [2] [ не удалось пройти проверку ] [3] [ нужна цитата для проверки ]
В 1973 году археологи обнаружили в гробнице в Хубэе несколько деревянных надписей, датируемых периодом династии Хань (206 г. до н. э. — 220 г. н. э.). На одной из деревянных рукописей было написано: «当利二月定算𝍥». [ нужна ссылка ] Это один из самых ранних примеров использования счетных стержней в письменной форме.
Квадратная лаковая шкатулка, датируемая ок. 168 г. до н. э., содержащая квадратную шахматную доску с узорами TLV, шахматные фигуры, счетные стержни и другие предметы, была раскопана в 1972 году в Мавандуи M3, Чанша, провинция Хунань. [4] [5]
была обнаружена связка счетных стержней эпохи Западной Хань (202 г. до н. э. — 9 г. н. э.), сделанных из костей В 1976 году в округе Цяньян в провинции Шэньси . [6] [7] Использование счетных стержней должно было предшествовать этому; Сунци ( ок. 544–496 гг . До н.э.), военный стратег конца весеннего и осеннего периода 771 г. до н.э. – 5 в. до н.э., упоминает их использование для расчетов для победы в войнах перед вступлением в битву; [8] Лао-цзы (умер в 531 г. до н.э.), писавший в период Воюющих царств, сказал, что «хороший калькулятор не использует счетные стержни». [9] В «Книге Хань » (завершенной в 111 г. н.э.) записано: «Они рассчитывают с помощью бамбука диаметром один фен и длиной шесть цуней, сложенного в шестиугольный пучок из двухсот семидесяти одной части». [10]
Сначала счетные стержни были круглыми в поперечном сечении, но ко времени династии Суй (581–618 гг. н.э.) математики использовали треугольные стержни для обозначения положительных чисел и прямоугольные стержни для отрицательных чисел . [ нужна ссылка ]

После того, как счеты процветали [ когда? ] От счетных палочек отказались, за исключением Японии, где цифры на палочках превратились в символическое обозначение алгебры .
Использование счетных стержней [ править ]




Счетные палочки обозначают цифры по количеству палочек, а перпендикулярная палочка — пять. Чтобы избежать путаницы, попеременно используются вертикальные и горизонтальные формы. написано, Обычно вертикальные стержневые числа используются для обозначения позиций единиц, сотен, десятков тысяч и т. д., тогда как горизонтальные стержневые числа используются для десятков, тысяч, сотен тысяч и т. д. В Суньцзы Суаньцзин что «один вертикальен, десять — горизонтально». [11]
Красные стержни представляют положительные числа , а черные стержни представляют отрицательные числа . [12] Древние китайцы ясно понимали отрицательные числа и ноль (оставляя для него пустое место), хотя у них не было символа для последнего. В «Девяти главах математического искусства », которые в основном были написаны в первом веке нашей эры, говорилось: «(при использовании вычитания) вычитайте числа с одинаковым знаком, складывайте числа с разными знаками, вычитайте положительное число из нуля, чтобы получить отрицательное число, и вычитайте число отрицательное число от нуля до положительного числа». [13] [14] Позже камень го иногда использовался для обозначения нуля.
Такое чередование формы вертикальных и горизонтальных стержневых цифр очень важно для правильного понимания письменной транскрипции стержневых цифр в рукописях. Например, в Личэн суаньцзинь число 81 транскрибировалось как ![]()
![]() , а 108 транскрибировалось как
, а 108 транскрибировалось как ![]()
![]() ; ясно, что последний явно имел на «счетной доске» (т. е. полу или коврике) пустой ноль, хотя в письменной транскрипции пробела не было. В той же рукописи число 405 было записано как
; ясно, что последний явно имел на «счетной доске» (т. е. полу или коврике) пустой ноль, хотя в письменной транскрипции пробела не было. В той же рукописи число 405 было записано как ![]()
![]() , с пробелом между ними по понятным причинам и никоим образом не может быть интерпретировано как «45».
, с пробелом между ними по понятным причинам и никоим образом не может быть интерпретировано как «45». ![]()
![]() . Другими словами, записанные стержневые цифры могут быть не позиционными, но на счетной доске они позиционные.
. Другими словами, записанные стержневые цифры могут быть не позиционными, но на счетной доске они позиционные. ![]()
![]() представляет собой точное изображение счетной палочки номер 405 на столешнице или полу.
представляет собой точное изображение счетной палочки номер 405 на столешнице или полу.
Значение места [ править ]
Значение числа зависит от его физического положения на счетной доске. Цифра 9 в крайнем правом положении на доске соответствует цифре 9. Перемещение группы палочек, обозначающих 9, на одну позицию влево (т. е. на позицию десятков) дает 9[] или 90. Снова сдвиг влево на третью позицию (к разряду десятков). разряд сотен) дает 9[][] или 900. Каждый раз, когда кто-то сдвигает позицию номера один влево, он умножается на 10. Каждый раз, когда кто-то сдвигает позицию номер один вправо, он делится на 10. Это применимо к однозначным или многозначным числам.
Математик династии Сун Цзя Сянь использовал рукописные китайские десятичные порядки с шагом десятьсот миллионов в качестве разрядного значения стержневого числа, как видно из факсимиле со страницы Энциклопедии Юнлэ . Он расположил семьдесят одну тысячу восемьсот двадцать четыре как.
- 71824
- Тысячи шагов
Он рассматривал китайские порядковые номера как маркеры разрядного значения, а 七一八二四 стал десятичным числом разрядного значения. Затем он написал стержневые цифры в соответствии с их порядковым значением:
| Семь | один | восемь | два | Четыре |
|---|---|---|---|---|
| Десять тысяч | тысяча | сто | десять | шаг |
В Японии математики клали счетные стержни на счетную доску — лист ткани с сетками и использовали только вертикальные формы, опираясь на сетки. В японском учебнике математики XVIII века есть диаграмма шахматной счетной доски с символами порядка величин «千百十一分厘毛» (тысяча, сто, десять, единица, десятая, сотая, тысячная). [15]
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Вертикальный | ||||||||||
| Горизонтальный |
| 0 | −1 | −2 | −3 | −4 | −5 | −6 | −7 | −8 | −9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Вертикальный | ||||||||||
| Горизонтальный |
Примеры:
| 231 | ||||
|---|---|---|---|---|
| 5089 | ||||
| −407 | ||||
| −6720 |
Стержневые цифры [ править ]
Стержневые цифры представляют собой позиционную систему счисления, состоящую из форм счетных стержней. Положительные числа записываются такими, какие они есть, а отрицательные числа записываются с наклонной чертой у последней цифры. Вертикальная черта в горизонтальных формах 6–9 делается короче, чтобы иметь ту же высоту символов.
Круг (〇) используется для обозначения 0. Многие историки полагают, что он был импортирован из индийских цифр Гаутамой Сиддхом в 718 году. [13] но некоторые думают, что он был создан из китайского заполнителя текстового пространства «□», а другие думают, что индийцы приобрели его из Китая, потому что он напоминает конфуцианский философский символ, обозначающий «ничего». [16]
В 13 веке математики Южной Сун заменили цифры на 4, 5 и 9, чтобы уменьшить количество штрихов. [16] Новые горизонтальные формы в конечном итоге трансформировались в цифры Сучжоу . Японцы продолжали использовать традиционные формы.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Вертикальный | ||||||||||
| Горизонтальный |
| 0 | −1 | −2 | −3 | −4 | −5 | −6 | −7 | −8 | −9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Вертикальный | ||||||||||
| Горизонтальный |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Вертикальный | ||||||||||
| Горизонтальный |
Примеры:
| Традиционный | Южная песня | |
|---|---|---|
| 231 | ||
| 5089 | ||
| −407 | ||
| −6720 |
В Японии Сэки Такакадзу превратил стержневые цифры в символические обозначения алгебры и радикально усовершенствовал японскую математику . [13] После его периода была разработана позиционная система счисления с использованием китайских числовых символов , а стержневые цифры использовались только для знаков плюс и минус .
| западный | Секи | После Секи |
|---|---|---|
| х + у + 246 | ||
| 5 х - 6 лет | ||
| 7 ху | ||
| 8 раз / год | Н/Д | Второй |
Дроби [ править ]
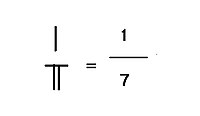
Дробь выражалась стержневыми цифрами в виде двух стержневых цифр, расположенных одна над другой (без какого-либо другого символа, как современная горизонтальная черта).
Стержневое исчисление [ править ]
Метод использования счетных стержней для математических расчетов назывался стержневым расчетом или стержневым исчислением (筹算). Стержневое исчисление можно использовать для широкого спектра вычислений, включая нахождение значения π , нахождение квадратных корней , кубических корней или корней более высокого порядка , а также решение системы линейных уравнений .
До введения письменного нуля для обозначения отсутствия единиц использовался пробел, а также был принят поворот символа в следующем столбце единиц на 90 °, чтобы уменьшить двусмысленность в записываемых значениях, рассчитанных на стержнях. [17] Например, 107 (𝍠 𝍧) и 17 (𝍩𝍧) будут различаться вращением, хотя несколько нулевых единиц могут привести к двусмысленности, например. 1007 (𝍩 𝍧) и 10007 (𝍠 𝍧). Как только в игру вступил письменный ноль, стержневые цифры стали независимыми, и их использование действительно пережило счетные стержни после их замены счетами . Один из вариантов горизонтальных стержневых цифр, цифры Сучжоу до сих пор используются для ведения бухгалтерского учета и в рецептах фитотерапии в китайских кварталах в некоторых частях мира.
Юникод [ править ]
Unicode 5.0 включает цифры счетных стержней в отдельный блок в дополнительной многоязычной плоскости (SMP) от U+1D360 до U+1D37F. Кодовые точки для горизонтальных цифр 1–9 — от U+1D360 до U+1D368, а кодовые точки для вертикальных цифр 1–9 — от U+1D369 до U+1D371. Первые называются единицами , вторые - десятками . [18] [19] что противоречит соглашению, описанному выше. Стандарт Unicode гласит, что ориентация символов Unicode соответствует соглашению династии Сун, которое отличается от практики династии Хань, которая представляла цифры в виде вертикальных линий, а десятки - в виде горизонтальных линий. [20] Ноль должен быть представлен U+3007 (〇, идеографическое число ноль), а отрицательный знак должен быть представлен U+20E5 (сочетание наложения обратной косой черты). [21] Поскольку они были недавно добавлены в набор символов и включены в SMP, поддержка шрифтов все еще может быть ограничена.
| Подсчет стержневых цифр [1] [2] Официальная таблица кодов Консорциума Unicode (PDF) | ||||||||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | А | Б | С | Д | И | Ф | |
| U + 1D36x | 𝍠 | 𝍡 | 𝍢 | 𝍣 | 𝍤 | 𝍥 | 𝍦 | 𝍧 | 𝍨 | 𝍩 | 𝍪 | 𝍫 | 𝍬 | 𝍭 | 𝍮 | 𝍯 |
| U + 1D37x | 𝍰 | 𝍱 | 𝍲 | 𝍳 | 𝍴 | 𝍵 | 𝍶 | 𝍷 | 𝍸 | |||||||
| Примечания | ||||||||||||||||
См. также [ править ]
Ссылки [ править ]
- ^ Лей-Йонг, Лам (1986). «Концептуальное происхождение нашей системы счисления и символической формы алгебры» . Архив истории точных наук . 36 (3): 183–195. ISSN 0003-9519 .
- ^ Математика Древнего Китая. Архивировано 26 января 2011 г. в Wayback Machine - Copyright © 2010 - TutorVista.com, Все права защищены.
- ^ Уникальный вычислительный инструмент Китая , заархивировано из оригинала 21 ноября 2007 г. , получено 16 декабря 2007 г.
- ^ ВОНГ, Пуй Инь Марианна (март 2006 г.). «Силин (четыре основных животных) в изобразительном искусстве Хань - том 1» (PDF) . СОАС : 370, 416.
- ^ «Блог BabelStone: Потерянная игра Любо, часть 4: Игровые доски и оборудование» . www.babelstone.co.uk . Проверено 05 августа 2020 г.
- ^ Изд. У Вэньцзюня, Большая серия истории китайской математики, том 1, стр. 371
- ^ Лам, Лэй Йонг; Анг, Тянь Се (2004). Мимолетные шаги: прослеживание концепции арифметики и алгебры в древнем Китае . Всемирная научная. ISBN 978-981-256-725-3 .
- ^ Сунь Цзы: Если муж еще не сражался и храм считается победителем, то победителем надо считать больше.
- ^ Лао Цзы: Тем, кто хорошо разбирается в цифрах, не нужно строить планы.
- ^ Чжу, Ивэнь (2018). «Как западные письменные вычисления были внедрены в Китай? — Анализ «Тунвэнь суаньчжи» (Руководство по арифметике на общем языке, 1613 г.)» . Исследовательские ворота . Проверено 05 августа 2020 г.
- ↑ Китайский викиисточник Сутра Сунь Цзы: Сначала узнайте положение: один из десяти горизонталей, сотни стоят и тысячи стоят, тысячи и десять смотрят друг на друга, и десятки тысяч равны.
- ^ Китайский Wikisource , письменный доклад Мэнси: Например, алгоритм использует красные и черные фишки, чтобы различать положительные и отрицательные числа.
- ^ Jump up to: Перейти обратно: а б с Ван, Цинсян (1999), Санги о коэта отоко (Человек, который превзошел счетные палочки) , Токио: Тойо Сётэн, ISBN 4-88595-226-3
- ^ Китайский Wikisource Искусство позитива и негатива гласит: одни и те же имена разделяют друг друга, разные имена приносят друг другу пользу, позитив не входит в негатив, а негатив не входит в позитив. Их разные имена исключают друг друга, и те, у кого одно и то же имя, приносят пользу друг другу. То, что правильно, не переходит в правильное, а отрицательное не переходит в отрицательное.
- ^ Карл Меннингер , Числовые слова и числовые символы, стр. 369, MIT Press, 1970.
- ^ Jump up to: Перейти обратно: а б Цянь, Баосун (1964), Чжунго Шусюэ Ши (История китайской математики) , Пекин: Кексюэ Чубанше
- ^ «Китайские цифры» . История математики . Проверено 28 апреля 2024 г.
- ^ Кристофер Каллен и Джон Х. Дженкинс, Предложение добавить китайские цифры на счетных стержнях в Unicode и ISO / IEC 10646 , 2004 г.
- ^ Стандарт Юникод, версия 5.0 – Электронное издание (PDF) , Unicode, Inc., 2006, стр. 558
- ^ Стандарт Unicode, версия 15.0 – электронное издание (PDF) , Unicode, Inc., 2022 г., стр. 869–870.
- ^ Стандарт Unicode, версия 5.0 – Электронное издание (PDF) , Unicode, Inc., 2006, стр. 499–500.
Внешние ссылки [ править ]
Чтобы увидеть древние счетные стержни и получить дополнительные объяснения, вы можете посетить сайты
- https://web.archive.org/web/20010217175749/http://www.math.sfu.ca/histmath/China/Beginning/Rod.html
- http://mathforum.org/library/drmath/view/52557.html
- Счетные палочки в Китае (на китайском языке) ( Перевести на английский: Google , Bing , Yandex )
- Счетные палочки и камни японского математика около 1872 года (на японском языке) ( Перевести на английский: Google , Bing , Yandex )