Квадратное уравнение

В математике квадратное уравнение (из латинского квадратуса « квадрат ») - это уравнение , которое можно переставить в стандартной форме, как ^{[ 1 ]} $ax^{2}+bx+c=0\,,$ где $x$ представляет неизвестное значение, а $A$ , $B$ и $C$ представляют известные числа, где $a ↓ 0$ . (Если $a = 0$ и $b \neq 0,$ то уравнение линейное , а не квадратичное.) Числа $A$ , $B$ и $C$ являются коэффициентами уравнения и могут быть различны, вызывая их, квадратичный коэффициент , линейный коэффициент и постоянный коэффициент или свободный термин . ^{[ 2 ]}

Значения $x$ называются решениями уравнения, а корни или нули выражения , которые удовлетворяют уравнению , на левой стороне. Квадратное уравнение имеет не более двух решений. Если есть только одно решение, одно говорит, что это двойной корень . Если все коэффициенты являются реальными числами , существуют либо два реальных решения, либо единый настоящий двойной корень, либо два сложных решения, которые являются сложными конъюгатами друг друга. Квадратное уравнение всегда имеет два корня, если комплексные корни включены, и двойной корень подсчитывается на двоих. Квадратное уравнение может быть учтено в эквивалентное уравнение ^{[ 3 ]} $ax^{2}+bx+c=a(x-r)(x-s)=0$ где $r$ и $s$ являются решения для $x$ .

Квадратичная формула $x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}$ выражает решения с точки $A$ , $B$ и $C.$ зрения Завершение квадрата является одним из нескольких способов получения формулы.

Решения проблем, которые могут быть выражены с точки зрения квадратичных уравнений, были известны уже в 2000 году до нашей эры. ^{[ 4 ]}^{[ 5 ]}

Поскольку квадратное уравнение включает в себя только один неизвестный, оно называется « одномерным ». Квадратное уравнение содержит только силы x $,$ которые являются неотрицательными целыми числами, и, следовательно, это полиномиальное уравнение . В частности, это полиномиальное уравнение второй степени , так как величайшая сила-две.

Решение квадратичного уравнения

Квадратное уравнение с реальными или сложными коэффициентами имеет два решения, называемые корнями . Эти два решения могут быть или не быть различными, и они могут быть или не быть реальными.

Факторинг по проверке

Может быть возможно выразить квадратичное уравнение $топор 2 + bx + c = 0$ как продукт $(px + q) (Rx + s) = 0$ . В некоторых случаях можно при простой проверке, чтобы определить значения P , Q , R и S , которые делают две формы эквивалентны друг другу. Если квадратное уравнение записано во второй форме, то «свойство нулевого фактора» утверждает, что квадратное уравнение выполнено, если $Px + Q = 0$ или $Rx + S = 0$ . Решение этих двух линейных уравнений обеспечивает корни квадратичного.

Для большинства студентов факторинг с помощью проверки является первым методом решения квадратичных уравнений, на которые они подвергаются. ^{[ 6 ]}^{: 202–207} Если одно издается квадратичное уравнение в форме $x 2 + bx + c = 0$ , востребованная факторизация имеет форму $(x + q) (x + s)$ , и нужно найти два числа $q$ и $s$ , которые добавляют к $B$ и чей продукт $C$ (это иногда называют » Правило Вьете " ^{[ 7 ]} и связан с формулами Вьете ). В качестве примера $x 2 + 5 x + 6$ факторов как $(x + 3) (x + 2)$ . Более общий случай, когда $A$ не равняется $1,$ может потребовать значительных усилий в пробных и ошибках, предполагая, что это может быть вообще учитывать при проверке.

За исключением особых случаев, таких как $B = 0$ или $C = 0$ , факторинг по проверке работает только для квадратичных уравнений, которые имеют рациональные корни. Это означает, что подавляющее большинство квадратичных уравнений, возникающих в практических приложениях, не может быть решено путем факторинга путем проверки. ^{[ 6 ]}^: 207

Завершая квадрат

Рисунок 2 иллюстрирует график XY квадратичной функции f x равен x квадрат минус x минус 2. координата x точек, где график пересекает ось x, x равно -1 и x равно 2, являются растворами Квадратное уравнение x квадрат минус X минус 2 равняется нулю. — Рисунок 2. Для квадратичной функции $y = x 2 -x, -2$ , точки, где график пересекает $ось x$ , $x = -1$ и $x = 2$ являются решения квадратичного уравнения $x 2 - x - 2 = 0$ .

Процесс завершения квадрата использует алгебраическую идентичность $x^{2}+2hx+h^{2}=(x+h)^{2},$ который представляет четко определенное алгоритм , который можно использовать для решения любого квадратичного уравнения. ^{[ 6 ]}^: 207 Начиная с квадратичного уравнения в стандартной форме, $AX 2 + bx + c = 0$

Разделите каждую сторону на $коэффициент$ квадратного термина.
Вычтите постоянный член $C / A$ с обеих сторон.
Добавьте квадрат половины $B / A$ , коэффициент $x$ , к обеим сторонам. Это «завершает квадрат», превращая левую сторону в идеальный квадрат.
Напишите левую сторону как квадрат и упростите правую сторону, если это необходимо.
Получить два линейных уравнения, приравнивая квадратный корень левой стороны с положительными и отрицательными квадратными корнями правой стороны.
Решите каждое из двух линейных уравнений.

Мы иллюстрируем использование этого алгоритма, решая $2 x 2 + 4 x - 4 = 0$ $2x^{2}+4x-4=0$ $\ x^{2}+2x-2=0$ $\ x^{2}+2x=2$ $\ x^{2}+2x+1=2+1$ $\left(x+1\right)^{2}=3$ $\ x+1=\pm {\sqrt {3}}$ $\ x=-1\pm {\sqrt {3}}$

Символ плюс -минуса «±» указывает, что как $x = -1 + \sqrt 3$ , так и $x = -1 - \sqrt 3$ являются растворами квадратичного уравнения. ^{[ 8 ]}

Квадратичная формула и ее вывод

Завершение квадрата может использоваться для получения общей формулы для решения квадратичных уравнений, называемой квадратичной формулой. ^{[ 9 ]} Математическое доказательство теперь будет кратко суммировано. ^{[ 10 ]} можно легко увидеть Полиномиальным расширением , что следующее уравнение эквивалентно квадратичному уравнению: $\left(x+{\frac {b}{2a}}\right)^{2}={\frac {b^{2}-4ac}{4a^{2}}}.$ Принимая квадратный корень с обеих сторон и изолируя $x$ , дает: $x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}.$

Некоторые источники, особенно более старые, используют альтернативные параметризации квадратичного уравнения, такие как $AX 2 + 2 bx + c = 0$ или $топор 2 - 2 bx + c = 0$ , ^{[ 11 ]} где $B$ имеет величину половину более распространенной, возможно, с противоположным знаком. Это приводит к немного разным формам для решения, но в противном случае эквивалентны.

ряд альтернативных производных В литературе можно найти . Эти доказательства проще, чем стандартный, заполняющий квадратный метод, представляют собой интересные приложения других часто используемых методов в алгебре или дают представление о других областях математики.

Менее известная квадратичная формула, используемая в методе Мюллера , обеспечивает те же корни через уравнение $x={\frac {2c}{-b\pm {\sqrt {b^{2}-4ac}}}}.$ Это может быть выведено из стандартной квадратичной формулы с помощью формул Vieta что продукт корней составляет $C / A.$ , которые утверждают , Это также следует от деления квадратного уравнения на $x^{2}$ дающий $cx^{-2}+bx^{-1}+a=0,$ Решение этого для $x^{-1},$ а затем инвертирование.

Одним из свойств этой формы является то, что он дает один действительный корень, когда $a = 0$ , в то время как другой корень содержит деление на ноль, потому что, когда $a = 0$ , квадратное уравнение становится линейным уравнением, которое имеет один корень. Напротив, в этом случае более распространенная формула имеет разделение на ноль для одного корня и неопределенную форму $0/0$ для другого корня. С другой стороны, когда $C = 0$ , более распространенная формула дает два правильных корня, тогда как эта форма дает нулевой корень и неопределенную форму $0/0$ .

Когда ни $A,$ ни $C$ не являются нулевыми, равенство между стандартной квадратичной формулой и методом Мюллера, ${\frac {2c}{-b-{\sqrt {b^{2}-4ac}}}}={\frac {-b+{\sqrt {b^{2}-4ac}}}{2a}}\,,$ может быть подтверждено перекрестным умножением , а также для другого выбора знаков.

Уменьшенное квадратное уравнение

Иногда удобно уменьшить квадратное уравнение, чтобы его ведущий коэффициент был одним. Это делается путем деления обеих сторон на $A$ , что всегда возможно, так как $A$ не нулевой. Это создает уменьшенное квадратное уравнение : ^{[ 12 ]}

$x^{2}+px+q=0,$

где $p = b / a$ и $q = c / a$ . Это моническое полиномиальное уравнение имеет те же решения, что и оригинал.

Квадратичная формула для решений уменьшенного квадратного уравнения, написанная в терминах его коэффициентов, $x=-{\frac {p}{2}}\pm {\sqrt {\left({\frac {p}{2}}\right)^{2}-q}}\,.$

Дискриминант

В квадратичной формуле выражение под квадратным корневым знаком называется дискриминантом квадратичного уравнения и часто представляется с использованием верхнего случая $D$ или греческой дельты верхнего чехла : ^{[ 13 ]} $\Delta =b^{2}-4ac.$ Квадратное уравнение с реальными коэффициентами может иметь либо одну или два различных настоящих корня или два различных сложных корня. В этом случае дискриминант определяет количество и природу корней. Есть три случая:

Если дискриминант положительный, то есть два различных корня ${\frac {-b+{\sqrt {\Delta }}}{2a}}\quad {\text{and}}\quad {\frac {-b-{\sqrt {\Delta }}}{2a}},$ Оба из которых являются реальными числами. Для квадратных уравнений с рациональными коэффициентами, если дискриминантом является квадратным числом , то корни рациональны - в других случаях они могут быть квадратичными иррациональными .
Если дискриминант равен нулю, то есть ровно один настоящий корень $-{\frac {b}{2a}},$ иногда называют повторяющимся или двойным корнем или двумя равными корнями.
Если дискриминант негативно, то нет настоящих корней. Скорее, есть два различных (нереальных) сложных корнях ^{[ 14 ]} $-{\frac {b}{2a}}+i{\frac {\sqrt {-\Delta }}{2a}}\quad {\text{and}}\quad -{\frac {b}{2a}}-i{\frac {\sqrt {-\Delta }}{2a}},$ которые являются сложными конъюгатами друг друга. В этих выражениях $я$ воображаемая единица .

Таким образом, корни различны, если и только тогда, когда дискриминант ненулевой, и корни реальны, если и только тогда, когда дискриминант неотрицательный.

Геометрическая интерпретация

Функция $f (x) = ax 2 + bx + c$ - квадратичная функция . ^{[ 16 ]} График любой квадратичной функции имеет ту же общую форму, которая называется параболой . Местоположение и размер параболы, а также от того, как она открывается, зависят от $A$ , $B$ и $C.$ значений Если $a > 0$ , парабола имеет минимальную точку и открывается вверх. Если $< 0$ , парабола имеет максимальную точку и открывается вниз. Чрезвычайная точка параболы, как минимум или максимум, соответствует его вершине . X $в$ -координата вершины будет расположена $\scriptstyle x={\tfrac {-b}{2a}}$ и $y$ -координата вершины может быть найдена путем замены этого $x$ -значения в функцию. Y $,$ -интерцепт находится в точке $(0 C)$ .

Решения $AX квадратичного уравнения 2 + bx + c = 0$ соответствует корням функции $f (x) = ax 2 + bx + c$ , поскольку они являются значениями $x,$ для которых $f (x) = 0$ . Если $A$ , $B$ и $C$ являются реальными числами , а домен F $-$ это набор реальных чисел, то корни $F$ являются именно $X$ - координатами точек, где график касается $оси x$ . Если дискриминант положительный, график касается $x$ оси в двух точках; Если ноль, график касается в одной точке; И если отрицательный, график не касается $оси x$ .

Квадратичная факторизация

Термин $x-r$ является фактором полинома $ax^{2}+bx+c$ Если и только тогда, когда $r$ является корнем квадратного уравнения $ax^{2}+bx+c=0.$ Это следует из квадратичной формулы, которая $ax^{2}+bx+c=a\left(x-{\frac {-b+{\sqrt {b^{2}-4ac}}}{2a}}\right)\left(x-{\frac {-b-{\sqrt {b^{2}-4ac}}}{2a}}\right).$ В специальном случае $B 2 = 4 ac$ , где квадратичный имеет только один отдельный корень ( то есть дискриминант равен нулю), квадратичный многочлен может быть учтено как $ax^{2}+bx+c=a\left(x+{\frac {b}{2a}}\right)^{2}.$

Графическое решение

Квадратичная функция без реального корня: y = ( x - 5) ² + 9 . «3» -воображаемая часть X -интерцепта. Реальная часть -это x -координата вершины. Таким образом, корни 5 ± 3 i .

Решения квадратичного уравнения $ax^{2}+bx+c=0$ может быть выведен из графика квадратичной функции $f(x)=ax^{2}+bx+c,$ которая является параболой .

Если парабола пересекает $оси x$ в двух точках, есть два настоящих корня , которые являются $x$ -координатами этих двух точек (также называемых $x$ -терцепт).

Если парабола касается оси $x$ , существует двойной корень, который представляет собой $x$ -координату точки контакта между графом и параболой.

Если парабола не пересекает $оси x$ , существуют два сложных сопряженных корня. Хотя эти корни не могут быть визуализированы на графике, их реальные и воображаемые части могут быть. ^{[ 17 ]}

Пусть $H$ и $K$ будут соответственно $x$ -координата и $y$ -координата вершины параболы (то есть точка с максимальным или минимальным $Y$ -координатом. Квадратичная функция может быть переписана $y=a(x-h)^{2}+k.$ Пусть $D$ -расстояние между точкой $y$ -координата $2 K$ на оси параболы, и точкой на параболе с одинаковой $Y$ -координат (см. Рисунок; есть две такие точки, которые дают одинаковое расстояние, из -за симметрии параболы). Тогда реальная часть корней - $H$ , а их воображаемая часть - $\pm d$ . То есть корни $h+id\quad {\text{and}}\quad h-id,$ или в случае примера рисунка $5+3i\quad {\text{and}}\quad 5-3i.$

Избегание потери значимости

Хотя квадратичная формула обеспечивает точное решение, результат не является точным, если реальные числа аппроксимированы во время вычисления, как обычно в численном анализе , где реальные числа аппроксимируются с помощью номеров с плавающими темпами (называемыми «реальными» во многих языках программирования ). В этом контексте квадратичная формула не является полностью стабильной .

Это происходит, когда корни имеют другой порядок , или, эквивалентно, когда $б 2$ и $б 2 - 4 AC$ близки по величине. В этом случае вычитание двух почти равных чисел приведет к потере значимости или катастрофической отмене в меньшем корне. Чтобы избежать этого, корень, который меньше по величине, $r$ , может быть рассчитан как $(c/a)/R$ где $r$ - корень, который больше по величине. Это эквивалентно использованию формулы

$x={\frac {-2c}{b\pm {\sqrt {b^{2}-4ac}}}}$

Использование знака плюс, если $b>0$ и знак минус, если $b<0.$

Вторая форма отмены может произойти между терминами $B 2$ и $4 AC$ дискриминанта, это когда два корня очень близки. Это может привести к потере до половины правильных значительных цифр в корнях. ^{[ 11 ]}^{[ 18 ]}

Примеры и приложения

Золотое соотношение обнаруживается как положительное решение квадратичного уравнения $x^{2}-x-1=0.$

Уравнения круга и других конических секций - эллипсы , параболы и гиперболы - имеют квадратичные уравнения в двух переменных.

Учитывая косинус или синус угла, поиск косинуса или синуса угла, который вдвое меньше, включает в себя решение квадратного уравнения.

Процесс упрощения выражений с участием квадратного корня выражения, включающего квадратный корень другого выражения, включает в себя поиск двух решений квадратного уравнения.

Теорема Декарта утверждает, что за каждые четыре поцелуя (взаимно касательные) круги их радиусы удовлетворяют конкретному квадратичному уравнению.

Уравнение, данное теоремой Фуса , давая связь между радиусом двухстороннего вписанного круга , радиус его ограниченного круга и расстояние между центрами этих кругов может быть выражено как квадратичное уравнение, для которого Расстояние между центрами двух кругов с точки зрения их радиусов является одним из решений. Другое решение того же уравнения с точки зрения соответствующих радиусов дает расстояние между центральным центром круга и центром экскурсий бывшего четырехугольника впаривания .

Критические точки и кубической функции точек перегиба квартирной функции обнаруживаются путем решения квадратичного уравнения.

В физике , для движения с постоянным ускорением $a$ , смещение или положение $x$ движущегося тела может быть выражена как функция времени квадратичная $t$ Учитывая начальную позицию $x_{0}$ и начальная скорость $v_{0}$ : ${\textstyle x=x_{0}+v_{0}t+{\frac {1}{2}}at^{2}}$ .

В химии рН основания раствора постоянной слабой кислоты можно рассчитать из логарифма отрицательного -10 положительного корня квадратичного уравнения с точки зрения кислотности и аналитической концентрации кислоты.

История

Вавилонские математики , еще в 2000 году до нашей эры (показанные на старых вавилонских глиняных таблетках ) могут решить проблемы, связанные с участками и сторонами прямоугольников. Существуют доказательства, датируемые этим алгоритмом еще в третьей династии Ур . ^{[ 19 ]} В современных обозначениях проблемы, обычно связанные с решением пары одновременных уравнений формы: $x+y=p,\ \ xy=q,$ что эквивалентно утверждению, что $x$ и $y$ являются корнями уравнения: ^{[ 20 ]}^: 86 $z^{2}+q=pz.$

Шаги, заданные вавилонскими книжниками для решения вышеуказанной проблемы с прямоугольником, с точки зрения $x$ и $y$ , были следующими:

Вычислить половину р .
Квадрат результат.
Вычтите q .
Найдите (положительный) квадратный корень, используя таблицу квадратов.
Соберите результаты шагов (1) и (4), чтобы дать $x$ .

В современной нотации это означает расчет $x={\frac {p}{2}}+{\sqrt {\left({\frac {p}{2}}\right)^{2}-q}}$ , что эквивалентно современной квадратичной формуле для более крупного настоящего корня (если есть) $x={\frac {-b+{\sqrt {b^{2}-4ac}}}{2a}}$ с $a = 1$ , $b = - p$ и $c = q$ .

Геометрические методы были использованы для решения квадратичных уравнений в Вавилонии, Египте, Греции, Китае и Индии. Египетский берлинский папирус , начиная с Среднего Королевства (от 2050 г. до н.э. до 1650 г. до н.э.), содержит решение для двухлетнего квадратного уравнения. ^{[ 21 ]} Вавилонские математики около 400 г. до н.э. и китайские математики из 200 до н.э. использовали геометрические методы рассечения для решения квадратичных уравнений с положительными корнями. ^{[ 22 ]}^{[ 23 ]} Правила для квадратичных уравнений были даны в девяти главах по математическому искусству , китайскому трактату по математике. ^{[ 23 ]}^{[ 24 ]} Эти ранние геометрические методы, по -видимому, не имели общей формулы. Евклид , греческий математик , создал более абстрактный геометрический метод около 300 г. до н.э. С чисто геометрическим подходом Pythagoras и Euclid создали общую процедуру для поиска решений квадратичного уравнения. В своей работе арифметика греческий математик Диофант решил квадратичное уравнение, но дал только один корень, даже когда оба корня были положительными. ^{[ 25 ]}

В 628 г. н.э. Брахмагупта , индийский математик , дал в своей книге Brāhmasphuṭasiddhānta первое явное (хотя и все еще не совсем общее) решение квадратичного уравнения $. 2 + bx = c$ следующим образом: «к абсолютному числу, умноженному в четыре раза выше [коэффициента] квадрата, добавьте квадрат [коэффициента] среднего члена; квадратный корень того же самого, меньше [коэффициент ] Средний термин, разделенный на два раза больше [коэффициента] квадрата - это значение ». ^{[ 26 ]} Это эквивалентно $x={\frac {{\sqrt {4ac+b^{2}}}-b}{2a}}.$ Рукопись Бахшали, написанная в Индии в 7 -м веке нашей эры, содержала алгебраическую формулу для решения квадратичных уравнений, а также линейные неопределенные уравнения (изначально из типа $AX / C = Y$ ). Мухаммед ибн Муса аль-Кхваризми (9-й век) разработал набор формул, которые работали на позитивные решения. Аль-Хваризми идет дальше, предоставляя полное решение общему квадратичному уравнению, принимая один или два численных ответа для каждого квадратичного уравнения, одновременно предоставляя геометрические доказательства в процессе. ^{[ 27 ]} Он также описал метод завершения квадрата и признал, что дискриминант должен быть положительным, ^{[ 27 ]}^{[ 28 ]}^: 230 что было доказано его современным «Абд аль-Хамидом ибн Турком » (Центральная Азия, 9-й век), который дал геометрические фигуры, чтобы доказать, что если дискриминант отрицательный, квадратное уравнение не имеет решения. ^{[ 28 ]}^: 234 В то время как сам аль-Хваризми не принимал негативные решения, более поздние исламские математики , которые сменили его, приняли негативные решения, ^{[ 27 ]}^: 191 а также иррациональные числа как решения. ^{[ 29 ]} Абу Камил Шуджа ибн Аслам (Египет, 10 -й век), в частности, был первым, кто принял иррациональные числа (часто в форме квадратного корня , корня куба или четвертого корня ) в качестве решений квадратичных уравнений или в качестве коэффициентов в уравнении. ^{[ 30 ]} Индийский математик 9 -го века Шридхара записал правила для решения квадратных уравнений. ^{[ 31 ]}

Еврейский математик Авраам Бар Хийя Ха-Наси (12 век, Испания) автором первой европейской книги, включающей полное решение общего квадратичного уравнения. ^{[ 32 ]} Его решение было в значительной степени основано на работе Аль-Хваризми. ^{[ 27 ]} Написание китайского математика Ян Хуи (1238–1298 гг. Н.) является первым известным, в котором появляются квадратичные уравнения с негативными коэффициентами «x», хотя он приписывает это более ранним Лю Йи . ^{[ 33 ]} К 1545 году Джероламо Кардано собрал работы, связанные с квадратичными уравнениями. Квадратичная формула, покрывающая все случаи, была впервые получена Саймоном Стевином в 1594 году. ^{[ 34 ]} В 1637 году René Decartes опубликовал La Géométrie, содержащую квадратичную формулу в той форме, которую мы знаем сегодня.

Расширенные темы

Альтернативные методы расчета корня

Формулы места

Формулы Вьете (названные в честь Франсуа Вейте ) являются отношениями $x_{1}+x_{2}=-{\frac {b}{a}},\quad x_{1}x_{2}={\frac {c}{a}}$ между корнями квадратичного полинома и его коэффициентами. Они являются результатом сравнения термина по термину отношения $\left(x-x_{1}\right)\left(x-x_{2}\right)=x^{2}-\left(x_{1}+x_{2}\right)x+x_{1}x_{2}=0$ с уравнением $x^{2}+{\frac {b}{a}}x+{\frac {c}{a}}=0.$

Первая формула Vieta полезна для графика квадратичной функции. Поскольку график симметричен относительно вертикальной линии через вершину -координата вершины $, x$ расположена со средним значением корней (или перехватов). Таким образом, $x$ -координата вершины $x_{V}={\frac {x_{1}+x_{2}}{2}}=-{\frac {b}{2a}}.$ -координата $Y$ может быть получена путем замены вышеупомянутого результата в данное квадратичное уравнение, давая $y_{V}=-{\frac {b^{2}}{4a}}+c=-{\frac {b^{2}-4ac}{4a}}.$ Кроме того, эти формулы для вершины могут быть выведены непосредственно из формулы (см. Завершение квадрата ) $ax^{2}+bx+c=a\left(x+{\frac {b}{2a}}\right)^{2}-{\frac {b^{2}-4ac}{4a}}.$

Для численных вычислений формулы Vieta обеспечивают полезный метод для поиска корней квадратичного уравнения в случае, когда один корень намного меньше, чем другой. Если $| x 2 | << | x 1 |$ , затем $x 1 + x 2 \approx x 1$ , и мы имеем оценку: $x_{1}\approx -{\frac {b}{a}}.$ Формула второй Vieta предоставляет: $x_{2}={\frac {c}{ax_{1}}}\approx -{\frac {c}{b}}.$ Эти формулы гораздо проще оценить, чем квадратичная формула при условии одного большого и одного маленького корня, потому что квадратичная формула оценивает небольшой корень как разницу двух почти равных чисел (случай большого $B$ ), который вызывает круглый -Ошибка в численной оценке. На рисунке показана разница между ^{[ нужно разъяснения ]} (i) Прямая оценка с использованием квадратичной формулы (точной, когда корни находятся рядом друг с другом по значению) и (ii) оценка, основанная на вышеуказанном приближении формул Vieta (точные, когда корни широко расставлены). По мере увеличения линейного коэффициента $B$ , первоначально квадратичная формула является точной, а приблизительная формула повышает точность, что приводит к меньшей разнице между методами с $B.$ увеличением Однако в какой -то момент квадратичная формула начинает терять точность из -за ошибки, в то время как приблизительный метод продолжает улучшаться. Следовательно, разница между методами начинает увеличиваться, поскольку квадратичная формула становится хуже и хуже.

Эта ситуация обычно возникает в конструкции усилителей, где требуются широко разделенные корни, чтобы обеспечить стабильную работу (см. Шаг ответ ).

Тригонометрическое решение

В дни до калькуляторов люди использовали математические таблицы - листы чисел, показывающие результаты расчета с различными аргументами - для упрощения и ускорения вычислений. Таблицы логарифмов и тригонометрических функций были распространены в учебниках по математике и науке. Специализированные таблицы были опубликованы для таких приложений, как астрономия, небесная навигация и статистика. Существовали методы численного приближения, называемые простафаферизом , который предлагал ярлыки вокруг трудоемких операций, таких как умножение и принятие полномочий и корней. ^{[ 35 ]} Астрономы, особенно, были связаны с методами, которые могли бы ускорить длинную серию вычислений, связанных с расчетами небесных механиков .

Именно в этом контексте мы можем понять разработку средств решения квадратичных уравнений с помощью тригонометрической замещения . Рассмотрим следующую альтернативную форму квадратного уравнения,

ax^{2}+bx\pm c=0,

( 1 )

где признак ± символ выбирается так, чтобы $A$ и $C$ могли быть положительными. Заменив

x={\textstyle {\sqrt {c/a}}}\tan \theta

( 2 )

а затем умножение на $cos 2 (θ) / c$ , получаем

\sin ^{2}\theta +{\frac {b}{\sqrt {ac}}}\sin \theta \cos \theta \pm \cos ^{2}\theta =0.

( 3 )

Введение функций $2 θ$ и перестановки, мы получаем

\tan 2\theta _{n}=+2{\frac {\sqrt {ac}}{b}},

( 4 )

\sin 2\theta _{p}=-2{\frac {\sqrt {ac}}{b}},

( 5 )

где подписки $N$ и $P$ соответственно соответственно, с использованием отрицательного или положительного знака в уравнении [1] . Заменить два значения $θ N$ или $θ P,$ найденные из уравнений [4] или [5] в [2], дает необходимые корни [1] . Сложные корни встречаются в решении, основанном на уравнении [5], если абсолютное значение $SIN 2 θ P$ превышает единство. Количество усилий, связанных с решением квадратичных уравнений с использованием этой смешанной тригонометрической и логарифмической стратегии поиска таблиц, составило две трети усилий с использованием только логарифмических таблиц. ^{[ 36 ]} Расчет сложных корней потребует использования другой тригонометрической формы. ^{[ 37 ]}

Чтобы проиллюстрировать, давайте предположим, что у нас были доступны логарифм и тригонометрические таблицы с семью местами, и хотелось бы решить следующую точность шестизначной фигуры: $4.16130x^{2}+9.15933x-11.4207=0$

В семи местах таблица поиска может иметь только 100 000 записей, а вычисление промежуточных результатов для семи мест, как правило, потребует интерполяции между соседними записями.
$\log a=0.6192290,\log b=0.9618637,\log c=1.0576927$
$2{\sqrt {ac}}/b=2\times 10^{(0.6192290+1.0576927)/2-0.9618637}=1.505314$
$\theta =(\tan ^{-1}1.505314)/2=28.20169^{\circ }{\text{ or }}-61.79831^{\circ }$
$\log |\tan \theta |=-0.2706462{\text{ or }}0.2706462$
$\log {\textstyle {\sqrt {c/a}}}=(1.0576927-0.6192290)/2=0.2192318$
$x_{1}=10^{0.2192318-0.2706462}=0.888353$ (округлен до шести важных цифр) $x_{2}=-10^{0.2192318+0.2706462}=-3.08943$

Решение для сложных корней в полярных координатах

Если квадратное уравнение $ax^{2}+bx+c=0$ с реальными коэффициентами имеет два сложных корня - случай, где $b^{2}-4ac<0,$ Требование A и C имело тот же знак, что и друг друга - затем решения для корней могут быть выражены в полярной форме, как и ^{[ 38 ]}

$x_{1},\,x_{2}=r(\cos \theta \pm i\sin \theta ),$

где $r={\sqrt {\tfrac {c}{a}}}$ и $\theta =\cos ^{-1}\left({\tfrac {-b}{2{\sqrt {ac}}}}\right).$

Геометрическое решение

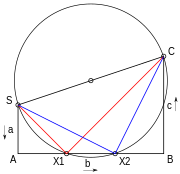
Квадратное уравнение может быть решено геометрически несколькими способами. Одним из способов является метод Лилла . Три коэффициента $A$ , $B$ , $C$ протянуты с прямыми углами между ними, как в SA, AB и BC на рисунке 6. Круг протягивается с начальной и конечной точкой SC в виде диаметра. Если это сокращает среднюю линию AB из трех, то уравнение имеет решение, и растворы даются отрицательными на расстоянии вдоль этой линии от деленного на первый коэффициент $A$ или SA. Если $A$ равен $1,$ коэффициенты могут быть считываются напрямую. Таким образом, растворы в диаграмме являются -Ax1/sa и -ax2/sa. ^{[ 39 ]}

Carlyle Circle из квадратного уравнения x ² - SX + P = 0.

Carlyle Circle , названный в честь Томаса Карлайла , обладает свойством, что решения квадратичного уравнения являются горизонтальными координатами пересечений круга с горизонтальной осью . ^{[ 40 ]} Круги Карлайла использовались для разработки правителей и коммерческих конструкций обычных многоугольников .

Обобщение квадратичного уравнения

Формула и ее вывод остаются правильными, если коэффициенты $A$ , $B$ и $C$ являются комплексными числами , или, в более общем смысле, члены любого поля которого , характеристика не составляет $2$ . (В поле Характеристики 2 элемент $2 A$ равен нулю, и его невозможно разделить.

Символ $\pm {\sqrt {b^{2}-4ac}}$ в формуле следует понимать как «любой из двух элементов, чей $квадрат 2 - 4 ac$ , если такие элементы существуют ». В некоторых полях у некоторых элементов нет квадратных корней, а у некоторых есть два; только ноль имеет только один квадратный корень, за исключением полей характеристики $2.$ Даже если поле не содержит квадратного корня Из некоторого числа всегда есть квадратичное поле расширения , поэтому квадратичная формула всегда будет иметь смысл в качестве формулы в этом поле расширения.

Характеристика 2

В поле Характеристики $2$ квадратичная формула, которая опирается на $2,$ является единицей , не удерживается. Рассмотрим монический квадратичный полином $x^{2}+bx+c$ над поле характеристики $2$ . Если $b = 0$ , то раствор уменьшается для извлечения квадратного корня, поэтому раствор $x={\sqrt {c}}$ И есть только один корень, так как $-{\sqrt {c}}=-{\sqrt {c}}+2{\sqrt {c}}={\sqrt {c}}.$ В итоге, $\displaystyle x^{2}+c=(x+{\sqrt {c}})^{2}.$ См. Квадратичный остаток для получения дополнительной информации об извлечении квадратных корней в конечных полях.

В том случае, если $B ↓ 0$ , есть два различных корня, но если полиномиально не подходит , они не могут быть выражены в терминах квадратных корней чисел в поле коэффициента. Вместо этого определить 2-root $(c) C$ как $r$ корень полинома $x 2 + x + c$ , элемент поля разделения этого полинома. Один проверяет, что $r (c) + 1$ также является корнем. С точки зрения операции с двумя корнями, два корня (немонического) квадратичного $топора 2 + bx + c$ ${\frac {b}{a}}R\left({\frac {ac}{b^{2}}}\right)$ и ${\frac {b}{a}}\left(R\left({\frac {ac}{b^{2}}}\right)+1\right).$

Например, пусть $a$ обозначает мультипликативный генератор группы единиц $F 4$ , поля Галуа -Ордена четвертого (таким образом, $A$ и $A + 1$ являются корнями $x 2 + x + 1$ над $F 4$ . Потому что $(а + 1) 2 = a$ , $a + 1$ - уникальное решение квадратичного уравнения $x 2 + a = 0$ . С другой стороны, полиномиальный $х 2 + ax + 1$ не подходит для $F 4$ , но он разбивает $F 16$ , где имеет два корня $Ab$ и $ab + a$ , где $B$ - корень $x 2 + x + a$ in $f 16$ .

Это особый случай теории Артин -Шриера .

Смотрите также

Ссылки

^ Чарльз П. МакКиг (2014). Промежуточная алгебра с тригонометрией (перепечатано изд.). Академическая пресса. п. 219. ISBN 978-1-4832-1875-5 Полем Извлечение страницы 219
^ Protters & Morrey: «исчисление и аналитическая геометрия. Первый курс».
^ Принстонский обзор (2020). Princeton Review Sat Prep, 2021: 5 Практические тесты + обзор и методы + онлайн -инструменты . Рэндом домик детские книги. п. 360. ISBN 978-0-525-56974-9 Полем Извлечение страницы 360
^ Дэвид Мамфорд; Серия Кэролайн; Дэвид Райт (2002). Жемчужина Индры: видение Феликса Кляйна (иллюстрировано, перепечатано изд.). Издательство Кембриджского университета. п. 37. ISBN 978-0-521-35253-6 Полем Извлечение страницы 37
^ Математика в ресурсной книге учителей. 4B (иллюстрированное изд.). Нельсон Торнс. 1996. с. 26. ISBN 978-0-17-431439-4 Полем Извлечение страницы 26
^ Jump up to: ^а ^{беременный} ^в Вашингтон, Аллин Дж. (2000). Основная техническая математика с исчислением, седьмое издание . Addison Wesley Longman, Inc. ISBN 978-0-201-35666-3 .
^ Ebbinghaus, Heinz-Dieter; Ewing, John H. (1991), Numbers , выпускники в математике, Vol. 123, Springer, p. 77, ISBN 9780387974972 .
^ Стерлинг, Мэри Джейн (2010), Алгебра I для чайников , Wiley Publishing, p. 219, ISBN 978-0-470-55964-2
^ Рич, Барнетт; Schmidt, Philip (2004), Схема теории и проблем начальной алгебры , McGraw-Hill Companies, ISBN 978-0-07-141083-0 , Глава 13 §4.4, с. 291
^ ГИМОНАС, Алекс. Исчисление для деловых и социальных наук , с. 64 (Richard Dennis Publications, 2001).
^ Jump up to: ^а ^{беременный} Кахан, Виллиан (20 ноября 2004 г.), о стоимости вычислений с плавающей точкой без дополнительной арифметики (PDF) , получен 2012-12-25
^ Alenit͡syn, Aleksandr и Butikov, evgeniĭ. Краткое руководство по математике и физике , с. 38 (CRC Press 1997)
дискриминант Diakrínousa , word Διακρίνουσα, Diakrínousa.
^ Ачац, Томас; Андерсон, Джон Г.; Маккензи, Кэтлин (2005). Технический магазин математика . Промышленная пресса. п. 277. ISBN 978-0-8311-3086-2 .
^ «Сложные корни стали видимыми - математические забавные факты» . Получено 1 октября 2016 года .
^ Wharton, P. (2006). Основы Edexcel GCSE Math/Higher . Лонсдейл. п. 63. ISBN 978-1-905-129-78-2 .
^ Алек Нортон, Бенджамин Лото (июнь 1984 г.), «Сложные корни, ставшие видимыми», The College Mathematic Journal , 15 (3): 248–249, doi : 10.2307/2686333 , JSTOR 2686333
^ Higham, Nicholas (2002), Точность и стабильность численных алгоритмов (2 -е изд.), Siam, p. 10, ISBN 978-0-89871-521-7
^ Friberg, Jöran (2009). «Геометрический алгоритм с решениями квадратичных уравнений в шумерском юридическом документе от UR III Umma» . Cuneiform Digital Library Journal . 3
^ Стиллвелл, Джон (2004). Математика и ее история (2 -е изд.) . Спрингер. ISBN 978-0-387-95336-6 .
^ Кембриджская древняя история, часть 2 Ранняя история Ближнего Востока . Издательство Кембриджского университета. 1971. с. 530. ISBN 978-0-521-07791-0 .
^ Хендерсон, Дэвид В. «Геометрические решения квадратичных и кубических уравнений» . Математический факультет, Корнелльский университет . Получено 28 апреля 2013 года .
^ Jump up to: ^а ^{беременный} Эйткен, Уэйн. «Китайская классика: девять глав» (PDF) . Математический факультет, Калифорнийский государственный университет . Получено 28 апреля 2013 года .
^ Смит, Дэвид Юджин (1958). История математики . Публикации курьера. п. 380. ISBN 978-0-486-20430-7 .
^ Смит, Дэвид Юджин (1958). История математики, том 1 . Публикации курьера. п. 134. ISBN 978-0-486-20429-1 Полем Извлечение страницы 134
^ Brāhmasphuṭasiddhānta, перевод Colebrook, 1817, стр. 346; цитируется Стиллвелл, Джон (2010). Математика и ее история (3 -е изд.) . Спрингер. п. 93. doi : 10.1007/978-1-4419-6053-5 . ISBN 978-0-387-95336-6 .
^ Jump up to: ^а ^{беременный} ^в ^{дюймовый} Кац, VJ; Бартон Б. (2006). «Стадии в истории алгебры с последствиями для обучения». Образовательные исследования по математике . 66 (2): 185–201. doi : 10.1007/s10649-006-9023-7 . S2CID 120363574 .
^ Jump up to: ^а ^{беременный} Бойер, Карл Б. (1991). Мерцбах, Ута С. (ред.). История математики . John Wiley & Sons, Inc. ISBN 978-0-471-54397-8 .
^ О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. (1999), «Математика арабской игры: забытый блеск?» , Архив истории макейторов Университет Сент -Эндрюса «Алгебра была объединяющей теорией, которая позволяла рациональному числам, иррациональным числам, геометрическим величинам и т. Д., Для всех рассматриваться как« алгебраические объекты »».
^ Жак Сесано, «Исламская математика», с. 148, в Селин, Героя ; D'Abrosio, Blind , eds. ( , ) 2000 , 978-1-4020-0260-1
^ Смит, Дэвид Юджин (1958). История математики . Публикации курьера. п. 280. ISBN 978-0-486-20429-1 .
^ Ливио, Марио (2006). Уравнение, которое не может быть решено . Саймон и Шустер. ISBN 978-0743258210 .
^ Ронан, Колин (1985). Более короткая наука и цивилизация в Китае . Издательство Кембриджского университета. п. 15. ISBN 978-0-521-31536-4 .
^ Струу, диджей; 1958) Стевин , , Саймон ( II - B, CV Swets & Zeitlinger, p. 470
^ Ballew, Pat. «Решение квадратичных уравнений - аналитическими и графическими методами; включая несколько методов, которые вы, возможно, никогда не видели» (PDF) . Архивировано из оригинала (PDF) 9 апреля 2011 года . Получено 18 апреля 2013 года .
^ Seares, FH (1945). «Тригонометрическое решение квадратичного уравнения» . Публикации Астрономического общества Тихого океана . 57 (339): 307–309. Bibcode : 1945pasp ... 57..307s . doi : 10.1086/125759 .
^ Aude, HTR (1938). «Решения квадратного уравнения, полученные с помощью тригонометрии». Национальный журнал по математике . 13 (3): 118–121. doi : 10.2307/3028750 . JSTOR 3028750 .
^ Саймонс, Стюарт, «Альтернативный подход к сложным корням реальных квадратичных уравнений», Математическая газетта 93, март 2009 г., 91–92.
^ Биксби, Уильям Герберт (1879), графический метод для с готовностью поиск реальных корней численных уравнений любой степени , Вест -Пойнт, Нью -Йорк
^ Вейсштейн, Эрик У. "Карлайл Круг" . От MathWorld - веб -ресурс Wolfram . Получено 21 мая 2013 года .

Внешние ссылки

[1] Чарльз П. МакКиг (2014). Промежуточная алгебра с тригонометрией (перепечатано изд.). Академическая пресса. п. 219. ISBN 978-1-4832-1875-5 Полем Извлечение страницы 219

[2] Protters & Morrey: «исчисление и аналитическая геометрия. Первый курс».

[3] Принстонский обзор (2020). Princeton Review Sat Prep, 2021: 5 Практические тесты + обзор и методы + онлайн -инструменты . Рэндом домик детские книги. п. 360. ISBN 978-0-525-56974-9 Полем Извлечение страницы 360

[4] Дэвид Мамфорд; Серия Кэролайн; Дэвид Райт (2002). Жемчужина Индры: видение Феликса Кляйна (иллюстрировано, перепечатано изд.). Издательство Кембриджского университета. п. 37. ISBN 978-0-521-35253-6 Полем Извлечение страницы 37

[5] Математика в ресурсной книге учителей. 4B (иллюстрированное изд.). Нельсон Торнс. 1996. с. 26. ISBN 978-0-17-431439-4 Полем Извлечение страницы 26

[Washington2000-6] Jump up to: ^а ^{беременный} ^в Вашингтон, Аллин Дж. (2000). Основная техническая математика с исчислением, седьмое издание . Addison Wesley Longman, Inc. ISBN 978-0-201-35666-3 .

[7] Ebbinghaus, Heinz-Dieter; Ewing, John H. (1991), Numbers , выпускники в математике, Vol. 123, Springer, p. 77, ISBN 9780387974972 .

[8] Стерлинг, Мэри Джейн (2010), Алгебра I для чайников , Wiley Publishing, p. 219, ISBN 978-0-470-55964-2

[9] Рич, Барнетт; Schmidt, Philip (2004), Схема теории и проблем начальной алгебры , McGraw-Hill Companies, ISBN 978-0-07-141083-0 , Глава 13 §4.4, с. 291

[10] ГИМОНАС, Алекс. Исчисление для деловых и социальных наук , с. 64 (Richard Dennis Publications, 2001).

[kahan-11] Jump up to: ^а ^{беременный} Кахан, Виллиан (20 ноября 2004 г.), о стоимости вычислений с плавающей точкой без дополнительной арифметики (PDF) , получен 2012-12-25

[12] Alenit͡syn, Aleksandr и Butikov, evgeniĭ. Краткое руководство по математике и физике , с. 38 (CRC Press 1997)

[13] дискриминант Diakrínousa , word Διακρίνουσα, Diakrínousa.

[14] Ачац, Томас; Андерсон, Джон Г.; Маккензи, Кэтлин (2005). Технический магазин математика . Промышленная пресса. п. 277. ISBN 978-0-8311-3086-2 .

[15] «Сложные корни стали видимыми - математические забавные факты» . Получено 1 октября 2016 года .

[16] Wharton, P. (2006). Основы Edexcel GCSE Math/Higher . Лонсдейл. п. 63. ISBN 978-1-905-129-78-2 .

[Norton1984-17] Алек Нортон, Бенджамин Лото (июнь 1984 г.), «Сложные корни, ставшие видимыми», The College Mathematic Journal , 15 (3): 248–249, doi : 10.2307/2686333 , JSTOR 2686333

[Higham2002-18] Higham, Nicholas (2002), Точность и стабильность численных алгоритмов (2 -е изд.), Siam, p. 10, ISBN 978-0-89871-521-7

[Friberg2009-19] Friberg, Jöran (2009). «Геометрический алгоритм с решениями квадратичных уравнений в шумерском юридическом документе от UR III Umma» . Cuneiform Digital Library Journal . 3

[Stillwell2004-20] Стиллвелл, Джон (2004). Математика и ее история (2 -е изд.) . Спрингер. ISBN 978-0-387-95336-6 .

[21] Кембриджская древняя история, часть 2 Ранняя история Ближнего Востока . Издательство Кембриджского университета. 1971. с. 530. ISBN 978-0-521-07791-0 .

[Henderson-22] Хендерсон, Дэвид В. «Геометрические решения квадратичных и кубических уравнений» . Математический факультет, Корнелльский университет . Получено 28 апреля 2013 года .

[Aitken-23] Jump up to: ^а ^{беременный} Эйткен, Уэйн. «Китайская классика: девять глав» (PDF) . Математический факультет, Калифорнийский государственный университет . Получено 28 апреля 2013 года .

[24] Смит, Дэвид Юджин (1958). История математики . Публикации курьера. п. 380. ISBN 978-0-486-20430-7 .

[25] Смит, Дэвид Юджин (1958). История математики, том 1 . Публикации курьера. п. 134. ISBN 978-0-486-20429-1 Полем Извлечение страницы 134

[26] Brāhmasphuṭasiddhānta, перевод Colebrook, 1817, стр. 346; цитируется Стиллвелл, Джон (2010). Математика и ее история (3 -е изд.) . Спрингер. п. 93. doi : 10.1007/978-1-4419-6053-5 . ISBN 978-0-387-95336-6 .

[Katz2007-27] Jump up to: ^а ^{беременный} ^в ^{дюймовый} Кац, VJ; Бартон Б. (2006). «Стадии в истории алгебры с последствиями для обучения». Образовательные исследования по математике . 66 (2): 185–201. doi : 10.1007/s10649-006-9023-7 . S2CID 120363574 .

[Boyer1991-28] Jump up to: ^а ^{беременный} Бойер, Карл Б. (1991). Мерцбах, Ута С. (ред.). История математики . John Wiley & Sons, Inc. ISBN 978-0-471-54397-8 .

[29] О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. (1999), «Математика арабской игры: забытый блеск?» , Архив истории макейторов Университет Сент -Эндрюса «Алгебра была объединяющей теорией, которая позволяла рациональному числам, иррациональным числам, геометрическим величинам и т. Д., Для всех рассматриваться как« алгебраические объекты »».

[30] Жак Сесано, «Исламская математика», с. 148, в Селин, Героя ; D'Abrosio, Blind , eds. ( , ) 2000 , 978-1-4020-0260-1

[31] Смит, Дэвид Юджин (1958). История математики . Публикации курьера. п. 280. ISBN 978-0-486-20429-1 .

[Livio2006-32] Ливио, Марио (2006). Уравнение, которое не может быть решено . Саймон и Шустер. ISBN 978-0743258210 .

[Ron-33] Ронан, Колин (1985). Более короткая наука и цивилизация в Китае . Издательство Кембриджского университета. п. 15. ISBN 978-0-521-31536-4 .

[34] Струу, диджей; 1958) Стевин , , Саймон ( II - B, CV Swets & Zeitlinger, p. 470

[Ballew2007-35] Ballew, Pat. «Решение квадратичных уравнений - аналитическими и графическими методами; включая несколько методов, которые вы, возможно, никогда не видели» (PDF) . Архивировано из оригинала (PDF) 9 апреля 2011 года . Получено 18 апреля 2013 года .

[Seares1945-36] Seares, FH (1945). «Тригонометрическое решение квадратичного уравнения» . Публикации Астрономического общества Тихого океана . 57 (339): 307–309. Bibcode : 1945pasp ... 57..307s . doi : 10.1086/125759 .

[Aude1938-37] Aude, HTR (1938). «Решения квадратного уравнения, полученные с помощью тригонометрии». Национальный журнал по математике . 13 (3): 118–121. doi : 10.2307/3028750 . JSTOR 3028750 .

[38] Саймонс, Стюарт, «Альтернативный подход к сложным корням реальных квадратичных уравнений», Математическая газетта 93, март 2009 г., 91–92.

[39] Биксби, Уильям Герберт (1879), графический метод для с готовностью поиск реальных корней численных уравнений любой степени , Вест -Пойнт, Нью -Йорк

[Wolfram-40] Вейсштейн, Эрик У. "Карлайл Круг" . От MathWorld - веб -ресурс Wolfram . Получено 21 мая 2013 года .

[ 1 ]

[ 2 ]

[ 3 ]

[ 4 ]

[ 5 ]

[ 6 ]

[ 7 ]

[ 8 ]

[ 9 ]

[ 10 ]

[ 11 ]

[ 12 ]

[ 13 ]

[ 14 ]

[ 15 ]

[ 16 ]

[ 17 ]

[ 18 ]

[ 19 ]

[ 20 ]

[ 21 ]

[ 22 ]

[ 23 ]

[ 24 ]

[ 25 ]

[ 26 ]

[ 27 ]

[ 28 ]

[ 29 ]

[ 30 ]

[ 31 ]

[ 32 ]

[ 33 ]

[ 34 ]

[ 35 ]

[ 36 ]

[ 37 ]

[ 38 ]

[ 39 ]

[ 40 ]

v Т и Полиномы и полиномиальные функции
По степени	Нулевой полином (степень не определена или -1 или −∞) Постоянная функция (0) Линейная функция (1) Линейное уравнение Квадратичная функция (2) Квадратное уравнение Кубическая функция (3) Кубическое уравнение Кварная функция (4) Квартическое уравнение Квинтетическая функция (5) Секстическое уравнение (6) Септическое уравнение (7)
По свойствам	Одномерный Двумерный Многомерный Мономиальный Биномиал Триномиал Неснижаемый Без квадратов Гомогенный Квази-гомогенный
Инструменты и алгоритмы	Факторизация Величайший общий делитель Разделение Метод оценки Хорнера Полиномиальная тестирование идентичности Результирующий Дискриминант Грёбнер База