сила Лоренца
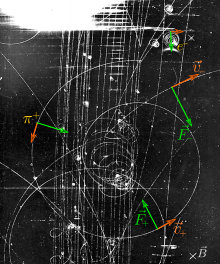
В физике , особенно в электромагнетизме , сила Лоренца (или электромагнитная сила ) представляет собой комбинацию электрической и магнитной силы, воздействующей на точечный заряд вследствие электромагнитных полей . На частицу заряда q, движущуюся со скоростью v в электрическом поле E и магнитном поле B, действует сила (в единицах СИ [1] [2] ) из
Вариации этой базовой формулы описывают магнитную силу, действующую на провод с током (иногда называемую силой Лапласа ), электродвижущую силу в проволочной петле, движущейся через магнитное поле (аспект закона индукции Фарадея ), и силу, действующую на движущееся тело. заряженная частица. [3]
Историки предполагают, что этот закон подразумевается в статье Джеймса Клерка Максвелла , опубликованной в 1865 году. [4] Хендрик Лоренц пришел к полному выводу в 1895 году. [5] определение вклада электрической силы через несколько лет после того, как Оливер Хевисайд правильно определил вклад магнитной силы. [6]
как определение E Закон силы Лоренца и B
Во многих учебниках по классическому электромагнетизму закон силы Лоренца используется в качестве определения электрических и магнитных E и B. полей [7] [8] [9] Говоря конкретнее, под силой Лоренца понимается следующее эмпирическое утверждение:
Электромагнитная сила F, действующая на пробный заряд в данную точку и время, представляет собой определенную функцию его заряда q и скорости v , которую можно параметризовать ровно двумя векторами E и B в функциональной форме :
Это справедливо даже для частиц, приближающихся к скорости света (то есть величиной с v , | v | ≈ c ). [10] Таким образом, два векторных поля E и B определяются в пространстве и времени и называются «электрическим полем» и «магнитным полем». Поля определяются повсюду в пространстве и времени относительно того, какую силу получит пробный заряд, независимо от того, присутствует ли заряд, испытывающий эту силу.
В качестве определения E и B сила Лоренца является лишь принципиальным определением, потому что реальная частица (в отличие от гипотетического «пробного заряда» бесконечно малых массы и заряда) будет генерировать свои собственные конечные E и B поля , которые изменит электромагнитную силу, которую он испытывает. [11] Кроме того, если заряд испытывает ускорение, как если бы его заставили двигаться по искривленной траектории, он испускает излучение, заставляющее его терять кинетическую энергию. См., например, тормозное излучение и синхротронный свет . Эти эффекты происходят как за счет прямого воздействия (называемого силой реакции излучения ), так и косвенно (путем воздействия на движение близлежащих зарядов и токов).
Уравнение [ править ]
Заряженная частица [ править ]

Сила F, действующая на частицу с электрическим зарядом q с мгновенной скоростью v , вызванная внешним электрическим полем E и магнитным полем B , определяется выражением (в единицах СИ [1] ): [12]
где × — векторное векторное произведение (все величины, выделенные жирным шрифтом, являются векторами). С точки зрения декартовых компонентов мы имеем:
В общем, электрические и магнитные поля являются функциями положения и времени. Поэтому в явном виде силу Лоренца можно записать как:
Положительно заряженная частица будет ускоряться в той же линейной ориентации, что и поле E , но будет изгибаться перпендикулярно как вектору мгновенной скорости v , так и полю B по правилу правой руки (подробнее, если пальцы правой руки вытянуты так, чтобы указывать в направлении v , а затем скручиваются так, чтобы указывать в направлении B , тогда вытянутый большой палец будет указывать в направлении F ).
Член qE , а называется электрической силой член q ( v × B ) называется магнитной силой . [13] Согласно некоторым определениям, термин «сила Лоренца» относится конкретно к формуле магнитной силы: [14] при этом суммарная электромагнитная сила (включая электрическую силу) получила другое (нестандартное) название. В этой статье не будет следовать этой номенклатуре: далее термин «сила Лоренца» будет относиться к выражению полной силы.
Магнитно-силовая составляющая силы Лоренца проявляется как сила, действующая на провод с током в магнитном поле. В этом контексте ее также называют силой Лапласа .
Сила Лоренца — это сила, действующая электромагнитным полем на заряженную частицу, то есть это скорость, с которой линейный импульс передается от электромагнитного поля к частице. С ним связана мощность, которая представляет собой скорость, с которой энергия передается от электромагнитного поля к частице. Эта сила
заряда Непрерывное распределение

Для непрерывного распределения заряда в движении уравнение силы Лоренца принимает вид:
Полная сила представляет собой объемный интеграл по распределению заряда:
Устранив и , используя уравнения Максвелла и управляя теоремами векторного исчисления , эту форму уравнения можно использовать для вывода тензора напряжений Максвелла. , в свою очередь это можно объединить с вектором Пойнтинга чтобы получить электромагнитный тензор энергии-напряжения T, используемый в общей теории относительности . [15]
С точки зрения и , другой способ записать силу Лоренца (на единицу объема): [15]
Плотность мощности, связанная с силой Лоренца в материальной среде, равна
Если мы разделим полный заряд и полный ток на свободную и связанную части, то получим, что плотность силы Лоренца равна
где: – плотность свободного заряда; – плотность поляризации ; – плотность свободного тока; и – плотность намагничивания . Таким образом, сила Лоренца может объяснить крутящий момент, приложенный к постоянному магниту магнитным полем. Плотность связанной мощности равна
Уравнения с условными единицами измерения CGS [ править ]
В вышеупомянутых формулах используются соглашения для определения электрического и магнитного поля, используемые в единицах СИ . Это самые распространенные. Однако возможны и используются другие соглашения с той же физикой (т.е. силы, действующие, например, на электрон). В соглашениях, используемых со старыми единицами CGS-Гаусса , которые несколько более распространены среди некоторых физиков-теоретиков, а также экспериментаторов конденсированного состояния, вместо этого используется
История [ править ]

Первые попытки количественного описания электромагнитной силы были предприняты в середине 18 века. предположили, что сила, действующая на магнитные полюса, В 1760 году Иоганн Тобиас Майер и другие [16] и электрически заряженные объекты, Генри Кавендиш в 1762 году. [17] подчинялся закону обратных квадратов . Однако в обоих случаях экспериментальное доказательство не было ни полным, ни убедительным. Лишь в 1784 году Шарль-Огюстен де Кулон , используя торсионные весы , смог окончательно доказать посредством эксперимента, что это правда. [18] Вскоре после открытия в 1820 году Гансом Христианом Эрстедом того, что на магнитную стрелку действует гальванический ток, Андре-Мари Ампер в том же году смог экспериментально разработать формулу угловой зависимости силы между двумя элементами с током. [19] [20] Во всех этих описаниях сила всегда описывалась с точки зрения свойств материи и расстояний между двумя массами или зарядами, а не с точки зрения электрического и магнитного полей. [21]
Современная концепция электрических и магнитных полей впервые возникла в теориях Майкла Фарадея , в частности в его идее силовых линий , позднее получившая полное математическое описание лордом Кельвином и Джеймсом Клерком Максвеллом . [22] С современной точки зрения можно идентифицировать в формулировке Максвеллом 1865 года его уравнений поля форму уравнения силы Лоренца по отношению к электрическим токам: [4] хотя во времена Максвелла не было очевидно, как его уравнения связаны с силами, действующими на движущиеся заряженные объекты. Дж. Дж. Томсон был первым, кто попытался вывести из уравнений поля Максвелла электромагнитные силы, действующие на движущийся заряженный объект, через свойства объекта и внешние поля. Заинтересовавшись определением электромагнитного поведения заряженных частиц в катодных лучах , Томсон опубликовал в 1881 году статью, в которой определил силу, действующую на частицы под действием внешнего магнитного поля, как [6] [23]
Траектории частиц, обусловленные силой Лоренца [ править ]

Во многих случаях, представляющих практический интерес, движение в магнитном поле частицы электрически заряженной (например, электрона или иона в плазме ) можно рассматривать как суперпозицию относительно быстрого кругового движения вокруг точки, называемой ведущим центром , и относительно медленный дрейф этой точки. Скорости дрейфа могут различаться для разных видов в зависимости от их зарядового состояния, массы или температуры, что может привести к возникновению электрических токов или химическому разделению.
Значение силы Лоренца [ править ]
В то время как современные уравнения Максвелла описывают, как электрически заряженные частицы и токи или движущиеся заряженные частицы создают электрические и магнитные поля, закон силы Лоренца дополняет эту картину, описывая силу, действующую на движущийся точечный заряд q в присутствии электромагнитных полей. [12] [29] Закон силы Лоренца описывает влияние E и B на точечный заряд, но такие электромагнитные силы не дают полной картины. Заряженные частицы, возможно, связаны с другими силами, особенно с гравитацией и ядерными силами. Таким образом, уравнения Максвелла не стоят отдельно от других физических законов, а связаны с ними через плотности заряда и тока. Реакция точечного заряда на закон Лоренца является одним из аспектов; генерация E и B токами и зарядами — другое.
В реальных материалах сила Лоренца недостаточна для описания коллективного поведения заряженных частиц как в принципе, так и с точки зрения вычислений. Заряженные частицы в материальной среде не только реагируют на поля E и B , но и порождают эти поля. Для определения временного и пространственного отклика зарядов необходимо решить сложные уравнения переноса, например, уравнение Больцмана , уравнение Фоккера-Планка или уравнения Навье-Стокса . Например, см. Магнитогидродинамика , Гидродинамика , Электрогидродинамика , Сверхпроводимость , Эволюция звезд . Разработан целый физический аппарат для решения этих вопросов. См., например, отношения Грина-Кубо и функцию Грина (теория многих тел) .
Сила на проводе с током [ править ]

Когда провод, по которому течет электрический ток, помещается в магнитное поле, каждый из движущихся зарядов, составляющих ток, испытывает действие силы Лоренца, и вместе они могут создавать на проводе макроскопическую силу (иногда называемую силой Лапласа ). Объединив приведенный выше закон силы Лоренца с определением электрического тока, получаем следующее уравнение в случае прямого неподвижного провода в однородном поле: [30]
Если проволока непрямая, силу, действующую на нее, можно вычислить, применив эту формулу к каждому бесконечно малому сегменту проволоки. , затем суммируем все эти силы путем интегрирования . Это приводит к тому же формальному выражению, но теперь ℓ следует понимать как вектор, соединяющий концы изогнутого провода с направлением от начальной до конечной точки обычного тока. Обычно также присутствует чистый крутящий момент .
Если, кроме того, магнитное поле неоднородно, результирующая сила, действующая на неподвижный жесткий провод, по которому течет постоянный ток I, определяется интегрированием по проводу:
Одним из применений этого является закон силы Ампера , который описывает, как два провода с током могут притягивать или отталкивать друг друга, поскольку каждый из них испытывает силу Лоренца со стороны магнитного поля другого.
ЭДС [ править ]
Компонент магнитной силы ( q v × B ) силы Лоренца отвечает за движущую электродвижущую силу (или движущуюся ЭДС ), явление, лежащее в основе многих электрических генераторов. Когда проводник перемещается через магнитное поле, магнитное поле оказывает противоположные силы на электроны и ядра в проводе, и это создает ЭДС. К этому явлению применяется термин «ЭДС движения», поскольку ЭДС возникает вследствие движения проволоки .
В других электрических генераторах магниты движутся, а проводники — нет. В этом случае ЭДС возникает из-за члена электрической силы ( q E ) в уравнении силы Лоренца. Рассматриваемое электрическое поле создается изменяющимся магнитным полем, в результате чего возникает индуцированная ЭДС, описываемая уравнением Максвелла-Фарадея (одним из четырех современных уравнений Максвелла ). [31]
Обе эти ЭДС, несмотря на кажущееся разное происхождение, описываются одним и тем же уравнением, а именно: ЭДС — это скорость изменения магнитного потока через провод. (Это закон индукции Фарадея, см. ниже Эйнштейна .) Специальная теория относительности была частично мотивирована желанием лучше понять эту связь между двумя эффектами. [31] Фактически, электрическое и магнитное поля являются разными гранями одного и того же электромагнитного поля, и при переходе от одной инерциальной системы к другой соленоидальная векторная часть Е -поля может полностью или частично измениться на В -поле или наоборот . [32]
Фарадея индукции закон Сила Лоренца и

Если петля провода находится в магнитном поле , закон индукции Фарадея гласит, что индуцированная электродвижущая сила (ЭДС) в проводе равна:
Знак ЭДС определяется законом Ленца . Обратите внимание, что это справедливо не только для неподвижного провода, но и для движущегося провода.
Из закона индукции Фарадея (который справедлив для движущегося провода, например, в двигателе) и уравнений Максвелла можно вывести силу Лоренца. Верно и обратное: сила Лоренца и уравнения Максвелла могут быть использованы для вывода закона Фарадея .
Пусть Σ( t ) — движущаяся проволока, движущаяся вместе без вращения и с постоянной скоростью v , а Σ( t ) — внутренняя поверхность проволоки. ЭДС на замкнутом пути ∂Σ( t ) определяется выражением: [33]
NB: И d ℓ, и d A имеют неоднозначность знака; чтобы получить правильный знак, используется правило правой руки , как объяснено в статье Теорема Кельвина – Стокса .
Приведенный выше результат можно сравнить с версией закона индукции Фарадея, которая появляется в современных уравнениях Максвелла, называемой здесь уравнением Максвелла – Фарадея :
Уравнение Максвелла–Фарадея также можно записать в интегральной форме, используя теорему Кельвина–Стокса . [34]
Итак, мы имеем уравнение Максвелла Фарадея:
Оба варианта эквивалентны, если провод не движется. Использование интегрального правила Лейбница и того, что div B = 0 , приводит к:
Закон индукции Фарадея действует независимо от того, является ли проволочная петля жесткой и неподвижной, находится в движении или находится в процессе деформации, а также независимо от того, является ли магнитное поле постоянным во времени или изменяющимся. Однако бывают случаи, когда закон Фарадея либо неадекватен, либо сложен в использовании, и необходимо применение основного закона силы Лоренца. См. неприменимость закона Фарадея .
Если магнитное поле фиксировано во времени и проводящая петля движется по полю, то магнитный поток Φ B, связывающий петлю, может меняться несколькими способами. Например, если B -поле меняется в зависимости от положения и контур перемещается в место с другим B -полем, Φ B изменится. Альтернативно, если петля меняет ориентацию относительно B -поля, дифференциальный элемент B ⋅ d A изменится из-за разного угла между B и d A , что также изменит Φ B . В качестве третьего примера, если часть контура проходит через однородное, независимое от времени B -поле, а другая часть контура удерживается неподвижно, поток, связывающий всю замкнутую цепь, может измениться из-за смещения относительного положения. частей схемы со временем (поверхность ∂Σ( t ) зависит от времени). Во всех трех случаях закон индукции Фарадея предсказывает ЭДС, создаваемую изменением Φ B .
Обратите внимание, что уравнение Максвелла Фарадея подразумевает, что электрическое поле E неконсервативно, когда магнитное поле B меняется во времени, и не выражается как градиент скалярного поля и не подчиняется теореме о градиенте , поскольку его ротор не равен нулю. [33] [35]
Сила Лоренца через потенциалы [ править ]
Поля E и B можно заменить магнитным векторным потенциалом A и ( скалярным ) электростатическим потенциалом φ на
Сила становится
Используя тождество тройного произведения, это можно переписать как:
(Обратите внимание, что координаты и компоненты скорости следует рассматривать как независимые переменные, поэтому оператор del действует только на , не на ; таким образом, нет необходимости использовать индекс Фейнмана в приведенном выше уравнении). Используя правило цепочки, полная производная от является:
так что приведенное выше выражение принимает вид:
При v = ẋ мы можем привести уравнение к удобной форме Эйлера – Лагранжа
где
Лоренца и аналитическая Сила механика
Лагранжиан энергии для заряженной частицы массы m и заряда q в электромагнитном поле эквивалентно описывает динамику частицы с точки зрения ее , а не силы, действующей на нее. Классическое выражение имеет вид: [36]
Для поля A частица, движущаяся со скоростью v = ṙ, имеет потенциальный импульс , поэтому его потенциальная энергия равна . Для поля φ потенциальная энергия частицы равна .
Тогда полная потенциальная энергия равна:
Уравнения Лагранжа:
приравнивая и упрощая:
и аналогично для направлений y и z . Следовательно, уравнение силы имеет вид:
Потенциальная энергия зависит от скорости частицы, поэтому сила зависит от скорости и не является консервативной.
Релятивистский лагранжиан – это
Действие представляет собой релятивистскую длину дуги пути частицы в пространстве-времени минус вклад потенциальной энергии плюс дополнительный вклад, который с квантовой механики является дополнительной фазой, которую получает заряженная частица, когда она движется вдоль векторного потенциала.
Уравнения движения, полученные путем экстремизации действия (обозначения см . в матричном исчислении ):
такие же, как уравнения движения Гамильтона :
оба эквивалентны неканонической форме:
Эта формула представляет собой силу Лоренца, представляющую скорость, с которой ЭМ поле придает частице релятивистский импульс.
силы Релятивистская форма Лоренца
силы Лоренца Ковариантная форма
Тензор поля [ править ]
Используя метрическую сигнатуру (1, −1, −1, −1) , силу Лоренца для заряда q можно записать в виде [38] Ковариантная форма :
где р а — четырехимпульс , определяемый как
τ собственное время частицы, F аб контравариантный электромагнитный тензор
U — ковариантная 4-скорость частицы, определяемая как:
Поля преобразуются в систему координат, движущуюся с постоянной относительной скоростью:
где Λ м α — тензор преобразования Лоренца .
Перевод в векторную нотацию [ править ]
= Компонент α 1 ( x -компонент) силы равен
Подстановка компонент ковариантного электромагнитного тензора F дает
Используя компоненты ковариантных четырехскоростных выходов
Расчет для α = 2, 3 (компоненты силы в направлениях y и z ) дает аналогичные результаты, поэтому 3 уравнения собираются в одно:
Это и есть закон силы Лоренца, однако важно отметить, что p — релятивистское выражение,
в алгебре пространства-времени ( Сила Лоренца STA )
Электрические и магнитные поля зависят от скорости наблюдателя , поэтому релятивистскую форму закона силы Лоренца лучше всего можно продемонстрировать, исходя из независимого от координат выражения для электромагнитного и магнитного полей. и произвольное направление времени, . Это можно решить с помощью алгебры пространства-времени (или геометрической алгебры пространства-времени), типа алгебры Клиффорда, определенной в псевдоевклидовом пространстве . [39] как
Правильная (инвариант — неподходящий термин, поскольку преобразование не было определено) форма закона силы Лоренца просто
Обратите внимание, что порядок важен, потому что скалярное произведение бивектора и вектора антисимметрично. При подобном расщеплении пространства-времени можно получить скорость и поля, как указано выше, что дает обычное выражение.
Сила Лоренца в общей теории относительности [ править ]
В общей теории относительности уравнение движения частицы с массой и зарядить , движущийся в пространстве с метрическим тензором и электромагнитное поле , дается как
Уравнение также можно записать как
Приложения [ править ]
Сила Лоренца возникает во многих устройствах, в том числе:
- Циклотроны с круговым движением и другие ускорители частиц
- Масс-спектрометры
- Фильтры скорости
- Микроволновые печи
- Силовая велосиметрия Лоренца
В своем проявлении как сила Лапласа, действующая на электрический ток в проводнике, эта сила встречается во многих устройствах, в том числе:
См. также [ править ]
| Статьи о |
| Электромагнетизм |
|---|
 |
- Эффект Холла
- Электромагнетизм
- Гравитомагнетизм
- Закон силы Ампера
- Хендрик Лоренц
- Уравнения Максвелла
- Формулировка уравнений Максвелла в специальной теории относительности
- Проблема с движущимся магнитом и проводником
- Сила Авраама – Лоренца
- Формула Лармора
- Циклотронное излучение
- Магнитосопротивление
- Скалярный потенциал
- Разложение Гельмгольца
- Руководящий центр
- Линия поля
- Закон Кулона
- Электромагнитная плавучесть
Сноски [ править ]
- ^ Jump up to: Перейти обратно: а б с В единицах СИ B измеряется в теслах (обозначение: T). В Гаусса-СГС единицах B измеряется в гауссах (обозначение: G). См., например «Часто задаваемые вопросы по геомагнетизму» . Национальный центр геофизических данных . Проверено 21 октября 2013 г. )
- ^ H - поле измеряется в амперах на метр (А/м) в единицах СИ и в эрстедах (Э) в единицах СГС. «Международная система единиц (СИ)» . Справочник NIST по константам, единицам измерения и неопределенности . Национальный институт стандартов и технологий. 12 апреля 2010 года . Проверено 9 мая 2012 г.
- ^ Хурей, Пол Г. (16 ноября 2009 г.). Уравнения Максвелла . Джон Уайли и сыновья. ISBN 978-0-470-54276-7 .
- ^ Jump up to: Перейти обратно: а б Урэй, Пол Г. (2010). Уравнения Максвелла . Вайли-IEEE. п. 22. ISBN 978-0-470-54276-7 .
- ^ Jump up to: Перейти обратно: а б Даль, Пер Ф. (1997). Вспышка катодных лучей: история электрона Дж. Дж. Томсона . ЦРК Пресс. п. 10.
- ^ Jump up to: Перейти обратно: а б с Пол Дж. Нахин, Оливер Хевисайд , JHU Press, 2002.
- ^ См., например, Джексон, стр. 777–8.
- ^ Дж. А. Уилер; К. Миснер; К. С. Торн (1973). Гравитация . WH Freeman & Co., стр. 72–73 . ISBN 0-7167-0344-0 . . Эти авторы используют силу Лоренца в тензорной форме в качестве определения электромагнитного тензора F полей E и B. , в свою очередь ,
- ^ ИС Грант; В. Р. Филлипс; Манчестерская физика (1990). Электромагнетизм (2-е изд.). Джон Уайли и сыновья. п. 122. ИСБН 978-0-471-92712-9 .
- ^ ИС Грант; В. Р. Филлипс; Манчестерская физика (1990). Электромагнетизм (2-е изд.). Джон Уайли и сыновья. п. 123. ИСБН 978-0-471-92712-9 .
- ^ «Фейнмановские лекции по физике, том II, глава 1: Электромагнетизм» . www.feynmanlectures.caltech.edu . Проверено 6 июля 2022 г.
- ^ Jump up to: Перейти обратно: а б См. Джексон, стр. 2. В книге перечислены четыре современных уравнения Максвелла, а затем говорится: «Для рассмотрения движения заряженных частиц также важно уравнение силы Лоренца F = q ( E + v × B ) , которое дает силу, действующую на точечный заряд q в присутствии электромагнитных полей».
- ^ См. Гриффитс, стр. 204.
- ^ Например, см. сайт Института Лоренца или Гриффитса.
- ^ Jump up to: Перейти обратно: а б с Гриффитс, Дэвид Дж. (1999). Введение в электродинамику . перепечатка. с корр. (3-е изд.). Река Аппер-Сэддл, Нью-Джерси [ua]: Прентис-Холл. ISBN 978-0-13-805326-0 .
- ^ Делон, Мишель (2001). Энциклопедия Просвещения . Чикаго, Иллинойс: Издательство Fitzroy Dearborn. п. 538. ИСБН 157958246X .
- ^ Гудвин, Эллиот Х. (1965). Новая Кембриджская современная история, том 8: Американская и французская революции, 1763–1793 гг . Кембридж: Издательство Кембриджского университета. п. 130. ИСБН 9780521045469 .
- ^ Мейер, Герберт В. (1972). История электричества и магнетизма . Норуолк, Коннектикут: Библиотека Бернди. стр. 30–31. ISBN 0-262-13070-Х .
- ^ Вершуур, Геррит Л. (1993). Скрытое притяжение: история и тайна магнетизма . Нью-Йорк: Издательство Оксфордского университета. стр. 78–79 . ISBN 0-19-506488-7 .
- ^ Дарригол, Оливье (2000). Электродинамика от Ампера до Эйнштейна . Оксфорд, [Англия]: Издательство Оксфордского университета. стр. 9 , 25. ISBN 0-19-850593-0 .
- ^ Вершуур, Геррит Л. (1993). Скрытое притяжение: история и тайна магнетизма . Нью-Йорк: Издательство Оксфордского университета. п. 76 . ISBN 0-19-506488-7 .
- ^ Дарригол, Оливье (2000). Электродинамика от Ампера до Эйнштейна . Оксфорд, [Англия]: Издательство Оксфордского университета. стр. 126–131 , 139–144. ISBN 0-19-850593-0 .
- ^ Массачусетс, Дж. Дж. Томсон (1 апреля 1881 г.). «XXXIII. Об электрических и магнитных эффектах, производимых движением наэлектризованных тел» . Лондонский, Эдинбургский и Дублинский философский журнал и научный журнал . 11 (68): 229–249. дои : 10.1080/14786448108627008 . ISSN 1941-5982 .
- ^ Дарригол, Оливье (2000). Электродинамика от Ампера до Эйнштейна . Оксфорд, [Англия]: Издательство Оксфордского университета. стр. 200 , 429–430. ISBN 0-19-850593-0 .
- ^ Хевисайд, Оливер (апрель 1889 г.). «Об электромагнитных эффектах, связанных с движением электризации через диэлектрик» . Философский журнал : 324.
- ^ Лоренц, Хендрик Антун, Попытка теории электрических и оптических явлений в движущихся телах , 1895.
- ^ Дарригол, Оливье (2000). Электродинамика от Ампера до Эйнштейна . Оксфорд, [Англия]: Издательство Оксфордского университета. п. 327 . ISBN 0-19-850593-0 .
- ^ Уиттакер, ET (1910). История теорий эфира и электричества: от эпохи Декарта до конца девятнадцатого века . Лонгманс, Грин и Ко, стр. 420–423. ISBN 1-143-01208-9 .
- ^ См. Гриффитс, стр. 326, где говорится, что уравнения Максвелла «вместе с законом силы [Лоренца] ... обобщают все теоретическое содержание классической электродинамики».
- ^ «Физические эксперименты» . www.Physicsexperiment.co.uk . Архивировано из оригинала 8 июля 2018 г. Проверено 14 августа 2018 г.
- ^ Jump up to: Перейти обратно: а б См. Гриффитс, стр. 301–3.
- ^ Тай Л. Чоу (2006). Электромагнитная теория . Садбери, Массачусетс: Джонс и Бартлетт. п. 395. ИСБН 0-7637-3827-1 .
- ^ Jump up to: Перейти обратно: а б Ландау, Л.Д.; Лифшиц, Э.М.; Питаевский, Л.П. (1984). Электродинамика сплошных сред; Том 8 Курс теоретической физики (Второе изд.). Оксфорд: Баттерворт-Хайнеманн. п. §63 (§49, стр. 205–207 в издании 1960 г.). ISBN 0-7506-2634-8 .
- ^ Роджер Ф. Харрингтон (2003). Введение в электромагнитную технику . Минеола, Нью-Йорк: Dover Publications. п. 56. ИСБН 0-486-43241-6 .
- ^ МНО Садику (2007). Элементы электромагнетизма (Четвертое изд.). Нью-Йорк/Оксфорд: Издательство Оксфордского университета. п. 391. ИСБН 978-0-19-530048-2 .
- ^ Киббл, TWB (1973). Классическая механика . Европейская серия по физике (2-е изд.). МакГроу Хилл. Великобритания. ISBN 0-07-084018-0 .
- ^ Ланцос, Корнелиус (январь 1986 г.). Вариационные принципы механики (Четвертое изд.). Нью-Йорк. ISBN 0-486-65067-7 . OCLC 12949728 .
{{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка ) - ^ Джексон, JD Глава 11
- ^ Хестенес, Дэвид . «Пространственно-временное исчисление» . Архивировано из оригинала 9 мая 2021 г. Проверено 20 ноября 2011 г.
Ссылки [ править ]
Пронумерованные ссылки частично относятся к приведенному ниже списку.
- Фейнман, Ричард Филлипс ; Лейтон, Роберт Б.; Сэндс, Мэтью Л. (2006). Фейнмановские лекции по физике (3 т.) . Пирсон / Аддисон-Уэсли. ISBN 0-8053-9047-2 . : том 2.
- Гриффитс, Дэвид Дж. (1999). Введение в электродинамику (3-е изд.). Река Аппер-Сэддл, [Нью-Джерси]: Прентис-Холл. ISBN 0-13-805326-Х .
- Джексон, Джон Дэвид (1999). Классическая электродинамика (3-е изд.). Нью-Йорк, [Нью-Йорк]: Уайли. ISBN 0-471-30932-Х .
- Сервей, Раймонд А.; Джуэтт, Джон В. младший (2004). Физика для ученых и инженеров, с современной физикой . Бельмонт, [Калифорния]: Томсон Брукс/Коул. ISBN 0-534-40846-Х .
- Средницкий, Марк А. (2007). Квантовая теория поля . Кембридж, [Англия]; Нью-Йорк [Нью-Йорк]: Издательство Кембриджского университета. ISBN 978-0-521-86449-7 .
Внешние ссылки [ править ]
- Сила Лоренца (демонстрация)
- Интерактивный Java-апплет о магнитном отклонении пучка частиц в однородном магнитном поле. Архивировано 13 августа 2011 г. в Wayback Machine Вольфгангом Бауэром.





![{\displaystyle {\begin{aligned}F_{x}&=q\left(E_{x}+v_{y}B_{z}-v_{z}B_{y}\right),\\[0.5ex ]F_{y}&=q\left(E_{y}+v_{z}B_{x}-v_{x}B_{z}\right),\\[0.5ex]F_{z}&=q \left(E_{z}+v_{x}B_{y}-v_{y}B_{x}\right).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b05eb7f10282a7cd046f2249de47a690233b5229)
![{\displaystyle \mathbf {F} \left(\mathbf {r} (t), {\dot {\mathbf {r} }}(t),t,q\right)=q\left[\mathbf {E } (\mathbf {r},t)+{\dot {\mathbf {r} }}(t)\times \mathbf {B} (\mathbf {r},t)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f4d9437434d618ba0ea1ac72354bba715c7f858)







































![{\displaystyle {\begin{aligned}\mathbf {E} &=-\nabla \phi - {\frac {\partial \mathbf {A} {\partial t}} \\[1ex]\mathbf {B} &=\nabla\times\mathbf{A}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/82e6cbe4f1afe1aa0e4af564c40ca86c526a60c7)
![{\displaystyle \mathbf {F} =q\left[-\nabla \phi - {\frac {\partial \mathbf {A} {\partial t}}+\mathbf {v} \times (\nabla \times \mathbf {A} )\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8fb4e9a877320ef94bcaaf59ed4b4cdcc3b46ac3)
![{\displaystyle \mathbf {F} =q\left[-\nabla \phi - {\frac {\partial \mathbf {A} {\partial t}}+\nabla \left(\mathbf {v} \cdot \mathbf {A} \right)-\left(\mathbf {v} \cdot \nabla \right)\mathbf {A} \right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eaeed018e78d24c910e10653ad0dd3c0627ed3d9)



![{\displaystyle \mathbf {F} =q\left[-\nabla (\phi -\mathbf {v} \cdot \mathbf {A}) - {\frac {\mathrm {d} \mathbf {A} } \mathrm {d}t}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f5a8760ee13f027e93853b21c3f945b749d98fcf)
![{\displaystyle \mathbf {F} =q\left[-\nabla _ {\mathbf {x} }(\phi - {\dot {\mathbf {x} }}\cdot \mathbf {A})+{\ frac {\mathrm {d} {\mathrm {d} t}}\nabla _ {\dot {\mathbf {x} }}(\phi - {\dot {\mathbf {x} }}\cdot \mathbf {A} )\вправо]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f9949c2ff8130b2afa9bc01498342a043eda8540)












![{\displaystyle {\begin{aligned}{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L}{\partial {\dot {x}}}}=m {\ddot {x}}+q{\frac {\mathrm {d} A_{x}}{\mathrm {d} t}}&=m{\ddot {x}}+{\frac {q} \mathrm {d} t}}\left[{\frac {\partial A_{x}}{\partial t}}dt+{\frac {\partial A_{x}}{\partial x}}dx+{\frac {\partial A_{x}}{\partial y}}dy+{\frac {\partial A_{x}}{\partial z}}dz\right]\\[1ex]&=m{\ddot {x} }+q\left[{\frac {\partial A_{x}}{\partial t}}+{\frac {\partial A_{x}}{\partial x}}{\dot {x}}+{ \frac {\partial A_{x}}{\partial y}}{\dot {y}}+{\frac {\partial A_{x}}{\partial z}}{\dot {z}}\right ]\\\конец{выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/894137c78e12c60be5406b313a79815e2d503fd9)


![{\displaystyle {\begin{aligned}F_{x}&=-q\left({\frac {\partial \phi }{\partial x}}+{\frac {\partial A_{x}}{\partial t}}\right)+q\left[{\dot {y}}\left({\frac {\partial A_{y}}{\partial x}}-{\frac {\partial A_{x}} {\partial y}}\right)+{\dot {z}}\left({\frac {\partial A_{z}}{\partial x}}-{\frac {\partial A_{x}}{ \partial z}}\right)\right]\\[1ex]&=qE_{x}+q[{\dot {y}}(\nabla \times \mathbf {A} )_{z}-{\ dot {z}}(\nabla \times \mathbf {A} )_{y}]\\[1ex]&=qE_{x}+q[\mathbf {\dot {r}} \times (\nabla \ times \mathbf {A} )]_{x}\\[1ex]&=qE_{x}+q(\mathbf {\dot {r}} \times \mathbf {B} )_{x}\end{ выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc41e9215e3f4c2a35e5f987d1e8fbbbba505764)














![{\displaystyle {\frac {\mathrm {d} p^{1}}{\mathrm {d} \tau }}=q\left[U_{0}\left({\frac {E_{x}}{ c}}\right)+U_{2}(-B_{z})+U_{3}(B_{y})\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa294150a56ff4b26e8662034d72dad77daacbca)
![{\displaystyle {\frac {\mathrm {d} p^{1}}{\mathrm {d} \tau }}=q\gamma \left[c\left({\frac {E_ {x}}{c }}\right)+(-v_{y})(-B_{z})+(-v_{z})(B_{y})\right]=q\gamma \left(E_{x}+v_ {y}B_{z}-v_{z}B_{y}\right)=q\gamma \left[E_{x}+\left(\mathbf {v} \times \mathbf {B} \right)_ {x}\вправо]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c2468a743c81d45a1015d8bb2efbd8e46123b15a)
























