Квантовый гармонический осциллятор

«QHO» перенаправляется сюда. Это также код аэропорта IATA для всех аэропортов в районе Хьюстона .

Некоторые траектории гармонического осциллятора согласно Ньютона законам классической механики (A–B) и уравнению Шрёдингера квантовой механики (C–H). В A–B частица (представленная в виде шара, прикрепленного к пружине ) колеблется вперед и назад. В C–H показаны некоторые решения уравнения Шредингера, где горизонтальная ось — это положение, а вертикальная ось — действительная часть (синий) или мнимая часть (красный) волновой функции . C, D, E, F, но не G, H, являются собственными энергетическими состояниями . H — когерентное состояние — квантовое состояние, аппроксимирующее классическую траекторию.

Квантовый гармонический осциллятор является квантовомеханическим аналогом классического гармонического осциллятора . Поскольку произвольный гладкий потенциал обычно можно аппроксимировать как гармонический потенциал вблизи точки устойчивого равновесия , он является одной из наиболее важных модельных систем в квантовой механике. Более того, это одна из немногих квантово-механических систем, для которой точное аналитическое решение . известно

Одномерный гармонический осциллятор

Гамильтониан и собственные состояния энергии

Представления волновой функции для первых восьми связанных собственных состояний, n = от 0 до 7. Горизонтальная ось показывает положение x .

Соответствующие плотности вероятности.

Гамильтониан частицы : $${\hat {H}}={\frac {{\hat {p}}^{2}}{2m}}+{\frac {1}{2}}k{\hat {x}}^{2}={\frac {{\hat {p}}^{2}}{2m}}+{\frac {1}{2}}m\omega ^{2}{\hat {x}}^{2}\,,$$где m — масса частицы, k — силовая постоянная, ${\textstyle \omega ={\sqrt {k/m}}}$ - угловая частота генератора, ${\hat {x}}$ - оператор положения (задаваемый x в координатной системе), и ${\hat {p}}$ — оператор импульса (задаваемый формулой ${\hat {p}}=-i\hbar \,\partial /\partial x$ в координатном базисе). Первый член гамильтониана представляет собой кинетическую энергию частицы, а второй член представляет ее потенциальную энергию, как в законе Гука .

Независимое от времени уравнение Шредингера : $${\hat {H}}\left|\psi \right\rangle =E\left|\psi \right\rangle ~,$$где $E$ обозначает действительное число (которое необходимо определить), которое будет определять независимый от времени уровень энергии или собственное значение , и решение $|\psi \rangle$ энергии этого уровня обозначает собственное состояние .

Затем решите дифференциальное уравнение, представляющее эту проблему собственных значений в координатном базисе, для волновой функции $\langle x|\psi \rangle =\psi (x)$, используя спектральный метод . Оказывается, существует семейство решений. В этом базисе они составляют функции Эрмита , $$\psi _{n}(x)={\frac {1}{\sqrt {2^{n}\,n!}}}\left({\frac {m\omega }{\pi \hbar }}\right)^{1/4}e^{-{\frac {m\omega x^{2}}{2\hbar }}}H_{n}\left({\sqrt {\frac {m\omega }{\hbar }}}x\right),\qquad n=0,1,2,\ldots .$$

Функции H _n физиков представляют собой полиномы Эрмита , $$H_{n}(z)=(-1)^{n}~e^{z^{2}}{\frac {d^{n}}{dz^{n}}}\left(e^{-z^{2}}\right).$$

Соответствующие энергетические уровни $$E_{n}=\hbar \omega {\bigl (}n+{\tfrac {1}{2}}{\bigr )}.$$Ожидаемые значения положения и импульса в сочетании с дисперсией каждой переменной могут быть получены из волновой функции, чтобы понять поведение собственных энергетических цепей. Они показаны как ${\textstyle \langle {\hat {x}}\rangle =0}$ и ${\textstyle \langle {\hat {p}}\rangle =0}$ в силу симметричности задачи, тогда как:

$\langle {\hat {x}}^{2}\rangle =(2n+1){\frac {\hbar }{2m\omega }}=\sigma _{x}^{2}$

$\langle {\hat {p}}^{2}\rangle =(2n+1){\frac {m\hbar \omega }{2}}=\sigma _{p}^{2}$

Наблюдается увеличение дисперсии как положения, так и импульса для более высоких энергетических уровней. Самый низкий энергетический уровень имеет значение ${\textstyle \sigma _{x}\sigma _{p}={\frac {\hbar }{2}}}$ что является его минимальным значением из-за соотношения неопределенностей и также соответствует гауссовой волновой функции.

Этот энергетический спектр примечателен по трем причинам. Во-первых, энергии квантуются, а это означает, что только дискретные значения энергии (целое число плюс половина, кратное ħω возможны ); это общая особенность квантово-механических систем, когда частица удерживается. Во-вторых, эти дискретные уровни энергии расположены на одинаковом расстоянии друг от друга, в отличие от Бора модели атома или частицы в ящике . В-третьих, наименьшая достижимая энергия (энергия состояния n = 0 , называемого основным состоянием ) не равна минимуму потенциальной ямы, а находится на ħω /2 выше нее; это называется энергией нулевой точки . Из-за энергии нулевой точки положение и импульс осциллятора в основном состоянии не фиксированы (как в классическом осцилляторе), а имеют небольшой диапазон отклонений в соответствии с принципом неопределенности Гейзенберга .

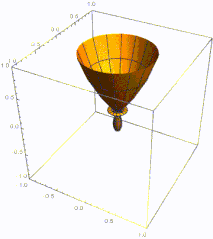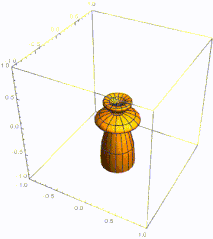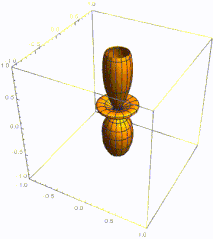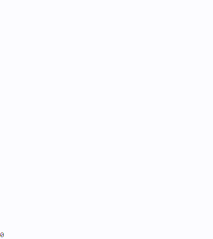
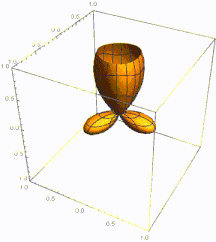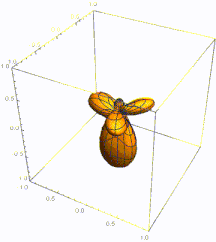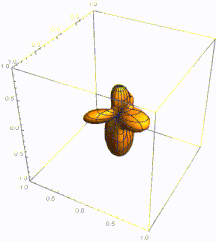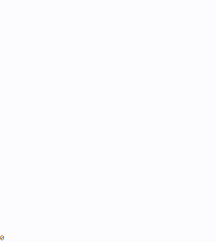
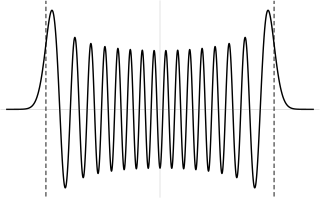
Плотность вероятности основного состояния сосредоточена в начале координат, что означает, что частица проводит большую часть своего времени на дне потенциальной ямы, как и следовало ожидать для состояния с небольшой энергией. По мере увеличения энергии плотность вероятности достигает максимума в классических «точках поворота», когда энергия состояния совпадает с потенциальной энергией. (См. обсуждение высоковозбужденных состояний ниже.) Это согласуется с классическим гармоническим осциллятором, в котором частица проводит большую часть своего времени (и, следовательно, с большей вероятностью ее можно обнаружить) вблизи точек поворота, где она перемещает самый медленный. Таким образом, принцип соответствия соблюдается. Более того, специальные недисперсионные волновые пакеты с минимальной неопределенностью, называемые когерентными состояниями, колеблются очень похоже на классические объекты, как показано на рисунке; они не являются собственными состояниями гамильтониана.

Метод лестничного оператора

Плотности вероятности | ψ _п ( Икс )| ² для связанных собственных состояний, начиная с основного состояния ( n = 0) внизу и увеличивая энергию кверху. Горизонтальная ось показывает положение x , а более яркие цвета обозначают более высокие плотности вероятности.

Метод « лестничного оператора », разработанный Полем Дираком , позволяет извлекать собственные значения энергии без непосредственного решения дифференциального уравнения. Его можно обобщить на более сложные задачи, особенно на квантовую теорию поля . Следуя этому подходу, мы определяем операторы a и сопряженный с ним a ^† , $${\begin{aligned}a&={\sqrt {m\omega \over 2\hbar }}\left({\hat {x}}+{i \over m\omega }{\hat {p}}\right)\\a^{\dagger }&={\sqrt {m\omega \over 2\hbar }}\left({\hat {x}}-{i \over m\omega }{\hat {p}}\right)\end{aligned}}$$Обратите внимание, что эти операторы классически являются в точности генераторами нормированного вращения в фазовом пространстве $x$ и $m{\frac {dx}{dt}}$, т.е. они описывают прямую и обратную эволюцию во времени классического гармонического осциллятора.

Эти операторы приводят к следующему представлению ${\hat {x}}$ и ${\hat {p}}$, $${\begin{aligned}{\hat {x}}&={\sqrt {\frac {\hbar }{2m\omega }}}(a^{\dagger }+a)\\{\hat {p}}&=i{\sqrt {\frac {\hbar m\omega }{2}}}(a^{\dagger }-a)~.\end{aligned}}$$

Оператор a не является эрмитовым , так как он сам и сопряженный с ним a ^† не равны. Собственные состояния энергии | n ⟩ , когда над ними работают эти лестничные операторы, дайте $${\begin{aligned}a^{\dagger }|n\rangle &={\sqrt {n+1}}|n+1\rangle \\a|n\rangle &={\sqrt {n}}|n-1\rangle .\end{aligned}}$$

Из приведенных выше соотношений мы также можем определить числовой оператор N , который обладает следующим свойством: $${\begin{aligned}N&=a^{\dagger }a\\N\left|n\right\rangle &=n\left|n\right\rangle .\end{aligned}}$$

Следующие коммутаторы можно легко получить, подставив каноническое коммутационное соотношение : $$[a,a^{\dagger }]=1,\qquad [N,a^{\dagger }]=a^{\dagger },\qquad [N,a]=-a,$$

а оператор Гамильтона можно выразить как $${\hat {H}}=\hbar \omega \left(N+{\frac {1}{2}}\right),$$

поэтому собственные состояния N также являются собственными состояниями энергии.Чтобы увидеть это, мы можем применить ${\hat {H}}$ в числовое состояние $|n\rangle$:

$${\hat {H}}|n\rangle =\hbar \omega \left({\hat {N}}+{\frac {1}{2}}\right)|n\rangle .$$

Использование свойства числового оператора ${\hat {N}}$:

$${\hat {N}}|n\rangle =n|n\rangle ,$$

мы получаем:

$${\hat {H}}|n\rangle =\hbar \omega \left(n+{\frac {1}{2}}\right)|n\rangle .$$

Таким образом, поскольку $|n\rangle$ решает TISE для гамильтониана ${\hat {H}}$, также является одним из его собственных состояний с соответствующим собственным значением:

$$E_{n}=\hbar \omega \left(n+{\frac {1}{2}}\right).$$

ЯВЛЯЕТСЯ

Свойство коммутации дает $${\begin{aligned}Na^{\dagger }|n\rangle &=\left(a^{\dagger }N+[N,a^{\dagger }]\right)|n\rangle \\&=\left(a^{\dagger }N+a^{\dagger }\right)|n\rangle \\&=(n+1)a^{\dagger }|n\rangle ,\end{aligned}}$$

и аналогично, $$Na|n\rangle =(n-1)a|n\rangle .$$

Это означает, что действует на | n ⟩ производить с точностью до мультипликативной константы | n –1⟩ и ​ ^† действует на | п ⟩ производить | п +1⟩ . По этой причине оператор а называется оператором уничтожения («оператором понижения»), а оператором а. ^† оператор создания («оператор повышения»). Два оператора вместе называются лестничными операторами .

Учитывая любое собственное состояние энергии, мы можем воздействовать на него с помощью понижающего оператора a , чтобы создать другое собственное состояние с энергией на ħω меньшей. Кажется, что путем многократного применения понижающего оператора мы можем создавать собственные состояния энергии вплоть до E = −∞ . Однако, поскольку $$n=\langle n|N|n\rangle =\langle n|a^{\dagger }a|n\rangle ={\Bigl (}a|n\rangle {\Bigr )}^{\dagger }a|n\rangle \geqslant 0,$$

наименьшее собственное значение числового оператора равно 0, а $$a\left|0\right\rangle =0.$$

В этом случае последующие применения понижающего оператора просто дадут ноль вместо дополнительных собственных состояний энергии. Более того, мы показали выше, что $${\hat {H}}\left|0\right\rangle ={\frac {\hbar \omega }{2}}\left|0\right\rangle$$

Наконец, воздействуя на |0⟩ с помощью оператора повышения и умножая на подходящие коэффициенты нормализации , мы можем создать бесконечный набор собственных состояний энергии $$\left\{\left|0\right\rangle ,\left|1\right\rangle ,\left|2\right\rangle ,\ldots ,\left|n\right\rangle ,\ldots \right\},$$

такой, что $${\hat {H}}\left|n\right\rangle =\hbar \omega \left(n+{\frac {1}{2}}\right)\left|n\right\rangle ,$$что соответствует энергетическому спектру, приведенному в предыдущем разделе.

Произвольные собственные состояния могут быть выражены через |0⟩, $$|n\rangle ={\frac {(a^{\dagger })^{n}}{\sqrt {n!}}}|0\rangle .$$

Доказательство

$${\begin{aligned}\langle n|aa^{\dagger }|n\rangle &=\langle n|\left([a,a^{\dagger }]+a^{\dagger }a\right)\left|n\right\rangle =\langle n|\left(N+1\right)|n\rangle =n+1\\[1ex]\Rightarrow a^{\dagger }|n\rangle &={\sqrt {n+1}}|n+1\rangle \\[1ex]\Rightarrow |n\rangle &={\frac {1}{\sqrt {n}}}a^{\dagger }\left|n-1\right\rangle ={\frac {1}{\sqrt {n(n-1)}}}\left(a^{\dagger }\right)^{2}\left|n-2\right\rangle =\cdots ={\frac {1}{\sqrt {n!}}}\left(a^{\dagger }\right)^{n}\left|0\right\rangle .\end{aligned}}$$

Аналитические вопросы

Предыдущий анализ является алгебраическим и использует только коммутационные соотношения между повышающими и понижающими операторами. После завершения алгебраического анализа следует обратиться к аналитическим вопросам. Сначала следует найти основное состояние, то есть решение уравнения $a\psi _{0}=0$. В позиционном представлении это дифференциальное уравнение первого порядка $$\left(x+{\frac {\hbar }{m\omega }}{\frac {d}{dx}}\right)\psi _{0}=0,$$решением которого легко найти гауссову $$\psi _{0}(x)=Ce^{-{\frac {m\omega x^{2}}{2\hbar }}}.$$Концептуально важно, что существует только одно решение этого уравнения; если бы существовало, скажем, два линейно независимых основных состояния, мы получили бы две независимые цепочки собственных векторов гармонического осциллятора. После того, как основное состояние вычислено, можно индуктивно показать, что возбужденные состояния представляют собой полиномы Эрмита, умноженные на гауссово основное состояние, используя явную форму повышающего оператора в представлении положения. Можно также доказать, что, как и ожидалось исходя из единственности основного состояния, собственные состояния энергии функций Эрмита $\psi _{n}$ построенные лестничным методом образуют полный ортонормированный набор функций.

Явно связываясь с предыдущим разделом, основное состояние |0⟩ в представлении положения определяется выражением $a|0\rangle =0$, $$\left\langle x\mid a\mid 0\right\rangle =0\qquad \Rightarrow \left(x+{\frac {\hbar }{m\omega }}{\frac {d}{dx}}\right)\left\langle x\mid 0\right\rangle =0\qquad \Rightarrow$$$$\left\langle x\mid 0\right\rangle =\left({\frac {m\omega }{\pi \hbar }}\right)^{\frac {1}{4}}\exp \left(-{\frac {m\omega }{2\hbar }}x^{2}\right)=\psi _{0}~,$$следовательно $$\langle x\mid a^{\dagger }\mid 0\rangle =\psi _{1}(x)~,$$так что $\psi _{1}(x,t)=\langle x\mid e^{-3i\omega t/2}a^{\dagger }\mid 0\rangle$, и так далее.

Естественная длина и энергетические масштабы

См. Также: Формулировка интеграла по траектории § Простой гармонический осциллятор.

Квантовый гармонический осциллятор обладает естественными масштабами длины и энергии, которые можно использовать для упрощения задачи. Их можно найти путем обезразмеривания .

В результате, если энергия измеряется в единицах ħω , а расстояние в единицах √ ħ /( mω ) , то гамильтониан упрощается до $$H=-{\frac {1}{2}}{d^{2} \over dx^{2}}+{\frac {1}{2}}x^{2},$$в то время как собственные функции и собственные значения энергии упрощаются до функций Эрмита и целых чисел, смещенных вдвое, $$\psi _{n}(x)=\left\langle x\mid n\right\rangle ={1 \over {\sqrt {2^{n}n!}}}~\pi ^{-1/4}\exp(-x^{2}/2)~H_{n}(x),$$$$E_{n}=n+{\tfrac {1}{2}}~,$$где Hn _. ( x ) — Эрмита полиномы

Во избежание путаницы эти «естественные единицы» в этой статье в большинстве случаев использоваться не будут. Однако они часто пригодятся при выполнении расчетов, позволяя избежать беспорядка.

Например, фундаментальное решение ( пропагатор ) H − i∂ _t , зависящего от времени оператора Шрёдингера для этого осциллятора, просто сводится к ядру Мелера , $$\langle x\mid \exp(-itH)\mid y\rangle \equiv K(x,y;t)={\frac {1}{\sqrt {2\pi i\sin t}}}\exp \left({\frac {i}{2\sin t}}\left((x^{2}+y^{2})\cos t-2xy\right)\right)~,$$где K ( Икс , y ;0) знак равно δ ( Икс - y ) . Тогда наиболее общее решение для данной начальной конфигурации ψ ( x ,0) будет просто $$\psi (x,t)=\int dy~K(x,y;t)\psi (y,0)\,.$$

Когерентные состояния

Основная статья: Когерентное состояние

Эволюция во времени распределения вероятностей (и фазы, показанной цветом) когерентного состояния с | α |=3.

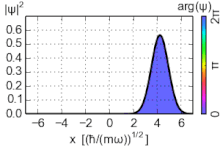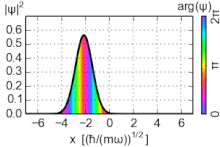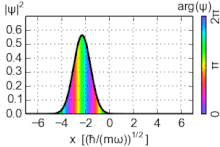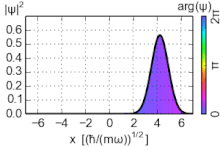
Когерентные состояния (также известные как глауберовые состояния) гармонического осциллятора представляют собой специальные недисперсионные волновые пакеты с минимальной неопределенностью σ _x σ _p = ℏ ⁄ 2 , чьи наблюдаемых ожидаемые значения развиваются как классическая система. Они являются собственными векторами оператора уничтожения, а не гамильтониана, и образуют сверхполный базис, который, следовательно, лишен ортогональности.

Когерентные состояния индексируются $\alpha \in \mathbb {C}$ и выражается в | n ⟩ базис как

$$|\alpha \rangle =\sum _{n=0}^{\infty }|n\rangle \langle n|\alpha \rangle =e^{-{\frac {1}{2}}|\alpha |^{2}}\sum _{n=0}^{\infty }{\frac {\alpha ^{n}}{\sqrt {n!}}}|n\rangle =e^{-{\frac {1}{2}}|\alpha |^{2}}e^{\alpha a^{\dagger }}e^{-{\alpha ^{*}a}}|0\rangle .$$

Поскольку когерентные состояния не являются собственными энергетическими состояниями, их эволюция во времени не является простым сдвигом фазы волновой функции. Однако развивающиеся во времени состояния также являются когерентными состояниями, но вместо этого имеют параметр фазового сдвига α : $\alpha (t)=\alpha (0)e^{-i\omega t}=\alpha _{0}e^{-i\omega t}$. $$|\alpha (t)\rangle =\sum _{n=0}^{\infty }e^{-i\left(n+{\frac {1}{2}}\right)\omega t}|n\rangle \langle n|\alpha \rangle =e^{\frac {-i\omega t}{2}}e^{-{\frac {1}{2}}|\alpha |^{2}}\sum _{n=0}^{\infty }{\frac {(\alpha e^{-i\omega t})^{n}}{\sqrt {n!}}}|n\rangle =e^{-{\frac {i\omega t}{2}}}|\alpha e^{-i\omega t}\rangle$$

Потому что $a\left|0\right\rangle =0$ и через тождество Кермака-МакКрея последняя форма эквивалентна унитарному оператору смещения, действующему на основное состояние: $|\alpha \rangle =e^{\alpha {\hat {a}}^{\dagger }-\alpha ^{*}{\hat {a}}}|0\rangle =D(\alpha )|0\rangle$. Вычисление ожидаемых значений:

$\langle {\hat {x}}\rangle _{\alpha (t)}={\sqrt {\frac {2\hbar }{m\omega }}}|\alpha _{0}|\cos {(\omega t-\phi )}$

$\langle {\hat {p}}\rangle _{\alpha (t)}=-{\sqrt {2m\hbar \omega }}|\alpha _{0}|\sin {(\omega t-\phi )}$

где $\phi$ — фаза, вносимая комплексом α . Эти уравнения подтверждают колебательное поведение частицы.

Неопределенности, рассчитанные с использованием численного метода, составляют:

$\sigma _{x}(t)={\sqrt {\frac {\hbar }{2m\omega }}}$

$\sigma _{p}(t)={\sqrt {\frac {m\hbar \omega }{2}}}$

что дает ${\textstyle \sigma _{x}(t)\sigma _{p}(t)={\frac {\hbar }{2}}}$. Поскольку единственная волновая функция, которая может иметь наименьшую неопределенность положения-импульса, ${\textstyle {\frac {\hbar }{2}}}$, является гауссовой волновой функцией, и поскольку волновая функция когерентного состояния имеет минимальную неопределенность положения-импульса, мы отмечаем, что общая гауссова волновая функция в квантовой механике имеет вид: $$\psi _{\alpha }(x')=\left({\frac {m\omega }{\pi \hbar }}\right)^{\frac {1}{4}}e^{{\frac {i}{\hbar }}\langle {\hat {p}}\rangle _{\alpha }(x'-{\frac {\langle {\hat {x}}\rangle _{\alpha }}{2}})-{\frac {m\omega }{2\hbar }}(x'-\langle {\hat {x}}\rangle _{\alpha })^{2}}.$$Подстановка значений ожидания как функции времени дает требуемую волновую функцию, изменяющуюся во времени.

Вероятность каждого собственного состояния энергии можно рассчитать, чтобы найти распределение энергии волновой функции:

$P(E_{n})=|\langle n|\alpha \rangle |^{2}={\frac {e^{-|\alpha |^{2}}|\alpha |^{2n}}{n!}}$

что соответствует распределению Пуассона .

Сильно возбужденные состояния

Волновая функция (вверху) и плотность вероятности (внизу) для n = 30 возбужденного состояния квантового гармонического осциллятора с . Вертикальные пунктирные линии обозначают классические точки поворота, а пунктирная линия представляет классическую плотность вероятности.

При больших n собственные состояния локализуются в классической разрешенной области, т. е. в области, в которой . _{классическая частица с энергией En} может двигаться Собственные состояния имеют максимум вблизи точек поворота: точек на концах классически разрешенной области, где классическая частица меняет направление. Это явление можно проверить с помощью асимптотики полиномов Эрмита , а также с помощью приближения ВКБ .

Частота колебаний в точке x пропорциональна импульсу p ( x ) классической частицы с энергией En _и положением x . Более того, квадрат амплитуды (определяющий плотность вероятности) обратно пропорционален p ( x ) , отражая время, в течение которого классическая частица проводит вблизи x . Поведение системы в малой окрестности точки поворота не имеет простого классического объяснения, но может быть смоделировано с помощью функции Эйри . Используя свойства функции Эйри, можно оценить вероятность обнаружения частицы вне классически разрешенной области приблизительно равной $${\frac {2}{n^{1/3}3^{2/3}\Gamma ^{2}({\tfrac {1}{3}})}}={\frac {1}{n^{1/3}\cdot 7.46408092658...}}$$Это также асимптотически определяется интегралом $${\frac {1}{2\pi }}\int _{0}^{\infty }e^{(2n+1)\left(x-{\tfrac {1}{2}}\sinh(2x)\right)}dx~.$$

Решения для фазового пространства

В формулировке квантовой механики в фазовом пространстве собственные состояния квантового гармонического осциллятора в нескольких различных представлениях распределения квазивероятностей могут быть записаны в замкнутой форме. Наиболее широко из них используется квазивероятностное распределение Вигнера .

Распределение квазивероятностей Вигнера для собственного состояния энергии | n ⟩ в натуральных единицах, описанных выше, $$F_{n}(x,p)={\frac {(-1)^{n}}{\pi \hbar }}L_{n}\left(2(x^{2}+p^{2})\right)e^{-(x^{2}+p^{2})}\,,$$где L _n — полиномы Лагерра . Этот пример иллюстрирует, как полиномы Эрмита и Лагерра связаны через карту Вигнера .

Между тем, Q-функция Хусими собственных состояний гармонического осциллятора имеет еще более простой вид. Если мы будем работать в натуральных единицах, описанных выше, мы получим $$Q_{n}(x,p)={\frac {(x^{2}+p^{2})^{n}}{n!}}{\frac {e^{-(x^{2}+p^{2})}}{\pi }}$$Это утверждение можно проверить с помощью преобразования Сигала – Баргмана . В частности, поскольку повышающий оператор в представлении Сигала – Баргмана представляет собой просто умножение на $z=x+ip$ а основное состояние — это постоянная функция 1, нормированные состояния гармонического осциллятора в этом представлении просто $z^{n}/{\sqrt {n!}}$ . На этом этапе мы можем обратиться к формуле для Q-функции Хусими в терминах преобразования Сигала – Баргмана.

N -мерный изотропный гармонический осциллятор

Одномерный гармонический осциллятор легко обобщается на N измерений, где N = 1, 2, 3,… . В одном измерении положение частицы задавалось координатой одной x . В N измерениях это заменяется N координатами положения, которые мы обозначаем x ₁ , …, x _N . Каждой координате положения соответствует импульс; мы обозначаем их p ₁ , …, p _N . Канонические коммутационные соотношения между этими операторами имеют вид $${\begin{aligned}{[}x_{i},p_{j}{]}&=i\hbar \delta _{i,j}\\{[}x_{i},x_{j}{]}&=0\\{[}p_{i},p_{j}{]}&=0\end{aligned}}$$

Гамильтониан для этой системы есть $$H=\sum _{i=1}^{N}\left({p_{i}^{2} \over 2m}+{1 \over 2}m\omega ^{2}x_{i}^{2}\right).$$

Как ясно видно из формы этого гамильтониана, N -мерный гармонический осциллятор точно аналогичен N независимым одномерным гармоническим осцилляторам с той же массой и жесткостью пружины. В этом случае величины x ₁ , ..., x _N будут относиться к положениям каждой из N частиц. Это удобное свойство r ² потенциал, позволяющий разделить потенциальную энергию на слагаемые, зависящие каждое от одной координаты.

Это наблюдение делает решение простым. Для определенного набора квантовых чисел $\{n\}\equiv \{n_{1},n_{2},\dots ,n_{N}\}$ собственные функции энергии N -мерного осциллятора выражаются через одномерные собственные функции как:

$$\langle \mathbf {x} |\psi _{\{n\}}\rangle =\prod _{i=1}^{N}\langle x_{i}\mid \psi _{n_{i}}\rangle$$

В методе лестничных операторов мы определяем N наборов лестничных операторов,

$${\begin{aligned}a_{i}&={\sqrt {m\omega \over 2\hbar }}\left(x_{i}+{i \over m\omega }p_{i}\right),\\a_{i}^{\dagger }&={\sqrt {m\omega \over 2\hbar }}\left(x_{i}-{i \over m\omega }p_{i}\right).\end{aligned}}$$

Затем, используя процедуру, аналогичную одномерному случаю, мы можем показать, что каждый из a _i и a ^† _i операторы понижают и повышают энергию на ℏω соответственно. Гамильтониан $$H=\hbar \omega \,\sum _{i=1}^{N}\left(a_{i}^{\dagger }\,a_{i}+{\frac {1}{2}}\right).$$Этот гамильтониан инвариантен относительно динамической группы симметрии U ( N ) (унитарной группы в N измерениях), определяемой формулой $$U\,a_{i}^{\dagger }\,U^{\dagger }=\sum _{j=1}^{N}a_{j}^{\dagger }\,U_{ji}\quad {\text{for all}}\quad U\in U(N),$$где $U_{ji}$ является элементом определяющего матричного представления U ( N ) .

Энергетические уровни системы $$E=\hbar \omega \left[(n_{1}+\cdots +n_{N})+{N \over 2}\right].$$$$n_{i}=0,1,2,\dots \quad ({\text{the energy level in dimension }}i).$$

Как и в одномерном случае, энергия квантуется. Энергия основного состояния в N раз превышает одномерную основную энергию, как и следовало ожидать, используя аналогию с N независимыми одномерными осцилляторами. Есть еще одно отличие: в одномерном случае каждому энергетическому уровню соответствует уникальное квантовое состояние. В N -мерностях, за исключением основного состояния, уровни энергии вырождены , то есть существует несколько состояний с одинаковой энергией.

Вырождение можно относительно легко вычислить. В качестве примера рассмотрим трехмерный случай: Определите n = n ₁ + n ₂ + n ₃ . Все состояния с одинаковым n будут иметь одинаковую энергию. Для данного n мы выбираем конкретное n ₁ . Тогда п ₂ + п ₃ знак равно п - п ₁ . Существует n − n ₁ + 1 возможных пар { n ₂ , n ₃ } . n ₂ может принимать значения от 0 до n − n ₁ , и для каждого n ₂ значение n ₃ фиксировано. Таким образом, степень вырождения равна: $$g_{n}=\sum _{n_{1}=0}^{n}n-n_{1}+1={\frac {(n+1)(n+2)}{2}}$$Формула для общих N и n [ g _n — размерность симметричного неприводимого представления n -й степени унитарной группы U ( N ) ]: $$g_{n}={\binom {N+n-1}{n}}$$ Приведенный выше частный случай N = 3 непосредственно следует из этого общего уравнения. Однако это верно только для различимых частиц или одной частицы в N измерениях (поскольку измерения различимы). В случае N бозонов в одномерной гармонической ловушке вырождение масштабируется как количество способов разбить целое число n, целые числа, меньшие или равные N. используя

$$g_{n}=p(N_{-},n)$$

Это возникает из-за ограничения помещения N квантов в состояние кет, где ${\textstyle \sum _{k=0}^{\infty }kn_{k}=n}$ и ${\textstyle \sum _{k=0}^{\infty }n_{k}=N}$, которые являются теми же ограничениями, что и в целочисленном разделе.

Пример: 3D изотропный гармонический генератор.

Трехмерные сферические гармонические орбитальные решения Шрёдингера на двумерных графиках плотности; исходный код Mathematica , который использовался для создания графиков, находится вверху.

Уравнение Шредингера для частицы в сферически-симметричном трехмерном гармоническом осцилляторе можно решить явно путем разделения переменных; см. эту статью для настоящего случая. Эта процедура аналогична разделению, выполненному в задаче о водородоподобном атоме , но с другим сферически-симметричным потенциалом. $$V(r)={1 \over 2}\mu \omega ^{2}r^{2},$$где ц — масса частицы. Поскольку m будет использоваться ниже для магнитного квантового числа, масса обозначается как μ вместо m , как ранее в этой статье.

Решение уравнения: $$\psi _{klm}(r,\theta ,\phi )=N_{kl}r^{l}e^{-\nu r^{2}}L_{k}^{\left(l+{1 \over 2}\right)}(2\nu r^{2})Y_{lm}(\theta ,\phi )$$где

$N_{kl}={\sqrt {{\sqrt {\frac {2\nu ^{3}}{\pi }}}{\frac {2^{k+2l+3}\;k!\;\nu ^{l}}{(2k+2l+1)!!}}}}~~$ – константа нормировки; $\nu \equiv {\mu \omega \over 2\hbar }~$;

${L_{k}}^{(l+{1 \over 2})}(2\nu r^{2})$

— обобщенные полиномы Лагерра ; Порядок k многочлена является неотрицательным целым числом;

• $Y_{lm}(\theta ,\phi )\,$ – сферическая гармоническая функция ;
• ħ — приведенная постоянная Планка : $\hbar \equiv {\frac {h}{2\pi }}~.$

Собственное значение энергии $$E=\hbar \omega \left(2k+l+{\frac {3}{2}}\right).$$Энергия обычно описывается одним квантовым числом $$n\equiv 2k+l\,.$$

Поскольку k — неотрицательное целое число, для каждого четного n имеем ℓ = 0, 2, …, n − 2, n, а для каждого нечетного n имеем ℓ = 1, 3, …, n − 2, n . Магнитное квантовое число m является целым числом, удовлетворяющим − ℓ ≤ m ≤ ℓ , поэтому для каждых n и ℓ существует 2 ℓ + 1 различных квантовых состояний , помеченных m . Таким образом, вырождение на уровне n равно $$\sum _{l=\ldots ,n-2,n}(2l+1)={(n+1)(n+2) \over 2}\,,$$где сумма начинается с 0 или 1, в зависимости от того, является ли n четным или нечетным.Этот результат соответствует приведенной выше формуле размерности и представляет собой размерность симметричного представления SU(3) , соответствующую группу вырождения.

Приложения

Решетка гармонических осцилляторов: фононы

Смотрите также: Каноническое квантование

Обозначение гармонического осциллятора можно распространить на одномерную решетку из многих частиц. Рассмотрим одномерную квантовомеханическую гармоническую цепочку из N одинаковых атомов. Это простейшая квантовомеханическая модель решетки, и мы увидим, как фононы из нее возникают . Формализм, который мы разработаем для этой модели, легко обобщается на два и три измерения.

Как и в предыдущем разделе, мы обозначаем положения масс через x ₁ , x ₂ , … , измеренные от их положений равновесия (т. е. x _i = 0, если частица i находится в положении равновесия). В двух или более измерениях x _i являются векторными величинами. Гамильтониан есть для этой системы

$$\mathbf {H} =\sum _{i=1}^{N}{p_{i}^{2} \over 2m}+{1 \over 2}m\omega ^{2}\sum _{\{ij\}(nn)}(x_{i}-x_{j})^{2}\,,$$где m — (предполагаемая однородная) масса каждого атома, а x _i и pi _— положения и импульса операторы i- го атома, а сумма производится по ближайшим соседям (nn). Однако принято переписывать гамильтониан в терминах нормальных мод а волнового вектора, не в терминах координат частицы, чтобы можно было работать в более удобном пространстве Фурье .

Суперпозиция трех колеблющихся диполей - иллюстрирует распространение во времени общей волновой функции для разных n,l,m.

Затем мы вводим набор из s и N _, « сопряженных импульсов N «нормальных координат» Qk, определенных как дискретные преобразования Фурье x » Π , определенных как преобразования Фурье p s, $$Q_{k}={1 \over {\sqrt {N}}}\sum _{l}e^{ikal}x_{l}$$$$\Pi _{k}={1 \over {\sqrt {N}}}\sum _{l}e^{-ikal}p_{l}\,.$$

Величина k _n окажется волновым числом фонона, т. е. 2 π, деленным на длину волны . Он принимает квантованные значения, поскольку число атомов конечно.

Это сохраняет желаемые коммутационные соотношения либо в реальном пространстве, либо в пространстве волновых векторов.

Другая иллюстрация распространения во времени общей волновой функции для трех разных атомов подчеркивает влияние углового момента на поведение распределения

$${\begin{aligned}\left[x_{l},p_{m}\right]&=i\hbar \delta _{l,m}\\\left[Q_{k},\Pi _{k'}\right]&={1 \over N}\sum _{l,m}e^{ikal}e^{-ik'am}[x_{l},p_{m}]\\&={i\hbar \over N}\sum _{m}e^{iam(k-k')}=i\hbar \delta _{k,k'}\\\left[Q_{k},Q_{k'}\right]&=\left[\Pi _{k},\Pi _{k'}\right]=0~.\end{aligned}}$$

Из общего результата $${\begin{aligned}\sum _{l}x_{l}x_{l+m}&={1 \over N}\sum _{kk'}Q_{k}Q_{k'}\sum _{l}e^{ial\left(k+k'\right)}e^{iamk'}=\sum _{k}Q_{k}Q_{-k}e^{iamk}\\\sum _{l}{p_{l}}^{2}&=\sum _{k}\Pi _{k}\Pi _{-k}~,\end{aligned}}$$с помощью элементарной тригонометрии легко показать, что член потенциальной энергии равен $${1 \over 2}m\omega ^{2}\sum _{j}(x_{j}-x_{j+1})^{2}={1 \over 2}m\omega ^{2}\sum _{k}Q_{k}Q_{-k}(2-e^{ika}-e^{-ika})={1 \over 2}m\sum _{k}{\omega _{k}}^{2}Q_{k}Q_{-k}~,$$где $$\omega _{k}={\sqrt {2\omega ^{2}(1-\cos(ka))}}~.$$

Гамильтониан можно записать в пространстве волновых векторов как $$\mathbf {H} ={1 \over {2m}}\sum _{k}\left({\Pi _{k}\Pi _{-k}}+m^{2}\omega _{k}^{2}Q_{k}Q_{-k}\right)~.$$

Обратите внимание, что связи между переменными положения были преобразованы; если бы Q и Π были эрмитовыми (а это не так), преобразованный гамильтониан описывал бы N несвязанных гармонических осцилляторов.

Форма квантования зависит от выбора граничных условий; для простоты мы налагаем периодические граничные условия, определяя ( N + 1) -й атом как эквивалентный первому атому. Физически это соответствует соединению концов цепи. Результирующее квантование

$$k=k_{n}={2n\pi \over Na}\quad {\hbox{for}}\ n=0,\pm 1,\pm 2,\ldots ,\pm {N \over 2}.$$

Верхняя граница n определяется минимальной длиной волны, которая в два раза превышает шаг решетки a , как обсуждалось выше.

Собственные значения или уровни энергии гармонического осциллятора для моды ω _k равны $$E_{n}=\left({1 \over 2}+n\right)\hbar \omega _{k}\quad {\hbox{for}}\quad n=0,1,2,3,\ldots$$

Если мы пренебрегаем нулевой энергией , то уровни будут равномерно распределены между собой. $${\tfrac {3}{2}}\hbar \omega ,\ {\tfrac {5}{2}}\hbar \omega ,\ {\tfrac {7}{2}}\hbar \omega \ \cdots$$

Таким образом, точное количество энергии ħω должно быть передано в решетку гармонического осциллятора, чтобы подтолкнуть ее на следующий энергетический уровень. По аналогии со случаем фотона , когда электромагнитное поле квантовано, квант колебательной энергии называется фононом .

Все квантовые системы обладают волновыми и корпускулярными свойствами. Частичноподобные свойства фонона лучше всего понять с помощью методов вторичного квантования и операторных методов, описанных в других источниках.

В континуума пределе a → 0 , N → ∞ , в то время как Na остается фиксированным. Канонические координаты Q _k переходят в несвязанные моды импульса скалярного поля: $\phi _{k}$, в то время как индекс местоположения i ( а не динамическая переменная смещения ) становится аргументом параметра x скалярного поля, $\phi (x,t)$.

Молекулярные вибрации

Основная статья: Молекулярная вибрация

• Колебания двухатомной молекулы являются примером двухчастичной версии квантового гармонического осциллятора. В этом случае угловая частота определяется выражением $$\omega ={\sqrt {\frac {k}{\mu }}}$$ где $\mu ={\frac {m_{1}m_{2}}{m_{1}+m_{2}}}$ это приведенная масса и $m_{1}$ и $m_{2}$ - массы двух атомов.
• Атом Гука — это простая модель атома гелия , использующая квантовый гармонический осциллятор.
• Моделирование фононов, как обсуждалось выше.
• Плата $q$ с массой $m$ в однородном магнитном поле $\mathbf {B}$ является примером одномерного квантового гармонического осциллятора: квантования Ландау .

См. также

• Столько же, сколько маятник
• Квантовая машина - созданное человеком устройство, коллективное движение которого подчиняется законам квантовой механики. Страницы, отображающие описания из Викиданных в качестве запасного варианта.
• Газ в гармонической ловушке – Квантовомеханическая модель
• Операторы рождения и уничтожения - операторы, полезные в квантовой механике.
• Когерентное состояние - особое квантовое состояние квантового гармонического осциллятора.
• Потенциал Морса - Модель потенциальной энергии двухатомной молекулы.
• Теорема Бертрана - Физическая теорема
• Ядро Мелера
• Молекулярная вибрация - периодическое движение атомов молекулы.

Библиография

• Гриффитс, Дэвид Дж. (2004). Введение в квантовую механику (2-е изд.). Прентис Холл. ISBN  978-0-13-805326-0 .
• Либофф, Ричард Л. (2002). Введение в квантовую механику . Аддисон-Уэсли. ISBN  978-0-8053-8714-8 .
• Цвибах, Бартон (2022). Освоение квантовой механики: основы, теория и приложения . С Прессой. ISBN  978-0-262-04613-8 .

Внешние ссылки

• Квантовый гармонический осциллятор
• Обоснование выбора лестничных операторов
• Живые трехмерные графики интенсивности квантового гармонического осциллятора. Архивировано 12 июля 2011 г. на Wayback Machine.
• Управляемый и затухающий квантовый гармонический генератор (конспект лекций курса «Квантовая оптика в электрических цепях»)