Преобразование Мёбиуса

Не путать с преобразованием Мёбиуса или функцией Мёбиуса .

В геометрии и комплексном анализе комплексной преобразование Мёбиуса плоскости представляет собой рациональную функцию вида $$f(z)={\frac {az+b}{cz+d}}$$одной комплексной переменной z ; здесь коэффициенты a , b , c , d являются комплексными числами, удовлетворяющими условию ad − bc ≠ 0 .

Геометрически преобразование Мёбиуса можно получить, сначала применив обратную стереографическую проекцию плоскости к единичной сфере , переместив и повернув сферу в новое место и ориентацию в пространстве, а затем применив стереографическую проекцию для отображения сферы обратно в самолет. Эти преобразования сохраняют углы, сопоставляют каждую прямую линию с линией или кругом и сопоставляют каждый круг с линией или кругом.

Преобразования Мёбиуса — это проективные преобразования комплексной проективной прямой . Они образуют группу , называемую группой Мёбиуса , которая является проективной линейной группой PGL(2, C ) . Вместе со своими подгруппами он имеет многочисленные приложения в математике и физике.

Геометрии Мёбиуса и их преобразования обобщают этот случай на любое количество измерений в других полях.

Преобразования Мёбиуса названы в честь Августа Фердинанда Мёбиуса ; они являются примером гомографий , дробно-линейных преобразований , билинейных преобразований и спиновых преобразований (в теории относительности).

Обзор

Преобразования Мёбиуса определены на расширенной комплексной плоскости ${\widehat {\mathbb {C} }}=\mathbb {C} \cup \{\infty \}$ (т.е. комплексная плоскость , дополненная бесконечной точкой ).

Стереографическая проекция определяет ${\widehat {\mathbb {C} }}$ со сферой, которую тогда называют сферой Римана ; альтернативно, ${\widehat {\mathbb {C} }}$ можно представить как комплексную проективную линию $\mathbb {C} \mathbb {P} ^{1}$. Преобразования Мёбиуса — это в точности биективные конформные отображения сферы Римана в себя, т. е. автоморфизмы сферы Римана как комплексного многообразия ; альтернативно, они являются автоморфизмами $\mathbb {C} \mathbb {P} ^{1}$ как алгебраическое многообразие. Следовательно, множество всех преобразований Мёбиуса образует группу по составу . Эту группу называют группой Мёбиуса и иногда обозначают $\operatorname {Aut} ({\widehat {\mathbb {C} }})$.

Группа Мёбиуса изоморфна группе сохраняющих ориентацию изометрий гиперболического 3-пространства и поэтому играет важную роль при изучении гиперболических 3-многообразий .

В физике единичная компонента группы Лоренца действует на небесную сферу так же, как группа Мёбиуса действует на сферу Римана. Фактически эти две группы изоморфны. Наблюдатель, который ускоряется до релятивистских скоростей, увидит, что структура созвездий, видимая вблизи Земли, постоянно трансформируется в соответствии с бесконечно малыми преобразованиями Мёбиуса. Это наблюдение часто принимают за отправную точку твисторной теории .

Некоторые подгруппы группы Мёбиуса образуют группы автоморфизмов других односвязных римановых поверхностей ( комплексной плоскости и гиперболической плоскости ). Таким образом, преобразования Мёбиуса играют важную роль в теории римановых поверхностей . Фундаментальная группа каждой римановой поверхности является дискретной подгруппой группы Мёбиуса (см. Фуксову группу и Клейнову группу ). Особенно важной дискретной подгруппой группы Мёбиуса является модулярная группа ; он занимает центральное место в теории многих фракталов , модулярных форм , эллиптических кривых и уравнений Пеллиана .

Преобразования Мёбиуса в более общем смысле можно определить в пространствах размерности n > 2 как биективные конформные, сохраняющие ориентацию отображения из n -сферы в n -сферу. Такое преобразование является наиболее общей формой конформного отображения области. Согласно теореме Лиувилля, преобразование Мёбиуса можно выразить как комбинацию сдвигов, подобий , ортогональных преобразований и инверсий.

Определение

Общий вид преобразования Мёбиуса имеет вид $$f(z)={\frac {az+b}{cz+d}},$$где a , b , c , d — любые комплексные числа , удовлетворяющие условию ad − bc ≠ 0 .

В случае c ≠ 0 это определение распространяется на всю сферу Римана , определяя $$f\left({\frac {-d}{c}}\right)=\infty {\text{ and }}f(\infty )={\frac {a}{c}}.$$

Если c = 0 , мы определяем $$f(\infty )=\infty .$$

Таким образом, преобразование Мёбиуса всегда является биективной голоморфной функцией из сферы Римана в сферу Римана.

Совокупность всех преобразований Мёбиуса образует группу по составу . Этой группе можно придать структуру комплексного многообразия таким образом, чтобы композиция и инверсия были голоморфными отображениями . Тогда группа Мёбиуса является комплексной группой Ли . Группу Мёбиуса обычно обозначают $\operatorname {Aut} ({\widehat {\mathbb {C} }})$ поскольку это группа автоморфизмов сферы Римана.

Если ad = bc , рациональная функция, определенная выше, является константой (если только c = d = 0 , когда она не определена): $${\frac {az+b}{cz+d}}={\frac {a}{c}}={\frac {b}{d}},$$где дробь с нулевым знаменателем игнорируется. Постоянная функция не является биективной и поэтому не считается преобразованием Мёбиуса.

Фиксированные точки

Каждое нетождественное преобразование Мёбиуса имеет две неподвижные точки. $\gamma _{1},\gamma _{2}$ на сфере Римана. Неподвижные точки здесь учитываются с кратностью ; параболические преобразования - это преобразования, в которых неподвижные точки совпадают. Одна или обе эти фиксированные точки могут быть точкой, находящейся на бесконечности.

Определение фиксированных точек

Фиксированные точки трансформации $$f(z)={\frac {az+b}{cz+d}}$$получаются путем решения уравнения неподвижной точки f ( γ ) = γ . При c ≠ 0 оно имеет два корня, полученные путем расширения этого уравнения до $$c\gamma ^{2}-(a-d)\gamma -b=0\ ,$$и применив квадратичную формулу . Корни $$\gamma _{1,2}={\frac {(a-d)\pm {\sqrt {(a-d)^{2}+4bc}}}{2c}}={\frac {(a-d)\pm {\sqrt {\Delta }}}{2c}}$$с дискриминантом $$\Delta =(\operatorname {tr} {\mathfrak {H}})^{2}-4\det {\mathfrak {H}}=(a+d)^{2}-4(ad-bc).$$Параболические преобразования имеют совпадающие неподвижные точки из-за нулевого дискриминанта. Для ненулевого и ненулевого дискриминанта c преобразование является эллиптическим или гиперболическим.

Когда c = 0 квадратное уравнение вырождается в линейное уравнение, и преобразование является линейным. Это соответствует ситуации, когда одной из неподвижных точек является точка, находящаяся на бесконечности. Когда a ≠ d, вторая неподвижная точка конечна и определяется выражением $$\gamma =-{\frac {b}{a-d}}.$$

В этом случае преобразование будет простым преобразованием, состоящим из перемещений , вращений и расширений : $$z\mapsto \alpha z+\beta .$$

Если c = 0 и a = d , то обе неподвижные точки находятся на бесконечности, а преобразование Мёбиуса соответствует чистому сдвигу: $$z\mapsto z+\beta .$$

Топологическое доказательство

Топологически тот факт, что (нетождественные) преобразования Мёбиуса фиксируют 2 точки (с кратностью), соответствует эйлеровой характеристике сферы, равной 2: $$\chi ({\hat {\mathbb {C} }})=2.$$

Во-первых, проективная линейная группа PGL(2, K ) точно 3-транзитивна – для любых двух упорядоченных троек различных точек существует единственное отображение, переводящее одну тройку в другую, так же, как и для преобразований Мёбиуса, и по тому же принципу. алгебраическое доказательство (по сути, подсчет размерностей , поскольку группа трехмерна). Таким образом, любая карта, на которой зафиксировано хотя бы 3 точки, является тождественной.

Далее, это можно увидеть, отождествив группу Мёбиуса с $\mathrm {PGL} (2,\mathbb {C} )$ что любая функция Мёбиуса гомотопна тождеству. Действительно, любой член общей линейной группы может быть сведен к тождественному отображению методом исключения Гаусса-Жордана. Это показывает, что проективная линейная группа также линейно связна, что обеспечивает гомотопию тождественного отображения. Теорема Лефшеца – Хопфа утверждает, что сумма индексов (в данном контексте кратности) неподвижных точек карты с конечным числом неподвижных точек равна числу Лефшеца карты, которое в данном случае является следом тождественного отображения. на группах гомологий, что является просто эйлеровой характеристикой.

Напротив, проективная линейная группа реальной проективной прямой PGL(2, R ) не требует фиксации каких-либо точек - например $(1+x)/(1-x)$ не имеет (реальных) неподвижных точек: как комплексное преобразование оно фиксирует ± i – в то время как отображение 2 x фиксирует две точки 0 и ∞. Это соответствует тому факту, что эйлерова характеристика окружности (вещественной проективной линии) равна 0, и, таким образом, теорема Лефшеца о неподвижной точке говорит только о том, что она должна фиксировать как минимум 0 точек, а возможно и больше.

Нормальная форма

Преобразования Мёбиуса также иногда записываются через их неподвижные точки в так называемой нормальной форме . Сначала мы рассмотрим непараболический случай, для которого имеются две различные неподвижные точки.

Непараболический случай :

Каждое непараболическое преобразование сопряжено с расширением/поворотом, т. е. преобразованием вида $$z\mapsto kz$$( k ∈ C ) с неподвижными точками в точках 0 и ∞. Чтобы увидеть это, определите карту $$g(z)={\frac {z-\gamma _{1}}{z-\gamma _{2}}}$$что переводит точки ( γ ₁ , γ ₂ ) в (0, ∞). Здесь мы предполагаем, что γ ₁ и γ ₂ различны и конечны. Если одна из них уже находится на бесконечности, то g можно изменить так, чтобы зафиксировать бесконечность и отправить другую точку в 0.

Если f имеет различные неподвижные точки ( γ ₁ , γ ₂ ), то преобразование $gfg^{-1}$ имеет фиксированные точки в точках 0 и ∞ и, следовательно, является расширением: $gfg^{-1}(z)=kz$. Тогда уравнение неподвижной точки для преобразования f можно записать $${\frac {f(z)-\gamma _{1}}{f(z)-\gamma _{2}}}=k{\frac {z-\gamma _{1}}{z-\gamma _{2}}}.$$

Решение для f дает (в матричной форме): $${\mathfrak {H}}(k;\gamma _{1},\gamma _{2})={\begin{pmatrix}\gamma _{1}-k\gamma _{2}&(k-1)\gamma _{1}\gamma _{2}\\1-k&k\gamma _{1}-\gamma _{2}\end{pmatrix}}$$или, если одна из фиксированных точек находится на бесконечности: $${\mathfrak {H}}(k;\gamma ,\infty )={\begin{pmatrix}k&(1-k)\gamma \\0&1\end{pmatrix}}.$$

Из приведенных выше выражений можно вычислить производные f в фиксированных точках: $$f'(\gamma _{1})=k$$ и $$f'(\gamma _{2})=1/k.$$

Заметьте, что, учитывая порядок неподвижных точек, мы можем выделить один из множителей ( ) f как характеристическую константу f k . Изменение порядка фиксированных точек на противоположный эквивалентно использованию обратного множителя для характеристической константы: $${\mathfrak {H}}(k;\gamma _{1},\gamma _{2})={\mathfrak {H}}(1/k;\gamma _{2},\gamma _{1}).$$

Для локсодромных преобразований всякий раз, когда | к | > 1 , говорят, что γ ₁ — отталкивающая неподвижная точка, а γ ₂ — притягивающая неподвижная точка. Для | к | < 1 , роли меняются.

Параболический случай :

В параболическом случае имеется только одна неподвижная точка γ . Преобразование, отправляющее эту точку в ∞, равно $$g(z)={\frac {1}{z-\gamma }}$$или тождество, если γ уже находится на бесконечности. Преобразование $gfg^{-1}$ фиксирует бесконечность и поэтому является переводом: $$gfg^{-1}(z)=z+\beta \,.$$

Здесь β называется длиной трансляции . Тогда формула фиксированной точки для параболического преобразования будет иметь вид $${\frac {1}{f(z)-\gamma }}={\frac {1}{z-\gamma }}+\beta .$$

Решение для f (в ​​матричной форме) дает $${\mathfrak {H}}(\beta ;\gamma )={\begin{pmatrix}1+\gamma \beta &-\beta \gamma ^{2}\\\beta &1-\gamma \beta \end{pmatrix}}$$Обратите внимание, что $\det {\mathfrak {H}}(\beta ;\gamma )=|{\mathfrak {H}}(\beta ;\gamma )|=\det {\begin{pmatrix}1+\gamma \beta &-\beta \gamma ^{2}\\\beta &1-\gamma \beta \end{pmatrix}}=1-\gamma ^{2}\beta ^{2}+\gamma ^{2}\beta ^{2}=1$

Если γ = ∞ : $${\mathfrak {H}}(\beta ;\infty )={\begin{pmatrix}1&\beta \\0&1\end{pmatrix}}$$

Обратите внимание, что β является не характеристической константой f , которая всегда равна 1 для параболического преобразования. Из приведенных выше выражений можно рассчитать: $$f'(\gamma )=1.$$

Полюса трансформации

Суть ${\textstyle z_{\infty }=-{\frac {d}{c}}}$ называется полюсом ​ ${\mathfrak {H}}$; это та точка, которая превращается в точку на бесконечности под действием ⁠ ${\mathfrak {H}}$⁠ .

Обратный полюс ${\textstyle Z_{\infty }={\frac {a}{c}}}$ это та точка, в которую преобразуется точка на бесконечности. Точка посередине между двумя полюсами всегда совпадает с точкой посередине между двумя фиксированными точками: $$\gamma _{1}+\gamma _{2}=z_{\infty }+Z_{\infty }.$$

Эти четыре точки являются вершинами параллелограмма , который иногда называют характеристическим параллелограммом преобразования.

Преобразование ${\mathfrak {H}}$ можно задать с двумя неподвижными точками γ ₁ , γ ₂ и полюсом $z_{\infty }$.

$${\mathfrak {H}}={\begin{pmatrix}Z_{\infty }&-\gamma _{1}\gamma _{2}\\1&-z_{\infty }\end{pmatrix}},\;\;Z_{\infty }=\gamma _{1}+\gamma _{2}-z_{\infty }.$$

Это позволяет нам вывести формулу для преобразования между k и $z_{\infty }$ данный $\gamma _{1},\gamma _{2}$: $$z_{\infty }={\frac {k\gamma _{1}-\gamma _{2}}{1-k}}$$$$k={\frac {\gamma _{2}-z_{\infty }}{\gamma _{1}-z_{\infty }}}={\frac {Z_{\infty }-\gamma _{1}}{Z_{\infty }-\gamma _{2}}}={\frac {a-c\gamma _{1}}{a-c\gamma _{2}}},$$что сводится к $$k={\frac {(a+d)+{\sqrt {(a-d)^{2}+4bc}}}{(a+d)-{\sqrt {(a-d)^{2}+4bc}}}}.$$

Последнее выражение совпадает с одним из (взаимно обратных) собственных значений отношений ${\textstyle {\frac {\lambda _{1}}{\lambda _{2}}}}$ матрицы $${\mathfrak {H}}={\begin{pmatrix}a&b\\c&d\end{pmatrix}}$$представление преобразования (сравните обсуждение характеристической константы преобразования в предыдущем разделе). Его характеристический полином равен $$\det(\lambda I_{2}-{\mathfrak {H}})=\lambda ^{2}-\operatorname {tr} {\mathfrak {H}}\,\lambda +\det {\mathfrak {H}}=\lambda ^{2}-(a+d)\lambda +(ad-bc)$$у которого есть корни $$\lambda _{i}={\frac {(a+d)\pm {\sqrt {(a-d)^{2}+4bc}}}{2}}={\frac {(a+d)\pm {\sqrt {(a+d)^{2}-4(ad-bc)}}}{2}}=c\gamma _{i}+d\,.$$

Простые преобразования Мёбиуса и композиция

Преобразование Мёбиуса можно составить как последовательность простых преобразований.

Следующие простые преобразования также являются преобразованиями Мёбиуса:

• $f(z)=z+b\quad (a=1,c=0,d=1)$ это перевод .
• $f(z)=az\quad (b=0,c=0,d=1)$ представляет собой комбинацию гомотетии и вращения . Если $|a|=1$ то это вращение, если $a\in \mathbb {R}$ тогда это гомотетия.
• $f(z)=1/z\quad (a=0,b=1,c=1,d=0)$ ( инверсия и отражение относительно действительной оси)

Композиция простых преобразований

Если $c\neq 0$, позволять:

• $f_{1}(z)=z+d/c\quad$ ( перевод ​ д / к )
• $f_{2}(z)=1/z\quad$ ( инверсия и отражение относительно действительной оси)
• $f_{3}(z)={\frac {bc-ad}{c^{2}}}z\quad$ ( гомотетия и вращение )
• $f_{4}(z)=z+a/c\quad$ (перевод а / с )

Затем эти функции можно составить , показав, что если $$f(z)={\frac {az+b}{cz+d}},$$у одного есть $$f=f_{4}\circ f_{3}\circ f_{2}\circ f_{1}.$$Другими словами, у человека есть $${\frac {az+b}{cz+d}}={\frac {a}{c}}+{\frac {e}{z+{\frac {d}{c}}}},$$с $$e={\frac {bc-ad}{c^{2}}}.$$

Это разложение делает очевидными многие свойства преобразования Мёбиуса.

Элементарные свойства

Преобразование Мёбиуса эквивалентно последовательности более простых преобразований. Композиция делает очевидными многие свойства преобразования Мёбиуса.

Формула обратного преобразования

Существование обратного преобразования Мёбиуса и его явная формула легко выводятся путем композиции обратных функций более простых преобразований. То есть определите функции g ₁ , g ₂ , g ₃ , g ₄ такие, что каждое является _gi обратным к f _i . Тогда композиция $$g_{1}\circ g_{2}\circ g_{3}\circ g_{4}(z)=f^{-1}(z)={\frac {dz-b}{-cz+a}}$$дает формулу обратного.

Сохранение углов и обобщенных окружностей.

Из этого разложения мы видим, что преобразования Мёбиуса переносят все нетривиальные свойства инверсии окружности . Например, сохранение углов сводится к доказательству того, что инверсия окружности сохраняет углы, поскольку другие типы преобразований — это расширения и изометрии (перенос, отражение, поворот), которые тривиально сохраняют углы.

Более того, преобразования Мёбиуса отображают обобщенные круги в обобщенные круги, поскольку инверсия круга обладает этим свойством. Обобщенный круг — это либо круг, либо линия, причем последняя рассматривается как круг, проходящий через точку, находящуюся в бесконечности. Обратите внимание, что преобразование Мёбиуса не обязательно отображает круги в круги, а линии в линии: оно может смешивать и то, и другое. Даже если он сопоставляет круг с другим кругом, он не обязательно сопоставляет центр первого круга с центром второго круга.

Сохранение перекрестного соотношения

Перекрестные отношения инвариантны относительно преобразований Мёбиуса. То есть, если преобразование Мёбиуса отображает четыре различные точки $z_{1},z_{2},z_{3},z_{4}$ четырем различным точкам $w_{1},w_{2},w_{3},w_{4}$ соответственно, тогда $${\frac {(z_{1}-z_{3})(z_{2}-z_{4})}{(z_{2}-z_{3})(z_{1}-z_{4})}}={\frac {(w_{1}-w_{3})(w_{2}-w_{4})}{(w_{2}-w_{3})(w_{1}-w_{4})}}.$$

Если одна из точек $z_{1},z_{2},z_{3},z_{4}$ если точка находится на бесконечности, то перекрестное отношение должно быть определено путем принятия соответствующего предела; например, перекрестное отношение $z_{1},z_{2},z_{3},\infty$ является $${\frac {(z_{1}-z_{3})}{(z_{2}-z_{3})}}.$$

Перекрестное отношение четырех различных точек вещественно тогда и только тогда, когда через них проходит прямая или окружность. Это еще один способ показать, что преобразования Мёбиуса сохраняют обобщенные окружности.

Спряжение

точки z1 _D и z2 _и сопряжены и относительно обобщенной окружности C , если дана обобщенная окружность через z1 z2 _Две , разрезающая _точки C в двух a и b , ( z1 _, точках z2 _{проходящая} ; a , b ) находятся в гармоническом перекрестном отношении (т.е. их перекрестное отношение равно -1). не зависит от выбора окружности D. Это свойство Это свойство также иногда называют симметричностью относительно линии или круга.

Две точки z , z ^∗ сопряжены относительно прямой, если они симметричны относительно прямой. Две точки сопряжены относительно окружности, если они меняются местами при инверсии относительно этой окружности.

Точка z ^∗ сопряжено с z , когда L — линия, определяемая вектором на основе e ^я , в точке z ₀ . Это может быть явно задано как $$z^{*}=e^{2i\theta }\,{\overline {z-z_{0}}}+z_{0}.$$

Точка z ^∗ сопряжен с z , когда C — круг радиуса r с центром вокруг z ₀ . Это может быть явно задано как $$z^{*}={\frac {r^{2}}{\overline {z-z_{0}}}}+z_{0}.$$

Поскольку преобразования Мёбиуса сохраняют обобщенные окружности и обратные отношения, они также сохраняют сопряжение.

Проективные матричные представления

Изоморфизм между группой Мёбиуса и PGL(2, C)

Естественное действие PGL (2, C ) на комплексной проективной прямой CP ¹ в точности является естественным действием группы Мёбиуса на сфере Римана.

Соответствие комплексной проективной прямой сфере Римана

Здесь проективная линия CP ¹ и сфера Римана отождествляются следующим образом: $$[z_{1}:z_{2}]\ \thicksim {\frac {z_{1}}{z_{2}}}.$$

Здесь [ z ₁ : z ₂ ] — однородные координаты на CP ¹ ; точка [1:0] соответствует точке ∞ сферы Римана. Используя однородные координаты, можно упростить многие вычисления, включающие преобразования Мёбиуса, поскольку не никаких различий в регистрах, касающихся ∞ требуется .

Действие PGL(2, C) на комплексной проективной прямой

Любая обратимая комплексная матрица 2×2. $${\mathfrak {H}}={\begin{pmatrix}a&b\\c&d\end{pmatrix}}$$действует на проективной прямой как $$z=[z_{1}:z_{2}]\mapsto w=[w_{1}:w_{2}],$$где $${\begin{pmatrix}w_{1}\\w_{2}\end{pmatrix}}={\begin{pmatrix}a&b\\c&d\end{pmatrix}}{\begin{pmatrix}z_{1}\\z_{2}\end{pmatrix}}={\begin{pmatrix}az_{1}+bz_{2}\\cz_{1}+dz_{2}\end{pmatrix}}.$$

Таким образом, результат $$w=[w_{1}:w_{2}]=[az_{1}+bz_{2}:cz_{1}+dz_{2}]$$

Что, используя приведенное выше отождествление, соответствует следующей точке на сфере Римана:

$$w=[az_{1}+bz_{2}:cz_{1}+dz_{2}]\thicksim {\frac {az_{1}+bz_{2}}{cz_{1}+dz_{2}}}={\frac {a{\frac {z_{1}}{z_{2}}}+b}{c{\frac {z_{1}}{z_{2}}}+d}}.$$

Эквивалентность преобразованию Мёбиуса на сфере Римана.

Поскольку приведенная выше матрица обратима тогда и только тогда, когда ее определитель ad − bc не равен нулю, это приводит к отождествлению действия группы преобразований Мёбиуса с действием PGL(2, C ) на комплексной проективной прямой. В этой идентификации приведенная выше матрица ${\mathfrak {H}}$ соответствует преобразованию Мёбиуса $z\mapsto {\frac {az+b}{cz+d}}.$

Это отождествление является групповым изоморфизмом , так как умножение ${\mathfrak {H}}$ ненулевым скаляром $\lambda$ не меняет элемент PGL(2, C ) и, поскольку это умножение состоит из умножения всех элементов матрицы на $\lambda ,$ это не меняет соответствующее преобразование Мёбиуса.

Другие группы

Для любого поля K аналогично можно отождествить группу PGL(2, K ) проективных линейных автоморфизмов с группой дробно-линейных преобразований. Это широко используется; например, при изучении гомографии действительной линии и ее приложениях в оптике .

Если разделить ${\mathfrak {H}}$ извлекая квадратный корень из определителя, получаем матрицу определителя единица. Это индуцирует гомоморфизм сюръективной группы из специальной линейной группы SL(2, C ) в PGL(2, C ) с $\pm I$ как его ядро.

Это позволяет показать, что группа Мёбиуса является 3-мерной комплексной группой Ли (или 6-мерной вещественной группой Ли), полупростой и некомпактной , и что SL(2, C ) является двойным накрытием PSL ( 2, С ) . Поскольку SL(2, C ) односвязна , она является универсальным накрытием группы Мёбиуса, а фундаментальной группой группы Мёбиуса является Z ₂ .

Задание преобразования по трем точкам

Дан набор из трех различных точек $z_{1},z_{2},z_{3}$ на сфере Римана и второй набор различных точек ⁠ $w_{1},w_{2},w_{3}$⁠ существует ровно одно преобразование Мёбиуса $f(z)$ с $f(z_{j})=w_{j}$ для ⁠ $j=1,2,3$⁠ . (Другими словами: действие группы Мёбиуса на сфере Римана является точно 3-транзитивным .) Существует несколько способов определения $f(z)$ из заданных наборов точек.

Сначала сопоставление с 0, 1, ∞

Легко проверить, что преобразование Мёбиуса $$f_{1}(z)={\frac {(z-z_{1})(z_{2}-z_{3})}{(z-z_{3})(z_{2}-z_{1})}}$$с матрицей $${\mathfrak {H}}_{1}={\begin{pmatrix}z_{2}-z_{3}&-z_{1}(z_{2}-z_{3})\\z_{2}-z_{1}&-z_{3}(z_{2}-z_{1})\end{pmatrix}}$$карты $z_{1},z_{2}{\text{ and }}z_{3}$ до ⁠ $0,1,\ {\text{and}}\ \infty$⁠ соответственно. Если один из $z_{j}$ является $\infty$, то правильная формула для ${\mathfrak {H}}_{1}$ получается из приведенного выше путем предварительного деления всех записей на $z_{j}$ а затем переходя к пределу ⁠ $z_{j}\to \infty$⁠ .

Если ${\mathfrak {H}}_{2}$ определяется аналогично отображению $w_{1},w_{2},w_{3}$ к $0,1,\ {\text{and}}\ \infty ,$ тогда матрица ${\mathfrak {H}}$ какие карты $z_{1,2,3}$ к $w_{1,2,3}$ становится $${\mathfrak {H}}={\mathfrak {H}}_{2}^{-1}{\mathfrak {H}}_{1}.$$

Стабилизатор $\{0,1,\infty \}$ (как неупорядоченное множество) представляет собой подгруппу, известную как ангармоническая группа .

Они явно определяют формулу

Уравнение $$w={\frac {az+b}{cz+d}}$$эквивалентно уравнению стандартной гиперболы $$cwz-az+dw-b=0$$в $(z,w)$-самолет. Задача построения преобразования Мёбиуса ${\mathfrak {H}}(z)$ отображение тройки $(z_{1},z_{2},z_{3})$ в другую тройку $(w_{1},w_{2},w_{3})$ таким образом, эквивалентно нахождению коэффициентов $a,b,c,d$ гиперболы, проходящей через точки ⁠ $(z_{i},w_{i})$⁠ . Явное уравнение можно найти, вычислив определитель $$\det {\begin{pmatrix}zw&z&w&1\\z_{1}w_{1}&z_{1}&w_{1}&1\\z_{2}w_{2}&z_{2}&w_{2}&1\\z_{3}w_{3}&z_{3}&w_{3}&1\end{pmatrix}}\,$$с помощью разложения Лапласа по первой строке. Это приводит к детерминантным формулам $$a=\det {\begin{pmatrix}z_{1}w_{1}&w_{1}&1\\z_{2}w_{2}&w_{2}&1\\z_{3}w_{3}&w_{3}&1\end{pmatrix}}$$$$b=\det {\begin{pmatrix}z_{1}w_{1}&z_{1}&w_{1}\\z_{2}w_{2}&z_{2}&w_{2}\\z_{3}w_{3}&z_{3}&w_{3}\end{pmatrix}}$$$$c=\det {\begin{pmatrix}z_{1}&w_{1}&1\\z_{2}&w_{2}&1\\z_{3}&w_{3}&1\end{pmatrix}}$$$$d=\det {\begin{pmatrix}z_{1}w_{1}&z_{1}&1\\z_{2}w_{2}&z_{2}&1\\z_{3}w_{3}&z_{3}&1\end{pmatrix}}$$для коэффициентов $a,b,c,d$ представляющей матрицы ⁠ ${\mathfrak {H}}={\begin{pmatrix}a&b\\c&d\end{pmatrix}}$⁠ . Построенная матрица ${\mathfrak {H}}$ имеет определитель, равный ⁠ $(z_{1}-z_{2})(z_{1}-z_{3})(z_{2}-z_{3})(w_{1}-w_{2})(w_{1}-w_{3})(w_{2}-w_{3})$⁠ , который не обращается в нуль, если $z_{j}$ соотв. $w_{j}$ попарно различны, поэтому преобразование Мёбиуса корректно определено. Если одна из точек $z_{j}$ или $w_{j}$ это ⁠ $\infty$⁠ , то сначала делим все четыре определителя на эту переменную, а затем переходим к пределу по мере приближения переменной ⁠ $\infty$⁠ .

Подгруппы группы Мёбиуса

Если нам нужны коэффициенты $a,b,c,d$ преобразования Мёбиуса быть действительными числами с ⁠ $ad-bc=1$⁠ , мы получаем подгруппу группы Мёбиуса, обозначенную как PSL(2, R ) . Это группа тех преобразований Мёбиуса, которые отображают верхнюю полуплоскость H = { x + i y : y > 0} в себя, и равна группе всех биголоморфных (или, что то же самое: биективных , конформных и сохраняющих ориентацию ) отображает ЧАС → ЧС . Если ввести правильную метрику , верхняя полуплоскость становится моделью гиперболической плоскости H ² , модель полуплоскости Пуанкаре , а PSL(2, R ) — группа всех сохраняющих ориентацию изометрий H ² в этой модели.

Подгруппа всех преобразований Мёбиуса, отображающих открытый круг D = { z : | г | < 1} в себя состоит из всех преобразований вида $$f(z)=e^{i\phi }{\frac {z+b}{{\bar {b}}z+1}}$$с $\phi$ ∈ R , b ∈ C и | б | < 1 . Это эквивалентно группе всех биголоморфных (или, что то же самое: биективных, сохраняющих угол и ориентацию) отображений D → D . Введением подходящей метрики открытый диск превращается в другую модель гиперболической плоскости, модель диска Пуанкаре , и эта группа представляет собой группу всех сохраняющих ориентацию изометрий H ² в этой модели.

Поскольку обе указанные подгруппы служат группами изометрий H ² , они изоморфны. Конкретный изоморфизм задается сопряжением с преобразованием $$f(z)={\frac {z+i}{iz+1}}$$который биективно отображает открытый единичный диск в верхнюю полуплоскость.

В качестве альтернативы рассмотрим открытый диск радиуса r с центром в точке r   i . Модель диска Пуанкаре в этом диске становится идентичной модели верхней полуплоскости при приближении r к ∞.

группы Максимальная компактная подгруппа Мёбиуса ${\mathcal {M}}$ дано ( Tóth 2002 ) $${\mathcal {M}}_{0}:=\left\{z\mapsto {\frac {uz-{\bar {v}}}{vz+{\bar {u}}}}:|u|^{2}+|v|^{2}=1\right\},$$и соответствует изоморфизму ${\mathcal {M}}\cong \operatorname {PSL} (2,\mathbb {C} )$ к проективной специальной унитарной группе PSU(2, C ), которая изоморфна специальной ортогональной группе SO(3) вращений в трех измерениях и может быть интерпретирована как вращения сферы Римана. Каждая конечная подгруппа сопряжена с этой максимальной компактной группой, и, таким образом, они в точности соответствуют группам многогранников, точечным группам в трех измерениях .

Икосаэдрические группы преобразований Мёбиуса использовались Феликсом Кляйном для получения аналитического решения уравнения пятой степени в ( Кляйн, 1913 ); современное изложение дано в ( Tóth 2002 ).

Если мы потребуем, чтобы коэффициенты a , b , c , d преобразования Мёбиуса были целыми числами с ad − bc = 1 , мы получим модулярную группу PSL(2, Z ) , дискретную подгруппу PSL(2, R ), важную в изучение решеток на комплексной плоскости, эллиптических функций и эллиптических кривых . Дискретные подгруппы PSL(2, R ) известны как фуксовы группы ; они важны при изучении римановых поверхностей .

Классификация

Показано гиперболическое преобразование. Прообразами единичного круга являются круги Аполлония с отношением расстояний c / a и фокусами в точках – b / a и – d / c .

Для тех же фокусов – b / a и – d / c красные кружки соответствуют лучам, проходящим через начало координат.

В дальнейшем обсуждении мы всегда будем предполагать, что представляющая матрица ${\mathfrak {H}}$ нормирован так, что ⁠ $\det {\mathfrak {H}}=ad-bc=1$⁠ .

Нетождественные преобразования Мёбиуса обычно разделяют на четыре типа: параболические , эллиптические , гиперболические и локсодромные , причем гиперболические являются подклассом локсодромных. Классификация имеет как алгебраическое, так и геометрическое значение. Геометрически разные типы приводят к разным преобразованиям комплексной плоскости, как показано на рисунках ниже.

Четыре типа можно различить, посмотрев на след. $\operatorname {tr} {\mathfrak {H}}=a+d$. След инвариантен относительно сопряжения , т. е. $$\operatorname {tr} \,{\mathfrak {GHG}}^{-1}=\operatorname {tr} \,{\mathfrak {H}},$$и поэтому каждый член класса сопряженности будет иметь один и тот же след. Каждое преобразование Мёбиуса можно записать так, что его представляющая матрица ${\mathfrak {H}}$ имеет определитель один (путем умножения записей на подходящий скаляр). Два преобразования Мёбиуса ${\mathfrak {H}},{\mathfrak {H}}'$ (оба не равны тождественному преобразованию) с $\det {\mathfrak {H}}=\det {\mathfrak {H}}'=1$ сопряжены тогда и только тогда, когда $\operatorname {tr} ^{2}{\mathfrak {H}}=\operatorname {tr} ^{2}{\mathfrak {H}}'.$

Параболические преобразования

Нетождественное преобразование Мёбиуса, определяемое матрицей ${\mathfrak {H}}$ определителя один называется параболическим, если $$\operatorname {tr} ^{2}{\mathfrak {H}}=(a+d)^{2}=4$$(так что трасса равна плюс или минус 2; для данного преобразования может возникнуть и то, и другое, поскольку ${\mathfrak {H}}$ определяется только до знака). Фактически один из вариантов ${\mathfrak {H}}$ имеет тот же характеристический полином X ² − 2 X + 1 как единичная матрица и, следовательно, унипотентна . Преобразование Мёбиуса является параболическим тогда и только тогда, когда оно имеет ровно одну неподвижную точку в расширенной комплексной плоскости. ${\widehat {\mathbb {C} }}=\mathbb {C} \cup \{\infty \}$, что происходит тогда и только тогда, когда оно может быть определено матрицей, сопряженной с $${\begin{pmatrix}1&1\\0&1\end{pmatrix}}$$которое описывает перевод в комплексной плоскости.

Набор всех параболических преобразований Мёбиуса с заданной неподвижной точкой в ${\widehat {\mathbb {C} }}$, вместе с единицей образует подгруппу , изоморфную группе матриц $$\left\{{\begin{pmatrix}1&b\\0&1\end{pmatrix}}\mid b\in \mathbb {C} \right\};$$это пример унипотентного радикала борелевской подгруппы (группы Мёбиуса или SL(2, C ) для матричной группы; это понятие определено для любой редуктивной группы Ли ).

Характеристическая константа

Все непараболические преобразования имеют две неподвижные точки и определяются матрицей, сопряженной с $${\begin{pmatrix}\lambda &0\\0&\lambda ^{-1}\end{pmatrix}}$$с комплексным числом λ, не равным 0, 1 или −1, что соответствует расширению/повороту путем умножения на комплексное число k = λ ² , называемая характеристической константой или множителем преобразования.

Эллиптические преобразования

Диаграмма Смита , используемая инженерами-электриками для анализа линий электропередачи , представляет собой визуальное изображение эллиптического преобразования Мёбиуса Γ = ( z − 1)/( z + 1) . Каждая точка на диаграмме Смита одновременно представляет как значение z (внизу слева), так и соответствующее значение Γ (внизу справа) для |Γ |<1.

Преобразование называется эллиптическим, если его можно представить матрицей ${\mathfrak {H}}$ чей след реален с $$0\leq \operatorname {tr} ^{2}{\mathfrak {H}}<4.$$

Преобразование является эллиптическим тогда и только тогда, когда | λ | знак равно 1 и λ ≠ ±1 . Письмо $\lambda =e^{i\alpha }$, эллиптическое преобразование сопряжено с $${\begin{pmatrix}\cos \alpha &-\sin \alpha \\\sin \alpha &\cos \alpha \end{pmatrix}}$$с α действительным.

Для любого ${\mathfrak {H}}$ с характеристической константой k , характеристическая константа ${\mathfrak {H}}^{n}$ это к ^н . Таким образом, все преобразования Мёбиуса конечного порядка являются эллиптическими преобразованиями, а именно теми, где λ — корень из единицы или, что то же самое, где α — рациональное кратное π . Простейшая возможность дробного кратного означает α = π /2 , что также является уникальным случаем $\operatorname {tr} {\mathfrak {H}}=0$, также обозначается как круговое преобразование ; геометрически это соответствует повороту на 180° вокруг двух фиксированных точек. Этот класс представлен в матричной форме как: $${\begin{pmatrix}0&-1\\1&0\end{pmatrix}}.$$Есть 3 представителя, фиксирующих {0, 1, ∞}, которые представляют собой три транспозиции в группе симметрии этих трех точек: $1/z,$ который фиксирует 1 и меняет 0 на ∞ (поворот на 180 ° вокруг точек 1 и −1), $1-z$, который фиксирует ∞ и меняет 0 на 1 (поворот на 180° вокруг точек 1/2 и ∞ ), и $z/(z-1)$ который фиксирует 0 и меняет 1 на ∞ (поворот на 180° вокруг точек 0 и 2).

Гиперболические преобразования

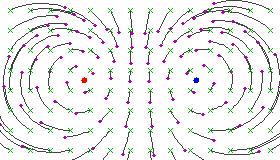
Преобразование называется гиперболическим, если его можно представить матрицей ${\mathfrak {H}}$ чей след реален с $$\operatorname {tr} ^{2}{\mathfrak {H}}>4.$$

Преобразование является гиперболическим тогда и только тогда, когда λ вещественно и λ ≠ ±1 .

Локсодромные преобразования

Преобразование называется локсодромным, если $\operatorname {tr} ^{2}{\mathfrak {H}}$ не находится в [0, 4] . Преобразование является локсодромным тогда и только тогда, когда $|\lambda |\neq 1$.

Исторически навигация по локсодрому или прямой линии относилась к пути постоянного пеленга ; результирующий путь представляет собой логарифмическую спираль , по форме похожую на преобразования комплексной плоскости, которые производит локсодромное преобразование Мёбиуса. Посмотрите геометрические фигуры ниже.

Общая классификация

Трансформация	Трассировка в квадрате	Множители	Представитель класса
Круговой	σ = 0	к = −1	${\begin{pmatrix}i&0\\0&-i\end{pmatrix}}$	г ↦ - г
Эллиптический	0 ≤ σ < 4	| к | = 1 $k=e^{\pm i\theta }\neq 1$	${\begin{pmatrix}e^{i\theta /2}&0\\0&e^{-i\theta /2}\end{pmatrix}}$	г ↦ е я С
Параболический	о = 4	к = 1	${\begin{pmatrix}1&a\\0&1\end{pmatrix}}$	г ↦ г + а
гиперболический	4 < σ < ∞	$k\in \mathbb {R} ^{+}$ $k=e^{\pm \theta }\neq 1$	${\begin{pmatrix}e^{\theta /2}&0\\0&e^{-\theta /2}\end{pmatrix}}$	г ↦ е я С
локсодромный	σ ∈ C \ [0,4]	$|k|\neq 1$ $k=\lambda ^{2},\lambda ^{-2}$	${\begin{pmatrix}\lambda &0\\0&\lambda ^{-1}\end{pmatrix}}$	от ↦ Кз

Реальный случай и замечание по терминологии

Над действительными числами (если коэффициенты должны быть действительными) негиперболические локсодромные преобразования отсутствуют, и классификация ведется на эллиптические, параболические и гиперболические, как и для действительных коник . Эта терминология обусловлена ​​тем, что половина абсолютного значения трассы, |tr|/2, рассматривается как эксцентриситет преобразования – деление на 2 вносит поправку на размерность, поэтому тождество имеет эксцентриситет 1 (tr/ n иногда используется как альтернатива трассе по этой причине), а абсолютное значение корректирует трассу, определяемую только с коэффициентом ±1 из-за работы в PSL. трассы В качестве альтернативы можно использовать половину квадрата в качестве показателя квадрата эксцентриситета, как это было сделано выше; эти классификации (но не точные значения эксцентриситета, поскольку возведение в квадрат и абсолютные значения различны) согласуются для реальных следов, но не для сложных следов. Та же самая терминология используется для классификации элементов SL(2, R ) (2-кратного накрытия), аналогичные классификации используются и в других местах. Локсодромные трансформации представляют собой по существу сложное явление и соответствуют сложным эксцентриситетам.

Геометрическая интерпретация характеристической константы

На следующем рисунке изображены (после стереографического преобразования сферы в плоскость) две неподвижные точки преобразования Мёбиуса в непараболическом случае:

Характеристическую константу можно выразить через логарифм : $$e^{\rho +\alpha i}=k.$$В таком виде действительное число ρ становится коэффициентом расширения. Оно указывает на то, насколько отталкивающей является неподвижная точка γ ₁ и насколько притягивающей является γ ₂ . Действительное число α является коэффициентом вращения, указывающим, в какой степени преобразование вращает плоскость против часовой стрелки относительно γ ₁ и по часовой стрелке вокруг γ ₂ .

Эллиптические преобразования

Если ρ = 0 , то неподвижные точки не являются ни притягивающими, ни отталкивающими, а индифферентными, и преобразование называется эллиптическим . Эти преобразования имеют тенденцию перемещать все точки по кругу вокруг двух фиксированных точек. Если одна из фиксированных точек находится на бесконечности, это эквивалентно аффинному вращению вокруг точки.

Если мы возьмем однопараметрическую подгруппу, порожденную любым эллиптическим преобразованием Мёбиуса, мы получим непрерывное преобразование, такое, что каждое преобразование в подгруппе фиксирует одни и те же две точки. Все остальные точки текут по семейству окружностей, вложенных между двумя неподвижными точками на сфере Римана. В общем, две фиксированные точки могут быть любыми двумя различными точками.

Это имеет важную физическую интерпретацию.Представьте себе, что некий наблюдатель вращается с постоянной угловой скоростью вокруг некоторой оси. Тогда мы можем принять две фиксированные точки за северный и южный полюса небесной сферы. Внешний вид ночного неба теперь непрерывно трансформируется точно так же, как это описывает однопараметрическая подгруппа эллиптических преобразований, разделяющая фиксированные точки 0, ∞ и с числом α, соответствующим постоянной угловой скорости нашего наблюдателя.

Вот несколько рисунков, иллюстрирующих влияние эллиптического преобразования Мёбиуса на сферу Римана (после стереографической проекции на плоскость):

Эти изображения иллюстрируют эффект одного преобразования Мёбиуса. Создаваемая им однопараметрическая подгруппа непрерывно перемещает точки по семейству дуг окружностей, предложенных изображениями.

Гиперболические преобразования

Если α равно нулю (или кратно 2 π ), то преобразование называется гиперболическим . Эти преобразования имеют тенденцию перемещать точки по круговым траекториям от одной фиксированной точки к другой.

Если мы возьмем однопараметрическую подгруппу, порожденную любым гиперболическим преобразованием Мёбиуса, мы получим непрерывное преобразование, такое, что каждое преобразование в подгруппе фиксирует одни и те же две точки. Все остальные точки текут по определенному семейству дуг окружностей от первой неподвижной точки к второй неподвижной точке. В общем, две неподвижные точки могут быть любыми двумя различными точками на сфере Римана.

Это также имеет важную физическую интерпретацию. Представьте себе, что наблюдатель ускоряется (с постоянной величиной ускорения) в направлении Северного полюса на своей небесной сфере. Тогда внешний вид ночного неба преобразуется точно так же, как это описывает однопараметрическая подгруппа гиперболических преобразований, разделяющая фиксированные точки 0, ∞, с действительным числом ρ, соответствующим величине его вектора ускорения. Кажется, что звезды движутся по долготе, от Южного полюса к Северному полюсу. (Долготы выглядят как круговые дуги в стереографической проекции сферы на плоскость.)

Вот несколько рисунков, иллюстрирующих влияние гиперболического преобразования Мёбиуса на сферу Римана (после стереографической проекции на плоскость):

Эти изображения напоминают силовые линии положительного и отрицательного электрического заряда, расположенные в фиксированных точках, поскольку круговые линии тока образуют постоянный угол между двумя фиксированными точками.

Локсодромные преобразования

Если и ρ , и α не равны нулю, то преобразование называется локсодромным . Эти преобразования имеют тенденцию перемещать все точки S-образных путей из одной фиксированной точки в другую.

Слово « локсодром » происходит от греческого: «λοξος (локсос), косой + δρόμος (дромос), ход ». При движении по постоянному курсу – если вы держите курс (скажем) на северо-восток, вы в конечном итоге будете плыть вокруг северного полюса по логарифмической спирали . В проекции Меркатора такой курс представляет собой прямую линию, поскольку северный и южный полюса уходят в бесконечность. Угол, который образует локсодром относительно линий долготы (т.е. его наклон, «плотность» спирали), является аргументом k . Конечно, преобразования Мёбиуса могут иметь две фиксированные точки где угодно, а не только на северном и южном полюсах. Но любое локсодромное преобразование будет сопряжено с преобразованием, перемещающим все точки по таким локсодромам.

Если мы возьмем однопараметрическую подгруппу, порожденную любым локсодромным преобразованием Мёбиуса, мы получим непрерывное преобразование, такое, что каждое преобразование в подгруппе фиксирует одни и те же две точки. Все остальные точки текут по определенному семейству кривых от первой неподвижной точки к второй неподвижной точке. В отличие от гиперболического случая, эти кривые не являются дугами окружности, а представляют собой определенные кривые, которые при стереографической проекции со сферы на плоскость выглядят как спиральные кривые, которые бесконечно часто закручиваются против часовой стрелки вокруг одной фиксированной точки и бесконечно часто закручиваются по часовой стрелке вокруг другой фиксированной точки. В общем, две неподвижные точки могут быть любыми двумя различными точками на сфере Римана.

Физическую интерпретацию, вероятно, можно догадаться в случае, когда две неподвижные точки равны 0, ∞: наблюдатель, одновременно вращающийся (с постоянной угловой скоростью) вокруг некоторой оси и движущийся вдоль той же оси, увидит вид ночного неба. преобразуют по однопараметрической подгруппе локсодромных преобразований с фиксированными точками 0, ∞ и с ρ , α, определяемыми соответственно величиной фактической линейной и угловой скоростей.

Стереографическая проекция

На этих изображениях показаны преобразования Мёбиуса , стереографически проецированные на сферу Римана . Обратите внимание, в частности, что при проецировании на сферу частный случай фиксированной точки, находящейся на бесконечности, ничем не отличается от фиксированных точек в произвольном месте.

Одна фиксированная точка на бесконечности
Эллиптический	гиперболический	локсодромный
Фиксированные точки диаметрально противоположны
Эллиптический	гиперболический	локсодромный
Фиксированные точки в произвольном месте
Эллиптический	гиперболический	локсодромный

Итерация преобразования

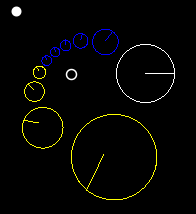
Если трансформация ${\mathfrak {H}}$ имеет неподвижные точки γ ₁ , γ ₂ и характеристическую константу k , то ${\mathfrak {H}}'={\mathfrak {H}}^{n}$ будет иметь $\gamma _{1}'=\gamma _{1},\gamma _{2}'=\gamma _{2},k'=k^{n}$.

Это можно использовать для повторения преобразования или для его анимации, разбив его на этапы.

На этих изображениях показаны три точки (красная, синяя и черная), непрерывно повторяющиеся при преобразованиях с различными характеристическими константами.

И эти изображения демонстрируют, что происходит, когда вы преобразуете круг с помощью гиперболических, эллиптических и локсодромных преобразований. На эллиптических и локсодромных изображениях значение α составляет 1/10.

Высшие измерения

более высоких измерениях преобразование Мёбиуса является гомеоморфизмом ⁠ В ${\overline {\mathbb {R} ^{n}}}$⁠ , одноточечная ⁠ компактификация $\mathbb {R} ^{n}$⁠ , представляющий собой конечную композицию инверсий в сферах и отражений в гиперплоскостях . Теорема Лиувилля в конформной геометрии утверждает, что в размерности не менее трех все конформные преобразования являются преобразованиями Мёбиуса. Любое преобразование Мёбиуса можно представить в виде $$f(x)=b+{\frac {\alpha A(x-a)}{|x-a|^{\varepsilon }}},$$где $a,b\in \mathbb {R} ^{n}$, $\alpha \in \mathbb {R}$, $A$ является ортогональной матрицей и $\varepsilon$ равен 0 или 2. Группу преобразований Мёбиуса также называют группой Мёбиуса .

Преобразования Мёбиуса, сохраняющие ориентацию, образуют компоненту связности тождества в группе Мёбиуса. В размерности n = 2 сохраняющие ориентацию преобразования Мёбиуса представляют собой в точности карты сферы Римана, рассматриваемые здесь. Из них путем комплексного сопряжения получаются меняющие ориентацию.

Область преобразований Мёбиуса, т.е. ⁠ ${\overline {\mathbb {R} ^{n}}}$⁠ , гомеоморфен n -мерной сфере $S^{n}$. Канонический изоморфизм между этими двумя пространствами — это преобразование Кэли , которое само по себе является преобразованием Мёбиуса ⁠ ${\overline {\mathbb {R} ^{n+1}}}$⁠ . Это отождествление означает, что преобразования Мёбиуса также можно рассматривать как конформные изоморфизмы $S^{n}$. - сфера n вместе с действием группы Мёбиуса представляет собой геометрическую структуру (в смысле Эрлангенской программы Клейна ), называемую геометрией Мёбиуса .

Приложения

Преобразование Лоренца

Основная статья: преобразование Лоренца

Изоморфизм группы Мёбиуса с группой Лоренца был отмечен рядом авторов: На основе предыдущих работ Феликса Клейна (1893, 1897) об автоморфных функциях, связанных с гиперболической геометрией и геометрией Мёбиуса, Густав Герглотц (1909) показал, что гиперболические движения (т.е. изометрические автоморфизмы гиперболического пространства ), переводящие единичную сферу в себя, соответствуют преобразованиям Лоренца, с помощью которых Герглотц смог классифицировать однопараметрические преобразования Лоренца на локсодромные, эллиптические, гиперболические и параболические группы. Среди других авторов - Эмиль Артин (1957), HSM Коксетер (1965), и Роджер Пенроуз , Вольфганг Риндлер (1984), Тристан Нидэм (1997) и В. М. Оливия (2002).

Пространство Минковского состоит из четырехмерного вещественного координатного пространства R ⁴ состоящий из пространства упорядоченных четверок ( x ₀ , x ₁ , x ₂ , x ₃ ) действительных чисел вместе с квадратичной формой $$Q(x_{0},x_{1},x_{2},x_{3})=x_{0}^{2}-x_{1}^{2}-x_{2}^{2}-x_{3}^{2}.$$

Заимствуя терминологию из специальной теории относительности , точки с Q > 0 считаются времениподобными ; кроме того, если x ₀ > 0 , то точка называется указывающей в будущее . Точки с Q < 0 называются пространственноподобными . Нулевой конус S состоит из тех точек, где Q = 0 ; будущий нулевой конус N ⁺ это точки на нулевом конусе с x ₀ > 0 . Тогда небесная сфера отождествляется с совокупностью лучей в N ⁺ начальная точка которого является началом координат R ⁴ . Коллекция линейных преобразований на R ⁴ с положительным определителем, сохраняющим квадратичную форму Q и сохраняющим направление времени из ограниченной группы Лоренца SO ⁺ (1, 3) .

В связи с геометрией небесной сферы группа преобразований SO ⁺ (1, 3) отождествляется с группой PSL(2, C ) преобразований Мёбиуса сферы. Каждому ( Икс ₀ , Икс ₁ , Икс ₂ , Икс ₃ ) ∈ R ⁴ , сопоставьте эрмитову матрицу $$X={\begin{bmatrix}x_{0}+x_{1}&x_{2}+ix_{3}\\x_{2}-ix_{3}&x_{0}-x_{1}\end{bmatrix}}.$$

Определитель ​ матрицы X равен Q ( x0 _​ , x1 _​ , x2 _​ , x3 _​ ) . Специальная линейная группа действует на пространстве таких матриц через

$X\mapsto AXA^{*}$ ( 1 )

для каждого A ∈ SL(2, C ) , и это действие SL(2, C ) сохраняет определитель X, поскольку det A = 1 . Поскольку определитель X отождествляется с квадратичной формой Q , SL(2, C ) действует посредством преобразований Лоренца. По соображениям размерности SL(2, C ) покрывает окрестность единицы SO(1, 3) . Поскольку SL(2, C ) связна, она покрывает всю ограниченную группу Лоренца SO ⁺ (1, 3) . При этом, поскольку ядром действия ( 1 ) является подгруппа {± I }, то переход к факторгруппе дает групповой изоморфизм

$\operatorname {PSL} (2,\mathbb {C} )\cong \operatorname {SO} ^{+}(1,3).$ ( 2 )

Теперь сосредоточим внимание на случае, когда ( x ₀ , x ₁ , x ₂ , x ₃ ) равно нулю, матрица X имеет нулевой определитель и, следовательно, распадается как внешнее произведение комплексного двухвектора ξ с его комплексно-сопряженным вектором:

$X=\xi {\bar {\xi }}^{\text{T}}=\xi \xi ^{*}.$ ( 3 )

На двухкомпонентный вектор ξ действует SL(2, C ) способом, совместимым с ( 1 ). Теперь ясно, что ядром представления SL(2, C ) на эрмитовых матрицах является {± I }.

Действие PSL(2, C ) на небесную сферу можно описать и геометрически, используя стереографическую проекцию . Рассмотрим сначала гиперплоскость в R ⁴ заданное выражением x ₀ = 1. Небесную сферу можно отождествить со сферой S ⁺ пересечения гиперплоскости с будущим нулевым конусом N ⁺ . Стереографическая проекция северного полюса (1, 0, 0, 1) этой сферы на плоскость x ₃ = 0 принимает точку с координатами (1, x ₁ , x ₂ , x ₃ ) с $$x_{1}^{2}+x_{2}^{2}+x_{3}^{2}=1$$в точку $$\left(1,{\frac {x_{1}}{1-x_{3}}},{\frac {x_{2}}{1-x_{3}}},0\right).$$

Введение комплексной координаты $$\zeta ={\frac {x_{1}+ix_{2}}{1-x_{3}}},$$обратная стереографическая проекция дает следующую формулу для точки ( x ₁ , x ₂ , x ₃ ) на S ⁺ :

${\begin{aligned}x_{1}&={\frac {\zeta +{\bar {\zeta }}}{\zeta {\bar {\zeta }}+1}}\\x_{2}&={\frac {\zeta -{\bar {\zeta }}}{i(\zeta {\bar {\zeta }}+1)}}\\x_{3}&={\frac {\zeta {\bar {\zeta }}-1}{\zeta {\bar {\zeta }}+1}}.\end{aligned}}$ ( 4 )

Действие СО ⁺ (1, 3) в точках N ⁺ не сохраняет гиперплоскость S ⁺ , но действуя на точки из S ⁺ а затем масштабирование так, чтобы результат снова был в S ⁺ дает действие SO ⁺ (1, 3) на сфере, которая переходит к действию на комплексную переменную ζ . На самом деле это действие осуществляется путем дробно-линейных преобразований, хотя из такого представления небесной сферы это нелегко увидеть. Обратно, для любого дробно-линейного преобразования переменной ζ происходит единственное преобразование Лоренца на N ⁺ , возможно, после подходящего (однозначно определенного) изменения масштаба.

Более инвариантное описание стереографической проекции, позволяющее более четко увидеть действие, состоит в том, чтобы рассматривать переменную ζ = z : w как отношение пары однородных координат для комплексной проективной прямой CP ¹ . Стереографическая проекция переходит к преобразованию из C ² − {0} до N ⁺ который является однородным второй степени относительно действительных скейлингов

$(z,w)\mapsto (x_{0},x_{1},x_{2},x_{3})=(z{\bar {z}}+w{\bar {w}},z{\bar {z}}-w{\bar {w}},z{\bar {w}}+w{\bar {z}},i^{-1}(z{\bar {w}}-w{\bar {z}}))$ ( 5 )

что согласуется с ( 4 ) при ограничении масштабами, в которых $z{\bar {z}}+w{\bar {w}}=1.$ Компоненты ( 5 ) — это именно те, которые получены из внешнего произведения $${\begin{bmatrix}x_{0}+x_{1}&x_{2}+ix_{3}\\x_{2}-ix_{3}&x_{0}-x_{1}\end{bmatrix}}=2{\begin{bmatrix}z\\w\end{bmatrix}}{\begin{bmatrix}{\bar {z}}&{\bar {w}}\end{bmatrix}}.$$

Таким образом, действие ограниченной группы Лоренца SO ⁺ (1,3) согласуется с уравнением группы Мёбиуса PSL(2, C ) . Это мотивирует следующее определение. В размерности n ≥ 2 группа Мёбиуса Möb( n ) представляет собой группу всех сохраняющих ориентацию конформных изометрий круглой сферы S ^н самому себе. Реализуя конформную сферу как пространство направленных в будущее лучей нулевого конуса в пространстве Минковского R ^1,n+1 , существует изоморфизм Möb( n ) с ограниченной группой Лоренца SO ⁺ (1, n +1) преобразований Лоренца с положительным определителем, сохраняющим направление времени.

Вместо этого Коксетер начал с эквивалентной квадратичной формы ⁠ $Q(x_{1},\ x_{2},\ x_{3}\ x_{4})=x_{1}^{2}+x_{2}^{2}+x_{3}^{2}-x_{4}^{2}$⁠ .

Он отождествил группу Лоренца с преобразованиями, для которых { x | Q( x ) = −1} стабилен . Затем он интерпретировал x как однородные координаты и { x | Q( x ) = 0}, нулевой конус , как абсолют Кэли для гиперболического пространства точек { x | Q( х ) <0}. Далее Коксетер ввел переменные $$\xi ={\frac {x_{1}}{x_{4}}},\ \eta ={\frac {x_{2}}{x_{4}}},\ \zeta ={\frac {x_{3}}{x_{4}}}$$так что лоренц-инвариантная квадрика соответствует сфере ⁠ $\xi ^{2}+\eta ^{2}+\zeta ^{2}=1$⁠ . Коксетер отмечает, что Феликс Кляйн также писал об этом соответствии, применяя стереографическую проекцию из (0, 0, 1) на комплексную плоскость. ${\textstyle z={\frac {\xi +i\eta }{1-\zeta }}.}$ Коксетер использовал тот факт, что окружности инверсивной плоскости представляют собой плоскости гиперболического пространства, а общая гомография является продуктом инверсий в двух или четырех окружностях, что соответствует общему гиперболическому смещению, которое является продуктом инверсий в двух или четырех плоскостях.

Гиперболическое пространство

Как было видно выше, группа Мёбиуса PSL(2, C ) действует на пространстве Минковского как группа тех изометрий, которые сохраняют начало координат, ориентацию пространства и направление времени. Ограничиваясь точками, где Q = 1 в положительном световом конусе, которые образуют модель гиперболического 3-пространства H ³ , мы видим, что группа Мёбиуса действует на H ³ как группу изометрий, сохраняющих ориентацию. Фактически группа Мёбиуса равна группе сохраняющих ориентацию изометрий гиперболического трёхмерного пространства. Если мы используем модель шара Пуанкаре , определяя единичный шар в R ³ с Н ³ , то мы можем думать о сфере Римана как о «конформной границе» H ³ . Любая сохраняющая ориентацию изометрия H ³ приводит к преобразованию Мёбиуса на сфере Римана и наоборот.

См. также

• Билинейное преобразование
• Конформная геометрия
• Фуксова группа
• Обобщенный круг
• Гиперболическая геометрия
• Бесконечные композиции аналитических функций
• Инверсионное преобразование
• Кляйнианская группа
• Геометрия сферы лжи
• Линейное дробное преобразование
• Теорема Лиувилля (конформные отображения)
• группа Лоренца
• Модульная группа
• Модель полуплоскости Пуанкаре
• Проективная геометрия
• Проективная линия над кольцом
• Теория представлений группы Лоренца
• группа Шоттки
• диаграмма Смита

Ссылки

Специфический

Общий

• Арнольд, Дуглас Н.; Рогнесс, Джонатан (2008), «Раскрытые преобразования Мёбиуса» (PDF) , Уведомления AMS , 55 (10): 1226–1231
• Бердон, Алан Ф. (1995), Геометрия дискретных групп , Нью-Йорк: Springer-Verlag, ISBN  978-0-387-90788-8
• Холл, GS (2004), Симметрии и структура кривизны в общей теории относительности , Сингапур: World Scientific, ISBN  978-981-02-1051-9 (См. главу 6, где представлена ​​классификация с точностью до сопряженности подалгебр Ли алгебры Ли группы Лоренца.)
• Каток, Светлана (1992), Фуксовы группы , Чикаго: University of Chicago Press, ISBN  978-0-226-42583-2 См. главу 2 .
• Кляйн, Феликс (1913) [1-е немецкое изд. 1884], Лекции по икосаэдру и решению уравнений пятой степени , перевод Морриса, Джорджа Гэвина (2-е изд.), Лондон: Кеган Пол, Тренч, Трюбнер и компания, перевод с Лекции об икосаэдре и решении уравнений пятой степени (на немецком языке), Тойбнер, 1884 г.
• Кнопп, Конрад (1952), Элементы теории функций , Нью-Йорк: Дувр, ISBN  978-0-486-60154-0 (См. главы 3–5 этой классической книги, где представлено прекрасное введение в сферу Римана, стереографическую проекцию и преобразования Мёбиуса.)
• Мамфорд, Дэвид ; Серия, Кэролайн; Райт, Дэвид (2002), Жемчуг Индры: видение Феликса Кляйна , издательство Кембриджского университета, ISBN  978-0-521-35253-6 (Рассчитано на нематематиков, содержит превосходное изложение теории и результатов, богато иллюстрированное диаграммами.)
• Нидэм, Тристан (1997), Анализ визуального комплекса , Оксфорд: Clarendon Press, ISBN  978-0-19-853446-4 (См. главу 3, где прекрасно иллюстрировано введение в преобразования Мёбиуса, включая их классификацию с точностью до сопряженности.)
• Пенроуз, Роджер ; Риндлер, Вольфганг (1984), Спиноры и пространство-время, Том 1: Двухспинорное исчисление и релятивистские поля , Cambridge University Press, ISBN  978-0-521-24527-2
• Швердтфегер, Ганс (1979), Геометрия комплексных чисел , Дувр, ISBN  978-0-486-63830-0 (Введение в преобразования Мёбиуса см. в главе 2.)
• Тот, Габор (2002), Конечные группы Мёбиуса, минимальные погружения сфер и модули

Дальнейшее чтение

• Лоусон, М.В. (1998). «Обратный моноид Мёбиуса» . Журнал алгебры . 200 (2): 428. doi : 10.1006/jabr.1997.7242 .

Внешние ссылки

• «Квазиконформное отображение» , Математическая энциклопедия , EMS Press , 2001 [1994]
• Галерея конформных карт
• Вайсштейн, Эрик В. «Дробно-линейное преобразование» . Математический мир .