Космическая группа

Пространственная группа гексагонального льда H ₂ O — P6 ₃ / mmc . Первый m обозначает плоскость зеркала, перпендикулярную оси c (a), второй m указывает плоскости зеркала, параллельные оси c (b), а c обозначает плоскости скольжения (b) и (c). Черные прямоугольники очерчивают элементарную ячейку.

В математике , физике и химии — пространственная группа это группа симметрии повторяющегося узора в пространстве, обычно в трёх измерениях . Элементы пространственной группы (ее операции симметрии ) — это жесткие преобразования образца, оставляющие его неизменным. В трех измерениях пространственные группы подразделяются на 219 различных типов или 230 типов, если киральные копии считаются отдельными. Пространственные группы — это дискретные ориентированного евклидова пространства кокомпактные группы изометрий любого числа измерений. В размерностях, отличных от 3, их иногда называют группами Бибербаха .

В кристаллографии пространственные группы также называются кристаллографическими или Федорова группами и представляют собой описание симметрии кристалла . Полным источником информации о трехмерных пространственных группах являются Международные таблицы кристаллографии Хана (2002) .

История

Пространственные группы в двух измерениях — это 17 групп обоев , которые известны уже несколько столетий, хотя доказательство полноты списка было дано только в 1891 году, после того как гораздо более сложная классификация пространственных групп была в основном завершена.

В 1879 году немецкий математик Леонхард Зонке перечислил 65 пространственных групп (называемых группами Зонке), элементы которых сохраняют киральность . Точнее, он перечислил 66 групп, но и русский математик и кристаллограф Евграф Федоров , и немецкий математик Артур Мориц Шенфлис заметили, что две из них на самом деле одинаковы. Пространственные группы в трех измерениях впервые перечислил Федоров в 1891 году. (в списке которых было два пропуска (I 4 3d и Fdd2) и одно дублирование (Fmm2)), а вскоре после этого, в 1891 году, они были независимо перечислены Шенфлисом. (в списке которых было четыре пропуска (I 4 3d, Pc, Cc, ?) и одно дублирование (P 4 2 ₁ m)). Правильный список из 230 пространственных групп был найден к 1892 году во время переписки Федорова и Шенфлиса. Уильям Барлоу ( 1894 ) позже перечислил группы другим методом, но опустил четыре группы (Fdd2, I 4 2d, P 4 2 ₁ d и P 4 2 ₁ c), хотя у него уже был правильный список из 230 групп из Федоров и Шенфлис; Распространенное утверждение о том, что Барлоу не знал об их работе, неверно. Буркхардт (1967) подробно описывает историю открытия космических групп.

Элементы

Пространственные группы в трех измерениях состоят из комбинаций 32 кристаллографических точечных групп с 14 решетками Браве , каждая из которых принадлежит одной из 7 решеточных систем . Это означает, что действие любого элемента данной пространственной группы может быть выражено как действие элемента соответствующей точечной группы, за которым необязательно следует перевод. Таким образом, пространственная группа представляет собой некоторую комбинацию трансляционной симметрии элементарной ячейки (включая центрирование решетки ), операций симметрии точечной группы отражения , вращения и неправильного вращения (также называемых ротоинверсией), а также операций симметрии оси винта и плоскости скольжения . Комбинация всех этих операций симметрии дает в общей сложности 230 различных пространственных групп, описывающих все возможные симметрии кристалла.

Таким образом, количество повторений асимметричной единицы в элементарной ячейке равно количеству точек решетки в ячейке, умноженному на порядок точечной группы. Это значение варьируется от 1 в случае пространственной группы P1 до 192 для такой пространственной группы, как Fm 3 m, структура NaCl .

Элементы, фиксирующие точку

Элементами пространственной группы, фиксирующими точку пространства, являются единичный элемент, отражения, вращения и несобственные вращения , включая точки инверсии .

Переводы

Трансляции образуют нормальную абелеву подгруппу ранга 3, называемую решеткой Браве (названной так в честь французского физика Огюста Браве ). Существует 14 возможных типов решетки Браве. Фактор точечных пространственной группы по решетке Браве — это конечная группа, которая является одной из 32 возможных групп .

Планирующие самолеты

Плоскость скольжения — это отражение в плоскости, за которым следует перемещение, параллельное этой плоскости. Это отмечает $a$, $b$, или $c$, в зависимости от того, по какой оси происходит скольжение. Существует также $n$ скольжение, то есть скольжение по половине диагонали лица, а $d$ скольжение, которое составляет четверть пути вдоль грани или пространственной диагонали элементарной ячейки. Последняя называется плоскостью скольжения алмаза, поскольку она является особенностью структуры алмаза . В 17 пространственных группах благодаря центрированию ячейки скольжение происходит одновременно в двух перпендикулярных направлениях, т.е. одна и та же плоскость скольжения может называться b или c , a или b , a или c . Например, группа Abm2 может также называться Acm2, группа Ccca может называться Cccb. В 1992 году было предложено использовать для таких самолетов обозначение е . Были изменены символы пяти пространственных групп:

Космическая группа №.	39	41	64	67	68
Новый символ	Аем2	Да2	Cmce	Давай	Ксс
Старый символ	Абм2	Аба2	смка	Хм	Кокка

Винтовые оси

Винтовая ось представляет собой вращение вокруг оси с последующим перемещением вдоль направления оси. Они обозначаются числом n для описания степени вращения, где число показывает, сколько операций необходимо выполнить для завершения полного вращения (например, 3 будет означать каждый раз поворот на одну треть вокруг оси). . Затем степень перевода добавляется в виде нижнего индекса, показывающего, насколько далеко по оси находится сдвиг, как часть вектора параллельной решетки. Итак, 2 ₁ — это двукратный поворот с последующим сдвигом 1/2 вектора решетки.

Общая формула

Общая формула действия элемента пространственной группы такова:

у = М. ​ х + Д

где M — его матрица, D — его вектор, и где элемент преобразует точку x в точку y . В общем, D = D ( решетка ) + D ( M ), где D ( M ) — уникальная функция от M , равная нулю, если M является единицей. Матрицы M образуют точечную группу , которая является базисом пространственной группы; решетка должна быть симметричной относительно этой точечной группы, но сама кристаллическая структура может не быть симметричной относительно этой точечной группы применительно к любой конкретной точке (то есть без перемещения). Например, кубическая структура ромба не имеет точки, к которой применима группа кубических точек .

Размер решетки может быть меньше общего размера, что приводит к образованию «субпериодической» пространственной группы. Для (габаритный размер, размер решетки):

• (1,1): Одномерные группы прямых
• (2,1): Двумерные группы линий : группы фризов
• (2,2): Группы обоев
• (3,1): Трехмерные группы линий ; с трехмерными кристаллографическими точечными группами, стержневыми группами
• (3,2): Группы слоев
• (3,3): Пространственные группы, обсуждаемые в этой статье.

Хиральность

65 пространственных групп «Зонке», не содержащих никаких зеркал, точек инверсии, несобственных вращений или плоскостей скольжения, дают киральные кристаллы, не идентичные своему зеркальному изображению; тогда как пространственные группы, которые включают хотя бы одну из них, дают ахиральные кристаллы. Ахиральные молекулы иногда образуют хиральные кристаллы, но хиральные молекулы всегда образуют хиральные кристаллы в одной из пространственных групп, которые это допускают.

Среди 65 групп Зонке 22 входят в 11 энантиоморфных пар.

Комбинации

В пространственной группе возможны только определенные комбинации элементов симметрии. Переводы присутствуют всегда, а пространственная группа P1 имеет только переводы и единичный элемент. Наличие зеркал подразумевает и плоскости скольжения, а наличие осей вращения подразумевает и винтовые оси, но обратное неверно. Инверсия и зеркало подразумевают двойные винтовые оси и так далее.

Обозначения

Дополнительная информация: Список космических групп.

Существует как минимум десять способов именования пространственных групп. Некоторые из этих методов могут присваивать одной и той же пространственной группе несколько разных имен, поэтому в целом существует много тысяч разных имен.

Число

Международный союз кристаллографии публикует таблицы всех типов пространственных групп и присваивает каждому уникальный номер от 1 до 230. Нумерация произвольна, за исключением того, что группам с одной и той же кристаллической системой или точечной группой присваиваются последовательные номера.

Обозначение международных символов

Обозначения Германа – Могена

Обозначение Германа – Могена (или международное) описывает решетку и некоторые генераторы группы. Он имеет сокращенную форму, называемую международным коротким символом , который наиболее часто используется в кристаллографии и обычно состоит из набора из четырех символов. Первый описывает центрирование решетки Браве ( P , A , C , I , R или F ). Следующие три описывают наиболее заметную операцию симметрии, видимую при проецировании вдоль одного из направлений высокой симметрии кристалла. Эти символы такие же, как и в группах точек , с добавлением плоскостей скольжения и оси винта, описанных выше. В качестве примера, пространственная группа кварца - P3 ₁ 21, что показывает, что он демонстрирует примитивное центрирование мотива (т.е. один раз на элементарную ячейку) с винтовой осью третьего порядка и осью вращения двойного порядка. Обратите внимание, что он явно не содержит кристаллическую систему , хотя она уникальна для каждой пространственной группы (в случае P 3 ₁ 21 она тригональна).

В международном коротком символе первый символ (3 ₁ в данном примере) обозначает симметрию вдоль большой оси (ось c в тригональных случаях), второй (в данном случае 2) — вдоль осей второстепенного значения (a и b) и третий символ симметрия в другом направлении. В тригональном случае также существует пространственная группа P3 ₁ 12. В этой пространственной группе оси второго порядка расположены не вдоль осей a и b, а в направлении, повернутом на 30°.

Международные символы и международные короткие символы для некоторых космических групп были немного изменены в период с 1935 по 2002 год, поэтому в нескольких космических группах используются четыре разных международных символа.

Направления обзора семи кристаллических систем показаны следующим образом.

Позиция в символе	Триклиника	Моноклиника	орторомбический	четырехугольный	Треугольный	Шестиугольный	Кубический
1	—	б	а	с	с	с	а
2	—		б	а	а	а	[111]
3	—		с	[110]	[210]	[210]	[110]

Обозначение Холла

Обозначение пространственной группы с явным происхождением. Символы вращения, перемещения и направления оси четко разделены, а центры инверсии четко определены. Конструкция и формат обозначений делают их особенно подходящими для компьютерной генерации информации о симметрии. Например, группа номер 3 имеет три символа Холла: P 2y (P 1 2 1), P 2 (P 1 1 2), P 2x (P 2 1 1).

Обозначение Шенфлиса

Пространственные группы с данной точечной группой нумеруются 1, 2, 3, ... (в том же порядке, что и их международный номер), и этот номер добавляется в качестве верхнего индекса к символу Шенфлиса для точечной группы. Например, группы с номерами от 3 до 5, точечная группа которых равна C _2, имеют символы Шенфлиса C. ¹
₂ , С ²
₂ , С ³
₂ .

Федорова Обозначение

Shubnikov symbol

Обозначение структурного отчета

Соответствующие обозначения кристаллических структур с буквой и индексом: A Элементы (одноатомные), B для соединений AB, C для соединений AB ₂ , D для соединений A _m B _n , ( E , F , ..., K Более сложные соединения ), L Сплавы, O Органические соединения, S Силикаты. Некоторые обозначения структур имеют одни и те же пространственные группы. Например, пространственная группа 225 — это A ₁ , B ₁ и C ₁ . Пространственная группа 221 — это A _h и B ₂ . Однако кристаллографы не будут использовать обозначение Strukturbericht для описания пространственной группы, а скорее будут использовать его для описания конкретной кристаллической структуры (например, пространственная группа + расположение атомов (мотив)).

Обозначение орбифолда (2D)

Обозначение фиброфолда (3D)

Как следует из названия, обозначение орбифолда описывает орбифолд, заданный фактором евклидова пространства по пространственной группе, а не генераторами пространственной группы. Он был введен Конвеем и Терстоном и мало используется за пределами математики. С некоторыми пространственными группами связано несколько разных волокон, поэтому они имеют несколько разных символов волокон.

Обозначение Кокстера

Группы пространственной и точечной симметрии, представленные как модификации чисто отражательных групп Кокстера .

Геометрические обозначения

Обозначение геометрической алгебры .

Системы классификации

Существует (по крайней мере) 10 различных способов классификации пространственных групп на классы. Отношения между некоторыми из них описаны в следующей таблице. Каждая система классификации является усовершенствованием предшествующих ей систем. Чтобы понять объяснение, данное здесь, возможно, потребуется понять следующее.

(Кристаллографические) типы пространственных групп (230 в трех измерениях)
Две пространственные группы, рассматриваемые как подгруппы группы аффинных преобразований пространства, имеют один и тот же тип пространственной группы, если они одинаковы с точностью до аффинного преобразования пространства, сохраняющего ориентацию . Таким образом, например, изменение угла между векторами трансляции не влияет на тип пространственной группы, если оно не добавляет или не удаляет какую-либо симметрию. Более формальное определение предполагает сопряженность (см. Группа симметрии ). В трех измерениях для 11 аффинных пространственных групп не существует сохраняющего киральность (т.е. сохраняющего ориентацию) отображения группы в ее зеркальное изображение, поэтому, если кто-то отличает группы от их зеркальных изображений, каждая из них распадается на два случая (например, как P4 1 и P4 3 ). Таким образом, вместо 54 аффинных пространственных групп, сохраняющих киральность, существует 54 + 11 = 65 типов пространственных групп, сохраняющих киральность ( группы Зонке ). Для большинства киральных кристаллов два энантиоморфа принадлежат к одной и той же кристаллографической пространственной группе, например P2 1. 3 для FeSi , но для других, таких как кварц , они принадлежат к двум энантиоморфным пространственным группам.
Типы аффинных пространственных групп (219 в трех измерениях)
Две пространственные группы, рассматриваемые как подгруппы группы аффинных преобразований пространства, имеют один и тот же тип аффинной пространственной группы, если они одинаковы с точностью до аффинного преобразования, даже если это меняет ориентацию. Тип аффинной пространственной группы определяется базовой абстрактной группой пространственной группы. В трех измерениях пятьдесят четыре типа аффинных пространственных групп сохраняют хиральность и образуют хиральные кристаллы. Два энантиоморфа хирального кристалла имеют одну и ту же аффинную пространственную группу.
Арифметические кристаллические классы (73 в трех измерениях)
Иногда их называют Z-классами. Они определяются группой точек вместе с действием группы точек на подгруппу переводов. Другими словами, арифметические кристаллические классы соответствуют классам сопряженности конечной подгруппы общей линейной группы GL n ( Z ) над целыми числами. Пространственная группа называется симморфной (или расщепленной ), если существует точка, все симметрии которой являются произведением симметрии, фиксирующей эту точку, и перевода. Эквивалентно, космическая группа является симморфной, если она является полупрямым произведением своей точечной группы с подгруппой трансляции. Существует 73 симморфных пространственных группы, по одной в каждом арифметическом кристаллическом классе. Существует также 157 типов несимморфных пространственных групп с разными номерами в арифметических кристаллических классах. Арифметические классы кристаллов можно интерпретировать как различные ориентации точечных групп в решетке, при этом матричные компоненты элементов группы ограничены целыми коэффициентами в пространстве решетки. Это довольно легко представить на примере двухмерной группы обоев . Некоторые группы точек имеют отражения, а линии отражения могут располагаться вдоль направлений решетки, на полпути между ними или по обоим направлениям. Нет: С 1 : р1; С2 : р2 ; С3 ; : р3 С 4 : р4; С 6 : стр.6 Вдоль: Д 1 : вечера, стр; D2 : пмм, пмг , пгг; Д 3 : стр31м Между: D 1 : см; Д 2 : смм; Д 3 : p3m1 Оба: D 4 : p4m, p4g; Д 6 : п6м
(геометрические) Классы кристаллов (32 в трех измерениях)	Стаи Браве (14 в трех измерениях)
Иногда их называют Q-классами. Кристаллический класс пространственной группы определяется ее точечной группой: фактором по подгруппе трансляций, действующих на решетку. Две пространственные группы принадлежат к одному и тому же кристаллическому классу тогда и только тогда, когда их точечные группы, являющиеся подгруппами GL n ( Z ), сопряжены в большей группе GL n ( Q ).	Они определяются основным типом решетки Браве. Они соответствуют классам сопряженности точечных групп решетки в GL n ( Z ), где точечная группа решетки - это группа симметрий базовой решетки, которая фиксирует точку решетки и содержит точечную группу.
Кристаллические системы (7 в трех измерениях)	Решётчатые системы (7 в трёх измерениях)
Кристаллические системы представляют собой специальную модификацию решетчатых систем, чтобы сделать их совместимыми с классификацией по точечным группам. Они отличаются от семейств кристаллов тем, что семейство гексагональных кристаллов разделено на два подмножества, называемые тригональной и гексагональной кристаллическими системами. Тригональная кристаллическая система больше, чем система ромбоэдрической решетки, гексагональная кристаллическая система меньше, чем система гексагональной решетки, а остальные кристаллические системы и системы решетки одинаковы.	Система решетки пространственной группы определяется классом сопряженности точечной группы решетки (подгруппы GL n ( Z )) в большей группе GL n ( Q ). В трех измерениях точечная группа решетки может иметь один из 7 различных порядков: 2, 4, 8, 12, 16, 24 или 48. Семейство гексагональных кристаллов разделено на два подмножества, называемые системами ромбоэдрической и гексагональной решетки.
Семейства кристаллов (6 в трех измерениях)
Точечная группа пространственной группы не совсем определяет ее систему решетки, поскольку иногда две пространственные группы с одной и той же точечной группой могут находиться в разных системах решетки. Семейства кристаллов образуются из систем решеток путем слияния двух систем решеток всякий раз, когда это происходит, так что кристаллическое семейство пространственной группы определяется либо ее системой решетки, либо ее точечной группой. В трехмерном пространстве единственные два семейства решеток, которые сливаются таким образом, — это системы гексагональной и ромбоэдрической решеток, которые объединяются в семейство гексагональных кристаллов. Шесть семейств кристаллов в трех измерениях называются триклинными, моноклинными, орторомбическими, тетрагональными, гексагональными и кубическими. Семейства кристаллов обычно используются в популярных книгах по кристаллам, где их иногда называют кристаллическими системами.

Конвей , Дельгадо Фридрихс и Хьюсон и др. ( 2001 ) дали другую классификацию пространственных групп, названную фибрифолдной нотацией , в соответствии с фибрифолдными структурами на соответствующем орбифолде . Они разделили 219 аффинных пространственных групп на приводимые и неприводимые группы. Приводимые группы распадаются на 17 классов, соответствующих 17 группам обоев , а остальные 35 неприводимых групп такие же, как кубические группы , и классифицируются отдельно.

В других измерениях

Теоремы Бибербаха

В n измерениях аффинная пространственная группа или группа Бибербаха представляет собой дискретную подгруппу изометрий n -мерного евклидова пространства с компактной фундаментальной областью. Бибербах ( 1911 , 1912 ) доказал, что подгруппа переводов любой такой группы содержит n линейно независимых сдвигов, является свободной абелевой подгруппой конечного индекса, а также единственной максимальной нормальной абелевой подгруппой. Он также показал, что в любом измерении n существует только конечное число возможностей для класса изоморфизма базовой группы пространственной группы, и, более того, действие группы в евклидовом пространстве уникально с точностью до сопряжения аффинными преобразованиями. Это частично отвечает на восемнадцатую проблему Гильберта . Зассенхаус (1948) показал, что, наоборот, любая группа, являющаяся расширением Z ​ ^н конечной группой, действующей точно, является аффинной пространственной группой. Объединение этих результатов показывает, что классификация пространственных групп в n измерениях с точностью до сопряжения аффинными преобразованиями по существу совпадает с классификацией классов изоморфизма для групп, которые являются расширениями Z. ^н конечной группой, действующей точно.

В теоремах Бибербаха важно предположить, что группа действует как изометрия; теоремы не распространяются на дискретные кокомпактные группы аффинных преобразований евклидова пространства. Контрпример дан трехмерной группой Гейзенберга целых чисел, действующей посредством сдвигов в группе Гейзенберга действительных чисел, отождествляемой с трехмерным евклидовым пространством. Это дискретная кокомпактная группа аффинных преобразований пространства, но не содержащая подгруппы Z ³ .

Классификация по малым размерам

В этой таблице указано количество типов пространственных групп в малых размерностях, включая количество различных классов пространственных групп. В скобках указано количество энантиоморфных пар.

Размеры	Семейства кристаллов, OEIS A004032 последовательность	Кристаллические системы, OEIS A004031 последовательность	Решетки Браве, OEIS A256413 последовательность	Абстрактные кристаллографические точечные группы, последовательность OEIS A006226	Геометрические классы кристаллов, Q-классы, кристаллографические точечные группы, последовательность OEIS A004028	Классы арифметических кристаллов, Z-классы, OEIS A004027 последовательность	Типы аффинных пространственных групп, OEIS A004029 последовательность	Типы кристаллографических пространственных групп, последовательность OEIS A006227
0	1	1	1	1	1	1	1	1
1	1	1	1	2	2	2	2	2
2	4	4	5	9	10	13	17	17
3	6	7	14	18	32	73	219 (+11)	230
4	23 (+6)	33 (+7)	64 (+10)	118	227 (+44)	710 (+70)	4783 (+111)	4894
5	32	59	189	239	955	6079	222018 (+79)	222097
6	91	251	841	1594	7103	85308 (+?)	28927915 (+?)	?

Магнитные группы и обращение времени

Основная статья: Магнитная космическая группа

Помимо кристаллографических пространственных групп существуют еще магнитные пространственные группы (также называемые двухцветными (черно-белыми) кристаллографическими группами или группами Шубникова ). Эти симметрии содержат элемент, известный как обращение времени. Они рассматривают время как дополнительное измерение, а элементы группы могут включать в себя обращение времени как отражение. Они играют важную роль в магнитных структурах , содержащих упорядоченные неспаренные спины, т. е. в ферро- , ферри- или антиферромагнитных структурах, изучаемых методом дифракции нейтронов . Элемент обращения времени переворачивает магнитный спин, оставляя всю остальную структуру прежней, и его можно комбинировать с рядом других элементов симметрии. С учетом обращения времени в 3D имеется 1651 магнитная пространственная группа ( Ким 1999 , стр.428). Также удалось построить магнитные версии для других габаритов и размеров решетки ( работы Даниэля Литвина , ( Литвин 2008 ), ( Литвин 2005 )). Группы фризов представляют собой магнитные группы 1D-линий, группы слоев — это группы магнитных обоев, а группы осевых 3D-точек — это магнитные 2D-группы точек. Количество исходных и магнитных групп по (общему, решеточному) размеру:( Палистрант 2012 )( Сувинье 2006 )

Общий измерение	Решетка измерение	Обычные группы			Магнитные группы
		Имя	Символ	Считать	Символ	Считать
0	0	Нульмерная группа симметрии	$G_{0}$	1	$G_{0}^{1}$	2
1	0	Одномерные точечные группы	$G_{10}$	2	$G_{10}^{1}$	5
	1	Одномерные дискретные группы симметрии	$G_{1}$	2	$G_{1}^{1}$	7
2	0	Двумерные точечные группы	$G_{20}$	10	$G_{20}^{1}$	31
	1	Фризовые группы	$G_{21}$	7	$G_{21}^{1}$	31
	2	Группы обоев	$G_{2}$	17	$G_{2}^{1}$	80
3	0	Трехмерные точечные группы	$G_{30}$	32	$G_{30}^{1}$	122
	1	Стержневые группы	$G_{31}$	75	$G_{31}^{1}$	394
	2	Группы слоев	$G_{32}$	80	$G_{32}^{1}$	528
	3	Трехмерные космические группы	$G_{3}$	230	$G_{3}^{1}$	1651
4	0	Четырехмерные точечные группы	$G_{40}$	271	$G_{40}^{1}$	1202
	1		$G_{41}$	343
	2		$G_{42}$	1091
	3		$G_{43}$	1594
	4	Четырехмерные дискретные группы симметрии	$G_{4}$	4894	$G_{4}^{1}$	62227

Таблица пространственных групп в 2 измерениях (группы обоев)

Таблица групп обоев с использованием классификации двумерных пространственных групп:

Кристаллическая система , Решетка Браве	Геометрический класс, точечная группа					Арифметика сорт	Группы обоев (схема ячеек)
	Международный	Хороший.	Орбифолд	Кокс.	Слово.
Косой	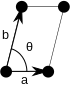1	С 1	(1)	[ ] +	1	Никто	п1 (1)
	2	С 2	(22)	[2] +	2	Никто	п2 (2222)
Прямоугольный	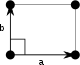м	Д 1	(*)	[ ]	2	Вдоль	вечер (**)		стр. (××)
	2 мм	DД2	(*22)	[2]	4	Вдоль	пмм (*2222)		пмг (22*)
Центрированный прямоугольный	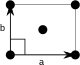м	Д 1	(*)	[ ]	2	Между	см (*×)
	2 мм	DД2	(*22)	[2]	4	Между	хмм (2*22)		пгг (22×)
Квадрат	4	С 4	(44)	[4] +	4	Никто	п4 (442)
	4 мм	Д 4	(*44)	[4]	8	Оба	п4м (*442)		п4г (4*2)
Шестиугольный	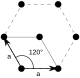3	С 3	(33)	[3] +	3	Никто	п3 (333)
	3m	Д 3	(*33)	[3]	6	Между	п3м1 (*333)		п31м (3*3)
	6	CС6	(66)	[6] +	6	Никто	стр.6 (632)
	6 мм	Д 6	(*66)	[6]	12	Оба	п6м (*632)

Для каждого геометрического класса возможны следующие арифметические классы:

• Нет: нет линий отражения.
• Вдоль: линии отражения вдоль направлений решетки.
• Между: линии отражения посередине между направлениями решетки.
• Оба: линии отражения как вдоль направлений решетки, так и между ними.

Таблица пространственных групп в 3 измерениях

Дополнительная информация: Список космических групп.

№	Кристаллическая система , (считать), Решетка Браве	Группа точек					Пространственные группы (международный короткий символ)
		Международный	Хороший.	Орбифолд	Кокс.	Слово.
1	Триклиника (2)	1	С 1	11	[ ] +	1	П1
2		1	CТам	1×	[2 + ,2 + ]	2	PП1
3–5	Моноклиника (13)	2	С 2	22	[2] +	2	П2, П2 1 С2
6–9		м	С с	*11	[ ]	2	ПМ, ПК См, Копия
10–15		2/м	С 2 часа	2*	[2,2 + ]	4	П2/м, П2 1 /м С2/м, П2/к, Р2 1 /к С2/с
16–24	орторомбический (59)	222	DД2	222	[2,2] +	4	P222, P222 1 , P2 1 2 1 2, P2 1 2 1 2 1 , C222 1 , C222, F222, I222, I2 1 2 1 2 1
25–46		мм2	С 2 в	*22	[2]	4	Pmm2, Pmc2 1 , Pcc2, Pma2, Pca2 1 , Pnc2, Pmn2 1 , Pba2, Pna2 1 , Pnn2 Cmm2, Cmc2 1 , Ccc2, Amm2, Aem2, Ama2, Aea2 Фмм2, Фдд2 Имм2, Иба2, Има2
47–74		М-м-м	Д 2 часа	*222	[2,2]	8	Пммм, Пннн, Пксм, Пбан, Пмма, Пнна, Пмна, Пкка, Пбам, Пккн, Пбкм, Пнм, Пммн, ПБЦн, Пбка, Пнма Cmcm, Cmce, Cmmm, Cccm, Cmme, Ccce Мммм, Фддд Иммм, Ибам, Ибша, Имма
75–80	четырехугольный (68)	4	С 4	44	[4] +	4	П4, П4 1 , П4 2 , П4 3 , И4, И4 1
81–82		4	С 4	2×	[2 + ,4 + ]	4	П 4 , Я 4
83–88		4/м	С 4 часа	4*	[2,4 + ]	8	П4/м, П4 2 /м, П4/н, П4 2 /н I4/м, I4 1 /а
89–98		422	Д 4	224	[2,4] +	8	P422, P42 1 2, P4 1 22, P4 1 2 1 2, P4 2 22, P4 2 2 1 2, P4 3 22, P4 3 2 1 2 И422, И4 1 22
99–110		4 мм	С 4В	*44	[4]	8	П4мм, П4бм, П4 2 см, П4 2 нм, П4сс, П4нк, П4 2 мк, П4 2 н.э. I4мм, I4см, I4 1 мкр, I4 1 кд
111–122		4 2 м	Д 2д	2*2	[2 + ,4]	8	П 4 2м, П 4 2в, П 4 2 1 м, П 4 2 1 в, П 4 м2, П 4 с2, П 4 б2, П 4 н2 Я 4 м2, Я 4 с2, Я 4 2м, Я 4 2д.
123–142		4/ммм	Д 4 часа	*224	[2,4]	16	P4/mmm, P4/mcc, P4/nbm, P4/nnc, P4/mbm, P4/mnc, P4/nmm, P4/ncc, P4 2 /mmc, P4 2 /mcm, P4 2 /nbc, P4 2 / nnm, P4 2 /mbc, P4 2 /mnm, P4 2 /nmc, P4 2 /ncm I4/mmm, I4/mcm, I4 1 /amd, I4 1 /acd
143–146	Треугольный (25)	3	С 3	33	[3] +	3	П3, П3 1 , П3 2 Р3
147–148		3	SS6	3×	[2 + ,6 + ]	6	П3 , Р3
149–155		32	Д 3	223	[2,3] +	6	П312, П321, П3 1 12, П3 1 21, П3 2 12, П3 2 21 Р32
156–161		3m	С 3В	*33	[3]	6	П3м1, П31м, П3с1, П31с Р3м, Р3с
162–167		3 m	Д 3д	2*3	[2 + ,6]	12	П 3 1м, П 3 1в, П 3 м1, П 3 с1 Р 3 м, Р 3 в
168–173	Шестиугольный (27)	6	CС6	66	[6] +	6	П6, П6 1 , П6 5 , П6 2 , П6 4 , П6 3
174		6	С 3 часа	3*	[2,3 + ]	6	П 6
175–176		6/м	С 6 часов	6*	[2,6 + ]	12	Р6/м, Р6 3 /м
177–182		622	Д 6	226	[2,6] +	12	P622, P6 1 22, P6 5 22, P6 2 22, P6 4 22, P6 3 22
183–186		6 мм	С 6в	*66	[6]	12	P6мм, P6cc, P6 3 см, P6 3 мк
187–190		6 м2	Д 3 часа	*223	[2,3]	12	П 6 м2, П 6 с2, П 6 2м, П 6 2в
191–194		6/ммм	Д 6ч	*226	[2,6]	24	P6/ммм, P6/мсм, P6 3 /мкм, P6 3 /ммк
195–199	Кубический (36)	23	Т	332	[3,3] +	12	П23, Ф23, И23 П2 1 3, И2 1 3
200–206		m 3	Т ч	3*2	[3 + ,4]	24	Пм3 , Пн3 , Фм3 , Фд3 , Им3 , Па3 , Иа3
207–214		432	ТО	432	[3,4] +	24	П432, П4 2 32 Ф432, Ф4 1 32 I432 П4 3 32, П4 1 32, И4 1 32
215–220		4 3м	Т д	*332	[3,3]	24	П 4 3м, Ж 4 3м, И 4 3м П 4 3н, Ф 4 3в, И 4 3д
221–230		м 3 м	Ой ​	*432	[3,4]	48	Пм 3 м, Пн 3 н, Пм 3 н, Пн 3 м Фм 3 м, Фм 3 в, Фд 3 м, Фд 3 в мне 3 м, мне 3 д

Примечание. Самолет e — это самолет с двойным скольжением, один из которых скользит в двух разных направлениях. Они встречаются в семи ромбических, пяти тетрагональных и пяти кубических пространственных группах, все с центрированной решеткой. Использование символа e стало официальным благодаря Хану (2002) .

Систему решетки можно найти следующим образом. Если кристаллическая система не тригональна, то и решётка того же типа. Если кристаллическая система тригональная, то система решетки является шестиугольной, если только пространственная группа не является одной из семи в ромбоэдрической системе решетки, состоящей из 7 тригональных пространственных групп в таблице выше, название которых начинается с буквы R. (Термин ромбоэдрическая система также иногда используется как альтернативное название всей тригональной системы.) Шестиугольная кристаллическая система больше, чем гексагональная кристаллическая система, и состоит из гексагональной кристаллической системы вместе с 18 группами тригональной кристаллической системы, кроме семи, названия которых начинаются с Р.

Решетка Браве пространственной группы определяется системой решетки вместе с начальной буквой ее названия, которая для неромбоэдрических групп - P, I, F, A или C, что означает главную, объемноцентрированную, гранецентрированную группу. , Решетки с центрированием грани А или С. Существует семь ромбоэдрических пространственных групп с начальной буквой R.

Вывод кристаллического класса из пространственной группы

1. Оставьте тип Браве
2. Преобразование всех элементов симметрии с трансляционными компонентами в соответствующие им элементы симметрии без трансляционной симметрии (плоскости скольжения преобразуются в простые зеркальные плоскости; оси винтов преобразуются в простые оси вращения).
3. Оси вращения, оси ротоинверсии и плоскости зеркал остаются неизменными.

Ссылки

• Барлоу, В. (1894), «О геометрических свойствах жестких структур и их применении к кристаллам», Journal of Crystallography , 23 : 1–63, doi : 10.1524/zkri.1894.23.1.1 , S2CID   102301331
• Бибербах, Людвиг (1911), «О группах жестких преобразований в евклидовых пространствах» , Mathematical Annals , 70 (3): 297–336, doi : 10.1007/BF01564500 , ISSN   0025-5831 , S2CID   124429194
• Бибербах, Людвиг (1912), «О группах жестких преобразований в евклидовых пространствах (Второе эссе.) Группы с конечной фундаментальной областью», Mathematical Annals , 72 (3): 400–412, doi : 10.1007/BF01456724 , ISSN   0025 -5831 , S2CID   119472023
• Браун, Гарольд; Бюлов, Рольф; Нойбюзер, Иоахим; Вондраччек, Ганс; Зассенхаус, Ганс (1978), Кристаллографические группы четырехмерного пространства , Нью-Йорк: Wiley-Interscience [John Wiley & Sons], ISBN  978-0-471-03095-9 , МР   0484179
• Буркхардт, Иоганн Якоб (1947), Группы кристаллографии жестких преобразований в , Учебники и монографии из областей точных наук, том. 13, Верлаг Биркхойзер, Базель, MR   0020553
• Буркхардт, Иоганн Якоб (1967), «К истории открытия 230 космических групп», Архив истории точных наук , 4 (3): 235–246, doi : 10.1007 /BF00412962 , ISSN   0003-9519 , MR   0220837 , S2CID   121994079
• Конвей, Джон Хортон ; Дельгадо Фридрихс, Олаф; Хьюсон, Дэниел Х.; Терстон, Уильям П. (2001), «О трехмерных пространственных группах» , Вклад в алгебру и геометрию , 42 (2): 475–507, ISSN   0138-4821 , MR   1865535
• Fedorov, E. S. (1891a), "Симметрія правильныхъ системъ фигуръ" [ Simmetriya pravil'nykh sistem figur , The symmetry of regular systems of figures], Записки Императорского С.-Петербургского Минералогического Общества (Zapiski Imperatorskova Sankt Petersburgskova Mineralogicheskova Obshchestva, Proceedings of the Imperial St. Petersburg Mineralogical Society) , 2nd series (in Russian), 28 (2): 1–146
  • Английский перевод: Федоров, Е.С. (1971). Симметрия кристаллов . Монография № 7 Американской кристаллографической ассоциации. Перевод Дэвида и Кэтрин Харкер. Буффало, Нью-Йорк: Американская кристаллографическая ассоциация. стр. 50–131.
• Fedorov, E. S. (1891b). "Симметрія на плоскости" [ Simmetrija na ploskosti , Symmetry in the plane]. Записки Императорского С.-Петербургского Минералогического Общества (Zapiski Imperatorskogo Sant-Petersburgskogo Mineralogicheskogo Obshchestva, Proceedings of the Imperial St. Petersburg Mineralogical Society) . 2nd series (in Russian). 28 : 345–390.
• Хан, Т. (2002), Хан, Тео (редактор), Международные таблицы для кристаллографии, Том A: Симметрия пространственной группы , том. А (5-е изд.), Берлин, Нью-Йорк: Springer-Verlag , doi : 10.1107/97809553602060000100 , ISBN  978-0-7923-6590-7
• Холл, SR (1981), «Обозначение пространственных групп с явным происхождением», Acta Crystallographica A , 37 (4): 517–525, Bibcode : 1981AcCrA..37..517H , doi : 10.1107/s0567739481001228
• Янссен, Т .; Бирман, Дж.Л.; Денуайе, Ф.; Копцик, В.А.; Вергер-Гогри, JL; Вайгель, Д.; Ямамото, А.; Абрахамс, Южная Каролина; Копский, В. (2002), «Отчет подкомитета по номенклатуре n -мерной кристаллографии. II. Символы арифметических кристаллических классов, классов Браве и пространственных групп», Acta Crystallographica A , 58 (Pt 6): 605–621 , doi : 10.1107/S010876730201379X , PMID   12388880
• Ким, Шуун К. (1999), Теоретико-групповые методы и приложения к молекулам и кристаллам , Cambridge University Press , doi : 10.1017/CBO9780511534867 , ISBN  978-0-521-64062-6 , МР   1713786 , S2CID   117849701
• Литвин, Д.Б. (май 2008 г.), «Таблицы кристаллографических свойств магнитных пространственных групп», Acta Crystallographica A , 64 (Pt 3): 419–24, Bibcode : 2008AcCrA..64..419L , doi : 10.1107/S010876730800768X , PMID   18421131
• Литвин, Д.Б. (май 2005 г.), «Таблицы свойств магнитных субпериодических групп» (PDF) , Acta Crystallographica A , 61 (Pt 3): 382–5, Bibcode : 2005AcCrA..61..382L , doi : 10.1107/S010876730500406X , PMID   15846043
• Нойбюзер, Дж.; Сувинье, Б.; Уондрачек, Х. (2002), «Поправки к кристаллографическим группам четырехмерного пространства Брауна и др. (1978) [Нью-Йорк: Wiley and Sons]», Acta Crystallographica A , 58 (Pt 3): 301, doi : 10.1107/S0108767302001368 , PMID   11961294
• Опгенорт, Дж; Плескен, Ж; Шульц, Т. (1998), «Кристаллографические алгоритмы и таблицы», Acta Crystallographica A , 54 (Pt 5): 517–531, Bibcode : 1998AcCrA..54..517O , doi : 10.1107/S010876739701547X
• Палистрант, А. Ф. (2012), «Полная схема групп четырехмерной кристаллографической симметрии», Crystallography Reports , 57 (4): 471–477, Bibcode : 2012CryRp..57..471P , doi : 10.1134/S1063774512040104 , S2CID   9568 0790
• Плескен, Вильгельм; Ханрат, В. (1984), "Решетки шестимерного пространства", Math. Комп. , 43 (168): 573–587, doi : 10.1090/s0025-5718-1984-0758205-5
• Плескен, Вильгельм; Шульц, Тилман (2000), «Подсчет кристаллографических групп в низких измерениях» , Экспериментальная математика , 9 (3): 407–411, doi : 10.1080/10586458.2000.10504417 , ISSN   1058-6458 , MR   1795312 , S2CID   405882 34
• Шёнфлис, Артур Мориц (1923), «Теория кристаллической структуры», Gebrüder Bornträger, Берлин
• Сувинье, Берн (2003), «Энантиоморфизм кристаллографических групп в более высоких измерениях с результатами в размерах до 6» (PDF) , Acta Crystallographica A , 59 (3): 210–220, doi : 10.1107/S0108767303004161 , PMID   12714771
• Сувинье, Берн (2006), «Четырехмерная магнитная точка и пространственные группы», Журнал кристаллографии , 221 : 77–82, Bibcode : 2006ZK...221...77S , doi : 10.1524/zkri.2006.221. , HDL : 2066/35218 , S2CID   99946564
• Винберг, Э. (2001) [1994], «Кристаллографическая группа» , Энциклопедия математики , EMS Press
• Зассенхаус, Ганс (1948), «Об алгоритме определения пространственных групп» , Commentarii Mathematici Helvetici , 21 : 117–141, doi : 10.1007/BF02568029 , ISSN   0010-2571 , MR   0024424 , S2CID   120651709

Внешние ссылки

• Международный союз кристаллографии
• Группы точек и решетки Браве, заархивировано 16 июля 2012 г. в Wayback Machine.
• [1] Кристаллографический сервер Бильбао
• Информация о космической группе (старая)
• Информация о космической группе (новая)
• Структуры кристаллической решетки: указатель по пространственной группе
• Полный список 230 кристаллографических пространственных групп
• Интерактивная 3D-визуализация всех 230 кристаллографических пространственных групп. Архивировано 18 апреля 2021 г. на Wayback Machine.
• Хьюсон, Дэниел Х. (1999), Обозначение волокон и классификация трехмерных пространственных групп (PDF)
• Центр геометрии: 2.1 Формулы симметрии в декартовых координатах (два измерения)
• Центр геометрии: 10.1 Формулы симметрии в декартовых координатах (трехмерные)