Двухщелевой эксперимент

Фотоны или материя (например, электроны) создают интерференционную картину, когда используются две щели.

Свет зеленого лазера, проходящий через две щели шириной 0,4 мм и на расстоянии 0,1 мм друг от друга.

В современной физике эксперимент с двумя щелями демонстрирует, что свет и материя могут удовлетворять, казалось бы, нелепым классическим определениям как волн , так и частиц. Эта двусмысленность считается свидетельством фундаментально вероятностной природы квантовой механики . Эксперименты такого типа были впервые проведены Томасом Янгом в 1801 году как демонстрация волнового поведения видимого света. ^[1] В 1927 году Дэвиссон и Гермер и независимо Джордж Пейджет Томсон и его студент-исследователь Александр Рид ^[2] продемонстрировали, что электроны демонстрируют такое же поведение, которое позже было распространено на атомы и молекулы. ^[3]^[4]^[5] Эксперимент Томаса Янга со светом был частью классической физики задолго до развития квантовой механики и концепции корпускулярно-волнового дуализма . Он считал, что это продемонстрировало Христиана Гюйгенса правильность волновой теории света , и его эксперимент иногда называют экспериментом Янга. ^[6] или щели Янга. ^[7]

Эксперимент принадлежит к общему классу экспериментов «двойного пути», в которых волна разделяется на две отдельные волны (волна обычно состоит из множества фотонов и ее лучше называть волновым фронтом, не путать со свойствами волны отдельного фотона), которые позже объединяются в одну волну. Изменения длины пути обеих волн приводят к фазовому сдвигу , создавая интерференционную картину . Другая версия — интерферометр Маха-Цендера , разделяющий луч с помощью светоделителя .

В базовой версии этого эксперимента источник когерентного света , например лазерный луч, освещает пластину, пронизанную двумя параллельными щелями, и свет, проходящий через щели, наблюдается на экране позади пластины. ^[8]^[9] Волновая природа света приводит к тому, что световые волны, проходящие через две щели, интерферируют , создавая яркие и темные полосы на экране – результат, которого нельзя было бы ожидать, если бы свет состоял из классических частиц. ^[8]^[10] Однако свет всегда поглощается экраном в отдельных точках в виде отдельных частиц (не волн); интерференционная картина проявляется за счет различной плотности попадания этих частиц на экран. ^[11] Более того, версии эксперимента, включающие детекторы в щелях, показывают, что каждый обнаруженный фотон проходит через одну щель (как в случае с классической частицей), а не через обе щели (как в случае с волной). ^[12]^[13]^[14]^[15]^[16] Однако такие эксперименты показывают, что частицы не образуют интерференционную картину, если определить, через какую щель они проходят. Эти результаты демонстрируют принцип корпускулярно-волнового дуализма . ^[17]^[18]

Обнаружено, что другие объекты атомного масштаба, такие как электроны , демонстрируют такое же поведение при попадании в двойную щель. ^[9] Кроме того, обнаружение отдельных дискретных воздействий носит вероятностный характер, что необъяснимо с точки зрения классической механики . ^[9]

Эксперимент можно провести с объектами, намного большими, чем электроны и фотоны, хотя с увеличением размера это становится сложнее. Самыми крупными объектами, для которых был проведен эксперимент с двумя щелями, были молекулы , каждая из которых содержала 2000 атомов (общая масса которых составляла 25 000 атомных единиц массы ). ^[19]

Эксперимент с двумя щелями (и его варианты) стал классикой благодаря своей ясности в выражении центральных загадок квантовой механики. Поскольку оно демонстрирует фундаментальное ограничение способности наблюдателя предсказывать результаты эксперимента, Ричард Фейнман назвал это «феноменом, который невозможно [...] объяснить никаким классическим способом и в котором заключена суть квантовой механики». , оно содержит единственную загадку [квантовой механики]». ^[9]

Обзор

Если бы свет состоял исключительно из обычных или классических частиц и эти частицы были выпущены по прямой линии через щель и могли попасть на экран на другой стороне, мы бы ожидали увидеть узор, соответствующий размеру и форме щели. Однако когда на самом деле проводится этот «однощелевой эксперимент», рисунок на экране представляет собой дифракционный рисунок , в котором свет распространяется. Чем меньше щель, тем больше угол раскрытия. В верхней части изображения показана центральная часть рисунка, образующегося при освещении щели красным лазером, и, если внимательно присмотреться, две слабые боковые полосы. Больше полос можно увидеть с помощью более совершенного аппарата. Дифракция объясняет этот узор результатом интерференции световых волн от щели.

Если осветить две параллельные щели, свет от двух щелей снова интерферирует. Здесь интерференция представляет собой более выраженный рисунок с серией чередующихся светлых и темных полос. Ширина полос зависит от частоты освещающего света. ^[20] (Смотрите нижнюю фотографию справа.)

Когда Томас Янг (1773–1829) впервые продемонстрировал это явление, это указывало на то, что свет состоит из волн, поскольку распределение яркости можно объяснить попеременно аддитивной и субтрактивной интерференцией волновых фронтов . ^[9] Эксперимент Юнга, проведенный в начале 1800-х годов, сыграл решающую роль в понимании волновой теории света, победив корпускулярную теорию света, предложенную Исааком Ньютоном , которая была принятой моделью распространения света в 17 и 18 веках.

Однако более позднее открытие фотоэлектрического эффекта продемонстрировало, что при различных обстоятельствах свет может вести себя так, как будто он состоит из дискретных частиц. Эти, казалось бы, противоречивые открытия заставили выйти за рамки классической физики и принять во внимание квантовую природу света.

Фейнман любил говорить, что всю квантовую механику можно почерпнуть, тщательно обдумав последствия этого единственного эксперимента. ^[21] Он также предположил (в качестве мысленного эксперимента), что если перед каждой щелью разместить детекторы, интерференционная картина исчезнет. ^[22]

Соотношение двойственности Энглерта -Гринбергера обеспечивает детальное рассмотрение математики двухщелевой интерференции в контексте квантовой механики.

Эксперимент с двумя щелями низкой интенсивности был впервые проведен Дж. И. Тейлором в 1909 году. ^[23] путем уменьшения уровня падающего света до тех пор, пока события испускания/поглощения фотонов не станут в основном неперекрывающимися. Эксперимент с интерференцией щелей не проводился ни с чем, кроме света, до 1961 года, когда Клаус Йонссон из Тюбингенского университета провел его с когерентными электронными лучами и несколькими щелями. ^[24]^[25] В 1974 году итальянские физики Пьер Джорджо Мерли, Джан Франко Миссироли и Джулио Поцци провели аналогичный эксперимент с использованием одиночных электронов из когерентного источника и светоделителя на бипризме, показав статистический характер формирования интерференционной картины, предсказанный квантовыми методами. теория. ^[26]^[27] В 2002 году одноэлектронная версия эксперимента была признана читателями журнала Physics World «самым красивым экспериментом» . ^[28] С тех пор был опубликован ряд подобных экспериментов, вызвавших небольшие разногласия. ^[29]

В 2012 году Стефано Фраббони и его коллеги отправили одиночные электроны в нанощели (шириной около 100 нм) и, обнаружив прошедшие электроны с помощью одноэлектронного детектора, они смогли продемонстрировать формирование интерференционной картины с двумя щелями. ^[30] Было проведено множество подобных экспериментов, связанных с когерентной интерференцией; они являются основой современной электронной дифракции, микроскопии и визуализации высокого разрешения. ^[31]^[32]

В 2018 году интерференция одиночных частиц антивещества была продемонстрирована в Лаборатории позитронов (L-NESS, Миланский политехнический университет ) Рафаэля Феррагута в Комо ( Италия ) группой под руководством Марко Джаммарки. ^[33]

Варианты эксперимента

Помехи от отдельных частиц

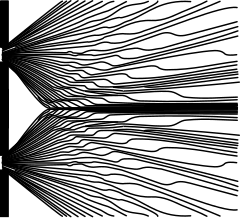
Важная версия этого эксперимента предполагает обнаружение одиночных частиц. Освещение двойной щели низкой интенсивностью приводит к тому, что отдельные частицы обнаруживаются в виде белых точек на экране. Примечательно, однако, что интерференционная картина возникает, когда этим частицам позволяют накапливаться одна за другой (см. изображение ниже).

Экспериментальная картина дифракции электронов на двойной щели. ^[34] В середине изображения вверху интенсивность меняется от высокой к низкой, показывая интерференцию сигнала из двух щелей. Внизу: видеоролик, на котором выстраивается точка за точкой узора. Нажмите на миниатюру, чтобы увеличить фильм.

Это демонстрирует корпускулярно-волновой дуализм , который утверждает, что вся материя обладает как волновыми, так и корпускулярными свойствами: частица измеряется как одиночный импульс в одной позиции, а квадрат модуля волны описывает вероятность обнаружения частицы в определенной точке. место на экране, дающее статистическую интерференционную картину. ^[35] Было показано, что это явление происходит с фотонами. ^[36] электроны, ^[37] атомы и даже некоторые молекулы: с бакминстерфуллереном ( C
₆₀ ) в 2001 году, ^[38]^[39]^[40]^[41] с 2 молекулами по 430 атомов ( C
₆₀ (С
₁₂ Ф
₂₅)
₁₀ и С
₁₆₈ ч.
₉₄ Ф
₁₅₂ О
₈ Н
₄4S
₄ ) в 2011 году, ^[42] и с молекулами до 2000 атомов в 2019 году. ^[43]Помимо интерференционных картин, построенных из отдельных частиц, до 4 запутанных фотонов. интерференционные картины могут также проявляться ^[44]

Интерферометр Маха-Цендера

Интерферометр Маха – Цендера можно рассматривать как упрощенную версию эксперимента с двумя щелями. Вместо того, чтобы распространяться в свободном пространстве после двух щелей и достигать любого положения на расширенном экране, в интерферометре фотоны могут распространяться только по двум путям и попадать на два дискретных фотодетектора. Это позволяет описать его с помощью простой линейной алгебры в размерности 2, а не дифференциальных уравнений.

Фотон, испускаемый лазером, попадает в первый светоделитель и затем оказывается в суперпозиции между двумя возможными путями. Во втором светоделителе эти пути интерферируют, в результате чего фотон попадает в фотодетектор справа с вероятностью единица и в фотодетектор внизу с вероятностью ноль. Интересно подумать, что произошло бы, если бы фотон определенно оказался на любом из путей между светоделителями. Этого можно добиться, заблокировав один из путей или, что то же самое, обнаружив там присутствие фотона. В обоих случаях интерференции между путями больше не будет, и оба фотоприемника будут поражены с вероятностью 1/2. Из этого мы можем заключить, что фотон не выбирает тот или иной путь после первого светоделителя, а скорее находится в настоящей квантовой суперпозиции двух путей. ^[45]

Эксперименты «в какую сторону» и принцип дополнительности

Известный мысленный эксперимент предсказывает, что если возле щелей разместить детекторы частиц, показывающие, через какую щель проходит фотон, интерференционная картина исчезнет. ^[9] Этот эксперимент «в какую сторону» иллюстрирует принцип дополнительности , согласно которому фотоны могут вести себя либо как частицы, либо как волны, но не могут наблюдаться как и то, и другое одновременно. ^[46]^[47]^[48]Несмотря на важность этого мысленного эксперимента в истории квантовой механики (см., например, обсуждение версии этого эксперимента Эйнштейна ), технически осуществимые реализации этого эксперимента не были предложены до 1970-х годов. ^[49] (Наивная реализация мысленного эксперимента из учебника невозможна, поскольку фотоны невозможно обнаружить без поглощения фотона.) В настоящее время проведено множество экспериментов, иллюстрирующих различные аспекты дополнительности. ^[50]

Эксперимент, проведенный в 1987 году. ^[51]^[52] дали результаты, которые продемонстрировали, что можно получить частичную информацию о том, по какому пути прошла частица, без полного устранения помех. Этот «компромисс между волной и частицей» принимает форму неравенства , касающегося видимости интерференционной картины и различимости траекторий движения. ^[53]

Отложенный выбор и варианты квантового ластика

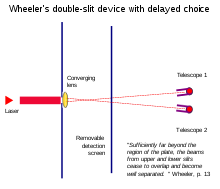
Эксперименты Уиллера с отложенным выбором показывают, что извлечение информации о том, какой путь после прохождения частицы через щели, может показаться задним числом изменить ее предыдущее поведение в щелях.

Эксперименты с квантовым ластиком показывают, что поведение волн можно восстановить, стирая или иным образом делая навсегда недоступной информацию о том, какой путь.

Простая иллюстрация феномена квантового ластика, выполненная в домашних условиях, была приведена в статье в журнале Scientific American . ^[54] Если перед каждой щелью установить поляризаторы так, чтобы их оси были ортогональны друг другу, интерференционная картина будет устранена. Поляризаторы можно рассматривать как средства, вводящие информацию о пути каждого луча. Введение перед детектором третьего поляризатора с осью 45° относительно остальных поляризаторов «стирает» эту информацию, позволяя интерференционной картине появиться вновь. Это также можно объяснить, рассматривая свет как классическую волну. ^[54]^: 91 а также при использовании круговых поляризаторов и одиночных фотонов. ^[55]^: 6 Реализации поляризаторов с использованием запутанных пар фотонов не имеют классического объяснения. ^[55]

Слабое измерение

В широко разрекламированном эксперименте 2012 года исследователи заявили, что определили путь, по которому прошла каждая частица, без каких-либо негативных последствий для интерференционной картины, создаваемой частицами. ^[56] Для этого они использовали установку, в которой частицы, попадающие на экран, были не от точечного источника, а от источника с двумя максимумами интенсивности. Однако такие комментаторы, как Свенссон ^[57] отметили, что на самом деле нет никакого конфликта между слабыми измерениями, выполненными в этом варианте эксперимента с двумя щелями, и принципом неопределенности Гейзенберга . Слабое измерение с последующим последующим отбором не позволило одновременно измерить положение и импульс для каждой отдельной частицы, а, скорее, позволило измерить среднюю траекторию частиц, прибывших в разные положения. Другими словами, экспериментаторы создавали статистическую карту полного ландшафта траекторий. ^[57]

Другие варианты

Лабораторная двухщелевая сборка; расстояние между верхними стойками составляет примерно 2,5 см (один дюйм).

В 1967 году Пфлигор и Мандель продемонстрировали интерференцию двух источников, используя два отдельных лазера в качестве источников света. ^[58]^[59]

В 1972 году экспериментально было показано, что в системе с двумя щелями, где в любой момент времени была открыта только одна щель, интерференция, тем не менее, наблюдалась при условии, что разность хода была такова, что обнаруженный фотон мог прийти из любой щели. ^[60]^[61] Условия эксперимента были таковы, что плотность фотонов в системе была значительно меньше единицы.

В 1991 году Карнал и Млинек провели классический эксперимент Янга с двумя щелями, в котором метастабильные атомы гелия проходили через щели микрометрового размера в золотой фольге. ^[62]^[63]

В 1999 году эксперимент по квантовой интерференции (с использованием дифракционной решетки, а не двух щелей) был успешно проведен с молекулами бакибола (каждая из которых содержит 60 атомов углерода). ^[38]^[64] Бакибол достаточно велик (диаметр около 0,7 нм , что почти в полмиллиона раз больше протона), чтобы его можно было увидеть в электронный микроскоп .

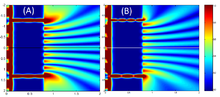
В 2002 году источник электронной эмиссии был использован для демонстрации эксперимента с двумя щелями. В этом эксперименте когерентная электронная волна излучалась из двух близко расположенных точек излучения на вершине иглы, которые действовали как двойные щели, разделяя волну на две когерентные электронные волны в вакууме. Тогда можно было наблюдать интерференционную картину между двумя электронными волнами. ^[65] В 2017 году исследователи провели эксперимент с двумя щелями, используя светоиндуцированные полевые эмиттеры электронов. С помощью этого метода места эмиссии можно оптически выбирать в масштабе десяти нанометров. Выборочно деактивировав (закрыв) одно из двух излучений (щелей), исследователи смогли показать, что интерференционная картина исчезла. ^[66]

В 2005 году Э.Р. Элиэль представил экспериментальное и теоретическое исследование оптического пропускания тонкого металлического экрана, перфорированного двумя субволновыми щелями, разделенными множеством оптических длин волн. Показано, что общая интенсивность двухщелевой структуры в дальней зоне уменьшается или увеличивается в зависимости от длины волны падающего светового луча. ^[67]

В 2012 году исследователи из Университета Небраски-Линкольна провели эксперимент с двумя щелями с электронами, как описано Ричардом Фейнманом , используя новые инструменты, которые позволяли контролировать передачу двух щелей и отслеживать события обнаружения одиночных электронов. Электроны выпускались из электронной пушки и проходили через одну или две щели шириной 62 нм и высотой 4 мкм. ^[68]

В 2013 году эксперимент по квантовой интерференции (с использованием дифракционных решеток, а не двух щелей) был успешно проведен с молекулами, каждая из которых состояла из 810 атомов (общая масса которых составляла более 10 000 атомных единиц массы ). ^[4]^[5] В 2019 году рекорд был поднят до 2000 атомов (25 000 а.е.м.). ^[19]

Гидродинамические аналоги пилотной волны

Были разработаны гидродинамические аналоги , которые могут воссоздать различные аспекты квантово-механических систем, включая интерференцию одной частицы через двойную щель. ^[69] Капля силиконового масла, подпрыгивая по поверхности жидкости, самодвижется за счет резонансного взаимодействия с собственным волновым полем. Капля мягко расплескивает жидкость при каждом отскоке. В то же время на его ход влияют волны прошлых отскоков. Взаимодействие капли с ее собственными волнами, которые образуют так называемую пилотную волну , заставляет ее демонстрировать поведение, которое ранее считалось свойственным элементарным частицам, включая поведение, обычно воспринимаемое как доказательство того, что элементарные частицы распространяются в пространстве, как волны, без каких-либо конкретном месте, пока они не будут измерены. ^[70]^[71]

Поведение, имитируемое этой гидродинамической системой пилот-волн, включает квантовую дифракцию одиночных частиц, ^[72] туннелирование, квантованные орбиты, расщепление орбитальных уровней, спин и мультимодальная статистика. Также возможно вывести отношения неопределенности и принципы исключения. Доступны видеоролики, иллюстрирующие различные функции этой системы. (См. Внешние ссылки.)

Однако более сложные системы, включающие две или более частиц в суперпозиции, не поддаются такому простому, классически интуитивному объяснению. ^[73] Соответственно, гидродинамический аналог запутывания не разработан. ^[69] Тем не менее, оптические аналоги возможны. ^[74]

Двухщелевой эксперимент вовремя

В 2023 году сообщалось об эксперименте по воссозданию интерференционной картины во времени путем освещения импульсом лазера накачки экрана, покрытого оксидом индия и олова (ITO), который изменил свойства электронов внутри материала из-за эффекта Керра , изменив его с от прозрачного до отражающего в течение примерно 200 фемтосекунд, когда последующий зондирующий лазерный луч, попадающий на экран ITO, затем увидит это временное изменение оптических свойств как щель во времени, а две из них - как двойную щель с разностью фаз, складывающейся деструктивно или конструктивно на каждая частотная составляющая приводит к интерференционной картине. ^[75]^[76]^[77] Аналогичные результаты были получены классически на волнах на воде. ^[75]^[77]

Классическая формулировка волновой оптики

Двухщелевая дифракционная картина с падающей плоской волной

Две щели освещаются плоской волной, показывая разность хода.

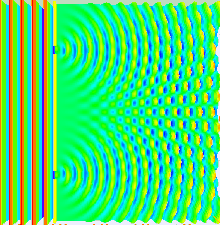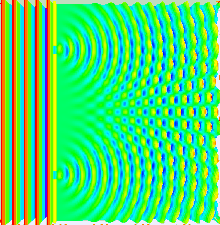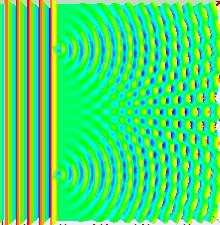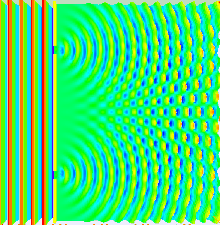
Большую часть поведения света можно смоделировать с помощью классической волновой теории. Принцип Гюйгенса-Френеля является одной из таких моделей; он утверждает, что каждая точка волнового фронта генерирует вторичный вейвлет и что возмущение в любой последующей точке можно найти путем суммирования вкладов отдельных вейвлетов в этой точке. При этом суммировании необходимо учитывать как фазу , так и амплитуду отдельных вейвлетов. Измерить можно только интенсивность светового поля — она пропорциональна квадрату амплитуды.

В эксперименте с двумя щелями две щели освещаются квазимонохроматическим светом одного лазера. Если ширина щелей достаточно мала (намного меньше длины волны лазерного света), щели преломляют свет на цилиндрические волны. Эти два цилиндрических волновых фронта накладываются, и амплитуда, а, следовательно, и интенсивность, в любой точке объединенных волновых фронтов зависит как от величины, так и от фазы двух волновых фронтов. Разница в фазе между двумя волнами определяется разницей в расстоянии, пройденном двумя волнами.

Если расстояние просмотра велико по сравнению с расстоянием между щелями ( дальнее поле ), разность фаз можно найти с помощью геометрии, показанной на рисунке внизу справа. Разность хода между двумя волнами, движущимися под углом $θ,$ определяется выражением:

d\sin \theta \approx d\theta

Где d — расстояние между двумя щелями. Когда две волны находятся в фазе, т. е. разность хода равна целому числу длин волн, суммарная амплитуда и, следовательно, суммарная интенсивность максимальны, а когда они находятся в противофазе, т. е. разность хода равна половине длина волны, полторы длины волны и т. д., тогда две волны компенсируются, и суммарная интенсивность равна нулю. Этот эффект известен как интерференция . Максимумы интерференционных полос располагаются под углами

~d\theta _{n}=n\lambda ,~n=0,1,2,\ldots

где λ — длина волны света. Угловое расстояние между полосами $θ f$ определяется выражением

\theta _{f}\approx \lambda /d

Расстояние между полосами на расстоянии $z$ от щелей определяется выражением

~w=z\theta _{f}=z\lambda /d

Например, если две щели расположены на расстоянии 0,5 мм ( $d$ ) и освещаются лазером с длиной волны 0,6 мкм ( $λ$ ), то на расстоянии 1 м ( $z$ ) расстояние между полосами составит 1,2 мм.

Если ширина щелей $b$ значительна по сравнению с длиной волны, то уравнение дифракции Фраунгофера необходимо для определения интенсивности дифрагированного света следующим образом: ^[78]

{\begin{aligned}I(\theta )&\propto \cos ^{2}\left[{\frac {\pi d\sin \theta }{\lambda }}\right]~\mathrm {sinc} ^{2}\left[{\frac {\pi b\sin \theta }{\lambda }}\right]\end{aligned}}

где функция sinc определяется как sinc( x ) = sin( x )/ x для x ≠ 0 и sinc(0) = 1.

Это проиллюстрировано на рисунке выше, где первая картина представляет собой картину дифракции одной щели, заданную функцией $sinc$ в этом уравнении, а второй рисунок показывает объединенную интенсивность света, дифрагированного от двух щелей, где $cos$ Функция представляет тонкую структуру, а более грубая структура представляет дифракцию на отдельных щелях, как описано функцией $sinc$ .

Аналогичные расчеты для ближнего поля можно провести, применив уравнение дифракции Френеля , которое подразумевает, что по мере приближения плоскости наблюдения к плоскости, в которой расположены щели, дифракционные картины, связанные с каждой щелью, уменьшаются в размерах, так что Область, в которой возникает интерференция, уменьшается и может вообще исчезнуть, если две дифрагированные картины не перекрываются. ^[79]

Формулировка интеграла по траектории

Эксперимент с двумя щелями может проиллюстрировать формулировку квантовой механики с интегралом по траекториям, предложенную Фейнманом. ^[80] Формулировка интеграла по путям заменяет классическое понятие единственной уникальной траектории системы суммой по всем возможным траекториям. Траектории складываются с помощью функционального интегрирования .

Каждый путь считается равновероятным и, следовательно, вносит одинаковую сумму. Однако фаза этого вклада в любой данной точке пути определяется действием на пути: $A_{\text{path}}(x,y,z,t)=e^{iS(x,y,z,t)}$

Все эти вклады затем складываются вместе, а величина конечного результата возводится в квадрат , чтобы получить распределение вероятностей положения частицы: $p(x,y,z,t)\propto \left\vert \int _{\text{all paths}}e^{iS(x,y,z,t)}\right\vert ^{2}$

Как всегда бывает при вычислении вероятности , результаты затем необходимо нормализовать , наложив: $\iiint _{\text{all space}}p(x,y,z,t)\,dV=1$

Распределение вероятностей результата представляет собой нормализованный квадрат нормы суперпозиции по всем путям от исходной точки до конечной точки волн, распространяющихся пропорционально действию на каждом пути. Различия в кумулятивном воздействии на разных путях (и, следовательно, в относительных фазах вкладов) создают интерференционную картину, наблюдаемую в эксперименте с двумя щелями. Фейнман подчеркнул, что его формулировка — это всего лишь математическое описание, а не попытка описать реальный процесс, который мы можем измерить.

Интерпретации эксперимента

Подобно с котом Шрёдингера мысленному эксперименту , эксперимент с двумя щелями часто используется для того, чтобы подчеркнуть различия и сходства между различными интерпретациями квантовой механики .

Копенгагенская интерпретация

Копенгагенская интерпретация — это совокупность взглядов на смысл квантовой механики , вытекающих из работ Нильса Бора , Вернера Гейзенберга , Макса Борна и других. Термин «копенгагенская интерпретация», по-видимому, был придуман Гейзенбергом в 1950-х годах для обозначения идей, разработанных в период 1925–1927 годов, сглаживая его разногласия с Бором. ^[81]^[82]^[83]^[84] Следовательно, не существует окончательного исторического утверждения о том, что влечет за собой эта интерпретация. Особенности, общие для всех версий Копенгагенской интерпретации, включают идею о том, что квантовая механика по своей сути индетерминистична , с вероятностями, рассчитываемыми с использованием правила Борна , и принцип дополнительности , который утверждает, что объекты обладают определенными парами дополнительных свойств, которые не могут наблюдаться или измеряться одновременно. . ^[85] Более того, акт «наблюдения» или «измерения» объекта необратим, и никакая истина не может быть приписана объекту, кроме как по результатам его измерения . Конкретный эксперимент может продемонстрировать поведение частицы (прохождение через определенную щель) или поведение волны (интерференция), но не то и другое одновременно. ^[86]^[87]^: 167^[88] Интерпретации копенгагенского типа утверждают, что квантовые описания объективны, поскольку они независимы от личных убеждений физиков и других произвольных ментальных факторов. ^[87]^: 85–90

Результаты самого простого эксперимента с двумя щелями — наблюдения интерференционной картины — объясняются интерференцией волн от двух путей к экрану от каждой из двух щелей. ^[9] Результаты для одной частицы показывают, что волны представляют собой амплитуды вероятности, квадрат которых образует распределение вероятностей. ^[9] Частицы дискретны и идентичны; многие из них необходимы для построения полной интерференционной картины. ^[9] Результаты некоторых экспериментов по определению направления описываются как наблюдения за дополнительностью: ^[89] изменение эксперимента для наблюдения за щелью подавляет интерференционную картину. ^[90]^: 155 Другие эксперименты, посвященные вопросу «пути», в своем анализе не упоминают о дополнительности. ^[91]

Реляционная интерпретация

Согласно реляционной интерпретации квантовой механики , впервые предложенной Карло Ровелли , ^[92] наблюдения, подобные наблюдениям в эксперименте с двумя щелями, являются результатом именно взаимодействия между наблюдателем (измерительным устройством) и наблюдаемым объектом (физически взаимодействующим с ним), а не каким-либо абсолютным свойством, которым обладает объект. В случае электрона, если он изначально «наблюдается» в определенной щели, то взаимодействие наблюдатель-частица (фотон-электрон) включает информацию о положении электрона. Это частично ограничивает возможное местоположение частицы на экране. Если он «наблюдается» (измеряется с помощью фотона) не на конкретной щели, а на экране, то в рамках взаимодействия нет информации о том, «какой путь» отсутствует, поэтому «наблюдаемое» положение электрона на экране определяется строго по его функции вероятности. Это делает результирующий рисунок на экране таким же, как если бы каждый отдельный электрон прошел через обе щели. ^{[ нужна ссылка ]}

Многомировая интерпретация

Как и в случае с Копенгагеном, существует множество вариантов интерпретации многих миров . Объединяющая тема заключается в том, что физическая реальность отождествляется с волновой функцией, и эта волновая функция всегда развивается унитарно, т.е. следует уравнению Шредингера без коллапса. ^[93]^[94] Следовательно, существует множество параллельных вселенных, которые взаимодействуют друг с другом только посредством интерференции. Дэвид Дойч утверждает, что эксперимент с двумя щелями можно понять так: в каждой вселенной частица проходит через определенную щель, но на ее движение влияет интерференция с частицами в других вселенных. Это создает наблюдаемые полосы. ^[95] Дэвид Уоллес, еще один сторонник многомировой интерпретации, пишет, что в знакомой постановке эксперимента с двумя щелями два пути недостаточно разделены, чтобы описание в терминах параллельных вселенных имело смысл. ^[96]

Теория де Бройля – Бома

Альтернатива стандартному пониманию квантовой механики, теория Де Бройля-Бома утверждает, что частицы также всегда имеют точное местоположение и что их скорости определяются волновой функцией. Таким образом, хотя в эксперименте с двумя щелями одна частица будет проходить через одну конкретную щель, так называемая «пилотная волна», влияющая на нее, будет проходить через обе. Две щелевые траектории де Бройля-Бома были впервые рассчитаны Крисом Дьюдни во время работы с Крисом Филиппидисом и Бэзилом Хили в Биркбек-колледже (Лондон). ^[97] Теория де Бройля-Бома дает те же статистические результаты, что и стандартная квантовая механика, но обходится без многих концептуальных трудностей, добавляя сложность за счет специального квантового потенциала, направляющего частицы. ^[98]

Хотя модель во многом похожа на уравнение Шредингера , известно, что она не работает в релятивистских случаях. ^[99] и не учитывает такие особенности, как рождение или уничтожение частиц в квантовой теории поля . Многие авторы, такие как нобелевские лауреаты Вернер Гейзенберг , ^[100] Сэр Энтони Джеймс Леггетт ^[101] и сэр Роджер Пенроуз ^[102] раскритиковали его за то, что он не добавил ничего нового.

Появились более сложные варианты этого типа подхода, например, трехволновая гипотеза. ^[103]^[104] Рышарда Городецкого, а также другие сложные комбинации волн де Бройля и Комптона. ^[105]^[106]^[107] На сегодняшний день нет никаких доказательств того, что они полезны.

Бомовы траектории

Траектории частиц в теории де Бройля–Бома в двухщелевом эксперименте.

100 траекторий, управляемых волновой функцией. В теории Де Бройля-Бома частица в любой момент времени представлена волновой функцией и положением (центром масс). Это своего рода дополненная реальность по сравнению со стандартной интерпретацией.

Численное моделирование двухщелевого эксперимента с электронами. Рисунок слева: эволюция (слева направо) интенсивности электронного пучка на выходе из щелей (слева) до экрана регистрации, расположенного на расстоянии 10 см после щелей (справа). Чем выше интенсивность, тем более светло-голубой цвет – Рисунок в центре: удары электронов, наблюдаемые на экране – Рисунок справа: интенсивность электронов в приближении дальнего поля (на экране). Численные данные эксперимента Клауса Йонссона (1961). Фотоны, атомы и молекулы следуют аналогичной эволюции.

См. также

Ссылки

^ Янг, Томас (1804). «Бекеровская лекция. Эксперименты и расчеты относительно физической оптики» . Философские труды Лондонского королевского общества . 94 : 1–16. дои : 10.1098/rstl.1804.0001 . S2CID 110408369 .
^ Наварро, Хауме (2010). «Дифракция электронов через Томсона: ранние ответы на квантовую физику в Великобритании» . Британский журнал истории науки . 43 (2): 245–275. дои : 10.1017/S0007087410000026 . ISSN 0007-0874 . S2CID 171025814 .
^ Томсон, врач общей практики; Рид, А. (1927). «Дифракция катодных лучей на тонкой пленке» . Природа . 119 (3007): 890. Бибкод : 1927Natur.119Q.890T . дои : 10.1038/119890a0 . ISSN 0028-0836 . S2CID 4122313 .
^ Перейти обратно: ^а ^б « Физики побили рекорд корпускулярно-волнового дуализма »
^ Перейти обратно: ^а ^б Эйбенбергер, Сандра; и др. (2013). «Интерференция материи и волн с частицами, выбранными из молекулярной библиотеки, с массой более 10000 а.е.м.». Физическая химия Химическая физика . 15 (35): 14696–14700. arXiv : 1310.8343 . Бибкод : 2013PCCP...1514696E . дои : 10.1039/C3CP51500A . ПМИД 23900710 . S2CID 3944699 .
↑
Хотя нет никаких сомнений в том, что демонстрация Янгом оптической интерференции с использованием солнечного света, точечных отверстий и карт сыграла жизненно важную роль в принятии волновой теории света, остается некоторый вопрос относительно того, действительно ли он когда-либо выполнял интерференцию с двумя щелями. эксперимент.
- Робинсон, Эндрю (2006). Последний человек, который знал всё . Нью-Йорк, штат Нью-Йорк: Pi Press. стр. 123–124 . ISBN 978-0-13-134304-7 .
^ Кипнис, Наум С. (1991). История принципа интерференции света . Спрингер. п. 65. ИСБН 978-0-8176-2316-6 .
^ Перейти обратно: ^а ^б Ледерман, Леон М.; Кристофер Т. Хилл (2011). Квантовая физика для поэтов . США: Книги Прометея. стр. 102–111. ISBN 978-1-61614-281-0 .
^ Перейти обратно: ^а ^б ^с ^д ^и ^ж ^г ^час ^я Фейнман, Ричард П.; Роберт Б. Лейтон; Мэтью Сэндс (1965). Фейнмановские лекции по физике, Vol. 3 . Аддисон-Уэсли. стр. 1.1–1.8. ISBN 978-0-201-02118-9 .
^ Фейнман, 1965, с. 1,5
^ Дорогая, Дэвид (2007). «Дуальность волны и частицы» . Интернет-энциклопедия науки . Миры Дэвида Дарлинга . Проверено 18 октября 2008 г.
^ Фейнман, 1965, с. 1,7
^ Леон Ледерман; Кристофер Т. Хилл (27 сентября 2011 г.). Квантовая физика для поэтов . Книги Прометея, Издательства. п. 109. ИСБН 978-1-61614-281-0 .
^ " ...если в двухщелевом эксперименте детекторы, регистрирующие вылетающие фотоны, располагаются сразу за диафрагмой с двумя щелями: Фотон регистрируется в одном детекторе, а не в обоих... " Мюллер-Кирстен, HJW (2006). Введение в квантовую механику: уравнение Шрёдингера и интеграл по траекториям . США: World Scientific. п. 14. ISBN 978-981-2566911 .
^ Плотницкий, Аркадий (2012). Нильс Бор и дополнительность: введение . США: Спрингер. стр. 75–76. ISBN 978-1-4614-4517-3 .
^ " Кажется, что свет проходит через одну или другую щель в виде фотонов, если мы поставим эксперимент, чтобы определить, через какую щель проходит фотон, но проходит через обе щели в виде волны, если мы проведем интерференционный эксперимент. " Рэй, Аластер IM (2004). Квантовая физика: иллюзия или реальность? . Великобритания: Издательство Кембриджского университета. стр. 9–10. ISBN 978-1-139-45527-5 .
^ Фейнман, Лекции Фейнмана по физике , 3 : Квантовая механика, стр. 1-1 «Однако есть один счастливый случай - электроны ведут себя точно так же, как свет».
^ См.: Эксперимент Дэвиссона-Гермера. Дэвиссон, CJ (1928). «Дифракция электронов на кристалле никеля». Технический журнал Bell System . 7 : 90–105. дои : 10.1002/j.1538-7305.1928.tb00342.x .
^ Перейти обратно: ^а ^б Яаков Ю. Фейн; Филипп Гейер; Патрик Цвик; Филип Кялка; Себастьян Педалино; Марсель Майор; Стефан Герлих; Маркус Арндт (сентябрь 2019 г.). «Квантовая суперпозиция молекул за пределами 25 кДа». Физика природы . 15 (12): 1242–1245. Бибкод : 2019NatPh..15.1242F . дои : 10.1038/s41567-019-0663-9 . S2CID 203638258 .
^
Чарльз Сандерс Пирс первым предложил использовать этот эффект в качестве независимого от артефактов эталонного стандарта длины.
- К. С. Пирс (июль 1879 г.). «Заметка о ходе экспериментов по сравнению длины волны с метровой». Американский журнал науки , по ссылке Криза, Роберта П. (2011). Мир на волоске: исторический поиск абсолютной системы измерения . Нью-Йорк: WW Нортон. п. 317. ISBN 978-0-393-07298-3 . п. 203.
^ Грин, Брайан (1999). Элегантная Вселенная: суперструны, скрытые измерения и поиск окончательной теории . Нью-Йорк: WW Нортон. стр. 97–109 . ISBN 978-0-393-04688-5 .
^ Фейнман, 1965, глава 3.
^ Сэр Джеффри, Ингрэм Тейлор (1909). «Интерференционные полосы слабого света». Профессор Кэм. Фил. Соц . 15 : 114.
^ Йонссон, Клаус (1 августа 1961 г.). «Электронная интерференция в нескольких искусственно созданных тонких щелях». Журнал физики (на немецком языке). 161 (4): 454–474. Бибкод : 1961ZPhy..161..454J . дои : 10.1007/BF01342460 . ISSN 0044-3328 . S2CID 121659705 .
^ Йонссон, Клаус (1 января 1974 г.). «Дифракция электронов на нескольких щелях». Американский журнал физики . 42 (1): 4–11. Бибкод : 1974AmJPh..42....4J . дои : 10.1119/1.1987592 . ISSN 0002-9505 .
^ Мерли, PG; Миссироли, Г.Ф.; Поцци, Дж. (1976). «О статистическом аспекте явлений электронной интерференции». Американский журнал физики . 44 (3): 306–307. Бибкод : 1976AmJPh..44..306M . дои : 10.1119/1.10184 .
^ Роза, Р. (2012). «Эксперимент Мерли-Миссироли-Поцци с двумя щелями электронной интерференции» . Физика в перспективе . 14 (2): 178–194. Бибкод : 2012ФП....14..178Р . дои : 10.1007/s00016-011-0079-0 . ПМЦ 4617474 . ПМИД 26525832 .
^ "Самый красивый эксперимент" . Мир физики 2002. Архивировано 24 мая 2021 года в Wayback Machine.
^ Стидс, Джон; Мерли, Пьер Джорджио; Поцци, Джулио; Миссироли, ДжанФранко; Тономура, Акира (2003). «Двущелевой эксперимент с одиночными электронами» . Мир физики . 16 (5): 20–21. дои : 10.1088/2058-7058/16/5/24 . ISSN 0953-8585 .
^ Фраббони, Стефано; Габриэлли, Алессандро; Карло Газзади, Джиан; Джорджи, Филиппо; Маттеуччи, Джорджио; Поцци, Джулио; Чезари, Никола Семприни; Вилла, Мауро; Зокколи, Антонио (май 2012 г.). «Эксперимент Янга-Фейнмана с двумя щелями с одиночными электронами: построение интерференционной картины и распределения времени прибытия с использованием пиксельного детектора с быстрым считыванием». Ультрамикроскопия . 116 :73–76. дои : 10.1016/j.ultramic.2012.03.017 . ISSN 0304-3991 .
^ Коули, Дж. М. (1995). Дифракционная физика . Личная библиотека Северной Голландии (3-е изд.). Амстердам: Эльзевир. ISBN 978-0-444-82218-5 .
^ Спенс, Джон Ч. (2017). Электронная микроскопия высокого разрешения (Четвертое издание, впервые опубликовано в мягкой обложке). Оксфорд: Издательство Оксфордского университета. ISBN 978-0-19-879583-4 .
^ Сала, С.; Арига, А.; Эредитато, А.; Феррагут, Р.; Джаммарки, М.; Леоне, М.; Пистилло, К.; Скамполи, П. (2019). «Первая демонстрация волновой интерферометрии антивещества» . Достижения науки . 5 (5): eaav7610. Бибкод : 2019SciA....5.7610S . дои : 10.1126/sciadv.aav7610 . ПМК 6499593 . ПМИД 31058223 .
^ Бах, Роджер; Папа, Дамиан; Лиу, Си-Хван; Бателаан, Герман (13 марта 2013 г.). «Управляемая дифракция электронов на двух щелях» . Новый журнал физики . 15 (3). Издание IOP: 033018. arXiv : 1210.6243 . Бибкод : 2013NJPh...15c3018B . дои : 10.1088/1367-2630/15/3/033018 . ISSN 1367-2630 . S2CID 832961 .
^ Грин, Брайан (2007). Ткань космоса: пространство, время и текстура реальности . ООО "Рэндом Хаус". п. 90. ИСБН 978-0-307-42853-0 .
^ Анантасвами, Анил (2018). Через две двери одновременно: элегантный эксперимент, раскрывающий загадку нашей квантовой реальности . Пингвин. п. 63. ИСБН 978-1-101-98611-0 .
^ Донати, О; Миссироли, Г.Ф.; Поцци, Дж. (1973). «Эксперимент по электронной интерференции». Американский журнал физики . 41 (5): 639–644. Бибкод : 1973AmJPh..41..639D . дои : 10.1119/1.1987321 .
^ Перейти обратно: ^а ^б Новый учёный: Квантовые чудеса: Корпускулы и бакиболлы, 2010 г. (Введение, для полного текста необходима подписка, полностью цитируется в [1]. Архивировано 25 сентября 2017 г. на Wayback Machine )
↑ Двойственность волновых частиц C60. Архивировано 31 марта 2012 г. в Wayback Machine.
^ Наирз, Олаф; Брезгер, Бьёрн; Арндт, Маркус; Цайлингер, Антон (2001). «Дифракция сложных молекул на структурах из света». Физ. Преподобный Летт . 87 (16): 160401. arXiv : quant-ph/0110012 . Бибкод : 2001PhRvL..87p0401N . дои : 10.1103/physrevlett.87.160401 . ПМИД 11690188 . S2CID 21547361 .
^ Наирз, О; Арндт, М; Цайлингер, А (2003). «Эксперименты по квантовой интерференции с большими молекулами» (PDF) . Американский журнал физики . 71 (4): 319–325. Бибкод : 2003AmJPh..71..319N . дои : 10.1119/1.1531580 . Архивировано из оригинала (PDF) 4 июня 2015 года . Проверено 4 июня 2015 г.
^ Стефан Герлих; и др. (5 апреля 2011 г.). «Квантовая интерференция крупных органических молекул» . Природные коммуникации . 2 : 263. Бибкод : 2011NatCo...2..263G . дои : 10.1038/ncomms1263 . ПМК 3104521 . ПМИД 21468015 .
^ Яаков Фейн; и др. (декабрь 2019 г.). «Квантовая суперпозиция молекул за пределами 25 кДа» . Физика природы . 15 (12): 1242–1245. Бибкод : 2019NatPh..15.1242F . дои : 10.1038/s41567-019-0663-9 . S2CID 203638258 .
^ Хессмо, Б., М.В. Митчелл и П. Вальтер. «Запутанные фотоны демонстрируют интерференцию и билокацию». Курьер ЦЕРН (2004): 11.
^ Ведрал, Влатко (2006). Введение в квантовую информатику . Издательство Оксфордского университета. ISBN 978-0-19-921570-6 . OCLC 442351498 .
^ Харрисон, Дэвид (2002). «Дополнительность и Копенгагенская интерпретация квантовой механики» . ВЫСОКИЙ . Кафедра физики Университета Торонто . Проверено 21 июня 2008 г.
^ Кэссиди, Дэвид (2008). «Квантовая механика 1925–1927: триумф копенгагенской интерпретации» . Вернер Гейзенберг . Американский институт физики. Архивировано из оригинала 14 января 2016 года . Проверено 21 июня 2008 г.
^ Боска Диас-Пинтадо, Мария К. (29–31 марта 2007 г.). «Обновление корпускулярно-волнового дуализма» . 15-я Британско-европейская встреча по основам физики . Лидс, Великобритания . Проверено 21 июня 2008 г.
^ Бартелл, Л. (1980). «Дополнительность в эксперименте с двумя щелями: о простых реализуемых системах для наблюдения промежуточного корпускулярно-волнового поведения». Физический обзор D . 21 (6): 1698–1699. Бибкод : 1980PhRvD..21.1698B . дои : 10.1103/PhysRevD.21.1698 .
^ Цайлингер, А. (1999). «Эксперимент и основы квантовой физики». Обзоры современной физики . 71 (2): С288–С297. Бибкод : 1999RvMPS..71..288Z . дои : 10.1103/RevModPhys.71.S288 .
^ П. Миттельштадт; А. Приер; Р. Шидер (1987). «Нерезкий корпускулярно-волновой дуализм в эксперименте с расщепленным пучком фотонов». Основы физики . 17 (9): 891–903. Бибкод : 1987FoPh...17..891M . дои : 10.1007/BF00734319 . S2CID 122856271 .
^ Д. М. Гринбергер и А. Ясин, «Одновременные знания о волнах и частицах в нейтронном интерферометре», Physics Letters A 128 , 391–4 (1988).
^ Сен, Д. (2014). «Соотношения неопределенностей в квантовой механике» . Современная наука . 107 (2): 203–218. ISSN 0011-3891 . JSTOR 24103129 . «Однако «компромисс между волной и частицей теперь выражается в терминах неравенства, известного как дуальность Энглерта-Гринбергера или просто отношение дуальности волна-частица». См. также ссылку 24 в этой работе.
^ Перейти обратно: ^а ^б Хиллмер, Р.; Квиат, П. (2007). «Квантовый ластик своими руками» . Научный американец . Том. 296, нет. 5. С. 90–95. Бибкод : 2007SciAm.296e..90H . doi : 10.1038/scientificamerican0507-90 . Проверено 11 января 2016 г.
^ Перейти обратно: ^а ^б Цзяо, Республика Корея; ПГ Квиат; Стейнберг, AM (1995). «Квантовая нелокальность в двухфотонных экспериментах в Беркли». Квантовая и полуклассическая оптика: Журнал Европейского оптического общества, часть B. 7 (3): 259–278. arXiv : Quant-ph/9501016 . Бибкод : 1995QuSOp...7..259C . дои : 10.1088/1355-5111/7/3/006 . S2CID 118987962 .
^ Фрэнсис, Мэтью (21 мая 2012 г.). «Распутывание корпускулярно-волнового дуализма в эксперименте с двумя щелями» . Арс Техника .
^ Перейти обратно: ^а ^б Свенссон, Бенгт Э.Ю. (2013). «Педагогический обзор квантовой теории измерений с акцентом на слабые измерения». Кванта . 2 (1): 18–49. arXiv : 1202.5148 . дои : 10.12743/quanta.v2i1.12 . S2CID 119242577 .
^ Пфлигор, РЛ; Мандель, Л. (июль 1967 г.). «Интерференция независимых фотонных пучков». Физический обзор . 159 (5): 1084–1088. Бибкод : 1967PhRv..159.1084P . дои : 10.1103/PhysRev.159.1084 .
^ «Интерференция независимых фотонных пучков: эксперимент Пфлигора-Манделя» . Архивировано из оригинала 3 января 2011 года . Проверено 16 июня 2011 г. >
^ Силлитто, РМ; Уайкс, Кэтрин (1972). «Интерференционный эксперимент со световыми лучами, модулированными в противофазе электрооптическим затвором». Буквы по физике А. 39 (4): 333–334. Бибкод : 1972PhLA...39..333S . дои : 10.1016/0375-9601(72)91015-8 .
^ " "К лёгкой частице" " .
^ Карнал, О.; Млынек, Дж. (май 1991 г.). «Двущелевой эксперимент Янга с атомами: простой атомный интерферометр» . Письма о физических отзывах . 66 (21): 2689–2694. Бибкод : 1991PhRvL..66.2689C . дои : 10.1103/PhysRevLett.66.2689 . ПМИД 10043591 .
^ Карнал, О.; Млынек, Дж. (1991). «Двущелевой эксперимент Янга с атомами: простой атомный интерферометр» . Письма о физических отзывах . 66 (21): 2689–2692. Бибкод : 1991PhRvL..66.2689C . дои : 10.1103/PhysRevLett.66.2689 . ПМИД 10043591 . Проверено 20 марта 2022 г. >
^ Арндт, Маркус; Наирз, Олаф; Вос-Андреа, Джулиан; Келлер, Клаудия; Ван Дер Зув, Гербранд; Цайлингер, Антон (1999). «Волново-частичный дуализм молекул C60». Природа . 401 (6754): 680–682. Бибкод : 1999Natur.401..680A . дои : 10.1038/44348 . ПМИД 18494170 . S2CID 4424892 .
^ Осима, К.; Мастуда, К.; Кона, Т.; Могами, Ю.; Комаки, М.; Мурата, Ю.; Ямасита, Т.; Кузумаки, Т.; Хориике, Ю. (4 января 2002 г.). «Интерференция электронов Янга в картинах автоэмиссии» . Письма о физических отзывах . 88 (3): 038301. Бибкод : 2002PhRvL..88c8301O . doi : 10.1103/PhysRevLett.88.038301 . ISSN 0031-9007 . ПМИД 11801091 .
^ Янагисава, Хирофуми; Чаппина, Марсело; Хафнер, Кристиан; Шец, Йоханнес; Остервальдер, Юрг; Клинг, Маттиас Ф. (4 октября 2017 г.). «Оптическое управление двухщелевым интерферометром Янга для лазерно-индуцированной эмиссии электронов из нано-иглы» . Научные отчеты . 7 (1): 12661. arXiv : 1710.02216 . Бибкод : 2017НацСР...712661Y . дои : 10.1038/s41598-017-12832-3 . ISSN 2045-2322 . ПМЦ 5627254 . ПМИД 28978914 .
^ Схоутен, ХФ; Кузьмин Н.; Дюбуа, Ж.; Виссер, Т.Д.; Гбур, Г. ; Алкемаде, ПФА; Блок, Х.; Хофт, ГВ; Ленстра, Д.; Элиэль, ER (7 февраля 2005 г.). «Двущелевая передача с плазмоном: новый взгляд на эксперимент Янга» . Физ. Преподобный Летт . 94 (5): 053901. Бибкод : 2005PhRvL..94e3901S . doi : 10.1103/physrevlett.94.053901 . hdl : 1887/71482 . ПМИД 15783641 . S2CID 19197175 .
^ Бах, Роджер; и др. (март 2013 г.). «Управляемая дифракция электронов на двух щелях». Новый журнал физики . 15 (3): 033018. arXiv : 1210.6243 . Бибкод : 2013NJPh...15c3018B . дои : 10.1088/1367-2630/15/3/033018 . S2CID 832961 .
^ Перейти обратно: ^а ^б Буш, Джон ВМ (2015). «Гидродинамика пилот-волны» (PDF) . Ежегодный обзор механики жидкости . 47 (1): 269–292. Бибкод : 2015АнРФМ..47..269Б . doi : 10.1146/annurev-fluid-010814-014506 . hdl : 1721.1/89790 . Архивировано (PDF) из оригинала 21 июня 2015 года . Проверено 21 июня 2015 г.
^ Буш, Джон ВМ (2010). «Квантовая механика в широком смысле» . ПНАС . 107 (41): 17455–17456. Бибкод : 2010PNAS..10717455B . дои : 10.1073/pnas.1012399107 . ПМЦ 2955131 .
^ Натали Волчовер (30 июня 2014 г.). «Неужели мы все это время неправильно интерпретировали квантовую механику?» . Проводной .
^ Кудер, Ю.; Форт, Э. (2012). «Вероятности и траектории в классическом корпускулярно-волновом дуализме» . Физический журнал: серия конференций . 361 (1): 012001. Бибкод : 2012JPhCS.361a2001C . дои : 10.1088/1742-6596/361/1/012001 .
^ Бэгготт, Джим (2011). Квантовая история: история за 40 мгновений . Нью-Йорк: Издательство Оксфордского университета. С. 76. («Волновая функция системы, содержащей N частиц, зависит от 3 N координат положения и является функцией в 3 N -мерном конфигурационном пространстве или «фазовом пространстве». Трудно представить себе реальность, состоящую из мнимых функций в абстрактное, многомерное пространство, однако, не возникает никаких затруднений, если мнимым функциям не требуется дать реальную интерпретацию».)
^ Ли, Пэнъюнь; Сунь, Ифань; Ян, Чжэньвэй; Сун, Синьбин; Чжан, Сяндун (2016). «Классическая гиперкорреляция и волновая оптика аналогии квантового сверхплотного кодирования» . Научные отчеты . 5 : 18574. Бибкод : 2015NatSR...518574L . дои : 10.1038/srep18574 . ПМЦ 4686973 . ПМИД 26689679 .
^ Перейти обратно: ^а ^б Бакот, Винсент; Лабусс, Матье; Эдди, Антонин; Финк, Матиас; Форт, Эммануэль (ноябрь 2016 г.). «Обращение времени и голография с преобразованиями пространства-времени» . Физика природы . 12 (10): 972–977. arXiv : 1510.01277 . Бибкод : 2016NatPh..12..972B . дои : 10.1038/nphys3810 . ISSN 1745-2481 . S2CID 53536274 .
^ Родригес-Фортуньо, Франсиско Х. (3 апреля 2023 г.). «Оптический двухщелевой эксперимент во времени» . Физика природы . 19 (7): 929–930. Бибкод : 2023NatPh..19..929R . дои : 10.1038/s41567-023-02026-2 . ISSN 1745-2481 . S2CID 257945438 .
^ Перейти обратно: ^а ^б Кастельвекки, Давиде (3 апреля 2023 г.). «Световые волны протиснулись сквозь «щели во времени» » . Природа . 616 (7956): 230. Бибкод : 2023Natur.616..230C . дои : 10.1038/d41586-023-00968-4 . ПМИД 37012471 . S2CID 257922697 .
^ Дженкинс Ф.А. и Уайт Х.Э., Основы оптики, 1967, МакГроу-Хилл, Нью-Йорк.
^ Longhurst RS, Физическая и геометрическая оптика, 1967, 2-е издание, Longmans
^ Зи, Энтони (2010). Квантовая теория поля в двух словах (2-е изд.). Издательство Принстонского университета. стр. 2–16. ISBN 978-0-691-14034-6 .
^ Фэй, Ян (2019). «Копенгагенская интерпретация квантовой механики» . В Залте, Эдвард Н. (ред.). Стэнфордская энциклопедия философии . Лаборатория метафизических исследований Стэнфордского университета.
^ Камиллери, К.; Шлоссхауэр, М. (2015). «Нильс Бор как философ эксперимента: бросает ли теория декогеренции вызов доктрине классических концепций Бора?». Исследования по истории и философии современной физики . 49 : 73–83. arXiv : 1502.06547 . Бибкод : 2015ШПМП..49...73С . дои : 10.1016/j.shpsb.2015.01.005 . S2CID 27697360 .
^ Шайбе, Эрхард (1973). Логический анализ квантовой механики . Пергамон Пресс. ISBN 978-0-08-017158-6 . OCLC 799397091 . [T]нет смысла искать копенгагенскую интерпретацию как единую и непротиворечивую логическую структуру. Такие термины, как «Копенгагенская интерпретация» или «Копенгагенская школа», основаны на истории развития квантовой механики; они представляют собой упрощенный и часто удобный способ ссылки на идеи ряда физиков, сыгравших важную роль в становлении квантовой механики и которые были сотрудниками Бора в его Институте или принимали участие в дискуссиях в решающие годы. При ближайшем рассмотрении довольно легко увидеть, что эти идеи расходятся в деталях и что, в частности, взгляды Бора, духовного лидера школы, образуют отдельную целостность, которую теперь можно понять только путем тщательного изучения как можно большего числа соответствующих публикаций самого Бора.
^ Мермин, Н. Дэвид (1 января 2017 г.). «Почему кбизм не является копенгагенской интерпретацией и что мог об этом подумать Джон Белл». В Бертльманне, Рейнгольде; Цайлингер, Антон (ред.). Квантовые [Un]Speakables II . Коллекция «Границы». Международное издательство Спрингер. стр. 83–93. arXiv : 1409.2454 . дои : 10.1007/978-3-319-38987-5_4 . ISBN 978-3-319-38985-1 . S2CID 118458259 .
^ Омнес, Роланд (1999). «Копенгагенская интерпретация». Понимание квантовой механики . Издательство Принстонского университета. стр. 41–54. дои : 10.2307/j.ctv173f2pm.9 . S2CID 203390914 .
^ Розенфельд, Л. (1953). «Спор о дополнительности». Прогресс науки (1933–) . 41 (163): 393–410. ISSN 0036-8504 . JSTOR 43414997 .
^ Перейти обратно: ^а ^б Омнес, Р. (1994). Интерпретация квантовой механики . Издательство Принстонского университета. ISBN 978-0-691-03669-4 . OCLC 439453957 .
^ Перес, Ашер (1995). Квантовая теория: концепции и методы . Академическое издательство Клувер. стр. 36–39. ISBN 0-7923-2549-4 .
^ Скалли, Мэриан О.; Энглерт, Бертольд-Георг; Вальтер, Герберт (май 1991 г.). «Квантово-оптические тесты дополнительности» . Природа . 351 (6322): 111–116. Бибкод : 1991Natur.351..111S . дои : 10.1038/351111a0 . ISSN 0028-0836 . S2CID 4311842 .
^ Мессия, Альберт (1966). Квантовая механика . Северная Голландия, Джон Уайли и сыновья. ISBN 0-486-40924-4 .
^ Фраббони, Стефано; Газзади, Джан Карло; Грилло, Винченцо; Поцци, Джулио (1 июля 2015 г.). «Упругие и неупругие электроны в эксперименте с двумя щелями: вариант установки Фейнмана с перекосом» . Ультрамикроскопия . 154 : 49–56. дои : 10.1016/j.ultramic.2015.03.006 . ISSN 0304-3991 . ПМИД 25799917 .
^ Ровелли, Карло (1996). «Реляционная квантовая механика». Международный журнал теоретической физики . 35 (8): 1637–1678. arXiv : Quant-ph/9609002 . Бибкод : 1996IJTP...35.1637R . дои : 10.1007/BF02302261 . S2CID 16325959 .
^ Кент, Адриан (февраль 2015 г.). «Есть ли смысл говорить о самоопределяющейся неопределенности в универсальной волновой функции? Замечания о Себенсе и Кэрролле». Основы физики . 45 (2): 211–217. arXiv : 1408.1944 . Бибкод : 2015FoPh...45..211K . дои : 10.1007/s10701-014-9862-5 . ISSN 0015-9018 . S2CID 118471198 .
^ Вайдман, Лев (5 августа 2021 г.). «Многомировая интерпретация квантовой механики» . В Залте, Эдвард Н. (ред.). Стэнфордская энциклопедия философии .
^ Дойч, Дэвид (1998). Ткань реальности . Лондон: Пингвин. стр. 40–53. ISBN 978-0-14-014690-5 .
^ Уоллес, Дэвид (2012). Возникающая мультивселенная . Оксфорд: Издательство Оксфордского университета. п. 382. ИСБН 978-0-19-954696-1 .
^ Филиппидис, К.; Дьюдни, К.; Хили, Би Джей (1979). «Квантовая интерференция и квантовый потенциал». Иль Нуово Чименто Б. 52 (1): 15–28. Бибкод : 1979NCimB..52...15P . дои : 10.1007/bf02743566 . ISSN 1826-9877 . S2CID 53575967 .
^ «Бомовская механика» . Стэнфордская энциклопедия философии . Лаборатория метафизических исследований Стэнфордского университета. 2017.
^ Гольдштейн, Шелдон (2021), «Бомианская механика» , в Залте, Эдвард Н. (редактор), Стэнфордская энциклопедия философии (изд. осенью 2021 г.), Лаборатория метафизических исследований, Стэнфордский университет , получено 14 августа 2023 г.
^ Гейзенберг, В. (1956). Паули, В. (ред.). « Нильс Бор и развитие физики: очерки, посвященные Нильсу Бору по случаю его семидесятилетия ». Физика сегодня . 9 (8): 12. дои : 10.1063/1.3060063 . ISSN 0031-9228 .
^ Леггетт, Эй Джей (2002). «Проверка пределов квантовой механики: мотивация, состояние дел, перспективы» . Физический журнал: конденсированное вещество . 14 (15): Р415–Р451. дои : 10.1088/0953-8984/14/15/201 . ISSN 0953-8984 . S2CID 250911999 .
^ Пенроуз, Роджер (2004). Дорога к реальности: Полное руководство по законам Вселенной . Лондон: Кейп. ISBN 978-0-224-04447-9 .
^ Городецкий, Р. (1981). «Волна де Бройля и ее двойная волна». Буквы по физике А. 87 (3): 95–97. Бибкод : 1981PhLA...87...95H . дои : 10.1016/0375-9601(81)90571-5 . ISSN 0375-9601 .
^ Городецкий, Р. (1983). «Сверхсветовая сингулярная двойная волна». Lettere al Nuovo Cimento . 36 (15): 509–511. дои : 10.1007/bf02817964 . ISSN 1827-613X . S2CID 120784358 .
^ Дас, С.Н. (1984). «Волна де Бройля и волна Комптона». Буквы по физике А. 102 (8): 338–339. Бибкод : 1984PhLA..102..338D . дои : 10.1016/0375-9601(84)90291-3 . ISSN 0375-9601 .
^ Мухопадьяй, П. (1986). «Корреляция между длиной волны Комптона и длиной волны де Бройля». Буквы по физике А. 114 (4): 179–182. Бибкод : 1986PhLA..114..179M . дои : 10.1016/0375-9601(86)90200-8 . ISSN 0375-9601 .
^ Эльбаз, Клод (1985). «О волнах де Бройля и волнах Комптона массивных частиц». Буквы по физике А. 109 (1–2): 7–8. Бибкод : 1985PhLA..109....7E . дои : 10.1016/0375-9601(85)90379-2 . ISSN 0375-9601 .

Дальнейшее чтение

Аль-Халили, Джим (2003). Квант: Путеводитель для недоумевающих . Лондон: Вайденфельд и Николсон. ISBN 978-0-297-84305-4 .
Анантасвами, Анил (2018). Через две двери одновременно: элегантный эксперимент, раскрывающий загадку нашей квантовой реальности . Даттон/Пингвин. ISBN 978-1-101-98609-7 .
Фейнман, Ричард П. (1988). КЭД: Странная теория света и материи . Издательство Принстонского университета. ISBN 978-0-691-02417-2 .
Франк, Филипп (1957). Философия науки . Прентис-Холл.
Французский, AP; Тейлор, Эдвин Ф. (1978). Введение в квантовую физику . Нортон. ISBN 978-0-393-09106-9 .
Грин, Брайан (2000). Элегантная Вселенная . Винтаж. ISBN 978-0-375-70811-4 .
Грин, Брайан (2005). Ткань Космоса . Винтаж. ISBN 978-0-375-72720-7 .
Гриббин, Джон (1999). Q означает «Квант: физика элементарных частиц от А до Я» . Вайденфельд и Николсон. ISBN 978-0-7538-0685-2 .
Привет, Тони (2003). Новая квантовая вселенная . Издательство Кембриджского университета. Бибкод : 2003nqu..book.....H . ISBN 978-0-521-56457-1 .
Сирс, Фрэнсис Уэстон (1949). Оптика . Эддисон Уэсли.
Типлер, Пол (2004). Физика для ученых и инженеров: электричество, магнетизм, свет и элементарная современная физика (5-е изд.). У. Х. Фриман. ISBN 978-0-7167-0810-0 .

Внешние ссылки

о двойной щелевой интерференции Лекция Уолтера Левина из Массачусетского технологического института

Интерактивная анимация

Гюйгенс и интерференция. Архивировано 28 октября 2007 года в Wayback Machine.

Эксперименты с одной частицей

Гидродинамический аналог

Компьютерное моделирование

[The_Bakerian_lecture-1] Янг, Томас (1804). «Бекеровская лекция. Эксперименты и расчеты относительно физической оптики» . Философские труды Лондонского королевского общества . 94 : 1–16. дои : 10.1098/rstl.1804.0001 . S2CID 110408369 .

[2] Наварро, Хауме (2010). «Дифракция электронов через Томсона: ранние ответы на квантовую физику в Великобритании» . Британский журнал истории науки . 43 (2): 245–275. дои : 10.1017/S0007087410000026 . ISSN 0007-0874 . S2CID 171025814 .

[3] Томсон, врач общей практики; Рид, А. (1927). «Дифракция катодных лучей на тонкой пленке» . Природа . 119 (3007): 890. Бибкод : 1927Natur.119Q.890T . дои : 10.1038/119890a0 . ISSN 0028-0836 . S2CID 4122313 .

[medium.com-4] Перейти обратно: ^а ^б « Физики побили рекорд корпускулярно-волнового дуализма »

[Eibenberger_2013_pp._14696–14700-5] Перейти обратно: ^а ^б Эйбенбергер, Сандра; и др. (2013). «Интерференция материи и волн с частицами, выбранными из молекулярной библиотеки, с массой более 10000 а.е.м.». Физическая химия Химическая физика . 15 (35): 14696–14700. arXiv : 1310.8343 . Бибкод : 2013PCCP...1514696E . дои : 10.1039/C3CP51500A . ПМИД 23900710 . S2CID 3944699 .

[6] Хотя нет никаких сомнений в том, что демонстрация Янгом оптической интерференции с использованием солнечного света, точечных отверстий и карт сыграла жизненно важную роль в принятии волновой теории света, остается некоторый вопрос относительно того, действительно ли он когда-либо выполнял интерференцию с двумя щелями. эксперимент.
Робинсон, Эндрю (2006). Последний человек, который знал всё . Нью-Йорк, штат Нью-Йорк: Pi Press. стр. 123–124 . ISBN 978-0-13-134304-7 .

[7] Робинсон, Эндрю (2006). Последний человек, который знал всё . Нью-Йорк, штат Нью-Йорк: Pi Press. стр. 123–124 . ISBN 978-0-13-134304-7 .

[7] Кипнис, Наум С. (1991). История принципа интерференции света . Спрингер. п. 65. ИСБН 978-0-8176-2316-6 .

[Lederman-8] Перейти обратно: ^а ^б Ледерман, Леон М.; Кристофер Т. Хилл (2011). Квантовая физика для поэтов . США: Книги Прометея. стр. 102–111. ISBN 978-1-61614-281-0 .

[Feynman-9] Перейти обратно: ^а ^б ^с ^д ^и ^ж ^г ^час ^я Фейнман, Ричард П.; Роберт Б. Лейтон; Мэтью Сэндс (1965). Фейнмановские лекции по физике, Vol. 3 . Аддисон-Уэсли. стр. 1.1–1.8. ISBN 978-0-201-02118-9 .

[10] Фейнман, 1965, с. 1,5

[11] Дорогая, Дэвид (2007). «Дуальность волны и частицы» . Интернет-энциклопедия науки . Миры Дэвида Дарлинга . Проверено 18 октября 2008 г.

[12] Фейнман, 1965, с. 1,7

[13] Леон Ледерман; Кристофер Т. Хилл (27 сентября 2011 г.). Квантовая физика для поэтов . Книги Прометея, Издательства. п. 109. ИСБН 978-1-61614-281-0 .

[Müller-Kirsten-14] " ...если в двухщелевом эксперименте детекторы, регистрирующие вылетающие фотоны, располагаются сразу за диафрагмой с двумя щелями: Фотон регистрируется в одном детекторе, а не в обоих... " Мюллер-Кирстен, HJW (2006). Введение в квантовую механику: уравнение Шрёдингера и интеграл по траекториям . США: World Scientific. п. 14. ISBN 978-981-2566911 .

[Plotnitsky-15] Плотницкий, Аркадий (2012). Нильс Бор и дополнительность: введение . США: Спрингер. стр. 75–76. ISBN 978-1-4614-4517-3 .

[Rae-16] " Кажется, что свет проходит через одну или другую щель в виде фотонов, если мы поставим эксперимент, чтобы определить, через какую щель проходит фотон, но проходит через обе щели в виде волны, если мы проведем интерференционный эксперимент. " Рэй, Аластер IM (2004). Квантовая физика: иллюзия или реальность? . Великобритания: Издательство Кембриджского университета. стр. 9–10. ISBN 978-1-139-45527-5 .

[17] Фейнман, Лекции Фейнмана по физике , 3 : Квантовая механика, стр. 1-1 «Однако есть один счастливый случай - электроны ведут себя точно так же, как свет».

[18] См.: Эксперимент Дэвиссона-Гермера. Дэвиссон, CJ (1928). «Дифракция электронов на кристалле никеля». Технический журнал Bell System . 7 : 90–105. дои : 10.1002/j.1538-7305.1928.tb00342.x .

[Yaakov_Y._Fein_1242–1245-19] Перейти обратно: ^а ^б Яаков Ю. Фейн; Филипп Гейер; Патрик Цвик; Филип Кялка; Себастьян Педалино; Марсель Майор; Стефан Герлих; Маркус Арндт (сентябрь 2019 г.). «Квантовая суперпозиция молекул за пределами 25 кДа». Физика природы . 15 (12): 1242–1245. Бибкод : 2019NatPh..15.1242F . дои : 10.1038/s41567-019-0663-9 . S2CID 203638258 .

[20] Чарльз Сандерс Пирс первым предложил использовать этот эффект в качестве независимого от артефактов эталонного стандарта длины.
К. С. Пирс (июль 1879 г.). «Заметка о ходе экспериментов по сравнению длины волны с метровой». Американский журнал науки , по ссылке Криза, Роберта П. (2011). Мир на волоске: исторический поиск абсолютной системы измерения . Нью-Йорк: WW Нортон. п. 317. ISBN 978-0-393-07298-3 . п. 203.

[22] К. С. Пирс (июль 1879 г.). «Заметка о ходе экспериментов по сравнению длины волны с метровой». Американский журнал науки , по ссылке Криза, Роберта П. (2011). Мир на волоске: исторический поиск абсолютной системы измерения . Нью-Йорк: WW Нортон. п. 317. ISBN 978-0-393-07298-3 . п. 203.

[Greene_1999-21] Грин, Брайан (1999). Элегантная Вселенная: суперструны, скрытые измерения и поиск окончательной теории . Нью-Йорк: WW Нортон. стр. 97–109 . ISBN 978-0-393-04688-5 .

[22] Фейнман, 1965, глава 3.

[23] Сэр Джеффри, Ингрэм Тейлор (1909). «Интерференционные полосы слабого света». Профессор Кэм. Фил. Соц . 15 : 114.

[24] Йонссон, Клаус (1 августа 1961 г.). «Электронная интерференция в нескольких искусственно созданных тонких щелях». Журнал физики (на немецком языке). 161 (4): 454–474. Бибкод : 1961ZPhy..161..454J . дои : 10.1007/BF01342460 . ISSN 0044-3328 . S2CID 121659705 .

[25] Йонссон, Клаус (1 января 1974 г.). «Дифракция электронов на нескольких щелях». Американский журнал физики . 42 (1): 4–11. Бибкод : 1974AmJPh..42....4J . дои : 10.1119/1.1987592 . ISSN 0002-9505 .

[26] Мерли, PG; Миссироли, Г.Ф.; Поцци, Дж. (1976). «О статистическом аспекте явлений электронной интерференции». Американский журнал физики . 44 (3): 306–307. Бибкод : 1976AmJPh..44..306M . дои : 10.1119/1.10184 .

[27] Роза, Р. (2012). «Эксперимент Мерли-Миссироли-Поцци с двумя щелями электронной интерференции» . Физика в перспективе . 14 (2): 178–194. Бибкод : 2012ФП....14..178Р . дои : 10.1007/s00016-011-0079-0 . ПМЦ 4617474 . ПМИД 26525832 .

[28] "Самый красивый эксперимент" . Мир физики 2002. Архивировано 24 мая 2021 года в Wayback Machine.

[29] Стидс, Джон; Мерли, Пьер Джорджио; Поцци, Джулио; Миссироли, ДжанФранко; Тономура, Акира (2003). «Двущелевой эксперимент с одиночными электронами» . Мир физики . 16 (5): 20–21. дои : 10.1088/2058-7058/16/5/24 . ISSN 0953-8585 .

[30] Фраббони, Стефано; Габриэлли, Алессандро; Карло Газзади, Джиан; Джорджи, Филиппо; Маттеуччи, Джорджио; Поцци, Джулио; Чезари, Никола Семприни; Вилла, Мауро; Зокколи, Антонио (май 2012 г.). «Эксперимент Янга-Фейнмана с двумя щелями с одиночными электронами: построение интерференционной картины и распределения времени прибытия с использованием пиксельного детектора с быстрым считыванием». Ультрамикроскопия . 116 :73–76. дои : 10.1016/j.ultramic.2012.03.017 . ISSN 0304-3991 .

[31] Коули, Дж. М. (1995). Дифракционная физика . Личная библиотека Северной Голландии (3-е изд.). Амстердам: Эльзевир. ISBN 978-0-444-82218-5 .

[32] Спенс, Джон Ч. (2017). Электронная микроскопия высокого разрешения (Четвертое издание, впервые опубликовано в мягкой обложке). Оксфорд: Издательство Оксфордского университета. ISBN 978-0-19-879583-4 .

[33] Сала, С.; Арига, А.; Эредитато, А.; Феррагут, Р.; Джаммарки, М.; Леоне, М.; Пистилло, К.; Скамполи, П. (2019). «Первая демонстрация волновой интерферометрии антивещества» . Достижения науки . 5 (5): eaav7610. Бибкод : 2019SciA....5.7610S . дои : 10.1126/sciadv.aav7610 . ПМК 6499593 . ПМИД 31058223 .

[Bach_Pope_Liou_Batelaan_2013_p=033018-34] Бах, Роджер; Папа, Дамиан; Лиу, Си-Хван; Бателаан, Герман (13 марта 2013 г.). «Управляемая дифракция электронов на двух щелях» . Новый журнал физики . 15 (3). Издание IOP: 033018. arXiv : 1210.6243 . Бибкод : 2013NJPh...15c3018B . дои : 10.1088/1367-2630/15/3/033018 . ISSN 1367-2630 . S2CID 832961 .

[35] Грин, Брайан (2007). Ткань космоса: пространство, время и текстура реальности . ООО "Рэндом Хаус". п. 90. ИСБН 978-0-307-42853-0 .

[Ananthaswamy-36] Анантасвами, Анил (2018). Через две двери одновременно: элегантный эксперимент, раскрывающий загадку нашей квантовой реальности . Пингвин. п. 63. ИСБН 978-1-101-98611-0 .

[37] Донати, О; Миссироли, Г.Ф.; Поцци, Дж. (1973). «Эксперимент по электронной интерференции». Американский журнал физики . 41 (5): 639–644. Бибкод : 1973AmJPh..41..639D . дои : 10.1119/1.1987321 .

[buckyballs-38] Перейти обратно: ^а ^б Новый учёный: Квантовые чудеса: Корпускулы и бакиболлы, 2010 г. (Введение, для полного текста необходима подписка, полностью цитируется в [1]. Архивировано 25 сентября 2017 г. на Wayback Machine )

[39] Двойственность волновых частиц C60. Архивировано 31 марта 2012 г. в Wayback Machine.

[40] Наирз, Олаф; Брезгер, Бьёрн; Арндт, Маркус; Цайлингер, Антон (2001). «Дифракция сложных молекул на структурах из света». Физ. Преподобный Летт . 87 (16): 160401. arXiv : quant-ph/0110012 . Бибкод : 2001PhRvL..87p0401N . дои : 10.1103/physrevlett.87.160401 . ПМИД 11690188 . S2CID 21547361 .

[41] Наирз, О; Арндт, М; Цайлингер, А (2003). «Эксперименты по квантовой интерференции с большими молекулами» (PDF) . Американский журнал физики . 71 (4): 319–325. Бибкод : 2003AmJPh..71..319N . дои : 10.1119/1.1531580 . Архивировано из оригинала (PDF) 4 июня 2015 года . Проверено 4 июня 2015 г.

[42] Стефан Герлих; и др. (5 апреля 2011 г.). «Квантовая интерференция крупных органических молекул» . Природные коммуникации . 2 : 263. Бибкод : 2011NatCo...2..263G . дои : 10.1038/ncomms1263 . ПМК 3104521 . ПМИД 21468015 .

[43] Яаков Фейн; и др. (декабрь 2019 г.). «Квантовая суперпозиция молекул за пределами 25 кДа» . Физика природы . 15 (12): 1242–1245. Бибкод : 2019NatPh..15.1242F . дои : 10.1038/s41567-019-0663-9 . S2CID 203638258 .

[44] Хессмо, Б., М.В. Митчелл и П. Вальтер. «Запутанные фотоны демонстрируют интерференцию и билокацию». Курьер ЦЕРН (2004): 11.

[vedral-45] Ведрал, Влатко (2006). Введение в квантовую информатику . Издательство Оксфордского университета. ISBN 978-0-19-921570-6 . OCLC 442351498 .

[46] Харрисон, Дэвид (2002). «Дополнительность и Копенгагенская интерпретация квантовой механики» . ВЫСОКИЙ . Кафедра физики Университета Торонто . Проверено 21 июня 2008 г.

[47] Кэссиди, Дэвид (2008). «Квантовая механика 1925–1927: триумф копенгагенской интерпретации» . Вернер Гейзенберг . Американский институт физики. Архивировано из оригинала 14 января 2016 года . Проверено 21 июня 2008 г.

[48] Боска Диас-Пинтадо, Мария К. (29–31 марта 2007 г.). «Обновление корпускулярно-волнового дуализма» . 15-я Британско-европейская встреча по основам физики . Лидс, Великобритания . Проверено 21 июня 2008 г.

[Bartell1980-49] Бартелл, Л. (1980). «Дополнительность в эксперименте с двумя щелями: о простых реализуемых системах для наблюдения промежуточного корпускулярно-волнового поведения». Физический обзор D . 21 (6): 1698–1699. Бибкод : 1980PhRvD..21.1698B . дои : 10.1103/PhysRevD.21.1698 .

[Zeilinger1999-50] Цайлингер, А. (1999). «Эксперимент и основы квантовой физики». Обзоры современной физики . 71 (2): С288–С297. Бибкод : 1999RvMPS..71..288Z . дои : 10.1103/RevModPhys.71.S288 .

[Mittelstaedt-51] П. Миттельштадт; А. Приер; Р. Шидер (1987). «Нерезкий корпускулярно-волновой дуализм в эксперименте с расщепленным пучком фотонов». Основы физики . 17 (9): 891–903. Бибкод : 1987FoPh...17..891M . дои : 10.1007/BF00734319 . S2CID 122856271 .

[52] Д. М. Гринбергер и А. Ясин, «Одновременные знания о волнах и частицах в нейтронном интерферометре», Physics Letters A 128 , 391–4 (1988).

[53] Сен, Д. (2014). «Соотношения неопределенностей в квантовой механике» . Современная наука . 107 (2): 203–218. ISSN 0011-3891 . JSTOR 24103129 . «Однако «компромисс между волной и частицей теперь выражается в терминах неравенства, известного как дуальность Энглерта-Гринбергера или просто отношение дуальности волна-частица». См. также ссылку 24 в этой работе.

[Hillmer2007-54] Перейти обратно: ^а ^б Хиллмер, Р.; Квиат, П. (2007). «Квантовый ластик своими руками» . Научный американец . Том. 296, нет. 5. С. 90–95. Бибкод : 2007SciAm.296e..90H . doi : 10.1038/scientificamerican0507-90 . Проверено 11 января 2016 г.

[Chiao1995-55] Перейти обратно: ^а ^б Цзяо, Республика Корея; ПГ Квиат; Стейнберг, AM (1995). «Квантовая нелокальность в двухфотонных экспериментах в Беркли». Квантовая и полуклассическая оптика: Журнал Европейского оптического общества, часть B. 7 (3): 259–278. arXiv : Quant-ph/9501016 . Бибкод : 1995QuSOp...7..259C . дои : 10.1088/1355-5111/7/3/006 . S2CID 118987962 .

[56] Фрэнсис, Мэтью (21 мая 2012 г.). «Распутывание корпускулярно-волнового дуализма в эксперименте с двумя щелями» . Арс Техника .

[Svensson2013-57] Перейти обратно: ^а ^б Свенссон, Бенгт Э.Ю. (2013). «Педагогический обзор квантовой теории измерений с акцентом на слабые измерения». Кванта . 2 (1): 18–49. arXiv : 1202.5148 . дои : 10.12743/quanta.v2i1.12 . S2CID 119242577 .

[58] Пфлигор, РЛ; Мандель, Л. (июль 1967 г.). «Интерференция независимых фотонных пучков». Физический обзор . 159 (5): 1084–1088. Бибкод : 1967PhRv..159.1084P . дои : 10.1103/PhysRev.159.1084 .

[59] «Интерференция независимых фотонных пучков: эксперимент Пфлигора-Манделя» . Архивировано из оригинала 3 января 2011 года . Проверено 16 июня 2011 г. >

[60] Силлитто, РМ; Уайкс, Кэтрин (1972). «Интерференционный эксперимент со световыми лучами, модулированными в противофазе электрооптическим затвором». Буквы по физике А. 39 (4): 333–334. Бибкод : 1972PhLA...39..333S . дои : 10.1016/0375-9601(72)91015-8 .

[61] " "К лёгкой частице" " .

[62] Карнал, О.; Млынек, Дж. (май 1991 г.). «Двущелевой эксперимент Янга с атомами: простой атомный интерферометр» . Письма о физических отзывах . 66 (21): 2689–2694. Бибкод : 1991PhRvL..66.2689C . дои : 10.1103/PhysRevLett.66.2689 . ПМИД 10043591 .

[63] Карнал, О.; Млынек, Дж. (1991). «Двущелевой эксперимент Янга с атомами: простой атомный интерферометр» . Письма о физических отзывах . 66 (21): 2689–2692. Бибкод : 1991PhRvL..66.2689C . дои : 10.1103/PhysRevLett.66.2689 . ПМИД 10043591 . Проверено 20 марта 2022 г. >

[64] Арндт, Маркус; Наирз, Олаф; Вос-Андреа, Джулиан; Келлер, Клаудия; Ван Дер Зув, Гербранд; Цайлингер, Антон (1999). «Волново-частичный дуализм молекул C60». Природа . 401 (6754): 680–682. Бибкод : 1999Natur.401..680A . дои : 10.1038/44348 . ПМИД 18494170 . S2CID 4424892 .

[65] Осима, К.; Мастуда, К.; Кона, Т.; Могами, Ю.; Комаки, М.; Мурата, Ю.; Ямасита, Т.; Кузумаки, Т.; Хориике, Ю. (4 января 2002 г.). «Интерференция электронов Янга в картинах автоэмиссии» . Письма о физических отзывах . 88 (3): 038301. Бибкод : 2002PhRvL..88c8301O . doi : 10.1103/PhysRevLett.88.038301 . ISSN 0031-9007 . ПМИД 11801091 .

[66] Янагисава, Хирофуми; Чаппина, Марсело; Хафнер, Кристиан; Шец, Йоханнес; Остервальдер, Юрг; Клинг, Маттиас Ф. (4 октября 2017 г.). «Оптическое управление двухщелевым интерферометром Янга для лазерно-индуцированной эмиссии электронов из нано-иглы» . Научные отчеты . 7 (1): 12661. arXiv : 1710.02216 . Бибкод : 2017НацСР...712661Y . дои : 10.1038/s41598-017-12832-3 . ISSN 2045-2322 . ПМЦ 5627254 . ПМИД 28978914 .

[67] Схоутен, ХФ; Кузьмин Н.; Дюбуа, Ж.; Виссер, Т.Д.; Гбур, Г. ; Алкемаде, ПФА; Блок, Х.; Хофт, ГВ; Ленстра, Д.; Элиэль, ER (7 февраля 2005 г.). «Двущелевая передача с плазмоном: новый взгляд на эксперимент Янга» . Физ. Преподобный Летт . 94 (5): 053901. Бибкод : 2005PhRvL..94e3901S . doi : 10.1103/physrevlett.94.053901 . hdl : 1887/71482 . ПМИД 15783641 . S2CID 19197175 .

[68] Бах, Роджер; и др. (март 2013 г.). «Управляемая дифракция электронов на двух щелях». Новый журнал физики . 15 (3): 033018. arXiv : 1210.6243 . Бибкод : 2013NJPh...15c3018B . дои : 10.1088/1367-2630/15/3/033018 . S2CID 832961 .

[Bush2015-69] Перейти обратно: ^а ^б Буш, Джон ВМ (2015). «Гидродинамика пилот-волны» (PDF) . Ежегодный обзор механики жидкости . 47 (1): 269–292. Бибкод : 2015АнРФМ..47..269Б . doi : 10.1146/annurev-fluid-010814-014506 . hdl : 1721.1/89790 . Архивировано (PDF) из оригинала 21 июня 2015 года . Проверено 21 июня 2015 г.

[Bush2010-70] Буш, Джон ВМ (2010). «Квантовая механика в широком смысле» . ПНАС . 107 (41): 17455–17456. Бибкод : 2010PNAS..10717455B . дои : 10.1073/pnas.1012399107 . ПМЦ 2955131 .

[71] Натали Волчовер (30 июня 2014 г.). «Неужели мы все это время неправильно интерпретировали квантовую механику?» . Проводной .

[CouderFort2012-72] Кудер, Ю.; Форт, Э. (2012). «Вероятности и траектории в классическом корпускулярно-волновом дуализме» . Физический журнал: серия конференций . 361 (1): 012001. Бибкод : 2012JPhCS.361a2001C . дои : 10.1088/1742-6596/361/1/012001 .

[Baggott,_Jim_2011_pp._76-73] Бэгготт, Джим (2011). Квантовая история: история за 40 мгновений . Нью-Йорк: Издательство Оксфордского университета. С. 76. («Волновая функция системы, содержащей N частиц, зависит от 3 N координат положения и является функцией в 3 N -мерном конфигурационном пространстве или «фазовом пространстве». Трудно представить себе реальность, состоящую из мнимых функций в абстрактное, многомерное пространство, однако, не возникает никаких затруднений, если мнимым функциям не требуется дать реальную интерпретацию».)

[74] Ли, Пэнъюнь; Сунь, Ифань; Ян, Чжэньвэй; Сун, Синьбин; Чжан, Сяндун (2016). «Классическая гиперкорреляция и волновая оптика аналогии квантового сверхплотного кодирования» . Научные отчеты . 5 : 18574. Бибкод : 2015NatSR...518574L . дои : 10.1038/srep18574 . ПМЦ 4686973 . ПМИД 26689679 .

[:0-75] Перейти обратно: ^а ^б Бакот, Винсент; Лабусс, Матье; Эдди, Антонин; Финк, Матиас; Форт, Эммануэль (ноябрь 2016 г.). «Обращение времени и голография с преобразованиями пространства-времени» . Физика природы . 12 (10): 972–977. arXiv : 1510.01277 . Бибкод : 2016NatPh..12..972B . дои : 10.1038/nphys3810 . ISSN 1745-2481 . S2CID 53536274 .

[76] Родригес-Фортуньо, Франсиско Х. (3 апреля 2023 г.). «Оптический двухщелевой эксперимент во времени» . Физика природы . 19 (7): 929–930. Бибкод : 2023NatPh..19..929R . дои : 10.1038/s41567-023-02026-2 . ISSN 1745-2481 . S2CID 257945438 .

[:1-77] Перейти обратно: ^а ^б Кастельвекки, Давиде (3 апреля 2023 г.). «Световые волны протиснулись сквозь «щели во времени» » . Природа . 616 (7956): 230. Бибкод : 2023Natur.616..230C . дои : 10.1038/d41586-023-00968-4 . ПМИД 37012471 . S2CID 257922697 .

[78] Дженкинс Ф.А. и Уайт Х.Э., Основы оптики, 1967, МакГроу-Хилл, Нью-Йорк.

[79] Longhurst RS, Физическая и геометрическая оптика, 1967, 2-е издание, Longmans

[80] Зи, Энтони (2010). Квантовая теория поля в двух словах (2-е изд.). Издательство Принстонского университета. стр. 2–16. ISBN 978-0-691-14034-6 .

[Faye-Stanford-81] Фэй, Ян (2019). «Копенгагенская интерпретация квантовой механики» . В Залте, Эдвард Н. (ред.). Стэнфордская энциклопедия философии . Лаборатория метафизических исследований Стэнфордского университета.

[camilleri2015-82] Камиллери, К.; Шлоссхауэр, М. (2015). «Нильс Бор как философ эксперимента: бросает ли теория декогеренции вызов доктрине классических концепций Бора?». Исследования по истории и философии современной физики . 49 : 73–83. arXiv : 1502.06547 . Бибкод : 2015ШПМП..49...73С . дои : 10.1016/j.shpsb.2015.01.005 . S2CID 27697360 .

[83] Шайбе, Эрхард (1973). Логический анализ квантовой механики . Пергамон Пресс. ISBN 978-0-08-017158-6 . OCLC 799397091 . [T]нет смысла искать копенгагенскую интерпретацию как единую и непротиворечивую логическую структуру. Такие термины, как «Копенгагенская интерпретация» или «Копенгагенская школа», основаны на истории развития квантовой механики; они представляют собой упрощенный и часто удобный способ ссылки на идеи ряда физиков, сыгравших важную роль в становлении квантовой механики и которые были сотрудниками Бора в его Институте или принимали участие в дискуссиях в решающие годы. При ближайшем рассмотрении довольно легко увидеть, что эти идеи расходятся в деталях и что, в частности, взгляды Бора, духовного лидера школы, образуют отдельную целостность, которую теперь можно понять только путем тщательного изучения как можно большего числа соответствующих публикаций самого Бора.

[Mermin_2017-84] Мермин, Н. Дэвид (1 января 2017 г.). «Почему кбизм не является копенгагенской интерпретацией и что мог об этом подумать Джон Белл». В Бертльманне, Рейнгольде; Цайлингер, Антон (ред.). Квантовые [Un]Speakables II . Коллекция «Границы». Международное издательство Спрингер. стр. 83–93. arXiv : 1409.2454 . дои : 10.1007/978-3-319-38987-5_4 . ISBN 978-3-319-38985-1 . S2CID 118458259 .

[85] Омнес, Роланд (1999). «Копенгагенская интерпретация». Понимание квантовой механики . Издательство Принстонского университета. стр. 41–54. дои : 10.2307/j.ctv173f2pm.9 . S2CID 203390914 .

[86] Розенфельд, Л. (1953). «Спор о дополнительности». Прогресс науки (1933–) . 41 (163): 393–410. ISSN 0036-8504 . JSTOR 43414997 .

[omnes-87] Перейти обратно: ^а ^б Омнес, Р. (1994). Интерпретация квантовой механики . Издательство Принстонского университета. ISBN 978-0-691-03669-4 . OCLC 439453957 .

[peres-88] Перес, Ашер (1995). Квантовая теория: концепции и методы . Академическое издательство Клувер. стр. 36–39. ISBN 0-7923-2549-4 .

[89] Скалли, Мэриан О.; Энглерт, Бертольд-Георг; Вальтер, Герберт (май 1991 г.). «Квантово-оптические тесты дополнительности» . Природа . 351 (6322): 111–116. Бибкод : 1991Natur.351..111S . дои : 10.1038/351111a0 . ISSN 0028-0836 . S2CID 4311842 .

[Messiah-90] Мессия, Альберт (1966). Квантовая механика . Северная Голландия, Джон Уайли и сыновья. ISBN 0-486-40924-4 .

[Frabboni-91] Фраббони, Стефано; Газзади, Джан Карло; Грилло, Винченцо; Поцци, Джулио (1 июля 2015 г.). «Упругие и неупругие электроны в эксперименте с двумя щелями: вариант установки Фейнмана с перекосом» . Ультрамикроскопия . 154 : 49–56. дои : 10.1016/j.ultramic.2015.03.006 . ISSN 0304-3991 . ПМИД 25799917 .

[92] Ровелли, Карло (1996). «Реляционная квантовая механика». Международный журнал теоретической физики . 35 (8): 1637–1678. arXiv : Quant-ph/9609002 . Бибкод : 1996IJTP...35.1637R . дои : 10.1007/BF02302261 . S2CID 16325959 .

[93] Кент, Адриан (февраль 2015 г.). «Есть ли смысл говорить о самоопределяющейся неопределенности в универсальной волновой функции? Замечания о Себенсе и Кэрролле». Основы физики . 45 (2): 211–217. arXiv : 1408.1944 . Бибкод : 2015FoPh...45..211K . дои : 10.1007/s10701-014-9862-5 . ISSN 0015-9018 . S2CID 118471198 .

[vaidman_stanfordencyclopedia-94] Вайдман, Лев (5 августа 2021 г.). «Многомировая интерпретация квантовой механики» . В Залте, Эдвард Н. (ред.). Стэнфордская энциклопедия философии .

[95] Дойч, Дэвид (1998). Ткань реальности . Лондон: Пингвин. стр. 40–53. ISBN 978-0-14-014690-5 .

[96] Уоллес, Дэвид (2012). Возникающая мультивселенная . Оксфорд: Издательство Оксфордского университета. п. 382. ИСБН 978-0-19-954696-1 .

[97] Филиппидис, К.; Дьюдни, К.; Хили, Би Джей (1979). «Квантовая интерференция и квантовый потенциал». Иль Нуово Чименто Б. 52 (1): 15–28. Бибкод : 1979NCimB..52...15P . дои : 10.1007/bf02743566 . ISSN 1826-9877 . S2CID 53575967 .

[98] «Бомовская механика» . Стэнфордская энциклопедия философии . Лаборатория метафизических исследований Стэнфордского университета. 2017.

[99] Гольдштейн, Шелдон (2021), «Бомианская механика» , в Залте, Эдвард Н. (редактор), Стэнфордская энциклопедия философии (изд. осенью 2021 г.), Лаборатория метафизических исследований, Стэнфордский университет , получено 14 августа 2023 г.

[100] Гейзенберг, В. (1956). Паули, В. (ред.). « Нильс Бор и развитие физики: очерки, посвященные Нильсу Бору по случаю его семидесятилетия ». Физика сегодня . 9 (8): 12. дои : 10.1063/1.3060063 . ISSN 0031-9228 .

[101] Леггетт, Эй Джей (2002). «Проверка пределов квантовой механики: мотивация, состояние дел, перспективы» . Физический журнал: конденсированное вещество . 14 (15): Р415–Р451. дои : 10.1088/0953-8984/14/15/201 . ISSN 0953-8984 . S2CID 250911999 .

[102] Пенроуз, Роджер (2004). Дорога к реальности: Полное руководство по законам Вселенной . Лондон: Кейп. ISBN 978-0-224-04447-9 .

[103] Городецкий, Р. (1981). «Волна де Бройля и ее двойная волна». Буквы по физике А. 87 (3): 95–97. Бибкод : 1981PhLA...87...95H . дои : 10.1016/0375-9601(81)90571-5 . ISSN 0375-9601 .

[104] Городецкий, Р. (1983). «Сверхсветовая сингулярная двойная волна». Lettere al Nuovo Cimento . 36 (15): 509–511. дои : 10.1007/bf02817964 . ISSN 1827-613X . S2CID 120784358 .

[105] Дас, С.Н. (1984). «Волна де Бройля и волна Комптона». Буквы по физике А. 102 (8): 338–339. Бибкод : 1984PhLA..102..338D . дои : 10.1016/0375-9601(84)90291-3 . ISSN 0375-9601 .

[106] Мухопадьяй, П. (1986). «Корреляция между длиной волны Комптона и длиной волны де Бройля». Буквы по физике А. 114 (4): 179–182. Бибкод : 1986PhLA..114..179M . дои : 10.1016/0375-9601(86)90200-8 . ISSN 0375-9601 .

[107] Эльбаз, Клод (1985). «О волнах де Бройля и волнах Комптона массивных частиц». Буквы по физике А. 109 (1–2): 7–8. Бибкод : 1985PhLA..109....7E . дои : 10.1016/0375-9601(85)90379-2 . ISSN 0375-9601 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[41]

[42]

[43]

[44]

[45]

[46]

[47]

[48]

[49]

[50]

[51]

[52]

[53]

[54]

[55]

[56]

[57]

[58]

[59]

[60]

[61]

[62]

[63]

[64]

[65]

[66]

[67]

[68]

[69]

[70]

[71]

[72]

[73]

[74]

[75]

[76]

[77]

[78]

[79]

[80]

[81]

[82]

[83]

[84]

[85]

[86]

[87]

[88]

[89]

[90]

[91]

[92]

[93]

[94]

[95]

[96]

[97]

[98]

[99]

[100]

v т и Квантовая механика
Background	Introduction History Timeline Classical mechanics Old quantum theory Glossary
Fundamentals	Born rule Bra–ket notation Complementarity Density matrix Energy level Ground state Excited state Degenerate levels Zero-point energy Entanglement Hamiltonian Interference Decoherence Measurement Nonlocality Quantum state Superposition Tunnelling Scattering theory Symmetry in quantum mechanics Uncertainty Wave function Collapse Wave–particle duality
Formulations	Formulations Heisenberg Interaction Matrix mechanics Schrödinger Path integral formulation Phase space
Equations	Dirac Klein–Gordon Pauli Rydberg Schrödinger
Interpretations	Bayesian Consistent histories Copenhagen de Broglie–Bohm Ensemble Hidden-variable Local Superdeterminism Many-worlds Objective collapse Quantum logic Relational Transactional Von Neumann–Wigner
Experiments	Bell test Davisson–Germer Delayed-choice quantum eraser Double-slit Franck–Hertz Mach–Zehnder interferometer Elitzur–Vaidman Popper Quantum eraser Stern–Gerlach Wheeler's delayed choice
Science	Quantum biology Quantum chemistry Quantum chaos Quantum cosmology Quantum differential calculus Quantum dynamics Quantum geometry Quantum measurement problem Quantum mind Quantum stochastic calculus Quantum spacetime
Technology	Quantum algorithms Quantum amplifier Quantum bus Quantum cellular automata Quantum finite automata Quantum channel Quantum circuit Quantum complexity theory Quantum computing Timeline Quantum cryptography Quantum electronics Quantum error correction Quantum imaging Quantum image processing Quantum information Quantum key distribution Quantum logic Quantum logic gates Quantum machine Quantum machine learning Quantum metamaterial Quantum metrology Quantum network Quantum neural network Quantum optics Quantum programming Quantum sensing Quantum simulator Quantum teleportation
Extensions	Quantum fluctuation Casimir effect Quantum statistical mechanics Quantum field theory History Quantum gravity Relativistic quantum mechanics
Related	Schrödinger's cat in popular culture Wigner's friend EPR paradox Quantum mysticism
Category