Законы де Моргана

Законы де Моргана представлены диаграммами Венна . В каждом случае результирующий набор представляет собой набор всех точек любого оттенка синего цвета.

В логике высказываний и булевой алгебре законы Моргана Де также известная как теорема Де Моргана , представляют собой пару правил преобразования, которые оба являются действительными правилами вывода . Они названы в честь Огастеса Де Моргана , британского математика XIX века. Правила позволяют выражать союзы и дизъюнкции исключительно через друг друга посредством отрицания .

Правила можно выразить на английском языке так:

• Отрицание «А и Б» то же самое, что «не А или не Б».
• Отрицание «А или Б» то же самое, что «не А и не Б».

или

• Дополнение . объединения двух множеств совпадает с пересечением их дополнений
• Дополнение пересечения двух множеств совпадает с объединением их дополнений.

или

• не (А или Б) = (не А) и (не Б)
• не (А и В) = (не А) или (не Б)

где «A или B» означает « включающее или », означающее по крайней мере одно из A или B, а не « исключительное или », которое означает ровно одно из A или B.

В теории множеств и булевой алгебре они формально записываются как

${\begin{aligned}{\overline {A\cup B}}&={\overline {A}}\cap {\overline {B}},\\{\overline {A\cap B}}&={\overline {A}}\cup {\overline {B}},\end{aligned}}$

где

• $A$ и $B$ это наборы,
• ${\overline {A}}$ является дополнением $A$,
• $\cap$ это пересечение , и
• $\cup$ это союз .

Эквивалентность ¬φ ∨ ¬ψ и ¬(φ ∧ ψ) отображается в этой таблице истинности.

На формальном языке правила записываются как

$\neg (P\lor Q)\iff (\neg P)\land (\neg Q),$

и

$\neg (P\land Q)\iff (\neg P)\lor (\neg Q)$

где

• P и Q — предложения,
• $\neg$ – логический оператор отрицания (НЕ),
• $\land$ – логический оператор конъюнкции (И),
• $\lor$ – логический оператор дизъюнкции (ИЛИ),
• $\iff$ — это металогический символ, означающий «может быть заменен в логическом доказательстве на», который часто читается как «тогда и только если». Для любой комбинации значений «истина/ложь» для P и Q левая и правая стороны стрелки после оценки будут иметь одно и то же значение истинности.

Закон де Моргана с операцией вычитания множеств.

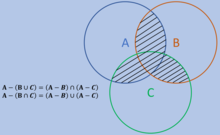
Другая форма закона Де Моргана выглядит следующим образом, как показано на рисунке справа.

$A-(B\cup C)=(A-B)\cap (A-C),$

$A-(B\cap C)=(A-B)\cup (A-C).$

Применение правил включает упрощение логических выражений в компьютерных программах и проектирование цифровых схем. Законы де Моргана являются примером более общей концепции математической двойственности .

Формальные обозначения

Правило отрицания конъюнкции можно записать в последовательных обозначениях:

${\begin{aligned}\neg (P\land Q)&\vdash (\neg P\lor \neg Q),{\text{and}}\\(\neg P\lor \neg Q)&\vdash \neg (P\land Q).\end{aligned}}$

Правило отрицания дизъюнкции можно записать так:

${\begin{aligned}\neg (P\lor Q)&\vdash (\neg P\land \neg Q),{\text{and}}\\(\neg P\land \neg Q)&\vdash \neg (P\lor Q).\end{aligned}}$

В форме правила : отрицание союза.

${\frac {\neg (P\land Q)}{\therefore \neg P\lor \neg Q}}\qquad {\frac {\neg P\lor \neg Q}{\therefore \neg (P\land Q)}}$

и отрицание дизъюнкции

${\frac {\neg (P\lor Q)}{\therefore \neg P\land \neg Q}}\qquad {\frac {\neg P\land \neg Q}{\therefore \neg (P\lor Q)}}$

и выражаются в виде функционально-истинных тавтологий или теорем логики высказываний:

${\begin{aligned}\neg (P\land Q)&\leftrightarrow (\neg P\lor \neg Q),\\\neg (P\lor Q)&\leftrightarrow (\neg P\land \neg Q).\\\end{aligned}}$

где $P$ и $Q$ Это предложения, выраженные в некоторой формальной системе.

Обобщенные законы Де Моргана обеспечивают эквивалентность для отрицания соединения или дизъюнкции, включающей несколько терминов.
Для набора предложений $P_{1},P_{2},\dots ,P_{n}$, обобщенные законы де Моргана таковы:

${\begin{aligned}\lnot (P_{1}\land P_{2}\land \dots \land P_{n})\leftrightarrow \lnot P_{1}\lor \lnot P_{2}\lor \ldots \lor \lnot P_{n}\\\lnot (P_{1}\lor P_{2}\lor \dots \lor P_{n})\leftrightarrow \lnot P_{1}\land \lnot P_{2}\land \ldots \land \lnot P_{n}\end{aligned}}$

Эти законы обобщают оригинальные законы Де Моргана об отрицании конъюнкций и дизъюнкций.

Форма замены

Законы де Моргана обычно изображаются в компактной форме выше: отрицание выходных данных слева и отрицание входных данных справа. Более четкую форму замены можно сформулировать так:

${\begin{aligned}(P\land Q)&\Longleftrightarrow \neg (\neg P\lor \neg Q),\\(P\lor Q)&\Longleftrightarrow \neg (\neg P\land \neg Q).\end{aligned}}$

Это подчеркивает необходимость инвертировать как входные, так и выходные данные, а также менять оператор при выполнении подстановки.

Теория множеств

В теории множеств и булевой алгебре это часто называют «обменом объединения и пересечения при дополнении». что формально можно выразить как:

${\begin{aligned}{\overline {A\cup B}}&={\overline {A}}\cap {\overline {B}},\\{\overline {A\cap B}}&={\overline {A}}\cup {\overline {B}},\end{aligned}}$

где:

• ${\overline {A}}$ это отрицание $A$, над чертой пишутся термины, которые нужно инвертировать,
• $\cap$ – оператор пересечения (И),
• $\cup$ — оператор объединения (ИЛИ).

Объединения и пересечения любого количества множеств

Обобщенная форма – это

${\begin{aligned}{\overline {\bigcap _{i\in I}A_{i}}}&\equiv \bigcup _{i\in I}{\overline {A_{i}}},\\{\overline {\bigcup _{i\in I}A_{i}}}&\equiv \bigcap _{i\in I}{\overline {A_{i}}},\end{aligned}}$

где I — некоторое, возможно счетное или несчетное бесконечное, индексное множество.

В установленных обозначениях законы Де Моргана можно запомнить, используя мнемонику «перервите линию, измените знак».

Инженерное дело

В электротехнике и вычислительной технике законы Де Моргана обычно записываются так:

${\overline {(A\cdot B)}}\equiv ({\overline {A}}+{\overline {B}})$

и

${\overline {A+B}}\equiv {\overline {A}}\cdot {\overline {B}},$

где:

• $\cdot$ это логическое И,
• $+$ это логическое ИЛИ,
• верхняя черта является логическим НЕ того, что находится под верхней чертой.

Текстовый поиск

Законы Де Моргана обычно применяются к текстовому поиску с использованием логических операторов И, ИЛИ и НЕ. Рассмотрим набор документов, содержащих слова «кошки» и «собаки». Законы де Моргана гласят, что эти два поиска вернут один и тот же набор документов:

Поиск A: НЕ (кошки ИЛИ собаки)

Поиск Б: (НЕ кошки) И (НЕ собаки)

Корпус документов, содержащих «кошки» или «собаки», может быть представлен четырьмя документами:

Документ 1: Содержит только слово «кошки».

Документ 2: Содержит только «собак».

Документ 3: содержит как «кошек», так и «собак».

Документ 4: Не содержит ни «кошек», ни «собак».

Чтобы оценить Поиск А, очевидно, что поиск «(кошки ИЛИ собаки)» попадет в Документы 1, 2 и 3. Таким образом, отрицание этого поиска (который является Поиском А) поразит все остальное, то есть Документ 4.

При оценке поиска B поиск «(НЕ кошки)» приведет к документам, которые не содержат слова «кошки», то есть к документам 2 и 4. Аналогичным образом поиск «(НЕ собаки)» приведет к документам 1 и 4. Применение Оператор И для этих двух поисков (поиск B) найдет документы, общие для этих двух поисков, то есть документ 4.

Подобную оценку можно применить, чтобы показать, что следующие два поиска вернут документы 1, 2 и 4:

Поиск C: НЕ (кошки И собаки),

Поиск D: (НЕ кошки) ИЛИ (НЕ собаки).

История

Законы названы в честь Огастеса Де Моргана (1806–1871). который представил формальную версию законов классической логики высказываний . На формулировку Де Моргана повлияла алгебраизация логики, предпринятая Джорджем Булем , которая позже закрепила претензии Де Моргана на находку. Тем не менее, подобное наблюдение было сделано Аристотелем и было известно греческим и средневековым логикам. Например, в 14 веке Уильям Оккам записывал слова, которые получались в результате чтения законов. Жан Буридан в своей «Сумме диалектики » также описывает правила конверсии, которые следуют законам Де Моргана. Тем не менее, Де Моргану отдают должное за то, что он сформулировал законы в терминах современной формальной логики и включил их в язык логики. Законы де Моргана легко доказать и даже могут показаться тривиальными. Тем не менее, эти законы помогают делать обоснованные выводы в доказательствах и дедуктивных аргументах.

доказательство

Теорема де Моргана может быть применена к отрицанию дизъюнкции или отрицанию союза во всей или части формулы.

Отрицание дизъюнкции

В случае его применения к дизъюнкции рассмотрим следующее утверждение: «ложно, что либо из A, либо B истинно», которое записывается как:

$\neg (A\lor B).$

Поскольку установлено, что ни А, ни В не истинно, из этого должно следовать, что и А неверно , и В неверно, что можно записать непосредственно как:

$(\neg A)\wedge (\neg B).$

Если бы либо А, либо В были истинны, то дизъюнкция А и В была бы истинной, а ее отрицание было бы ложным. Представленное на английском языке, это следует логике, согласно которой «поскольку обе вещи ложны, ложно также и то, что любая из них истинна».

Действуя в противоположном направлении, второе выражение утверждает, что A ложно, а B ложно (или, что то же самое, что «не A» и «не B» истинны). Зная это, дизъюнкция А и В также должна быть ложной. Таким образом, отрицание указанной дизъюнкции должно быть истинным, а результат идентичен первому утверждению.

Отрицание союза

Применение теоремы Де Моргана к конъюнкции очень похоже на ее применение к дизъюнкции как по форме, так и по смыслу. Рассмотрим следующее утверждение: «Неверно, что A и B истинны», которое записывается как:

$\neg (A\land B).$

Для того чтобы это утверждение было истинным, любое из A или B или оба должны быть ложными, поскольку, если бы они оба были истинными, тогда соединение A и B было бы истинным, что делало бы его отрицание ложным. Таким образом, одно (по крайней мере) или несколько из A и B должны быть ложными (или, что то же самое, одно или несколько из «не A» и «не B» должны быть истинными). Это можно записать прямо так:

$(\neg A)\lor (\neg B).$

Представленное на английском языке, это следует логике, согласно которой «поскольку две вещи являются истинными, ложно, по крайней мере одна из них должна быть ложной».

Снова работая в противоположном направлении, второе выражение утверждает, что по крайней мере одно из «не A» и «не B» должно быть истинным, или, что то же самое, что по крайней мере одно из «A» и «B» должно быть ложным. Поскольку хотя бы один из них должен быть ложным, то и их соединение также будет ложным. Таким образом, отрицание указанного союза приводит к истинному выражению, и это выражение идентично первому утверждению.

Официальное доказательство

Здесь мы используем ${\overline {A}}$ для обозначения дополнения к A, как указано выше в § Теория множеств и булева алгебра . Доказательство того, что ${\overline {A\cap B}}={\overline {A}}\cup {\overline {B}}$ завершается в два этапа, доказывая оба ${\overline {A\cap B}}\subseteq {\overline {A}}\cup {\overline {B}}$ и ${\overline {A}}\cup {\overline {B}}\subseteq {\overline {A\cap B}}$.

Часть 1

Позволять $x\in {\overline {A\cap B}}$. Затем, $x\not \in A\cap B$.

Потому что $A\cap B=\{\,y\ |\ y\in A\wedge y\in B\,\}$, должно быть так, что $x\not \in A$ или $x\not \in B$.

Если $x\not \in A$, затем $x\in {\overline {A}}$, так $x\in {\overline {A}}\cup {\overline {B}}$.

Аналогично, если $x\not \in B$, затем $x\in {\overline {B}}$, так $x\in {\overline {A}}\cup {\overline {B}}$.

Таким образом, $\forall x{\Big (}x\in {\overline {A\cap B}}\implies x\in {\overline {A}}\cup {\overline {B}}{\Big )}$;

то есть, ${\overline {A\cap B}}\subseteq {\overline {A}}\cup {\overline {B}}$.

Часть 2

Чтобы доказать обратное направление, пусть $x\in {\overline {A}}\cup {\overline {B}}$, и от противного предположим $x\not \in {\overline {A\cap B}}$.

Согласно этому предположению, должно быть так, что $x\in A\cap B$,

отсюда следует, что $x\in A$ и $x\in B$, и таким образом $x\not \in {\overline {A}}$ и $x\not \in {\overline {B}}$.

Однако это означает $x\not \in {\overline {A}}\cup {\overline {B}}$, что противоречит гипотезе о том, что $x\in {\overline {A}}\cup {\overline {B}}$,

следовательно, предположение $x\not \in {\overline {A\cap B}}$ не должно быть так, а это означает, что $x\in {\overline {A\cap B}}$.

Следовательно, $\forall x{\Big (}x\in {\overline {A}}\cup {\overline {B}}\implies x\in {\overline {A\cap B}}{\Big )}$,

то есть, ${\overline {A}}\cup {\overline {B}}\subseteq {\overline {A\cap B}}$.

Заключение

Если ${\overline {A}}\cup {\overline {B}}\subseteq {\overline {A\cap B}}$ и ${\overline {A\cap B}}\subseteq {\overline {A}}\cup {\overline {B}}$, затем ${\overline {A\cap B}}={\overline {A}}\cup {\overline {B}}$; на этом завершается доказательство закона Де Моргана.

Другой закон Де Моргана: ${\overline {A\cup B}}={\overline {A}}\cap {\overline {B}}$, доказывается аналогично.

Де

Законы де Моргана представлены в виде схемы с логическими элементами ( схемы Международной электротехнической комиссии ).

В расширениях классической логики высказываний двойственность по-прежнему сохраняется (т. е. к любому логическому оператору всегда можно найти его двойственный оператор), поскольку при наличии тождеств, управляющих отрицанием, всегда можно ввести оператор, который является двойственным по Де Моргану оператору. другой. Это приводит к важному свойству логики, основанной на классической логике , а именно к существованию нормальных форм отрицания : любая формула эквивалентна другой формуле, где отрицания происходят только в применении к нелогическим атомам формулы. Существование нормальных форм отрицания стимулирует множество приложений, например, в проектировании цифровых схем , где оно используется для управления типами логических элементов , и в формальной логике, где необходимо найти конъюнктивную нормальную форму и дизъюнктивную нормальную форму . формула. Программисты используют их для упрощения или правильного отрицания сложных логических условий . Они также часто полезны в вычислениях по элементарной теории вероятностей .

Пусть двойственный к любому пропозициональному оператору P( p , q , ...) в зависимости от элементарных предложений p , q , ... определим как оператор ${\mbox{P}}^{d}$ определяется

${\mbox{P}}^{d}(p,q,...)=\neg P(\neg p,\neg q,\dots ).$

Расширение предикативной и модальной логики

Эту двойственность можно обобщить на кванторы, так, например, квантор универсальности и квантор существования являются двойственными:

$\forall x\,P(x)\equiv \neg [\exists x\,\neg P(x)]$

$\exists x\,P(x)\equiv \neg [\forall x\,\neg P(x)]$

Чтобы связать эту двойственность кванторов с законами Де Моргана, создайте модель с небольшим количеством элементов в ее области D , например:

D знак равно { а , б , с }.

Затем

$\forall x\,P(x)\equiv P(a)\land P(b)\land P(c)$

и

$\exists x\,P(x)\equiv P(a)\lor P(b)\lor P(c).$

Но, используя законы Де Моргана,

$P(a)\land P(b)\land P(c)\equiv \neg (\neg P(a)\lor \neg P(b)\lor \neg P(c))$

и

$P(a)\lor P(b)\lor P(c)\equiv \neg (\neg P(a)\land \neg P(b)\land \neg P(c)),$

проверка кванторной двойственности в модели.

Затем двойственность кванторов может быть расширена до модальной логики , связывая операторы коробки («необходимо») и ромба («возможно»):

$\Box p\equiv \neg \Diamond \neg p,$

$\Diamond p\equiv \neg \Box \neg p.$

В применении к алетическим модальностям возможности и необходимости Аристотель наблюдал этот случай, и в случае нормальной модальной логики связь этих модальных операторов с количественной оценкой можно понять, создав модели с использованием семантики Крипке .

В интуиционистской логике

Три из четырех следствий законов де Моргана справедливы для интуиционистской логики . В частности, у нас есть

$\neg (P\lor Q)\,\leftrightarrow \,{\big (}(\neg P)\land (\neg Q){\big )},$

и

${\big (}(\neg P)\lor (\neg Q){\big )}\,\to \,\neg (P\land Q).$

Обратное к последнему импликации не справедливо в чистой интуиционистской логике. То есть несостоятельность совместного предложения $P\land Q$ не обязательно может быть разрешено неудачей любого из двух конъюнктов . Например, зная, что Алиса и Боб не явились на свидание, не следует, кто не пришел. Последний принцип эквивалентен принципу слабого исключенного среднего. ${\mathrm {WPEM} }$,

$(\neg P)\lor \neg (\neg P).$

Эту слабую форму можно использовать как основу для промежуточной логики . Усовершенствованную версию ошибочного закона, касающегося экзистенциальных утверждений, см. в менее ограниченном принципе всеведения. ${\mathrm {LLPO} }$, который, однако, отличается от ${\mathrm {WLPO} }$.

Справедливость остальных трех законов Де Моргана остается верной, если отрицать $\neg P$ заменяется импликацией $P\to C$ для некоторого произвольного постоянного предиката C, что означает, что приведенные выше законы по-прежнему верны в минимальной логике .

Аналогично предыдущему, законы кванторов:

$\forall x\,\neg P(x)\,\leftrightarrow \,\neg \exists x\,P(x)$

и

$\exists x\,\neg P(x)\,\to \,\neg \forall x\,P(x).$

являются тавтологиями даже в минимальной логике, где отрицание заменяется подразумеванием фиксированного $Q$, тогда как обратное к последнему закону вообще не обязательно должно быть верным.

Далее, еще есть

$(P\lor Q)\,\to \,\neg {\big (}(\neg P)\land (\neg Q){\big )},$

$(P\land Q)\,\to \,\neg {\big (}(\neg P)\lor (\neg Q){\big )},$

$\forall x\,P(x)\,\to \,\neg \exists x\,\neg P(x),$

$\exists x\,P(x)\,\to \,\neg \forall x\,\neg P(x),$

но их инверсия подразумевает исключенную середину , ${\mathrm {PEM} }$.

В компьютерной инженерии

Законы де Моргана широко используются в вычислительной технике и цифровой логике с целью упрощения схемотехники.

См. также

• Изоморфизм - оператор NOT как изоморфизм между положительной логикой и отрицательной логикой
• Список тем по булевой алгебре
• Список установленных личностей и отношений
• Позитивная логика
• Двойственность конъюнкции/дизъюнкции

Внешние ссылки

• «Принцип двойственности» , Математическая энциклопедия , EMS Press , 2001 [1994]
• Вайсштейн, Эрик В. «Законы де Моргана» . Математический мир .
• Законы де Моргана в PlanetMath .
• Двойственность в логике и языке , Интернет-энциклопедия философии .