Воздушный змей (геометрия)

Видеть
Видеть
	Воздушный змей, показывающий пары с равной длиной и вписанный круг.
Тип	Четырехугольник
Края и вершины	4
Группа симметрии	D 1 (*)
Двойной многоугольник	Isocseles Trapezoid

В евклидовой геометрии воздушный змей представляет собой четырехугольник с симметрией отражения по диагонали . Из-за этой симметрии воздушный змей имеет два равных угла и две пары смежных сторон равной длины. Воздушные змеи также известны как Deltoids , ^{[ 1 ]} Но слово Deltoid также может относиться к дельтовидной кривой , не связанного геометрического объекта, который иногда изучался в связи с четырехугольниками. ^{[ 2 ]}^{[ 3 ]} Воздушный змей также можно назвать дротиком , ^{[ 4 ]} Особенно, если это не выпуклое. ^{[ 5 ]}^{[ 6 ]}

Каждый воздушный змей представляет собой ортодиагональный четырехугольник (его диагонали находятся под прямым углом) и, когда выпуклый тангенциальный четырехугольник (его стороны касаются надписанного круга). Выпуклые воздушные змеи - это именно то, что четырехугольники являются как ортодиагональными, так и тангенциальными. Они включают в себя в качестве особых случаев « Правые воздушные змеи» , с двумя противоположными прямыми углами; Ромби ; , с двумя диагональными осями симметрии и квадраты , которые также являются особыми случаями как правых воздушных змеев, так и Rhombi.

Четвертистороннее с наибольшим соотношением периметра к диаметру представляет собой воздушный змей, с 60 °, 75 ° и 150 ° углов. Воздушные воздушные змеи из двух форм (одна выпуклая и одна невыпуктная) образуют прототили одной из форм пенроуза . Воздушные воздушные змеи также образуют лица нескольких симметричных лицевых многогранников и тесселяций и были изучены в связи с внешними бильярдными , что является проблемой в продвинутой математике динамических систем .

Определение и классификация

Воздушник - это четырехугольник с симметрией отражения в одной из его диагонали. Эквивалентно, это четырехугольник, чьи четыре стороны могут быть сгруппированы в две пары соседних сторон равной длины. ^{[ 1 ]}^{[ 7 ]} Воздушник может быть построен из центров и точек пересечения любых двух пересекающихся кругов . ^{[ 8 ]} Воздушные змеи, как описано здесь, могут быть либо выпуклыми , либо вогнутыми , хотя некоторые источники ограничивают воздушных змеев только выпуклыми воздушными змеями. Четвертисторонний змей - это воздушный змей, если и только если какое -либо из следующих условий верно:

Четыре стороны могут быть разделены на две пары смежных сторон равной длины. ^{[ 7 ]}
Один диагональный пересекает среднюю точку другой диагонали под прямым углом, образуя его перпендикулярный бисектор . ^{[ 9 ]} (В вогнутом случае линия через одну из диагоналей делится пополам другой.)
Один диагональ - это линия симметрии. Он делит четырехугольник на два конгруэнтных треугольника, которые являются зеркальными изображениями друг друга. ^{[ 7 ]}
Один диагональный потрохим пополам оба угла на двух его концах. ^{[ 7 ]}

Четырехугородные змея названы в честь ветряных летающих воздушных змеев , которые часто имеют такую форму ^{[ 10 ]}^{[ 11 ]} и которые, в свою очередь, названы в честь парящей птицы и звука, которую он издает. ^{[ 12 ]}^{[ 13 ]} По словам Олауса Хенрири , название «Воздушник» было дано этим формам Джеймса Джозефа Сильвестра . ^{[ 14 ]}

Четырехугородки могут быть классифицированы иерархически , что означает, что некоторые классы четырехсторонности включают в себя другие классы или частично , что означает, что каждый четырехугольник находится только в одном классе. В классифицированных иерархически, воздушные змеи включают Rhombi (четырехугольника с четырьмя равными сторонами) и квадраты . Все равносторонние воздушные змеи - Rhombi, а все эк -юношные воздушные змеи - квадраты. При классификации разделяются ромби и квадраты не будут воздушными змеями, потому что они принадлежат к другому классу четырехсторонних; Точно так же, правые воздушные змеи, обсуждаемые ниже, не будут воздушными змеями. Остальная часть этой статьи следует иерархической классификации; Ромби, квадраты и правые воздушные змеи считаются воздушными змеями. Избегая необходимости рассмотреть особые случаи, эта классификация может упростить некоторые факты о воздушных змеях. ^{[ 15 ]}

Как и воздушные змеи, параллелограмм также имеет две пары сторон равной длины, но они противоположны друг другу, а не прилегают. Любая не с пересеченная четырехугольника, которая имеет ось симметрии, должна быть либо воздушным змеем, с диагональной осью симметрии; Или трапециевид из изоптаров , с осью симметрии через середины двух сторон. Они включают в себя в качестве особых случаев ромб и прямоугольник соответственно, а также квадрат, который является особым случаем обоих. ^{[ 1 ]} Самостоятельный четырехугольник включает в себя еще один класс симметричных четырехугольников, антипараллелограммы . ^{[ 16 ]}

Особые случаи

Правый воздушный змей

Equidiagonal Kite в треугольнике Reuleaux

Лютня Пифагора

Правые воздушные змеи имеют два противоположных правых углов . ^{[ 15 ]}^{[ 16 ]} Правые воздушные змеи - это именно те воздушные змеи, которые являются циклическими четырехугольниками , что означает, что есть круг, который проходит через все их вершины. ^{[ 17 ]} Циклические четырехугольники могут эквивалентно определяться как четырехугольники, в которых два противоположных угла являются дополнительными (они добавляют к 180 °); Если одна пара дополнительная, другая тоже. ^{[ 9 ]} Следовательно, правые воздушные змеи представляют собой воздушные змеи с двумя противоположными дополнительными углами, для любой из двух противоположных пар углов. Поскольку правые воздушные воздушные змеи описают один кружок и вписаны в другой круг, они представляют собой бицентричные четырехугольники (на самом деле трицентричный, поскольку они также имеют третий круг снаружи, касающийся удлинения их бок ). ^{[ 16 ]} Если размеры вставленного и ограниченного круга фиксируются, правый воздушный змей имеет самую большую площадь любой четырехугольной заперты между ними. ^{[ 18 ]}

Среди всех четырехсторонних, форма, которая имеет наибольшее соотношение его периметра к его диаметру (максимальное расстояние между любыми двумя точками), представляет собой эквидиагональный воздушный змей с углами 60 °, 75 °, 150 °, 75 °. Его четыре вершины лежат на трех углах и в одном из боковых средних точек треугольника Рейуле . ^{[ 19 ]}^{[ 20 ]} Когда эквидиагональный воздушный змей имеет боковые длины меньше или равную его диагонали, например, этот или квадрат, он является одним из четырехсторонних с наибольшим соотношением площади к диаметру . ^{[ 21 ]}

Воздушный змей с тремя углами 108 ° и одним углом 36 ° образует выпуклый корпус лютней пифагор , фрактал, изготовленный из вложенных пентаграммов . ^{[ 22 ]} Четыре стороны этого воздушного змея лежат на четырех сторонах обычного Пентагона , с золотым треугольником, приклеенным на пятую сторону. ^{[ 16 ]}

Есть только восемь многоугольников, которые могут плит плоскость так, что отражение любой плитки по любому из его краев производит еще одну плитку; Эта договоренность называется краем . Одним из них является плитка правым воздушным змеем с углом 60 °, 90 ° и 120 °. Он производит дельтовидную тригексагональную плитку (см. § Tilings и Polyhedra ). ^{[ 23 ]} Прототиль, изготовленный восьми из этих змеев плитки, плоскость только апериодически , ключ к заявленному решению проблемы Эйнштейна . ^{[ 24 ]}

В неэвклидовой геометрии воздушное змея может иметь три прямых углов и один не правый угол, образуя особый случай четырехстороннего четырехугольника Ламберта . Четвертый угол является острым в гиперболической геометрии и тупой в сферической геометрии . ^{[ 25 ]}

Характеристики

Диагонали, углы и область

Каждый воздушный змей является ортодиагональным четырехугольником , что означает, что две его диагонали находятся под прямым углом друг к другу. Более того, одна из двух диагоналей (ось симметрии) является перпендикулярным бисектором другого, а также является угловым бисектором двух углов, которые он встречается. ^{[ 1 ]} Из -за своей симметрии два других угла змея должны быть равны. ^{[ 10 ]}^{[ 11 ]} Диагональная ось симметрии выпуклого воздушного змея делит его на два конгруэнтных треугольника ; Другая диагональ делит его на два треугольника издебля . ^{[ 1 ]}

Как и в более общем плане для любого ортодиагонального четырехугольника, область $A$ воздушного змея может быть рассчитана как половина продукта длины диагонали $p$ и $q$ : ^{[ 10 ]} $A={\frac {p\cdot q}{2}}.$ В качестве альтернативы, область может быть рассчитана путем деления воздушного змея на два конгруэнтных треугольника и применения формулы SAS для их области. Если $a$ и $b$ длины две стороны воздушного змея, и $\theta$ это угол между, тогда область ^{[ 26 ]} $\displaystyle A=ab\cdot \sin \theta .$

Вписанный круг

Два круга, касающихся по бокам, и расширенные стороны выпуклых воздушных змеев (вверху), невыпуклых воздушных змеев (средний) и антипараллелограмма (внизу). Четыре линии по бокам каждого четырехугольника - это битангенты кругов.

Каждый выпуклый воздушный змей также является тангенциальным четырехугольником , четырехугольником, который имеет вписанный круг . То есть существует круг, касающийся всех четырех сторон. Кроме того, если выпуклый воздушный змей не является ромбом, за пределами воздушного змея есть круг, который касается расширений четырех сторон; Следовательно, каждый выпуклый воздушный змей, который не является ромбом, является бывшим врожденным четырехугольником . Выпуклые воздушные змеи, которые не являются Rhombi, являются именно тем, которые являются как тангенциальными, так и эксплуатационными. ^{[ 16 ]} На каждом вогнутом воздушном змее существует два круга, касающихся двух сторон и наращивание двух других: один - внутреннее змее и касается двух сторон напротив вогнутого угла, в то время как другой кружок находится в воздухе и касается Воздушный змей на двух краях инцидент к вогнутому углу. ^{[ 27 ]}

Для выпуклого воздушного воздушного змея с диагональной длиной $p$ и $q$ и длина боковых $a$ и $b$ , радиус $r$ вписанного круга $r={\frac {pq}{2(a+b)}},$ и радиус $\rho$ бывшего круга ^{[ 16 ]} $\rho ={\frac {pq}{2|a-b|}}.$

Тангенциальное четырехугольник также является воздушным змеем, если и только если какое -либо из следующих условий верно: ^{[ 28 ]}

Область составляет половину продукта диагонали .
Диагонали перпендикулярно . (Таким образом, воздушные змеи являются именно тем четырехугородными, которые являются тангенциальными и ортодиагональными .
Два сегмента линии, соединяющих противоположные точки касания, имеют одинаковую длину.
Тангационные длины , расстояния от точки касания до прилегающей вершины четырехсторонней, равны в двух противоположных вершинах четырехсторонней. (В каждой вершине есть две соседние точки касания, но они одинаковые расстояния, что и друг от друга от вершины, поэтому каждая вершина имеет одну касальную длину.)
Два бимедиане , линии, соединяющие средние точки противоположных краев, имеют одинаковую длину.
Продукты противоположной длины стороны равны.
Центр инцидента лежит на линии симметрии, которая также является диагональю.

Если диагонали в тангенциальном четырехугольнике $ABCD$ пересечь в $P$ и окружение треугольников $ABP$ , $BCP$ , $CDP$ , $DAP$ есть радиусы $r_{1}$ , $r_{2}$ , $r_{3}$ , и $r_{4}$ соответственно, тогда четырехугольник - это воздушный змей и только тогда, когда ^{[ 28 ]} $r_{1}+r_{3}=r_{2}+r_{4}.$ Если сухожилия к тем же четырем треугольникам напротив вершины $P$ есть радиусы $R_{1}$ , $R_{2}$ , $R_{3}$ , и $R_{4}$ соответственно, тогда четырехугольник - это воздушный змей и только тогда, когда ^{[ 28 ]} $R_{1}+R_{3}=R_{2}+R_{4}.$

Двойственность

Воздушные воздушные змеи и изобранные трапеции являются двойными друг для друга, что означает, что между ними существует соответствие, которое меняет размер их частей, доставляя вершины по бокам и сторонам вершинам. От любого воздушного змея вписанный кружок касается его четырех сторон на четырех вершинах трапециера из изобилия. Для любых трапециевых, касательных линий, касающихся, касающихся окружающего круга в его четырех вершинах образуют четыре стороны воздушного змея. Это соответствие также можно рассматривать как пример полярной взаимной взаимности , общий метод для соответствующих точек с линиями и наоборот, с учетом фиксированного круга. Хотя они не касаются круга, четыре вершины воздушных змеев являются взаимными в этом смысле к четырем сторонам трапеции Isosceles. ^{[ 29 ]} Особенности воздушных змеев и трапеций, которые соответствуют друг другу под этой двойственностью, сравниваются в таблице ниже. ^{[ 7 ]}

Isocseles Trapezoid	Видеть
Две пары равных соседних углов	Две пары равных соседних сторон
Две равные противоположные стороны	Два равных противоположных углах
Две противоположные стороны с общим перпендикулярным бисектором	Два противоположных углы с общим углом бисектора
Ось симметрии через две противоположные стороны	Ось симметрии через два противоположных угла
Описанный круг по всем вершинам	Вписанный круг, касаясь всех сторон

Рассечение

Проблема по равенству касается подразделения полигонов в треугольники, которые имеют равные участки. В этом контексте спектр многоугольника является набором чисел $n$ так, что многоугольник имеет равенство в $n$ Равные треугольники. Из -за своей симметрии спектр воздушного змея содержит все даже целые числа. Некоторые специальные воздушные змеи также содержат некоторые нечетные числа в своих спектрах. ^{[ 30 ]}^{[ 31 ]}

Каждый треугольник может быть подразделен на три правых воздушных змеях, собравшихся в центре его вписанного круга. В целом, метод, основанный на упаковке круга, может использоваться для подразделения любого многоугольника с $n$ стороны в $O(n)$ воздушные змеи, встреча с краем до края. ^{[ 32 ]}

Пять и многогранника

Рекурсивная конструкция змея и дрэк -пенроуза

Фрактальная розетка из пенроуза воздушных змеев

Все воздушные змеи плютируют плоскость с помощью повторяющегося точечного отражения вокруг средних точек их краев, как и в целом, все четырехугольники. ^{[ 33 ]} Воздушные змеи и дротики с углами 72 °, 72 °, 72 °, 144 ° и 36 °, 72 °, 36 °, 216 °, соответственно, образуют прототили одной версии пенурозной плитки , апериодическое плит Математический физик Роджер Пенроуз . ^{[ 5 ]} Когда змея имеют углы, которые на вершине и одной стороне суммируют $\pi (1-{\tfrac {1}{n}})$ Для некоторого положительного целого числа $n$ , затем масштабированные копии этого воздушного змея могут быть использованы для плитки плоскости в фрактальной розетке, в которой последовательно большие кольца $n$ воздушные змеи окружают центральную точку. ^{[ 34 ]} Эти розетки могут быть использованы для изучения явления неэластичного коллапса, в котором система движущихся частиц, встречающихся в неэластичных столкновениях, все объединяются в общей точке. ^{[ 35 ]}

Воздушный змей с углами 60 °, 90 °, 120 °, 90 ° также может также пенить плоскость повторным отражением по его краям; Полученная тесселяция, дельтоидальная тригексагональная плитка , суперпозирует тесселяцию плоскости регулярными гексагонами и изобранными треугольниками. ^{[ 16 ]} Дельтоидальный икоситетрахедрон , дельтоидальный гексеконтахедрон и трапецирдрон - многогранники с конгруэнтными змеями в форме змеев , ^{[ 36 ]} который альтернативно может рассматриваться как уточнения сферы конгруэнтными сферическими воздушными змеями. ^{[ 37 ]} Есть бесконечно много симметричных лиц гиперболической плоскости воздушными змеями. ^{[ 38 ]} Эти многогранники (эквивалентно, сферические уклонки), квадратные и дельтоидные тригексагогоговые уточнения евклидовой плоскости и некоторые пьесы гиперболической плоскости показаны в таблице ниже, помеченные конфигурацией лица (количество соседей каждого из четырех вершин каждая плитка). Некоторые многогранники и пьесы появляются дважды, под двумя разными конфигурациями лица.

Полигранра			Евклидовый
V4.3.4.3	V4.3.4.4	V4.3.4.5	V4.3.4.6
Полигранра	Евклидовый	Гиперболические уточнения
V4.4.4.3	V4.4.4.4	V4.4.4.5	V4.4.4.6
Полигранра	Гиперболические уточнения
V4.3.4.5	V4.4.4.5	V4.5.4.5	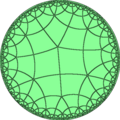V4.6.4.5
Евклидовый	Гиперболические уточнения
V4.3.4.6	V4.4.4.6	V4.5.4.6	V4.6.4.6

Трапезоидры . -это еще одна семья многогранников, которые имеют конгруэнтные лица в форме воздушных змеев В этих многогранниках края одной из двух боковых длин воздушных змеев встречаются на двух «полюсных» вершинах, в то время как края другой длины образуют экваториальную зигзагообразную траекторию вокруг многогранника. Они являются двойными многоградами однородных антипризмов . ^{[ 36 ]} Обычно заметным примером является пентагональный трапецировку , используемый для десятисторонних костей . ^{[ 16 ]}

Внешние бильярд

Математик Ричард Шварц изучал внешних бильярд на воздушных змеях. Внешние бильярды - это динамическая система , в которой из точки за пределами данного компактного выпуклости, установленного в плоскости, один вытягивает касательную линию к набору выпуклы, перемещается от начальной точки вдоль этой линии в другую точку, одинаково далеко от точки опадения , а затем повторяет тот же процесс. Это было открыто с 1950 -х годов, может ли какая -либо система, определенная таким образом, может создать пути, которые произвольно становятся далеко от их отправной точки, и в статье 2007 года Шварц решил эту проблему, обнаружив безграничные бильярдные пути для кайта с углами 72 °, 72 ° , 72 °, 144 °, так же, как и в плюше. ^{[ 39 ]} Позже он написал монографию , анализирующую внешние бильярды для змеев в целом. Для этой проблемы любая аффинная преобразование воздушного змея сохраняет на нем динамические свойства внешних бильярдов, и можно преобразовать любое воздушное здание в форму, где три вершины находятся в точках $(-1,0)$ и $(0,\pm 1)$ , с четвертым в $(\alpha ,0)$ с $\alpha$ в интервале открытого блока $(0,1)$ Полем Поведение внешних бильярдов на любом воздушном змее сильно зависит от параметра $\alpha$ И в частности, является ли это рациональным . Для случая воздушного змея, $\alpha =1/\varphi ^{3}$ , иррациональное число, где $\varphi =(1+{\sqrt {5}})/2$ Золотое соотношение . ^{[ 40 ]}

Ссылки

^ Jump up to: ^а ^{беременный} ^в ^{дюймовый} ^и Halsted, George Bruce (1896), «Глава XIV. Симметричные четырехугольники» , Элементарная синтетическая геометрия , J. Wiley & Sons, с. 49–53
^ Goormaghtigh, R. (1947), «Ортополярные и изополярные линии в циклическом четырехугольнике», американский математический месяц , 54 (4): 211–214, doi : 10.1080/00029890.1947.11991815 , JSTOR 2304700, MR 001993444415, JSTOR 2304700, MR 0019934444415, JSTOR 2304700, MR 00199344444415 , JSTOR 2304700 , MR 0019934444
^ См HSM Обзор Grünbaum (1960) . Grünbaum ( 1960 ) 0125489 : «К сожалению, автор использует вместо« кайта », название« deltoid », которое более правильно принадлежит кривой, с тремя сопостальными гипоциклоидом».
^ Хартия, Кевин; Роджерс, Томас (1993), «Динамика четырехсторонней складывания» , Экспериментальная математика , 2 (3): 209–222, doi : 10.1080/10586458.1993.10504278 , MR 1273409
^ Jump up to: ^а ^{беременный} Гарднер, Мартин (январь 1977 г.), «Чрезвычайная непериодическая плитка, которая обогащает теорию плиток», Математические игры, Scientific American , Vol. 236, нет. 1, с. 110–121, Bibcode : 1977Sciam.236a.110G , doi : 10.1038/Scientificamerican0177-110 , JSTOR 24953856
^ Терстон, Уильям П. (1998), «Формы многогранников и триангуляции сферы», в Ривине, Игорь ; Рурк, Колин; Серия, Кэролайн (ред.), Эпштейнский день рождения , «Геометрия и топология монографии», вып. 1, Coventry, стр. 511–549, arxiv : математика/9801088 , doi : 10.2140/gtm.1998.1.511 , MR 1668340 , S2CID 8686884 {{citation}}: CS1 Maint: местоположение отсутствует издатель ( ссылка )
^ Jump up to: ^а ^{беременный} ^в ^{дюймовый} ^и De Villiers, Michael (2009), Некоторые приключения в евклидовой геометрии , динамическое обучение математике, с. 16, 55, ISBN 978-0-557-10295-2
^ Szecsei, Denise (2004), Полное идиотское руководство по геометрии , Penguin, с. 290–291, ISBN 9781592571833
^ Jump up to: ^а ^{беременный} Усискин, Залман; Гриффин, Дженнифер (2008), Классификация четырехсторонних: исследование определения , публикация информационного возраста , стр. 49–52, 63–67
^ Jump up to: ^а ^{беременный} ^в Бимер, Джеймс Э. (май 1975), «Сказка о воздушном змее», учитель арифметики , 22 (5): 382–386, doi : 10.5951/at.22.5.0382 , JStor 41188788
^ Jump up to: ^а ^{беременный} Александр, Даниэль С.; Koeberlein, Geralyn M. (2014), Элементарная геометрия для студентов колледжа (6 -е изд.), Cengage Learning , с. 180–181, ISBN 9781285965901
^ Суэй, Джон Майкл; 2014 ) Дэвид Тейран , ( (2): 439–463, doi:,
^ Liberman, Anatoly (2009), Word Origins ... и откуда мы их знаем: этимология для всех , издательство Оксфордского университета , с. 17, ISBN 9780195387070
^ Henrici, Olaus (1879), Elementary Geometry: конгруэнтные фигуры , Longmans, Green, p. XIV
^ Jump up to: ^а ^{беременный} Де Вилльерс, Майкл (февраль 1994 г.), «Роль и функция иерархической классификации четырехугольника», для изучения математики , 14 (1): 11–18, JSTOR 40248098
^ Jump up to: ^а ^{беременный} ^в ^{дюймовый} ^и ^фон ^глин ^час Алсина, Клауди; Нельсен, Роджер Б. (2020), «Раздел 3.4: воздушные змеи» , рогнукопия четырехсторонних , математические экспозиции Dolciani, vol. 55, Провиденс, Род -Айленд: Maa Press и Американское математическое общество, с. 73–78, ISBN 978-1-4704-5312-1 , MR 4286138 ; См. Также антипараллелограммы, с. 212
^ Гант, П. (1944), «Примечание о четырехтерапии», Математическая газетта , 28 (278): 29–30, doi : 10.2307/3607362 , JSTOR 3607362 , S2CID 250436895
^ Josefsson, Martin (2012), «Максимальная площадь двухстороннего четырехугольника» (PDF) , Forum Geometricorum , 12 : 237–241, MR 2990945
^ Ball, DG (1973), «Обобщение $\pi$ ", Математическая газета , 57 (402): 298–303, doi : 10.2307/3616052 , JSTOR 3616052 , S2CID 125396664
^ Гриффитс, Дэвид; Culpin, David (1975), «Пиоптимальные многоугольники», Математическая газетта , 59 (409): 165–175, doi : 10.2307/3617699 , JSTOR 3617699 , S2CID 126325288
^ Одет, Чарльз; Хансен, Пьер; Svrtan, Dragutin (2021), «Использование символических расчетов для определения самых больших небольших полигонов», Journal of Global Optimization , 81 (1): 261–268, DOI : 10.1007/S10898-020-00908-W , MR 4299185 , S2CID 203042405
^ Дарлинг, Дэвид (2004), Универсальная книга математики: от Абракадабра до парадоксов Зено , Джон Вили и сыновья , с. 260, ISBN 9780471667001
^ Кирби, Мэтью; Умбл, Рональд (2011), «Тесселяции края и складывание штампов», Mathematic Magazine , 84 (4): 283–289, arxiv : 0908.3257 , doi : 10.4169/math.mag.84.4.283, MR 2843659, S2CID 1235793888888888, MR 2843659, S2CID 123579388888888, MR 2843659, S2CID 12357788888888 , MR 2843659 , S2CID 1235778888888, MR 2843659 , S2CID 123577888888,
^ Смит, Дэвид; Майерс, Джозеф Самуэль; Каплан, Крейг С.; Гудман-Страсс, Хаим (март 2023 г.), апериодический монотиль , arxiv : 2303.10798
^ Eves, Howard Whitley (1995), Геометрия колледжа , Jones & Bartlett Learning , p. 245, ISBN 9780867204759
^ «OC506» (PDF) , Олимпиадские угловые решения, Cross Mathematics , 47 (5): 241, май 2021 г.
^ Wheeler, Roger F. (1958), «Четырехугольные», Математическая газетта , 42 (342): 275–276, doi : 10.2307/3610439 , JSTOR 3610439 , S2CID 250434576
^ Jump up to: ^а ^{беременный} ^в Josefsson, Martin (2011), «Когда он касается четырехстороннего воздушного змея?» (PDF) , Forum Geometricorum , 11 : 165–174
^ Робертсон, С.А. (1977), «Классификация треугольников и четырехугольников», Математическая газетта , 61 (415): 38–49, doi : 10.2307/3617441 , JSTOR 3617441 , S2CID 125355481
^ Касиматис, Элейн А .; Stein, Sherman K. (декабрь 1990 г.), «Раквидации полигонов», дискретная математика , 85 (3): 281–294, doi : 10.1016/0012-365x (90) 90384-T , MR 1081836 , ZBL 0736.05028
^ Джепсен, Чарльз Х.; Седберри, Тревор; Hoyer, Rolf (2009), «Эквидиссии четырехугольников в форме воздушных змеев» (PDF) , вовлеченность: журнал по математике , 2 (1): 89–93, doi : 10.2140/into.2009.2.89 , Mr 2501347
^ Берн, Маршалл; Eppstein, David (2000), «Четырехсторонняя сетка с кружкой упаковкой», Международный журнал вычислительной геометрии и применения , 10 (4): 347–360, arxiv : cs.cg/9908016 , doi : 10.1142/s0218195900000206 , Mr 1791192 , S2CID . 12228995
^ Schattschneider, Doris (1993), «Увлечение плитки» , в Emmer, Michele (ed.), The Visual Mind: Art and Mathematics , серия книг Леонардо, Кембридж, Массачусетс: MIT Press , с. 157–164, ISBN 0-262-05048-х , MR 1255846
^ Fathauer, Robert (2018), «Искусство и развлекательная математика, основанная на розетках для змеев» , в Торренсе, Ева ; Торренс, Брюс; Séquin, Carlo ; Fenyvesi, Kristóf (Eds.), Trootings of Bridges 2018: математика, искусство, музыка, архитектура, образование, культура , Феникс, Аризона: Tessellations Publishing, стр. 15–22, ISBN 978-1-938664-27-4
^ Шазель, Бернард ; Картикун, Криткорн; Чжэн, Юфэй (2022), «Геометрический подход к неэластичному коллапсу», Журнал вычислительной геометрии , 13 (1): 197–203, doi : 10.20382/jocg.v13i1a7 , MR 4414332
^ Jump up to: ^а ^{беременный} Grünbaum, B. (1960), «On Polyherra in $E^{3}$ Все лица конгруэнтны », Бюллетень Исследовательского совета Израиля , 8F : 215–218 (1960), MR 0125489
^ Скажи, Юдай; Akama, Yohji (2015), «Аноэдральные сферические треугольники и классификация сферических печьи конгруэнтными змеями, дротиками и римби» Хиросимы Математический журнал , 45 (3): 309–339 doi : 10.3 , , 3429167 , S2CID 123859584
^ Данхэм, Дуглас; Линдгрен, Джон; Витте, Дейв (1981), «Создание повторяющихся гиперболических паттернов», в зеленом, Дуг; Люсидо, Тони; Фукс, Генри (ред.), графике и интерактивным методам, Siggraph 1981, Даллас, Техас, США, 3–7 августа , компьютерной г. Труды 8 -й ежегодной конференции по 1981 10.1145/800224.806808 , s2cid 2255628
^ Evan 2007 ) , Richard Schwartz ( . , S2CID 119146537
^ Шварц, Ричард Эван (2009), Внешние бильярд на воздушных змеях , Анналы исследований математики, Vol. 171, Принстон, Нью -Джерси: издательство Принстонского университета , doi : 10.1515/9781400831975 , ISBN 978-0-691-14249-4 , MR 2562898

Внешние ссылки

Вейсштейн, Эрик У. , "Кайт" , Mathworld
Формулы области с интерактивной анимацией на mathopenref.com

[halsted-1] Jump up to: ^а ^{беременный} ^в ^{дюймовый} ^и Halsted, George Bruce (1896), «Глава XIV. Симметричные четырехугольники» , Элементарная синтетическая геометрия , J. Wiley & Sons, с. 49–53

[goormaghtigh-2] Goormaghtigh, R. (1947), «Ортополярные и изополярные линии в циклическом четырехугольнике», американский математический месяц , 54 (4): 211–214, doi : 10.1080/00029890.1947.11991815 , JSTOR 2304700, MR 001993444415, JSTOR 2304700, MR 0019934444415, JSTOR 2304700, MR 00199344444415 , JSTOR 2304700 , MR 0019934444

[3] См HSM Обзор Grünbaum (1960) . Grünbaum ( 1960 ) 0125489 : «К сожалению, автор использует вместо« кайта », название« deltoid », которое более правильно принадлежит кривой, с тремя сопостальными гипоциклоидом».

[charter-rogers-4] Хартия, Кевин; Роджерс, Томас (1993), «Динамика четырехсторонней складывания» , Экспериментальная математика , 2 (3): 209–222, doi : 10.1080/10586458.1993.10504278 , MR 1273409

[gardner-5] Jump up to: ^а ^{беременный} Гарднер, Мартин (январь 1977 г.), «Чрезвычайная непериодическая плитка, которая обогащает теорию плиток», Математические игры, Scientific American , Vol. 236, нет. 1, с. 110–121, Bibcode : 1977Sciam.236a.110G , doi : 10.1038/Scientificamerican0177-110 , JSTOR 24953856

[thurston-6] Терстон, Уильям П. (1998), «Формы многогранников и триангуляции сферы», в Ривине, Игорь ; Рурк, Колин; Серия, Кэролайн (ред.), Эпштейнский день рождения , «Геометрия и топология монографии», вып. 1, Coventry, стр. 511–549, arxiv : математика/9801088 , doi : 10.2140/gtm.1998.1.511 , MR 1668340 , S2CID 8686884 {{citation}}: CS1 Maint: местоположение отсутствует издатель ( ссылка )

[devilliers-adventures-7] Jump up to: ^а ^{беременный} ^в ^{дюймовый} ^и De Villiers, Michael (2009), Некоторые приключения в евклидовой геометрии , динамическое обучение математике, с. 16, 55, ISBN 978-0-557-10295-2

[idiot-8] Szecsei, Denise (2004), Полное идиотское руководство по геометрии , Penguin, с. 290–291, ISBN 9781592571833

[usiskin-griffin-9] Jump up to: ^а ^{беременный} Усискин, Залман; Гриффин, Дженнифер (2008), Классификация четырехсторонних: исследование определения , публикация информационного возраста , стр. 49–52, 63–67

[beamer-10] Jump up to: ^а ^{беременный} ^в Бимер, Джеймс Э. (май 1975), «Сказка о воздушном змее», учитель арифметики , 22 (5): 382–386, doi : 10.5951/at.22.5.0382 , JStor 41188788

[alexander-koeberlein-11] Jump up to: ^а ^{беременный} Александр, Даниэль С.; Koeberlein, Geralyn M. (2014), Элементарная геометрия для студентов колледжа (6 -е изд.), Cengage Learning , с. 180–181, ISBN 9781285965901

[nuncius-12] Суэй, Джон Майкл; 2014 ) Дэвид Тейран , ( (2): 439–463, doi:,

[liberman-13] Liberman, Anatoly (2009), Word Origins ... и откуда мы их знаем: этимология для всех , издательство Оксфордского университета , с. 17, ISBN 9780195387070

[henrici-14] Henrici, Olaus (1879), Elementary Geometry: конгруэнтные фигуры , Longmans, Green, p. XIV

[devilliers-role-15] Jump up to: ^а ^{беременный} Де Вилльерс, Майкл (февраль 1994 г.), «Роль и функция иерархической классификации четырехугольника», для изучения математики , 14 (1): 11–18, JSTOR 40248098

[alsina-nelson-16] Jump up to: ^а ^{беременный} ^в ^{дюймовый} ^и ^фон ^глин ^час Алсина, Клауди; Нельсен, Роджер Б. (2020), «Раздел 3.4: воздушные змеи» , рогнукопия четырехсторонних , математические экспозиции Dolciani, vol. 55, Провиденс, Род -Айленд: Maa Press и Американское математическое общество, с. 73–78, ISBN 978-1-4704-5312-1 , MR 4286138 ; См. Также антипараллелограммы, с. 212

[gant-17] Гант, П. (1944), «Примечание о четырехтерапии», Математическая газетта , 28 (278): 29–30, doi : 10.2307/3607362 , JSTOR 3607362 , S2CID 250436895

[josefsson-area-18] Josefsson, Martin (2012), «Максимальная площадь двухстороннего четырехугольника» (PDF) , Forum Geometricorum , 12 : 237–241, MR 2990945

[ball-19] Ball, DG (1973), «Обобщение $\pi$ ", Математическая газета , 57 (402): 298–303, doi : 10.2307/3616052 , JSTOR 3616052 , S2CID 125396664

[griffiths-culpin-20] Гриффитс, Дэвид; Culpin, David (1975), «Пиоптимальные многоугольники», Математическая газетта , 59 (409): 165–175, doi : 10.2307/3617699 , JSTOR 3617699 , S2CID 126325288

[audet-hansen-svrtan-21] Одет, Чарльз; Хансен, Пьер; Svrtan, Dragutin (2021), «Использование символических расчетов для определения самых больших небольших полигонов», Journal of Global Optimization , 81 (1): 261–268, DOI : 10.1007/S10898-020-00908-W , MR 4299185 , S2CID 203042405

[darling-22] Дарлинг, Дэвид (2004), Универсальная книга математики: от Абракадабра до парадоксов Зено , Джон Вили и сыновья , с. 260, ISBN 9780471667001

[kirby-umble-23] Кирби, Мэтью; Умбл, Рональд (2011), «Тесселяции края и складывание штампов», Mathematic Magazine , 84 (4): 283–289, arxiv : 0908.3257 , doi : 10.4169/math.mag.84.4.283, MR 2843659, S2CID 1235793888888888, MR 2843659, S2CID 123579388888888, MR 2843659, S2CID 12357788888888 , MR 2843659 , S2CID 1235778888888, MR 2843659 , S2CID 123577888888,

[smkg-24] Смит, Дэвид; Майерс, Джозеф Самуэль; Каплан, Крейг С.; Гудман-Страсс, Хаим (март 2023 г.), апериодический монотиль , arxiv : 2303.10798

[eves-25] Eves, Howard Whitley (1995), Геометрия колледжа , Jones & Bartlett Learning , p. 245, ISBN 9780867204759

[crux-26] «OC506» (PDF) , Олимпиадские угловые решения, Cross Mathematics , 47 (5): 241, май 2021 г.

[wheeler-27] Wheeler, Roger F. (1958), «Четырехугольные», Математическая газетта , 42 (342): 275–276, doi : 10.2307/3610439 , JSTOR 3610439 , S2CID 250434576

[josefsson-when-28] Jump up to: ^а ^{беременный} ^в Josefsson, Martin (2011), «Когда он касается четырехстороннего воздушного змея?» (PDF) , Forum Geometricorum , 11 : 165–174

[robertson-29] Робертсон, С.А. (1977), «Классификация треугольников и четырехугольников», Математическая газетта , 61 (415): 38–49, doi : 10.2307/3617441 , JSTOR 3617441 , S2CID 125355481

[kasimitis-stein-30] Касиматис, Элейн А .; Stein, Sherman K. (декабрь 1990 г.), «Раквидации полигонов», дискретная математика , 85 (3): 281–294, doi : 10.1016/0012-365x (90) 90384-T , MR 1081836 , ZBL 0736.05028

[jepsen-sedberry-hoyer-31] Джепсен, Чарльз Х.; Седберри, Тревор; Hoyer, Rolf (2009), «Эквидиссии четырехугольников в форме воздушных змеев» (PDF) , вовлеченность: журнал по математике , 2 (1): 89–93, doi : 10.2140/into.2009.2.89 , Mr 2501347

[bern-eppstein-32] Берн, Маршалл; Eppstein, David (2000), «Четырехсторонняя сетка с кружкой упаковкой», Международный журнал вычислительной геометрии и применения , 10 (4): 347–360, arxiv : cs.cg/9908016 , doi : 10.1142/s0218195900000206 , Mr 1791192 , S2CID . 12228995

[schattschneider-33] Schattschneider, Doris (1993), «Увлечение плитки» , в Emmer, Michele (ed.), The Visual Mind: Art and Mathematics , серия книг Леонардо, Кембридж, Массачусетс: MIT Press , с. 157–164, ISBN 0-262-05048-х , MR 1255846

[fathauer-34] Fathauer, Robert (2018), «Искусство и развлекательная математика, основанная на розетках для змеев» , в Торренсе, Ева ; Торренс, Брюс; Séquin, Carlo ; Fenyvesi, Kristóf (Eds.), Trootings of Bridges 2018: математика, искусство, музыка, архитектура, образование, культура , Феникс, Аризона: Tessellations Publishing, стр. 15–22, ISBN 978-1-938664-27-4

[chazelle-karntikoon-zheng-35] Шазель, Бернард ; Картикун, Криткорн; Чжэн, Юфэй (2022), «Геометрический подход к неэластичному коллапсу», Журнал вычислительной геометрии , 13 (1): 197–203, doi : 10.20382/jocg.v13i1a7 , MR 4414332

[grunbaum-36] Jump up to: ^а ^{беременный} Grünbaum, B. (1960), «On Polyherra in $E^{3}$ Все лица конгруэнтны », Бюллетень Исследовательского совета Израиля , 8F : 215–218 (1960), MR 0125489

[sakano-akama-37] Скажи, Юдай; Akama, Yohji (2015), «Аноэдральные сферические треугольники и классификация сферических печьи конгруэнтными змеями, дротиками и римби» Хиросимы Математический журнал , 45 (3): 309–339 doi : 10.3 , , 3429167 , S2CID 123859584

[dunham-lindgren-witte-38] Данхэм, Дуглас; Линдгрен, Джон; Витте, Дейв (1981), «Создание повторяющихся гиперболических паттернов», в зеленом, Дуг; Люсидо, Тони; Фукс, Генри (ред.), графике и интерактивным методам, Siggraph 1981, Даллас, Техас, США, 3–7 августа , компьютерной г. Труды 8 -й ежегодной конференции по 1981 10.1145/800224.806808 , s2cid 2255628

[schwartz-unbounded-39] Evan 2007 ) , Richard Schwartz ( . , S2CID 119146537

[schwartz-monograph-40] Шварц, Ричард Эван (2009), Внешние бильярд на воздушных змеях , Анналы исследований математики, Vol. 171, Принстон, Нью -Джерси: издательство Принстонского университета , doi : 10.1515/9781400831975 , ISBN 978-0-691-14249-4 , MR 2562898

[ 1 ]

[ 2 ]

[ 3 ]

[ 4 ]

[ 5 ]

[ 6 ]

[ 7 ]

[ 8 ]

[ 9 ]

[ 10 ]

[ 11 ]

[ 12 ]

[ 13 ]

[ 14 ]

[ 15 ]

[ 16 ]

[ 17 ]

[ 18 ]

[ 19 ]

[ 20 ]

[ 21 ]

[ 22 ]

[ 23 ]

[ 24 ]

[ 25 ]

[ 26 ]

[ 27 ]

[ 28 ]

[ 29 ]

[ 30 ]

[ 31 ]

[ 32 ]

[ 33 ]

[ 34 ]

[ 35 ]

[ 36 ]

[ 37 ]

[ 38 ]

[ 39 ]

[ 40 ]