Воздушный змей (геометрия)

Видеть
Видеть
	Воздушный змей с парами сторон одинаковой длины и вписанным кругом.
Тип	Четырехугольник
Ребра и вершины	4
Группа симметрии	Д 1 (*)
Двойной полигон	Равнобедренная трапеция

В евклидовой геометрии воздушный змей представляет собой четырехугольник с симметрией отражения по диагонали . Из-за этой симметрии воздушный змей имеет два равных угла и две пары смежных сторон одинаковой длины. Воздушных змеев также называют дельтоидами . ^[1] но слово «дельтоида» может также относиться к дельтовидной кривой , несвязанному геометрическому объекту, который иногда изучают в связи с четырехугольниками. ^[2]^[3] Воздушного змея также можно назвать дротиком . ^[4] особенно если он не выпуклый. ^[5]^[6]

Каждый воздушный змей представляет собой ортодиагональный четырехугольник (его диагонали под прямым углом) и, если он выпуклый, тангенциальный четырехугольник (его стороны касаются вписанной окружности). Выпуклые воздушные змеи представляют собой в точности четырехугольники, которые являются как ортодиагональными, так и касательными. В качестве особых случаев они включают в себя правые воздушные змеи с двумя противоположными прямыми углами; ромбики ; с двумя диагональными осями симметрии и квадраты , которые также являются частными случаями как правых воздушных змеев, так и ромбов.

Четырехугольник с наибольшим отношением периметра к диаметру представляет собой воздушный змей с углами 60°, 75° и 150°. Воздушные змеи двух форм (одна выпуклая и одна невыпуклая) образуют прототипы одной из форм мозаики Пенроуза . Воздушные змеи также образуют грани нескольких гране-симметричных многогранников и мозаик и изучались в связи с внешним бильярдом — проблемой высшей математики динамических систем .

Определение и классификация

Воздушный змей представляет собой четырехугольник с симметрией отражения по одной из диагоналей. Другими словами, это четырехугольник, четыре стороны которого можно сгруппировать в две пары смежных сторон одинаковой длины. ^[1]^[7] Воздушный змей можно построить из центров и точек пересечения любых двух пересекающихся кругов . ^[8] Описанные здесь воздушные змеи могут быть как выпуклыми , так и вогнутыми , хотя в некоторых источниках под «воздушным змеем» подразумеваются только выпуклые воздушные змеи. Четырехугольник является воздушным змеем тогда и только тогда, когда выполняется любое из следующих условий:

Четыре стороны можно разделить на две пары смежных сторон одинаковой длины. ^[7]
Одна диагональ пересекает середину другой диагонали под прямым углом, образуя ее биссектрису . ^[9] (В вогнутом случае линия, проходящая через одну из диагоналей, делит другую пополам.)
Одна диагональ представляет собой линию симметрии. Он делит четырехугольник на два равных треугольника, которые являются зеркальными отражениями друг друга. ^[7]
Одна диагональ делит пополам оба угла на двух своих концах. ^[7]

Четырехугольные воздушные змеи названы в честь летающих воздушных змеев , которые часто имеют такую форму. ^[10]^[11] и которые, в свою очередь, названы в честь парящей птицы и звука, который она издает. ^[12]^[13] По словам Олауса Хенрици , название «воздушный змей» этим формам дал Джеймс Джозеф Сильвестр . ^[14]

Четырехугольники можно классифицировать иерархически , что означает, что некоторые классы четырехугольников включают другие классы, или раздельно , что означает, что каждый четырехугольник принадлежит только одному классу. По иерархической классификации воздушные змеи включают ромбы (четырехугольники с четырьмя равными сторонами) и квадраты . Все равносторонние воздушные змеи — ромбы, а все равноугольные — квадраты. При раздельной классификации ромбы и квадраты не были бы воздушными змеями, поскольку они принадлежат к другому классу четырехугольников; Точно так же правильные воздушные змеи , обсуждаемые ниже, не будут воздушными змеями. Оставшаяся часть этой статьи соответствует иерархической классификации; ромбы, квадраты и правые воздушные змеи считаются воздушными змеями. Избегая необходимости рассматривать особые случаи, эта классификация может упростить некоторые факты о воздушных змеях. ^[15]

Как и воздушные змеи, параллелограмм также имеет две пары сторон одинаковой длины, но они расположены напротив друг друга, а не рядом. Любой несамопересекающийся четырехугольник, имеющий ось симметрии, должен быть либо воздушным змеем с диагональной осью симметрии; или равнобедренная трапеция с осью симметрии, проходящей через середины двух сторон. К ним относятся в качестве особых случаев ромб и прямоугольник соответственно, а также квадрат, который является частным случаем обоих. ^[1] Самопересекающиеся четырехугольники включают еще один класс симметричных четырехугольников — антипараллелограммы . ^[16]

Особые случаи

Правый змей

Равнодиагональный змей в треугольнике Рело

Лютня Пифагора

Правильные воздушные змеи имеют два противоположных прямых угла . ^[15]^[16] Правильные воздушные змеи — это именно те воздушные змеи, которые представляют собой циклические четырехугольники , а это означает, что через все их вершины проходит окружность. ^[17] Вписанные четырехугольники можно эквивалентно определить как четырехугольники, в которых два противоположных угла являются дополнительными (они в сумме составляют 180 °); если одна пара является дополнительной, то и другая тоже. ^[9] Следовательно, правильные воздушные змеи — это воздушные змеи с двумя противоположными дополнительными углами для любой из двух противоположных пар углов. Поскольку правые воздушные змеи описывают одну окружность и вписаны в другую окружность, они представляют собой бицентрические четырехугольники (на самом деле трехцентрические, поскольку у них также есть третий круг, касающийся снаружи продолжений их сторон ). ^[16] Если размеры вписанной и описанной окружностей фиксированы, то правый змей имеет наибольшую площадь среди всех четырехугольников, оказавшихся между ними. ^[18]

Среди всех четырехугольников фигурой, которая имеет наибольшее отношение периметра к диаметру ( максимальное расстояние между любыми двумя точками), является равнодиагональный змей с углами 60°, 75°, 150°, 75°. Его четыре вершины лежат в трех углах и одной из боковых середин треугольника Рело . ^[19]^[20] Когда длина сторон равнодиагонального воздушного змея меньше или равна его диагоналям, как у этого или квадрата, это один из четырехугольников с наибольшим соотношением площади к диаметру . ^[21]

Воздушный змей с тремя углами 108° и одним углом 36° образует выпуклую оболочку лютни Пифагора , фрактал, состоящий из вложенных пентаграмм . ^[22] Четыре стороны этого воздушного змея лежат на четырех сторонах правильного пятиугольника , а золотой треугольник . к пятой стороне приклеен ^[16]

Есть только восемь многоугольников, которые могут замостить плоскость так, что при отражении любой плитки через любой из ее краев образуется другая плитка; такое расположение называется краевой тесселяцией . Один из них — замощение прямым воздушным змеем с углами 60°, 90° и 120°. Он создает дельтовидную тригексагональную мозаику (см. § Тайлинги и многогранники ). ^[23] Прототип , созданный восемью из этих воздушных змеев, лишь апериодически закрывает плоскость плиткой , что является ключом к заявленному решению проблемы Эйнштейна . ^[24]

В неевклидовой геометрии воздушный змей может иметь три прямых угла и один непрямой угол, образуя частный случай четырехугольника Ламберта . Четвертый угол острый в гиперболической геометрии и тупой в сферической геометрии . ^[25]

Характеристики

Диагонали, углы и площадь

Каждый воздушный змей представляет собой ортодиагональный четырехугольник , то есть две его диагонали расположены под прямым углом друг к другу. Более того, одна из двух диагоналей (ось симметрии) является биссектрисой другой, а также биссектрисой двух углов, с которыми она пересекается. ^[1] Из-за симметрии два других угла кайта должны быть равны. ^[10]^[11] Диагональная ось симметрии выпуклого воздушного змея делит его на два равных треугольника ; другая диагональ делит его на два равнобедренных треугольника . ^[1]

Как и в более общем смысле для любого ортодиагонального четырехугольника, площадь $A$ воздушного змея можно рассчитать как половину произведения длин диагоналей. $p$ и $q$ : ^[10] $A={\frac {p\cdot q}{2}}.$ Альтернативно, площадь можно рассчитать, разделив кайт на два равных треугольника и применив формулу SAS для определения их площади. Если $a$ и $b$ - длины двух сторон воздушного змея, а $\theta$ - угол между ними, то площадь равна ^[26] $\displaystyle A=ab\cdot \sin \theta .$

Вписанный круг

Две окружности, касающиеся сторон и расширенных сторон выпуклого воздушного змея (вверху), невыпуклого воздушного змея (в центре) и антипараллелограмма (внизу). Четыре прямые, проходящие через стороны каждого четырехугольника, являются касательными к окружностям.

Каждый выпуклый воздушный змей также является касательным четырехугольником , четырехугольником, в который вписана окружность . То есть существует окружность, касающаяся всех четырех сторон. Кроме того, если выпуклый воздушный змей не является ромбом, снаружи воздушного змея есть круг, касающийся продолжений четырех сторон; следовательно, каждый выпуклый змей, не являющийся ромбом, является экскасательным четырехугольником . Выпуклые воздушные змеи, не являющиеся ромбами, представляют собой в точности четырехугольники, которые являются как тангенциальными, так и экстангенциальными. ^[16] Для каждого вогнутого змея существуют две окружности, касающиеся двух сторон и продолжения двух других: одна находится внутри змея и касается двух сторон, противоположных вогнутому углу, тогда как другая окружность находится снаружи змея и касается змей на двух краях, прилегающих к вогнутому углу. ^[27]

Для выпуклого воздушного змея с диагональной длиной $p$ и $q$ и длины сторон $a$ и $b$ , радиус $r$ вписанной окружности $r={\frac {pq}{2(a+b)}},$ и радиус $\rho$ внекасательной окружности ^[16] $\rho ={\frac {pq}{2|a-b|}}.$

Касательный четырехугольник также является воздушным змеем тогда и только тогда, когда выполняется любое из следующих условий: ^[28]

Площадь равна половине произведения диагоналей .
Диагонали перпендикулярны . (Таким образом, воздушные змеи представляют собой в точности четырехугольники, которые одновременно являются тангенциальными и ортодиагональными .)
Два отрезка, соединяющие противоположные точки касания, имеют одинаковую длину.
Касательные длины , расстояния от точки касания до соседней вершины четырехугольника, равны в двух противоположных вершинах четырехугольника. (В каждой вершине есть две соседние точки касания, но они находятся на одинаковом расстоянии друг от друга от вершины, поэтому каждая вершина имеет одну касательную длину.)
Две бимедианы , отрезки, соединяющие середины противоположных ребер, имеют одинаковую длину.
Произведения противоположных сторон равны.
Центр вписанной окружности лежит на линии симметрии, которая также является диагональю.

Если диагонали касательного четырехугольника $ABCD$ пересекаться в $P$ , и вписанные в треугольники окружности $ABP$ , $BCP$ , $CDP$ , $DAP$ иметь радиусы $r_{1}$ , $r_{2}$ , $r_{3}$ , и $r_{4}$ соответственно, то четырехугольник является воздушным змеем тогда и только тогда, когда ^[28] $r_{1}+r_{3}=r_{2}+r_{4}.$ Если вписанная окружность тех же четырех треугольников, лежащих напротив вершины $P$ иметь радиусы $R_{1}$ , $R_{2}$ , $R_{3}$ , и $R_{4}$ соответственно, то четырехугольник является воздушным змеем тогда и только тогда, когда ^[28] $R_{1}+R_{3}=R_{2}+R_{4}.$

Двойственность

Воздушные змеи и равнобедренные трапеции двойственны друг другу, а это означает, что между ними существует соответствие, которое меняет размерность их частей на противоположные, превращая вершины в стороны, а стороны в вершины. Для любого воздушного змея вписанная окружность касается четырех его сторон в четырех вершинах равнобедренной трапеции. Для любой равнобедренной трапеции касательные к описанной окружности в ее четырех вершинах образуют четыре стороны воздушного змея. Это соответствие также можно рассматривать как пример полярного возвратно-поступательного движения , общего метода сопоставления точек с линиями и наоборот с учетом фиксированного круга. Хотя они и не касаются круга, четыре вершины воздушного змея в этом смысле обратны четырем сторонам равнобедренной трапеции. ^[29] Характеристики воздушных змеев и равнобедренных трапеций, соответствующих друг другу в рамках этой двойственности, сравниваются в таблице ниже. ^[7]

Равнобедренная трапеция	Видеть
Две пары равных смежных углов	Две пары равных смежных сторон
Две равные противоположные стороны	Два равных противоположных угла
Две противоположные стороны с общим серединным перпендикуляром.	Два противоположных угла с общей биссектрисой.
Ось симметрии, проходящая через две противоположные стороны	Ось симметрии, проходящая через два противоположных угла
Описанная окружность через все вершины	Вписанная окружность, касательная ко всем сторонам

Диссекция

Проблема равнорассечения касается разделения многоугольников на треугольники, имеющие равные площади. В этом контексте спектр многоугольника представляет собой набор чисел $n$ такой, что многоугольник имеет равнорассечение на $n$ равновеликие треугольники. Из-за своей симметрии спектр воздушного змея содержит все четные целые числа. Некоторые специальные воздушные змеи также содержат в своем спектре нечетные числа. ^[30]^[31]

Каждый треугольник можно разделить на три правых змея, встречающихся в центре вписанного в него круга. В более общем смысле метод, основанный на упаковке кругов, можно использовать для разделения любого многоугольника с помощью $n$ стороны в $O(n)$ воздушные змеи, встречающиеся от края до края. ^[32]

Тайлинги и многогранники

Рекурсивное построение мозаики Пенроуза из воздушного змея и дротика

Фрактальная розетка воздушных змеев Пенроуза

Все воздушные змеи замостили плоскость путем многократного точечного отражения вокруг середин своих краев, как и все четырехугольники в целом. ^[33] Воздушные змеи и дротики с углами 72°, 72°, 72°, 144° и 36°, 72°, 36°, 216° соответственно образуют прототипы одной из версий мозаики Пенроуза — апериодической мозаики плоскости, открытой физик-математик Роджер Пенроуз . ^[5] Если у воздушного змея углы на вершине и на одной стороне в сумме равны $\pi (1-{\tfrac {1}{n}})$ для некоторого положительного целого числа $n$ , то масштабированные копии этого воздушного змея можно использовать для того, чтобы замостить плоскость фрактальной розеткой, в которой последовательно увеличиваются кольца из $n$ воздушные змеи окружают центральную точку. ^[34] Эти розетки можно использовать для изучения явления неупругого коллапса, при котором система движущихся частиц, встречающихся в неупругих столкновениях, объединяется в общей точке. ^[35]

Воздушный змей с углами 60°, 90°, 120°, 90° также может замостить плоскость за счет многократного отражения от ее краев; результирующая мозаика, дельтовидная тригексагональная мозаика , накладывает мозаику плоскости правильными шестиугольниками и равнобедренными треугольниками. ^[16] Дельтоидный икоситетраэдр , дельтоидный шестиконтаэдр и трапецоэдр представляют собой многогранники в форме воздушного змея с конгруэнтными гранями . ^[36] которые альтернативно можно рассматривать как мозаику сферы, состоящую из конгруэнтных сферических змеев. ^[37] Существует бесконечно много гранесимметричных замощений гиперболической плоскости воздушными змеями. ^[38] Эти многогранники (эквивалентно сферическим мозаикам), квадратные и дельтовидные тригексагональные мозаики евклидовой плоскости, а также некоторые мозаики гиперболической плоскости показаны в таблице ниже, помечены конфигурацией грани (числом соседей каждой из четырех вершин каждая плитка). Некоторые многогранники и мозаики появляются дважды, под двумя разными конфигурациями граней.

Многогранники			евклидов
Версия 4.3.4.3	Версия 4.3.4.4	Версия 4.3.4.5	Версия 4.3.4.6
Многогранники	евклидов	Гиперболические мозаики
Версия 4.4.4.3	Версия 4.4.4.4	Версия 4.4.4.5	Версия 4.4.4.6
Многогранники	Гиперболические мозаики
Версия 4.3.4.5	Версия 4.4.4.5	Версия 4.5.4.5	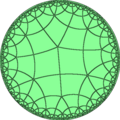Версия 4.6.4.5
евклидов	Гиперболические мозаики
Версия 4.3.4.6	Версия 4.4.4.6	Версия 4.5.4.6	Версия 4.6.4.6

Трапецоэдры — еще одно семейство многогранников , имеющих конгруэнтные грани в форме воздушного змея. В этих многогранниках края одной из двух сторон змея встречаются в двух «полюсных» вершинах, а края другой длины образуют экваториальный зигзагообразный путь вокруг многогранника. Они представляют собой двойственные многогранники однородных антипризм . ^[36] Часто встречающийся пример — пятиугольный трапецоэдр , используемый для изготовления десятигранных игральных костей . ^[16]

Внешний бильярд

Математик Ричард Шварц изучал внешний бильярд на воздушных змеях. Внешний бильярд — это динамическая система , в которой из точки, находящейся вне данного компактного выпуклого множества на плоскости, проводят касательную к выпуклому множеству, проходят от начальной точки по этой прямой до другой точки, равно удаленной от точки касания. , а затем повторяет тот же процесс. С 1950-х годов было открыто, может ли какая-либо система, определенная таким образом, создавать пути, которые уходят сколь угодно далеко от их начальной точки, и в статье 2007 года Шварц решил эту проблему, найдя неограниченные бильярдные траектории для воздушного змея с углами 72 °, 72 °. , 72°, 144°, такие же, как и в мозаике Пенроуза. ^[39] Позже он написал монографию, анализирующую внешний бильярд на предмет форм воздушных змеев в более общем плане. Для этой задачи любое аффинное преобразование воздушного змея сохраняет на нем динамические свойства внешнего биллиарда, и можно преобразовать любой воздушный змей в форму, в которой три вершины находятся в точках $(-1,0)$ и $(0,\pm 1)$ , с четвертым в $(\alpha ,0)$ с $\alpha$ в открытом единичном интервале $(0,1)$ . Поведение внешнего бильярда на любом кайте сильно зависит от параметра $\alpha$ и, в частности, является ли оно рациональным . В случае с воздушным змеем Пенроуза: $\alpha =1/\varphi ^{3}$ , иррациональное число, где $\varphi =(1+{\sqrt {5}})/2$ это золотое сечение . ^[40]

Ссылки

^ Jump up to: ^а ^б ^с ^д ^и Холстед, Джордж Брюс (1896), «Глава XIV. Симметричные четырехугольники» , «Элементарная синтетическая геометрия » , Дж. Уайли и сыновья, стр. 49–53.
^ Гурмахиг, Р. (1947), «Ортополярные и изополярные линии в циклическом четырехугольнике», The American Mathematical Monthly , 54 (4): 211–214, doi : 10.1080/00029890.1947.11991815 , JSTOR 2304700 , MR 0019934
^ См. HSM Coxeter обзор Грюнбаума (1960) в MR. 0125489 : «К сожалению, автор использует вместо слова «воздушный змей» название «дельтовидная мышца», которое больше соответствует кривой, трехбугорной гипоциклоиде».
^ Чартер, Кевин; Роджерс, Томас (1993), «Динамика четырехстороннего складывания» , Экспериментальная математика , 2 (3): 209–222, doi : 10.1080/10586458.1993.10504278 , MR 1273409
^ Jump up to: ^а ^б Гарднер, Мартин (январь 1977 г.), «Необычайное непериодическое замощение, которое обогащает теорию плиток», Mathematical Games, Scientific American , vol. 236, нет. 1, стр. 110–121, Bibcode : 1977SciAm.236a.110G , doi : 10.1038/scientificamerican0177-110 , JSTOR 24953856
^ Терстон, Уильям П. (1998), «Формы многогранников и триангуляции сферы», Ривин, Игорь ; Рурк, Колин; Серия, Кэролайн (ред.), День рождения Эпштейна , Монографии по геометрии и топологии, том. 1, Ковентри, стр. 511–549, arXiv : math/9801088 , doi : 10.2140/gtm.1998.1.511 , MR 1668340 , S2CID 8686884 {{citation}}: CS1 maint: отсутствует местоположение издателя ( ссылка )
^ Jump up to: ^а ^б ^с ^д ^и Де Вильерс, Майкл (2009), Некоторые приключения в евклидовой геометрии , Динамическое изучение математики, стр. 16, 55, ISBN 978-0-557-10295-2
^ Сечеи, Дениз (2004), Полное руководство идиота по геометрии , Penguin, стр. 290–291, ISBN 9781592571833
^ Jump up to: ^а ^б Усиськин, Залман; Гриффин, Дженнифер (2008), Классификация четырехугольников: исследование определения , Information Age Publishing , стр. 49–52, 63–67.
^ Jump up to: ^а ^б ^с Бимер, Джеймс Э. (май 1975 г.), «Сказка о воздушном змее», Учитель арифметики , 22 (5): 382–386, doi : 10.5951/at.22.5.0382 , JSTOR 41188788
^ Jump up to: ^а ^б Александр, Дэниел С.; Кеберлейн, Джералин М. (2014), Элементарная геометрия для студентов колледжей (6-е изд.), Cengage Learning , стр. 180–181, ISBN 9781285965901
^ Суай, Хуан Мигель; Тейра, Дэвид (2014), «Воздушные змеи: взлет и падение научного объекта» (PDF) , Нунциус , 29 (2): 439–463, doi : 10.1163/18253911-02902004
^ Либерман, Анатолий (2009), Происхождение слов... и как мы их знаем: этимология для всех , Oxford University Press , стр. 17, ISBN 9780195387070
^ Хенрици, Олаус (1879), «Элементарная геометрия: конгруэнтные фигуры» , Лонгманс, Грин, с. xiv
^ Jump up to: ^а ^б Де Вильерс, Майкл (февраль 1994 г.), «Роль и функция иерархической классификации четырехугольников», For the Learning of Mathematics , 14 (1): 11–18, JSTOR 40248098
^ Jump up to: ^а ^б ^с ^д ^и ^ж ^г ^час Альсина, Клауди; Нельсен, Роджер Б. (2020), «Раздел 3.4: Воздушные змеи» , Рог изобилия четырехугольников , Математические объяснения Дольчиани, том. 55, Провиденс, Род-Айленд: MAA Press и Американское математическое общество, стр. 73–78, ISBN. 978-1-4704-5312-1 , МР 4286138 ; см. также антипараллелограммы, с. 212
^ Гант, П. (1944), «Заметки о четырехугольниках», The Mathematical Gazette , 28 (278): 29–30, doi : 10.2307/3607362 , JSTOR 3607362 , S2CID 250436895
^ Йозефссон, Мартин (2012), «Максимальная площадь бицентрического четырехугольника» (PDF) , Forum Geometricorum , 12 : 237–241, MR 2990945
^ Болл, Д.Г. (1973), «Обобщение $\pi$ ", The Mathematical Gazette , 57 (402): 298–303, doi : 10.2307/3616052 , JSTOR 3616052 , S2CID 125396664
^ Гриффитс, Дэвид; Калпин, Дэвид (1975), «Пи-оптимальные многоугольники», The Mathematical Gazette , 59 (409): 165–175, doi : 10.2307/3617699 , JSTOR 3617699 , S2CID 126325288
^ Одет, Чарльз; Хансен, Пьер; Свртан, Драгутин (2021), «Использование символических вычислений для определения крупнейших маленьких многоугольников», Journal of Global Optimization , 81 (1): 261–268, doi : 10.1007/s10898-020-00908-w , MR 4299185 , S2CID 203042405
^ Дарлинг, Дэвид (2004), Универсальная книга по математике: от абракадабры до парадоксов Зенона , John Wiley & Sons , стр. 260, ISBN 9780471667001
^ Кирби, Мэтью; Умбл, Рональд (2011), «Тесселяции края и складывание штампов», Mathematic Magazine , 84 (4): 283–289, Arxiv : 0908.3257 , doi : , S2CID 123579388888888, MR 2843659, S2CID 123577888888888, г -н 2843659, S2CID 123579388888888 10.4169/math.mag.84.4.283 , MR 2843659 , MR 2843659, S2CID 12357938888888, MR 2843659 , S2CID 1235778888888 .
^ Смит, Дэвид; Майерс, Джозеф Сэмюэл; Каплан, Крейг С.; Гудман-Штраус, Хаим (март 2023 г.), Апериодический монотиль , arXiv : 2303.10798
^ Ивс, Ховард Уитли (1995), Геометрия колледжа , Jones & Bartlett Learning , стр. 245, ISBN 9780867204759
^ «OC506» (PDF) , Olympiad Corner Solutions, Crux Mathematicorum , 47 (5): 241, май 2021 г.
^ Уилер, Роджер Ф. (1958), «Четырехугольники», The Mathematical Gazette , 42 (342): 275–276, doi : 10.2307/3610439 , JSTOR 3610439 , S2CID 250434576
^ Jump up to: ^а ^б ^с Йозефссон, Мартин (2011), «Когда касательный четырехугольник становится воздушным змеем?» (PDF) , Forum Geometricorum , 11 : 165–174.
^ Робертсон, С.А. (1977), «Классификация треугольников и четырехугольников», The Mathematical Gazette , 61 (415): 38–49, doi : 10.2307/3617441 , JSTOR 3617441 , S2CID 125355481
^ Касиматис, Элейн А .; Штейн, Шерман К. (декабрь 1990 г.), «Равноразрезание многоугольников», Discrete Mathematics , 85 (3): 281–294, doi : 10.1016/0012-365X(90)90384-T , MR 1081836 , Zbl 0736.05028
^ Джепсен, Чарльз Х.; Седберри, Тревор; Хойер, Рольф (2009), «Равнорассечение четырехугольников в форме воздушного змея» (PDF) , Involve: A Journal of Mathematics , 2 (1): 89–93, doi : 10.2140/involve.2009.2.89 , MR 2501347
^ Берн, Маршалл; Эппштейн, Дэвид (2000), «Четырехсторонняя сетка путем упаковки кругов», Международный журнал вычислительной геометрии и приложений , 10 (4): 347–360, arXiv : cs.CG/9908016 , doi : 10.1142/S0218195900000206 , MR 1791192 , S2CID 12228995
^ Шатшнайдер, Дорис (1993), «Очарование плитки» , в Эммер, Мишель (редактор), «Визуальный разум: искусство и математика» , серия книг Леонардо, Кембридж, Массачусетс: MIT Press , стр. 157–164, ISBN 0-262-05048-Х , МР 1255846
^ Фатауэр, Роберт (2018), «Искусство и развлекательная математика, основанная на розетках из воздушных змеев» , в Торренсе, Ева ; Торренс, Брюс; Секин, Карло ; Фенивеси, Кристоф (ред.), Proceedings of Bridges 2018: Mathematics, Art, Music, Architecture, Education, Culture , Phoenix, Arizona: Tessellations Publishing, стр. 15–22, ISBN 978-1-938664-27-4
^ Шазель, Бернар ; Карнтикун, Криткорн; Чжэн, Юфэй (2022), «Геометрический подход к неупругому разрушению», Журнал вычислительной геометрии , 13 (1): 197–203, doi : 10.20382/jocg.v13i1a7 , MR 4414332
^ Jump up to: ^а ^б Грюнбаум, Б. (1960), «О многогранниках в $E^{3}$ иметь все лица конгруэнтными», Бюллетень Исследовательского совета Израиля , 8F : 215–218 (1960), MR 0125489.
^ Закхей, Иуда; Акама, Йоджи (2015), «Анизоэдрические сферические треугольники и классификация сферических мозаик с помощью конгруэнтных воздушных змеев, дротиков и ромбов» , Hiroshima Mathematical Journal , 45 (3):309–339, doi : 10.32917/hmj/1448323768 , MR 3429167 , S2CID 123859584
^ Данэм, Дуглас; Линдгрен, Джон; Витте, Дэйв (1981), «Создание повторяющихся гиперболических паттернов», Грин, Дуг; Люсидо, Тони; Фукс, Генри (ред.), Труды 8-й ежегодной конференции по компьютерной графике и интерактивным технологиям, SIGGRAPH 1981, Даллас, Техас, США, 3–7 августа 1981 г. , Ассоциация вычислительной техники , стр. 215–223, doi : 10.1145/800224.806808 , S2CID 2255628
^ Шварц, Ричард Эван (2007), «Неограниченные орбиты для внешнего биллиарда, I», Journal of Modern Dynamics , 1 (3): 371–424, arXiv : math/0702073 , doi : 10.3934/jmd.2007.1.371 , MR 2318496 , S2CID 119146537
^ Шварц, Ричард Эван (2009), Внешний бильярд на воздушных змеях , Анналы математических исследований, том. 171, Принстон, Нью-Джерси: Princeton University Press , номер номера : 10.1515/9781400831975 , ISBN. 978-0-691-14249-4 , МР 2562898

Внешние ссылки

Вайсштейн, Эрик В. , «Воздушный змей» , MathWorld
формулы площади с интерактивной анимацией на Mathopenref.com

[halsted-1] Jump up to: ^а ^б ^с ^д ^и Холстед, Джордж Брюс (1896), «Глава XIV. Симметричные четырехугольники» , «Элементарная синтетическая геометрия » , Дж. Уайли и сыновья, стр. 49–53.

[goormaghtigh-2] Гурмахиг, Р. (1947), «Ортополярные и изополярные линии в циклическом четырехугольнике», The American Mathematical Monthly , 54 (4): 211–214, doi : 10.1080/00029890.1947.11991815 , JSTOR 2304700 , MR 0019934

[3] См. HSM Coxeter обзор Грюнбаума (1960) в MR. 0125489 : «К сожалению, автор использует вместо слова «воздушный змей» название «дельтовидная мышца», которое больше соответствует кривой, трехбугорной гипоциклоиде».

[charter-rogers-4] Чартер, Кевин; Роджерс, Томас (1993), «Динамика четырехстороннего складывания» , Экспериментальная математика , 2 (3): 209–222, doi : 10.1080/10586458.1993.10504278 , MR 1273409

[gardner-5] Jump up to: ^а ^б Гарднер, Мартин (январь 1977 г.), «Необычайное непериодическое замощение, которое обогащает теорию плиток», Mathematical Games, Scientific American , vol. 236, нет. 1, стр. 110–121, Bibcode : 1977SciAm.236a.110G , doi : 10.1038/scientificamerican0177-110 , JSTOR 24953856

[thurston-6] Терстон, Уильям П. (1998), «Формы многогранников и триангуляции сферы», Ривин, Игорь ; Рурк, Колин; Серия, Кэролайн (ред.), День рождения Эпштейна , Монографии по геометрии и топологии, том. 1, Ковентри, стр. 511–549, arXiv : math/9801088 , doi : 10.2140/gtm.1998.1.511 , MR 1668340 , S2CID 8686884 {{citation}}: CS1 maint: отсутствует местоположение издателя ( ссылка )

[devilliers-adventures-7] Jump up to: ^а ^б ^с ^д ^и Де Вильерс, Майкл (2009), Некоторые приключения в евклидовой геометрии , Динамическое изучение математики, стр. 16, 55, ISBN 978-0-557-10295-2

[idiot-8] Сечеи, Дениз (2004), Полное руководство идиота по геометрии , Penguin, стр. 290–291, ISBN 9781592571833

[usiskin-griffin-9] Jump up to: ^а ^б Усиськин, Залман; Гриффин, Дженнифер (2008), Классификация четырехугольников: исследование определения , Information Age Publishing , стр. 49–52, 63–67.

[beamer-10] Jump up to: ^а ^б ^с Бимер, Джеймс Э. (май 1975 г.), «Сказка о воздушном змее», Учитель арифметики , 22 (5): 382–386, doi : 10.5951/at.22.5.0382 , JSTOR 41188788

[alexander-koeberlein-11] Jump up to: ^а ^б Александр, Дэниел С.; Кеберлейн, Джералин М. (2014), Элементарная геометрия для студентов колледжей (6-е изд.), Cengage Learning , стр. 180–181, ISBN 9781285965901

[nuncius-12] Суай, Хуан Мигель; Тейра, Дэвид (2014), «Воздушные змеи: взлет и падение научного объекта» (PDF) , Нунциус , 29 (2): 439–463, doi : 10.1163/18253911-02902004

[liberman-13] Либерман, Анатолий (2009), Происхождение слов... и как мы их знаем: этимология для всех , Oxford University Press , стр. 17, ISBN 9780195387070

[henrici-14] Хенрици, Олаус (1879), «Элементарная геометрия: конгруэнтные фигуры» , Лонгманс, Грин, с. xiv

[devilliers-role-15] Jump up to: ^а ^б Де Вильерс, Майкл (февраль 1994 г.), «Роль и функция иерархической классификации четырехугольников», For the Learning of Mathematics , 14 (1): 11–18, JSTOR 40248098

[alsina-nelson-16] Jump up to: ^а ^б ^с ^д ^и ^ж ^г ^час Альсина, Клауди; Нельсен, Роджер Б. (2020), «Раздел 3.4: Воздушные змеи» , Рог изобилия четырехугольников , Математические объяснения Дольчиани, том. 55, Провиденс, Род-Айленд: MAA Press и Американское математическое общество, стр. 73–78, ISBN. 978-1-4704-5312-1 , МР 4286138 ; см. также антипараллелограммы, с. 212

[gant-17] Гант, П. (1944), «Заметки о четырехугольниках», The Mathematical Gazette , 28 (278): 29–30, doi : 10.2307/3607362 , JSTOR 3607362 , S2CID 250436895

[josefsson-area-18] Йозефссон, Мартин (2012), «Максимальная площадь бицентрического четырехугольника» (PDF) , Forum Geometricorum , 12 : 237–241, MR 2990945

[ball-19] Болл, Д.Г. (1973), «Обобщение $\pi$ ", The Mathematical Gazette , 57 (402): 298–303, doi : 10.2307/3616052 , JSTOR 3616052 , S2CID 125396664

[griffiths-culpin-20] Гриффитс, Дэвид; Калпин, Дэвид (1975), «Пи-оптимальные многоугольники», The Mathematical Gazette , 59 (409): 165–175, doi : 10.2307/3617699 , JSTOR 3617699 , S2CID 126325288

[audet-hansen-svrtan-21] Одет, Чарльз; Хансен, Пьер; Свртан, Драгутин (2021), «Использование символических вычислений для определения крупнейших маленьких многоугольников», Journal of Global Optimization , 81 (1): 261–268, doi : 10.1007/s10898-020-00908-w , MR 4299185 , S2CID 203042405

[darling-22] Дарлинг, Дэвид (2004), Универсальная книга по математике: от абракадабры до парадоксов Зенона , John Wiley & Sons , стр. 260, ISBN 9780471667001

[kirby-umble-23] Кирби, Мэтью; Умбл, Рональд (2011), «Тесселяции края и складывание штампов», Mathematic Magazine , 84 (4): 283–289, Arxiv : 0908.3257 , doi : , S2CID 123579388888888, MR 2843659, S2CID 123577888888888, г -н 2843659, S2CID 123579388888888 10.4169/math.mag.84.4.283 , MR 2843659 , MR 2843659, S2CID 12357938888888, MR 2843659 , S2CID 1235778888888 .

[smkg-24] Смит, Дэвид; Майерс, Джозеф Сэмюэл; Каплан, Крейг С.; Гудман-Штраус, Хаим (март 2023 г.), Апериодический монотиль , arXiv : 2303.10798

[eves-25] Ивс, Ховард Уитли (1995), Геометрия колледжа , Jones & Bartlett Learning , стр. 245, ISBN 9780867204759

[crux-26] «OC506» (PDF) , Olympiad Corner Solutions, Crux Mathematicorum , 47 (5): 241, май 2021 г.

[wheeler-27] Уилер, Роджер Ф. (1958), «Четырехугольники», The Mathematical Gazette , 42 (342): 275–276, doi : 10.2307/3610439 , JSTOR 3610439 , S2CID 250434576

[josefsson-when-28] Jump up to: ^а ^б ^с Йозефссон, Мартин (2011), «Когда касательный четырехугольник становится воздушным змеем?» (PDF) , Forum Geometricorum , 11 : 165–174.

[robertson-29] Робертсон, С.А. (1977), «Классификация треугольников и четырехугольников», The Mathematical Gazette , 61 (415): 38–49, doi : 10.2307/3617441 , JSTOR 3617441 , S2CID 125355481

[kasimitis-stein-30] Касиматис, Элейн А .; Штейн, Шерман К. (декабрь 1990 г.), «Равноразрезание многоугольников», Discrete Mathematics , 85 (3): 281–294, doi : 10.1016/0012-365X(90)90384-T , MR 1081836 , Zbl 0736.05028

[jepsen-sedberry-hoyer-31] Джепсен, Чарльз Х.; Седберри, Тревор; Хойер, Рольф (2009), «Равнорассечение четырехугольников в форме воздушного змея» (PDF) , Involve: A Journal of Mathematics , 2 (1): 89–93, doi : 10.2140/involve.2009.2.89 , MR 2501347

[bern-eppstein-32] Берн, Маршалл; Эппштейн, Дэвид (2000), «Четырехсторонняя сетка путем упаковки кругов», Международный журнал вычислительной геометрии и приложений , 10 (4): 347–360, arXiv : cs.CG/9908016 , doi : 10.1142/S0218195900000206 , MR 1791192 , S2CID 12228995

[schattschneider-33] Шатшнайдер, Дорис (1993), «Очарование плитки» , в Эммер, Мишель (редактор), «Визуальный разум: искусство и математика» , серия книг Леонардо, Кембридж, Массачусетс: MIT Press , стр. 157–164, ISBN 0-262-05048-Х , МР 1255846

[fathauer-34] Фатауэр, Роберт (2018), «Искусство и развлекательная математика, основанная на розетках из воздушных змеев» , в Торренсе, Ева ; Торренс, Брюс; Секин, Карло ; Фенивеси, Кристоф (ред.), Proceedings of Bridges 2018: Mathematics, Art, Music, Architecture, Education, Culture , Phoenix, Arizona: Tessellations Publishing, стр. 15–22, ISBN 978-1-938664-27-4

[chazelle-karntikoon-zheng-35] Шазель, Бернар ; Карнтикун, Криткорн; Чжэн, Юфэй (2022), «Геометрический подход к неупругому разрушению», Журнал вычислительной геометрии , 13 (1): 197–203, doi : 10.20382/jocg.v13i1a7 , MR 4414332

[grunbaum-36] Jump up to: ^а ^б Грюнбаум, Б. (1960), «О многогранниках в $E^{3}$ иметь все лица конгруэнтными», Бюллетень Исследовательского совета Израиля , 8F : 215–218 (1960), MR 0125489.

[sakano-akama-37] Закхей, Иуда; Акама, Йоджи (2015), «Анизоэдрические сферические треугольники и классификация сферических мозаик с помощью конгруэнтных воздушных змеев, дротиков и ромбов» , Hiroshima Mathematical Journal , 45 (3):309–339, doi : 10.32917/hmj/1448323768 , MR 3429167 , S2CID 123859584

[dunham-lindgren-witte-38] Данэм, Дуглас; Линдгрен, Джон; Витте, Дэйв (1981), «Создание повторяющихся гиперболических паттернов», Грин, Дуг; Люсидо, Тони; Фукс, Генри (ред.), Труды 8-й ежегодной конференции по компьютерной графике и интерактивным технологиям, SIGGRAPH 1981, Даллас, Техас, США, 3–7 августа 1981 г. , Ассоциация вычислительной техники , стр. 215–223, doi : 10.1145/800224.806808 , S2CID 2255628

[schwartz-unbounded-39] Шварц, Ричард Эван (2007), «Неограниченные орбиты для внешнего биллиарда, I», Journal of Modern Dynamics , 1 (3): 371–424, arXiv : math/0702073 , doi : 10.3934/jmd.2007.1.371 , MR 2318496 , S2CID 119146537

[schwartz-monograph-40] Шварц, Ричард Эван (2009), Внешний бильярд на воздушных змеях , Анналы математических исследований, том. 171, Принстон, Нью-Джерси: Princeton University Press , номер номера : 10.1515/9781400831975 , ISBN. 978-0-691-14249-4 , МР 2562898

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]