Рейтинговые пары
| Из «Политика и экономика». серии |
| Избирательные системы |
|---|
 |
Ранговые пары ( RP ) — это турнирная система ранжированного голосования, впервые предложенная Николаусом Тайдманом в 1987 году. [1] [2]
Рейтинговые пары начинаются с кругового турнира , в котором сравниваются шансы на победу один на один для каждого кандидата, чтобы найти кандидата, предпочитаемого большинством ; если такой кандидат существует, он избирается немедленно. В противном случае, если существует цикл Кондорсе (последовательность типа «камень-ножницы-бумага») A > B > C > A – цикл разрывается путем исключения «самых слабых» выборов в цикле, то есть тех, которые наиболее близки к ничьей. . [3]
Процедура
[ редактировать ]Процедура ранжирования пар следующая:
- Рассмотрите каждую пару кандидатов по круговой системе и рассчитайте парный перевес в победе для каждого в матче один на один.
- Отсортируйте пары по ( абсолютному ) перевесу в порядке от наибольшего к наименьшему.
- Просматривая список, проверьте, не создаст ли добавление каждого совпадения цикл . Если да, то вычеркните выборы; это будут выборы в цикле с наименьшим перевесом в победу (почти равные шансы). [примечание 1]
В конце этой процедуры все циклы будут исключены, и останется единственный победитель, который выиграет каждый матч один на один (который не был вычеркнут). Отсутствие циклов означает, что кандидатов можно ранжировать непосредственно на основе оставшихся матчей.
Пример
[ редактировать ]Ситуация
[ редактировать ]Предположим, что в Теннесси проводятся выборы по вопросу о местонахождении своей столицы . Население сосредоточено вокруг четырех крупных городов. Все избиратели хотят, чтобы столица была как можно ближе к ним. Возможные варианты:
- Мемфис , крупнейший город, но далекий от остальных (42% избирателей)
- Нэшвилл , недалеко от центра штата (26% избирателей)
- Чаттануга , немного восточнее (15% избирателей)
- Ноксвилл , далеко на северо-востоке (17% избирателей)
Предпочтения избирателей каждого региона таковы:
| 42% избирателей Дальний Запад | 26% избирателей Центр | 15% избирателей Центр-Восток | 17% избирателей Дальний Восток |
|---|---|---|---|
|
|
|
|
Результаты сведены в следующую таблицу:
А Б | Мемфис | Нэшвилл | Чаттануга | Ноксвилл |
| Мемфис | [А] 58% [Б] 42% | [А] 58% [Б] 42% | [А] 58% [Б] 42% | |
| Нэшвилл | [А] 42% [Б] 58% | [А] 32% [Б] 68% | [А] 32% [Б] 68% | |
| Чаттануга | [А] 42% [Б] 58% | [А] 68% [Б] 32% | [А] 17% [Б] 83% | |
| Ноксвилл | [А] 42% [Б] 58% | [А] 68% [Б] 32% | [А] 83% [Б] 17% |
- [A] обозначает избирателей, которые предпочли кандидата, указанного в заголовке столбца, кандидату, указанному в заголовке строки.
- [B] обозначает избирателей, которые предпочли кандидата, указанного в заголовке строки, кандидату, указанному в заголовке столбца.
Талли
[ редактировать ]Сначала перечислите каждую пару и определите победителя:
| Пара | Победитель |
|---|---|
| Мемфис (42%) против Нэшвилла (58%) | Нэшвилл 58% |
| Мемфис (42%) против Чаттануги (58%) | Чаттануга 58% |
| Мемфис (42%) против Ноксвилла (58%) | Ноксвилл 58% |
| Нэшвилл (68%) против Чаттануги (32%) | Нэшвилл 68% |
| Нэшвилл (68%) против Ноксвилла (32%) | Нэшвилл 68% |
| Чаттануга (83%) против Ноксвилла (17%) | Чаттануга: 83% |
Затем голоса сортируются. Наибольшее большинство - это «Чаттануга над Ноксвиллем»; 83% избирателей предпочитают Чаттанугу. Таким образом, пары сверху будут отсортированы следующим образом:
| Пара | Победитель |
|---|---|
| Чаттануга (83%) против Ноксвилла (17%) | Чаттануга 83% |
| Нэшвилл (68%) против Ноксвилла (32%) | Нэшвилл 68% |
| Нэшвилл (68%) против Чаттануги (32%) | Нэшвилл 68% |
| Мемфис (42%) против Нэшвилла (58%) | Нэшвилл 58% |
| Мемфис (42%) против Чаттануги (58%) | Чаттануга 58% |
| Мемфис (42%) против Ноксвилла (58%) | Ноксвилл 58% |
Замок
[ редактировать ]Затем пары фиксируются по порядку, пропуская любые пары, которые могут создать цикл:
- Блокировка Чаттануги над Ноксвиллем.
- Зафиксируйте Нэшвилл над Ноксвиллом.
- Зафиксируйте Нэшвилл над Чаттанугой.
- Зафиксируйте Нэшвилл над Мемфисом.
- Блокировка Чаттануги над Мемфисом.
- Зафиксируйте Ноксвилл над Мемфисом.
В этом случае ни одна из пар не создает циклов, поэтому каждая из них заблокирована.
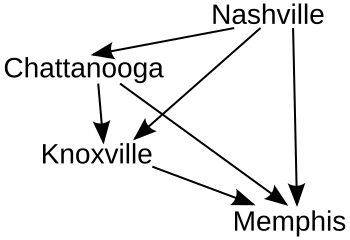
Каждая «фиксация» добавляла к графику еще одну стрелку, показывающую отношения между кандидатами. Вот окончательный график (где стрелки указывают в сторону от победителя).
В этом примере Нэшвилл является победителем при использовании процедуры ранжированных пар. За Нэшвиллом следуют Чаттануга, Ноксвилл и Мемфис, занявшие второе, третье и четвертое места соответственно.
Краткое содержание
[ редактировать ]В примере выборов победителем является Нэшвилл. Это справедливо для любого метода Кондорсе .
При системе «первым прошедшим большинство» и некоторых других системах Мемфис выиграл бы выборы, набрав наибольшее количество людей, даже несмотря на то, что Нэшвилл сразу выиграл все смоделированные парные выборы. Использование мгновенного второго тура голосования в этом примере приведет к победе Ноксвилла, хотя больше людей предпочитают Нэшвилл Ноксвиллу.
Критерии
[ редактировать ]Из формальных критериев голосования метод ранжированных пар проходит критерий большинства , критерий монотонности , критерий Смита (который подразумевает критерий Кондорсе ), критерий проигравшего Кондорсе и критерий независимости клонов . Ранжированные пары не соответствуют критерию согласованности и критерию участия . Хотя ранжированные пары не являются полностью независимыми от нерелевантных альтернатив , они по-прежнему удовлетворяют локальной независимости от нерелевантных альтернатив. [ сломанный якорь ] и независимость альтернатив, в которых доминирует Смит , что означает, что он, вероятно, примерно удовлетворит IIA «на практике».
Независимость нерелевантных альтернатив
[ редактировать ]Ранжированные пары не обладают независимостью от нерелевантных альтернатив , как и все другие ранжированные системы голосования . Однако этот метод придерживается менее строгого свойства, иногда называемого независимостью альтернатив, в которых доминирует Смит (ISDA). В нем говорится, что если один кандидат (X) выиграет выборы и будет добавлена новая альтернатива (Y), X выиграет выборы, если Y не входит в набор Смита . ISDA подразумевает критерий Кондорсе.
Сравнительная таблица
[ редактировать ]В следующей таблице сравниваются ранжированные пары с другими методами выборов с одним победителем:
Примечания
[ редактировать ]- ^ Вместо того, чтобы вычеркивать близкие к ничьей, шаг 3 иногда описывается как движение вниз по списку и подтверждение («фиксация») крупнейших побед, которые не создают цикл, с последующим игнорированием любых побед, которые не зафиксированы.
Ссылки
[ редактировать ]- ^ Тайдман, Теннесси (1 сентября 1987 г.). «Независимость клонов как критерий правил голосования» . Социальный выбор и благосостояние . 4 (3): 185–206. дои : 10.1007/BF00433944 . ISSN 1432-217X . S2CID 122758840 .
- ^ Шульце, Маркус (октябрь 2003 г.). «Новый монотонный и независимый от клонов метод выборов с одним победителем» . Голосование имеет значение (www.votingmatters.org.uk) . 17 . Макдугалл Траст. Архивировано из оригинала 11 июля 2020 г. Проверено 2 февраля 2021 г.
- ^ Мангер, Чарльз Т. (2022). «Лучший метод выборов, совместимый с Кондорсе: ранжированные пары» . Конституционная политическая экономия . 34 (3): 434–444. дои : 10.1007/s10602-022-09382-w .
Внешние ссылки
[ редактировать ]- Описания методов ранжированного голосования Роба ЛеГранда
- Пример реализации JS от Асафа Хаддада
- Парный рейтинг рубинового камня от Бала Паранджа
- PHP-реализация ранговых пар Tideman на основе маржи
- Реализация ранговых пар в Rust от Кори Диксона