Сравнение избирательных систем

Основная ветвь теории социального выбора посвящена сравнению избирательных систем , иначе известных как функции социального выбора . С точки зрения политологии , избирательные системы — это правила проведения выборов и определения победителей по поданным бюллетеням. С точки зрения экономики , математики и философии , функция социального выбора — это математическая функция , которая определяет, как общество должно делать выбор, учитывая совокупность индивидуальных предпочтений.

В данной статье рассматриваются методы и результаты сравнения различных систем. Существует два основных способа сравнения систем голосования:

Показатели удовлетворенности избирателей, полученные с помощью моделирования или опроса.
Соблюдение логических критериев .

Оценка по метрикам

Модели избирательного процесса

Методы голосования можно оценить путем измерения их точности при случайных смоделированных выборах, стремясь обеспечить соответствие свойствам выборов в реальной жизни. Первая такая оценка была проведена Чемберлином и Коэном в 1978 году, которые измерили частоту, с которой некоторые системы, не относящиеся к Кондорсе, избирали победителей Кондорсе. ^[1]

Модель жюри Кондорсе

Маркиз де Кондорсе рассматривал выборы как аналог голосования присяжных, где каждый член выражает независимое суждение о качестве кандидатов. Кандидаты различаются по объективным достоинствам, но избиратели имеют неполную информацию об относительных достоинствах кандидатов. Такие модели присяжных иногда называют валентными моделями . Кондорсе и его современник Лаплас продемонстрировали, что в такой модели теорию голосования можно свести к вероятности путем определения ожидаемого качества каждого кандидата. ^[2]

Модель жюри подразумевает несколько естественных концепций точности систем голосования в рамках разных моделей:

Если в оценках избирателей есть ошибки, соответствующие нормальному распределению , идеальной процедурой является голосование по баллам .
Если доступна только информация о рейтинге и избирателей намного больше, чем кандидатов, любой метод Кондорсе приведет к одному победителю Кондорсе, который будет иметь наибольшую вероятность стать лучшим кандидатом. ^[3]

Однако модель Кондорсе основана на чрезвычайно сильном предположении о независимых ошибках , т.е. избиратели не будут систематически предвзяты в пользу той или иной группы кандидатов. Обычно это нереально: избиратели склонны общаться друг с другом, формировать партии или политические идеологии и совершать другие действия, которые могут привести к коррелирующим ошибкам .

Пространственная модель Блэка

Дункан Блэк предложил одномерную пространственную модель голосования в 1948 году, рассматривая выборы как идеологически мотивированные. ^[4] Его идеи позже были расширены Энтони Даунсом. ^[5] Мнения избирателей рассматриваются как позиции в пространстве одного или нескольких измерений; кандидаты занимают должности в одной и той же сфере; а избиратели выбирают кандидатов в порядке близости (измеренной по евклидову расстоянию или какой-либо другой метрике).

Пространственные модели предполагают другое представление о достоинстве избирательных систем: чем более приемлемым может быть победивший кандидат в качестве параметра местоположения для распределения избирателей, тем лучше система. Политический спектр — это одномерная пространственная модель.

Нейтральные модели

Модели нейтрального голосования пытаются минимизировать количество параметров и, как пример принципа «ничего в рукаве» . Наиболее распространенной такой моделью является модель беспристрастной анонимной культуры (или модель Дирихле ). Эти модели предполагают, что избиратели назначают каждому кандидату полезность совершенно случайно (из равномерного распределения ).

Сравнение моделей

Тайдман и Плассманн провели исследование, которое показало, что двумерная пространственная модель дает разумное соответствие сокращению на 3 кандидата большого набора электоральных рейтингов. Модели жюри, нейтральные модели и одномерные пространственные модели оказались неадекватными. ^[6] Они изучили циклы Кондорсе в предпочтениях избирателей (примером которых является то, что большинство избирателей предпочитают A перед B, B перед C и C перед A) и обнаружили, что их количество соответствует эффектам малой выборки, и пришли к выводу, что «Циклы голосования будут происходить очень редко, если вообще возникнут, на выборах с большим количеством избирателей». Актуальность размера выборки ранее изучалась Гордоном Таллоком , который наглядно доказал, что, хотя ограниченный электорат будет склонен к циклам, область, в которой кандидаты могут вызвать цикличность, сокращается по мере увеличения числа избирателей. ^[7]

Утилитарные модели

Утилитарная модель рассматривает избирателей как кандидатов , ранжирующих их по степени полезности. Законным победителем в этой модели является кандидат, который максимизирует общую социальную полезность. Утилитарная модель отличается от пространственной модели по нескольким важным параметрам:

Это требует дополнительного предположения, что избиратели мотивированы исключительно осознанными личными интересами, без какого-либо идеологического пятна в их предпочтениях.
Это требует замены метрики расстояния пространственной модели точной мерой полезности.
Следовательно, этот показатель должен будет различаться для разных избирателей. Часто случается, что на одну группу избирателей сильно повлияет выбор между двумя кандидатами, в то время как на другую группу мало что поставлено; тогда метрика должна быть сильно асимметричной.

Из последнего свойства следует, что ни одна система голосования, которая дает равное влияние всем избирателям, скорее всего, не достигнет максимальной социальной полезности. Крайние случаи конфликта между требованиями утилитаризма и демократии называются « тиранией большинства ». См. комментарии Ласлиера, Мерлина и Нурми в рецензии Ласлиера. ^[8]

Джеймс Милль , кажется, был первым, кто заявил о существовании априорной связи между демократией и утилитаризмом – см. статью в Стэнфордской энциклопедии. ^[9]

Сравнения по модели жюри

Предположим, что я ^й кандидат на выборах имеет заслуги x _i (можно считать, что x _i ~ N (0,σ ²) ^[10]), и что уровень одобрения избирателем j кандидата i может быть записан как x _i + ε _ij (мы будем предполагать, что ε _ij равны iid. N (0,τ ²)). Мы предполагаем, что избиратель ранжирует кандидатов в порядке убывания одобрения. Мы можем интерпретировать ε _ij как ошибку в оценке избирателем j кандидата i и рассматривать метод голосования как задачу поиска кандидата с наибольшими достоинствами.

Каждый избиратель будет оценивать лучшего из двух кандидатов выше, чем менее хорошего с определенной вероятностью p (которая в рамках изложенной здесь нормальной модели равна ${\tfrac {1}{2}}\!+\!{\tfrac {1}{\pi }}{\textrm {tan}}^{-1}{\tfrac {\sigma }{\tau }}$ , что можно подтвердить из стандартной формулы для гауссовских интегралов по квадранту ^{[ нужна ссылка ]}). Теорема присяжных Кондорсе показывает, что до тех пор, пока p > 1 ⁄ 2 , большинство голосов жюри будет лучшим показателем относительных достоинств двух кандидатов, чем мнение любого отдельного члена.

Пейтон Янг показал, что к голосам между произвольным числом кандидатов применимы еще три свойства, предполагая, что Кондорсе знал о первом и третьем из них. ^[11]

Если p близко к 1 ⁄ 2 , то победителем Борда является оценщик максимального правдоподобия лучшего кандидата.
если p близко к 1, то победителем Minimax является оценка максимального правдоподобия лучшего кандидата.
Для любого p рейтинг Кемени-Янга является оценкой максимального правдоподобия истинного порядка достоинств.

Роберт Ф. Бордли построил «утилитарную» модель, которая представляет собой небольшой вариант модели присяжных Кондорсе. ^[12] Он рассматривал задачу метода голосования как задачу поиска кандидата, который имеет наибольшее общее одобрение со стороны избирателей, т.е. наибольшую сумму уровней одобрения отдельных избирателей. Эта модель имеет смысл даже при σ ² = 0, и в этом случае p принимает значение ${\tfrac {1}{2}}\!+\!{\tfrac {1}{\pi }}{\textrm {tan}}^{-1}{\tfrac {1}{n-1}}$ где n – количество избирателей. Он провел оценку по этой модели и, как и ожидалось, обнаружил, что подсчет Борда был наиболее точным.

Имитация выборов в рамках пространственных моделей

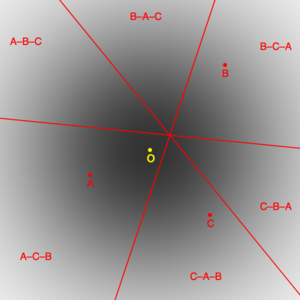
Моделирование выборов в двух измерениях — A simulated election in two dimensions

Симулированные выборы могут быть построены на основе распределения избирателей в подходящем пространстве. На рисунке показаны избиратели, удовлетворяющие двумерному распределению Гаусса с центром в O. Есть 3 случайно сгенерированных кандидата: A, B и C. Пространство разделено на 6 сегментов 3 линиями, причем избиратели в каждом сегменте имеют одинаковые предпочтения кандидатов. Доля избирателей, выбирающих кандидатов каким-либо образом, определяется интегралом распределения избирателей по соответствующему сегменту.

Пропорции, соответствующие шести возможным порядкам кандидатов, определяют результаты, полученные при различных системах голосования. Считается, что те, кто избирает лучшего кандидата, то есть кандидата, ближайшего к О (в данном случае А), дали правильный результат, а те, кто выбирает кого-то другого, показали ошибку. Анализируя результаты для большого числа случайно сгенерированных кандидатов, можно измерить эмпирические свойства систем голосования.

Описанный здесь протокол оценки создан по образцу протокола, описанного Тайдеманом и Плассманном. ^[6]Оценки этого типа наиболее распространены для избирательных систем с одним победителем. Системы ранжированного голосования наиболее естественно вписываются в эту структуру, но другие типы голосования (такие как FPTP и одобрительное голосование ) могут быть реализованы с меньшими или большими усилиями.

Протокол оценки может варьироваться по-разному:

Число избирателей можно сделать конечным и варьировать по размеру. На практике это почти всегда делается в многомерных моделях, при этом избиратели отбираются по их распределению, а результаты для больших электоратов используются для демонстрации ограничивающего поведения.
Количество кандидатов может быть разным.
Распределение избирателей могло быть различным; например, можно изучить влияние асимметричного распределения. Небольшое отклонение от нормальности вызвано эффектами случайной выборки, когда число избирателей конечно. Более систематические отклонения (по-видимому, принимающие форму модели гауссовой смеси ) были исследованы Джеймсоном Куинном в 2017 году. ^[13]

Оценка точности

м метод	3	6	10	15	25	40
ФПТП	70.6	35.5	21.1	14.5	9.3	6.4
АВ/ИРВ	85.2	50.1	31.5	21.6	12.9	7.9
Край	87.6	82.1	74.2	67.0	58.3	50.1
Кондорсе	100.0	100.0	100.0	100.0	100.0	100.0

Одним из основных применений оценок является сравнение точности систем голосования, когда избиратели голосуют искренне. Если бесконечное число избирателей удовлетворяет распределению Гаусса, то законным победителем выборов можно считать кандидата, наиболее близкого к среднему/медиане, а точность метода можно определить по доле выборов, на которых законный победитель выборов победитель выбран. Теорема о медианном избирателе гарантирует, что все системы Кондорсе дадут 100% точность (то же самое относится и к методу Кумбса). ^[14]).

В оценках, опубликованных в исследовательских статьях, используются многомерные гауссианы, что затрудняет численные расчеты. ^[1]^[15]^[16]^[17] Число избирателей остается ограниченным, а число кандидатов обязательно невелико.

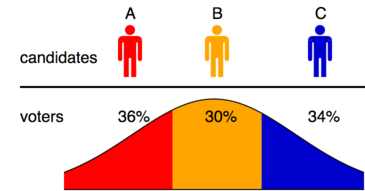
B выбывает в первом раунде IRV. — B is eliminated in the first round under IRV

Вычисления гораздо проще в одном измерении, что допускает бесконечное количество избирателей и произвольное количество m кандидатов. Результаты для этого простого случая показаны в первой таблице, которая напрямую сопоставима с таблицей 5 (1000 избирателей, средняя дисперсия) цитируемой статьи Чемберлина и Коэна. единственный метод Кондорсе ( Минимакс Кандидаты были выбраны случайным образом из распределения избирателей, и в испытания для подтверждения был включен ).

м метод	10
ФПТП	0.166
АВ/ИРВ	0.058
Край	0.016
Кондорсе	0.010

Относительно низкие результаты альтернативного голосования (IRV) объясняются хорошо известным и распространенным источником ошибок, показанным на диаграмме, на которой выборы удовлетворяют одномерной пространственной модели, а законный победитель B будет исключен в первом туре. Подобная проблема существует во всех измерениях.

Альтернативной мерой точности является среднее расстояние избирателей от победителя (где меньше означает лучше). Это вряд ли изменит рейтинг методов голосования, но его предпочитают люди, которые интерпретируют расстояние как бесполезность. Во второй таблице показано среднее расстояние (в стандартных отклонениях) минус ${\sqrt {\tfrac {2}{\pi }}}$ (что представляет собой среднее расстояние переменной от центра стандартного распределения Гаусса) для 10 кандидатов в рамках одной и той же модели.

Оценка устойчивости к тактическому голосованию

Джеймс Грин-Армитаж и др. опубликовали исследование, в котором оценили уязвимость нескольких систем голосования к манипуляциям со стороны избирателей. ^[18] Они мало говорят о том, как адаптировали свою оценку для этой цели, просто упоминая, что она «требует творческого программирования». Более ранняя статья первого автора дает немного больше подробностей. ^[19]

Число кандидатов на смоделированных выборах было ограничено тремя. Это устраняет различие между определенными системами; например, метод Блэка и метод Дасгупта-Маскина эквивалентны для трех кандидатов.

Выводы исследования трудно обобщить, но подсчет Борда показал плохие результаты; Минимакс был несколько уязвим; и IRV был очень устойчивым. Авторы показали, что ограничение любого метода выборами без победителя Кондорсе (выбор победителя Кондорсе, когда он есть) никогда не увеличит его восприимчивость к тактическому голосованию . Они сообщили, что система «Кондорсе-Хара», которая использует IRV в качестве тай-брейка для выборов, не решенных по критерию Кондорсе, была столь же устойчива к тактическому голосованию, как и IRV сама по себе, и более точна. Кондорсе-Хара эквивалентен методу Коупленда с тай-брейком IRV на выборах с тремя кандидатами.

Оценка эффекта распределения кандидатов

х м	0	0.25	0.5	1	1.5
3	87.6	87.9	88.9	93.0	97.4
6	82.1	80.2	76.2	71.9	79.9
10	74.1	70.1	61.2	47.6	54.1
15	66.9	60.6	46.4	26.6	30.8
25	58.3	47.0	26.3	8.1	10.1
40	50.2	33.3	11.3	1.5	2.1

Некоторые системы, в частности система подсчета голосов в Борде, уязвимы, когда распределение кандидатов смещается относительно распределения избирателей. В прилагаемой таблице показана точность подсчета Борда (в процентах), когда бесконечная совокупность избирателей удовлетворяет одномерному распределению Гаусса, а m кандидатов выбираются из аналогичного распределения, смещенного на x стандартных распределений. Красным цветом обозначены цифры, которые хуже случайных. Напомним, что все методы Кондорсе дают 100% точность решения этой задачи. (И обратите внимание, что снижение точности по мере увеличения x не наблюдается, когда есть только три кандидата.)

Чувствительность к распределению кандидатов можно рассматривать либо как вопрос точности, либо как вопрос устойчивости к манипуляциям. Если ожидать, что в ходе событий кандидаты естественным образом будут принадлежать к тому же распределению, что и избиратели, то любое перемещение будет рассматриваться как попытка подрывной деятельности; но если кто-то думает, что факторы, определяющие жизнеспособность кандидата (например, финансовая поддержка), могут быть коррелированы с идеологической позицией, то он будет рассматривать это более с точки зрения точности.

Опубликованные оценки отражают различные взгляды на распределение кандидатов. Некоторые просто предполагают, что кандидаты принадлежат к тому же распределению, что и избиратели. ^[16]^[18] Некоторые старые газеты предполагают равные средства, но допускают, чтобы распределение кандидатов было более или менее плотным, чем распределение избирателей. ^[20]^[1] В статье Тайдмана и Плассмана аппроксимируется взаимосвязь между распределением кандидатов и избирателей на основе эмпирических измерений. ^[15] Это менее реалистично, чем может показаться, поскольку не допускает возможности корректировки распределения кандидатов с целью использования любой слабости в системе голосования. В статье Джеймса Грин-Армитажа распределение кандидатов рассматривается как отдельная проблема, рассматривая его как форму манипуляции и измеряя эффекты стратегического входа и выхода. Неудивительно, что он считает, что граф Борда особенно уязвим. ^[19]

Оценка других объектов недвижимости

Как упоминалось ранее, Чемберлин и Коэн измерили частоту, с которой определенные системы, не относящиеся к Кондорсе, выбирают победителей Кондорсе. В пространственной модели с равным распределением избирателей и кандидатов частоты составляют 99% ( Кумбс ), 86% (Борда), 60% (IRV) и 33% (FPTP). ^[1] Иногда это называют эффективностью Кондорсе .
Дарлингтон измерил частоту, с которой метод Коупленда дает единственного победителя на выборах без победителя Кондорсе. Он обнаружил, что для полей до 10 кандидатов этот показатель составляет менее 50%. ^[17]

Экспериментальные метрики

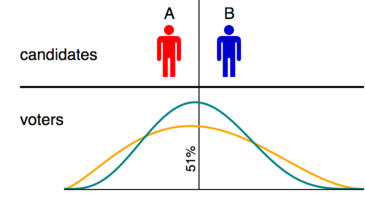
Две выборы с одними и теми же кандидатами — Two elections with the same candidates

Задача системы голосования в рамках пространственной модели — выявить кандидата, позиция которого наиболее точно отражает распределение мнений избирателей. Это означает выбор параметра местоположения для распределения из множества альтернатив, предложенных кандидатами. Параметры местоположения могут основываться на среднем значении, медиане или моде; но поскольку ранжированные бюллетени о предпочтениях предоставляют только порядковую информацию, медиана является единственной приемлемой статистикой.

Это видно из диаграммы, которая иллюстрирует два смоделированных выборов с одними и теми же кандидатами, но с разным распределением избирателей. В обоих случаях средняя точка между кандидатами составляет 51-й процентиль распределения избирателей; следовательно, 51% избирателей предпочитают A, а 49% предпочитают B. Если мы считаем метод голосования правильным, если он избирает кандидата, наиболее близкого к медиане числа избирателей, то, поскольку медиана обязательно находится немного левее 51% линии, метод голосования будет считаться правильным, если в каждом случае он выберет вариант А.

Среднее значение бирюзового распределения также находится немного левее линии 51%, а среднее значение оранжевого распределения — немного правее. Следовательно, если мы считаем метод голосования правильным, если он выбирает кандидата, наиболее близкого к среднему числу избирателей, тогда метод не сможет получить полные оценки, если он не выявит разных победителей из одних и тех же бюллетеней на двух выборах. Очевидно, что это приведет к ложным ошибкам в методах голосования. Та же проблема возникнет и для любой кардинальной меры местоположения; только медиана дает последовательные результаты.

Медиана не определена для многомерных распределений, но одномерная медиана обладает свойством, которое удобно обобщать. Медиана распределения — это положение, среднее расстояние которого от всех точек распределения наименьшее. Это определение обобщается на геометрическую медиану в нескольких измерениях. избирателя Расстояние часто определяют как функцию бесполезности .

Если у нас есть набор кандидатов и совокупность избирателей, то нет необходимости решать сложную в вычислительном отношении задачу нахождения геометрической медианы избирателей, а затем идентифицировать ближайшего к ней кандидата; вместо этого мы можем определить кандидата, чья средняя дистанция от избирателей минимальна. Это показатель, который обычно используется начиная с Merrill; ^[20] см. также Грин-Армитаж и Дарлингтон. ^[19]^[16]

Кандидата, наиболее близкого к геометрическому медианному распределению избирателей, можно назвать «пространственным победителем».

Оценка реальными выборами

Данные реальных выборов можно проанализировать для сравнения эффектов различных систем либо путем сравнения между странами, либо путем применения альтернативных избирательных систем к реальным данным выборов. Результаты выборов можно сравнить с помощью индексов демократии , показателей политической фрагментации , явки избирателей , ^[21]^[22] политическая эффективность и различные экономические и юридические показатели. Практические критерии оценки реальных выборов включают долю потерянных голосов , сложность подсчета голосов , пропорциональность и барьеры для входа новых политических движений. ^[23] Дополнительные возможности для сравнения реальных выборов возникают благодаря избирательным реформам .

Канадский пример такой возможности можно увидеть в городе Эдмонтон (Канада), который перешел от голосования первым прошедшим на всеобщих выборах в Альберте 1917 года из пяти членов к голосованию блоком плюралистического большинства на всеобщих выборах в мандатному голосованию на всеобщих выборах в Альберте 1921 года Альберте 1921 года , а затем к пяти- . член с одним передаваемым голосованием на всеобщих выборах в Альберте 1926 года , затем снова в FPTP на всеобщих выборах в Альберте 1959 года . Одна партия получила все места в Эдмонтоне в 1917, 1921 и 1959 годах. Под STV в 1926 году были избраны два консерватора, один либерал, один лейборист и один United Farmers MLA.

Сравнение методов голосования с одним победителем

Логические критерии выборов с одним победителем

Традиционно достоинства различных избирательных систем аргументировались с помощью логических критериев. Они имеют форму правил вывода для избирательных решений, разрешающих вывод, например, что «если E и E ' являются выборами такими, что R ( E , E '), и если A является законным победителем E , то A является законным обладателем премии E '".

Критерии столь же спорны, как и сами системы голосования. Здесь мы кратко обсуждаем соображения, выдвинутые относительно их обоснованности, а затем суммируем наиболее важные критерии, показывая в таблице, какие из основных систем голосования им удовлетворяют.

Критерии результата (абсолютные)

Теперь мы обратимся к самим логическим критериям, начиная с абсолютных критериев, которые гласят, что если набор бюллетеней составлен определенным образом, определенный кандидат должен или не должен победить.

Критерии результата (абсолютные)
Критерий	Описание
Критерий большинства	Всегда ли победит кандидат, которого большинство избирателей считает единственным фаворитом? Этот критерий существует в двух вариантах: Критерий ранжированного большинства , при котором побеждает вариант, который большинство просто предпочитает другим. (Прохождение рейтингового MC отмечено « да » в таблице ниже, поскольку это подразумевает также прохождение следующего:) рейтингового Критерий большинства , при котором побеждать должен только тот вариант, которому однозначно дает высший большинство рейтинг. Ранжированные и рейтинговые MC являются синонимами ранжированных методов голосования, но не рейтинговых или градуированных. Ранжированный MC, но не рейтинговый MC, несовместим с критерием независимости нерелевантных альтернатив, описанным ниже.
Критерий проигравшего большинства	если большинство избирателей предпочитают любого другого кандидата данному кандидату, то разве этот кандидат не победит?
Критерий взаимного большинства	Всегда ли победивший кандидат будет принадлежать к группе кандидатов, которых большинство избирателей оценивает выше всех остальных?
Критерий победителя Кондорсе	Если кандидат побеждает любого другого кандидата в личных встречах, всегда ли этот кандидат победит на выборах? (Это подразумевает критерий большинства, описанный выше.)
Критерий проигравшего Кондорсе	Если кандидат проигрывает любому другому кандидату в личных встречах, всегда ли этот кандидат проиграет выборы?

Критерии результата (относительные)

Это критерии, которые гласят, что если определенный кандидат побеждает в одном случае, тот же кандидат должен (или не должен) победить в аналогичном случае.

Критерии результата (относительные)
Критерон	Описание
Независимость альтернатив, в которых доминирует Смит (Смит-IAA)	Неужели результат никогда не изменится, если кандидат, в котором доминирует Смит, будет добавлен или удален, при условии, что голоса в отношении других кандидатов не изменились? Кандидат C является доминируемым по Смиту, если существует какой-то другой кандидат A, такой, что C проигрывает A , и каждый кандидат B , который не проигрывает A и т. д. Обратите внимание, что, хотя этот критерий классифицируется здесь как относительный к номиналу, он имеет сильный абсолютный критерий. компонент исключения кандидатов, в которых доминирует Смит, от победы. Фактически, это подразумевает все вышеперечисленные абсолютные критерии. ^{[ указать ]}
Независимость нерелевантных альтернатив (IIA)	Никогда ли результат не изменится, если проигравший кандидат будет добавлен или удален, при условии, что предпочтения избирателей относительно других кандидатов не изменились? ^[24] Например, правило большинства не соответствует требованиям IIA; добавление кандидата X может привести к смене победителя с W на Y, даже если Y получит не больше голосов, чем раньше.
Местная независимость нерелевантных альтернатив (LIIA)	Неужели результат никогда не изменится, если будет удалена альтернатива, которая финишировала последней? И может ли альтернатива, занявшая второе место, не стать победителем, если победитель будет удален?
Независимость альтернатив клонов (cloneproof)	Никогда ли результат не изменится, если добавить невыигравших кандидатов, похожих на существующего кандидата? Существует три различные ситуации, которые могут привести к тому, что метод не будет соответствовать этому критерию: Спойлеры Кандидаты, которые уменьшают вероятность победы любого из похожих или клонированных кандидатов, также известный как эффект спойлера . Команды Наборы похожих кандидатов, одно лишь присутствие которых увеличивает шансы на победу любого из них. Толпы Дополнительные кандидаты, которые влияют на исход выборов, не помогая и не вредя шансам своей фракционной группы, а вместо этого влияя на другую группу.
Критерий монотонности (монотонный)	Если кандидат W победит в одном наборе бюллетеней, всегда ли W будет побеждать, если эти бюллетени изменятся, чтобы увеличить поддержку W ? Это также означает, что вы не можете добиться победы проигравшего кандидата, уменьшив его поддержку.
Критерий согласованности	Если кандидат W' побеждает в одном наборе бюллетеней, всегда ли W победит, если эти бюллетени изменятся путем добавления другого набора бюллетеней, в котором W также победит?
Критерий участия	Всегда ли честно голосовать лучше, чем вообще не голосовать? (Этот критерий сгруппирован с разными, но схожими критериями согласованности в таблице ниже. ^[25])
Обратная симметрия	Если индивидуальные предпочтения каждого избирателя перевернуты, неужели первоначальный победитель никогда не победит?

Критерии подсчета голосов

Это критерии, которые относятся к процессу подсчета голосов и определения победителя.

Критерии подсчета голосов
Критерий	Описание
Полиномиальное время	Можно ли вычислить победителя за время выполнения, полиномиальное по числу кандидатов и линейное по числу избирателей?
разрешимый	Можно ли во всех случаях (за исключением точного равенства по подсчету бюллетеней) определить победителя без использования каких-либо случайных процессов, таких как подбрасывание монет? То есть, являются ли точные равенства, при которых победителем может стать один из двух или более кандидатов, исчезающе редкой вещью на крупных выборах?
Суммируемость	Можно ли определить победителя путем подсчета бюллетеней на каждом избирательном участке отдельно и простого сложения индивидуальных результатов? Количество информации, необходимой для таких подсчетов, выражается как функция порядка числа кандидатов N. Медленнорастущие функции, такие как O(N) или O(N ²) облегчают подсчет, в то время как быстрорастущие функции, такие как O(N!), могут затруднить выполнение того же самого.

Критерии стратегии

Это критерии, которые связаны со стимулом избирателя использовать определенные формы стратегии. Их также можно рассматривать как критерии относительного результата; однако, в отличие от критериев этого раздела, эти критерии имеют непосредственное отношение к избирателям; тот факт, что метод соответствует этим критериям, может упростить процесс определения оптимального стратегического голосования.

Критерии стратегии
Критерий	Описание
Критерий отсутствия вреда в дальнейшем	Могут ли избиратели быть уверены, что добавление более низкого предпочтения в избирательный бюллетень не повредит какому-либо более предпочтительному кандидату, уже включенному в список?
критерий отсутствия помощи позже	Могут ли избиратели быть уверены, что добавление более низкого предпочтения в избирательный бюллетень не поможет любому более предпочтительному кандидату, уже включенному в список? ^[26]
Нет любимого критерия предательства	Могут ли избиратели быть уверены, что им не нужно поддерживать какого-либо другого кандидата, превосходящего их фаворита, чтобы получить желаемый результат? ^[27]

Формат голосования

Избирательные бюллетени в целом делятся на две категории: кардинальные и порядковые , где кардинальные бюллетени запрашивают индивидуальные меры поддержки для каждого кандидата, а порядковые бюллетени запрашивают относительные меры поддержки. Некоторые методы не попадают в одну категорию, например, STAR, который просит избирателя дать независимые оценки каждому кандидату, но для определения победителя использует как абсолютные, так и относительные рейтинги. Сравнение двух методов, основанных только на типе бюллетеня, в основном зависит от предпочтений избирателя, если только тип бюллетеня не связан с одним из других математических критериев, перечисленных здесь.

Относительная сила

Критерий A «сильнее», чем B, если удовлетворение A подразумевает удовлетворение B. Например, критерий Кондорсе сильнее критерия большинства, потому что все победители большинства являются победителями Кондорсе. Таким образом, любой метод голосования, удовлетворяющий критерию Кондорсе, должен удовлетворять и критерию большинства.

Соответствие выбранным методам единственного победителя

В следующей таблице показано, каким из вышеуказанных критериев соответствуют несколько методов с одним победителем. Не все критерии указаны.

Сравнение систем голосования с одним победителем
Критерий Метод	Большинство	Проигравший большинства	Взаимное большинство	Победитель Кондорсе ^{[Тн 1]}	Кондорсе неудачник	Смит ^{[Тн 1]}	Смит-IIA ^{[Тн 1]}	ТАМ / ЛИЯ ^{[Тн 1]}	Cloneproof	Monotone	Участие	Позже без вреда ^{[Тн 1]}	Позже-без помощи ^{[Тн 1]}	Нет любимого предательства ^{[Тн 1]}	бюллетень тип
Антиплюрализм	Нет	Да	Нет	Нет	Нет	Нет	Нет	Нет	Нет	Да	Да	Нет	Нет	Да	Единая отметка
Одобрение	Да	Нет	Нет	Нет	Нет	Нет	Нет	Да ^{[Тн 2]}	Да	Да	Да	Нет	Да	Да	Approvals
Болдуин	Да	Да	Да	Да	Да	Да	Нет	Нет	Нет	Нет	Нет	Нет	Нет	Нет	Ranking
Черный	Да	Да	Нет	Да	Да	Нет	Нет	Нет	Нет	Да	Нет	Нет	Нет	Нет	Ranking
Край	Нет	Да	Нет	Нет	Да	Нет	Нет	Нет	Нет	Да	Да	Нет	Да	Нет	Ranking
Баклин	Да	Да	Да	Нет	Нет	Нет	Нет	Нет	Нет	Да	Нет	Нет	Да	Нет	Ranking
Кумбс	Да	Да	Да	Нет	Да	Нет	Нет	Нет	Нет	Нет	Нет	Нет	Нет	Да	Ranking
Коупленд	Да	Да	Да	Да	Да	Да	Да	Нет	Нет	Да	Нет	Нет	Нет	Нет	Ranking
Доджсон	Да	Нет	Нет	Да	Нет	Нет	Нет	Нет	Нет	Нет	Нет	Нет	Нет	Нет	Ranking
Самая высокая медиана	Да	Да ^{[Тн 3]}	Нет ^{[Тн 4]}	Нет	Нет	Нет	Нет	Да ^{[Тн 2]}	Да	Да	Нет ^{[Тн 5]}	Нет	Да	Да	Результаты
Мгновенный сток	Да	Да	Да	Нет	Да	Нет	Нет	Нет	Да	Нет	Нет	Да	Да	Нет	Ranking
Кемени-Янг	Да	Да	Да	Да	Да	Да	Да	Только ЛИИА	Нет	Да	Нет	Нет	Нет	Нет	Ranking
Минимакс	Да	Нет	Нет	Да ^{[Тн 6]}	Нет	Нет	Нет	Нет	Нет	Да	Нет	Нет ^{[Тн 6]}	Нет	Нет	Ranking
Нансон	Да	Да	Да	Да	Да	Да	Нет	Нет	Нет	Нет	Нет	Нет	Нет	Нет	Ranking
Множество	Да	Нет	Нет	Нет	Нет	Нет	Нет	Нет	Нет	Да	Да	Да	Да	Нет	Единая отметка
Случайное голосование ^{[Тн 7]}	Нет	Нет	Нет	Нет	Нет	Нет	Нет	Да	Да	Да	Да	Да	Да	Да	Единая отметка
Рейтинговые пары	Да	Да	Да	Да	Да	Да	Да	Только ЛИИА	Да	Да	Нет ^{[Тн 5]}	Нет	Нет	Нет	Ranking
Сток	Да	Да	Нет	Нет	Да	Нет	Нет	Нет	Нет	Нет	Нет	Да	Да	Нет	Единая отметка
Шульце	Да	Да	Да	Да	Да	Да	Да	Нет	Да	Да	Нет ^{[Тн 5]}	Нет	Нет	Нет	Ranking
Счет	Нет	Нет	Нет	Нет	Нет	Нет	Нет	Да ^{[Тн 2]}	Да	Да	Да	Нет	Да	Да	Результаты
Жеребьевка ^{[Тн 8]}	Нет	Нет	Нет	Нет	Нет	Нет	Нет	Да	Нет	Да	Да	Да	Да	Да	Никто
ЗВЕЗДА	Нет	Да	Нет	Нет	Да	Нет	Нет	Нет	Нет	Да	Нет	Нет	Нет	Нет	Результаты
Альтернатива Тайдману	Да	Да	Да	Да	Да	Да	Да	Нет	Да	Нет	Нет	Нет	Нет	Нет	Ranking
Примечания к таблице	^ Перейти обратно: ^а ^б ^с ^д ^и ^ж ^г Критерий Кондорсе несовместим с критериями последовательности , участия , «позже без вреда» , «позже без помощи » и искреннего любимца . ^ Перейти обратно: ^а ^б ^с Голосование за одобрение, голосование по баллам и решение большинства удовлетворяют требованиям IIA, если предположить, что избиратели оценивают кандидатов независимо, используя свою собственную абсолютную шкалу . Чтобы это произошло, на некоторых выборах некоторые избиратели должны использовать меньше своих полномочий, несмотря на наличие значимых предпочтений среди жизнеспособных кандидатов. ^ Решение большинства может избрать кандидата, однозначно наименее предпочитаемого более чем половиной избирателей, но никогда не избирает кандидата с однозначно наименьшим рейтингом более чем половиной избирателей. ^ Решение большинства не соответствует критерию взаимного большинства, но удовлетворяет критерию, если большинство ставит взаимно предпочтительный набор выше заданной абсолютной оценки, а все остальные - ниже этой оценки. ^ Перейти обратно: ^а ^б ^с При голосовании по наивысшей медиане, рейтинговых парах и голосовании Шульце для любого избирателя всегда есть получестное голосование без сожалений, при этом все остальные бюллетени остаются неизменными и при условии, что он достаточно знает о том, как будут голосовать другие. В таких обстоятельствах у избирателя всегда есть хотя бы один способ принять участие, не ставя при этом менее предпочтительного кандидата выше более предпочтительного. ^ Перейти обратно: ^а ^б Вариант Минимакса, который учитывает только парную оппозицию, а не оппозицию минус поддержка, не соответствует критерию Кондорсе и соответствует принципу «позже не будет причинен вред». ^ Победитель определяется случайным образом выбранным бюллетенем. Этот и тесно связанные с ним методы представляют математический интерес и включены сюда, чтобы продемонстрировать, что даже необоснованные методы могут соответствовать критериям метода голосования. ^ Если победитель выбирается случайным образом из кандидатов, проводится жеребьевка, чтобы продемонстрировать, что даже методы без голосования могут соответствовать некоторым критериям.

Практические факторы

Высказанные выше опасения используются теоретиками социального выбора для разработки систем, которые являются точными и устойчивыми к манипуляциям. Однако существуют и практические причины, по которым одна система может быть более социально приемлемой, чем другая, и которые подпадают под сферу общественного выбора и политической науки . ^[8]^[16] Важные практические соображения включают в себя:

Легкость объяснения . Некоторые правила голосования трудно объяснить избирателям так, чтобы они могли их интуитивно понять, что может подорвать общественное доверие к выборам. ^[8]^{[ не удалось пройти проверку ]} Например, хотя правило Шульце хорошо работает по многим из приведенных выше критериев, оно требует подробного объяснения путей ударов .
Удобство голосования . Различные виды бюллетеней, возможно, будет легче заполнить; например, исследования обычно показывают, что избиратели обычно считают рейтинговое голосование сложным и запутанным по сравнению с рейтинговым голосованием или множественным голосованием .

Другие соображения включают барьеры для входа в политическую конкуренцию. ^[28] и вероятность того, что правительство зайдет в тупик . ^[29]

Сравнение систем с несколькими победителями

Избирательные системы с несколькими победителями в лучшем случае стремятся создать представительные собрания в более широком смысле, чем принятие тех же решений, которые были бы приняты при голосовании с одним победителем. непропорциональная система, такая как множественное блочное голосование или билетное голосование Они также могут быть направлены на однопартийное перераспределение мест в городе, если используется .

Метрики для оценок с участием нескольких победителей

Оценка эффективности методов голосования с несколькими победителями требует других показателей, чем те, которые используются для систем с одним победителем. Было предложено следующее.

Эффективность комитета Кондорсе (CCE) измеряет вероятность того, что группа избранных победителей победит всех проигравших в парных гонках. ^[30]
Индекс Галлахера и индекс Лусмора-Хэнби (LH) измеряют пропорциональность между долей мест и долей партийных голосов. Галлахер обычно использует общий процент голосов или голосов партий по сравнению с процентом мест для оценки пропорциональности, поэтому игнорирует наличие округов, если таковые имеются.
Потери голосов измеряют долю избирателей, не представленных ни одним представителем.

Таблицы критериев

В следующей таблице показано, каким из вышеуказанных критериев соответствуют несколько методов многократного победителя.

Критерий Метод	Пропорциональный	Monotone	Consistency	Participation	Нет Любимый Предательство	Semihonest	Кандидаты, пользующиеся всеобщим признанием
Последовательное пропорциональное одобрение	Да	Да		Нет	Нет	Нет	Нет
Перевзвешенный диапазон	Да	Да		Нет	Нет	Нет	Нет
Пропорциональное одобрение	Да	Да		Да	Нет	Нет	Нет
Один передаваемый голос	Да	Нет	Нет	Нет	Нет	Нет	Да
CPO-STV	Да	Нет	Нет	Нет	Нет	Нет	Да
Шульце СТВ	Да	Да	Нет	Нет	Нет	Нет	Да
Фрагмены
Система квот Борда
Единый непередаваемый голос	Нет	Да	Да	Да	Нет	Нет	— (не пропорционально)
Ограниченное голосование	Нет	Да	Да	Да	Нет ^[31]	Нет	— (не пропорционально)
кумулятивное голосование	Нет	Да	Да	Да	Нет ^[31]	Нет	— (не пропорционально)
Жеребьевка , произвольный победитель	Нет	Да	Да	Да	Да	Да	— (не пропорционально)

См. также

Ссылки

^ Перейти обратно: ^а ^б ^с ^д Чемберлин, Джон Р.; Коэн, Майкл Д. (декабрь 1978 г.). «На пути к применимой теории социального выбора: сравнение функций социального выбора при предположениях пространственной модели» . Американский обзор политической науки . 72 (4): 1341–1356. дои : 10.2307/1954543 . ISSN 0003-0554 . JSTOR 1954543 . S2CID 155928569 .
^ МЖАН де Карита, маркиз де Кондорсе. Его книга была опубликована в 1785 году. Название можно перевести как «Очерк применения теории вероятностей к голосованию большинством».
^ О Кондорсе и Лапласе см. Г. Г. Шпиро, «Правило чисел» (2010).
^ Блэк, Дункан (1948). «Обоснование группового принятия решений» . Журнал политической экономии . 56 (1): 23–34. дои : 10.1086/256633 . ISSN 0022-3808 . S2CID 153953456 .
^ Энтони Даунс, « Экономическая теория демократии » (1957).
^ Перейти обратно: ^а ^б Тайдман, Т. Николаус; Плассманн, Флоренц (2012), Фельсенталь, Дэн С.; Мачовер, Моше (ред.), «Моделирование результатов подсчета голосов на реальных выборах» , Избирательные системы , Берлин, Гейдельберг: Springer Berlin Heidelberg, стр. 217–251, номер документа : 10.1007/978-3-642-20441- 8_9 , ISBN 978-3-642-20440-1 , получено 2 апреля 2023 г.
^ Таллок, Гордон (1967). «Общая неуместность общей теоремы невозможности» . Ежеквартальный экономический журнал . 81 (2): 256–270. дои : 10.2307/1879585 . JSTOR 1879585 .
^ Перейти обратно: ^а ^б ^с Жан-Франсуа Ласлье (2011). И проигравшим становится... Множественное голосование . ISBN 978-3-642-42955-2 . ISSN 2267-828X . Викиданные Q108664719 . {{cite book}}: |journal= игнорируется ( помогите )
^ Болл, Теренс и Антис Лоизидис, «Джеймс Милль» , Стэнфордская энциклопедия философии (зимнее издание 2020 г.), Эдвард Н. Залта (ред.).
^ Обозначения определены в статье Нормальное распределение§Notation . Предположение о нормальности удобно и обеспечивает генеративную модель, пригодную для использования в симуляциях, но результаты Кондорсе и Янга не полагаются на него, поскольку они получены из чистой теории вероятностей.
^ Янг, HP (1988). «Теория голосования Кондорсе» . Американский обзор политической науки . 82 (4): 1231–1244. дои : 10.2307/1961757 . ISSN 0003-0554 . JSTOR 1961757 . S2CID 14908863 .
^ Бордли, Роберт Ф. (март 1983 г.). «Прагматический метод оценки избирательных схем посредством моделирования» . Американский обзор политической науки . 77 (1): 123–141. дои : 10.2307/1956015 . ISSN 0003-0554 . JSTOR 1956015 . S2CID 147689260 .
^ Куинн, Джеймсон (10 февраля 2017 г.). «Часто задаваемые вопросы по эффективности удовлетворенности избирателей» . Страницы GitHub . Проверено 24 июля 2019 г.
^ Грофман, Бернард; Фельд, Скотт Л. (декабрь 2004 г.). «Если вам нравится альтернативное голосование (то есть мгновенный второй тур), то вам следует знать о правиле Кумбса» . Электоральные исследования . 23 (4): 641–659. doi : 10.1016/j.electstud.2003.08.001 .
^ Перейти обратно: ^а ^б Тайдман, Т. Николаус; Плассманн, Флоренц (март 2014 г.). «Какое правило голосования с наибольшей вероятностью позволит выбрать «лучшего» кандидата?» . Общественный выбор . 158 (3–4): 331–357. дои : 10.1007/s11127-012-9935-y . ISSN 0048-5829 . S2CID 189841413 .
^ Перейти обратно: ^а ^б ^с ^д Дарлингтон, Ричард Б. (2018). «Являются ли системы голосования Кондорсе и минимакс лучшими?». arXiv : 1807.01366v8 [ physical.soc-ph ].
^ Перейти обратно: ^а ^б Дарлингтон, Ричард Б. (2016). «В конце концов, Минимакс - лучшая избирательная система». arXiv : 1606.04371 [ stat.ME ].
^ Перейти обратно: ^а ^б Грин-Армитейдж, Джеймс; Тайдман, Т. Николаус; Косман, Рафаэль (январь 2016 г.). «Статистическая оценка правил голосования» (PDF) . Социальный выбор и благосостояние . 46 (1): 183–212. дои : 10.1007/s00355-015-0909-0 . ISSN 0176-1714 . S2CID 253842768 .
^ Перейти обратно: ^а ^б ^с Грин-Армитаж, Джеймс (январь 2014 г.). «Стратегическое голосование и номинирование» . Социальный выбор и благосостояние . 42 (1): 111–138. дои : 10.1007/s00355-013-0725-3 . ISSN 0176-1714 . S2CID 253847024 .
^ Перейти обратно: ^а ^б Меррилл, Сэмюэл (февраль 1984 г.). «Сравнение эффективности избирательных систем с несколькими кандидатами» . Американский журнал политической науки . 28 (1): 23–48. дои : 10.2307/2110786 . JSTOR 2110786 – через JSTOR.
^ Лейпхарт, Аренд (март 1997 г.). «Неравное участие: нерешенная дилемма демократии». Американский обзор политической науки . 91 (1): 1–14. дои : 10.2307/2952255 . JSTOR 2952255 . S2CID 143172061 .
^ Бле, Андре (1990). «Повышает ли пропорциональное представительство явку избирателей?». Европейский журнал политических исследований . 18 (2): 167–181. дои : 10.1111/j.1475-6765.1990.tb00227.x .
^ Таллок, Гордон (1965). «Входные барьеры в политику» . Американский экономический обзор . 55 (1/2). Американская экономическая ассоциация: 458–466. ISSN 0002-8282 . JSTOR 1816288 . Проверено 3 апреля 2024 г.
^ Васильев, Сергей (1 апреля 2008 г.), Кардинальное голосование: способ избежать невозможности социального выбора , Электронная библиотека SSRN, SSRN 1116545
^ Последовательность подразумевает участие, но не наоборот. Например, голосование по диапазону соответствует участию и последовательности, но медианные рейтинги удовлетворяют участию и не соответствуют последовательности.
^ Вудалл, Дуглас (декабрь 1994 г.), «Свойства правил преференциальных выборов» , Вопросы голосования (3)
^ Смолл, Алекс (22 августа 2010 г.), «Геометрическое построение методов голосования, защищающих первый выбор избирателей», arXiv : 1008.4331 [ cs.GT ]
^ Таллок, Гордон (1965). «Входные барьеры в политику» . Американский экономический обзор . 55 (1/2): 458–466. JSTOR 1816288 .
^ Макганн, Энтони Дж. и Майкл Латнер. «Расчет консенсусной демократии: переосмысление моделей демократии без игроков с правом вето». Сравнительные политические исследования 46.7 (2013): 823-850.
^ Дисс, Мостафа; Догми, Ахмед (2016). «Методы выборов с множественным победителем: последовательность и парадоксы Кондорсе» . Общественный выбор . 169 (1–2): 97–116. дои : 10.1007/s11127-016-0376-x . ISSN 0048-5829 . S2CID 73721191 .
^ Перейти обратно: ^а ^б Эми, Дуглас Дж.; За урной для голосования: Руководство для граждан по системам голосования , с. 120 ISBN 0275965864

[condorcet-iia-incompatibility-28] Перейти обратно: ^а ^б ^с ^д ^и ^ж ^г Критерий Кондорсе несовместим с критериями последовательности , участия , «позже без вреда» , «позже без помощи » и искреннего любимца .

[IIA_rating_methods-29] Перейти обратно: ^а ^б ^с Голосование за одобрение, голосование по баллам и решение большинства удовлетворяют требованиям IIA, если предположить, что избиратели оценивают кандидатов независимо, используя свою собственную абсолютную шкалу . Чтобы это произошло, на некоторых выборах некоторые избиратели должны использовать меньше своих полномочий, несмотря на наличие значимых предпочтений среди жизнеспособных кандидатов.

[30] Решение большинства может избрать кандидата, однозначно наименее предпочитаемого более чем половиной избирателей, но никогда не избирает кандидата с однозначно наименьшим рейтингом более чем половиной избирателей.

[mjmmc-31] Решение большинства не соответствует критерию взаимного большинства, но удовлетворяет критерию, если большинство ставит взаимно предпочтительный набор выше заданной абсолютной оценки, а все остальные - ниже этой оценки.

[semipc-32] Перейти обратно: ^а ^б ^с При голосовании по наивысшей медиане, рейтинговых парах и голосовании Шульце для любого избирателя всегда есть получестное голосование без сожалений, при этом все остальные бюллетени остаются неизменными и при условии, что он достаточно знает о том, как будут голосовать другие. В таких обстоятельствах у избирателя всегда есть хотя бы один способ принять участие, не ставя при этом менее предпочтительного кандидата выше более предпочтительного.

[MinimaxVarient-33] Перейти обратно: ^а ^б Вариант Минимакса, который учитывает только парную оппозицию, а не оппозицию минус поддержка, не соответствует критерию Кондорсе и соответствует принципу «позже не будет причинен вред».

[34] Победитель определяется случайным образом выбранным бюллетенем. Этот и тесно связанные с ним методы представляют математический интерес и включены сюда, чтобы продемонстрировать, что даже необоснованные методы могут соответствовать критериям метода голосования.

[35] Если победитель выбирается случайным образом из кандидатов, проводится жеребьевка, чтобы продемонстрировать, что даже методы без голосования могут соответствовать некоторым критериям.

[chamberlin-1] Перейти обратно: ^а ^б ^с ^д Чемберлин, Джон Р.; Коэн, Майкл Д. (декабрь 1978 г.). «На пути к применимой теории социального выбора: сравнение функций социального выбора при предположениях пространственной модели» . Американский обзор политической науки . 72 (4): 1341–1356. дои : 10.2307/1954543 . ISSN 0003-0554 . JSTOR 1954543 . S2CID 155928569 .

[2] МЖАН де Карита, маркиз де Кондорсе. Его книга была опубликована в 1785 году. Название можно перевести как «Очерк применения теории вероятностей к голосованию большинством».

[3] О Кондорсе и Лапласе см. Г. Г. Шпиро, «Правило чисел» (2010).

[black-4] Блэк, Дункан (1948). «Обоснование группового принятия решений» . Журнал политической экономии . 56 (1): 23–34. дои : 10.1086/256633 . ISSN 0022-3808 . S2CID 153953456 .

[downs-5] Энтони Даунс, « Экономическая теория демократии » (1957).

[tidemanplassmann-6] Перейти обратно: ^а ^б Тайдман, Т. Николаус; Плассманн, Флоренц (2012), Фельсенталь, Дэн С.; Мачовер, Моше (ред.), «Моделирование результатов подсчета голосов на реальных выборах» , Избирательные системы , Берлин, Гейдельберг: Springer Berlin Heidelberg, стр. 217–251, номер документа : 10.1007/978-3-642-20441- 8_9 , ISBN 978-3-642-20440-1 , получено 2 апреля 2023 г.

[7] Таллок, Гордон (1967). «Общая неуместность общей теоремы невозможности» . Ежеквартальный экономический журнал . 81 (2): 256–270. дои : 10.2307/1879585 . JSTOR 1879585 .

[laslier11-8] Перейти обратно: ^а ^б ^с Жан-Франсуа Ласлье (2011). И проигравшим становится... Множественное голосование . ISBN 978-3-642-42955-2 . ISSN 2267-828X . Викиданные Q108664719 . {{cite book}}: |journal= игнорируется ( помогите )

[9] Болл, Теренс и Антис Лоизидис, «Джеймс Милль» , Стэнфордская энциклопедия философии (зимнее издание 2020 г.), Эдвард Н. Залта (ред.).

[10] Обозначения определены в статье Нормальное распределение§Notation . Предположение о нормальности удобно и обеспечивает генеративную модель, пригодную для использования в симуляциях, но результаты Кондорсе и Янга не полагаются на него, поскольку они получены из чистой теории вероятностей.

[young-11] Янг, HP (1988). «Теория голосования Кондорсе» . Американский обзор политической науки . 82 (4): 1231–1244. дои : 10.2307/1961757 . ISSN 0003-0554 . JSTOR 1961757 . S2CID 14908863 .

[bordley-12] Бордли, Роберт Ф. (март 1983 г.). «Прагматический метод оценки избирательных схем посредством моделирования» . Американский обзор политической науки . 77 (1): 123–141. дои : 10.2307/1956015 . ISSN 0003-0554 . JSTOR 1956015 . S2CID 147689260 .

[:22-13] Куинн, Джеймсон (10 февраля 2017 г.). «Часто задаваемые вопросы по эффективности удовлетворенности избирателей» . Страницы GitHub . Проверено 24 июля 2019 г.

[coombs-14] Грофман, Бернард; Фельд, Скотт Л. (декабрь 2004 г.). «Если вам нравится альтернативное голосование (то есть мгновенный второй тур), то вам следует знать о правиле Кумбса» . Электоральные исследования . 23 (4): 641–659. doi : 10.1016/j.electstud.2003.08.001 .

[tp2-15] Перейти обратно: ^а ^б Тайдман, Т. Николаус; Плассманн, Флоренц (март 2014 г.). «Какое правило голосования с наибольшей вероятностью позволит выбрать «лучшего» кандидата?» . Общественный выбор . 158 (3–4): 331–357. дои : 10.1007/s11127-012-9935-y . ISSN 0048-5829 . S2CID 189841413 .

[darlington-16] Перейти обратно: ^а ^б ^с ^д Дарлингтон, Ричард Б. (2018). «Являются ли системы голосования Кондорсе и минимакс лучшими?». arXiv : 1807.01366v8 [ physical.soc-ph ].

[darlington16-17] Перейти обратно: ^а ^б Дарлингтон, Ричард Б. (2016). «В конце концов, Минимакс - лучшая избирательная система». arXiv : 1606.04371 [ stat.ME ].

[jga-18] Перейти обратно: ^а ^б Грин-Армитейдж, Джеймс; Тайдман, Т. Николаус; Косман, Рафаэль (январь 2016 г.). «Статистическая оценка правил голосования» (PDF) . Социальный выбор и благосостояние . 46 (1): 183–212. дои : 10.1007/s00355-015-0909-0 . ISSN 0176-1714 . S2CID 253842768 .

[jga2-19] Перейти обратно: ^а ^б ^с Грин-Армитаж, Джеймс (январь 2014 г.). «Стратегическое голосование и номинирование» . Социальный выбор и благосостояние . 42 (1): 111–138. дои : 10.1007/s00355-013-0725-3 . ISSN 0176-1714 . S2CID 253847024 .

[merrill-20] Перейти обратно: ^а ^б Меррилл, Сэмюэл (февраль 1984 г.). «Сравнение эффективности избирательных систем с несколькими кандидатами» . Американский журнал политической науки . 28 (1): 23–48. дои : 10.2307/2110786 . JSTOR 2110786 – через JSTOR.

[21] Лейпхарт, Аренд (март 1997 г.). «Неравное участие: нерешенная дилемма демократии». Американский обзор политической науки . 91 (1): 1–14. дои : 10.2307/2952255 . JSTOR 2952255 . S2CID 143172061 .

[22] Бле, Андре (1990). «Повышает ли пропорциональное представительство явку избирателей?». Европейский журнал политических исследований . 18 (2): 167–181. дои : 10.1111/j.1475-6765.1990.tb00227.x .

[TullockBarriers-23] Таллок, Гордон (1965). «Входные барьеры в политику» . Американский экономический обзор . 55 (1/2). Американская экономическая ассоциация: 458–466. ISSN 0002-8282 . JSTOR 1816288 . Проверено 3 апреля 2024 г.

[24] Васильев, Сергей (1 апреля 2008 г.), Кардинальное голосование: способ избежать невозможности социального выбора , Электронная библиотека SSRN, SSRN 1116545

[25] Последовательность подразумевает участие, но не наоборот. Например, голосование по диапазону соответствует участию и последовательности, но медианные рейтинги удовлетворяют участию и не соответствуют последовательности.

[26] Вудалл, Дуглас (декабрь 1994 г.), «Свойства правил преференциальных выборов» , Вопросы голосования (3)

[27] Смолл, Алекс (22 августа 2010 г.), «Геометрическое построение методов голосования, защищающих первый выбор избирателей», arXiv : 1008.4331 [ cs.GT ]

[36] Таллок, Гордон (1965). «Входные барьеры в политику» . Американский экономический обзор . 55 (1/2): 458–466. JSTOR 1816288 .

[McGann-37] Макганн, Энтони Дж. и Майкл Латнер. «Расчет консенсусной демократии: переосмысление моделей демократии без игроков с правом вето». Сравнительные политические исследования 46.7 (2013): 823-850.

[38] Дисс, Мостафа; Догми, Ахмед (2016). «Методы выборов с множественным победителем: последовательность и парадоксы Кондорсе» . Общественный выбор . 169 (1–2): 97–116. дои : 10.1007/s11127-016-0376-x . ISSN 0048-5829 . S2CID 73721191 .

[Behind-39] Перейти обратно: ^а ^б Эми, Дуглас Дж.; За урной для голосования: Руководство для граждан по системам голосования , с. 120 ISBN 0275965864

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[Тн 1]

[Тн 2]

[Тн 3]

[Тн 4]

[Тн 5]

[Тн 6]

[Тн 7]

[Тн 8]

[28]

[29]

[30]

[31]