Динамические бильярд

Частица, движущаяся на стадионе Бунимовича, известный хаотичный бильярд. См. Раздел программного обеспечения для создания такой анимации.

Динамический бильярд - это динамическая система , в которой частица чередуется между свободным движением (обычно в виде прямой линии) и зеркальные отражения из границы. Когда частица достигает границы, она отражается из нее без потери скорости (то есть упругие столкновения). Бильярды - это гамильтонианские идеализации игры в бильярд , но там, где регион, содержащий границу, может иметь формы, отличные от прямоугольных и даже многомерных. Динамические бильярды также могут быть изучены на неяклидовой геометрии ; Действительно, первые исследования бильярдов установили их эргодическое движение на поверхностях постоянной негативной кривизны . Изучение бильярдов, которые не допускаются в регионе, а не хранятся в регионе, известно как внешнего бильярда теория .

Движение частицы в бильярде представляет собой прямую линию, с постоянной энергией, между отражениями с границей ( геодезическая , если риманновой метрика бильярда не является плоским). Все отражения являются зеркальными : угол падения непосредственно перед столкновением равна углу отражения сразу после столкновения. Последовательность , отражений описывается бильярдной картой которая полностью характеризует движение частицы.

Бильярды отражают всю сложность гамильтонианских систем, от интегрируемости до хаотического движения , без трудностей интеграции уравнений движения для определения его карты Пуанкаре . Биркхофф показал, что бильярдная система с эллиптической таблицей интегрируется.

Уравнения движения

Гамильтониан движущейся для частицы массы М, свободно без трения на поверхности:

$H(p,q)={\frac {p^{2}}{2m}}+V(q)$

где $V(q)$ это потенциал, предназначенный для нуля внутри региона $\Omega$ в котором частица может перемещаться, и в противном случае бесконечность:

$V(q)={\begin{cases}0&q\in \Omega \\\infty &q\notin \Omega \end{cases}}$

Эта форма потенциального гарантирует зеркальное отражение на границе. Кинетический термин гарантирует, что частица движется по прямой линии, без каких -либо изменений в энергии. Если частица должна перемещаться по неяклидовому коллектору , то гамильтониан заменяется:

$H(p,q)={\frac {1}{2m}}p^{i}p^{j}g_{ij}(q)+V(q)$

где $g_{ij}(q)$ Метрический тензор в точке $q\;\in \;\Omega$Полем Из -за очень простой структуры этого гамильтониана уравнения движения для частицы, уравнения Гамильтона -Якоби , являются ничем иным, как геодезическими уравнениями на многообразии: частица движется по геодезике .

Примечательные бильярдные и бильярдные классы

Бильярд Хадамарда

Основная статья: динамическая система Адамарда

Бильярд Хадамарда касается движения частицы свободной точки на поверхности постоянной негативной кривизны, в частности, самой простой компактной поверхности римана с отрицательной кривизны, поверхностью рода 2 (дончик с двумя вырубками). Модель точно решается и дается геодезическим потоком на поверхности. Это самый ранний пример детерминированного хаоса , когда -либо изучавшегося, который был представлен Жаком Хадамардом в 1898 году.

Артин Билл

Основная статья: Артин Бильярд

Бильярд Артины рассматривает свободное движение точечной частицы на поверхности постоянной негативной кривизны, в частности, самой простой некомпактной поверхности Римана , поверхности с одним пульсом. Это примечательно быть точно решаемым, и все же не только эргодичное , но и сильно смешивание . Это пример системы Anosov . Эта система была впервые изучена Эмилем Артин в 1924 году.

Рассеивание и полудисперсные бильярдные

Пусть M будет полным гладким римановым коллектором без границ, максимальная кривиза секции , не больше k , и с радиусом инъективности $\rho >0$Полем Рассмотрим коллекцию n геодезически выпуклых подмножеств (стены) $B_{i}\subset M$, $i=1,\ldots ,n$, так что их границы являются гладкими подмены Codimension One. Позволять $B=M\ (\bigcup _{i=1}^{n}\operatorname {Int} (B_{i}))$, где $\operatorname {Int} (B_{i})$ обозначает интерьер набора $B_{i}$Полем Набор $B\subset M$ Будет называться бильярдом. Рассмотрим теперь частицу, которая перемещается внутрь B с скоростью единицы вдоль геодезии, пока Он достигает одного из наборов B _i (такое событие называется столкновением), где он отражает в соответствии с законом «угол падения равна углу отражения» (если он достигает одного из наборов $B_{i}\cap B_{j}$ , $i\neq j$, траектория не определена после этого момента). Такая динамическая система называется полудисперсным биллиардом . Если стены строго выпуклые, то бильярд называется диспергированием . Название мотивируется наблюдением, что локально параллельный луч траекторий рассеивается после столкновения со строго выпуклой частью стены, но остается локально параллельными после столкновения с плоской секцией стены.

Распределение границы играет ту же роль для бильярда, что и негативная кривизна для геодезических потоков, вызывая экспоненциальную нестабильность динамики. Именно этот механизм рассеивания дает рассеиванию бильярдов свои самые сильные хаотические свойства, так как он был установлен Якова Г. Синай . А именно, бильярды являются эргодическими , смешивающими , Бернулли , имеют положительную энтропию -Синай и экспоненциальное распад корреляций Колмогоров .

Хаотические свойства общих полудисперсных бильярдов не понимаются, что хорошо, однако, с одного важного типа полудисперсных бильярдов, с некоторыми деталями были изучены жесткие шариковые газы в некоторых деталях (см. Следующий раздел).

Общие результаты Дмитрия Буры и Сержа Ферлегера По единой оценке количества столкновений в полудиспержильных бильярдных, не связанных с дегурации, позволяет установить ограничение своей топологической энтропии и не более, чем экспоненциальный рост периодических траекторий. Напротив, дегенератные полудисперширующие бильярд могут иметь бесконечную топологическую энтропию.

Lorentz Gas, AKA Sinai Billiard

Частица, движущаяся внутри синайского бильярда, также известная как газ Лоренца.

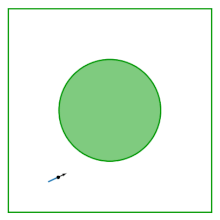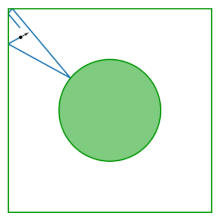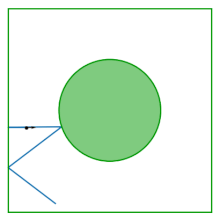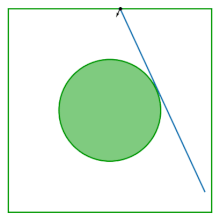
Таблица газа Лоренца (также известный как синайский бильярд) представляет собой квадрат с диском, удаленным из его центра; Стол плоский, не имеет кривизны. Бильярд возникает из -за изучения поведения двух взаимодействующих дисков, подпрыгивающих внутри квадрата, отражающих границы квадрата и друг от друга. Устранение центра массы в качестве переменной конфигурации, динамика двух взаимодействующих дисков сводится к динамике в бильярде Синай.

Бильярд был представлен Яковом Г. Синайем в качестве примера взаимодействующей гамильтонианской системы , которая демонстрирует физические термодинамические свойства: почти все (вплоть до нуля) ее возможных траекторий являются эргодическими и имеют положительный показатель Льяпунова .

Большое достижение Синай с этой моделью состояло в том, чтобы показать, что классический ансамбль Больцмана -Гиббс для идеального газа по сути является максимально хаотичным бильярдным хадамардом.

Запрыгивающий мяч бильярд

Частица подвержена постоянной силе (например, гравитация Земли) и неластично рассеивает на периодически гофрированном вибрирующем поле. Когда пол сделан по дуге или кругам - в определенном интервале частот - можно дать полуаналитические оценки скорости экспоненциального разделения траекторий.

Стадион Бунимовича

Стол, называемый стадион Bunimovich, представляет собой прямоугольник, покрытый полукругами, формой, называемой стадионом . До тех пор, пока он не был введен Леонидом Бунимовичем бильярды с позитивными показателями Ляпунова , считалось, что нуждаются в выпуклых рассеяниях, таких как диск в бильярде Синай, для получения экспоненциальной дивергенции орбит. Бунимович показал, что, рассматривая орбиты за пределами точки фокусировки вогнутой области, можно было получить экспоненциальную дивергенцию.

Магнитные бильярдные

Движение заряженной частицы внутри синайского бильярда с перпендикулярным магнитным полем.

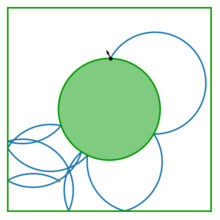
Магнитные бильярды представляют собой бильярд, где заряженная частица распространяется в присутствии перпендикулярного магнитного поля. В результате траектория частиц изменяется с прямой линии в дугу круга. Радиус этого круга обратно пропорционален силе магнитного поля. Такие бильярд были полезны в реальных приложениях бильярдных, обычно моделируя наноуродиции (см. Приложения).

Общие бильярд

Обобщенные бильярд (ГБ) описывают движение точки массы (частица) внутри закрытого домена $\Pi \,\subset \,\mathbb {R} ^{n}$ С помощью гладкой границы $\Gamma$Полем На границе $\Gamma$ Скорость точки трансформируется, поскольку частица претерпела действие обобщенного закона о бильярде. ГБ был введен Лев Д. Пустил'никовым в общем случае, и в случае, когда $\Pi$ это параллелепип в связи с оправданием второго закона термодинамики . С физической точки зрения GB описывает газ, состоящий из конечно, многие частицы, движущиеся в сосуде, в то время как стены сосуда нагреваются или остывают. Суть обобщения - следующее. Как частица попадает в границу $\Gamma$, его скорость преобразуется с помощью данной функции $f(\gamma ,\,t)$, определено на прямом продукте $\Gamma \,\times \,\mathbb {R} ^{1}$ (где $\mathbb {R} ^{1}$ настоящая линия, $\gamma \,\in \,\Gamma$ является точкой границы и $t\,\in \,\mathbb {R} ^{1}$ время), согласно следующему закону. Предположим, что траектория частицы, которая движется со скоростью $v$, пересекаются $\Gamma$ в точке $\gamma \,\in \,\Gamma$ в момент времени $t^{*}$Полем Тогда в момент времени $t^{*}$ частица получает скорость $v^{*}$, как будто он подвергся упругому толчке из бесконечно тяжелой плоскости $\Gamma ^{*}$, что касается $\Gamma$ в точке $\gamma$и в то время $t^{*}$ движется вдоль нормального к $\Gamma$ в $\gamma$ со скоростью $\textstyle {\frac {\partial f}{\partial t}}(\gamma ,\,t^{*})$Полем Мы подчеркиваем, что положение самой границы фиксируется, в то время как ее действие на частицу определяется через функцию $f$.

Мы поднимаем позитивное направление движения плоскости $\Gamma ^{*}$ быть сторону в $\Pi$Полем Таким образом, если производная $\textstyle {\frac {\partial f}{\partial t}}(\gamma ,\,t)\;>\;0$, затем частица ускоряется после удара.

Если скорость $v^{*}$Приобретено частицей в результате вышеуказанного закона о отражении, направлен на внутреннюю часть домена $\Pi$, тогда частица покинет границу и продолжит двигаться в $\Pi$ до следующего столкновения с $\Gamma$Полем Если скорость $v^{*}$ направлен на внешнюю часть $\Pi$, тогда частица остается на $\Gamma$ в точке $\gamma$ пока что -нибудь ${\tilde {t}}\;>\;t^{*}$ Взаимодействие с границей заставит частицу оставить ее.

Если функция $f(\gamma ,\,t)$ не зависит от времени $t$; Т.е. $\textstyle {\frac {\partial f}{\partial t}}\;=\;0$, генерализованный бильярд совпадает с классическим.

Этот обобщенный закон отражения очень естественный. Во -первых, это отражает очевидный факт, что стены сосуда с газом неподвижны. Во -вторых, действие стены на частицу по -прежнему является классическим эластичным толчком. По сути, мы рассматриваем бесконечно -лискую движущуюся границы с заданными скоростями.

Это считается отражением от границы $\Gamma$ Как в рамках классической механики (ньютоновский случай), так и теории относительности (релятивистский случай).

Основные результаты: в ньютоновском случае энергия частицы ограничена, энтропия Гиббса является постоянной, (в примечаниях) и в релятивистском случае энергия частицы, энтропия Гиббса, энтропия относительно объема фазы, растущая до бесконечности, (В примечаниях), ссылки на обобщенные бильярд.

Сколько хаоса

Квантовая версия бильярда легко изучается несколькими способами. Классический гамильтониан для бильярда, приведенный выше, заменяется уравнением Шердингера стационарного государства $H\psi \;=\;E\psi$ или, точнее,

$-{\frac {\hbar ^{2}}{2m}}\nabla ^{2}\psi _{n}(q)=E_{n}\psi _{n}(q)$

где $\nabla ^{2}$ это лапласиан . Потенциал, который бесконечен за пределами региона $\Omega$ Но ноль внутри него переводится на граничные условия Дирихле :

$\psi _{n}(q)=0\quad {\mbox{for}}\quad q\notin \Omega$

Как обычно, волновые функции считаются ортонормальными :

$\int _{\Omega }{\overline {\psi _{m}}}(q)\psi _{n}(q)\,dq=\delta _{mn}$

Любопытно, что уравнение Schrödinger свободного поля совпадает с уравнением Гельмгольца ,

$\left(\nabla ^{2}+k^{2}\right)\psi =0$

с

$k^{2}={\frac {1}{\hbar ^{2}}}2mE_{n}$

Это подразумевает, что два и трехмерные квантовые бильярды могут быть смоделированы классическими резонансными способами радарной полости данной формы, тем самым открывая дверь для экспериментальной проверки. (Изучение мод радиолокационной полости должно быть ограничено поперечными магнитными (TM) модами, так как они подчиняются условиям границ Дирихле).

Полуклассический предел соответствует $\hbar \;\to \;0$ что можно считать эквивалентным $m\;\to \;\infty$, масса увеличивается так, что она ведет себя классическим.

В качестве общего утверждения можно сказать, что всякий раз, когда классические уравнения движения интегрируются ( например, прямоугольные или круглые бильярдные таблицы), тогда квантово-механическая версия бильярда полностью разрешается. Когда классическая система хаотична, квантовая система, как правило, не совсем растворяется и представляет многочисленные трудности в ее квантовании и оценке. Общее исследование хаотических квантовых систем известно как квантовый хаос .

Особенно поразительный пример рубцов на эллиптической таблице приведен в связи с наблюдением так называемого квантового миража .

Приложения

Бильярд, как квантовые, так и классические, были применены в нескольких областях физики для моделирования довольно разнообразных систем реального мира. Примеры включают Ray-Optics , лазеры , акустика , оптические волокна (например, двойные волокна ), или квантово-классическая соответствие. Одним из наиболее частых применений является моделирование частиц, движущихся внутри нанодевисов, например, квантовых точек , PN-соединения , антидоновые суперреативы, среди других. Причина этого широко распространенного эффективности бильярда, поскольку физические модели заключается в том факте, что в ситуациях с небольшим количеством расстройства или шума движение EG частиц, таких как электроны, или световые лучи, очень похоже на движение точки. частицы в бильярде. Кроме того, энергия сохраняющая природа столкновений частиц является прямым отражением энергосбережения гамильтонианской механики.

Программное обеспечение

Программное обеспечение с открытым исходным кодом для имитации бильярдов существует для различных языков программирования. От самых последних до старейшего, существующего программного обеспечения: DynamicalBilliards.jl (Julia), Bill2d (C ++) и бильярд -симулятор (MATLAB). Анимации, присутствующие на этой странице, были сделаны с помощью DynamicalBilliards.jl.

Смотрите также

• Модель Ферми -Улама (бильярд с колеблющимися стенами)
• Любачевский -Стиллингер сжатия Лубачевский алгоритм
• Арифметические бильярд
• Проблема освещения

Ссылки

Бильярд Синай

• Синай, ты. Г. (1963). «[О основаниях эргодической гипотезы для динамической системы статистической механики]». Doklady Akademii Nauk SSSR (на русском языке). 153 (6): 1261–1264. (на английском языке, Sov. Math Dokl. 4 (1963) с. 1818–1822).
• Я. Г. Синай, «Динамические системы с упругими отражениями», Российские математические обследования , 25 , (1970) с. 137–191.
• Vi Arnold и A. Имеют эргодическую теорию динамических систем , (1967), Gauthier-Villars, Paris. (Английское издание: Бенджамин-Каммингс, Рединг, Массачусетс 1968). (Обсуждение и ссылки на бильярды Синай.)
• D. Heitmann, JP Kotthaus, «Спектроскопия массивов квантовых точек», Physics Today (1993) с. 56–63. (Предоставляет обзор экспериментальных тестов квантовых версий бильярдов Синай, реализованных как наномасштабные (мезоскопические) структуры на кремниевых пластинах.)
• S. Sridhar и WT Lu, « Синайские бильярдные, Руэль-Зета-Функции и резонансы Ruelle: микроволновые эксперименты », (2002) Журнал статистической физики , Vol. 108 № 5/6, с. 755–766.
• Linas Vepstas, бильярд Синай , (2001). (Предоставляет лучшие изображения бильярда Синай в трехмерном пространстве. Эти изображения обеспечивают графическую, интуитивную демонстрацию сильной эргодичности системы.)
• Н. Чернов и Р. Маркарян, «Хаотические бильярд», 2006, Математическая обследование и монографии № 127, AMS.

Странные бильярд

• Т. Шюрманн и И. Хоффманн, Энтропия странных бильярдов внутри н-симплексов. J. Phys A28, Page 5033ff, 1995. PDF-Document

Стадион Бунимовича

• Лабунимович (1979). «О эргодических свойствах нигде диспергирующих бильярд» . Commun Math Phys . 65 (3): 295–312. Bibcode : 1979cmaph..65..295b . doi : 10.1007/bf01197884 . S2CID   120456503 .
• Labunimovich & Ya. Г. Синай (1980). «Марковки разделяются на рассеянные бильярд» . Commun Math Phys . 78 (2): 247–280. Bibcode : 1980cmaph..78..247b . doi : 10.1007/bf01942372 . S2CID   123383548 .
• Флэш -анимация, иллюстрирующая стадион хаотика Bunimovich

Общие бильярд

• MV Deryabin и LD Pustyl'nikov, «Обобщенные релятивистские бильярды», рег. и хаотичный дин. 8 (3), с. 283–296 (2003).
• MV Deryabin и LD Pustyl'nikov, «О генерализованных релятивистских бильярдах во внешних силах», буквы в математической физике , 63 (3), с. 195–207 (2003).
• MV Deryabin и LD Pustyl'nikov, «Экспоненциальные аттракторы в обобщенных релятивистских бильярд», Comm. Математика Физический 248 (3), с. 527–552 (2004).

Внешние ссылки

• Вейсштейн, Эрик У. "Бильярд" . MathWorld .
• Ученическая запись о динамических бильярдах (Леонид Бунимович)
• Введение в динамические системы с использованием бильярдов , Институт физики сложных систем Макса Планка