Магнитный монополь

невозможно сделать магнитные монополи Из стержневого магнита . Если стержневой магнит разрезать пополам, это не значит, что одна половина имеет северный полюс, а другая половина — южный полюс. Вместо этого у каждой части есть свои северный и южный полюса. Магнитный монополь не может быть создан из обычной материи, такой как атомы и электроны , а вместо этого будет новой элементарной частицей .

В физике элементарных частиц магнитный монополь — это гипотетическая элементарная частица , представляющая собой изолированный магнит только с одним магнитным полюсом (северный полюс без южного полюса или наоборот). Магнитный монополь будет иметь суммарный северный или южный «магнитный заряд». Современный интерес к этой концепции проистекает из теорий частиц , особенно теорий великого объединения и суперструн , которые предсказывают их существование. Известные элементарные частицы, обладающие электрическим зарядом, являются электрическими монополями.

Магнетизм в стержневых магнитах и ​​электромагнитах не вызван магнитными монополями, и действительно, нет известных экспериментальных или наблюдательных доказательств существования магнитных монополей.

Некоторые конденсированные системы содержат эффективные (неизолированные) магнитные монопольные квазичастицы . или содержат явления, математически аналогичные магнитным монополям.

Историческая справка

наука и

Многие ранние учёные приписывали магнетизм магнитов двум разным «магнитным жидкостям» («effluvia»): жидкости северного полюса на одном конце и жидкости южного полюса — на другом, которые притягивали и отталкивали друг друга по аналогии с положительными и отрицательными жидкостями. отрицательный электрический заряд . Однако улучшение понимания электромагнетизма в девятнадцатом веке показало, что магнетизм магнитов правильно объяснялся не магнитными монопольными жидкостями, а скорее комбинацией электрических токов , магнитного момента электрона и магнитных моментов других частиц. Закон Гаусса для магнетизма , одно из уравнений Максвелла , представляет собой математическое утверждение о том, что магнитных монополей не существует. Тем не менее, Пьер Кюри отметил в 1894 г. что магнитные монополи предположительно могут существовать, хотя до сих пор они не наблюдались.

Квантовая механика

Квантовая теория магнитного заряда началась со статьи физика Поля Дирака в 1931 году. В этой статье Дирак показал, что если квантован во Вселенной существуют магнитные монополи, то весь электрический заряд во Вселенной должен быть ( условие квантования Дирака). Электрический заряд . фактически квантуется, что согласуется (но не доказывает) с существованием монополей

Со времени публикации Дирака было проведено несколько систематических поисков монополей. Эксперименты 1975 года и 1982 год породили события-кандидаты, которые первоначально интерпретировались как монополии, но теперь считаются неубедительными. Поэтому вопрос о существовании монополей остается открытым. Дальнейшие достижения в теоретической физике элементарных частиц , особенно разработки в области теорий великого объединения и квантовой гравитации , привели к появлению более убедительных аргументов (подробно описанных ниже) о том, что монополи действительно существуют. Джозеф Полчински , теоретик струн, описал существование монополей как «одну из самых безопасных ставок, которые можно сделать в отношении еще невиданной физики». Эти теории не обязательно противоречат экспериментальным данным. В некоторых теоретических моделях магнитные монополи вряд ли будут наблюдаться, поскольку они слишком массивны, чтобы их можно было создать в ускорителях частиц (см. § Поиски магнитных монополей ниже), а также слишком редки во Вселенной, чтобы попасть в детектор частиц . с большой вероятностью

Некоторые системы с конденсированным веществом предлагают структуру, внешне похожую на магнитный монополь, известную как магнитная трубка . Концы силовой трубки образуют магнитный диполь , но, поскольку они движутся независимо, во многих целях их можно рассматривать как независимые квазичастицы магнитного монополя . С 2009 года многочисленные новостные сообщения популярных СМИ ошибочно описали эти системы как долгожданное открытие магнитных монополей, но эти два явления лишь поверхностно связаны друг с другом. Эти системы конденсированного состояния остаются областью активных исследований. (См . § «Монополи» в конденсированных системах ниже.)

Полюса и магнетизм в обычной материи

Основная статья: Магнетизм

Вся материя, изолированная на сегодняшний день, включая каждый атом в таблице Менделеева и каждую частицу в Стандартной модели , имеет нулевой магнитный монопольный заряд. Следовательно, обычные явления магнетизма и магнитов не происходят от магнитных монополей.

Вместо этого магнетизм в обычной материи возникает из двух источников. Во-первых, электрические токи создают магнитные поля по закону Ампера . Во-вторых, многие элементарные частицы обладают собственным магнитным моментом , наиболее важным из которых является магнитный дипольный момент электрона , который связан с его квантовомеханическим спином .

Математически магнитное поле объекта часто описывается в терминах мультипольного разложения . Это выражение поля как суммы составляющих полей с определенными математическими формами. Первый член в разложении называется монопольным , второй — дипольным , затем квадрупольным , затем октупольным и так далее. в мультипольном разложении электрического поля Любой из этих членов может присутствовать , например, . Однако в мультипольном разложении магнитного поля «монопольный» член всегда равен нулю (для обычной материи). Магнитный монополь, если бы он существовал, имел бы определяющее свойство создавать магнитное поле, монопольный член которого не равен нулю.

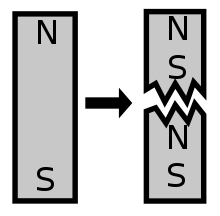
Магнитный диполь — это нечто, магнитное поле которого преимущественно или точно описывается магнитно-дипольным членом мультипольного расширения. Термин «диполь» означает два полюса , что соответствует тому факту, что дипольный магнит обычно содержит северный полюс с одной стороны и южный полюс с другой стороны. Это аналогично электрическому диполю , который имеет положительный заряд с одной стороны и отрицательный заряд с другой. Однако электрический диполь и магнитный диполь принципиально совершенно разные. В электрическом диполе, состоящем из обычного вещества, положительный заряд состоит из протонов , а отрицательный заряд состоит из электронов , но магнитный диполь не имеет разных типов материи, образующих северный и южный полюс. Вместо этого два магнитных полюса возникают одновременно в результате совокупного воздействия всех токов и собственных моментов во всем магните. Из-за этого два полюса магнитного диполя всегда должны иметь равную и противоположную силу, и эти два полюса не могут быть отделены друг от друга.

Уравнения Максвелла

Максвелла Уравнения электромагнетизма связывают электрические и магнитные поля друг с другом, а также с распределением электрического заряда и тока. Стандартные уравнения учитывают электрический заряд, но они предполагают нулевые магнитный заряд и ток. За исключением этого ограничения, уравнения симметричны относительно обмена электрическими и магнитными полями . Уравнения Максвелла симметричны, когда заряд и плотность электрического тока всюду равны нулю, как в вакууме.

Уравнения Максвелла также можно записать в полностью симметричной форме, если учесть «магнитный заряд», аналогичный электрическому. С включением переменной плотности магнитного заряда, скажем, ρ _m также появляется переменная « плотность магнитного тока , в уравнениях » j _m .

Если магнитный заряд не существует – или если он существует, но отсутствует в некоторой области пространства – тогда все новые члены в уравнениях Максвелла равны нулю, и расширенные уравнения сводятся к обычным уравнениям электромагнетизма, таким как ∇ ⋅ B = 0 ( где ∇⋅ — оператор дивергенции , а B — плотность магнитного потока ).

Слева: поля стационарных электрических и магнитных монополей.
Справа: при движении ( скорость v ) электрический заряд индуцирует поле B , а магнитный заряд индуцирует E. поле

Вверху: электронное поле, обусловленное электрическим дипольным моментом d .
Внизу слева: поле B , создаваемое магнитным диполем m, образованным двумя гипотетическими магнитными монополями.
Внизу справа: поле B , возникающее из-за естественного магнитного дипольного момента m, обнаруженного в обычной материи ( не из-за магнитных монополей). (На правом нижнем изображении не должно быть красных и синих кругов.)

Поля E электрического и B возникают из-за заряда (черный/белый) и магнитного заряда (красный/синий).

В гауссовских единицах СГС

Расширенные уравнения Максвелла имеют следующий вид в СГС-Гаусса : единицах

Уравнения Максвелла и уравнение силы Лоренца с магнитными монополями: единицы СГС-Гаусса.

Имя	Без магнитных монополей	С магнитными монополями
Закон Гаусса	$\nabla \cdot \mathbf {E} =4\pi \rho _{\mathrm {e} }$
Закон Ампера (с расширением Максвелла)	$\nabla \times \mathbf {B} -{\frac {1}{c}}{\frac {\partial \mathbf {E} }{\partial t}}={\frac {4\pi }{c}}\mathbf {j} _{\mathrm {e} }$
Закон Гаусса для магнетизма	$\nabla \cdot \mathbf {B} =0$	$\nabla \cdot \mathbf {B} =4\pi \rho _{\mathrm {m} }$
Закон индукции Фарадея	$-\nabla \times \mathbf {E} -{\frac {1}{c}}{\frac {\partial \mathbf {B} }{\partial t}}=0$	$-\nabla \times \mathbf {E} -{\frac {1}{c}}{\frac {\partial \mathbf {B} }{\partial t}}={\frac {4\pi }{c}}\mathbf {j} _{\mathrm {m} }$
силы Лоренца Закон	$\mathbf {F} =q_{\mathrm {e} }\left(\mathbf {E} +{\frac {\mathbf {v} }{c}}\times \mathbf {B} \right)$	$\mathbf {F} =q_{\mathrm {e} }\left(\mathbf {E} +{\frac {\mathbf {v} }{c}}\times \mathbf {B} \right)+q_{\mathrm {m} }\left(\mathbf {B} -{\frac {\mathbf {v} }{c}}\times \mathbf {E} \right)$

В этих уравнениях ρ _m — плотность магнитного заряда , j _m — плотность магнитного тока и q _m — магнитный заряд пробной частицы, все они определяются аналогично соответствующим величинам электрического заряда и тока; v — скорость частицы, а c — скорость света . Все остальные определения и подробности см. в уравнениях Максвелла . Для уравнений в безразмерной форме удалите факторы c .

В единицах СИ

В Международной системе величин, используемой в системе СИ , существует два соглашения для определения магнитного заряда qm _, каждое из которых имеет разные единицы измерения: вебер (Вб) и амперметр (А⋅м). Преобразование между ними равно q _m ^[Вб] = µ ₀ q _м ^[A⋅m] , поскольку единицами являются 1 Wb = 1 H⋅A = (1 H⋅m ⁻¹ )(1 А⋅м) , где H — генри – единица индуктивности в системе СИ .

Уравнения Максвелла тогда принимают следующий вид (с использованием тех же обозначений, что и выше):

Уравнения Максвелла и уравнение силы Лоренца с магнитными монополями: единицы СИ.

Имя	Без магнитного монополии	С магнитными монополями
		Веберовская конвенция	Условное обозначение амперметра
Закон Гаусса	$\nabla \cdot \mathbf {E} ={\frac {\rho _{\mathrm {e} }}{\varepsilon _{0}}}$
Закон Ампера (с расширением Максвелла)	$\nabla \times \mathbf {B} -{\frac {1}{c^{2}}}{\frac {\partial \mathbf {E} }{\partial t}}=\mu _{0}\mathbf {j} _{\mathrm {e} }$
Закон Гаусса для магнетизма	$\nabla \cdot \mathbf {B} =0$	$\nabla \cdot \mathbf {B} =\rho _{\mathrm {m} }$	$\nabla \cdot \mathbf {B} =\mu _{0}\rho _{\mathrm {m} }$
Закон индукции Фарадея	$-\nabla \times \mathbf {E} -{\frac {\partial \mathbf {B} }{\partial t}}=0$	$-\nabla \times \mathbf {E} -{\frac {\partial \mathbf {B} }{\partial t}}=\mathbf {j} _{\mathrm {m} }$	$-\nabla \times \mathbf {E} -{\frac {\partial \mathbf {B} }{\partial t}}=\mu _{0}\mathbf {j} _{\mathrm {m} }$
Уравнение силы Лоренца	$\mathbf {F} =q_{\mathrm {e} }\left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right)$	${\begin{aligned}\mathbf {F} ={}&q_{\mathrm {e} }\left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right)+\\&{\frac {q_{\mathrm {m} }}{\mu _{0}}}\left(\mathbf {B} -\mathbf {v} \times {\frac {\mathbf {E} }{c^{2}}}\right)\end{aligned}}$	${\begin{aligned}\mathbf {F} ={}&q_{\mathrm {e} }\left(\mathbf {E} +\mathbf {v} \times \mathbf {B} \right)+\\&q_{\mathrm {m} }\left(\mathbf {B} -\mathbf {v} \times {\frac {\mathbf {E} }{c^{2}}}\right)\end{aligned}}$

Возможная

Уравнения Максвелла также можно выразить через потенциалы следующим образом:

Имя	Гауссовы единицы	Единицы СИ (Вб)	Единицы СИ (А⋅м)
Уравнения Максвелла (при условии, что используется калибр Лоренца )	${\begin{aligned}\Box \phi _{\mathrm {e} }=&-4\pi \rho _{\mathrm {e} }\\\Box \mathbf {A} _{\mathrm {e} }=&-{\frac {4\pi }{c}}\mathbf {j} _{\mathrm {e} }\\\Box \phi _{\mathrm {m} }=&-4\pi \rho _{\mathrm {m} }\\\Box \mathbf {A} _{\mathrm {m} }=&-{\frac {4\pi }{c}}\mathbf {j} _{\mathrm {m} }\\\end{aligned}}$	${\begin{aligned}\Box \phi _{\mathrm {e} }=&-{\frac {\rho _{\mathrm {e} }}{\varepsilon _{0}}}\\\Box \mathbf {A} _{\mathrm {e} }=&-\mu _{0}\mathbf {j} _{\mathrm {e} }\\\Box \phi _{\mathrm {m} }=&-{\frac {\rho _{\mathrm {m} }}{\mu _{0}}}\\\Box \mathbf {A} _{\mathrm {m} }=&-\varepsilon _{0}\mathbf {j} _{\mathrm {m} }\\\end{aligned}}$	${\begin{aligned}\Box \phi _{\mathrm {e} }=&-{\frac {\rho _{\mathrm {e} }}{\varepsilon _{0}}}\\\Box \mathbf {A} _{\mathrm {e} }=&-\mu _{0}\mathbf {j} _{\mathrm {e} }\\\Box \phi _{\mathrm {m} }=&-\rho _{\mathrm {m} }\\\Box \mathbf {A} _{\mathrm {m} }=&-{\frac {\mathbf {j} _{\mathrm {m} }}{c^{2}}}\\\end{aligned}}$
Состояние датчика Лоренца	${\begin{aligned}&{\frac {1}{c}}{\frac {\partial }{\partial t}}\phi _{\mathrm {e} }+\nabla \cdot \mathbf {A} _{\mathrm {e} }=0\\&{\frac {1}{c}}{\frac {\partial }{\partial t}}\phi _{\mathrm {m} }+\nabla \cdot \mathbf {A} _{\mathrm {m} }=0\\\end{aligned}}$	${\begin{aligned}&{\frac {1}{c^{2}}}{\frac {\partial }{\partial t}}\phi _{\mathrm {e} }+\nabla \cdot \mathbf {A} _{\mathrm {e} }=0\\&{\frac {1}{c^{2}}}{\frac {\partial }{\partial t}}\phi _{\mathrm {m} }+\nabla \cdot \mathbf {A} _{\mathrm {m} }=0\\\end{aligned}}$
Связь с полями	${\begin{aligned}\mathbf {E} =&-\nabla \phi _{\mathrm {e} }-{\frac {1}{c}}{\frac {\partial \mathbf {A} _{\mathrm {e} }}{\partial t}}-\nabla \times \mathbf {A} _{\mathrm {m} }\\\mathbf {B} =&-\nabla \phi _{\mathrm {m} }-{\frac {1}{c}}{\frac {\partial \mathbf {A} _{\mathrm {m} }}{\partial t}}+\nabla \times \mathbf {A} _{\mathrm {e} }\\\end{aligned}}$	${\begin{aligned}\mathbf {E} =&-\nabla \phi _{\mathrm {e} }-{\frac {\partial \mathbf {A} _{\mathrm {e} }}{\partial t}}-{\frac {1}{\varepsilon _{0}}}\nabla \times \mathbf {A} _{\mathrm {m} }\\\mathbf {B} =&-\mu _{0}\nabla \phi _{\mathrm {m} }-\mu _{0}{\frac {\partial \mathbf {A} _{\mathrm {m} }}{\partial t}}+\nabla \times \mathbf {A} _{\mathrm {e} }\\\end{aligned}}$

где

$\Box =\nabla ^{2}-{\frac {1}{c^{2}}}{\frac {\partial ^{2}}{{\partial t}^{2}}}$

Тензорная

Уравнения Максвелла на языке тензоров проясняют ковариацию Лоренца . В этой статье мы вводим электромагнитные тензоры и предварительные четырехвекторы следующим образом:

Имя	Обозначения	Гауссовы единицы	Единицы СИ (Вб или А⋅м)
Электромагнитный тензор	$F^{\alpha \beta }=(F^{01},F^{02},F^{03},\;F^{23},F^{31},F^{12})$	$(-\mathbf {E} ,\;-\mathbf {B} )$	$(-\mathbf {E} /c,\;-\mathbf {B} )$
Двойной электромагнитный тензор	${\tilde {F}}^{\alpha \beta }=({\tilde {F}}^{01},{\tilde {F}}^{02},{\tilde {F}}^{03},\;{\tilde {F}}^{23},{\tilde {F}}^{31},{\tilde {F}}^{12})$	$(-\mathbf {B} ,\;\mathbf {E} )$	$(-\mathbf {B} ,\;\mathbf {E} /c)$
Четырехточечный	$J_{\mathrm {e} }^{\alpha }=(J_{\mathrm {e} }^{0},J_{\mathrm {e} }^{1},J_{\mathrm {e} }^{2},J_{\mathrm {e} }^{3})$	$(c\rho _{\mathrm {e} },\;\mathbf {j} _{\mathrm {e} })$
	$J_{\mathrm {m} }^{\alpha }=(J_{\mathrm {m} }^{0},J_{\mathrm {m} }^{1},J_{\mathrm {m} }^{2},J_{\mathrm {m} }^{3})$	$(c\rho _{\mathrm {m} },\;\mathbf {j} _{\mathrm {m} })$
Четырехпотенциальный	$A_{\mathrm {e} }^{\alpha }=(A_{\mathrm {e} }^{0},A_{\mathrm {e} }^{1},A_{\mathrm {e} }^{2},A_{\mathrm {e} }^{3})$	$(\phi _{\mathrm {e} },\mathbf {A} _{\mathrm {e} })$	$(\phi _{\mathrm {e} }/c,\;\mathbf {A} _{\mathrm {e} })$
	$A_{\mathrm {m} }^{\alpha }=(A_{\mathrm {m} }^{0},A_{\mathrm {m} }^{1},A_{\mathrm {m} }^{2},A_{\mathrm {m} }^{3})$	$(\phi _{\mathrm {m} },\mathbf {A} _{\mathrm {m} })$	$(\phi _{\mathrm {m} }/c,\;\mathbf {A} _{\mathrm {m} })$
Четыре силы	$f_{\alpha }=(f_{0},f_{1},f_{2},f_{3})$	${\frac {1}{\sqrt {1-v^{2}/c^{2}}}}(\mathbf {F} \cdot \mathbf {v} ,\;-\mathbf {F} )$

где:

• Сигнатура метрики Минковского : (+ − − −) .
• Электромагнитный тензор и его двойник Ходжа являются антисимметричными тензорами :

  $F^{\alpha \beta }=-F^{\beta \alpha },\quad {\tilde {F}}^{\alpha \beta }=-{\tilde {F}}^{\beta \alpha }$

Обобщенные уравнения:

Уравнения Максвелла	Гауссовы единицы	Единицы СИ (Вб)	Единицы СИ (А⋅м)
Закон Ампера – Гаусса	$\partial _{\alpha }F^{\alpha \beta }={\frac {4\pi }{c}}J_{\mathrm {e} }^{\beta }$	$\partial _{\alpha }F^{\alpha \beta }=\mu _{0}J_{\mathrm {e} }^{\beta }$
Закон Фарадея – Гаусса	$\partial _{\alpha }{{\tilde {F}}^{\alpha \beta }}={\frac {4\pi }{c}}J_{\mathrm {m} }^{\beta }$	$\partial _{\alpha }{{\tilde {F}}^{\alpha \beta }}={\frac {1}{c}}J_{\mathrm {m} }^{\beta }$	$\partial _{\alpha }{{\tilde {F}}^{\alpha \beta }}={\frac {\mu _{0}}{c}}J_{\mathrm {m} }^{\beta }$
Закон силы Лоренца	$f_{\alpha }=\left[q_{\mathrm {e} }F_{\alpha \beta }+q_{\mathrm {m} }{{\tilde {F}}_{\alpha \beta }}\right]{\frac {v^{\beta }}{c}}$	$f_{\alpha }=\left[q_{\mathrm {e} }F_{\alpha \beta }+{\frac {q_{\mathrm {m} }}{\mu _{0}c}}{{\tilde {F}}_{\alpha \beta }}\right]v^{\beta }$	$f_{\alpha }=\left[q_{\mathrm {e} }F_{\alpha \beta }+{\frac {q_{\mathrm {m} }}{c}}{{\tilde {F}}_{\alpha \beta }}\right]v^{\beta }$

Альтернативно,

Имя	Гауссовы единицы	Единицы СИ (Вб)	Единицы СИ (А⋅м)
Уравнения Максвелла	$\partial ^{\alpha }\partial _{\alpha }A_{\mathrm {e} }^{\beta }-\partial ^{\beta }\partial _{\alpha }A_{\mathrm {e} }^{\alpha }={\frac {4\pi }{c}}J_{\mathrm {e} }^{\beta }$	$\partial ^{\alpha }\partial _{\alpha }A_{\mathrm {e} }^{\beta }-\partial ^{\beta }\partial _{\alpha }A_{\mathrm {e} }^{\alpha }=\mu _{0}J_{\mathrm {e} }^{\beta }$
	$\partial ^{\alpha }\partial _{\alpha }A_{\mathrm {m} }^{\beta }-\partial ^{\beta }\partial _{\alpha }A_{\mathrm {m} }^{\alpha }={\frac {4\pi }{c}}J_{\mathrm {m} }^{\beta }$	$\partial ^{\alpha }\partial _{\alpha }A_{\mathrm {m} }^{\beta }-\partial ^{\beta }\partial _{\alpha }A_{\mathrm {m} }^{\alpha }=\varepsilon _{0}J_{\mathrm {m} }^{\beta }$	${\text{...}}={\frac {1}{c^{2}}}J_{\mathrm {m} }^{\beta }$
Состояние датчика Лоренца	$\partial _{\alpha }A_{\mathrm {e} }^{\alpha }=0,\quad \partial _{\alpha }A_{\mathrm {m} }^{\alpha }=0$
Связь с полями ( Отношения Кабиббо -Феррари-Шанмугадхасан)	$F^{\alpha \beta }=\partial ^{\alpha }A_{\mathrm {e} }^{\beta }-\partial ^{\beta }A_{\mathrm {e} }^{\alpha }-\varepsilon ^{\alpha \beta \mu \nu }\partial _{\mu }A_{{\mathrm {m} }\nu }$ ${\tilde {F}}^{\alpha \beta }=\partial ^{\alpha }A_{\mathrm {m} }^{\beta }-\partial ^{\beta }A_{\mathrm {m} }^{\alpha }+\varepsilon ^{\alpha \beta \mu \nu }\partial _{\mu }A_{{\mathrm {e} }\nu }$	$F^{\alpha \beta }=\partial ^{\alpha }A_{\mathrm {e} }^{\beta }-\partial ^{\beta }A_{\mathrm {e} }^{\alpha }-\mu _{0}c\varepsilon ^{\alpha \beta \mu \nu }\partial _{\mu }A_{{\mathrm {m} }\nu }$ ${\tilde {F}}^{\alpha \beta }=\mu _{0}c(\partial ^{\alpha }A_{\mathrm {m} }^{\beta }-\partial ^{\beta }A_{\mathrm {m} }^{\alpha })+\varepsilon ^{\alpha \beta \mu \nu }\partial _{\mu }A_{{\mathrm {e} }\nu }$

где ε ^авмн является символом Леви-Чивита .

Трансформация дуальности

Обобщенные уравнения Максвелла обладают определенной симметрией, называемой преобразованием двойственности . Можно выбрать любой действительный угол ξ и одновременно изменить поля и заряды повсюду во Вселенной следующим образом (в гауссовских единицах):

Заряды и токи	Поля
${\begin{pmatrix}\rho _{\mathrm {e} }\\\rho _{\mathrm {m} }\end{pmatrix}}={\begin{pmatrix}\cos \xi &-\sin \xi \\\sin \xi &\cos \xi \\\end{pmatrix}}{\begin{pmatrix}\rho _{\mathrm {e} }'\\\rho _{\mathrm {m} }'\end{pmatrix}}$	${\begin{pmatrix}\mathbf {E} \\\mathbf {H} \end{pmatrix}}={\begin{pmatrix}\cos \xi &-\sin \xi \\\sin \xi &\cos \xi \\\end{pmatrix}}{\begin{pmatrix}\mathbf {E'} \\\mathbf {H'} \end{pmatrix}}$
${\begin{pmatrix}\mathbf {J} _{\mathrm {e} }\\\mathbf {J} _{\mathrm {m} }\end{pmatrix}}={\begin{pmatrix}\cos \xi &-\sin \xi \\\sin \xi &\cos \xi \\\end{pmatrix}}{\begin{pmatrix}\mathbf {J} _{\mathrm {e} }'\\\mathbf {J} _{\mathrm {m} }'\end{pmatrix}}$	${\begin{pmatrix}\mathbf {D} \\\mathbf {B} \end{pmatrix}}={\begin{pmatrix}\cos \xi &-\sin \xi \\\sin \xi &\cos \xi \\\end{pmatrix}}{\begin{pmatrix}\mathbf {D'} \\\mathbf {B'} \end{pmatrix}}$

где величины со штрихом — это заряды и поля до преобразования, а величины без штриха — после преобразования. Поля и заряды после этого преобразования по-прежнему подчиняются тем же уравнениям Максвелла.

Из-за преобразования дуальности невозможно однозначно решить, имеет ли частица электрический заряд, магнитный заряд или и то, и другое, просто наблюдая за ее поведением и сравнивая его с уравнениями Максвелла. Например, это просто соглашение, а не требование уравнений Максвелла, что электроны имеют электрический заряд, но не магнитный заряд; после преобразования ξ = π /2 все будет наоборот. Ключевым эмпирическим фактом является то, что все когда-либо наблюдавшиеся частицы имеют одинаковое соотношение магнитного заряда и электрического заряда. Преобразования дуальности могут изменить соотношение на любое произвольное числовое значение, но не могут изменить соотношение всех частиц. Поскольку это так, можно провести дуальное преобразование, которое установит это соотношение равным нулю, так что все частицы не будут иметь магнитного заряда. Этот выбор лежит в основе «традиционных» определений электричества и магнетизма.

Квантование Дирака

Одним из определяющих достижений квантовой теории стала Поля Дирака работа по развитию релятивистского квантового электромагнетизма. До его формулировки наличие электрического заряда просто «вставлялось» в уравнения квантовой механики (КМ), но в 1931 году Дирак показал, что дискретный заряд естественным образом «выпадает» из КМ. Другими словами, мы можем сохранить форму уравнений Максвелла и при этом иметь магнитные заряды.

Рассмотрим систему, состоящую из одного стационарного электрического монополя (скажем, электрона) и одного стационарного магнитного монополя, которые не оказывают друг на друга никаких сил. Классически окружающее их электромагнитное поле имеет плотность импульса, определяемую вектором Пойнтинга , а также полный угловой момент , который пропорционален произведению q _e q _m и не зависит от расстояния между ними.

Однако квантовая механика требует, чтобы угловой момент квантовался как кратный ħ , поэтому произведение q _e q _m также должно быть квантовано. Это означает, что если бы во Вселенной существовал хотя бы один магнитный монополь и форма уравнений Максвелла верна, все электрические заряды тогда были бы квантованы .

Хотя в приведенном выше примере можно было бы просто интегрировать по всему пространству, чтобы найти полный угловой момент, Дирак применил другой подход. Это привело его к новым идеям. Он рассматривал точечный магнитный заряд, магнитное поле которого ведет себя как q _м / р  ² и направлена ​​в радиальном направлении, расположенном в начале координат. Поскольку дивергенция B равна нулю везде, кроме места магнитного монополя при = 0 , можно локально определить векторный потенциал так, чтобы ротор векторного потенциала A был равен магнитному полю B. r

Однако векторный потенциал не может быть определен глобально именно потому, что дивергенция магнитного поля пропорциональна дельта -функции Дирака в начале координат. Мы должны определить один набор функций для векторного потенциала в «северном полушарии» (полупространство z ​​> 0 над частицей) и другой набор функций для «южного полушария». Эти два векторных потенциала согласованы на «экваторе» (плоскость z = 0 , проходящая через частицу) и отличаются калибровочным преобразованием . Волновая функция электрически заряженной частицы («зондовый заряд»), вращающейся вокруг «экватора», обычно изменяется по фазе, во многом как в эффекте Ааронова-Бома . Эта фаза пропорциональна электрическому заряду q _e зонда, а также магнитному заряду q _m источника. Первоначально Дирак рассматривал электрон , волновая функция которого описывается уравнением Дирака .

Поскольку электрон возвращается в ту же точку после полного обхода экватора, фаза φ его волновой функции e ^iφ должна быть неизменной, а это означает, что добавленная к волновой функции фаза φ должна быть кратна 2 π . Это известно как условие квантования Дирака . В различных единицах это условие можно выразить так:

Единицы	Состояние
Единицы СИ ( Вебера ) конвенция	${\frac {q_{\mathrm {e} }q_{\mathrm {m} }}{2\pi \hbar }}\in \mathbb {Z}$
Единицы СИ ( условное обозначение амперметра )	${\frac {q_{\mathrm {e} }q_{\mathrm {m} }}{2\pi \varepsilon _{0}\hbar c^{2}}}\in \mathbb {Z}$
Единицы Гаусса-СГС	$2{\frac {q_{\mathrm {e} }q_{\mathrm {m} }}{\hbar c}}\in \mathbb {Z}$

где ε ₀ — диэлектрическая проницаемость вакуума , ħ = h /2 π — приведенная постоянная Планка , c — скорость света , и $\mathbb {Z}$ представляет собой набор целых чисел .

Гипотетическое существование магнитного монополя означало бы, что электрический заряд должен быть квантован в определенных единицах; кроме того, существование электрических зарядов означает, что магнитные заряды гипотетических магнитных монополей, если они существуют, должны быть квантованы в единицах, обратно пропорциональных элементарному электрическому заряду.

В то время было неясно, существует ли такая вещь или вообще должна ли она существовать. В конце концов, могла бы появиться другая теория, которая объяснила бы квантование заряда без необходимости использования монополя. Эта концепция оставалась чем-то вроде курьезности. Однако за время, прошедшее после публикации этой плодотворной работы, не появилось никакого другого общепринятого объяснения квантования заряда. (Концепция локальной калибровочной инвариантности — см. Калибровочная теория — дает естественное объяснение квантования заряда, не вызывая необходимости в магнитных монополях; но только если калибровочная группа U (1) компактна, и в этом случае у нас все равно есть магнитные монополи. )

Если максимально расширить определение векторного потенциала для южного полушария, то он будет определен везде, кроме полубесконечной линии, протянутой от начала координат в направлении к северному полюсу. Эта полубесконечная линия называется струной Дирака , и ее влияние на волновую функцию аналогично влиянию соленоида в эффекте Ааронова-Бома . Условие квантования исходит из требования, чтобы фазы вокруг струны Дирака были тривиальны, а это означает, что струна Дирака должна быть нефизической. Струна Дирака — это всего лишь артефакт используемой координатной карты, и ее не следует воспринимать всерьез.

Монополь Дирака является сингулярным решением уравнения Максвелла (поскольку оно требует удаления мировой линии из пространства-времени); в более сложных теориях его заменяет гладкое решение, такое как монополь 'т Хоофта – Полякова .

интерпретация

Строка Дирака

Основная статья: струна Дирака

Калибровочная теория , такая как электромагнетизм, определяется калибровочным полем, которое связывает групповой элемент с каждым путем в пространстве-времени. Для бесконечно малых путей групповой элемент близок к единице, тогда как для более длинных путей групповой элемент представляет собой последовательное произведение бесконечно малых групповых элементов на этом пути.

В электродинамике эта группа — это U(1) — единичные комплексные числа при умножении. Для бесконечно малых путей элементом группы является 1 + iA _µ dx ^м из чего следует, что для конечных путей, параметризованных s , групповым элементом является:

$\prod _{s}\left(1+ieA_{\mu }{dx^{\mu } \over ds}\,ds\right)=\exp \left(ie\int A\cdot dx\right).$

Отображение путей к элементам группы называется петлей Вильсона или голономией , а для калибровочной группы U (1) это фазовый коэффициент, который приобретает волновая функция заряженной частицы при прохождении пути. Для цикла:

$e\oint _{\partial D}A\cdot dx=e\int _{D}(\nabla \times A)\,dS=e\int _{D}B\,dS.$

Таким образом, фаза, которую приобретает заряженная частица при движении по петле, представляет собой магнитный поток через петлю. Когда небольшой соленоид имеет магнитный поток, возникают интерференционные полосы для заряженных частиц, которые движутся вокруг соленоида или вокруг разных сторон соленоида, что указывает на его присутствие.

Но если заряды всех частиц кратны e , соленоиды с потоком 2 π / e не имеют интерференционных полос, поскольку фазовый фактор для любой заряженной частицы равен exp(2 π i ) = 1 . Такой соленоид, если он достаточно тонкий, квантово-механически невидим. Если бы такой соленоид переносил поток 2 π / e , то, когда поток вытекал бы из одного из его концов, он был бы неотличим от монополя.

Решение монополя Дирака фактически описывает бесконечно малый линейный соленоид, заканчивающийся в точке, а местоположение соленоида является сингулярной частью решения, струной Дирака. Струны Дирака связывают монополи и антимонополи с противоположным магнитным зарядом, хотя в версии Дирака струна просто уходит в бесконечность. Строка ненаблюдаема, поэтому ее можно разместить где угодно, а с помощью двух участков координат поле в каждом фрагменте можно сделать несингулярным, переместив строку туда, где ее нельзя увидеть.

Теории Великого объединения

Main article: 't Hooft–Polyakov monopole

В калибровочной группе U(1) с квантованным зарядом группа представляет собой круг радиуса 2 π / e . Такая калибровочная группа U(1) называется компактной . Любая U(1), возникшая из теории великого объединения (GUT), компактна, потому что смысл имеют только компактные группы с более высокой калибровкой. Размер калибровочной группы является мерой обратной константы связи, так что в пределе калибровочной группы большого объема взаимодействие любого фиксированного представления стремится к нулю.

Случай калибровочной группы U(1) является особым случаем, поскольку все ее неприводимые представления имеют одинаковый размер – заряд больше на целое число, но поле по-прежнему представляет собой просто комплексное число – так что в U(1 ) теории калибровочного поля можно без противоречия взять декомпактифицированный предел. Квант заряда становится мал, но каждая заряженная частица имеет огромное количество квантов заряда, поэтому ее заряд остается конечным. В некомпактной теории калибровочной группы U (1) заряды частиц, как правило, не являются целыми кратными одной единицы. Поскольку квантование заряда является экспериментальной достоверностью, ясно, что калибровочная группа электромагнетизма U (1) компактна.

GUT приводят к компактным калибровочным группам U(1), поэтому они объясняют квантование заряда способом, который кажется логически независимым от магнитных монополей. Однако объяснение, по сути, то же самое, поскольку в любой ТЕ, которая распадается на калибровочную группу U(1) на больших расстояниях, существуют магнитные монополи.

Аргумент топологический:

1. Голономия калибровочного поля отображает петли в элементы калибровочной группы. Бесконечно малые циклы отображаются на элементы группы, бесконечно близкие к единице.
2. Если вы вообразите большую сферу в космосе, вы можете деформировать бесконечно малую петлю, которая начинается и заканчивается на северном полюсе, следующим образом: растяните петлю над западным полушарием, пока она не превратится в большой круг (который по-прежнему начинается и заканчивается на северном полюсе). ), а затем дайте ему снова сжаться в небольшую петлю, проходя через восточное полушарие. Это называется арканом сферы .
3. Лассо — это последовательность петель, поэтому голономия отображает его в последовательность элементов группы, непрерывный путь в калибровочной группе. Поскольку петля в начале аркана такая же, как петля в конце, путь в группе замкнутый.
4. Если групповой путь, связанный с процедурой аркана, обвивает U(1), сфера содержит магнитный заряд. Во время аркана голономия меняется на величину магнитного потока через сферу.
5. Поскольку голономия в начале и в конце тождественна, полный магнитный поток квантовается. Магнитный заряд пропорционален числу витков N , магнитный поток через сферу равен 2 π N / e . Это условие квантования Дирака, и это топологическое условие, которое требует, чтобы конфигурации калибровочного поля U (1) на больших расстояниях были согласованными.
6. Когда калибровочная группа U(1) возникает в результате разрушения компактной группы Ли , путь, который достаточное количество раз обходит группу U(1), топологически тривиален в большой группе. В не-U(1) компактной группе Ли накрывающее пространство представляет собой группу Ли с той же алгеброй Ли , но где все замкнутые петли стягиваемы . Группы Ли однородны, так что любой цикл в группе можно переместить так, чтобы он начинался с единицы, затем его подъем до накрывающей группы заканчивался в точке P , что является подъемом единицы. Обойдя цикл дважды, вы доберетесь до P. ² , три раза на P ³ , все лифты тож. Но лифтов тождества конечное число, потому что лифты не могут накапливаться. Количество раз, которое нужно пройти по циклу, чтобы сделать его сжимаемым, невелико, например, если группа GUT — SO(3), покрывающая группа — SU(2), и обхода любого цикла дважды достаточно.
7. Это означает, что наличие непрерывной конфигурации калибровочного поля в группе GUT позволяет конфигурации монополя U(1) раскручиваться на коротких расстояниях за счет того, что она не остается в U(1). Чтобы сделать это с как можно меньшей энергией, следует оставить только калибровочную группу U(1) в окрестности одной точки, которая называется ядром монополя . Вне сердечника монополь обладает только энергией магнитного поля.

Следовательно, монополь Дирака является топологическим дефектом в компактной калибровочной теории U(1). Когда нет ТВО, дефект представляет собой сингулярность – ядро ​​сжимается в точку. Но когда в пространстве-времени есть какой-то регулятор на малых расстояниях, монополи имеют конечную массу. Монополи возникают в решетке U(1) , и там размер ядра равен размеру решетки. В общем, ожидается, что они будут происходить всякий раз, когда есть регулятор ближнего действия.

Теория струн

Во Вселенной квантовая гравитация является регулятором. С учетом гравитации монопольная сингулярность может представлять собой черную дыру, а при больших магнитных заряде и массе масса черной дыры равна заряду черной дыры, так что масса магнитной черной дыры не бесконечна. Если черная дыра может полностью распасться излучением Хокинга , то легчайшие заряженные частицы не могут быть слишком тяжелыми. Самый легкий монополь должен иметь массу, меньшую или сравнимую с его зарядом в натуральных единицах .

Итак, в последовательной голографической теории, единственным известным примером которой является теория струн , всегда существуют монополи конечной массы. Для обычного электромагнетизма верхняя граница массы не очень полезна, поскольку она примерно того же размера, что и планковская масса .

формулировка

В математике (классическое) калибровочное поле определяется как связность над главным G-расслоением в пространстве-времени. G — калибровочная группа, действующая на каждом слое расслоения отдельно.

Соединение -пучке подскажет вам , на G склеить волокна в соседних точках M. как Он начинается с непрерывной группы симметрии G , которая действует на слое F , а затем сопоставляет элемент группы с каждым бесконечно малым путем. Групповое умножение вдоль любого пути подскажет вам, как перемещаться из одной точки пучка в другую, используя элемент G связанный с путем, действующим на волокно F. ,

В математике определение пучка призвано подчеркнуть топологию, поэтому понятие связи добавляется второстепенно. В физике связь является фундаментальным физическим объектом. Одно из фундаментальных наблюдений теории характеристических классов в алгебраической топологии состоит в том, что многие гомотопические структуры нетривиальных главных расслоений могут быть выражены как интеграл от некоторого многочлена по любой связности над ним. Обратите внимание, что связность над тривиальным расслоением никогда не может дать нам нетривиальное главное расслоение.

Если пространство-время $\mathbb {R} ^{4}$ пространство всех возможных связностей G -расслоения связно . Но представьте, что произойдет, если мы удалим времяподобную мировую линию из пространства-времени. Полученное пространство-время гомотопически эквивалентно сфере топологической S ² .

Главное G -расслоение над S ² определяется покрытием S ² двумя картами , каждая из которых гомеоморфна открытому 2-шару, и их пересечение гомеоморфно полосе S ¹ × Я. ​2-шары гомотопически тривиальны, а полоса гомотопически эквивалентна окружности S ¹ . Таким образом, топологическая классификация возможных связей сводится к классификации функций перехода. Функция перехода отображает полосу в G различные способы отображения полосы в G задаются первой гомотопической G. , а группой

Таким образом, в формулировке G -расслоения калибровочная теория допускает монополи Дирака при условии, что G не является односвязным , всякий раз, когда существуют пути, огибающие группу, которые не могут быть деформированы в постоянный путь (путь, образ которого состоит из одной точки). U(1), имеющая квантованные заряды, не является односвязной и может иметь монополи Дирака, а $\mathbb {R}$, ее универсальная накрывающая группа , односвязна , не имеет квантованных зарядов и не допускает монополей Дирака. Математическое определение эквивалентно физическому определению при условии, что, следуя Дираку, допускаются калибровочные поля, которые определяются только по участкам, а калибровочные поля на разных участках склеиваются после калибровочного преобразования.

Полный магнитный поток есть не что иное, как первое число Черна главного пучка и зависит только от выбора главного пучка, а не от конкретной связи над ним. Другими словами, это топологический инвариант.

Этот аргумент в пользу монополей является повторением аргумента лассо для чистой теории U(1). Он обобщается на измерения d + 1 с d ≥ 2 несколькими способами. Один из способов — расширить все на дополнительные измерения, чтобы монополи U(1) стали листами размерности d − 3 . Другой способ — изучить тип топологической особенности в точке с гомотопической группой π _{d −2} (G) .

Теории Великого объединения

В последние годы новый класс теорий также предположил существование магнитных монополей.

В начале 1970-х годов успехи квантовой теории поля и калибровочной теории в развитии электрослабой теории и математики сильного ядерного взаимодействия побудили многих теоретиков перейти к попыткам объединить их в единую теорию, известную как Теория Великого Объединения (Теория Великого Объединения ). ГУТ). Было предложено несколько GUT, большинство из которых предполагало наличие реальной частицы магнитного монополя. Точнее, GUT предсказал ряд частиц, известных как дионы , из которых самым основным состоянием был монополь. Заряд магнитных монополей, предсказанный GUT, составляет либо 1, либо 2 гД , в зависимости от теории.

Большинство частиц, появляющихся в любой квантовой теории поля, нестабильны и распадаются на другие частицы в ходе множества реакций, которые должны удовлетворять различным законам сохранения . Стабильные частицы стабильны, потому что не существует более легких частиц, на которые они могли бы распадаться и при этом удовлетворять законам сохранения. Например, электрон имеет лептонное число , равное единице, и электрический заряд, равный единице, и не существует более легких частиц, сохраняющих эти значения. С другой стороны, мюон , по сути, тяжелый электрон, может распасться на электрон плюс два кванта энергии, и, следовательно, он нестабилен.

Дионы в этих GUT также стабильны, но по совершенно другой причине. Ожидается, что дионы будут существовать как побочный эффект «замораживания» условий ранней Вселенной или нарушения симметрии . В этом сценарии дионы возникают из-за конфигурации вакуума в определенной области Вселенной, согласно оригинальной теории Дирака. Они остаются стабильными не из-за условия сохранения, а потому, что не существует более простого топологического состояния, в которое они могут распасться.

Масштаб длины, в котором существует эта особая вакуумная конфигурация, называется корреляционной длиной системы. Длина корреляции не может быть больше, чем причинность позволяет , поэтому длина корреляции для создания магнитных монополей должна быть по крайней мере такой же большой, как размер горизонта, определяемый метрикой расширяющейся Вселенной . Согласно этой логике, на объем горизонта должен приходиться хотя бы один магнитный монополь, как это было при нарушении симметрии.

Космологические модели событий, последовавших за Большим взрывом, позволяют предсказывать объем горизонта, что приводит к предсказаниям современной плотности монополей. Ранние модели предсказывали огромную плотность монополей, что явно противоречило экспериментальным данным. Это называлось « проблемой монополя ». Его широко признанное решение заключалось не в изменении предсказаний физики частиц о монополях, а скорее в космологических моделях, используемых для вывода об их современной плотности. В частности, более поздние теории космической инфляции резко сокращают предсказанное количество магнитных монополей до достаточно малой плотности, чтобы неудивительно, что люди никогда их не видели. Это решение «проблемы монополя» рассматривалось как успех теории космической инфляции . (Однако, конечно, это будет заметным успехом только в том случае, если предсказание монополя физики элементарных частиц верно. По этим причинам монополи стали основным интересом в 1970-х и 80-х годах, наряду с другими «достижимыми» предсказаниями Великого Объединения, такими как распад протона .

Многие другие частицы, предсказанные этими теориями Великого Объединения, оказались за пределами возможностей обнаружения в текущих экспериментах. Например, предсказано, что широкий класс частиц, известных как X- и Y-бозоны, будет опосредовать взаимодействие электрослабого и сильного взаимодействий, но эти частицы чрезвычайно тяжелы и находятся далеко за пределами возможностей любого разумного ускорителя частиц .

Поиски

Экспериментальные поиски магнитных монополей можно отнести к одной из двух категорий: те, которые пытаются обнаружить ранее существовавшие магнитные монополи, и те, которые пытаются создать и обнаружить новые магнитные монополи.

Прохождение магнитного монополя через катушку с проводом индуцирует в катушке чистый ток. Это не относится к магнитному диполю или магнитному полюсу более высокого порядка, для которого суммарный индуцированный ток равен нулю, и, следовательно, этот эффект можно использовать в качестве однозначного теста на наличие магнитных монополей. В проводе с конечным сопротивлением индуцированный ток быстро рассеивает свою энергию в виде тепла, но в сверхпроводящей петле индуцированный ток длится долго. Используя высокочувствительное «сверхпроводящее квантовое интерференционное устройство» ( СКВИД ), в принципе можно обнаружить даже один магнитный монополь.

Согласно стандартной инфляционной космологии, магнитные монополи, возникшие до инфляции, сегодня были бы разбавлены до чрезвычайно низкой плотности. Магнитные монополи также могли быть получены термическим путем после инфляции, в период повторного нагрева. Однако текущие ограничения температуры повторного нагрева составляют 18 порядков, и, как следствие, плотность магнитных монополей сегодня не очень хорошо ограничена теорией.

Было много поисков ранее существовавших магнитных монополей. Хотя было зарегистрировано одно дразнящее событие, произошедшее Бласом Кабрерой Наварро в ночь на 14 февраля 1982 года (поэтому его иногда называют « Монополем Дня святого Валентина »). ), никогда не было воспроизводимых доказательств существования магнитных монополей. Отсутствие таких событий накладывает верхний предел на число монополей примерно в один монополь на 10. ²⁹ нуклоны .

Результатом другого эксперимента 1975 года стало сообщение об обнаружении движущегося магнитного монополя в космических лучах группой под руководством П. Буфорда Прайса . Позже Прайс отказался от своего заявления, а возможное альтернативное объяснение предложил Луис Вальтер Альварес . В его работе было продемонстрировано, что путь события космических лучей, заявленный как следствие магнитного монополя, может быть воспроизведен путем платины ядра распада сначала на осмий , а затем на тантал .

Коллайдеры частиц высоких энергий использовались для создания магнитных монополей. Из-за сохранения магнитного заряда магнитные монополи должны создаваться парами: один северный, другой южный. Благодаря сохранению энергии могут быть созданы только магнитные монополи с массами, меньшими половины энергии центра масс сталкивающихся частиц. Помимо этого, теоретически очень мало известно о создании магнитных монополей при столкновениях частиц высоких энергий. Это связано с их большим магнитным зарядом, который делает недействительными все обычные методы расчета. Как следствие, поиск магнитных монополей на коллайдерах пока не может дать нижние границы массы магнитных монополей. Однако они могут обеспечить верхние границы вероятности (или сечения) образования пар в зависимости от энергии.

Эксперимент ATLAS на Большом адронном коллайдере в настоящее время имеет самые строгие пределы сечения для магнитных монополей с 1 и 2 зарядами Дирака, производимых посредством образования пар Дрелла-Яна . Команда под руководством Венди Тейлор ищет эти частицы, основываясь на теориях, которые определяют их как долгоживущие (они не распадаются быстро), а также сильно ионизирующие (их взаимодействие с веществом преимущественно ионизирующее). В 2019 году поиск магнитных монополей в детекторе ATLAS сообщил о своих первых результатах на основе данных, собранных в результате столкновений LHC Run 2 с энергией центра масс 13 ТэВ, что при энергии 34,4 ФБ. ⁻¹ это самый большой набор данных, проанализированный на сегодняшний день.

Эксперимент MoEDAL , установленный на Большом адронном коллайдере, в настоящее время занимается поиском магнитных монополей и крупных суперсимметричных частиц с использованием детекторов ядерных треков и алюминиевых стержней вокруг LHCb детектора VELO . Частицы, которые он ищет, на своем пути повреждают пластиковые листы, из которых состоят детекторы ядерных треков, с различными отличительными признаками. Кроме того, алюминиевые стержни могут улавливать достаточно медленно движущиеся магнитные монополи. Затем бруски можно проанализировать, пропустив их через СКВИД.

Астрофизик Игорь Новиков утверждает, что поля макроскопических черных дыр являются потенциальными магнитными монополями, представляющими собой вход в мост Эйнштейна-Розена .

«Монополи» в конденсированных системах

Примерно с 2003 года различные группы физики конденсированного состояния использовали термин «магнитный монополь» для описания другого и во многом несвязанного явления.

Настоящий магнитный монополь был бы новой элементарной частицей и нарушал бы закон Гаусса для магнетизма ∇⋅ B = 0 . Монополь такого типа, который помог бы объяснить закон квантования заряда , сформулированный Полем Дираком в 1931 году: никогда не наблюдалось в экспериментах.

Монополи, изучаемые группами конденсированного состояния, не обладают ни одним из этих свойств. Они не являются новой элементарной частицей, а скорее возникающим явлением в системах повседневных частиц ( протонов , нейтронов , электронов , фотонов ); другими словами, они являются квазичастицами . Они не являются источниками B -поля (т.е. не нарушают ∇⋅ B = 0 ); вместо этого они являются источниками для других полей, например H -поля , « B * -поле» (связанное со сверхтекучей завихренностью), или различные другие квантовые поля. Они не имеют прямого отношения к теориям великого объединения или другим аспектам физики элементарных частиц и не помогают объяснить квантование заряда — за исключением тех случаев, когда исследования аналогичных ситуаций могут помочь подтвердить, что используемый математический анализ верен.

есть ряд примеров В физике конденсированного состояния , когда коллективное поведение приводит к возникновению явлений, в некоторых отношениях напоминающих магнитные монополи. включая, прежде всего, материалы спинового льда . Хотя их не следует путать с гипотетическими элементарными монополями, существующими в вакууме, они, тем не менее, обладают схожими свойствами и могут быть исследованы с использованием аналогичных методов.

Некоторые исследователи используют термин «магнетичность» для описания манипуляций с магнитными монопольными квазичастицами в спиновом льду . по аналогии со словом «электричество».

Одним из примеров работ по магнитным монопольным квазичастицам является статья, опубликованная в журнале Science в сентябре 2009 года, в которой исследователи описали наблюдение квазичастиц, напоминающих магнитные монополи. Монокристалл спинового льда материала титаната диспрозия был охлажден до температуры от 0,6 до 2,0 кельвина . Используя наблюдения за рассеянием нейтронов , было показано, что магнитные моменты выстраиваются в переплетенные трубчатые пучки, напоминающие струны Дирака . На дефекте, образованном концом каждой трубки, магнитное поле имеет вид монополя. Используя приложенное магнитное поле для нарушения симметрии системы, исследователи смогли контролировать плотность и ориентацию этих струн. Описан также вклад в теплоемкость системы эффективного газа этих квазичастиц. Это исследование было удостоено премии Еврофизики 2012 года в области физики конденсированного состояния.

В другом примере статья в журнале Nature Physics от 11 февраля 2011 года описывает создание и измерение долгоживущих магнитных монопольных токов квазичастиц в спиновом льду. Приложив импульс магнитного поля к кристаллу титаната диспрозия при температуре 0,36 К, авторы создали релаксирующий магнитный ток, который длился несколько минут. Они измерили ток с помощью электродвижущей силы, которую он индуцировал в соленоиде, соединенном с чувствительным усилителем, и количественно описали его, используя химико-кинетическую модель точечных зарядов, подчиняющихся механизму диссоциации и рекомбинации носителей Онзагера-Вина. Таким образом, они получили микроскопические параметры движения монополя в спиновом льду и определили различные роли свободных и связанных магнитных зарядов.

В сверхтекучих средах существует поле B * , связанное со сверхтекучей завихренностью, которое математически аналогично магнитному B -полю. Из-за сходства поле B * называют «синтетическим магнитным полем». В январе 2014 года сообщалось, что монопольные квазичастицы для поля B * были созданы и исследованы в спинорном бозе-эйнштейновском конденсате. Это первый пример квазимагнитного монополя, наблюдаемого в системе, подчиняющейся квантовой теории поля.

Обновления теоретических и экспериментальных поисков материи можно найти в докладах Дж. Джакомелли (2000) и С. Балестры (2011) в разделе «Библиография».

См. также

• Уравнения Богомольного
• струна Дирака
• Там
• Феликс Эренхафт
• Проблема плоскостности
• Закон Гаусса для магнетизма
• Теория Гинзбурга – Ландау
• Массив Хальбаха
• Проблема горизонта
• Инстантон
• Проблема магнитного монополя
• Есть
• Солитон
• 't Hooft–Polyakov monopole
• Монополь Ву – Янга
• Магнитный ток

Ссылки

Библиография

• Атья, МФ; Хитчин, Н. (1988). Геометрия и динамика магнитных монополей . Издательство Принстонского университета. ISBN  0-691-08480-7 .
• Балестра, С. (2011), Библиография магнитных монополей-II , arXiv : 1105.5587
• Брау, Калифорния (2004). Современные проблемы классической электродинамики . Издательство Оксфордского университета. ISBN  978-0-19-514665-3 .
• Хитчин, Нью-Джерси; Мюррей, МК (1988). «Спектральные кривые и метод ADHM» . Комм. Математика. Физ . 114 (3): 463–474. Бибкод : 1988CMaPh.114..463H . дои : 10.1007/BF01242139 . S2CID   123573860 .
• Джакомелли, Г. (2000), Библиография по магнитным монополям (PDF)
• Джексон, JD (1999). Классическая электродинамика (3-е изд.). Уайли. ISBN  978-0-471-30932-1 .
• Лакава, Ф. (2022). Классическая электродинамика: от зарядов изображения к массе фотона и магнитным монополям (2-е изд.). Спрингер. ISBN  978-3-031-05098-5 .
• Лехнер, К. (2018). Классическая электродинамика: современный взгляд . Спрингер. ISBN  978-3-319-91808-2 .
• Лочак Г.; Штумпф, Х. (2015). Лептонный магнитный монополь: теория и эксперименты . Эльзевир. ISBN  978-0-12-802463-8 .
• Милтон, Калифорния (2006). «Теоретическое и экспериментальное состояние магнитных монополей». Отчеты о прогрессе в физике . 69 (6): 1637–1711. arXiv : hep-ex/0602040 . Бибкод : 2006РПФ...69.1637М . дои : 10.1088/0034-4885/69/6/R02 . S2CID   119061150 .
• Шнир, Ю.М. (2005). Магнитные монополи . Спрингер. ISBN  978-3-540-25277-1 .
• Сатклифф, премьер-министр (1997). «Монополи БПС». Межд. Дж. Мод. Физ. А. ​ 12 (26): 4663–4706. arXiv : hep-th/9707009 . Бибкод : 1997IJMPA..12.4663S . дои : 10.1142/S0217751X97002504 . S2CID   16765577 .
• Вонсовский, С.В. (1975). Магнетизм элементарных частиц . Издательство «Мир».

Внешние ссылки

В этой статье использованы материалы из Н. Хитчин (2001) [1994], «Магнитный монополь» , Энциклопедия математики , EMS Press , лицензия на которую распространяется по лицензии Creative Commons Attribution/Share-Alike и лицензии GNU Free Documentation License .