Крутящий момент

Крутящий момент
Крутящий момент
	Связь между силой F , крутящим моментом τ , линейным моментом p и угловым моментом L в системе, вращение которой ограничено только одной плоскостью (силы и моменты, возникающие под действием силы тяжести и трения, не учитываются).
Общие символы	, М
единица СИ	N⋅m
Другие подразделения	фунт-сила-фут , фунт-сила ⋅дюйм, унция⋅дюйм
В базовых единицах СИ	kg⋅m 2 ⋅s −2
Измерение

В физике и механике . момент является вращательным аналогом линейной силы крутящий ^[1] Его также называют моментом силы (также сокращенно момент ). Символ крутящего момента обычно ${\boldsymbol {\tau }}$ , строчная греческая буква тау . Когда его называют моментом обычно обозначают $М.$ силы, его Точно так же, как линейная сила — это толчок или притяжение, приложенное к телу, крутящий момент можно рассматривать как поворот, приложенный к объекту относительно выбранной точки; например, при завинчивании винта используется крутящий момент, который прикладывается отверткой, вращающейся вокруг своей оси . сила в три ньютона, приложенная в двух метрах Например, от точки опоры, оказывает тот же крутящий момент, что и сила в один ньютон, приложенная в шести метрах от точки опоры.

История

Эта концепция возникла в результате исследований Архимедом использования рычагов , что отражено в его знаменитой цитате: «Дайте мне рычаг и точку опоры, и я переверну Землю». Термин «крутящий момент» (от латинского torquere — «скручивать»), как говорят, был предложен Джеймсом Томсоном и появился в печати в апреле 1884 года. ^[2]^[3]^[4] Использование засвидетельствовано в том же году Сильванусом П. Томпсоном в первом издании Dynamo-Electric Machinery . ^[4] Томпсон мотивирует этот термин следующим образом: ^[3]

Точно так же, как ньютоновское определение силы — это сила, которая производит или стремится вызвать движение (вдоль линии), так и крутящий момент можно определить как силу, которая вызывает или стремится вызвать кручение (вокруг оси). Лучше использовать термин, рассматривающий это действие как единую определенную сущность, чем использовать такие термины, как « пара » и « момент », которые предполагают более сложные идеи. Единственное понятие поворота, применяемого для поворота вала, лучше, чем более сложное понятие приложения линейной силы (или пары сил) с определенным рычагом.

Сегодня крутящий момент называют разным словарем в зависимости от географического положения и области исследования. Эта статья следует определению, используемому в американской физике при использовании слова «крутящий момент» . ^[5]

В Великобритании и в машиностроении США крутящий момент называют моментом силы , обычно сокращаемым до момента . ^[6] Эту терминологию можно проследить по крайней мере до 1811 года в Симеона Дени Пуассона «Трактате о механике» . ^[7] Английский перевод работы Пуассона появляется в 1842 году.

Определение и связь с другими физическими величинами

Сила, приложенная перпендикулярно рычагу, умноженная на расстояние от точки опоры рычага (длину плеча рычага ), является его крутящим моментом. Следовательно, крутящий момент определяется как произведение величины перпендикулярной составляющей силы и расстояния линии действия силы от точки, вокруг которой она определяется. В трех измерениях крутящий момент представляет собой псевдовектор ; для точечных частиц оно определяется векторным произведением вектора смещения и вектора силы. Направление крутящего момента можно определить, воспользовавшись правилом хвата правой рукой : если пальцы правой руки согнуты от направления плеча рычага к направлению силы, то большой палец указывает в направлении крутящего момента. ^[8] Отсюда следует, что вектор крутящего момента перпендикулярен векторам положения и силы и определяет плоскость, в которой лежат два вектора. Направление результирующего вектора крутящего момента определяется по правилу правой руки. Следовательно, любая сила, направленная параллельно вектору положения частицы, не создает крутящего момента. ^[9]^[10] Величина крутящего момента, приложенного к твердому телу, зависит от трех величин: приложенной силы, вектора плеча рычага. ^[11] соединение точки, относительно которой измеряется крутящий момент, с точкой приложения силы и углом между векторами силы и плеча рычага. В символах:

${\boldsymbol {\tau }}=\mathbf {r} \times \mathbf {F} \implies \tau =rF_{\perp }=rF\sin \theta$

где

${\boldsymbol {\tau }}$ вектор крутящего момента и $\tau$ - величина крутящего момента,
$\mathbf {r}$ – вектор положения (вектор от точки, относительно которой измеряется крутящий момент, до точки приложения силы), а r – величина вектора положения,
$\mathbf {F}$ — вектор силы, F — величина вектора силы, а F _⊥ — величина силы, направленной перпендикулярно положению частицы,
$\times$ обозначает векторное произведение , которое дает вектор, перпендикулярный как к $r,$ так и к $F,$ в соответствии с правилом правой руки ,
$\theta$ - угол между вектором силы и вектором плеча рычага.

Единицей в системе СИ крутящего момента является ньютон-метр (Нм). Дополнительную информацию о единицах крутящего момента см. в § Единицы измерения .

Связь с угловым моментом

Чистый крутящий момент тела определяет скорость изменения углового момента тела .

${\boldsymbol {\tau }}={\frac {\mathrm {d} \mathbf {L} }{\mathrm {d} t}}$

где L — вектор углового момента, а t — время. Для движения точечной частицы

$\mathbf {L} =I{\boldsymbol {\omega }},$

где ${\textstyle I=mr^{2}}$ – момент инерции , ω – псевдовектор орбитальной угловой скорости . Отсюда следует, что

${\boldsymbol {\tau }}_{\mathrm {net} }=I_{1}{\dot {\omega _{1}}}{\hat {\boldsymbol {e_{1}}}}+I_{2}{\dot {\omega _{2}}}{\hat {\boldsymbol {e_{2}}}}+I_{3}{\dot {\omega _{3}}}{\hat {\boldsymbol {e_{3}}}}+I_{1}\omega _{1}{\frac {d{\hat {\boldsymbol {e_{1}}}}}{dt}}+I_{2}\omega _{2}{\frac {d{\hat {\boldsymbol {e_{2}}}}}{dt}}+I_{3}\omega _{3}{\frac {d{\hat {\boldsymbol {e_{3}}}}}{dt}}=I{\boldsymbol {\dot {\omega }}}+{\boldsymbol {\omega }}\times (I{\boldsymbol {\omega }})$

производной вектора использование ${d{\boldsymbol {\hat {e_{i}}}} \over dt}={\boldsymbol {\omega }}\times {\boldsymbol {\hat {e_{i}}}}$ Это уравнение является вращательным аналогом второго закона Ньютона для точечных частиц и справедливо для любого типа траектории. В некоторых простых случаях, например, при вращающемся диске, где на оси вращения действует только момент инерции, второй закон Ньютона вращения может быть равен: ${\boldsymbol {\tau }}=I{\boldsymbol {\alpha }}$ где ${\boldsymbol {\alpha }}={\dot {\boldsymbol {\omega }}}$ .

Доказательство эквивалентности определений

Определение углового момента для одиночной точечной частицы: $\mathbf {L} =\mathbf {r} \times \mathbf {p}$ где p частицы — линейный импульс , а r — вектор положения от начала координат. Производная по времени:

${\frac {\mathrm {d} \mathbf {L} }{\mathrm {d} t}}=\mathbf {r} \times {\frac {\mathrm {d} \mathbf {p} }{\mathrm {d} t}}+{\frac {\mathrm {d} \mathbf {r} }{\mathrm {d} t}}\times \mathbf {p} .$

Этот результат легко доказать, разбив векторы на компоненты и применив правило произведения . Но поскольку скорость изменения импульса равна силе ${\textstyle \mathbf {F} }$ а скорость изменения положения - это скорость ${\textstyle \mathbf {v} }$ ,

${\frac {\mathrm {d} \mathbf {L} }{\mathrm {d} t}}=\mathbf {r} \times \mathbf {F} +\mathbf {v} \times \mathbf {p}$

Перекрестное произведение импульса $\mathbf {p}$ с соответствующей скоростью $\mathbf {v}$ равно нулю, поскольку скорость и импульс параллельны, поэтому второй член обращается в нуль. Следовательно, крутящий момент частицы равен первой производной ее углового момента по времени. Если приложено несколько сил, согласно второму закону Ньютона следует, что ${\frac {\mathrm {d} \mathbf {L} }{\mathrm {d} t}}=\mathbf {r} \times \mathbf {F} _{\mathrm {net} }={\boldsymbol {\tau }}_{\mathrm {net} }.$

Это общее доказательство для точечных частиц, но его можно обобщить и на систему точечных частиц, применив приведенное выше доказательство к каждой точечной частице и затем просуммировав по всем точечным частицам. Точно так же доказательство можно обобщить на непрерывную массу, применив приведенное выше доказательство к каждой точке внутри массы, а затем проинтегрировав по всей массе.

Производные крутящего момента

В физике . вращение — это производная крутящего момента по времени ^[12]

$\mathbf {P} ={\frac {\mathrm {d} {\boldsymbol {\tau }}}{\mathrm {d} t}},$

где τ — крутящий момент.

Это слово происходит от латинского слова rotātus, означающего «вращать», но термин «rotatum» не является общепризнанным, но широко используется. Не существует общепринятого лексикона для обозначения последовательных производных от Rotatum, даже если иногда делались различные предложения.

Отношения с властью и энергией

Закон сохранения энергии также можно использовать для понимания крутящего момента. Если силе разрешено действовать на расстоянии, она совершает механическую работу . Аналогично, если крутящему моменту разрешено действовать посредством углового смещения, он совершает работу. Математически при вращении вокруг неподвижной оси, проходящей через центр масс , работу W можно выразить как

$W=\int _{\theta _{1}}^{\theta _{2}}\tau \ \mathrm {d} \theta ,$

где τ — крутящий момент, а θ ₁ и θ ₂ представляют (соответственно) начальное и конечное угловые положения тела. ^[13]

следует принципа работы-энергии , что W также представляет собой изменение кинетической энергии вращения Er _Из тела, определяемое выражением

$E_{\mathrm {r} }={\tfrac {1}{2}}I\omega ^{2},$

где I — момент инерции тела, а ω — его угловая скорость . ^[13]

Мощность – это работа в единицу времени , определяемая формулой

$P={\boldsymbol {\tau }}\cdot {\boldsymbol {\omega }},$

где P — мощность, τ — крутящий момент, ω — угловая скорость , а $\cdot$ представляет скалярное произведение .

Алгебраически уравнение можно перестроить, чтобы вычислить крутящий момент для заданной угловой скорости и выходной мощности. Мощность, вводимая крутящим моментом, зависит только от мгновенной угловой скорости, а не от того, увеличивается ли угловая скорость, уменьшается или остается постоянной во время приложения крутящего момента (это эквивалентно линейному случаю, когда мощность, вводимая силой, зависит только от мгновенной скорости, а не от результирующего ускорения, если таковое имеется).

Доказательство

Работа, совершаемая переменной силой, действующей на конечное линейное перемещение $s$ определяется путем интегрирования силы по элементарному линейному смещению $\mathrm {d} \mathbf {s}$

$W=\int _{s_{1}}^{s_{2}}\mathbf {F} \cdot \mathrm {d} \mathbf {s}$

Однако бесконечно малое линейное перемещение $\mathrm {d} \mathbf {s}$ связано с соответствующим угловым смещением $\mathrm {d} {\boldsymbol {\theta }}$ и радиус-вектор $\mathbf {r}$ как

$\mathrm {d} \mathbf {s} =\mathrm {d} {\boldsymbol {\theta }}\times \mathbf {r}$

Подстановка в приведенное выше выражение для работы дает $W=\int _{s_{1}}^{s_{2}}\mathbf {F} \cdot \mathrm {d} {\boldsymbol {\theta }}\times \mathbf {r}$

Выражение внутри интеграла представляет собой скалярное тройное произведение $\mathbf {F} \cdot \mathrm {d} {\boldsymbol {\theta }}\times \mathbf {r} =\mathbf {r} \times \mathbf {F} \cdot \mathrm {d} {\boldsymbol {\theta }}$ , но согласно определению крутящего момента и поскольку параметр интегрирования был изменен с линейного смещения на угловое, уравнение принимает вид

$W=\int _{\theta _{1}}^{\theta _{2}}{\boldsymbol {\tau }}\cdot \mathrm {d} {\boldsymbol {\theta }}$

Если крутящий момент и угловое смещение направлены в одном направлении, то скалярное произведение сводится к произведению величин; то есть, ${\boldsymbol {\tau }}\cdot \mathrm {d} {\boldsymbol {\theta }}=\left|{\boldsymbol {\tau }}\right|\left|\mathrm {d} {\boldsymbol {\theta }}\right|\cos 0=\tau \,\mathrm {d} \theta$ предоставление

$W=\int _{\theta _{1}}^{\theta _{2}}\tau \,\mathrm {d} \theta$

Принцип моментов

Принцип моментов, также известный как теорема Вариньона (не путать с одноименной геометрической теоремой ), гласит, что результирующие крутящие моменты, вызванные действием нескольких сил, приложенных к одной точке, равны сумме соответствующих крутящих моментов:

$\tau =\mathbf {r} _{1}\times \mathbf {F} _{1}+\mathbf {r} _{2}\times \mathbf {F} _{2}+\ldots +\mathbf {r} _{N}\times \mathbf {F} _{N}.$

Отсюда следует, что крутящие моменты, возникающие в результате действия N сил, действующих вокруг оси вращения объекта, уравновешиваются, когда

$\mathbf {r} _{1}\times \mathbf {F} _{1}+\mathbf {r} _{2}\times \mathbf {F} _{2}+\ldots +\mathbf {r} _{N}\times \mathbf {F} _{N}=\mathbf {0} .$

Единицы

Крутящий момент имеет размерность силы, умноженной на расстояние , символически T. ⁻²л ²М , и эти фундаментальные измерения такие же, как для энергии или работы . В официальной по системе СИ литературе указано, что ньютон-метр правильно обозначается как Нм, как единица крутящего момента; это хотя по размерам эквивалентно джоулю , который является единицей энергии, последний никогда не может использоваться для измерения крутящего момента. ^[14]^[15] В случае крутящего момента единица присваивается вектору , тогда как для энергии она присваивается скаляру . Это означает, что размерная эквивалентность ньютон-метра и джоуля может применяться в первом, но не во втором случае. Эта проблема решается в ориентационном анализе , который рассматривает радиан как базовую единицу, а не как безразмерную единицу. ^[16]

Традиционными британскими единицами измерения крутящего момента являются фунт-фут (фунт-сила-фут) или, для небольших значений, фунт-дюйм (фунт-сила-дюйм). В США крутящий момент чаще всего называют фут-фунт (обозначается как фунт-фут или фут-фунт) и дюйм-фунт (обозначается как дюйм-фунт). ^[17]^[18] Практики полагаются на контекст и дефис в аббревиатуре, чтобы знать, что они относятся к крутящему моменту, а не к энергии или моменту массы (как правильно подразумевает символизм ft-lb).

Преобразование в другие единицы

Коэффициент преобразования может потребоваться при использовании разных единиц мощности или крутящего момента. Например, если измерения: радиан в секунду) используется скорость вращения вместо угловой скорости (единица $(единица: оборот в минуту или секунду), мы должны умножить ее на 2 π$ радиан за оборот. В следующих формулах P — мощность, τ — крутящий момент, а ν ( греческая буква nu ) — скорость вращения.

$P=\tau \cdot 2\pi \cdot \nu$

Показаны единицы:

$P_{\rm {W}}=\tau _{\rm {N{\cdot }m}}\cdot 2\pi _{\rm {rad/rev}}\cdot \nu _{\rm {rev/s}}$

Разделив на 60 секунд в минуту, получим следующее.

$P_{\rm {W}}={\frac {\tau _{\rm {N{\cdot }m}}\cdot 2\pi _{\rm {rad/rev}}\cdot \nu _{\rm {rev/min}}}{\rm {60~s/min}}}$

где скорость вращения выражена в оборотах в минуту (об/мин, об/мин).

Некоторые люди (например, американские инженеры-автомобилестроители) используют лошадиные силы (механические) для мощности, футы-фунты (фунт-силы-футы) для крутящего момента и обороты в минуту для скорости вращения. В результате формула изменится на:

$P_{\rm {hp}}={\frac {\tau _{\rm {lbf{\cdot }ft}}\cdot 2\pi _{\rm {rad/rev}}\cdot \nu _{\rm {rev/min}}}{33,000}}.$

Приведенная ниже константа (в фут-фунтах в минуту) меняется в зависимости от определения мощности; например, если использовать метрическую мощность, она составит примерно 32 550.

Использование других единиц (например, БТЕ в час для мощности) потребует другого пользовательского коэффициента пересчета.

Вывод

Для вращающегося объекта линейное расстояние, пройденное по окружности вращения, представляет собой произведение радиуса на пройденный угол. То есть: линейное расстояние = радиус × угловое расстояние. И по определению линейное расстояние = линейная скорость × время = радиус × угловая скорость × время.

По определению крутящего момента: крутящий момент = радиус × сила. Мы можем изменить это, чтобы определить силу = крутящий момент ÷ радиус. Эти два значения можно подставить в определение мощности :

${\begin{aligned}{\text{power}}&={\frac {{\text{force}}\cdot {\text{linear distance}}}{\text{time}}}\\[6pt]&={\frac {\left({\dfrac {\text{torque}}{r}}\right)\cdot (r\cdot {\text{angular speed}}\cdot t)}{t}}\\[6pt]&={\text{torque}}\cdot {\text{angular speed}}.\end{aligned}}$

Радиус r и время t выпали из уравнения. Однако угловая скорость должна выражаться в радианах на единицу времени, исходя из предполагаемой прямой зависимости между линейной скоростью и угловой скоростью в начале вывода. Если скорость вращения измеряется в оборотах в единицу времени, линейная скорость и расстояние увеличиваются пропорционально на 2 $π$ в приведенном выше выводе, что дает:

${\text{power}}={\text{torque}}\cdot 2\pi \cdot {\text{rotational speed}}.\,$

Если крутящий момент выражен в ньютон-метрах, а скорость вращения — в оборотах в секунду, приведенное выше уравнение дает мощность в ньютон-метрах в секунду или ваттах. Если используются британские единицы измерения и если крутящий момент выражен в фунтах-силах-футах, а скорость вращения — в оборотах в минуту, приведенное выше уравнение дает мощность в футах-фунтах-силах в минуту. Затем формула уравнения для мощности в лошадиных силах получается путем применения коэффициента пересчета 33 000 фут-фунт-сила/мин на лошадиную силу:

${\begin{aligned}{\text{power}}&={\text{torque}}\cdot 2\pi \cdot {\text{rotational speed}}\cdot {\frac {{\text{ft}}{\cdot }{\text{lbf}}}{\text{min}}}\cdot {\frac {\text{horsepower}}{33,000\cdot {\frac {{\text{ft}}\cdot {\text{lbf}}}{\text{min}}}}}\\[6pt]&\approx {\frac {{\text{torque}}\cdot {\text{RPM}}}{5,252}}\end{aligned}}$

потому что $5252.113122\approx {\frac {33,000}{2\pi }}.\,$

Особые случаи и другие факты

Формула плеча момента

Очень полезный частный случай, который часто называют определением крутящего момента в других областях, помимо физики, выглядит следующим образом:

$\tau =({\text{moment arm}})({\text{force}}).$

Конструкция «плеча момента» показана на рисунке справа вместе с векторами r и F. упомянутыми выше Проблема с этим определением заключается в том, что оно не дает направления крутящего момента, а только его величину, и, следовательно, его трудно использовать в трехмерных случаях. Если сила перпендикулярна вектору перемещения r , то плечо момента будет равно расстоянию до центра, а крутящий момент будет максимальным для данной силы. Уравнение для величины крутящего момента, возникающего под действием перпендикулярной силы:

$\tau =({\text{distance to centre}})({\text{force}}).$

Например, если человек прикладывает силу 10 Н к концевому концу гаечного ключа длиной 0,5 м (или силу 10 Н, действующую на расстоянии 0,5 м от точки закручивания ключа любой длины), крутящий момент будет 5 Н⋅м – при условии, что человек перемещает ключ, прилагая силу в плоскости движения и перпендикулярно ключу.

Крутящий момент, вызванный двумя противоположными силами F _g и − F _g, вызывает изменение углового момента L в направлении этого крутящего момента. вершины Это приводит к прецессии .

Статическое равновесие

Чтобы объект находился в статическом равновесии , не только сумма сил должна быть равна нулю, но и сумма крутящих моментов (моментов) относительно любой точки. Для двумерной ситуации с горизонтальными и вертикальными силами сумма требований к силам представляет собой два уравнения: $Σ H = 0$ и $Σ V = 0$ , а крутящий момент – третье уравнение: $Σ τ = 0$ . То есть для решения статически определимых задач равновесия в двумерном пространстве используются три уравнения.

Чистая сила в зависимости от крутящего момента

Когда чистая сила, действующая на систему, равна нулю, крутящий момент, измеренный из любой точки пространства, одинаков. Например, крутящий момент на контуре с током в однородном магнитном поле одинаков независимо от точки отсчета. Если чистая сила $\mathbf {F}$ не равен нулю, и ${\boldsymbol {\tau }}_{1}$ крутящий момент, измеренный от $\mathbf {r} _{1}$ , то крутящий момент, измеренный от $\mathbf {r} _{2}$ является ${\boldsymbol {\tau }}_{2}={\boldsymbol {\tau }}_{1}+(\mathbf {r} _{2}-\mathbf {r} _{1})\times \mathbf {F}$

Крутящий момент машины

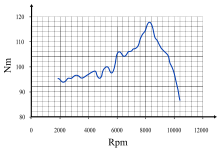
Крутящий момент является частью базовой характеристики двигателя : выходная мощность двигателя выражается как его крутящий момент, умноженный на угловую скорость приводного вала. Двигатели внутреннего сгорания производят полезный крутящий момент только в ограниченном диапазоне скоростей вращения (обычно около 1000–6000 об / мин для небольшого автомобиля). Можно измерить изменяющийся выходной крутящий момент в этом диапазоне с помощью динамометра и отобразить его в виде кривой крутящего момента. Паровые двигатели и электродвигатели, как правило, создают максимальный крутящий момент, близкий к нулю, при этом крутящий момент уменьшается по мере увеличения скорости вращения (из-за увеличения трения и других ограничений). Поршневые паровые машины и электродвигатели могут запускать тяжелые нагрузки с нулевых оборотов без сцепления .

На практике взаимосвязь между мощностью и крутящим моментом можно наблюдать на велосипедах : велосипеды обычно состоят из двух опорных катков, передней и задней шестерен (называемых звездочками ), сцепленных с цепью , и механизма переключения передач , если система трансмиссии велосипеда допускает несколько используемые передаточные числа (например, многоскоростной велосипед ), все из которых прикреплены к раме . Велосипедист проворачивая , человек, который ездит на велосипеде, обеспечивает входную мощность, поворачивая педали, тем самым переднюю звездочку (обычно называемую звездочкой ). Входная мощность, обеспечиваемая велосипедистом, равна произведению угловой скорости (т. е. числа оборотов педали в минуту, умноженного на 2 π ) и крутящего момента на шпинделе велосипеда шатуна . велосипеда Трансмиссия передает входную мощность на опорное колесо , которое, в свою очередь, передает полученную мощность на дорогу в качестве выходной мощности велосипеда. В зависимости от передаточного числа велосипеда _{входная} пара (крутящий момент, угловая скорость) преобразуется в (крутящий момент, угловая скорость) _{выходная} пара. При использовании большей задней передачи или переключении на более низкую передачу в многоскоростных велосипедах угловая скорость опорных катков уменьшается, а крутящий момент увеличивается, произведение которого (т.е. мощность) не меняется.

Множитель крутящего момента

Крутящий момент можно увеличить тремя способами: расположив точку опоры таким образом, чтобы длина рычага увеличилась; используя более длинный рычаг; или с помощью понижающей передачи или коробки передач . Такой механизм многократно увеличивает крутящий момент, поскольку снижается скорость вращения.

См. также

Ссылки

^ Сервей, Р.А. и Джуэтт, Дж.В. младший (2003). Физика для ученых и инженеров . 6-е изд. Брукс Коул. ISBN 0-534-40842-7 .
^ Томсон, Джеймс; Лармор, Джозеф (1912). Сборник статей по физике и технике . Университетское издательство. п. гражданский
^ Jump up to: ^а ^б Томпсон, Сильванус Филлипс (1893). Динамоэлектрические машины: Учебное пособие для студентов-электротехников (4-е изд.). Нью-Йорк, Гарвардское издательство. п. 108.
^ Jump up to: ^а ^б «крутящий момент» . Оксфордский словарь английского языка . 1933 год.
↑ «Физика для инженерии» , Хендрикс, Субрамони и Ван Блерк, Chinappi, стр. 148, веб-ссылка. Архивировано 11 июля 2017 г. на Wayback Machine.
^ Кейн, Т.Р. Кейн и Д.А. Левинсон (1985). Динамика, теория и приложения, стр. 90–99: скачать бесплатно. Архивировано 19 июня 2015 г. на Wayback Machine .
^ Пуассон, Симеон-Дени (1811). Трактат по механике, том первый . п. 67 .
^ «Правило правой руки для крутящего момента» . Архивировано из оригинала 19 августа 2007 г. Проверено 8 сентября 2007 г.
^ Холлидей, Дэвид; Резник, Роберт (1970). Основы физики . Джон Уайли и сыновья. стр. 184–85.
^ Найт, Рэндалл; Джонс, Брайан; Филд, Стюарт (2016). Колледжская физика: стратегический подход (3-е изд. Обновление технологий). Бостон: Пирсон. п. 199. ИСБН 9780134143323 . OCLC 922464227 .
^ Типлер, Пол (2004). Физика для ученых и инженеров: Механика, колебания и волны, Термодинамика (5-е изд.). У. Х. Фриман. ISBN 0-7167-0809-4 .
^ «Обзор сотрудничества человека и робота в промышленных условиях: осведомленность, интеллект и соответствие» .
^ Jump up to: ^а ^б Клеппнер, Дэниел; Коленков, Роберт (1973). Введение в механику . МакГроу-Хилл. стр. 267–268 . ISBN 9780070350489 .
^ С официального сайта SI. Архивировано 19 апреля 2021 г. в Wayback Machine , Международная система единиц - 9-е издание - Текст на английском языке, раздел 2.3.4: «Например, количественный крутящий момент представляет собой векторное произведение вектора положения и вектор силы. Единицей СИ является ньютон-метр. Несмотря на то, что крутящий момент имеет ту же размерность, что и энергия (единица СИ, джоуль), джоуль никогда не используется для выражения крутящего момента».
^ «Брошюра СИ, изд. 9, раздел 2.3.4» (PDF) . Международное бюро мер и веса. 2019. Архивировано (PDF) из оригинала 26 июля 2020 г. Проверено 29 мая 2020 г.
^ Пейдж, Честер Х. (1979). «Опровержение «Групповых свойств величин и единиц» де Бура ». Американский журнал физики . 47 (9): 820. Бибкод : 1979AmJPh..47..820P . дои : 10.1119/1.11704 .
^ «Динамометрические ключи с циферблатом от Grainger» . Грейнджер. 2020. Демонстрация того, что, как и в большинстве промышленных предприятий США, диапазоны крутящих моментов указаны в фут-фунтах, а не в фунт-силах-футах.
^ Эрьявец, Джек (22 января 2010 г.). Механические коробки передач и коробки передач: Учебное пособие . Cengage Обучение. п. 38. ISBN 978-1-4354-3933-7 .

Внешние ссылки

«Лошадиная сила и крутящий момент». Архивировано 28 марта 2007 г. в Wayback Machine. Статья показывает, как мощность, крутящий момент и передача влияют на характеристики автомобиля.
Крутящий момент и угловой момент при круговом движении в проекте PHYSNET .
Интерактивное моделирование крутящего момента
Конвертер единиц крутящего момента
Ощущение крутящего момента. Архивировано 8 мая 2021 г. на Wayback Machine. Интерактив на порядок величины.

[1] Сервей, Р.А. и Джуэтт, Дж.В. младший (2003). Физика для ученых и инженеров . 6-е изд. Брукс Коул. ISBN 0-534-40842-7 .

[2] Томсон, Джеймс; Лармор, Джозеф (1912). Сборник статей по физике и технике . Университетское издательство. п. гражданский

[thompson1-3] Jump up to: ^а ^б Томпсон, Сильванус Филлипс (1893). Динамоэлектрические машины: Учебное пособие для студентов-электротехников (4-е изд.). Нью-Йорк, Гарвардское издательство. п. 108.

[oed1933-4] Jump up to: ^а ^б «крутящий момент» . Оксфордский словарь английского языка . 1933 год.

[Hendricks-5] «Физика для инженерии» , Хендрикс, Субрамони и Ван Блерк, Chinappi, стр. 148, веб-ссылка. Архивировано 11 июля 2017 г. на Wayback Machine.

[Kane-6] Кейн, Т.Р. Кейн и Д.А. Левинсон (1985). Динамика, теория и приложения, стр. 90–99: скачать бесплатно. Архивировано 19 июня 2015 г. на Wayback Machine .

[7] Пуассон, Симеон-Дени (1811). Трактат по механике, том первый . п. 67 .

[8] «Правило правой руки для крутящего момента» . Архивировано из оригинала 19 августа 2007 г. Проверено 8 сентября 2007 г.

[halliday_184-85-9] Холлидей, Дэвид; Резник, Роберт (1970). Основы физики . Джон Уайли и сыновья. стр. 184–85.

[10] Найт, Рэндалл; Джонс, Брайан; Филд, Стюарт (2016). Колледжская физика: стратегический подход (3-е изд. Обновление технологий). Бостон: Пирсон. п. 199. ИСБН 9780134143323 . OCLC 922464227 .

[11] Типлер, Пол (2004). Физика для ученых и инженеров: Механика, колебания и волны, Термодинамика (5-е изд.). У. Х. Фриман. ISBN 0-7167-0809-4 .

[12] «Обзор сотрудничества человека и робота в промышленных условиях: осведомленность, интеллект и соответствие» .

[kleppner_267-68-13] Jump up to: ^а ^б Клеппнер, Дэниел; Коленков, Роберт (1973). Введение в механику . МакГроу-Хилл. стр. 267–268 . ISBN 9780070350489 .

[BIPM222-14] С официального сайта SI. Архивировано 19 апреля 2021 г. в Wayback Machine , Международная система единиц - 9-е издание - Текст на английском языке, раздел 2.3.4: «Например, количественный крутящий момент представляет собой векторное произведение вектора положения и вектор силы. Единицей СИ является ньютон-метр. Несмотря на то, что крутящий момент имеет ту же размерность, что и энергия (единица СИ, джоуль), джоуль никогда не используется для выражения крутящего момента».

[BIPM_5.1-15] «Брошюра СИ, изд. 9, раздел 2.3.4» (PDF) . Международное бюро мер и веса. 2019. Архивировано (PDF) из оригинала 26 июля 2020 г. Проверено 29 мая 2020 г.

[16] Пейдж, Честер Х. (1979). «Опровержение «Групповых свойств величин и единиц» де Бура ». Американский журнал физики . 47 (9): 820. Бибкод : 1979AmJPh..47..820P . дои : 10.1119/1.11704 .

[GRAINGER-17] «Динамометрические ключи с циферблатом от Grainger» . Грейнджер. 2020. Демонстрация того, что, как и в большинстве промышленных предприятий США, диапазоны крутящих моментов указаны в фут-фунтах, а не в фунт-силах-футах.

[18] Эрьявец, Джек (22 января 2010 г.). Механические коробки передач и коробки передач: Учебное пособие . Cengage Обучение. п. 38. ISBN 978-1-4354-3933-7 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]