Ускорение

Ускорение
Ускорение
	В вакууме (нет сопротивления воздуха ) объекты, притягиваемые Землей, набирают скорость с постоянной скоростью.
Общие символы	а
И объединились	РС 2 , РС −2 , РС −2
Выводы из ; другие количества
Измерение

Дрэг-рейсинг — это вид спорта, в котором специально построенные автомобили соревнуются за то, чтобы быстрее всех ускориться со старта с места.

В механике . ускорение — это скорость изменения скорости объекта по отношению ко времени Ускорение — одна из нескольких составляющих кинематики , изучающей движение . Ускорения являются векторными величинами (в том смысле, что они имеют величину и направление ). ^[1]^[2] Ориентация ускорения объекта задается ориентацией результирующей силы , действующей на этот объект. Величина ускорения объекта, описанная вторым законом Ньютона , ^[3] представляет собой совокупное действие двух причин:

чистый баланс всех внешних сил , действующих на этот объект — величина прямо пропорциональна этой чистой результирующей силе;
этого объекта масса в зависимости от материалов, из которых он сделан — величина обратно пропорциональна массе объекта.

Единицей в системе СИ ускорения является метр на секунду в квадрате ( м⋅с ⁻², $\mathrm {\tfrac {m}{s^{2}}}$ ).

Например, когда транспортное средство трогается с места (нулевая скорость в инерциальной системе отсчета ) и движется по прямой с возрастающей скоростью, оно ускоряется в направлении движения. Если автомобиль поворачивает, происходит ускорение в новом направлении и изменяется вектор движения. Ускорение транспортного средства в текущем направлении движения называется линейным (или тангенциальным при круговых движениях ) ускорением, реакцию на которое пассажиры на борту испытывают как силу, толкающую их обратно на сиденья. При изменении направления оказывающее воздействие ускорение называется радиальным (или центростремительным при круговых движениях) ускорением, реакцию на которое пассажиры испытывают как центробежную силу . Если скорость транспортного средства уменьшается, это ускорение в направлении, противоположном вектору скорости (математически отрицательное , если движение одномерное, а скорость положительная), иногда называемое замедлением. ^[4]^[5] или замедление , и пассажиры воспринимают реакцию на замедление как инерционную силу, толкающую их вперед. Такие отрицательные ускорения часто достигаются за счет сжигания тормозных ракет в космических кораблях . ^[6] И ускорение, и замедление рассматриваются одинаково, поскольку оба они представляют собой изменения скорости. Каждое из этих ускорений (тангенциальное, радиальное, замедление) ощущается пассажирами до тех пор, пока их относительная (дифференциальная) скорость не нейтрализуется по отношению к ускорению, вызванному изменением скорости.

Определение и свойства

Кинематические величины классической частицы: масса $m$ , положение $r$ , скорость $v$ , ускорение $a$ .

Среднее ускорение

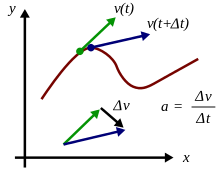
Среднее ускорение объекта за определенный период времени — это изменение его скорости . $\Delta \mathbf {v}$ , разделенный на продолжительность периода, $\Delta t$ . Математически, ${\bar {\mathbf {a} }}={\frac {\Delta \mathbf {v} }{\Delta t}}.$

Мгновенное ускорение

Между тем мгновенное ускорение является пределом среднего ускорения за бесконечно малый интервал времени. С точки зрения исчисления мгновенное ускорение является производной вектора скорости по времени: $\mathbf {a} =\lim _{{\Delta t}\to 0}{\frac {\Delta \mathbf {v} }{\Delta t}}={\frac {d\mathbf {v} }{dt}}.$ Поскольку ускорение определяется как производная скорости $v$ по времени $t,$ а скорость определяется как производная положения $x$ по времени, ускорение можно рассматривать как вторую производную $x$ по $t$ : $\mathbf {a} ={\frac {d\mathbf {v} }{dt}}={\frac {d^{2}\mathbf {x} }{dt^{2}}}.$

(Здесь и далее, если движение прямолинейное , векторные можно заменить скалярами величины в уравнениях .)

По основной теореме исчисления можно видеть, что интеграл функции ускорения $a (t)$ есть функция скорости $v (t)$ ; то есть площадь под кривой графика зависимости ускорения от времени ( $a$ vs. $t$ ) соответствует изменению скорости. $\mathbf {\Delta v} =\int \mathbf {a} \,dt.$

Аналогично, интеграл от рывка функции $j (t)$ , производной функции ускорения, можно использовать для нахождения изменения ускорения в определенный момент времени: $\mathbf {\Delta a} =\int \mathbf {j} \,dt.$

Единицы

Ускорение имеет размеры скорости (L/T), деленной на время, т.е. L T ⁻². Единицей в системе СИ ускорения является метр на секунду в квадрате (мс). ⁻²); или «метр в секунду в секунду», поскольку скорость в метрах в секунду меняется на значение ускорения каждую секунду.

Другие формы

Объект, движущийся по кругу, например спутник, вращающийся вокруг Земли, ускоряется из-за изменения направления движения, хотя его скорость может быть постоянной. В этом случае говорят, что он испытывает центростремительное (направленное к центру) ускорение.

Правильное ускорение , ускорение тела относительно состояния свободного падения, измеряется инструментом, называемым акселерометром .

В классической механике для тела с постоянной массой (векторное) ускорение центра масс тела пропорционально вектору результирующей силы (т. е. сумме всех сил), действующей на него ( второй закон Ньютона ): $\mathbf {F} =m\mathbf {a} \quad \implies \quad \mathbf {a} ={\frac {\mathbf {F} }{m}},$ где $F$ — результирующая сила, действующая на тело, $m$ — масса тела, $а$ — ускорение центра масс. По мере того как скорости приближаются к скорости света , релятивистские эффекты становятся все более значительными.

Тангенциальное и центростремительное ускорение

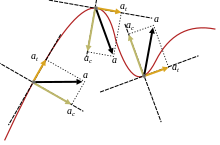
Скорость частицы, движущейся по криволинейной траектории, как функцию времени, можно записать как: $\mathbf {v} (t)=v(t){\frac {\mathbf {v} (t)}{v(t)}}=v(t)\mathbf {u} _{\mathrm {t} }(t),$ где $v (t)$ равно скорости движения по пути, и $\mathbf {u} _{\mathrm {t} }={\frac {\mathbf {v} (t)}{v(t)}}\,,$ единичный вектор, касательный к пути, указывающему направление движения в выбранный момент времени. Принимая во внимание как изменяющуюся скорость $v (t),$ так и изменяющееся направление $u t$ , ускорение частицы, движущейся по криволинейной траектории, можно записать с помощью цепного правила дифференцирования ^[7] для произведения двух функций времени как:

${\begin{alignedat}{3}\mathbf {a} &={\frac {d\mathbf {v} }{dt}}\\&={\frac {dv}{dt}}\mathbf {u} _{\mathrm {t} }+v(t){\frac {d\mathbf {u} _{\mathrm {t} }}{dt}}\\&={\frac {dv}{dt}}\mathbf {u} _{\mathrm {t} }+{\frac {v^{2}}{r}}\mathbf {u} _{\mathrm {n} }\ ,\end{alignedat}}$

где $un —$ единичный (внутренний) вектор нормали к траектории частицы (также называемый главной нормалью ), а $r$ — ее мгновенный радиус кривизны, основанный на соприкасающейся окружности в момент времени $t$ . Компоненты

\mathbf {a} _{\mathrm {t} }={\frac {dv}{dt}}\mathbf {u} _{\mathrm {t} }\quad {\text{and}}\quad \mathbf {a} _{\mathrm {c} }={\frac {v^{2}}{r}}\mathbf {u} _{\mathrm {n} }

называются тангенциальным ускорением и нормальным или радиальным ускорением (или центростремительным ускорением при круговом движении, см. также круговое движение и центростремительную силу ) соответственно.

Геометрический анализ трехмерных пространственных кривых, объясняющий касательную, (главную) нормаль и бинормаль, описывается формулами Френе-Серре . ^[8]^[9]

Особые случаи

Равномерное ускорение

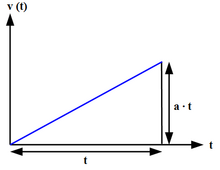
Равномерное или постоянное ускорение — это тип движения, при котором скорость объекта изменяется на одинаковую величину за каждый равный период времени.

Часто цитируемый пример равномерного ускорения — это объект, находящийся в свободном падении в однородном гравитационном поле. Ускорение падающего тела при отсутствии сопротивления движению зависит только от гравитационного поля напряженности $g$ (его еще называют ускорением силы тяжести ). По Ньютона сила второму закону $\mathbf {F_{g}}$ Действие на тело определяется: $\mathbf {F_{g}} =m\mathbf {g} .$

Из-за простых аналитических свойств случая постоянного ускорения существуют простые формулы, связывающие перемещение , начальную и зависящую от времени скорости , а также ускорение с прошедшим временем : ^[10] ${\begin{aligned}\mathbf {s} (t)&=\mathbf {s} _{0}+\mathbf {v} _{0}t+{\tfrac {1}{2}}\mathbf {a} t^{2}=\mathbf {s} _{0}+{\tfrac {1}{2}}\left(\mathbf {v} _{0}+\mathbf {v} (t)\right)t\\\mathbf {v} (t)&=\mathbf {v} _{0}+\mathbf {a} t\\{v^{2}}(t)&={v_{0}}^{2}+2\mathbf {a\cdot } [\mathbf {s} (t)-\mathbf {s} _{0}],\end{aligned}}$

где

$t$ это прошедшее время,
$\mathbf {s} _{0}$ - начальное смещение от начала координат,
$\mathbf {s} (t)$ это смещение от начала координат во времени $t$ ,
$\mathbf {v} _{0}$ - начальная скорость,
$\mathbf {v} (t)$ это скорость во времени $t$ , и
$\mathbf {a}$ - равномерная скорость ускорения.

В частности, движение можно разделить на две ортогональные части: одну с постоянной скоростью, а другую в соответствии с приведенными выше уравнениями. Как показал Галилей , конечным результатом является параболическое движение, описывающее, например, траекторию снаряда в вакууме вблизи поверхности Земли. ^[11]

Круговое движение

Вектор положения r всегда указывает радиально от начала координат.

Вектор скорости v , всегда касательный к траектории движения.

Вектор ускорения a не параллелен радиальному движению, а смещен угловым ускорением и ускорением Кориолиса, не касается траектории, а смещен центростремительным и радиальным ускорениями.

Кинематические векторы в плоских полярных координатах . Обратите внимание, что установка не ограничена двумерным пространством, но может представлять соприкасающуюся плоскость в точке произвольной кривой в любом более высоком измерении.

При равномерном круговом движении , то есть движущемся с постоянной скоростью по круговой траектории, частица испытывает ускорение, возникающее в результате изменения направления вектора скорости, при этом ее величина остается постоянной. Производная положения точки на кривой по времени, т. е. ее скорость, оказывается всегда точно касательной к кривой и соответственно ортогональной радиусу в этой точке. Поскольку при равномерном движении скорость в тангенциальном направлении не меняется, ускорение должно быть в радиальном направлении, направленном к центру круга. Это ускорение постоянно меняет направление скорости на касательное в соседней точке, тем самым вращая вектор скорости по окружности.

Для заданной скорости $v$ , величина этого геометрически обусловленного ускорения (центростремительного ускорения) обратно пропорциональна радиусу $r$ окружности и увеличивается пропорционально квадрату этой скорости: $a_{c}={\frac {v^{2}}{r}}\,.$
Для заданной угловой скорости $\omega$ , центростремительное ускорение прямо пропорционально радиусу $r$ . Это связано с зависимостью скорости $v$ по радиусу $r$ . $v=\omega r.$

Выразив вектор центростремительного ускорения в полярных компонентах, где $\mathbf {r}$ представляет собой вектор из центра круга к частице с величиной, равной этому расстоянию, и, учитывая ориентацию ускорения к центру, дает $\mathbf {a_{c}} =-{\frac {v^{2}}{|\mathbf {r} |}}\cdot {\frac {\mathbf {r} }{|\mathbf {r} |}}\,.$

Как обычно при вращениях, скорость $v$ частицы может быть выражена как угловая скорость относительно точки на расстоянии $r$ как $\omega ={\frac {v}{r}}.$

Таким образом $\mathbf {a_{c}} =-\omega ^{2}\mathbf {r} \,.$

Это ускорение и масса частицы определяют необходимую центростремительную силу , направленную к центру круга, как чистую силу, действующую на эту частицу, чтобы удерживать ее в этом равномерном круговом движении. Так называемая « центробежная сила », действующая наружу на тело, представляет собой так называемую псевдосилу, испытываемую в системе отсчета тела тела, совершающего круговое движение, из-за линейного импульса , вектора, касательного окружности. движения.

При неравномерном круговом движении, т. е. скорости по криволинейной траектории меняется, ускорение имеет ненулевую составляющую, касательную к кривой, и не ограничивается главной нормалью , направленной к центру соприкасающейся окружности, что определяет радиус $r$ для центростремительного ускорения. Тангенциальная составляющая определяется угловым ускорением $\alpha$ , то есть скорость изменения $\alpha ={\dot {\omega }}$ угловой скорости $\omega$ раз радиус $r$ . То есть, $a_{t}=r\alpha .$

Знак тангенциальной составляющей ускорения определяется знаком углового ускорения ( $\alpha$ ), а касательная всегда направлена под прямым углом к радиусу-вектору.

Системы координат

В многомерных декартовых системах координат ускорение разбивается на компоненты, соответствующие каждой размерной оси системы координат. В двумерной системе, где есть ось X и ось Y, соответствующие компоненты ускорения определяются как ^[12] $a_{x}=dv_{x}/dt=d^{2}x/dt^{2},$ $a_{y}=dv_{y}/dt=d^{2}y/dt^{2}.$ Тогда двумерный вектор ускорения определяется как ${\textbf {a}}=<a_{x},a_{y}>$ . Величина этого вектора находится по формуле расстояния как $|a|={\sqrt {a_{x}^{2}+a_{y}^{2}}}.$ В трехмерных системах, где имеется дополнительная ось z, соответствующая компонента ускорения определяется как $a_{z}=dv_{z}/dt=d^{2}z/dt^{2}.$ Вектор трехмерного ускорения определяется как ${\textbf {a}}=<a_{x},a_{y},a_{z}>$ причем его величина определяется $|a|={\sqrt {a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}}.$

Отношение к теории относительности

Специальная теория относительности

Специальная теория относительности описывает поведение объектов, движущихся относительно других объектов со скоростями, приближающимися к скорости света в вакууме. Как выяснилось, ньютоновская механика является приближением к реальности и действительна с большой точностью на более низких скоростях. Поскольку соответствующие скорости увеличиваются до скорости света, ускорение больше не подчиняется классическим уравнениям.

По мере приближения скорости к скорости света ускорение, создаваемое данной силой, уменьшается, становясь бесконечно малым по мере приближения к скорости света; объект с массой может асимптотически приближаться к этой скорости , но никогда ее не достичь.

Общая теория относительности

Если не известно состояние движения объекта, невозможно отличить, вызвана ли наблюдаемая сила гравитацией или ускорением — сила тяжести и инерционное ускорение имеют одинаковые эффекты. Альберт Эйнштейн назвал это принципом эквивалентности и сказал, что только наблюдатели, которые вообще не чувствуют никакой силы, включая силу гравитации, имеют право заключить, что они не ускоряются. ^[13]

Конверсии

Преобразования между общепринятыми единицами ускорения
Базовая стоимость	( Гал , или см/с ²)	( фут/с ²)	( РС ²)	( Стандартная плотность , г ₀ )
1 гал или см/с ²	1	0.032 8084	0.01	1.019 72 × 10 ⁻³
1 фут/с ²	30.4800	1	0.304 800	0.031 0810
1 м/с ²	100	3.280 84	1	0.101 972
1 г ₀	980.665	32.1740	9.806 65	1

См. также

Ускорение (дифференциальная геометрия)
Четырехвекторность : явная связь между пространством и временем.
Гравитационное ускорение
Инерция
Порядки величины (ускорение)
Удар (механика)
Регистратор данных ударов и вибрации
измерение 3-осевого ускорения
Космические путешествия с постоянным ускорением
Удельная сила

Ссылки

^ Бонди, Герман (1980). Относительность и здравый смысл . Публикации Courier Dover. стр. 3 . ISBN 978-0-486-24021-3 .
^ Лерман, Роберт Л. (1998). Физика: простой способ . Образовательная серия Бэррона. стр. 27 . ISBN 978-0-7641-0236-3 .
^ Экипаж, Генри (2008). Принципы механики . БиблиоБазар, ООО. п. 43. ИСБН 978-0-559-36871-4 .
^ П. Смит; Р. К. Смит (1991). Механика (2-е, иллюстрированное, переиздание). Джон Уайли и сыновья. п. 39. ИСБН 978-0-471-92737-2 . Выдержка со страницы 39
^ Джон Д. Катнелл; Кеннет В. Джонсон (2014). Физика, том первый: главы 1–17, том 1 (1st0, иллюстрированное изд.). Джон Уайли и сыновья. п. 36. ISBN 978-1-118-83688-0 . Выдержка со страницы 36
^ Раймонд А. Сервей; Крис Вуйль; Джерри С. Фон (2008). Колледж физики, том 10 . Сенгаге. п. 32. ISBN 9780495386933 .
^ Вайсштейн, Эрик В. «Правило цепи» . Вольфрам Математический мир . Вольфрам Исследования . Проверено 2 августа 2016 г.
^ Ларри К. Эндрюс; Рональд Л. Филлипс (2003). Математические методы для инженеров и ученых . СПАЙ Пресс. п. 164. ИСБН 978-0-8194-4506-3 .
^ Глава V Рамана Мурти; Н. К. Шринивас (2001). Прикладная математика . Нью-Дели: С. Чанд и Ко. с. 337. ИСБН 978-81-219-2082-7 .
^ Кейт Джонсон (2001). Физика для вас: пересмотренное издание национальной учебной программы для GCSE (4-е изд.). Нельсон Торнс. п. 135. ИСБН 978-0-7487-6236-1 .
^ Дэвид К. Кэссиди; Джеральд Джеймс Холтон; Ф. Джеймс Резерфорд (2002). Понимание физики . Биркхойзер. п. 146. ИСБН 978-0-387-98756-9 .
^ «Лекции Фейнмана по физике, том I, глава 9: Законы динамики Ньютона» . www.feynmanlectures.caltech.edu . Проверено 4 января 2024 г.
^ Брайан Грин, Ткань космоса: пространство, время и текстура реальности , страница 67. Винтаж. ISBN 0-375-72720-5

Внешние ссылки

Калькулятор ускорения Простой конвертер единиц ускорения
Калькулятор ускорения Калькулятор преобразования ускорения преобразует единицы измерения из метра в секунду в квадрате, километра в секунду в квадрате, миллиметра в секунду в квадрате и т. д. с помощью метрического преобразования.

[1] Бонди, Герман (1980). Относительность и здравый смысл . Публикации Courier Dover. стр. 3 . ISBN 978-0-486-24021-3 .

[2] Лерман, Роберт Л. (1998). Физика: простой способ . Образовательная серия Бэррона. стр. 27 . ISBN 978-0-7641-0236-3 .

[3] Экипаж, Генри (2008). Принципы механики . БиблиоБазар, ООО. п. 43. ИСБН 978-0-559-36871-4 .

[4] П. Смит; Р. К. Смит (1991). Механика (2-е, иллюстрированное, переиздание). Джон Уайли и сыновья. п. 39. ИСБН 978-0-471-92737-2 . Выдержка со страницы 39

[5] Джон Д. Катнелл; Кеннет В. Джонсон (2014). Физика, том первый: главы 1–17, том 1 (1st0, иллюстрированное изд.). Джон Уайли и сыновья. п. 36. ISBN 978-1-118-83688-0 . Выдержка со страницы 36

[6] Раймонд А. Сервей; Крис Вуйль; Джерри С. Фон (2008). Колледж физики, том 10 . Сенгаге. п. 32. ISBN 9780495386933 .

[7] Вайсштейн, Эрик В. «Правило цепи» . Вольфрам Математический мир . Вольфрам Исследования . Проверено 2 августа 2016 г.

[Andrews-8] Ларри К. Эндрюс; Рональд Л. Филлипс (2003). Математические методы для инженеров и ученых . СПАЙ Пресс. п. 164. ИСБН 978-0-8194-4506-3 .

[Chand-9] Глава V Рамана Мурти; Н. К. Шринивас (2001). Прикладная математика . Нью-Дели: С. Чанд и Ко. с. 337. ИСБН 978-81-219-2082-7 .

[10] Кейт Джонсон (2001). Физика для вас: пересмотренное издание национальной учебной программы для GCSE (4-е изд.). Нельсон Торнс. п. 135. ИСБН 978-0-7487-6236-1 .

[11] Дэвид К. Кэссиди; Джеральд Джеймс Холтон; Ф. Джеймс Резерфорд (2002). Понимание физики . Биркхойзер. п. 146. ИСБН 978-0-387-98756-9 .

[12] «Лекции Фейнмана по физике, том I, глава 9: Законы динамики Ньютона» . www.feynmanlectures.caltech.edu . Проверено 4 января 2024 г.

[13] Брайан Грин, Ткань космоса: пространство, время и текстура реальности , страница 67. Винтаж. ISBN 0-375-72720-5

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]