0.999...

Стилистическое впечатление от числа, показывающее, как его десятичные дроби продолжаются бесконечно.

В математике 0,999 ... (также пишется как 0,9 . , 0 ... 9 или 0.(9) ) обозначает наименьшее число, большее, чем каждое в последовательности (0,9, 0,99, 0,999,...) число Можно доказать, что это число равно 1; то есть,

0.999...=1.

Другими словами, 0,999... это не «почти точно 1» или «очень, очень почти, но не совсем 1»; скорее, 0,999... и "1" - это одно и то же число.

Ниже приводится элементарное доказательство, которое включает в себя только элементарную арифметику и тот факт, что не существует положительного действительного числа меньше всех 1/10. ^$н$, где $n$ — натуральное число, свойство, которое непосредственно следует из архимедова свойства действительных чисел .

Есть много других способов доказать это равенство: от интуитивных аргументов до математически строгих доказательств . Интуитивные аргументы обычно основаны на свойствах конечных десятичных дробей , которые без доказательства распространяются на бесконечные десятичные дроби. Доказательства обычно основаны на основных свойствах действительных чисел и методах исчисления , таких как ряды и пределы . Вопрос, изучаемый в рамках математического образования , заключается в том, почему некоторые люди отвергают это равенство.

В других системах счисления 0,999... может иметь то же значение, другое определение или быть неопределенным. Каждая ненулевая конечная десятичная дробь имеет два равных представления (например, 8,32000... и 8,31999...). Наличие значений с несколькими представлениями является особенностью всех позиционных систем счисления , которые представляют действительные числа.

Элементарное доказательство

Свойство Архимеда : любая точка

x

перед финишной чертой лежит между двумя точками

P n

(включительно).

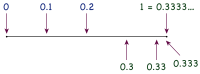
можно доказать, Уравнение 0,999... = 1 используя только математические инструменты сравнения и сложения (конечных) десятичных чисел , без каких-либо ссылок на более сложные темы, такие как ряды и пределы . доказательство Приведенное ниже представляет собой прямую формализацию интуитивного факта, что если провести на числовой прямой 0,9, 0,99, 0,999 и т. д. , то между ними и 1 не останется места для размещения числа. Смысл обозначения 0,999 ... является наименьшей точкой на числовой прямой, лежащей справа от всех чисел 0,9, 0,99, 0,999 и т. д. Поскольку в конечном итоге между 1 и этими числами нет места, точка 1 должна быть этой наименьшей точкой, и итак 0,999... = 1 .

Интуитивное объяснение

Если разместить на числовой прямой 0,9, 0,99, 0,999 и т. д. , то сразу видно, что все эти точки находятся левее 1 и что они становятся все ближе и ближе к 1. Для любого числа $x$ то есть меньше 1, последовательность 0,9, 0,99, 0,999 и т. д. в конечном итоге достигнет числа, большего, чем ⁠. $x$ ⁠ . Таким образом, нет смысла отождествлять 0,999... с любым числом меньшим 1. Между тем, каждое число больше 1 будет больше любой десятичной дроби вида 0,999...9 для любого конечного числа девяток. Следовательно, 0,999... также нельзя отождествить с каким-либо числом больше 1. Поскольку 0,999... не может быть больше 1 или меньше 1, оно должно равняться 1, если оно вообще должно быть действительным числом. ^[1]^[2]

Строгое доказательство

Обозначим через 0.(9) _$n$ число 0,999...9, причем $n$ девятки после запятой. Таким образом, 0.(9) ₁ = 0,9 , 0.(9) ₂ = 0,99 , 0.(9) ₃ = 0,999 и так далее. Один имеет 1 - 0.(9) ₁ = 0,1 = ⁠ $\textstyle {\frac {1}{10}}$ ⁠ , 1 − 0.(9) ₂ = 0.01 = ⁠ $\textstyle {\frac {1}{10^{2}}}$ ⁠ и так далее; то есть 1 − 0.(9) _$n$ = ${\textstyle {\frac {1}{10^{n}}}}$ для каждого натурального числа ⁠ $n$ ⁠ .

Позволять $x$ быть числом не больше 1 и больше 0,9, 0,99, 0,999 и т. д.; то есть 0.(9) _$n$ < $x$ ≤ 1 , для каждого ⁠ $n$ ⁠ . Вычитая эти неравенства из 1, получаем 0 ≤ 1 — $x$ < ⁠ $\textstyle {\frac {1}{10^{n}}}$ ⁠ .

Для завершения доказательства необходимо, чтобы не существовало положительного числа, меньшего ${\textstyle {\frac {1}{10^{n}}}}$ для всех ⁠ $n$ ⁠ . Это одна из версий свойства Архимеда , справедливая для действительных чисел. ^[3]^[4]

Из этого свойства следует, таким образом, что левое неравенство не может быть строгим ; таким образом $x$ = 1 и 1 — это наименьшее число, которое больше всех 0,9, 0,99, 0,999 и т. д. То есть 1 = 0,999... .

Это доказательство опирается на архимедово свойство рациональных и действительных чисел. Действительные числа могут быть расширены до систем счисления , таких как гипердействительные числа , с бесконечно малыми числами ( бесконечно малыми ) и бесконечно большими числами ( бесконечными числами ). ^[5]^[6] , нет наименьшего числа _{$При использовании таких систем обозначение 0,999... обычно не используется, так как среди чисел, больших всех 0.(9) n$} . ^[а]

Наименьшие верхние границы и полнота

Частично этот аргумент показывает, что существует наименьшая верхняя граница последовательности 0,9, 0,99, 0,999 и т. д.: наименьшее число, которое больше, чем все члены последовательности. Одной из аксиом системы действительных чисел является аксиома полноты , которая гласит, что каждая ограниченная последовательность имеет наименьшую верхнюю границу. ^[7]^[8] Эта наименьшая верхняя граница является одним из способов определения бесконечных десятичных разложений: действительное число, представленное бесконечной десятичной дробью, является наименьшей верхней границей его конечных усечений. ^[9] Аргумент здесь не обязательно предполагает полноту, поскольку он показывает, что эта конкретная последовательность рациональных чисел имеет наименьшую верхнюю границу и что эта наименьшая верхняя граница равна единице.

Алгебраические аргументы

Было приведено множество алгебраических аргументов, которые предполагают, что 1 = 0,999... ‍ . Они не являются строгими математическими доказательствами , поскольку обычно основаны на предположении, что правила сложения и умножения конечных десятичных дробей распространяются на бесконечные десятичные дроби. Распространение этих правил на бесконечные десятичные дроби интуитивно и правильно, но требует обоснования.

Простые алгебраические иллюстрации равенства являются предметом педагогических дискуссий и критики. Байерс (2007) обсуждает аргумент, согласно которому в начальной школе учат, что ${\textstyle {\frac {1}{3}}}$ = 0,333... , поэтому, игнорируя все существенные тонкости, "умножая" это тождество на 3, получаем 1 = 0,999... . Далее он говорит, что этот аргумент неубедителен из-за неразрешенной двусмысленности значения знака равенства ; студент может подумать: «Это, конечно, не означает, что число 1 идентично тому, которое подразумевается под обозначением 0,999... ^[10] Ричман (1999) обсуждает, как «этот аргумент получает свою силу от того факта, что большинству людей внушили принять первое уравнение, не задумываясь», но также предполагает, что этот аргумент может заставить скептиков усомниться в этом предположении. ^[11]

Байерс также приводит следующий аргумент.

{\begin{aligned}x&=0.999\ldots \\10x&=9.999\ldots &&{\text{by multiplying by }}10\\10x&=9+0.999\ldots &&{\text{by splitting off integer part}}\\10x&=9+x&&{\text{by definition of }}x\\9x&=9&&{\text{by subtracting }}x\\x&=1&&{\text{by dividing by }}9\end{aligned}}

Студенты, не принявшие первый аргумент, иногда принимают второй аргумент, но, по мнению Байерса, до сих пор не разрешили двусмысленность и, следовательно, не понимают представления бесконечных десятичных дробей. Перессини и Перессини (2007) , представляя тот же аргумент, также заявляют, что он не объясняет равенство, указывая на то, что такое объяснение, вероятно, будет включать в себя концепции бесконечности и полноты . ^[12] Болдуин и Нортон (2012) , цитируя Каца и Каца (2010a) , также приходят к выводу, что трактовка идентичности, основанная на подобных аргументах, без формальной концепции предела, является преждевременной. ^[13] Ченг (2023) соглашается, утверждая, что знание того, что можно умножить 0,999... на 10, сдвинув десятичную запятую, предполагает ответ на более глубокий вопрос о том, как придать смысл выражению 0,999... вообще. ^[14]

Тот же аргумент приводится Ричманом (1999) , который отмечает, что скептики могут сомневаться в том, что $x$ упразднима – то есть имеет ли смысл вычитать $x$ с обеих сторон. ^[11]

Аналитические доказательства

Реальный анализ — это изучение логических основ исчисления , включая поведение последовательностей и рядов действительных чисел. ^[15] Доказательства в этом разделе устанавливают 0,999... = 1, используя методы, знакомые из реального анализа.

Бесконечные серии и последовательности

Обычное развитие десятичных разложений состоит в том, чтобы определить их как суммы бесконечных рядов . В общем: $b_{0}.b_{1}b_{2}b_{3}b_{4}\ldots =b_{0}+b_{1}\left({\tfrac {1}{10}}\right)+b_{2}\left({\tfrac {1}{10}}\right)^{2}+b_{3}\left({\tfrac {1}{10}}\right)^{3}+b_{4}\left({\tfrac {1}{10}}\right)^{4}+\cdots .$

Для 0,999... можно применить теорему сходимости относительно геометрических рядов , утверждающую, что если ⁠ $\vert r\vert$ ⁠ < 1 , тогда: ^[16] $ar+ar^{2}+ar^{3}+\cdots ={\frac {ar}{1-r}}.$

Поскольку 0,999... – это такая сумма с $a=9$ и общее соотношение ⁠ $\textstyle r={\frac {1}{10}}$ ⁠ , теорема быстро решает вопрос: $0.999\ldots =9\left({\tfrac {1}{10}}\right)+9\left({\tfrac {1}{10}}\right)^{2}+9\left({\tfrac {1}{10}}\right)^{3}+\cdots ={\frac {9\left({\tfrac {1}{10}}\right)}{1-{\tfrac {1}{10}}}}=1.$ Это доказательство появляется уже в 1770 году в » Леонарда Эйлера «Элементах алгебры . ^[17]

Сумма геометрической прогрессии сама по себе является результатом даже старше Эйлера. В типичном выводе 18-го века использовалась почленная манипуляция, аналогичная алгебраическому доказательству, приведенному выше, и еще в 1811 году в учебнике Бонникасла «Введение в алгебру» такой аргумент для геометрических рядов используется для обоснования того же маневра на 0,999. . ‍ ^[18] Реакция XIX века против таких либеральных методов суммирования привела к определению, которое до сих пор доминирует: сумма ряда определяется как предел последовательности его частичных сумм. Соответствующее доказательство теоремы явно вычисляет эту последовательность; его можно найти в любом основанном на доказательствах введении в исчисление или анализ. ^[19]

Последовательность ( $x_{0}$ , $x_{1}$ , $x_{2}$ , ...) имеет значение $x$ как его предел, если расстояние $\left\vert x-x_{n}\right\vert$ становится сколь угодно малым, так как $n$ увеличивается. Утверждение о том, что 0,999... = 1 само по себе можно интерпретировать и доказать как предел: ^[б] $0.999\ldots \ {\overset {\underset {\mathrm {def} }{}}{=}}\ \lim _{n\to \infty }0.\underbrace {99\ldots 9} _{n}\ {\overset {\underset {\mathrm {def} }{}}{=}}\ \lim _{n\to \infty }\sum _{k=1}^{n}{\frac {9}{10^{k}}}=\lim _{n\to \infty }\left(1-{\frac {1}{10^{n}}}\right)=1-\lim _{n\to \infty }{\frac {1}{10^{n}}}=1-0=1.$ Первые два равенства можно интерпретировать как сокращенные определения символов. Остальные равенства можно доказать. Последний шаг, который 10 ^$н$ приближается к 0, поскольку $n$ приближается к бесконечности ( ⁠ $\infty$ ⁠ ), часто оправдывается архимедовым свойством действительных чисел. Такое ограниченное отношение к 0,999... часто выражается в более запоминающихся, но менее точных терминах. Например, в учебнике « Университетская арифметика» 1846 года объясняется: «0,999 +, продолжается до бесконечности = 1, потому что каждое присоединение 9 приближает значение к 1»; 1895 года В «Арифметике для школ» говорится: «Когда берется большое количество девяток, разница между 1 и 0,99999... становится непостижимо малой». ^[20] Студенты часто неправильно интерпретируют такую эвристику , предполагая, что 0,999... само по себе меньше 1. ^[21]

Вложенные интервалы и наименьшие верхние границы

Приведенное выше определение ряда определяет действительное число, названное десятичным представлением. Дополнительный подход адаптирован к противоположному процессу: для данного действительного числа определите десятичное расширение(я), чтобы дать ему имя.

Если действительное число $x$ известно, что он лежит в замкнутом интервале [0, 10] (то есть он больше или равен 0 и меньше или равен 10), можно представить себе разделение этого интервала на десять частей, которые перекрываются только в своих конечных точках: [0, 1] , [1, 2] , [2, 3] и так далее до [9, 10] . Число $x$ должен принадлежать к одному из них; если он принадлежит [2, 3] , то записывают цифру «2» и делят этот интервал на [2, 2.1] , [2.1, 2.2] , ..., [2.8, 2.9] , [2.9, 3] . Продолжение этого процесса дает бесконечную последовательность вложенных интервалов , помеченных бесконечной последовательностью цифр ⁠ $b_{1}$ ⁠ , ⁠ $b_{2}$ ⁠ , ⁠ $b_{3}$ ⁠ , ..., и один пишет $x=b_{0}.b_{1}b_{2}b_{3}\ldots \,.$

В этом формализме тождества 1 = 0,999... и 1 = 1,000... отражают соответственно тот факт, что 1 лежит в обоих [0, 1] . и [1, 2] , поэтому при нахождении его цифр можно выбрать любой подинтервал. Чтобы гарантировать, что эта запись не злоупотребляет знаком «=", нужен способ восстановить уникальное действительное число для каждого десятичного числа. Это можно сделать с ограничениями, но другие конструкции продолжают тему упорядочивания. ^[22]

Одним из простых вариантов является теорема о вложенных интервалах , которая гарантирует, что при наличии последовательности вложенных замкнутых интервалов, длина которых становится сколь угодно малой, интервалы содержат ровно одно действительное число в своем пересечении . Итак ⁠ $b_{1}$ ⁠ , ⁠ $b_{2}$ ⁠ , ⁠ $b_{3}$ ⁠ , ... определяется как уникальное число, содержащееся во всех интервалах [ $b_{0}$ , $b_{0}$ + 1] , [ $b_{0}.b_{1}$ , $b_{0}.b_{1}$ + 0,1] и так далее. 0,999... тогда является уникальным действительным числом, которое лежит во всех интервалах [0, 1] , [0,9, 1] , [0,99, 1] и [0,99...9, 1] для каждой конечной строки 9 с. Поскольку 1 является элементом каждого из этих интервалов, 0,999... = 1 . ^[23]

Теорема о вложенных интервалах обычно основана на более фундаментальной характеристике действительных чисел: существовании наименьших верхних границ или супремумов . Чтобы напрямую использовать эти объекты, можно определить ⁠ $b_{0}.b_{1}b_{2}b_{3}$ ⁠ ... быть наименьшей верхней границей множества аппроксимаций ⁠ $b_{0}$ ⁠ , ⁠ $b_{0}.b_{1}$ ⁠ , ⁠ $b_{0}.b_{1}b_{2}$ ⁠ , ... ‍ . ^[24] Затем можно показать, что это определение (или определение вложенных интервалов) согласуется с процедурой подразделения, что снова подразумевает 0,999... = 1 . Том Апостол заключает: «Тот факт, что действительное число может иметь два разных десятичных представления, является просто отражением того факта, что два разных набора действительных чисел могут иметь одинаковую верхнюю границу». ^[25]

Доказательства из построения действительных чисел

Некоторые подходы явно определяют действительные числа как определенные структуры, построенные на рациональных числах , используя аксиоматическую теорию множеств . Натуральные числа {0, 1, 2, 3, ...} начинаются с 0 и продолжаются вверх, так что у каждого числа есть преемник. Можно расширить натуральные числа их отрицательными числами, чтобы получить все целые числа , а затем расширить их до отношений, получив рациональные числа . Эти системы счисления сопровождаются арифметикой сложения, вычитания, умножения и деления. ^[26]^[27] Более тонко они включают в себя упорядочивание , так что одно число можно сравнить с другим и определить, что оно меньше, больше или равно другому числу. ^[28]

Шаг от рационального к реальному является важным расширением. Существует по крайней мере два популярных способа достижения этого шага, оба опубликованы в 1872 году: разрезы Дедекинда и последовательности Коши . Доказательства того, что 0,999... = 1 , напрямую использующие эти конструкции, не встречаются в учебниках по реальному анализу, где современной тенденцией последних нескольких десятилетий было использование аксиоматического анализа. Даже когда предлагается конструкция, она обычно применяется для доказательства аксиом действительных чисел, которые затем подтверждают приведенные выше доказательства. Однако некоторые авторы высказывают мнение, что начинать с конструкции логичнее, а полученные доказательства более самостоятельны. ^[с]

Дедекинд сокращает

В подходе Дедекинда каждое действительное число $x$ определяется как бесконечное множество всех рациональных чисел меньше ⁠ $x$ ⁠ . ^[д] В частности, действительное число 1 — это совокупность всех рациональных чисел, меньших 1. ^[и] Каждое положительное десятичное разложение легко определяет дедекиндовое сечение: набор рациональных чисел, меньших некоторой стадии разложения. Итак, действительное число 0,999... представляет собой набор рациональных чисел. $r$ такой, что $r$ < 0 или $r$ < 0,9 или $r$ < 0,99 или $r$ меньше некоторого другого числа вида ^[29] $1-{\frac {1}{10^{n}}}=0.(9)_{n}=0.\underbrace {99\ldots 9} _{n{\text{ nines}}}.$

Каждый элемент 0,999... меньше 1, поэтому он является элементом действительного числа 1. И наоборот, все элементы 1 являются рациональными числами, которые можно записать как ${\frac {a}{b}}<1,$ с $b>0$ и ⁠ $b>a$ ⁠ . Это подразумевает $1-{\frac {a}{b}}={\frac {b-a}{b}}\geq {\frac {1}{b}}>{\frac {1}{10^{b}}},$ и таким образом ${\frac {a}{b}}<1-{\frac {1}{10^{b}}}.$

С $1-{\frac {1}{10^{b}}}=0.(9)_{b}<0.999\ldots ,$ по приведенному выше определению каждый элемент 1 также является элементом 0,999..., и в сочетании с приведенным выше доказательством того, что каждый элемент 0,999... также является элементом 1, множества 0,999... и 1 содержат одни и те же рациональные числа и, следовательно, представляют собой один и тот же набор, то есть 0,999... = 1 .

Определение действительных чисел как делений Дедекинда было впервые опубликовано Ричардом Дедекиндом в 1872 году. ^[30]Вышеупомянутый подход к присвоению действительного числа каждому десятичному разложению основан на пояснительной статье под названием «Является ли 0,999 ... = 1 ?» Фреда Ричмана в журнале Mathematics Magazine . ^[11] Ричман отмечает, что дедекиндовские разрезы любого плотного подмножества рациональных чисел дают те же результаты; в частности, он использует десятичные дроби , для которых доказательство более непосредственное. Он также отмечает, что обычно определения допускают { $x$ | $x$ < 1} будет разрезом, но не { $x$ | $x$ ≤ 1} (или наоборот). ^[31] Дальнейшая модификация процедуры приводит к другой структуре, в которой они не равны. Несмотря на последовательность, многие общие правила десятичной арифметики больше не соблюдаются, например, дробь ${\textstyle {\frac {1}{3}}}$ не имеет представительства; см. § Альтернативные системы счисления ниже.

Последовательности Коши

Другой подход состоит в том, чтобы определить действительное число как предел последовательности Коши рациональных чисел. Эта конструкция действительных чисел менее напрямую использует порядок рациональных чисел. Во-первых, расстояние между $x$ и $y$ определяется как абсолютное значение ⁠ $\left\vert x-y\right\vert$ ⁠ , где абсолютное значение $\left\vert z\right\vert$ определяется как максимум $z$ и ⁠ $-z$ ⁠ , поэтому никогда не бывает отрицательным. Затем действительные числа определяются как последовательности рациональных чисел, которые обладают свойством последовательности Коши с использованием этого расстояния. То есть в последовательности ⁠ $x_{0}$ ⁠ , ⁠ $x_{1}$ ⁠ , ⁠ $x_{2}$ ⁠ , ..., отображение натуральных чисел в рациональные числа для любого положительного рационального числа $\delta$ есть $N$ такой, что $\left\vert x_{m}-x_{n}\right\vert \leq \delta$ для всех ⁠ $m,n>N$ ⁠ ; расстояние между членами становится меньше любого положительного рационального. ^[32]

Если $(x_{n})$ и $(y_{n})$ являются двумя последовательностями Коши, то они определяются как равные действительным числам, если последовательность $(x_{n}-y_{n})$ имеет предел 0. Усечение десятичного числа ⁠ $b_{0}.b_{1}b_{2}b_{3}$ ⁠ ... сгенерировать последовательность рациональных чисел, которая является Коши; это необходимо для определения реального значения числа. ^[33] Таким образом, в этом формализме задача состоит в том, чтобы показать, что последовательность рациональных чисел $\left(1-0,1-{9 \over 10},1-{99 \over 100},\ldots \right)=\left(1,{1 \over 10},{1 \over 100},\ldots \right)$ имеет предел 0. Учитывая ⁠ $n$ ⁠- й член последовательности, для ⁠ $n\in \mathbb {N}$ ⁠ , поэтому необходимо показать, что $\lim _{n\rightarrow \infty }{\frac {1}{10^{n}}}=0.$ Это можно доказать определением предела . Итак, еще раз: 0,999... = 1 . ^[34]

Определение действительных чисел как последовательностей Коши было впервые опубликовано отдельно Эдуардом Гейне и Георгом Кантором также в 1872 году. ^[30] Вышеупомянутый подход к десятичным разложениям, включая доказательство того, что 0,999... = 1 , во многом соответствует работе Гриффитса и Хилтона 1970 года «Полный учебник классической математики: современная интерпретация» . ^[35]

Бесконечное десятичное представление

Обычно в рамках математического образования в средних школах действительные числа строятся путем определения числа с использованием целого числа, за которым следует точка системы счисления , и бесконечная последовательность, записанная в виде строки, представляющая дробную часть любого данного действительного числа. В этой конструкции набор любой комбинации целого числа и цифр после десятичной точки (или точки счисления в системах счисления, отличных от 10) представляет собой набор действительных чисел. Можно строго показать, что эта конструкция удовлетворяет всем реальным аксиомам после определения отношения эквивалентности на множестве, которое определяет 1 = _eq 0,999... а также для любых других ненулевых десятичных дробей с конечным числом ненулевых членов в десятичной строке с ее завершающая версия 9s. ^[36] При таком построении действительных чисел все доказательства утверждения « 1 = 0,999... » можно рассматривать как неявное предположение о равенстве при выполнении каких-либо операций с действительными числами.

Плотный порядок

Одним из понятий, которое может решить эту проблему, является требование плотного упорядочения действительных чисел. Плотный порядок подразумевает, что если между двумя элементами набора нет нового элемента, эти два элемента должны считаться равными. Следовательно, если бы 0,99999... отличалось от 1, между ними должно было бы быть еще одно действительное число, но его нет: ни в одном из двух чисел нельзя изменить одну цифру, чтобы получить такое число. ^[37]

Обобщения

Результат 0,999... = 1 легко обобщается двумя способами. Во-первых, каждое ненулевое число с конечной десятичной записью (эквивалентно бесконечным конечным нулям) имеет аналог с конечными девятками. Например, 0,24999... равно 0,25, точно так же, как и в рассмотренном частном случае. Эти числа представляют собой в точности десятичные дроби и являются плотными . ^[38]^[9]

Во-вторых, аналогичная теорема применима к каждому основанию или основанию . Например, в базе 2 ( двоичная система счисления ) 0,111... равно 1, а в базе 3 ( тройная система счисления ) 0,222... равно 1. В общем, любая конечная система счисления $b$ выражение имеет аналог с повторяющимися конечными цифрами, равными $b$ − 1 . Учебники реального анализа, скорее всего, пропустят пример 0,999... и представят одно или оба этих обобщения с самого начала. ^[39]

Альтернативные представления 1 также встречаются в нецелочисленных основаниях. Например, в базе золотого сечения два стандартных представления — это 1,000... и 0,101010..., и существует бесконечно много других представлений, включающих соседние единицы. Как правило, почти для всех $q$ между 1 и 2 имеется бесчисленное множество оснований . $q$ разложения на 1. Напротив, их еще неисчислимо много ⁠ $q$ ⁠ , включая все натуральные числа больше 1, для которых имеется только одно основание. $q$ расширение 1, кроме тривиального 1.000... ‍ . Этот результат был впервые получен Паулем Эрдешем , Миклошем Хорватом и Иштваном Йоо примерно в 1990 году. В 1998 году Вилмос Коморник и Паола Лорети определили наименьшее такое основание - константу Коморника-Лорети. $q$ = 1,787231650... ‍ . В этой базе 1 = 0,11010011001011010010110011010011... ; цифры задаются последовательностью Туэ-Морса , которая не повторяется. ^[40]

Более далеко идущее обобщение касается наиболее общих позиционных систем счисления . У них тоже есть несколько представительств, и в некотором смысле трудности еще хуже. Например: ^[41]

В сбалансированной тройной системе ${\textstyle {\frac {1}{2}}}$ = 0.111... = 1. 111 ... ‍ .
В обратной факториальной системе счисления (с использованием оснований 2!, 3!, 4!, ... для позиций после десятичной точки) 1 = 1,000... = 0,1234... ‍ .

Петковшек (1990) доказал, что для любой позиционной системы, которая называет все действительные числа, множество действительных чисел с множественными представлениями всегда плотно. Он называет доказательство «поучительным упражнением в элементарной топологии множества точек »; он предполагает рассмотрение наборов позиционных значений как пространств Стоуна и замечание того, что их реальные представления задаются непрерывными функциями . ^[42]

Приложения

Одно из применений числа 0,999... как представления единицы встречается в элементарной теории чисел . В 1802 году Х. Гудвин опубликовал наблюдение о появлении девяток в повторяющихся десятичных представлениях дробей, знаменателями которых являются определенные простые числа . ^[43] Примеры включают в себя:

${\textstyle {\frac {1}{7}}}$ = 0,142857 и 142 + 857 = 999 .
${\textstyle {\frac {1}{73}}}$ = 0.01369863 и 0136 + 9863 = 9999 .

Э. Миди доказал общий результат о таких дробях, который теперь называется теоремой Миди , в 1836 году. Публикация была малоизвестной, и неясно, включало ли его доказательство непосредственно 0,999..., но по крайней мере одно современное доказательство Уильяма Г. Ливитта это делает. . Если можно доказать, что если десятичная дробь вида ⁠ $0.b_{1}b_{2}b_{3}$ ⁠ ... является положительным целым числом, то оно должно быть 0,999..., что является источником девяток в теореме. ^[44] Исследования в этом направлении могут мотивировать такие понятия, как наибольшие общие делители , модульная арифметика , простые числа Ферма , порядок элементов группы и квадратичная взаимность . ^[45]

Возвращаясь к реальному анализу, аналог по основанию 3 0,222... = 1 играет ключевую роль в характеристике одного из простейших фракталов средней трети , набора Кантора : точка в единичном интервале лежит в множестве Кантора, если и только если его можно представить в троичной форме, используя только цифры 0 и 2.

⁠ $n$ ⁠- я цифра изображения отражает положение точки в ⁠ $n$ ⁠ -й этап строительства. Например, точка ${\textstyle {\frac {2}{3}}}$ дается обычное представление 0,2 или 0,2000..., поскольку оно находится справа от первого удаления и слева от каждого последующего удаления. Суть ${\textstyle {\frac {1}{3}}}$ представлено не как 0,1, а как 0,0222..., поскольку оно находится слева от первой делеции и справа от каждой последующей делеции. ^[46]

Повторяющиеся девятки встречаются и еще в одном произведении Георга Кантора. Их необходимо принять во внимание, чтобы построить достоверное доказательство , применяя его диагональный аргумент 1891 года к десятичным разложениям несчетности единичного интервала . Такое доказательство должно иметь возможность объявить определенные пары действительных чисел разными на основе их десятичных представлений, поэтому следует избегать таких пар, как 0,2 и 0,1999... Простой метод представляет все числа с бесконечными расширениями; противоположный метод исключает повторение девяток. ^[ф] Вариант, который может быть ближе к исходному аргументу Кантора, использует базу 2, и, превратив расширения с основанием 3 в расширения с основанием 2, можно также доказать несчетность множества Кантора. ^[47]

Скептицизм в образовании

Студенты-математики часто отвергают равенство 0,999... и 1 по самым разным причинам, от их несопоставимого внешнего вида до глубоких опасений по поводу концепции предела и разногласий по поводу природы бесконечно малых величин . Есть много общих факторов, способствующих путанице:

Студенты часто «мысленно придерживаются идеи, что число может быть представлено одним и только одним способом десятичной дроби». Видение двух явно разных десятичных знаков, представляющих одно и то же число, кажется парадоксом , который усугубляется появлением, казалось бы, хорошо понятного числа 1. ^[г]
Некоторые студенты интерпретируют «0,999...» (или подобное обозначение) как большую, но конечную строку из девяток, возможно, с переменной, неопределенной длиной. Если они примут бесконечную последовательность девяток, они все равно могут ожидать, что последняя девятка будет «в бесконечности». ^[48]
Интуиция и неоднозначное преподавание заставляют учащихся думать о пределе последовательности как о своего рода бесконечном процессе, а не как о фиксированном значении, поскольку последовательность не обязательно должна достигать своего предела. Если учащиеся принимают разницу между последовательностью чисел и ее пределом, они могут прочитать «0,999...» как означающее последовательность, а не ее предел. ^[49]

Эти идеи ошибочны в контексте стандартных действительных чисел, хотя некоторые из них могут быть справедливы и в других системах счисления, изобретенных либо ради их общей математической полезности, либо в качестве поучительных контрпримеров для лучшего понимания 0,999...; см. § В альтернативных системах счисления ниже.

Многие из этих объяснений были найдены Дэвидом Таллом , который изучал особенности преподавания и познания, которые приводят к некоторым недопониманиям, с которыми он сталкивался со своими студентами колледжа. Опрашивая своих студентов, чтобы определить, почему подавляющее большинство изначально отвергло равенство, он обнаружил, что «студенты продолжали воспринимать 0,999... как последовательность чисел, приближающуюся все ближе и ближе к 1, а не как фиксированное значение, потому что «вы не указано количество знаков» или «это ближайшая возможная десятичная дробь ниже 1 » . ^[21]

Элементарный аргумент умножения 0,333... = ${\textstyle {\frac {1}{3}}}$ на 3 может убедить сопротивляющихся студентов, что 0,999... = 1. Тем не менее, столкнувшись с конфликтом между верой в первое уравнение и неверием во второе, некоторые студенты либо начинают не верить первому уравнению, либо просто разочаровываются. ^[50] Более сложные методы также не являются надежными: учащиеся, которые полностью способны применять строгие определения, все равно могут прибегнуть к интуитивным изображениям, когда их удивляет результат в высшей математике, включая 0,999... ‍ . Например, один настоящий студент-аналитик смог доказать, что 0,333... = ${\textstyle {\frac {1}{3}}}$ используя определение супремума , но затем настояла на том, что 0,999... <1, основываясь на ее более раннем понимании деления в столбики . ^[51] Другие еще могут это доказать ${\textstyle {\frac {1}{3}}}$ = 0,333... , но, столкнувшись с дробным доказательством , настаивают на том, что «логика» заменяет математические вычисления.

Мазур (2005) рассказывает историю о своем блестящем ученике по математическому анализу, который «бросал вызов почти всему, что я говорил в классе, но никогда не подвергал сомнению его калькулятор» и который пришел к выводу, что девять цифр — это все, что нужно для занятий математикой, включая вычисления. квадратный корень из 23. Студенту не нравился ограничивающий аргумент, что 9,99... = 10 , и он называл это «дико воображаемым бесконечным растущим процессом». ^[52]

В рамках APOS теории математического обучения Дубинский и др. (2005) предполагают, что студенты, которые представляют 0,999... как конечную, неопределенную строку с бесконечно малым расстоянием от 1, «еще не создали полную концепцию процесса бесконечной десятичной дроби». Другие студенты, у которых есть полное представление о процессе 0,999... возможно, еще не способны "инкапсулировать" этот процесс в "концепцию объекта", как у них есть концепция объекта 1, и поэтому они рассматривают процесс 0,999... и объект 1 как несовместимый. Они также связывают умственную способность инкапсуляции с просмотром ${\textstyle {\frac {1}{3}}}$ как число само по себе и иметь дело с множеством натуральных чисел в целом. ^[53]

Культурный феномен

С появлением Интернета дебаты о 0,999... стали обычным явлением в группах новостей и на досках объявлений , в том числе во многих из них, номинально имеющих мало общего с математикой. В группе новостей sci.math , спорящий о 0,999... описывается как «популярный вид спорта», и это один из вопросов, на которые есть ответы в FAQ . ^[54]^[55] Часто задаваемые вопросы кратко описывают ⁠ $\textstyle {\frac {1}{3}}$ ⁠ , умножение на 10 и пределы, а также отсылают к последовательностям Коши.

В выпуске общедоступной газетной колонки The Straight Dope за 2003 год обсуждается 0,999... через ${\textstyle {\frac {1}{3}}}$ и ограничения, говоря о заблуждениях,

Низший примат в нас все еще сопротивляется, говоря: .999~ на самом деле представляет собой не число , а процесс . Чтобы найти число, нам нужно остановить процесс, и в этот момент вещь .999~ = 1 разваливается.Ерунда. ^[56]

В статье Slate сообщается, что концепция 0,999... «горячо обсуждается на различных веб-сайтах, от досок объявлений World of Warcraft до форумов Айн Рэнд ». ^[57] Точно так же вопрос о 0,999... оказался настолько популярной темой в первые семь лет существования Blizzard Entertainment от форумов Battle.net 2004 года компания выпустила «пресс-релиз», в котором , что в День дурака говорилось, что это 1. :

Мы очень рады закрыть книгу по этой теме раз и навсегда. Мы стали свидетелями душевной боли и беспокойства по поводу того, равно ли .999~ 1, и мы гордимся тем, что следующее доказательство окончательно и убедительно решает проблему для наших клиентов. ^[58]

Затем предлагаются два доказательства, основанные на пределах и умножении на 10.

0,999... встречается также в математических шутках , таких как: ^[59]

Вопрос: Сколько математиков нужно, чтобы вкрутить лампочку ?
А: 0,999999....

В альтернативных системах счисления

Хотя действительные числа образуют чрезвычайно полезную систему счисления , решение интерпретировать обозначение «0,999...» как обозначение действительного числа в конечном итоге является соглашением, и Тимоти Гауэрс утверждает в книге «Математика: очень краткое введение» , что полученное тождество 0,999. .. = 1 также является соглашением:

Однако это ни в коем случае не произвольное соглашение, поскольку непринятие его заставляет либо изобретать странные новые объекты, либо отказываться от некоторых знакомых правил арифметики. ^[60]

Бесконечно малые

Некоторые доказательства того, что 0,999... = 1, основаны на архимедовом свойстве действительных чисел: не существует ненулевых бесконечно малых чисел . В частности, разница 1 - 0,999... должна быть меньше любого положительного рационального числа, поэтому она должна быть бесконечно малой; но поскольку действительные числа не содержат ненулевых бесконечно малых чисел, разница равна нулю, и, следовательно, эти два значения одинаковы.

Однако существуют математически последовательные упорядоченные алгебраические структуры , включая различные альтернативы действительным числам, которые не являются архимедовыми. Нестандартный анализ предоставляет систему счисления с полным набором бесконечно малых чисел (и обратных им). ^[час] А. Х. Лайтстоун разработал десятичное расширение для гипердействительных чисел в (0, 1). ^∗. Лайтстоун показывает, как связать каждое число с последовательностью цифр. $0.d_{1}d_{2}d_{3}\ldots ;\ldots d_{\infty -1}d_{\infty }d_{\infty +1}\ldots ,$ индексируются сверхнатуральными числами. Хотя он и не говорит напрямую о 0,999..., он показывает реальную цифру ${\textstyle {\frac {1}{3}}}$ представлено 0,333...;...333..., что является следствием принципа переноса . Как следствие число 0.999...;...999... = 1 . При таком типе десятичного представления не каждое расширение представляет число. В частности, "0,333...;...000..." и "0,999...;...000..." не соответствуют никакому числу. ^[61]

Стандартное определение числа 0,999... является пределом последовательности 0,9, 0,99, 0,999, ... ‍ . Другое определение включает ультрапредел , то есть класс эквивалентности [(0,9, 0,99, 0,999, ...)] этой последовательности в конструкции сверхстепени , который представляет собой число, которое не достигает 1 на бесконечно малую величину. ^[62] В более общем смысле, гипердействительное число $u_{H}$ = 0,999...;...999000... , с последней цифрой 9 в бесконечном сверхъестественном ранге ⁠ $H$ ⁠ , удовлетворяет строгому неравенству ⁠ $u_{H}<1$ ⁠ . Соответственно, альтернативная интерпретация выражения «ноль, за которым следует бесконечное количество девяток» может быть такой: ^[63] ${\underset {H}{0.\underbrace {999\ldots } }}\;=1\;-\;{\frac {1}{10^{H}}}.$ Все подобные интерпретации «0,999...» бесконечно близки к 1. Ян Стюарт характеризует эту интерпретацию как «вполне разумный» способ строго оправдать интуицию о том, что «кое-чего не хватает» от 1 из 0,999.... ^[я] Наряду с Кацем и Кацем (2010b) , Эли (2010) также ставит под сомнение предположение о том, что представления студентов о 0,999... < 1 являются ошибочными интуициями о действительных числах, интерпретируя их скорее как нестандартные интуиции, которые могут быть полезны при изучении исчисление. ^[64]

Хакенбуш

Комбинаторная теория игр предлагает обобщенное понятие числа, которое включает в себя действительные числа и многое другое. ^[65] Например, в 1974 году Элвин Берлекамп описал соответствие между строками красных и синих сегментов в Хакенбуше и двоичным разложением действительных чисел, мотивированное идеей сжатия данных . Например, значение строки Хакенбуша LRRLRLRL... равно 0,010101... ₂ = ${\textstyle {\frac {1}{3}}}$ . Однако значение LRLLL... (соответствующее 0,111... ₂ бесконечно меньше 1. Разница между ними представляет собой сюрреалистическое число). ${\textstyle {\frac {1}{\omega }}}$ , где $\omega$ — первый бесконечный порядковый номер ; соответствующая игра — LRRRR... или 0.000... ₂ . ^[Дж]

Это справедливо для двоичных разложений многих рациональных чисел, где значения чисел равны, но соответствующие пути двоичного дерева различны. Например, 0,10111... ₂ = 0,11000... ₂ , оба значения равны ⁠. $\textstyle {\frac {3}{4}}$ ⁠ , но первое представление соответствует пути двоичного дерева LRLRLLL..., а второе соответствует другому пути LRLLRRR... ‍ .

Возвращаясь к вычитанию

Другой способ, которым доказательства могут быть подорваны, - это если 1 - 0,999... просто не существует, потому что вычитание не всегда возможно. К математическим структурам с операцией сложения, но без операции вычитания относятся коммутативные полугруппы , коммутативные моноиды и полукольца . Ричман (1999) рассматривает две такие системы, спроектированные так, что 0,999... < 1 . ^[11]

Во-первых, Ричман (1999) определяет неотрицательное десятичное число как буквальное десятичное расширение. Он определяет лексикографический порядок и операцию сложения, отмечая, что 0,999... <1 просто потому, что 0 <1 в одном месте, но для любого незавершающего ⁠ $x$ ⁠ , у одного 0,999... + $x$ = 1 + ⁠ $x$ ⁠ . Итак, одна из особенностей десятичных чисел состоит в том, что сложение не всегда можно отменить; во-вторых, никакое десятичное число не соответствует ⁠ $\textstyle {\frac {1}{3}}$ ⁠ . После определения умножения десятичные числа образуют положительное, полностью упорядоченное, коммутативное полукольцо. ^[66]

В процессе определения умножения Ричман также определяет еще одну систему, которую он называет «сокращение ⁠ $D$ ⁠ ", который представляет собой набор дедекиндовых разрезов десятичных дробей. Обычно это определение приводит к действительным числам, но для десятичной дроби $d$ он допускает оба разреза ( ⁠ $-\infty$ ⁠ , ⁠ $d$ ⁠ ) и «основная версия» ( ⁠ $-\infty$ ⁠ , ⁠ $d$ ⁠ ] . В результате действительные числа «непросто уживаются» с десятичными дробями. Опять 0,999... <1 . В разрезе нет положительных бесконечно малых ⁠ $D$ ⁠ , но есть «своего рода отрицательная бесконечно малая», 0 ⁻, который не имеет десятичного расширения. Он заключает, что 0,999... = 1 + 0. ⁻, а уравнение " 0,999... + $x$ = 1 » не имеет решения. ^[к]

p -адические числа

Когда их спрашивают о 0,999..., новички часто полагают, что должна быть «конечная 9», полагая, что 1 - 0,999... является положительным числом, которое они записывают как «0,000...1». Независимо от того, имеет ли это смысл, интуитивная цель ясна: добавление 1 к последним 9 в 0,999... превратит все 9 в 0 и оставит 1 на месте единиц. Помимо прочего, эта идея терпит неудачу, потому что в 0,999... ‍ нет «последней девятки» . ^[67] Однако существует система, которая содержит бесконечную строку девяток, включая последнюю девятку.

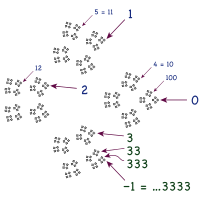
The $p$ - Адические числа представляют собой альтернативную систему счисления, представляющую интерес в теории чисел . Как и реальные цифры, $p$ - адические числа могут быть построены из рациональных чисел с помощью последовательностей Коши ; в конструкции используется другая метрика, в которой 0 ближе к ⁠ $p$ ⁠ и гораздо ближе к ⁠ $p^{n}$ ⁠ , чем 1. ^[68] $p$ - адические числа образуют поле для простых чисел $p$ и кольцо для остальных ⁠ $p$ ⁠ , в том числе 10. Таким образом, арифметику можно выполнять в $p$ - Адики, а бесконечно малых не бывает.

В 10-адических числах аналоги десятичных разложений идут влево. В 10-адическом расширении ...999 есть последние 9 и нет первых 9. К единицам можно добавить 1, и после переноса останутся только 0: 1 + ...999 = ...000 = 0 , и поэтому ...999 = −1 . ^[69] Другой вывод использует геометрическую серию. Бесконечный ряд, подразумеваемый «...999», не сходится в действительных числах, но сходится в 10-адических числах, поэтому можно повторно использовать знакомую формулу: ^[70] $\ldots 999=9+9(10)+9(10)^{2}+9(10)^{3}+\cdots ={\frac {9}{1-10}}=-1.$

Сравните с серией в разделе выше . Третий вывод был изобретен семиклассницей, которая сомневалась в ограничивающем аргументе своего учителя о том, что 0,999... = 1 доказательство умножения на 10 , но была вдохновлена применить приведенное выше в противоположном направлении: если $x$ = ...999 , затем 10 $x$ = ...990 , поэтому 10 $x$ = $x$ − 9 , следовательно $x$ = −1 снова. ^[69]

В качестве окончательного расширения, поскольку 0,999... = 1 (в действительных числах) и ... 999 = -1 (в 10-адических числах), то путем «слепой веры и беззастенчивого жонглирования символами» ^[71] можно сложить два уравнения и получить ...999,999... = 0 . Это уравнение не имеет смысла ни как 10-адическое разложение, ни как обычное десятичное разложение, но оно оказывается значимым и верным в дважды бесконечном десятичном разложении , 10-адического соленоида с повторяющимися левыми концами для представления действительного числа. числа и, в конечном итоге, повторяющиеся правые концы для обозначения 10-адических чисел. ^[72]

Связанные вопросы

Парадоксы Зенона , особенно парадокс бегуна, напоминают очевидный парадокс того, что 0,999... и 1 равны. Парадокс бегуна можно смоделировать математически, а затем, как и в случае с 0,999..., разрешить с помощью геометрической прогрессии. Однако неясно, решает ли эта математическая трактовка основные метафизические проблемы, которые исследовал Зенон. ^[73]

Отрицательный ноль — еще одна избыточная особенность многих способов записи чисел. В системах счисления, таких как действительные числа, где «0» обозначает аддитивную единицу и не является ни положительным, ни отрицательным, обычная интерпретация «-0» заключается в том, что она должна обозначать аддитивную обратную величину 0, что приводит к равенству -0 = 0 . ^[74] Тем не менее, в некоторых научных приложениях используются отдельные положительные и отрицательные нули, как и в некоторых вычислительных двоичных системах счисления (например, целые числа, хранящиеся в формате знака и величины или в формате дополнения до единиц , или числа с плавающей запятой, как указано в стандарте IEEE с плавающей запятой ). ^[75]

См. также

Примечания

^ Например, это можно показать следующим образом: если $x$ — любое число такое, что 0.(9) _$n$ ≤ $x < 1$ , то 0.(9) _{$n$ −1} ≤ 10 $x$ − 9 < $x$ < 1 . Таким образом, если $x$ обладает этим свойством для всех $n$ , то и меньшее число 10 $x$ − 9 тоже имеет это свойство.
^ Предел следует, например, из Рудина (1976) , с. 57, теорема 3.20д. Более прямой подход см. также в Finney, Weir & Giordano (2001) , раздел 8.1, пример 2(a), пример 6(b).
^ Исторический синтез заявлен Гриффитсом и Хилтоном (1970) , с. xiv и снова Пью (2002) , с. 10; оба на самом деле предпочитают сокращения Дедекинда аксиомам. Информацию об использовании сокращений в учебниках см. Pugh (2002) , с. 17 или Рудин (1976) , с. 17. Точки зрения на логику см. Pugh (2002) , с. 10, Рудин (1976) , с.ix, или Мункрес (2000) , с. 30.
^ Эндертон (1977) , с. 113 уточняет это описание: «Идея, лежащая в основе дедекиндовых сокращений, заключается в том, что действительное число $x$ можно назвать, задав бесконечный набор рациональных чисел, а именно все рациональные числа, меньшие, чем $x$ . Фактически мы определим $x$ как набор рациональных чисел, меньших, чем $x. x$ , чтобы избежать цикличности в определении, мы должны уметь характеризовать множества рациональных чисел, получаемые таким образом...»
^ Рудин (1976) , стр. 17–20, Ричман (1999) , стр. 17–20. 399, или Эндертон (1977) , с. 119. Точнее, Рудин, Ричман и Эндертон называют этот разрез 1∗, 1 ₋ и 1 _R соответственно; все трое отождествляют его с традиционным вещественным числом 1. Обратите внимание, что то, что Рудин и Эндертон называют разрезом Дедекинда, Ричман называет «неосновным разрезом Дедекинда».
^ Маор (1987) , с. 60 и Манкевич (2000) , с. 151 рассмотрите первый метод; Манкевич приписывает это Кантору, но первоисточник неясен. Мункрес (2000) , с. 50 упоминает последний метод.
^ Банч (1982) , с. 119; Талл и Шварценбергер (1978) , с. 6. Последнее предложение принадлежит Барреллу (1998) , с. 28: «Возможно, самое обнадеживающее из всех чисел — это 1… Поэтому особенно тревожно, когда кто-то пытается выдать 0,9~ за 1».
^ Полную информацию о нестандартных числах см. в Robinson (1996) .
^ Стюарт (2009) , с. 175; полное обсуждение 0,999... распространяется на стр. 172–175.
^ Berlekamp, Conway & Guy (1982) , стр. 79–80, 307–311, обсуждаются 1 и ⁠ 1 / 3 ⁠ и нажмите ⁠ 1 / $ω$ ⁠ . Игра на 0,111... ₂ непосредственно следует из правила Берлекампа.
^ Ричман (1999) , стр. 398–400. Рудин (1976) , с. 23 назначает эту альтернативную конструкцию (но без рациональных оснований) последним упражнением главы 1.

Ссылки

^ Ченг (2023) , с. 141.
^ Даймонд (1955) .
^ Болдуин и Нортон (2012) .
^ Мейер и Смит (2017) , §8.2.
^ Стюарт (2009) , с. 175.
^ Пропп (2023) .
^ Стиллвелл (1994) , с. 42.
^ Эрл и Николсон (2021) , «связанный».
^ Перейти обратно: ^а ^б Розенлихт (1985) , с. 27.
^ Байерс (2007) , с. 39.
^ Перейти обратно: ^а ^б ^с ^д Ричман (1999) .
^ Перессини и Перессини (2007) , с. 186 .
^ Болдуин и Нортон (2012) ; Кац и Кац (2010а) .
^ Ченг (2023) , с. 136.
^ Люди (2003) .
^ Рудин (1976) , с. 61, теорема 3.26; Стюарт (1999) , с. 706.
^ Эйлер (1822) , с. 170.
^ Граттан-Гиннесс (1970) , с. 69; Бонникасл (1806) , с. 177.
^ Стюарт (1999) , с. 706; Рудин (1976) , с. 61; Проттер и Морри (1991) , с. 213; Пью (2002) , с. 180; Конвей (1978) , с. 31.
^ Дэвис (1846) , с. 175; Смит и Харрингтон (1895) , с. 115.
^ Перейти обратно: ^а ^б Высокий (2000) , с. 221.
^ Билз (2004) , с. 22; Стюарт (2009) , с. 34.
^ Бартл и Шерберт (1982) , стр. 60–62; Педрик (1994) , с. 29; Сохраб (2003) , с. 46.
^ Апостол (1974) , стр. 107-1. 9, 11–12; Билз (2004) , с. 22; Розенлихт (1985) , с. 27.
^ Апостол (1974) , с. 12.
^ Ченг (2023) , стр. 153–156.
^ Конвей (2001) , стр. 25–27.
^ Рудин (1976) , стр. 3, 8.
^ Ричман (1999) , с. 399.
^ Перейти обратно: ^а ^б О'Коннор и Робертсон (2005) .
^ Ричман (1999) , с. 398–399. , чтобы исключить существование различных чисел 0,9 и 1. [...] Итак, мы видим, что в традиционном определении действительных чисел уравнение 0,9 «Зачем это делать? Именно для того = 1 встроено в начало."
^ Гриффитс и Хилтон (1970) , с. 386, §24.2 «Последовательности».
^ Гриффитс и Хилтон (1970) , стр. 388, 393.
^ Гриффитс и Хилтон (1970) , с. 395.
^ Гриффитс и Хилтон (1970) , стр. viii, 395.
^ Это (2011) .
^ Артиг (2002) , с. 212, «...упорядочение действительных чисел признается плотным порядком. Однако, в зависимости от контекста, учащиеся могут совместить это свойство с существованием чисел непосредственно перед или после данного числа (0,999... таким образом часто рассматривается как предшественник 1).".
^ Петковшек (1990) , с. 408.
^ Проттер и Морри (1991) , с. 503; Бартл и Шерберт (1982) , с. 61.
^ Коморник и Лорети (1998) , стр. 636.
^ Кемпнер (1936) , с. 611; Петковшек (1990) , с. 409.
^ Петковшек (1990) , стр. 410–411.
^ Гудвин (1802) ; Диксон (1919) , стр. 161.
^ Ливитт (1984) , с. 301.
^ Гинзберг (2004) , стр. 26–30; Левиттс (2006) , стр. 1–3; Ливитт (1967) , стр. 669, 673; Шрейдер-Фрешетт (1978) , стр. 96–98.
^ Пью (2002) , с. 97; Аллигуд, Зауэр и Йорк (1996) , стр. 150–152; Проттер и Морри (1991) , с. 507; Педрик (1994) , с. 29.
^ Рудин (1976) , с. 50; Пью (2002) , с. 98.
^ Талл и Шварценбергер (1978) , стр. 6–7; Высокий (2000) , с. 221.
^ Талл и Шварценбергер (1978) , с. 6; Высокий (2000) , с. 221.
^ Высокий (1976) , стр. 10–14.
^ Пинто и Талл (2001) , стр. 5; Эдвардс и Уорд (2004) , стр. 416–417.
^ Мазур (2005) , стр. 137–141.
^ Дубинский и др. (2005) , стр. 261–262.
^ Ричман (1999) , с. 396.
^ Врейта (1994) .
^ Адамс (2003) .
^ Элленберг, Иордания (6 июня 2014 г.). «Разве 0,999... = 1 ? И являются ли расходящиеся ряды изобретением дьявола?» . Сланец . Архивировано из оригинала 8 августа 2023 года.
^ «Blizzard Entertainment объявляет, что 0,999~ (повторяется) = 1» (пресс-релиз). Близзард Развлечения . 1 апреля 2004 г. Архивировано из оригинала 4 ноября 2009 г. Проверено 16 ноября 2009 г.
^ Renteln & Dundes (2005) , с. 27.
^ Гауэрс (2002) , с. 60.
^ Лайтстоун (1972) , стр. 245–247.
^ Люди (2012) , стр. 156–180.
^ Кац и Кац (2010a) .
^ Кац и Кац (2010b) ; Эли (2010) .
^ Конвей (2001) , стр. 3–5, 12–13, 24–27.
^ Ричман (1999) , стр. 397–399.
^ Гардинер (2003) , с. 98; Гауэрс (2002) , с. 60.
^ Маскари и Миола (1988) , с. 83–84 .
^ Перейти обратно: ^а ^б Фьелстад (1995) , стр. 11.
^ Фьелстад (1995) , стр. 14–15.
^ ДеСуа (1960) , с. 901.
^ ДеСуа (1960) , с. 902–903.
^ Уоллес (2003) , с. 51; Маор (1987) , с. 17.
^ Мункрес (2000) , с. 34, Упражнение 1(в).
^ Кремер и Киттель (1980) , с. 462. «Типы с плавающей запятой» . Спецификация языка MSDN C# . Архивировано из оригинала 24 августа 2006 года . Проверено 29 августа 2006 г.

Источники

Адамс, Сесил (11 июля 2003 г.). «Бесконечный вопрос: почему .999~ не = 1?» . Прямой наркотик . Чикагский читатель . Архивировано из оригинала 15 августа 2006 года . Проверено 6 сентября 2006 г.
Аллигуд, Коннектикут; Зауэр, Т.Д.; Йорк, Дж.А. (1996). «4.1 Канторовы множества». Хаос: Введение в динамические системы . Спрингер. ISBN 978-0-387-94677-1 .
Этот вводный учебник по динамическим системам предназначен для студентов и начинающих аспирантов. (стр. ix)
Апостол, Том М. (1974). Математический анализ (2-е изд.). Аддисон-Уэсли. ISBN 978-0-201-00288-1 .
Переход от исчисления к расширенному анализу. Математический анализ призван быть «честным, строгим, современным и в то же время не слишком педантическим». (прив.) В разработке Апостолом действительных чисел используется аксиома наименьшей верхней границы, а двумя страницами позже вводятся бесконечные десятичные дроби. (стр. 9–11)
Артиг, Мишель (2002). Холтон, Дерек; Артиг, Мишель; Кирхгребер, Урс; Гиллель, Джоэл; Нисс, Могенс; Шенфельд, Алан (ред.). Преподавание и изучение математики на университетском уровне . Новая серия исследований ICMI. Том. 7. Спрингер, Дордрехт. дои : 10.1007/0-306-47231-7 . ISBN 978-0-306-47231-2 .
Болдуин, Майкл; Нортон, Андерсон (2012). «Действительно ли 0,999… равно 1?» . Учитель математики . 21 (2): 58–67.
Бартл, РД ; Шерберт, доктор медицинских наук (1982). Введение в реальный анализ . Уайли. ISBN 978-0-471-05944-8 .
Этот текст призван стать «доступным, разумным учебником, посвященным фундаментальным концепциям и методам реального анализа». Его развитие действительных чисел основано на аксиоме супремума. (стр. vii–viii)
Билз, Ричард (2004). Анализ: Введение . Издательство Кембриджского университета. ISBN 978-0-521-60047-7 .
Берлекамп, ER ; Конвей, Дж. Х. ; Гай, РК (1982). Пути выигрыша в математических играх . Академическая пресса. ISBN 978-0-12-091101-1 .
Бонникасл, Джон (1806). Введение в алгебру; с примечаниями и наблюдениями: предназначен для использования в школах и местах народного образования (Первое американское изд.). Филадельфия. hdl : 2027/mdp.39015063620382 .
Банч, Брайан Х. (1982). Математические заблуждения и парадоксы . Ван Ностранд Рейнхольд. ISBN 978-0-442-24905-2 .
В этой книге представлен анализ парадоксов и заблуждений как инструмент для исследования ее центральной темы - «довольно тонкой связи между математической реальностью и физической реальностью». Он предполагает изучение алгебры на первом курсе средней школы; В книге развивается дальнейшая математика, включая геометрические ряды в главе 2. Хотя 0,999... не является одним из парадоксов, требующих полного рассмотрения, оно кратко упоминается во время разработки диагонального метода Кантора. (стр. ix-xi, 119)
Баррелл, Брайан (1998). Руководство Мерриам-Вебстера по повседневной математике: справочник для дома и бизнеса . Мерриам-Вебстер. ISBN 978-0-87779-621-3 .
Байерс, Уильям (2007). Как мыслят математики: использование двусмысленности, противоречий и парадоксов для создания математики . Издательство Принстонского университета. ISBN 978-0-691-12738-5 .
Ченг, Евгения (2023). Реальна ли математика? Как простые вопросы ведут нас к глубочайшим математическим истинам . Основные книги. ISBN 978-1-541-6-01826 .
Конвей, Джон Б. (1978) [1973]. Функции одной комплексной переменной I (2-е изд.). Спрингер-Верлаг. ISBN 978-0-387-90328-6 .
Конвей, Джон Х. (2001). О числах и играх (2-е изд.). АК Петерс. ISBN 1-56881-127-6 .
Дэвис, Чарльз (1846). Университетская арифметика: изучение науки о числах и их многочисленные приложения . АС Барнс. п. 175 . Проверено 4 июля 2011 г.
де Врейт, Ганс (1994). "Часто задаваемые вопросы по sci.math: Почему 0,9999... = 1?" . Архивировано из оригинала 29 сентября 2007 года . Проверено 29 июня 2006 г.
ДеСуа, Фрэнк К. (ноябрь 1960 г.). «Система, изоморфная реальным» . Американский математический ежемесячник . 67 (9): 900–903. дои : 10.2307/2309468 . JSTOR 2309468 .
Даймонд, Луи Э. (1955). «Иррациональные числа». Журнал «Математика» . 29 (2). Математическая ассоциация Америки: 89–99. дои : 10.2307/3029588 . JSTOR 3029588 .
Диксон, Леонард Юджин (1919). История теории чисел . Том. 1. Институт Карнеги в Вашингтоне.
Дубинский, Эд; Веллер, Кирк; Макдональд, Майкл; Браун, Энн (2005). «Некоторые исторические проблемы и парадоксы, касающиеся концепции бесконечности: анализ APOS: часть 2» . Образовательные исследования по математике . 60 (2): 253–266. дои : 10.1007/s10649-005-0473-0 . S2CID 45937062 .
Эрл, Ричард; Николсон, Джеймс (2021). Краткий Оксфордский математический словарь (6-е изд.). Издательство Оксфордского университета. ISBN 978-0-192-58405-2 .
Эдвардс, Барбара; Уорд, Майкл (май 2004 г.). «Сюрпризы исследования математического образования: (неправильное) использование студентами математических определений» (PDF) . Американский математический ежемесячник . 111 (5): 411–425. CiteSeerX 10.1.1.453.7466 . дои : 10.2307/4145268 . JSTOR 4145268 . Архивировано из оригинала (PDF) 22 июля 2011 года . Проверено 4 июля 2011 г.
Эли, Роберт (2010). «Нестандартные студенческие представления о бесконечно малых» . Журнал исследований в области математического образования . 41 (2): 117–146. doi : 10.5951/jresematheduc.41.2.0117 .
Эта статья представляет собой практическое исследование с участием студентки, которая разработала теорию бесконечно малых в стиле Лейбница, чтобы помочь ей понять исчисление и, в частности, объяснить, почему 0,999... не соответствует 1 на бесконечно малые 0,000...1.
Эндертон, Герберт Б. (1977). Элементы теории множеств . Эльзевир. ISBN 978-0-12-238440-0 .
Вводный учебник по теории множеств для бакалавров, который «не предполагает какой-либо конкретной подготовки». Он написан для изучения курса, посвященного аксиоматической теории множеств или построению систем счисления; аксиоматический материал помечен так, что его можно преуменьшить. (стр. xi–xii)
Эйлер, Леонард (1822) [1770]. Элементы алгебры . Джон Хьюлетт и Фрэнсис Хорнер, английские переводчики (3-е английское изд.). Орм Лонгман. п. 170 . ISBN 978-0-387-96014-2 . Проверено 4 июля 2011 г.
Финни, Росс Л.; Вейр, Морис Д.; Джордано, Фрэнк Р. (2001). Исчисление Томаса: ранние трансценденталии (10-е изд.). Нью-Йорк: Аддисон-Уэсли.
Фьелстад, Пол (январь 1995 г.). «Парадокс повторяющихся целых чисел» . Математический журнал колледжа . 26 (1): 11–15. дои : 10.2307/2687285 . JSTOR 2687285 .
Гардинер, Энтони (2003) [1982]. Понимание бесконечности: математика бесконечных процессов . Дувр. ISBN 978-0-486-42538-2 .
Гинзберг, Брайан (2004). «(Почти) секретная теорема Миди – продление через 165 лет» . Математический журнал колледжа . 35 (1): 26–30. дои : 10.1080/07468342.2004.11922047 .
Гудвин, Х. (1802 г.). «Любопытные свойства простых чисел, принимаемых за делители единицы. Корреспондент» . Журнал естественной философии, химии и искусств . Новая серия. 1 : 314–316.
Гауэрс, Тимоти (2002). Математика: очень краткое введение . Издательство Оксфордского университета. ISBN 978-0-19-285361-5 .
Граттан-Гиннесс, Айвор (1970). Развитие основ математического анализа от Эйлера до Римана . МТИ Пресс. ISBN 978-0-262-07034-8 .
Гриффитс, HB; Хилтон, Пи Джей (1970). Комплексный учебник классической математики: современная интерпретация . Лондон: Ван Ностранд Рейнхольд. ISBN 978-0-442-02863-3 . ЖКК QA37.2 G75 .
Эта книга стала результатом курса для Бирмингема учителей математики средней школы . Курс был предназначен для того, чтобы передать взгляд на школьную математику на университетском уровне , и книга предназначена для студентов, «которые достигли примерно уровня завершения одного года специального математического обучения в университете». Действительные числа построены в главе 24, «возможно, самой трудной главе во всей книге», хотя авторы приписывают большую часть трудностей использованию идеальной теории , которая здесь не воспроизводится. (стр. VII, XIV)
Кац, Карин Усади; Кац, Михаил Георгиевич (2010а). «Когда 0,999… меньше 1?» . Энтузиаст математики из Монтаны . 7 (1): 3–30. arXiv : 1007.3018 . Бибкод : 2010arXiv1007.3018U . дои : 10.54870/1551-3440.1381 . S2CID 11544878 . Архивировано из оригинала 20 июля 2011 года . Проверено 4 июля 2011 г.
Кац, Карин Усади; Кац, Михаил Георгиевич (2010б). «Увеличение бесконечно малого 1 − 0,9… в эпоху посттриумвирата». Образовательные исследования по математике . 74 (3): 259. arXiv : 1003.1501 . Бибкод : 2010arXiv1003.1501K . дои : 10.1007/s10649-010-9239-4 . S2CID 115168622 .
Кемпнер, Обри Дж. (декабрь 1936 г.). «Анормальные системы счисления». Американский математический ежемесячник . 43 (10): 610–617. дои : 10.2307/2300532 . JSTOR 2300532 .
Коморник, Вилмос; Лорети, Паола (1998). «Уникальные разработки в области нецелочисленных базисов». Американский математический ежемесячник . 105 (7): 636–639. дои : 10.2307/2589246 . JSTOR 2589246 .
Кремер, Герберт ; Киттель, Чарльз (1980). Теплофизика (2-е изд.). У. Х. Фриман. п. 462. ИСБН 978-0-7167-1088-2 .
Ли, Лянпань (март 2011 г.). «Новый подход к действительным числам». arXiv : 1101.1800 [ math.CA ].
Ливитт, Уильям Г. (1967). «Теорема о повторяющихся десятичных дробях» . Американский математический ежемесячник . 74 (6): 669–673. дои : 10.2307/2314251 . JSTOR 2314251 .
Ливитт, Уильям Г. (сентябрь 1984 г.). «Повторяющиеся десятичные дроби» . Математический журнал колледжа . 15 (4): 299–308. дои : 10.2307/2686394 . JSTOR 2686394 .
Левиттс, Джозеф (2006). «Теорема Миди для периодических десятичных дробей». arXiv : math.NT/0605182 .
Лайтстоун, Альберт Х. (март 1972 г.). «Бесконечно малые» . Американский математический ежемесячник . 79 (3): 242–251. дои : 10.2307/2316619 . JSTOR 2316619 .
Манкевич, Ричард (2000). История математики . Касселл. ISBN 978-0-304-35473-3 .
Манкевич стремится представить «историю математики в доступном стиле», сочетая визуальные и качественные аспекты математики, сочинения математиков и исторические очерки. (стр. 8)
Маскари, Джанфранко; Миола, Альфонсо (1988). «Об интеграции числовых и алгебраических вычислений». В Бет, Томас; Клаузен, Майкл (ред.). Применимая алгебра, коды, исправляющие ошибки, комбинаторика и компьютерная алгебра . дои : 10.1007/BFb0039172 . ISBN 978-3-540-39133-3 .
Маор, Эли (1987). К бесконечности и за ее пределами: Культурная история бесконечности . Биркхойзер. ISBN 978-3-7643-3325-6 .
Эта книга, представляющая собой скорее актуальный, чем хронологический обзор бесконечности, «предназначена для широкого читателя», но «рассказана с точки зрения математика». По поводу дилеммы строгости и читабельности языка Маор комментирует: «Надеюсь, мне удалось правильно решить эту проблему». (стр. x-xiii)
Мазур, Джозеф (2005). Евклид в тропическом лесу: открытие универсальных истин в логике и математике . Пирсон: Пи Пресс. ISBN 978-0-13-147994-4 .
Мейер, Джон; Смит, Дерек (2017). Изучение математики: увлекательное введение в доказательство . Издательство Кембриджского университета. ISBN 978-1-107-12898-9 .
Манкрес, Джеймс Р. (2000) [1975]. Топология (2-е изд.). Прентис-Холл. ISBN 978-0-13-181629-9 .
Задумано как введение «на уровне старшего или первого курса магистратуры» без каких-либо формальных предпосылок: «Я даже не предполагаю, что читатель хорошо знает теорию множеств». (стр. xi) Трактовка Мункресом реальности является аксиомой; он заявляет о конструкциях голыми руками: «Такой подход к предмету требует много времени и усилий и представляет больший логический, чем математический интерес». (стр. 30)
Наварро, Мария Анхелес; Каррерас, Педро Перес (2010). «Сократовское методологическое предложение по изучению равенства 0,999...=1» (PDF) . Преподавание математики . 13 (1): 17–34 . Проверено 4 июля 2011 г.
О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. (октябрь 2005 г.), «Действительные числа: от Стевина до Гильберта» , Архив истории математики MacTutor , Университет Сент-Эндрюс
Педрик, Джордж (1994). Первый курс анализа . Спрингер. ISBN 978-0-387-94108-0 .
Перессини, Энтони; Перессини, Доминик (2007). «Философия математики и математическое образование». В ван Керхове, Барт; ван Бендегем, Жан Поль (ред.). Перспективы математических практик . Логика, эпистемология и единство науки. Том. 5. Спрингер. ISBN 978-1-4020-5033-6 .
Петковшек, Марко (май 1990 г.). «Неоднозначные числа плотны» . Американский математический ежемесячник . 97 (5): 408–411. дои : 10.2307/2324393 . JSTOR 2324393 .
Пинто, Марсия; Высокий, Дэвид О. (2001). PME25: Наблюдение за развитием студентов на традиционном университетском курсе анализа (PDF) . стр. т. 4: 57–64. Архивировано из оригинала (PDF) 30 мая 2009 года . Проверено 3 мая 2009 г.
Пропп, Джеймс (17 сентября 2015 г.). «Эпизод о .999...» Математические чары . Проверено 24 мая 2024 г.
Пропп, Джеймс (17 января 2023 г.). «Знаменатели и двойники» . Математические чары . Проверено 16 апреля 2024 г.
Проттер, Мюррей Х .; Морри, Чарльз Б. младший (1991). Первый курс реального анализа (2-е изд.). Спрингер. ISBN 978-0-387-97437-8 .
Целью этой книги является «представить теоретическую основу анализа, подходящую для студентов, прошедших стандартный курс математического анализа». (стр. vii) В конце главы 2 авторы принимают в качестве аксиомы для действительных чисел сходимость ограниченных неубывающих последовательностей, позже доказывая теорему о вложенных интервалах и свойство наименьшей верхней границы. (стр. 56–64) Десятичные разложения приведены в Приложении 3 «Разложение действительных чисел по любому основанию». (стр. 503–507)
Пью, Чарльз Чепмен (2002). Реальный математический анализ . Спрингер-Верлаг. ISBN 978-0-387-95297-0 .
Предполагая, что он знаком с рациональными числами, Пью вводит дедекиндовские сокращения как можно скорее , говоря об аксиоматической трактовке: «Это своего рода мошенничество, учитывая, что вся структура анализа построена на действительной системе счисления». (стр. 10) После доказательства свойства наименьшей верхней границы и некоторых сопутствующих фактов разрезы не используются в остальной части книги.
Рентельн, Пол; Дандес, Алан (январь 2005 г.). «Защита от дурака: образцы математического народного юмора» (PDF) . Уведомления АМС . 52 (1): 24–34. Архивировано из оригинала (PDF) 25 февраля 2009 года . Проверено 3 мая 2009 г.
Ричман, Фред (декабрь 1999 г.). «0,999... = 1?» . Журнал «Математика» . 72 (5): 396–400. дои : 10.2307/2690798 . JSTOR 2690798 . Бесплатный HTML-препринт: Ричман, Фред (июнь 1999 г.). «0,999... = 1?» . Архивировано из оригинала 2 сентября 2006 года . Проверено 23 августа 2006 г. Примечание: журнальная статья содержит материал и формулировки, отсутствующие в препринте.
Робинсон, Авраам (1996). Нестандартный анализ (пересмотренная ред.). Издательство Принстонского университета. ISBN 978-0-691-04490-3 . JSTOR j.ctt1cx3vb6 .
Розенлихт, Максвелл (1985). Введение в анализ . Дувр. ISBN 978-0-486-65038-8 . Эта книга представляет собой «тщательное и строгое» введение в настоящий анализ. Он дает аксиомы действительных чисел, а затем строит их (стр. 27–31) в виде бесконечных десятичных дробей с 0,999... = 1 как часть определения.
Рудин, Вальтер (1976) [1953]. Принципы математического анализа (3-е изд.). МакГроу-Хилл. ISBN 978-0-07-054235-8 .
Учебник для продвинутого курса бакалавриата. «Опыт убедил меня, что педагогически неразумно (хотя и логически правильно) начинать с построения действительных чисел из рациональных. В начале большинство учащихся просто не осознают необходимости этого. Соответственно, реальная Система счисления представлена как упорядоченное поле со свойством наименьшей верхней границы, и быстро делается несколько интересных применений этого свойства. Однако конструкция Дедекинда не опущена теперь в приложении к главе 1, где она может быть опущена. изучайте и наслаждайтесь, когда придет время». (стр. ix)
Шрейдер-Фрешетт, Морис (март 1978 г.). «Дополнительные рациональные числа». Журнал «Математика» . 51 (2): 90–98. дои : 10.2307/2690144 . JSTOR 2690144 .
Смит, Чарльз; Харрингтон, Чарльз (1895). Арифметика для школы . Макмиллан. п. 115 . ISBN 978-0-665-54808-6 . Проверено 4 июля 2011 г.
Сохраб, Хоушанг (2003). Базовый реальный анализ . Биркгаузер. ISBN 978-0-8176-4211-2 .
Стюарт, Ян (2009). Клад математических сокровищ профессора Стюарта . Профильные книги. ISBN 978-1-84668-292-6 .
Стюарт, Джеймс (1999). Исчисление: ранние трансцендентальные теории (4-е изд.). Брукс/Коул. ISBN 978-0-534-36298-0 .
Целью этой книги является «помочь студентам в изучении исчисления» и «способствовать концептуальному пониманию». (p. v) В нем отсутствуют доказательства основ исчисления.
Стиллвелл, Джон (1994), Элементы алгебры: геометрия, числа, уравнения , Springer, ISBN 9783540942900
Высокий, Дэвид ; Шварценбергер, RLE (1978). «Конфликты при изучении действительных чисел и пределов» (PDF) . Преподавание математики . 82 : 44–49. Архивировано из оригинала (PDF) 30 мая 2009 года . Проверено 3 мая 2009 г.
Высокий, Дэвид О. (1976). «Конфликты и катастрофы в изучении математики» (PDF) . Математическое образование для преподавания . 2 (4): 2–18. Архивировано из оригинала (PDF) 26 марта 2009 года . Проверено 3 мая 2009 г.
Высокий, Дэвид (2000). «Когнитивное развитие в области высшей математики с использованием технологий» (PDF) . Журнал исследований математического образования . 12 (3): 210–230. Бибкод : 2000MEdRJ..12..196T . дои : 10.1007/BF03217085 . S2CID 143438975 . Архивировано из оригинала (PDF) 30 мая 2009 года . Проверено 3 мая 2009 г.
Тао, Теренс (2012). Анализ Фурье высшего порядка (PDF) . Американское математическое общество.
Тао, Теренс (2003). «Математика 131AH: неделя 1» (PDF) . Анализ с отличием . Математика Калифорнийского университета в Лос-Анджелесе . Проверено 23 мая 2024 г.
Уоллес, Дэвид Фостер (2003). Все и даже больше: компактная история бесконечности . Нортон. ISBN 978-0-393-00338-3 .

Дальнейшее чтение

Бесвик, Ким (2004). «Почему 0,999... = 1?: Вечный вопрос и чувство числа» . Учитель математики из Австралии . 60 (4): 7–9.
Бурков С.Е. (1987). «Одномерная модель квазикристаллического сплава». Журнал статистической физики . 47 (3/4): 409–438. Бибкод : 1987JSP....47..409B . дои : 10.1007/BF01007518 . S2CID 120281766 .
Берн, Боб (март 1997 г.). «81.15 Случай конфликта» . Математический вестник . 81 (490): 109–112. дои : 10.2307/3618786 . JSTOR 3618786 . S2CID 187823601 .
Калверт, Дж. Б.; Таттл, скорая помощь; Мартин, Майкл С.; Уоррен, Питер (февраль 1981 г.). «Эпоха Ньютона: интенсивный междисциплинарный курс» . Учитель истории . 14 (2): 167–190. дои : 10.2307/493261 . JSTOR 493261 .
Чхве, Ёнги; До, Чонхун (ноябрь 2005 г.). «Равенство участвует в 0,999... и (-8)1/3». Для изучения математики . 25 (3): 13–15, 36. JSTOR 40248503 .
Чунг, Кентукки; Дайкин, Делавэр; Рэтбоун, Чехия (апрель 1971 г.). «Рациональные приближения к π» . Математика вычислений . 25 (114): 387–392. дои : 10.2307/2004936 . JSTOR 2004936 .
Эдвардс, Б. (1997). «Понимание и использование студентами математических определений в реальном анализе». В Досси, Дж.; Сваффорд, Джо; Парментье, М.; Досси, А.Э. (ред.). Материалы 19-го ежегодного собрания Североамериканского отделения Международной группы по психологии математического образования . Том. 1. Колумбус, Огайо: Информационный центр ERIC по науке, математике и экологическому образованию. стр. 17–22.
Эйзенманн, Петр (2008). «Почему это неправда, что 0,999... < 1?» (PDF) . Преподавание математики . 11 (1): 35–40 . Проверено 4 июля 2011 г.
Феррини-Манди, Дж.; Грэм, К. (1994). Капут, Дж.; Дубинский Э. (ред.). «Исследования в области математического анализа: понимание пределов, производных и интегралов». Примечания MAA: Проблемы исследования в изучении математики на бакалавриате . 33 : 31–45.
Гардинер, Тони (июнь 1985 г.). «Бесконечные процессы в элементарной математике: что нужно рассказывать детям?» . Математический вестник . 69 (448): 77–87. дои : 10.2307/3616921 . JSTOR 3616921 . S2CID 125222118 .
Монаган, Джон (декабрь 1988 г.). «Настоящая математика: один аспект будущего A-Level» . Математический вестник . 72 (462): 276–281. дои : 10.2307/3619940 . JSTOR 3619940 . S2CID 125825964 .
Нуньес, Рафаэль (2006). «Действительно ли действительные числа движутся? Язык, мысль и жест: воплощенные когнитивные основы математики» . 18 нетрадиционных эссе о природе математики . Спрингер. стр. 160–181. ISBN 978-0-387-25717-4 . Архивировано из оригинала 18 июля 2011 года . Проверено 4 июля 2011 г.
Пшениосло, Малгожата (март 2004 г.). «Образы предела функции, сложившиеся в ходе математических занятий в университете». Образовательные исследования по математике . 55 (1–3): 103–132. дои : 10.1023/B:EDUC.0000017667.70982.05 . S2CID 120453706 .
Сандефур, Джеймс Т. (февраль 1996 г.). «Использование самоподобия для определения длины, площади и размера» . Американский математический ежемесячник . 103 (2): 107–120. дои : 10.2307/2975103 . JSTOR 2975103 .
Серпинская, Анна (ноябрь 1987 г.). «Студенты-гуманитарии и эпистемологические препятствия, связанные с ограничениями». Образовательные исследования по математике . 18 (4): 371–396. дои : 10.1007/BF00240986 . JSTOR 3482354 . S2CID 144880659 .
Старберд, Майкл ; Старберд, Томас (март 1992 г.). «Требуемая избыточность в представлении действительных чисел» . Труды Американского математического общества . 114 (3): 769–774. дои : 10.1090/S0002-9939-1992-1086343-5 . JSTOR 2159403 .
Шидлик, Дженнифер Эрлз (май 2000 г.). «Математические убеждения и концептуальное понимание предела функции». Журнал исследований в области математического образования . 31 (3): 258–276. дои : 10.2307/749807 . JSTOR 749807 .
Высокий, Дэвид О. (2009). «Динамическая математика и смешение структур знаний в исчислении». ЗДМ Математическое образование . 41 (4): 481–492. дои : 10.1007/s11858-009-0192-6 . S2CID 14289039 .
Высокий, Дэвид О. (май 1981 г.). «Интуиция бесконечности» . Математика в школе . 10 (3): 30–33. JSTOR 30214290 .

Внешние ссылки

Послушайте эту статью ( 50 минут )

Этот аудиофайл был создан на основе редакции этой статьи от 19 октября 2006 г. и не отражает последующие изменения.

[7] Например, это можно показать следующим образом: если $x$ — любое число такое, что 0.(9) _$n$ ≤ $x < 1$ , то 0.(9) _{$n$ −1} ≤ 10 $x$ − 9 < $x$ < 1 . Таким образом, если $x$ обладает этим свойством для всех $n$ , то и меньшее число 10 $x$ − 9 тоже имеет это свойство.

[21] Предел следует, например, из Рудина (1976) , с. 57, теорема 3.20д. Более прямой подход см. также в Finney, Weir & Giordano (2001) , раздел 8.1, пример 2(a), пример 6(b).

[31] Исторический синтез заявлен Гриффитсом и Хилтоном (1970) , с. xiv и снова Пью (2002) , с. 10; оба на самом деле предпочитают сокращения Дедекинда аксиомам. Информацию об использовании сокращений в учебниках см. Pugh (2002) , с. 17 или Рудин (1976) , с. 17. Точки зрения на логику см. Pugh (2002) , с. 10, Рудин (1976) , с.ix, или Мункрес (2000) , с. 30.

[32] Эндертон (1977) , с. 113 уточняет это описание: «Идея, лежащая в основе дедекиндовых сокращений, заключается в том, что действительное число $x$ можно назвать, задав бесконечный набор рациональных чисел, а именно все рациональные числа, меньшие, чем $x$ . Фактически мы определим $x$ как набор рациональных чисел, меньших, чем $x. x$ , чтобы избежать цикличности в определении, мы должны уметь характеризовать множества рациональных чисел, получаемые таким образом...»

[33] Рудин (1976) , стр. 17–20, Ричман (1999) , стр. 17–20. 399, или Эндертон (1977) , с. 119. Точнее, Рудин, Ричман и Эндертон называют этот разрез 1∗, 1 ₋ и 1 _R соответственно; все трое отождествляют его с традиционным вещественным числом 1. Обратите внимание, что то, что Рудин и Эндертон называют разрезом Дедекинда, Ричман называет «неосновным разрезом Дедекинда».

[52] Маор (1987) , с. 60 и Манкевич (2000) , с. 151 рассмотрите первый метод; Манкевич приписывает это Кантору, но первоисточник неясен. Мункрес (2000) , с. 50 упоминает последний метод.

[54] Банч (1982) , с. 119; Талл и Шварценбергер (1978) , с. 6. Последнее предложение принадлежит Барреллу (1998) , с. 28: «Возможно, самое обнадеживающее из всех чисел — это 1… Поэтому особенно тревожно, когда кто-то пытается выдать 0,9~ за 1».

[68] Полную информацию о нестандартных числах см. в Robinson (1996) .

[72] Стюарт (2009) , с. 175; полное обсуждение 0,999... распространяется на стр. 172–175.

[75] Berlekamp, Conway & Guy (1982) , стр. 79–80, 307–311, обсуждаются 1 и ⁠ 1 / 3 ⁠ и нажмите ⁠ 1 / $ω$ ⁠ . Игра на 0,111... ₂ непосредственно следует из правила Берлекампа.

[77] Ричман (1999) , стр. 398–400. Рудин (1976) , с. 23 назначает эту альтернативную конструкцию (но без рациональных оснований) последним упражнением главы 1.

[FOOTNOTECheng2023141-1] Ченг (2023) , с. 141.

[FOOTNOTEDiamond1955-2] Даймонд (1955) .

[FOOTNOTEBaldwinNorton2012-3] Болдуин и Нортон (2012) .

[FOOTNOTEMeierSmith2017§8.2-4] Мейер и Смит (2017) , §8.2.

[FOOTNOTEStewart2009175-5] Стюарт (2009) , с. 175.

[FOOTNOTEPropp2023-6] Пропп (2023) .

[FOOTNOTEStillwell199442-8] Стиллвелл (1994) , с. 42.

[FOOTNOTEEarlNicholson2021"bound"-9] Эрл и Николсон (2021) , «связанный».

[FOOTNOTERosenlicht198527-10] Перейти обратно: ^а ^б Розенлихт (1985) , с. 27.

[FOOTNOTEByers200739-11] Байерс (2007) , с. 39.

[FOOTNOTERichman1999-12] Перейти обратно: ^а ^б ^с ^д Ричман (1999) .

[FOOTNOTEPeressiniPeressini2007[httpsarchiveorgdetailsperspectivesonma0000unse_f3x1page186mode1upqequalityviewtheater_186]-13] Перессини и Перессини (2007) , с. 186 .

[FOOTNOTEBaldwinNorton2012KatzKatz2010a-14] Болдуин и Нортон (2012) ; Кац и Кац (2010а) .

[FOOTNOTECheng2023136-15] Ченг (2023) , с. 136.

[FOOTNOTETao2003-16] Люди (2003) .

[FOOTNOTERudin197661Theorem_3.26Stewart1999706-17] Рудин (1976) , с. 61, теорема 3.26; Стюарт (1999) , с. 706.

[FOOTNOTEEuler1822170-18] Эйлер (1822) , с. 170.

[FOOTNOTEGrattan-Guinness197069Bonnycastle1806177-19] Граттан-Гиннесс (1970) , с. 69; Бонникасл (1806) , с. 177.

[FOOTNOTEStewart1999706Rudin197661ProtterMorrey1991213Pugh2002180Conway197831-20] Стюарт (1999) , с. 706; Рудин (1976) , с. 61; Проттер и Морри (1991) , с. 213; Пью (2002) , с. 180; Конвей (1978) , с. 31.

[FOOTNOTEDavies1846175SmithHarrington1895115-22] Дэвис (1846) , с. 175; Смит и Харрингтон (1895) , с. 115.

[FOOTNOTETall2000221-23] Перейти обратно: ^а ^б Высокий (2000) , с. 221.

[FOOTNOTEBeals200422Stewart200934-24] Билз (2004) , с. 22; Стюарт (2009) , с. 34.

[FOOTNOTEBartleSherbert198260–62Pedrick199429Sohrab200346-25] Бартл и Шерберт (1982) , стр. 60–62; Педрик (1994) , с. 29; Сохраб (2003) , с. 46.

[FOOTNOTEApostol19749,_11–12Beals200422Rosenlicht198527-26] Апостол (1974) , стр. 107-1. 9, 11–12; Билз (2004) , с. 22; Розенлихт (1985) , с. 27.

[FOOTNOTEApostol197412-27] Апостол (1974) , с. 12.

[FOOTNOTECheng2023153–156-28] Ченг (2023) , стр. 153–156.

[FOOTNOTEConway200125–27-29] Конвей (2001) , стр. 25–27.

[FOOTNOTERudin19763,_8-30] Рудин (1976) , стр. 3, 8.

[FOOTNOTERichman1999399-34] Ричман (1999) , с. 399.

[FOOTNOTEO'ConnorRobertson2005-35] Перейти обратно: ^а ^б О'Коннор и Робертсон (2005) .

[36] Ричман (1999) , с. 398–399. , чтобы исключить существование различных чисел 0,9 и 1. [...] Итак, мы видим, что в традиционном определении действительных чисел уравнение 0,9 «Зачем это делать? Именно для того = 1 встроено в начало."

[FOOTNOTEGriffithsHilton1970386§24.2_"Sequences"-37] Гриффитс и Хилтон (1970) , с. 386, §24.2 «Последовательности».

[FOOTNOTEGriffithsHilton1970388,_393-38] Гриффитс и Хилтон (1970) , стр. 388, 393.

[FOOTNOTEGriffithsHilton1970395-39] Гриффитс и Хилтон (1970) , с. 395.

[FOOTNOTEGriffithsHilton1970viii,_395-40] Гриффитс и Хилтон (1970) , стр. viii, 395.

[FOOTNOTELi2011-41] Это (2011) .

[FOOTNOTEArtigue2002212"..._the_ordering_of_the_real_numbers_is_recognized_as_a_dense_order._However,_depending_on_the_context,_students_can_reconcile_this_property_with_the_existence_of_numbers_just_before_or_after_a_given_number_(0.999..._is_thus_often_seen_as_the_predecessor_of&nbsp;1)."-42] Артиг (2002) , с. 212, «...упорядочение действительных чисел признается плотным порядком. Однако, в зависимости от контекста, учащиеся могут совместить это свойство с существованием чисел непосредственно перед или после данного числа (0,999... таким образом часто рассматривается как предшественник 1).".

[FOOTNOTEPetkovšek1990408-43] Петковшек (1990) , с. 408.

[FOOTNOTEProtterMorrey1991503BartleSherbert198261-44] Проттер и Морри (1991) , с. 503; Бартл и Шерберт (1982) , с. 61.

[FOOTNOTEKomornikLoreti1998636-45] Коморник и Лорети (1998) , стр. 636.

[FOOTNOTEKempner1936611Petkovšek1990409-46] Кемпнер (1936) , с. 611; Петковшек (1990) , с. 409.

[FOOTNOTEPetkovšek1990410–411-47] Петковшек (1990) , стр. 410–411.

[FOOTNOTEGoodwyn1802Dickson1919161-48] Гудвин (1802) ; Диксон (1919) , стр. 161.

[FOOTNOTELeavitt1984301-49] Ливитт (1984) , с. 301.

[FOOTNOTEGinsberg200426–30Lewittes20061–3Leavitt1967669,_673Shrader-Frechette197896–98-50] Гинзберг (2004) , стр. 26–30; Левиттс (2006) , стр. 1–3; Ливитт (1967) , стр. 669, 673; Шрейдер-Фрешетт (1978) , стр. 96–98.

[FOOTNOTEPugh200297AlligoodSauerYorke1996150–152ProtterMorrey1991507Pedrick199429-51] Пью (2002) , с. 97; Аллигуд, Зауэр и Йорк (1996) , стр. 150–152; Проттер и Морри (1991) , с. 507; Педрик (1994) , с. 29.

[FOOTNOTERudin197650Pugh200298-53] Рудин (1976) , с. 50; Пью (2002) , с. 98.

[FOOTNOTETallSchwarzenberger19786–7Tall2000221-55] Талл и Шварценбергер (1978) , стр. 6–7; Высокий (2000) , с. 221.

[FOOTNOTETallSchwarzenberger19786Tall2000221-56] Талл и Шварценбергер (1978) , с. 6; Высокий (2000) , с. 221.

[FOOTNOTETall197610–14-57] Высокий (1976) , стр. 10–14.

[FOOTNOTEPintoTall20015EdwardsWard2004416–417-58] Пинто и Талл (2001) , стр. 5; Эдвардс и Уорд (2004) , стр. 416–417.

[FOOTNOTEMazur2005137–141-59] Мазур (2005) , стр. 137–141.

[FOOTNOTEDubinskyWellerMcDonaldBrown2005261–262-60] Дубинский и др. (2005) , стр. 261–262.

[FOOTNOTERichman1999396-61] Ричман (1999) , с. 396.

[FOOTNOTEde_Vreught1994-62] Врейта (1994) .

[FOOTNOTEAdams2003-63] Адамс (2003) .

[64] Элленберг, Иордания (6 июня 2014 г.). «Разве 0,999... = 1 ? И являются ли расходящиеся ряды изобретением дьявола?» . Сланец . Архивировано из оригинала 8 августа 2023 года.

[65] «Blizzard Entertainment объявляет, что 0,999~ (повторяется) = 1» (пресс-релиз). Близзард Развлечения . 1 апреля 2004 г. Архивировано из оригинала 4 ноября 2009 г. Проверено 16 ноября 2009 г.

[FOOTNOTERentelnDundes200527-66] Renteln & Dundes (2005) , с. 27.

[FOOTNOTEGowers200260-67] Гауэрс (2002) , с. 60.

[FOOTNOTELightstone1972245–247-69] Лайтстоун (1972) , стр. 245–247.

[FOOTNOTETao2012156–180-70] Люди (2012) , стр. 156–180.

[FOOTNOTEKatzKatz2010a-71] Кац и Кац (2010a) .

[FOOTNOTEKatzKatz2010bEly2010-73] Кац и Кац (2010b) ; Эли (2010) .

[FOOTNOTEConway20013–5,_12–13,_24–27-74] Конвей (2001) , стр. 3–5, 12–13, 24–27.

[FOOTNOTERichman1999397–399-76] Ричман (1999) , стр. 397–399.

[FOOTNOTEGardiner200398Gowers200260-78] Гардинер (2003) , с. 98; Гауэрс (2002) , с. 60.

[FOOTNOTEMascariMiola1988[httpsbooksgooglecombooksidYVKzPSseyu4CpgPA83_83&ndash;84]-79] Маскари и Миола (1988) , с. 83–84 .

[FOOTNOTEFjelstad199511-80] Перейти обратно: ^а ^б Фьелстад (1995) , стр. 11.

[FOOTNOTEFjelstad199514–15-81] Фьелстад (1995) , стр. 14–15.

[FOOTNOTEDeSua1960901-82] ДеСуа (1960) , с. 901.

[FOOTNOTEDeSua1960902&ndash;903-83] ДеСуа (1960) , с. 902–903.

[FOOTNOTEWallace200351Maor198717-84] Уоллес (2003) , с. 51; Маор (1987) , с. 17.

[FOOTNOTEMunkres200034Exercise_1(c)-85] Мункрес (2000) , с. 34, Упражнение 1(в).

[86] Кремер и Киттель (1980) , с. 462. «Типы с плавающей запятой» . Спецификация языка MSDN C# . Архивировано из оригинала 24 августа 2006 года . Проверено 29 августа 2006 г.

[1]

[2]

[3]

[4]

[5]

[6]

[а]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[б]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[с]

[д]

[и]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[41]

[42]

[43]

[44]

[45]

[46]

[ф]

[47]

[г]

[48]

[49]

[50]

[51]

[52]

[53]

[54]

[55]

[56]

[57]

[58]

[59]

[60]

[час]

[61]

[62]

[63]

[я]

[64]

[65]

[Дж]

[66]

[к]

[67]

[68]

[69]

[70]

[71]

[72]

[73]

[74]

[75]