0.999...

Стилистическое впечатление от числа, показывающее, как его десятичные дроби продолжаются бесконечно.

В математике 0,999 ... (также пишется как 0,9 , , 0 ... 9 или 0.(9) ) — это обозначение повторяющейся десятичной дроби состоящей из бесконечной последовательности девяток после десятичной точки . Эта повторяющаяся десятичная дробь представляет собой число , которое представляет наименьшее число, не меньшее, чем каждое число в последовательности. $(0.9,0.99,0.999,\ldots )$ ; то есть верхняя грань этой последовательности. ^[а]Это число равно 1. Другими словами, «0,999...» — это не «почти точно 1» или «очень, очень почти, но не совсем 1»; скорее, «0,999...» и «1» представляют собой одно и то же число.

Существует много способов доказать это равенство: от интуитивных аргументов до математически строгих доказательств . Используемый метод зависит от целевой аудитории, исходных предположений, исторического контекста и предпочтительного развития действительных чисел , системы, в которой обычно определяется 0,999.... В других системах 0,999... может иметь то же значение, другое определение или быть неопределенным.

В более общем смысле, каждая ненулевая конечная десятичная дробь имеет два равных представления (например, 8,32000... и 8,31999...), что является свойством всех представлений позиционных систем счисления независимо от базы . Утилитарное предпочтение конечного десятичного представления способствует ошибочному представлению о том, что это единственное представление. По этой и другим причинам (например, строгие доказательства, основанные на неэлементарных методах, свойствах или дисциплинах) некоторые люди могут найти равенство настолько нелогичным, что они подвергнут сомнению или отвергнут его. Это было предметом нескольких исследований в области математического образования .

Элементарное доказательство [ править ]

: Свойство Архимеда любая точка

x

перед финишной чертой лежит между двумя точками

P n

(включительно).

Можно доказать уравнение $0.999\ldots =1$ используя только математические инструменты сравнения и сложения (конечных) десятичных чисел , без каких-либо ссылок на более сложные темы, такие как ряды и пределы . доказательство Приведенное ниже представляет собой прямую формализацию интуитивного факта, что если нарисовать $0.9$ , $0.99$ , $0.999$ и т. д. на числовой прямой не остается места для размещения числа между ними и 1. Смысл обозначения 0,999... — это наименьшая точка на числовой прямой, лежащая справа от всех чисел. $0.9$ , $0.99$ , $0.999$ и т. д. Поскольку в конечном итоге между 1 и этими числами нет места, точка 1 должна быть этой наименьшей точкой, и поэтому $0.999\ldots =1$ .

Интуитивное объяснение [ править ]

Если разместить $0.9$ , $0.99$ , $0.999$ и т. д. на числовой прямой сразу видно, что все эти точки находятся левее 1 и что они все ближе и ближе приближаются к 1. Для любого числа $x$ то есть меньше 1, последовательность $0.9$ , $0.99$ , $0.999$ и т. д. в конечном итоге достигнет числа, большего, чем $x$ . Поэтому нет смысла определять $0.999\ldots$ с любым числом меньше 1. Между тем, каждое число больше 1 будет больше любой десятичной дроби в форме $0.999\ldots 9$ для любого конечного числа девяток. Поэтому, $0.999\ldots$ также не может быть отождествлено с каким-либо числом больше 1. Потому что $0.999\ldots$ не может быть больше 1 или меньше 1, оно должно равняться 1, если оно вообще должно быть действительным числом. ^[1]^[2]

Строгое доказательство [ править ]

Обозначим как $0.(9)_{n}$ номер $0.999\ldots 9$ , с $n$ девятки после запятой. Таким образом $0.(9)_{1}=0.9$ , $0.(9)_{2}=0.99$ , $0.(9)_{3}=0.999,$ и так далее. Надо ${\textstyle 1-0.(9)_{1}=0.1={\frac {1}{10}},}$ ${\textstyle 1-0.(9)_{2}=0.01={\frac {1}{10^{2}}},}$ и так далее; то есть, ${\textstyle 1-0.(9)_{n}={\frac {1}{10^{n}}}}$ для каждого натурального числа $n.$

Позволять $x$ быть числом не больше $1$ и не больше $0.9,0.99,0.999,$ и т. д.; то есть, $0.(9)_{n}<x\leq 1,$ для каждого $n.$ Вычитая эти неравенства из 1, получаем ${\textstyle 0\leq 1-x<{\frac {1}{10^{n}}}.}$

Для завершения доказательства необходимо, чтобы не существовало положительного числа, меньшего ${\textstyle {\frac {1}{10^{n}}}}$ для всех $n$ . Это одна из версий свойства Архимеда , справедливая для действительных чисел. ^[3]^[4]

Из этого свойства следует, таким образом, что левое неравенство не может быть строгим ; таким образом $x=1$ а $1$ — наименьшее число, которое больше всех $0.9,0.99,0.999,$ и т. д. То есть, $1=0.999\ldots$ .

Это доказательство опирается на архимедово свойство рациональных и действительных чисел. Действительные числа могут быть расширены до систем счисления , таких как гипердействительные числа , с бесконечно малыми числами ( бесконечно малыми ) и бесконечно большими числами ( бесконечными числами ). ^[5]^[6] При использовании таких систем обозначение 0,999... обычно не используется, так как среди чисел, больших всех, нет наименьшего числа. $0.(9)_{n}$ . ^[б]

границы и полнота Наименьшие верхние

Частично этот аргумент показывает, что существует наименьшая верхняя граница последовательности $0.9$ , $0.99$ , $0.999$ и т. д.: наименьшее число, большее всех членов последовательности. Одной из аксиом системы действительных чисел является аксиома полноты , которая гласит, что каждая ограниченная последовательность имеет наименьшую верхнюю границу. ^[7]^[8] Эта наименьшая верхняя граница является одним из способов определения бесконечных десятичных разложений: действительное число, представленное бесконечной десятичной дробью, является наименьшей верхней границей его конечных усечений. ^[9] Аргумент здесь не обязательно предполагает полноту, поскольку он показывает, что эта конкретная последовательность рациональных чисел имеет наименьшую верхнюю границу и что эта наименьшая верхняя граница равна единице.

аргументы Алгебраические

Было приведено множество алгебраических аргументов, которые предполагают, что $1=0.999\ldots$ Они не являются строгими математическими доказательствами , поскольку обычно основаны на предположении, что правила сложения и умножения конечных десятичных дробей распространяются на бесконечные десятичные дроби. Распространение этих правил на бесконечные десятичные дроби интуитивно и правильно, но требует обоснования.

Простые алгебраические иллюстрации равенства являются предметом педагогических дискуссий и критики. Байерс (2007) обсуждает аргумент, согласно которому в начальной школе учат, что ${\textstyle {\frac {1}{3}}=0.333\ldots }$ , так что, игнорируя все существенные тонкости, "умножив" это тождество на $3$ дает $1=0.999\ldots$ . Далее он говорит, что этот аргумент неубедителен из-за неразрешенной двусмысленности значения знака равенства ; студент может подумать: «Это, конечно, не означает, что число 1 идентично тому, которое подразумевается под обозначением $0.999\ldots$ Большинство студентов-математиков, с которыми столкнулся Байерс, считают, что, хотя $0.999\ldots$ «очень близко» к 1 на основании этого аргумента, причем некоторые даже говорят, что оно «бесконечно близко», но они не готовы сказать, что оно равно 1. ^[10] Ричман (1999) обсуждает, как «этот аргумент получает свою силу от того факта, что большинству людей внушили принять первое уравнение, не задумываясь», но также предполагает, что этот аргумент может заставить скептиков усомниться в этом предположении. ^[11]

Байерс также приводит следующий аргумент.

{\begin{aligned}x&=0.999\ldots \\10x&=9.999\ldots &&{\text{by multiplying by }}10\\10x&=9+0.999\ldots &&{\text{by splitting off integer part}}\\10x&=9+x&&{\text{by definition of }}x\\9x&=9&&{\text{by subtracting }}x\\x&=1&&{\text{by dividing by }}9\end{aligned}}

Студенты, не принявшие первый аргумент, иногда принимают второй аргумент, но, по мнению Байерса, до сих пор не разрешили двусмысленность и, следовательно, не понимают представления бесконечных десятичных дробей. Перессини и Перессини (2007) , представляя тот же аргумент, также заявляют, что он не объясняет равенство, указывая на то, что такое объяснение, вероятно, будет включать концепции бесконечности и полноты . ^[12] Болдуин и Нортон (2012) , цитируя Каца и Каца (2010a) , также приходят к выводу, что трактовка идентичности, основанная на подобных аргументах, без формальной концепции предела, является преждевременной. ^[13] Ченг (2023) соглашается, утверждая, что, зная, можно умножать $0.999\ldots$ на 10 путем смещения десятичной точки предполагает ответ на более глубокий вопрос о том, как придать смысл выражению $0.999\ldots$ совсем. ^[14]

Тот же аргумент приводится Ричманом (1999) , который отмечает, что скептики могут сомневаться в том, что $x$ упразднима – то есть имеет ли смысл вычитать $x$ с обеих сторон. ^[11]

Аналитические доказательства [ править ]

Реальный анализ — это изучение логических основ исчисления , включая поведение последовательностей и рядов действительных чисел. ^[15] Доказательства в этом разделе устанавливают $0.999\ldots =1$ используя методы, знакомые из реального анализа.

Бесконечные серии и последовательности [ править ]

Обычное развитие десятичных разложений состоит в том, чтобы определить их как суммы бесконечных рядов . В общем:

b_{0}.b_{1}b_{2}b_{3}b_{4}\ldots =b_{0}+b_{1}\left({\tfrac {1}{10}}\right)+b_{2}\left({\tfrac {1}{10}}\right)^{2}+b_{3}\left({\tfrac {1}{10}}\right)^{3}+b_{4}\left({\tfrac {1}{10}}\right)^{4}+\cdots .

Для 0,999... можно применить теорему сходимости относительно геометрических рядов , утверждающую, что если $|r|<1$ , затем: ^[16]

ar+ar^{2}+ar^{3}+\cdots ={\frac {ar}{1-r}}.

Поскольку 0,999... – это такая сумма с $a=9$ и общее соотношение ${\textstyle r={\frac {1}{10}}}$ , теорема быстро решает вопрос:

0.999\ldots =9\left({\tfrac {1}{10}}\right)+9\left({\tfrac {1}{10}}\right)^{2}+9\left({\tfrac {1}{10}}\right)^{3}+\cdots ={\frac {9\left({\tfrac {1}{10}}\right)}{1-{\tfrac {1}{10}}}}=1.

Это доказательство появляется уже в 1770 году в » Леонарда Эйлера «Элементах алгебры . ^[17]

Сумма геометрической прогрессии сама по себе является результатом даже старше Эйлера. В типичном выводе 18-го века использовалась почленная манипуляция, аналогичная алгебраическому доказательству , приведенному выше, и еще в 1811 году в учебнике Бонникасла « Введение в алгебру» такой аргумент для геометрических рядов используется для обоснования того же маневра на 0,999. . ^[18]Реакция XIX века против таких либеральных методов суммирования привела к появлению определения, которое до сих пор доминирует: сумма ряда определяется как предел последовательности его частичных сумм. Соответствующее доказательство теоремы явно вычисляет эту последовательность; его можно найти в любом основанном на доказательствах введении в исчисление или анализ. ^[19]

Последовательность $(x_{0},x_{1},x_{2},\ldots )$ имеет значение $x$ как его предел , если расстояние $\left|x-x_{n}\right|$ становится сколь угодно малым, так как $n$ увеличивается. Заявление о том, что $0.999\ldots =1$ само по себе может быть интерпретировано и доказано как предел: ^[с]

0.999\ldots \ {\overset {\underset {\mathrm {def} }{}}{=}}\ \lim _{n\to \infty }0.\underbrace {99\ldots 9} _{n}\ {\overset {\underset {\mathrm {def} }{}}{=}}\ \lim _{n\to \infty }\sum _{k=1}^{n}{\frac {9}{10^{k}}}=\lim _{n\to \infty }\left(1-{\frac {1}{10^{n}}}\right)=1-\lim _{n\to \infty }{\frac {1}{10^{n}}}=1-0=1.

Первые два равенства можно интерпретировать как сокращенные определения символов. Остальные равенства можно доказать. Последний шаг, который

10^{n}

приближается к 0, так как

n

приближается к бесконечности (

\infty

), часто оправдывается архимедовым свойством действительных чисел. Такое ограниченное отношение к

0.999\ldots

часто выражается более выразительно, но менее точно. Например, в учебнике «Университетская арифметика» 1846 года объясняется: «0,999 +, продолжается до бесконечности = 1, потому что каждое присоединение 9 приближает значение к 1»; » 1895 года В «Арифметике для школ говорится: «Когда берется большое количество девяток, разница между 1 и 0,99999... становится непостижимо малой». ^[20] такую эвристику Студенты часто неправильно интерпретируют

, предполагая, что 0,999...

само по себе меньше 1. ^[21]

Вложенные интервалы и наименьшие верхние границы [ править ]

Приведенное выше определение ряда определяет действительное число, названное десятичным представлением. Дополнительный подход адаптирован к противоположному процессу: для данного действительного числа определите десятичное расширение(я), чтобы дать ему имя.

Если известно, что действительное число $x$ лежит в замкнутом интервале $[0,10]$ (то есть он больше или равен 0 и меньше или равен 10), можно представить себе разделение этого интервала на десять частей, которые перекрываются только в своих конечных точках: $[0,1]$ , $[1,2]$ , $[2,3]$ и так далее до $[9,10]$ . Номер $x$ должен принадлежать к одному из них; если он принадлежит [2, 3], то записывают цифру «2» и делят этот интервал на $[2,2.1]$ , $[2.1,2.2]$ , ..., $[2.8,2.9]$ , $[2.9,3]$ . Продолжение этого процесса дает бесконечную последовательность вложенных интервалов , помеченных бесконечной последовательностью цифр. $b_{1},b_{2},b_{3},\ldots$ , и один пишет

x=b_{0}.b_{1}b_{2}b_{3}\ldots .

В этом формализме тождества 1 = 0,999... и 1 = 1,000... отражают соответственно тот факт, что 1 лежит в обоих $[0,1]$ . и $[1,2]$ , поэтому при нахождении его цифр можно выбрать любой подинтервал. Чтобы гарантировать, что эта запись не злоупотребляет знаком «=", нужен способ восстановить уникальное действительное число для каждого десятичного числа. Это можно сделать с ограничениями, но другие конструкции продолжают тему упорядочивания. ^[22]

Одним из простых вариантов является теорема о вложенных интервалах , которая гарантирует, что при наличии последовательности вложенных замкнутых интервалов, длина которых становится сколь угодно малой, интервалы содержат ровно одно действительное число в своем пересечении . Так $b_{1},b_{2},b_{3},\ldots$ определяется как уникальное число, содержащееся во всех интервалах $[b_{0},b_{0}+1]$ , $[b_{0}.b_{1},b_{0}.b_{1}+0.1]$ , и так далее. 0,999... тогда это уникальное действительное число, лежащее во всех интервалах. $[0,1]$ , $[0.9,1]$ , $[0.99,1]$ , и $[0.99...9,1]$ для каждой конечной строки девяток. Поскольку 1 является элементом каждого из этих интервалов, $0.999...=1$ . ^[23]

Теорема о вложенных интервалах обычно основана на более фундаментальной характеристике действительных чисел: существовании наименьших верхних границ или супремумов . Чтобы напрямую использовать эти объекты, можно определить $b_{0}.b_{1}b_{2}b_{3}\ldots$ быть наименьшей верхней границей набора аппроксимантов $b_{0},b_{0}.b_{1},b_{0}.b_{1}b_{2},\ldots$ . ^[24] Затем можно показать, что это определение (или определение вложенных интервалов) согласуется с процедурой подразделения, подразумевая $0.999...=1$ снова. Том Апостол заключает: «Тот факт, что действительное число может иметь два разных десятичных представления, является просто отражением того факта, что два разных набора действительных чисел могут иметь одинаковую верхнюю границу». ^[25]

Доказательства из построения действительных чисел [ править ]

Некоторые подходы явно определяют действительные числа как определенные структуры, построенные на рациональных числах , используя аксиоматическую теорию множеств . Натуральные числа $\{0,1,2,3,\ldots \}$ начинаются с 0 и продолжаются вверх, чтобы у каждого числа был преемник. Можно расширить натуральные числа их отрицательными числами, чтобы получить все целые числа , а затем расширить их до отношений, получив рациональные числа . Эти системы счисления сопровождаются арифметикой сложения, вычитания, умножения и деления. ^[26]^[27] Более тонко они включают в себя упорядочивание , так что одно число можно сравнить с другим и определить, что оно меньше, больше или равно другому числу. ^[28]

Шаг от рационального к реальному является важным расширением. Существует по крайней мере два популярных способа достижения этого шага, оба опубликованы в 1872 году: разрезы Дедекинда и последовательности Коши . Доказательства того, что $0.999\ldots =1$ которые непосредственно используют эти конструкции, не встречаются в учебниках по реальному анализу, где современная тенденция последних нескольких десятилетий заключалась в использовании аксиоматического анализа. Даже когда предлагается конструкция, она обычно применяется для доказательства аксиом действительных чисел, которые затем подтверждают приведенные выше доказательства. Однако некоторые авторы высказывают мнение, что начинать с конструкции логичнее, а полученные доказательства более самостоятельны. ^[д]

Дедекинд сокращает

В подходе Дедекинда каждое действительное число $x$ определяется как бесконечное множество всех рациональных чисел , меньших $x$ . ^[Это] В частности, действительное число 1 — это совокупность всех рациональных чисел, меньших 1. ^[ф]Каждое положительное десятичное разложение легко определяет дедекиндовое сечение: набор рациональных чисел, меньших некоторой стадии разложения. Итак, действительное число 0,999... представляет собой набор рациональных чисел. $r$ такой, что $r<0$ , или $r<0.9$ , или $r<0.99$ , или $r$ меньше некоторого другого числа вида ^[29]

1-{\frac {1}{10^{n}}}=0.(9)_{n}=0.\underbrace {99\ldots 9} _{n{\text{ nines}}}.

Каждый элемент 0,999... меньше 1, поэтому он является элементом действительного числа 1. И наоборот, все элементы 1 являются рациональными числами, которые можно записать как

{\frac {a}{b}}<1,

с

b>0

и

b>a

. Из этого следует

1-{\frac {a}{b}}={\frac {b-a}{b}}\geq {\frac {1}{b}}>{\frac {1}{10^{b}}},

и поэтому

{\frac {a}{b}}<1-{\frac {1}{10^{b}}}.

С

1-{\frac {1}{10^{b}}}=0.(9)_{b}<0.999\ldots ,

по приведенному выше определению каждый элемент 1 также является элементом 0,999..., и в сочетании с приведенным выше доказательством того, что каждый элемент 0,999... также является элементом 1, множества 0,999... и 1 содержат одни и те же рациональные числа и, следовательно, представляют собой один и тот же набор, то есть

0.999...=1

.

Определение действительных чисел как сокращений Дедекинда было впервые опубликовано Ричардом Дедекиндом в 1872 году. ^[30]Вышеупомянутый подход к присвоению действительного числа каждому десятичному разложению основан на пояснительной статье под названием «Является ли 0,999 ... = 1?» Фреда Ричмана в журнале Mathematics Magazine . ^[11]Ричман отмечает, что дедекиндовские разрезы любого плотного подмножества рациональных чисел дают те же результаты; в частности, он использует десятичные дроби , для которых доказательство более непосредственное. Он также отмечает, что обычно определения позволяют $\{x\colon x<1\}$ быть разрезом, но не $\{x\colon x\leq 1\}$ (или наоборот). ^[31]Дальнейшая модификация процедуры приводит к другой структуре, в которой они не равны. Несмотря на последовательность, многие общие правила десятичной арифметики больше не соблюдаются, например, дробь ${\textstyle {\frac {1}{3}}}$ не имеет представительства; см. § Альтернативные системы счисления ниже.

Последовательности Коши [ править ]

Другой подход состоит в том, чтобы определить действительное число как предел последовательности Коши рациональных чисел. Эта конструкция действительных чисел использует порядок рациональных чисел менее непосредственно. Во-первых, расстояние между $x$ и $y$ определяется как абсолютное значение $\left|x-y\right|$ , где абсолютное значение $\left|z\right|$ определяется как максимум $z$ и $-z$ , поэтому никогда не бывает отрицательным. Затем действительные числа определяются как последовательности рациональных чисел, которые обладают свойством последовательности Коши с использованием этого расстояния. То есть в последовательности $x_{0},x_{1},x_{2},\ldots$ , отображение натуральных чисел в рациональные, для любого положительного рационального $\delta$ есть $N$ такой, что $\left|x_{m}-x_{n}\right|\leq \delta$ для всех $m,n>N$ ; расстояние между членами становится меньше любого положительного рационального. ^[32]

Если $(x_{n})$ и $(y_{n})$ являются двумя последовательностями Коши, то они определяются как равные действительным числам, если последовательность $(x_{n}-y_{n})$ имеет предел 0. Усечение десятичного числа $b_{0}.b_{1}b_{2}b_{3}\ldots$ сгенерировать последовательность рациональных чисел, которая является Коши; это необходимо для определения реального значения числа. ^[33] Таким образом, в этом формализме задача состоит в том, чтобы показать, что последовательность рациональных чисел

\left(1-0,1-{9 \over 10},1-{99 \over 100},\dots \right)=\left(1,{1 \over 10},{1 \over 100},\dots \right)

имеет предел 0. Учитывая

n

--й член последовательности, для

n\in \mathbb {N}

, поэтому необходимо показать, что

\lim _{n\rightarrow \infty }{\frac {1}{10^{n}}}=0.

Это можно доказать определением предела . Итак, еще раз,

0.999\ldots =1

. ^[34]

Определение действительных чисел как последовательностей Коши было впервые опубликовано отдельно Эдуардом Гейне и Георгом Кантором также в 1872 году. ^[30] Описанный выше подход к десятичным разложениям, включая доказательство того, что $0.999\ldots =1$ , внимательно следует за работой Гриффитса и Хилтона 1970 года «Полный учебник классической математики: современная интерпретация» . ^[35]

Бесконечное десятичное представление [ править ]

Обычно в рамках математического образования в средних школах действительные числа строятся путем определения числа с использованием целого числа, за которым следует точка системы счисления , и бесконечная последовательность, записанная в виде строки, представляющая дробную часть любого данного действительного числа. В этой конструкции набор любой комбинации целого числа и цифр после десятичной точки (или точки счисления в системах с основанием не 10) представляет собой набор действительных чисел. Можно строго показать, что эта конструкция удовлетворяет всем действительным аксиомам после определения отношения эквивалентности на множестве, которое определяет 1 = _eq 0,999... а также для любых других ненулевых десятичных дробей с конечным числом ненулевых членов в десятичной строке с ее завершающая версия 9s. ^[36] При таком построении действительных чисел все доказательства утверждения «1 = 0,999...» можно рассматривать как неявное предположение о равенстве при выполнении каких-либо операций с действительными числами.

Плотный порядок [ править ]

Одним из понятий, которое может решить эту проблему, является требование плотного упорядочения действительных чисел. Плотный порядок подразумевает, что если между двумя элементами набора нет нового элемента, эти два элемента должны считаться равными. Следовательно, если $0.99999...$ должны были отличаться от $1$ , между ними должно быть еще одно действительное число, но его нет: ни одну цифру нельзя изменить ни в одном из двух, чтобы получить такое число. ^[37]

Обобщения [ править ]

Результат, который $0.999\ldots =1$ легко обобщается двумя способами. Во-первых, каждое ненулевое число с конечной десятичной записью (эквивалентно бесконечным конечным нулям) имеет аналог с конечными девятками. Например, 0,24999... равно 0,25, точно так же, как и в рассмотренном частном случае. Эти числа представляют собой в точности десятичные дроби и являются плотными . ^[38]^[9]

Во-вторых, аналогичная теорема применима к каждому основанию или основанию . Например, в базе 2 ( двоичная система счисления ) 0,111... равно 1, а в базе 3 ( тройная система счисления ) 0,222... равно 1. В общем, любая конечная система счисления $b$ выражение имеет аналог с повторяющимися конечными цифрами, равными $b-1$ . Учебники реального анализа, скорее всего, пропустят пример 0,999... и представят одно или оба этих обобщения с самого начала. ^[39]

Альтернативные представления единицы также встречаются в нецелочисленных основаниях. Например, в базе золотого сечения два стандартных представления: $1.000\ldots$ и $0.101010\ldots$ , и существует бесконечно много других представлений, включающих соседние единицы. Как правило, почти для всех $q$ между 1 и 2 имеется бесчисленное множество оснований. $q$ разложения на 1. Напротив, существует еще несчетное количество $q$ , включая все натуральные числа больше 1, у которых есть только одно основание. $q$ расширение 1, кроме тривиального $1.000\ldots$ . Этот результат был впервые получен Паулем Эрдешем , Миклошем Хорватом и Иштваном Йоо примерно в 1990 году. В 1998 году Вилмос Коморник и Паола Лорети определили наименьшее такое основание - константу Коморника-Лорети. $q=1.787231650\ldots$ . В этой базе $1=0.11010011001011010010110011010011\ldots$ ; цифры задаются последовательностью Туэ-Морса , которая не повторяется. ^[40]

Более далеко идущее обобщение касается наиболее общих позиционных систем счисления . У них тоже есть несколько представительств, и в каком-то смысле трудности еще хуже. Например: ^[41]

В сбалансированной тройной системе ${\textstyle {\frac {1}{2}}=0.111\ldots =1.{\underline {111}}\ldots }$ .
В обратной факториальной системе счисления (с использованием оснований $2!,3!,4!,\ldots$ для позиций после десятичной точки), $1=1.000\ldots =0.1234\ldots$ .

Невозможность однозначного представления [ править ]

То, что все эти различные системы счисления страдают от множественного представления некоторых действительных чисел, можно объяснить фундаментальным различием между действительными числами как упорядоченным набором и коллекциями бесконечных строк символов, упорядоченных лексикографически . Действительно, следующие два свойства объясняют трудность:

Если интервал действительных чисел разбить на две непустые части $L$ , $R$ , такой, что каждый элемент $L$ (строго) меньше любого элемента $R$ , то либо $L$ содержит наибольший элемент или $R$ содержит наименьший элемент, но не оба.
Совокупность бесконечных строк символов, взятых из любого конечного «алфавита», лексикографически упорядоченных, можно разделить на две непустые части. $L$ , $R$ , такой, что каждый элемент $L$ меньше, чем каждый элемент $R$ , пока $L$ содержит самый большой элемент и $R$ содержит наименьший элемент. Действительно, достаточно взять два конечных префикса (начальных подстроки) $p_{1},p_{2}$ элементов из коллекции так, что они отличаются только своим конечным символом, для которого они имеют последовательные значения, и принимают за $L$ набор всех строк в коллекции, соответствующий префикс которых не превышает $p_{1}$ , и для $R$ остаток — строки в коллекции, соответствующий префикс которых не менее $p_{2}$ . Затем $L$ имеет самый большой элемент, начиная с $p_{1}$ и выбираем самый крупный доступный символ во всех следующих позициях. В отличие, $R$ имеет наименьший элемент, полученный следующим образом $p_{2}$ по наименьшему символу во всех позициях.

Первый пункт вытекает из основных свойств действительных чисел: $L$ имеет высшую и $R$ имеет инфимум , которые, как легко видеть, равны; будучи действительным числом, оно либо лежит в $R$ или в $L$ , но не то и другое, поскольку $L$ и $R$ должны быть непересекающимися . Второй пункт обобщает пару 0,999.../1,000..., полученную для $p_{1}=0$ , $p_{2}=1$ . Нет необходимости использовать один и тот же алфавит для всех позиций (чтобы, например, можно было включить смешанные системы счисления) или рассматривать полный набор возможных строк; Единственные важные моменты заключаются в том, что в каждой позиции может быть выбран конечный набор символов (который может даже зависеть от предыдущих символов) (это необходимо для обеспечения максимального и минимального выбора), и что правильный выбор для любой позиции должен быть сделан. в результате получится действительная бесконечная строка (поэтому нельзя допускать «9» в каждой позиции и одновременно запрещать бесконечную последовательность «9»). При этих предположениях приведенный выше аргумент показывает, что сохраняющее порядок отображение набора строк в интервал действительных чисел не может быть биекцией : либо некоторые числа не соответствуют ни одной строке, либо некоторые из них соответствуют более чем одной строке. .

Петковшек (1990) доказал, что для любой позиционной системы, в которой именуются все действительные числа, множество действительных чисел с множественными представлениями всегда плотно. Он называет доказательство «поучительным упражнением в элементарной топологии множества точек »; он предполагает рассмотрение наборов позиционных значений как пространств Стоуна и замечание того, что их реальные представления задаются непрерывными функциями . ^[42]

Приложения [ править ]

Одно из применений числа 0,999... как представления единицы встречается в элементарной теории чисел . В 1802 году Х. Гудвин опубликовал наблюдение о появлении девяток в повторяющихся десятичных представлениях дробей, знаменателями которых являются определенные простые числа . ^[43] Примеры включают в себя:

${\textstyle {\frac {1}{7}}=0.{\overline {142857}}}$ и $142+857=999$ .
${\textstyle {\frac {1}{73}}=0.{\overline {01369863}}}$ и $0136+9863=9999$ .

Э. Миди доказал общий результат о таких дробях, который теперь называется теоремой Миди , в 1836 году. Публикация была малоизвестной, и неясно, включало ли его доказательство непосредственно 0,999..., но по крайней мере одно современное доказательство Уильяма Г. Ливитта это делает. . Если можно доказать, что если десятичная дробь вида $0.b_{1}b_{2}b_{3}\ldots$ является положительным целым числом, то оно должно быть 0,999..., что и является источником девяток в теореме. ^[44] Исследования в этом направлении могут мотивировать такие понятия, как наибольшие общие делители , модульная арифметика , простые числа Ферма , порядок элементов группы и квадратичная взаимность . ^[45]

Возвращаясь к реальному анализу, аналог по основанию 3 $0.222\ldots =1$ играет ключевую роль в характеристике одного из простейших фракталов средней трети , множества Кантора : точка в единичном интервале лежит в множестве Кантора тогда и только тогда, когда ее можно представить в троичной форме, используя только цифры 0 и 2.

The $n$ -я цифра изображения отражает положение точки в $n$ - Этап строительства. Например, точка ${\textstyle {\frac {2}{3}}}$ дается обычное представление 0,2 или 0,2000..., поскольку оно находится справа от первого удаления и слева от каждого последующего удаления. Смысл ${\textstyle {\frac {1}{3}}}$ представлено не как 0,1, а как 0,0222..., поскольку оно находится слева от первой делеции и справа от каждой последующей делеции. ^[46]

Повторяющиеся девятки встречаются и еще в одном произведении Георга Кантора. Их необходимо принять во внимание, чтобы построить достоверное доказательство , применяя его диагональный аргумент 1891 года к десятичным разложениям несчетности единичного интервала . Такое доказательство должно иметь возможность объявить определенные пары действительных чисел разными на основе их десятичных представлений, поэтому следует избегать таких пар, как 0,2 и 0,1999... Простой метод представляет все числа с бесконечными расширениями; противоположный метод исключает повторение девяток. ^[г] Вариант, который может быть ближе к исходному аргументу Кантора, использует базу 2, и, превратив разложения по основанию 3 в расширения по основанию 2, можно также доказать несчетность множества Кантора. ^[47]

в образовании Скептицизм

Студенты-математики часто отвергают равенство 0,999... и 1 по причинам, варьирующимся от их несопоставимого внешнего вида до глубоких опасений по поводу концепции предела и разногласий по поводу природы бесконечно малых величин . Есть много общих факторов, способствующих путанице:

Студенты часто «мысленно придерживаются идеи, что число может быть представлено одним и только одним способом десятичной дроби». Видеть две явно разные десятичные дроби, представляющие одно и то же число, кажется парадоксом , который усугубляется появлением, казалось бы, хорошо понятного числа 1. ^[час]
Некоторые студенты интерпретируют «0,999...» (или подобное обозначение) как большую, но конечную строку из девяток, возможно, с переменной, неопределенной длиной. Если они примут бесконечную последовательность девяток, они все равно могут ожидать, что последняя девятка будет «в бесконечности». ^[48]
Интуиция и неоднозначное преподавание заставляют учащихся думать о пределе последовательности как о своего рода бесконечном процессе, а не как о фиксированном значении, поскольку последовательность не обязательно должна достигать своего предела. Если учащиеся принимают разницу между последовательностью чисел и ее пределом, они могут прочитать «0,999...» как означающее последовательность, а не ее предел. ^[49]

Эти идеи ошибочны в контексте стандартных действительных чисел, хотя некоторые из них могут быть справедливы и в других системах счисления, изобретенных либо ради их общей математической полезности, либо в качестве поучительных контрпримеров для лучшего понимания 0,999...; см . ниже .

Многие из этих объяснений были найдены Дэвидом Таллом , который изучал особенности преподавания и познания, которые приводят к некоторым недоразумениям, с которыми он сталкивался со своими студентами колледжа. Опрашивая своих студентов, чтобы определить, почему подавляющее большинство изначально отвергло равенство, он обнаружил, что «студенты продолжали воспринимать 0,999... как последовательность чисел, приближающуюся все ближе и ближе к 1, а не как фиксированное значение, потому что «вы не указано количество знаков» или «это ближайшая возможная десятичная дробь ниже 1 » . ^[21]

Элементарный аргумент умножения ${\textstyle 0.333\ldots ={\frac {1}{3}}}$ на 3 может убедить сопротивляющихся учеников, что $0.999\ldots =1$ . Тем не менее, столкнувшись с конфликтом между верой в первое уравнение и неверием во второе, некоторые студенты либо начинают не верить первому уравнению, либо просто разочаровываются. ^[50] Более сложные методы также не являются надежными: учащиеся, которые полностью способны применять строгие определения, все равно могут прибегнуть к интуитивным изображениям, когда их удивляет результат в высшей математике, в том числе $0.999\ldots$ . Например, один настоящий студент-аналитик смог доказать, что ${\textstyle 0.333\ldots ={\frac {1}{3}}}$ используя определение супремума , но затем настоял на том, что $0.999\ldots <1$ на основе ее более раннего понимания длинного деления . ^[51] Другие еще могут это доказать ${\textstyle {\frac {1}{3}}=0.333\ldots }$ , но, столкнувшись с дробным доказательством , настаивают на том, что «логика» превосходит математические вычисления.

Мазур (2005) рассказывает историю о своем блестящем студенте, изучавшем математический анализ, который «бросал вызов почти всему, что я говорил в классе, но никогда не подвергал сомнению его калькулятор» и который пришел к убеждению, что девять цифр — это все, что нужно для занятий математикой, включая вычисления. квадратный корень из 23. Студенту не нравился ограничивающий аргумент, что $9.99\ldots =10$ , назвав это «дико воображаемым бесконечным процессом роста». ^[52]

В рамках теории математического обучения APOS Эда Дубински он и его коллеги (2005) предполагают, что студенты, которые представляют 0,999... как конечную, неопределенную строку с бесконечно малым расстоянием от 1, «еще не создали полную концепцию процесса». бесконечной десятичной дроби». Другие студенты, у которых есть полное представление о процессе 0,999... возможно, еще не способны "инкапсулировать" этот процесс в "концепцию объекта", как у них есть концепция объекта 1, и поэтому они рассматривают процесс 0,999... и объект 1 как несовместимый. Дубинский и др. также свяжите эту умственную способность инкапсуляции с просмотром ${\textstyle {\frac {1}{3}}}$ как число само по себе и иметь дело с множеством натуральных чисел в целом. ^[53]

Культурный феномен [ править ]

С появлением Интернета дебаты о 0,999... стали обычным явлением в группах новостей и на досках объявлений , в том числе во многих из них, номинально имеющих мало общего с математикой. В группе новостей sci.math , спорящий о 0,999... описывается как «популярный вид спорта», и это один из вопросов, на которые есть ответы в FAQ . ^[54]^[55] Часто задаваемые вопросы кратко описывают ${\textstyle {\frac {1}{3}}}$ , умножение на 10 и пределы, а также отсылают к последовательностям Коши.

В выпуске общедоступной газетной колонки The Straight Dope за 2003 год обсуждается 0,999... через ${\textstyle {\frac {1}{3}}}$ и ограничения, говоря о заблуждениях,

Низший примат в нас все еще сопротивляется, говоря: .999~ на самом деле представляет собой не число , а процесс . Чтобы найти число, нам нужно остановить процесс, и в этот момент вещь .999~ = 1 разваливается. Ерунда. ^[56]

В статье Slate сообщается, что концепция 0,999... «горячо обсуждается на различных веб-сайтах, от World of Warcraft досок объявлений до форумов Айн Рэнд ». ^[57] Точно так же вопрос о 0,999... оказался настолько популярной темой в первые семь лет существования Blizzard Entertainment от форумов Battle.net 2004 года компания выпустила «пресс-релиз», , что в День дурака в котором говорилось, что это 1. :

Мы очень рады закрыть книгу по этой теме раз и навсегда. Мы стали свидетелями душевной боли и беспокойства по поводу того, равно ли .999~ 1, и мы гордимся тем, что следующее доказательство окончательно и убедительно решает проблему для наших клиентов. ^[58]

Затем предлагаются два доказательства, основанные на пределах и умножении на 10.

0,999... встречается также в математических шутках , таких как: ^[59]

Вопрос: Сколько математиков нужно, чтобы вкрутить лампочку ?
А: 0,999999....

В альтернативных системах счисления [ править ]

Хотя действительные числа образуют чрезвычайно полезную систему счисления , решение интерпретировать обозначение «0,999...» как обозначение действительного числа в конечном итоге является соглашением, и Тимоти Гауэрс в книге «Математика: очень краткое введение» утверждает , что полученное тождество $0.999\ldots =1$ также является соглашением:

Однако это ни в коем случае не произвольное соглашение, поскольку непринятие его заставляет либо изобретать странные новые объекты, либо отказываться от некоторых знакомых правил арифметики. ^[60]

Бесконечно малые [ править ]

Некоторые доказательства того, что $0.999\ldots =1$ полагаться на архимедово свойство действительных чисел: не существует ненулевых бесконечно малых чисел . В частности, разница $1-0.999\ldots$ должно быть меньше любого положительного рационального числа, поэтому оно должно быть бесконечно малым; но поскольку действительные числа не содержат ненулевых бесконечно малых чисел, разница равна нулю, и, следовательно, эти два значения одинаковы.

Однако существуют математически последовательные упорядоченные алгебраические структуры , включая различные альтернативы действительным числам, которые не являются архимедовыми. Нестандартный анализ предоставляет систему счисления с полным набором бесконечно малых чисел (и обратных им). ^[я] А. Х. Лайтстоун разработал десятичное расширение для гипердействительных чисел в (0, 1). ^∗. Лайтстоун показывает, как связать каждое число с последовательностью цифр.

0.d_{1}d_{2}d_{3}\dots ;\dots d_{\infty -1}d_{\infty }d_{\infty +1}\dots ,

индексируются сверхнатуральными числами. Хотя он и не говорит напрямую о 0,999..., он показывает реальную цифру

{\textstyle {\frac {1}{3}}}

представлен

0.333\ldots ;\ldots 333\ldots

, что является следствием принципа переноса . Как следствие, число

0.999\ldots ;\ldots 999\ldots =1

. При таком типе десятичного представления не каждое расширение представляет число. В частности "

0.333\ldots ;\ldots 000\ldots

" и "

0.999\ldots ;\ldots 000\ldots

" не соответствуют ни одному числу. ^[61]

Стандартное определение числа 0,999... является пределом последовательности. $0.9,0.99,0.999,\ldots$ . Другое определение включает ультрапредел , т. е. класс эквивалентности. $[(0.9,0.99,0.999,\ldots )]$ этой последовательности в сверхстепенной конструкции , которая представляет собой число, которое не достигает 1 на бесконечно малую величину. ^[62] В более общем смысле, гипердействительное число $u_{H}=0.999\ldots ;\ldots 999000\ldots$ , с последней цифрой 9 в бесконечном сверхъестественном ранге $H$ , удовлетворяет строгому неравенству $u_{H}<1$ . Соответственно, альтернативная интерпретация выражения «ноль, за которым следует бесконечное количество девяток» может быть такой: ^[63]

{\underset {H}{0.\underbrace {999\ldots } }}\;=1\;-\;{\frac {1}{10^{H}}}.

Все подобные интерпретации «0,999...» бесконечно близки к 1. Ян Стюарт характеризует эту интерпретацию как «вполне разумный» способ строго оправдать интуицию о том, что «кое-чего не хватает» от 1 из 0,999.... ^[Дж] Наряду с Katz & Katz (2010b) , Роберт Эли также подвергает сомнению предположение о том, что представления студентов о

0.999\ldots <1

являются ошибочными представлениями о действительных числах, интерпретируя их скорее как нестандартные интуиции, которые могут быть полезны при изучении исчисления. ^[64]

Хакенбуш [ править ]

Комбинаторная теория игр предлагает обобщенное понятие числа, которое включает в себя действительные числа и многое другое. ^[65]Например, в 1974 году Элвин Берлекамп описал соответствие между строками красных и синих сегментов в Хакенбуше и двоичным разложением действительных чисел, мотивированное идеей сжатия данных . Например, значение строки Хакенбуша $LRRLRLRL\ldots$ является ${\textstyle 0.010101_{2}\ldots ={\frac {1}{3}}}$ . Однако ценность $LRLLL\ldots$ (соответствует $0.111\ldots _{2}$ бесконечно меньше 1. Разница между ними - сюрреалистическое число ${\textstyle {\frac {1}{\omega }}}$ , где $\omega$ — первый бесконечный порядковый номер ; соответствующая игра $LRRRR\ldots$ или $0.000\ldots _{2}$ . ^[к]

Это справедливо для двоичных разложений многих рациональных чисел, где значения чисел равны, но соответствующие пути двоичного дерева различны. Например, $0.10111\ldots _{2}=0.11000\ldots _{2}$ , которые оба равны ${\textstyle {\frac {3}{4}}}$ , но первое представление соответствует пути двоичного дерева $LRLRLLL\ldots$ , а второй соответствует другому пути $LRLLRRR\ldots$ .

Возвращаясь к вычитанию [ править ]

Другой способ, которым доказательства могут быть подорваны, состоит в том, что $1-0.999\ldots$ просто не существует, потому что вычитание не всегда возможно. К математическим структурам с операцией сложения, но без операции вычитания относятся коммутативные полугруппы , коммутативные моноиды и полукольца . Ричман рассматривает две такие системы, спроектированные таким образом, что $0.999\ldots <1$ .

Во-первых, Ричман (1999) определяет неотрицательное десятичное число как буквальное десятичное расширение. Он определяет лексикографический порядок и операцию сложения, отмечая, что $0.999\ldots <1$ просто потому что $0<1$ в одном месте, но для любого бесконечного $x$ , надо $0.999\ldots +x=1+x$ . Итак, одна из особенностей десятичных чисел состоит в том, что сложение не всегда можно отменить; другое заключается в том, что никакое десятичное число не соответствует ${\textstyle {\frac {1}{3}}}$ . После определения умножения десятичные числа образуют положительное, полностью упорядоченное, коммутативное полукольцо. ^[66]

В процессе определения умножения Ричман также определяет другую систему, которую он называет «сокращением». $D$ ", который представляет собой набор дедекиндовых разрезов десятичных дробей. Обычно это определение приводит к действительным числам, но для десятичной дроби $d$ он позволяет оба разреза $(-\infty ,d)$ и "основной разрез" $(-\infty ,d]$ . В результате действительные числа «неспокойно уживаются» с десятичными дробями. Снова $0.999\ldots <1$ . В разрезе нет положительных бесконечно малых $D$ , но существует «своего рода отрицательная бесконечно малая», $0^{-}$ , который не имеет десятичного расширения. Он заключает, что $0.999\ldots =1+0^{-}$ , а уравнение " $0.999\ldots +x=1$ " не имеет решения. ^[л]

$p -$ адические числа [ править ]

Когда их спрашивают о 0,999..., новички часто полагают, что должна быть «конечная девятка», полагая, что $1-0.999\ldots$ быть положительным числом, которое они записывают как «0,000...1». Независимо от того, имеет ли это смысл, интуитивная цель ясна: добавление 1 к последним 9 в 0,999... превратит все 9 в 0 и оставит 1 на месте единиц. Среди других причин, эта идея провалилась, потому что в 0,999 нет «последней девятки».... ^[67] Однако существует система, которая содержит бесконечную строку девяток, включая последнюю девятку.

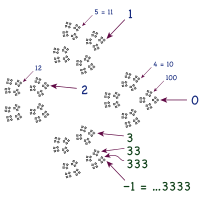
The $p$ - Адические числа представляют собой альтернативную систему счисления, представляющую интерес в теории чисел . Как и реальные цифры, $p$ - адические числа могут быть построены из рациональных чисел с помощью последовательностей Коши ; в конструкции используется другая метрика, в которой 0 ближе к $p$ и гораздо ближе к $p^{n}$ , чем 1. ^[68] $p$ - адические числа образуют поле для простых чисел $p$ и кольцо для другого $p$ , в том числе 10. Таким образом, арифметику можно выполнять в $p$ - Адики, а бесконечно малых не бывает.

В 10-адических числах аналоги десятичных разложений идут влево. В 10-адическом расширении ...999 есть последние 9 и нет первых 9. К единицам можно добавить 1, и после переноса останутся только 0: $1+\ldots 999=\ldots 000=0$ , и так $\ldots 999=-1$ . ^[69]Другой вывод использует геометрическую серию. Бесконечный ряд, подразумеваемый «...999», не сходится в действительных числах, но сходится в 10-адических числах, поэтому можно повторно использовать знакомую формулу: ^[70]

\ldots 999=9+9(10)+9(10)^{2}+9(10)^{3}+\cdots ={\frac {9}{1-10}}=-1.

Сравните с серией в разделе выше . Третий вывод был изобретен семиклассницей, которая сомневалась в ограничивающем аргументе своего учителя о том, что 0,999... = 1, но была вдохновлена применить приведенное выше доказательство умножения на 10 в противоположном направлении: если $x=\ldots 999$ , затем $10x=\ldots 990$ , так $10x=x-9$ , следовательно $x=-1$ снова. ^[69]

В качестве окончательного расширения, поскольку $0.999\ldots =1$ (в реалах) и $\ldots 999=-1$ (в 10-адике), затем «слепой верой и беззастенчивым жонглированием символами» ^[71] можно сложить два уравнения и получить $\ldots 999.999\ldots =0$ . Это уравнение не имеет смысла ни как 10-адическое разложение, ни как обычное десятичное разложение, но оно оказывается значимым и верным в дважды бесконечном десятичном разложении , 10-адического соленоида с повторяющимися левыми концами для представления действительного числа. числа и, в конечном итоге, повторяющиеся правые концы для обозначения 10-адических чисел. ^[72]

Связанные вопросы [ править ]

Парадоксы Зенона , особенно парадокс бегуна, напоминают очевидный парадокс того, что 0,999... и 1 равны. Парадокс бегуна можно смоделировать математически, а затем, как и в случае с 0,999..., разрешить с помощью геометрической прогрессии. Однако неясно, касается ли эта математическая трактовка основных метафизических проблем, которые исследовал Зенон. ^[73]

Отрицательный ноль — еще одна избыточная особенность многих способов записи чисел. В системах счисления, таких как действительные числа, где «0» обозначает аддитивную единицу и не является ни положительным, ни отрицательным, обычная интерпретация «-0» заключается в том, что она должна обозначать аддитивную инверсию 0, что заставляет $-0=0$ . ^[74] Тем не менее, в некоторых научных приложениях используются отдельные положительные и отрицательные нули, как и в некоторых вычислительных двоичных системах счисления (например, целые числа, хранящиеся в формате знака и величины или в формате дополнения до единиц , или числа с плавающей запятой, как указано в стандарте IEEE с плавающей запятой ). ^[75]

См. также [ править ]

Примечания [ править ]

^ Это определение эквивалентно определению десятичных чисел как пределов их суммированных компонентов, что в случае 0,999... является пределом последовательности (0,9, 0,99, 0,999, ...). Эквивалентность возникает из-за ограниченных возрастающих последовательностей, предел которых всегда равен их наименьшей верхней границе .
^ Например, это можно показать так: если $x$ любое число такое, что $0.(9)_{n}\leq x<1$ , затем $0.(9)_{n-1}\leq 10x-9<x<1$ . Таким образом, если $x$ имеет это свойство для всех $n$ , меньшее число $10x-9$ тоже делает.
^ Предел следует, например, из Рудина (1976) , с. 57, теорема 3.20д. Более прямой подход см. также в Finney, Weir & Giordano (2001) , раздел 8.1, пример 2(a), пример 6(b).
^ Исторический синтез заявлен Гриффитсом и Хилтоном (1970) , с. xiv и снова Пью (2002) , с. 10; оба на самом деле предпочитают сокращения Дедекинда аксиомам. Информацию об использовании сокращений в учебниках см. Pugh (2002) , с. 17 или Рудин (1976) , с. 17. Точки зрения на логику см. Pugh (2002) , с. 10, Рудин (1976) , с.ix, или Мункрес (2000) , с. 30.
^ Эндертон (1977) , с. 113 уточняет это описание: «Идея сокращений Дедекинда состоит в том, что действительное число $x$ можно назвать, задав бесконечное множество рациональных чисел, а именно все рациональные числа, меньшие, чем $x$ . Мы фактически определим $x$ быть множеством рациональных чисел, меньших, чем $x$ . Чтобы избежать цикличности в определении, мы должны уметь характеризовать множества рациональных чисел, получаемые таким образом...»
^ Рудин (1976) , стр. 17–20, Ричман (1999) , стр. 17–20. 399, или Эндертон (1977) , с. 119. Если быть точным, Рудин, Ричман и Эндертон называют этот разрез $1*$ , $1_{-}$ , и $1_{R}$ , соответственно; все трое отождествляют его с традиционным действительным числом 1. Обратите внимание, что то, что Рудин и Эндертон называют разрезом Дедекинда, Ричман называет «неглавным разрезом Дедекинда».
^ Маор (1987) , с. 60 и Манкевич (2000) , с. 151 рассмотрите первый метод; Манкевич приписывает это Кантору, но первоисточник неясен. Мункрес (2000) , с. 50 упоминает последний метод.
^ Банч (1982) , с. 119; Талл и Шварценбергер (1978) , с. 6. Последнее предложение принадлежит Барреллу (1998) , с. 28: «Возможно, самое обнадеживающее из всех чисел — это 1… Поэтому особенно тревожно, когда кто-то пытается выдать 0,9~ за 1».
^ Полную информацию о нестандартных числах см. в Robinson (1996) .
^ Стюарт (2009) , с. 175; полное обсуждение 0,999... распространяется на стр. 172–175.
^ Berlekamp, Conway & Guy (1982) , стр. 79–80, 307–311, обсуждаются 1 и ${\textstyle {\frac {1}{3}}}$ и коснитесь ${\textstyle {\frac {1}{\omega }}}$ . Игра для $0.111\dots _{2}$ следует непосредственно из правила Берлекампа.
^ Ричман (1999) , стр. 398–400. Рудин (1976) , с. 23 назначает эту альтернативную конструкцию (но без рациональных оснований) последним упражнением главы 1.

Ссылки [ править ]

^ Ченг (2023) , стр. 141.
^ Даймонд (1955) .
^ Болдуин и Нортон (2012) .
^ Мейер и Смит (2017) , §8.2.
^ Стюарт (2009) , с. 175.
^ Пропп (2023) .
^ Стиллвелл (1994) , с. 42.
^ Эрл и Николсон (2021) , «связанный».
^ Перейти обратно: ^а ^б Розенлихт (1985) , с. 27.
^ Байерс (2007) , с. 39.
^ Перейти обратно: ^а ^б ^с Ричман (1999) .
^ Перессини и Перессини (2007) , с. 186 .
^ Болдуин и Нортон (2012) ; Кац и Кац (2010а) .
^ Ченг (2023) , стр. 136.
^ Люди (2003) .
^ Рудин (1976) , с. 61, теорема 3.26; Стюарт (1999) , с. 706.
^ Эйлер (1822) , с. 170.
^ Граттан-Гиннесс (1970) , с. 69; Бонникасл (1806) , с. 177.
^ Стюарт (1999) , с. 706; Рудин (1976) , с. 61; Проттер и Морри (1991) , с. 213; Пью (2002) , с. 180; Конвей (1978) , с. 31.
^ Дэвис (1846) , с. 175; Смит и Харрингтон (1895) , с. 115.
^ Перейти обратно: ^а ^б Высокий (2000) , с. 221.
^ Билз (2004) , с. 22; Стюарт (2009) , с. 34.
^ Бартл и Шерберт (1982) . 60–62; Педрик (1994) , с. 29; Сохраб (2003) , с. 46.
^ Апостол (1974) , стр. 107-1. 9, 11–12; Билз (2004) , с. 22; Розенлихт (1985) , с. 27.
^ Апостол (1974) , с. 12.
^ Ченг (2023) , стр. 153–156.
^ Конвей (2001) , стр. 25–27.
^ Рудин (1976) , стр. 3 и 8.
^ Ричман (1999) , с. 399.
^ Перейти обратно: ^а ^б О'Коннор и Робертсон (2005) .
^ Ричман (1999) , с. 398–399. «Зачем это делать? Именно для того, чтобы исключить существование различных чисел. ${\textstyle 0.{\overline {9}}}$ и $1$ . [...] Итак, мы видим, что в традиционном определении действительных чисел уравнение ${\textstyle 0.{\overline {9}}=1}$ встроено в начале».
^ Гриффитс и Хилтон (1970) , с. 386, §24.2 «Последовательности».
^ Гриффитс и Хилтон (1970) , стр. 388, 393.
^ Гриффитс и Хилтон (1970) , с. 395.
^ Гриффитс и Хилтон (1970) , стр. viii, 395.
^ Это (2011) .
^ Артиг (2002) , с. 212, «...упорядочение действительных чисел признается плотным порядком. Однако, в зависимости от контекста, учащиеся могут совместить это свойство с существованием чисел непосредственно перед или после данного числа (0,999... таким образом часто рассматривается как предшественник 1).".
^ Петковшек (1990) , с. 408.
^ Проттер и Морри (1991) , с. 503; Бартл и Шерберт (1982) , с. 61.
^ Коморник и Лорети (1998) , стр. 636.
^ Кемпнер (1936) , с. 611; Петковшек (1990) , с. 409.
^ Петковшек (1990) , стр. 410–411.
^ Гудвин (1802) ; Диксон (1919) , стр. 161.
^ Ливитт (1984) , с. 301.
^ Гинзберг (2004) , стр. 26–30; Левиттс (2006) , стр. 1–3; Ливитт (1967) , стр. 669, 673; Шрейдер-Фрешетт (1978) , стр. 96–98.
^ Пью (2002) , с. 97; Аллигуд, Зауэр и Йорк (1996) . 150–152; Проттер и Морри (1991) , с. 507; Педрик (1994) , с. 29.
^ Рудин (1976) , с. 50; Пью (2002) , с. 98.
^ Талл и Шварценбергер (1978) , стр. 6–7; Высокий (2000) , с. 221.
^ Талл и Шварценбергер (1978) , с. 6; Высокий (2000) , с. 221.
^ Высокий (1976) , стр. 10–14.
^ Пинто и Талл (2001) , стр. 5; Эдвардс и Уорд (2004) , стр. 101–111. 416–417.
^ Мазур (2005) , стр. 137–141.
^ Дубинский и др. (2005) , стр. 101-1. 261–262.
^ Ричман (1999) , с. 396.
^ Врейта (1994) .
^ Адамс (2003) .
^ Элленберг, Иордания (6 июня 2014 г.). «Разве 0,999... = 1? И являются ли расходящиеся ряды изобретением дьявола?» . Сланец . Архивировано из оригинала 8 августа 2023 года.
^ «Blizzard Entertainment объявляет, что 0,999~ (повторяется) = 1» (пресс-релиз). Близзард Энтертейнмент . 1 апреля 2004 г. Архивировано из оригинала 4 ноября 2009 г. Проверено 16 ноября 2009 г.
^ Renteln & Dundes (2005) , с. 27.
^ Гауэрс (2002) , с. 60.
^ Лайтстоун (1972) , стр. 245–247.
^ Люди (2012) , стр. 156–180.
^ Кац и Кац (2010a) .
^ Кац и Кац (2010b) ; Эли (2010) .
^ Конвей (2001) , стр. 3–5, 12–13, 24–27.
^ Ричман (1999) , стр. 397–399.
^ Гардинер (2003) , с. 98; Гауэрс (2002) , с. 60.
^ Маскари и Миола (1988) , с. 83–84 .
^ Перейти обратно: ^а ^б Фьелстад (1995) , стр. 11.
^ Фьелстад (1995) , стр. 14–15.
^ ДеСуа (1960) , с. 901.
^ ДеСуа (1960) , с. 902–903.
^ Уоллес (2003) , с. 51; Маор (1987) , с. 17.
^ Мункрес (2000) , с. 34, Упражнение 1(в).
^ Кремер и Киттель (1980) , с. 462. «Типы с плавающей запятой» . MSDN Спецификация языка C# . Архивировано из оригинала 24 августа 2006 года . Проверено 29 августа 2006 г.

Источники [ править ]

Адамс, Сесил (11 июля 2003 г.). «Бесконечный вопрос: почему .999~ не = 1?» . Прямой наркотик . Чикагский читатель . Архивировано из оригинала 15 августа 2006 года . Проверено 6 сентября 2006 г.
Аллигуд, Коннектикут; Зауэр, Т.Д.; Йорк, Дж.А. (1996). «4.1 Канторовы множества». Хаос: Введение в динамические системы . Спрингер. ISBN 978-0-387-94677-1 .
Этот вводный учебник по динамическим системам предназначен для студентов и начинающих аспирантов. (стр. ix)
Апостол, Том М. (1974). Математический анализ (2-е изд.). Аддисон-Уэсли. ISBN 978-0-201-00288-1 .
Переход от исчисления к расширенному анализу. Математический анализ призван быть «честным, строгим, современным и в то же время не слишком педантическим». (прив.) В разработке Апостолом действительных чисел используется аксиома наименьшей верхней границы, а двумя страницами позже вводятся бесконечные десятичные дроби. (стр. 9–11)
Артиг, Мишель (2002). Холтон, Дерек; Артиг, Мишель; Кирхграбер, Урс; Гиллель, Джоэл; Нисс, Могенс; Шенфельд, Алан (ред.). Преподавание и изучение математики на университетском уровне Новая серия исследований ICMI. Том. 7. Спрингер, Дордрехт. дои : 10.1007/ 0-306-47231-7 ISBN 978-0-306-47231-2 .
Болдуин, Майкл; Нортон, Андерсон (2012). «Действительно ли 0,999… равно 1?» . Учитель математики . 21 (2): 58–67.
Бартл, РД ; Шерберт, доктор медицинских наук (1982). Введение в реальный анализ . Уайли. ISBN 978-0-471-05944-8 .
Этот текст призван стать «доступным, разумным учебником, посвященным фундаментальным концепциям и методам реального анализа». Его развитие действительных чисел основано на аксиоме супремума. (стр. vii–viii)
Билз, Ричард (2004). Анализ: Введение . Издательство Кембриджского университета. ISBN 978-0-521-60047-7 .
Берлекамп, ER ; Конвей, Дж. Х. ; Гай, РК (1982). Пути выигрыша в математических играх . Академическая пресса. ISBN 978-0-12-091101-1 .
Бонникасл, Джон (1806). Введение в алгебру; с примечаниями и наблюдениями: предназначен для использования в школах и местах народного образования (Первое американское изд.). Филадельфия. hdl : 2027/mdp.39015063620382 .
Банч, Брайан Х. (1982). Математические заблуждения и парадоксы . Ван Ностранд Рейнхольд. ISBN 978-0-442-24905-2 .
В этой книге представлен анализ парадоксов и заблуждений как инструмент для исследования ее центральной темы - «довольно тонкой связи между математической реальностью и физической реальностью». Он предполагает изучение алгебры на первом курсе средней школы; В книге развивается дальнейшая математика, включая геометрические ряды в главе 2. Хотя 0,999... не является одним из парадоксов, требующих полного рассмотрения, оно кратко упоминается во время разработки диагонального метода Кантора. (стр. ix-xi, 119)
Баррелл, Брайан (1998). Руководство Мерриам-Вебстера по повседневной математике: справочник для дома и бизнеса . Мерриам-Вебстер. ISBN 978-0-87779-621-3 .
Байерс, Уильям (2007). Как мыслят математики: использование двусмысленности, противоречий и парадоксов для создания математики . Издательство Принстонского университета. ISBN 978-0-691-12738-5 .
Ченг, Евгения (2023). Реальна ли математика? Как простые вопросы ведут нас к глубочайшим математическим истинам . Основные книги. ISBN 978-1-541-6-01826 .
Конвей, Джон Б. (1978) [1973]. Функции одной комплексной переменной I (2-е изд.). Спрингер-Верлаг. ISBN 978-0-387-90328-6 .
Конвей, Джон Х. (2001). О числах и играх (2-е изд.). АК Петерс. ISBN 1-56881-127-6 .
Дэвис, Чарльз (1846). Университетская арифметика: изучение науки о числах и их многочисленные приложения . АС Барнс. п. 175 . Проверено 4 июля 2011 г.
де Врейт, Ганс (1994). "Часто задаваемые вопросы по sci.math: Почему 0,9999... = 1?" . Архивировано из оригинала 29 сентября 2007 года . Проверено 29 июня 2006 г.
ДеСуа, Фрэнк К. (ноябрь 1960 г.). «Система, изоморфная реальным» . Американский математический ежемесячник . 67 (9): 900–903. дои : 10.2307/2309468 . JSTOR 2309468 .
Даймонд, Луи Э. (1955). "Иррациональные числа". Журнал «Математика» . 29 (2). Математическая ассоциация Америки: 89–99. дои : 10.2307/3029588 . JSTOR 3029588 .
Диксон, Леонард Юджин (1919). История теории чисел . Том. 1. Институт Карнеги в Вашингтоне.
Дубинский, Эд; Веллер, Кирк; Макдональд, Майкл; Браун, Энн (2005). «Некоторые исторические проблемы и парадоксы, касающиеся концепции бесконечности: анализ APOS: часть 2» . Образовательные исследования по математике . 60 (2): 253–266. дои : 10.1007/s10649-005-0473-0 . S2CID 45937062 .
Эрл, Ричард; Николсон, Джеймс (2021). Краткий Оксфордский математический словарь (6-е изд.). Издательство Оксфордского университета. ISBN 978-0-192-58405-2 .
Эдвардс, Барбара; Уорд, Майкл (май 2004 г.). «Сюрпризы исследования математического образования: (неправильное) использование студентами математических определений» (PDF) . Американский математический ежемесячник . 111 (5): 411–425. CiteSeerX 10.1.1.453.7466 . дои : 10.2307/4145268 . JSTOR 4145268 . Архивировано из оригинала (PDF) 22 июля 2011 года . Проверено 4 июля 2011 г.
Эли, Роберт (2010). «Нестандартные студенческие представления о бесконечно малых» . Журнал исследований в области математического образования . 41 (2): 117–146. doi : 10.5951/jresematheduc.41.2.0117 .
Эта статья представляет собой практическое исследование с участием студентки, которая разработала теорию бесконечно малых в стиле Лейбница, чтобы помочь ей понять исчисление и, в частности, объяснить, почему 0,999... не соответствует 1 на бесконечно малые 0,000...1.
Эндертон, Герберт Б. (1977). Элементы теории множеств . Эльзевир. ISBN 978-0-12-238440-0 .
Вводный учебник по теории множеств для студентов, который «не предполагает какой-либо конкретной подготовки». Он написан для изучения курса, посвященного аксиоматической теории множеств или построению систем счисления; аксиоматический материал помечен так, что его можно преуменьшить. (стр. xi–xii)
Эйлер, Леонард (1822) [1770]. Элементы алгебры . Джон Хьюлетт и Фрэнсис Хорнер, английские переводчики (3-е английское изд.). Орм Лонгман. п. 170 . ISBN 978-0-387-96014-2 . Проверено 4 июля 2011 г.
Финни, Росс Л.; Вейр, Морис Д.; Джордано, Фрэнк Р. (2001). Исчисление Томаса: ранние трансценденталии (10-е изд.). Нью-Йорк: Аддисон-Уэсли.
Фьелстад, Пол (январь 1995 г.). «Парадокс повторяющихся целых чисел» . Математический журнал колледжа . 26 (1): 11–15. дои : 10.2307/2687285 . JSTOR 2687285 .
Гардинер, Энтони (2003) [1982]. Понимание бесконечности: математика бесконечных процессов . Дувр. ISBN 978-0-486-42538-2 .
Гинзберг, Брайан (2004). «(Почти) секретная теорема Миди – продление через 165 лет» . Математический журнал колледжа . 35 (1). дои : 10.1080/07468342.2004.11922047 .
Гудвин, Х. (1802 г.). «Любопытные свойства простых чисел, принимаемых за делители единицы. Корреспондент» . Жур. Нат. Фил. хим. Новая серия искусств . 1 : 314–316.
Гауэрс, Тимоти (2002). Математика: очень краткое введение . Издательство Оксфордского университета. ISBN 978-0-19-285361-5 .
Граттан-Гиннесс, Айвор (1970). Развитие основ математического анализа от Эйлера до Римана . МТИ Пресс. ISBN 978-0-262-07034-8 .
Гриффитс, HB; Хилтон, Пи Джей (1970). Комплексный учебник классической математики: современная интерпретация . Лондон: Ван Ностранд Рейнхольд. ISBN 978-0-442-02863-3 . ЖКК QA37.2 G75 .
Эта книга стала результатом курса для Бирмингема учителей математики средней школы . Курс был предназначен для того, чтобы передать взгляд на школьную математику на университетском уровне , и книга предназначена для студентов, «которые достигли примерно уровня завершения одного года специального математического обучения в университете». Действительные числа построены в главе 24, «возможно, самой трудной главе во всей книге», хотя авторы приписывают большую часть трудностей использованию идеальной теории , которая здесь не воспроизводится. (стр. VII, XIV)
Кац, Карин Усади; Кац, Михаил Георгиевич (2010а). «Когда 0,999… меньше 1?» . Энтузиаст математики из Монтаны . 7 (1): 3–30. arXiv : 1007.3018 . Бибкод : 2010arXiv1007.3018U . дои : 10.54870/1551-3440.1381 . S2CID 11544878 . Архивировано из оригинала 20 июля 2011 года . Проверено 4 июля 2011 г.
Кац, Карин Усади; Кац, Михаил Георгиевич (2010б). «Увеличение бесконечно малого 1 − 0,9… в эпоху посттриумвирата». Образовательные исследования по математике . 74 (3): 259. arXiv : 1003.1501 . Бибкод : 2010arXiv1003.1501K . дои : 10.1007/s10649-010-9239-4 . S2CID 115168622 .
Кемпнер, Обри Дж. (декабрь 1936 г.). «Анормальные системы счисления». Американский математический ежемесячник . 43 (10): 610–617. дои : 10.2307/2300532 . JSTOR 2300532 .
Коморник, Вилмос; Лорети, Паола (1998). «Уникальные разработки в области нецелочисленных базисов». Американский математический ежемесячник . 105 (7): 636–639. дои : 10.2307/2589246 . JSTOR 2589246 .
Кремер, Герберт ; Киттель, Чарльз (1980). Теплофизика (2-е изд.). У. Х. Фриман. п. 462. ИСБН 978-0-7167-1088-2 .
Ли, Лянпань (март 2011 г.). «Новый подход к действительным числам». arXiv : 1101.1800 [ math.CA ].
Ливитт, Уильям Г. (1967). «Теорема о повторяющихся десятичных дробях» . Американский математический ежемесячник . 74 (6): 669–673. дои : 10.2307/2314251 . JSTOR 2314251 .
Ливитт, Уильям Г. (сентябрь 1984 г.). «Повторяющиеся десятичные дроби» . Математический журнал колледжа . 15 (4): 299–308. дои : 10.2307/2686394 . JSTOR 2686394 .
Левиттс, Джозеф (2006). «Теорема Миди для периодических десятичных дробей». arXiv : math.NT/0605182 .
Лайтстоун, Альберт Х. (март 1972 г.). «Бесконечно малые» . Американский математический ежемесячник . 79 (3): 242–251. дои : 10.2307/2316619 . JSTOR 2316619 .
Манкевич, Ричард (2000). История математики . Касселл. ISBN 978-0-304-35473-3 .
Манкевич стремится представить «историю математики в доступном стиле», сочетая визуальные и качественные аспекты математики, сочинения математиков и исторические очерки. (стр. 8)
Маскари, Джанфранко; Миола, Альфонсо (1988). «Об интеграции числовых и алгебраических вычислений». В Бет, Томас; Клаузен, Майкл (ред.). Применимая алгебра, коды, исправляющие ошибки, комбинаторика и компьютерная алгебра . дои : 10.1007/BFb0039172 . ISBN 978-3-540-39133-3 .
Маор, Эли (1987). К бесконечности и за ее пределами: Культурная история бесконечности . Биркхойзер. ISBN 978-3-7643-3325-6 .
Эта книга, представляющая собой скорее актуальный, чем хронологический обзор бесконечности, «предназначена для широкого читателя», но «рассказана с точки зрения математика». По поводу дилеммы строгости и читабельности языка Маор комментирует: «Надеюсь, мне удалось правильно решить эту проблему». (стр. x-xiii)
Мазур, Джозеф (2005). Евклид в тропическом лесу: открытие универсальных истин в логике и математике . Пирсон: Пи Пресс. ISBN 978-0-13-147994-4 .
Мейер, Джон; Смит, Дерек (2017). Изучение математики: увлекательное введение в доказательство . Издательство Кембриджского университета. ISBN 978-1-107-12898-9 .
Манкрес, Джеймс Р. (2000) [1975]. Топология (2-е изд.). Прентис-Холл. ISBN 978-0-13-181629-9 .
Задумано как введение «на уровне старшего или первого курса магистратуры» без каких-либо формальных предпосылок: «Я даже не предполагаю, что читатель хорошо знает теорию множеств». (стр. xi) Трактовка Мункресом реальности является аксиомой; он заявляет о конструкциях, построенных голыми руками: «Такой подход к предмету требует много времени и усилий и представляет больший логический, чем математический интерес». (стр. 30)
Наварро, Мария Анхелес; Каррерас, Педро Перес (2010). «Сократовское методологическое предложение по изучению равенства 0,999...=1» (PDF) . Преподавание математики . 13 (1): 17–34 . Проверено 4 июля 2011 г.
О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. (октябрь 2005 г.), «Действительные числа: от Стевина до Гильберта» , Архив истории математики MacTutor , Университет Сент-Эндрюс
Педрик, Джордж (1994). Первый курс анализа . Спрингер. ISBN 978-0-387-94108-0 .
Перессини, Энтони; Перессини, Доминик (2007). «Философия математики и математическое образование». В ван Керхове, Барт; ван Бендегем, Жан Поль (ред.). Перспективы математических практик . Логика, эпистемология и единство науки. Том. 5. Спрингер. ISBN 978-1-4020-5033-6 .
Петковшек, Марко (май 1990 г.). «Неоднозначные числа плотны» . Американский математический ежемесячник . 97 (5): 408–411. дои : 10.2307/2324393 . JSTOR 2324393 .
Пинто, Марсия; Высокий, Дэвид О. (2001). PME25: Наблюдение за развитием студентов на традиционном университетском курсе анализа (PDF) . стр. т. 4: 57–64. Архивировано из оригинала (PDF) 30 мая 2009 года . Проверено 3 мая 2009 г.
Пропп, Джеймс (17 сентября 2015 г.). «Эпизод о .999...» Математические чары . Проверено 24 мая 2024 г.
Пропп, Джеймс (17 января 2023 г.). «Знаменатели и двойники» . Математические чары . Проверено 16 апреля 2024 г.
Проттер, Мюррей Х .; Морри, Чарльз Б. младший (1991). Первый курс реального анализа (2-е изд.). Спрингер. ISBN 978-0-387-97437-8 .
Цель этой книги — «представить теоретическую основу анализа, подходящую для студентов, прошедших стандартный курс математического анализа». (стр. vii) В конце главы 2 авторы принимают в качестве аксиомы для действительных чисел сходимость ограниченных неубывающих последовательностей, позже доказывая теорему о вложенных интервалах и свойство наименьшей верхней границы. (стр. 56–64) Десятичные разложения приведены в Приложении 3 «Разложение действительных чисел по любому основанию». (стр. 503–507)
Пью, Чарльз Чепмен (2002). Реальный математический анализ . Спрингер-Верлаг. ISBN 978-0-387-95297-0 .
Предполагая знакомство с рациональными числами, Пью вводит дедекиндовские сокращения как можно скорее , говоря об аксиоматической трактовке: «Это своего рода мошенничество, учитывая, что вся структура анализа построена на действительной системе счисления». (стр. 10) После доказательства свойства наименьшей верхней границы и некоторых сопутствующих фактов разрезы не используются в остальной части книги.
Рентельн, Пол; Дандес, Алан (январь 2005 г.). «Защита от дурака: образцы математического народного юмора» (PDF) . Уведомления АМС . 52 (1): 24–34. Архивировано из оригинала (PDF) 25 февраля 2009 года . Проверено 3 мая 2009 г.
Ричман, Фред (декабрь 1999 г.). «0,999... = 1?» . Журнал «Математика» . 72 (5): 396–400. дои : 10.2307/2690798 . JSTOR 2690798 . Бесплатный HTML-препринт: Ричман, Фред (июнь 1999 г.). «0,999... = 1?» . Архивировано из оригинала 2 сентября 2006 года . Проверено 23 августа 2006 г. Примечание: журнальная статья содержит материал и формулировки, отсутствующие в препринте.
Робинсон, Авраам (1996). Нестандартный анализ (пересмотренная ред.). Издательство Принстонского университета. ISBN 978-0-691-04490-3 . JSTOR j.ctt1cx3vb6 .
Розенлихт, Максвелл (1985). Введение в анализ . Дувр. ISBN 978-0-486-65038-8 . Эта книга представляет собой «тщательное и строгое» введение в настоящий анализ. Он дает аксиомы действительных чисел, а затем строит их (стр. 27–31) как бесконечные десятичные дроби с 0,999... = 1 как часть определения.
Рудин, Вальтер (1976) [1953]. Принципы математического анализа (3-е изд.). МакГроу-Хилл. ISBN 978-0-07-054235-8 .
Учебник для продвинутого курса бакалавриата. «Опыт убедил меня, что педагогически неразумно (хотя и логически правильно) начинать с построения действительных чисел из рациональных. В начале большинство учащихся просто не осознают необходимости этого. Соответственно, реальная Система счисления представлена как упорядоченное поле со свойством наименьшей верхней границы, и быстро делается несколько интересных применений этого свойства. Однако конструкция Дедекинда не опущена теперь в Приложении к Главе 1, где она может быть опущена. изучайте и наслаждайтесь, когда придет время». (стр. ix)
Шрейдер-Фрешетт, Морис (март 1978 г.). «Дополнительные рациональные числа». Журнал «Математика» . 51 (2): 90–98. дои : 10.2307/2690144 . JSTOR 2690144 .
Смит, Чарльз; Харрингтон, Чарльз (1895). Арифметика для школы . Макмиллан. п. 115 . ISBN 978-0-665-54808-6 . Проверено 4 июля 2011 г.
Сохраб, Хоушанг (2003). Базовый реальный анализ . Биркхойзер. ISBN 978-0-8176-4211-2 .
Стюарт, Ян (2009). Клад математических сокровищ профессора Стюарта . Профильные книги. ISBN 978-1-84668-292-6 .
Стюарт, Джеймс (1999). Исчисление: ранние трансцендентальные теории (4-е изд.). Брукс/Коул. ISBN 978-0-534-36298-0 .
Целью этой книги является «помочь студентам в изучении исчисления» и «способствовать концептуальному пониманию». (p. v) В нем отсутствуют доказательства основ исчисления.
Стиллвелл, Джон (1994), Элементы алгебры: геометрия, числа, уравнения , Springer, ISBN 9783540942900
Высокий, Дэвид ; Шварценбергер, RLE (1978). «Конфликты при изучении действительных чисел и пределов» (PDF) . Преподавание математики . 82 : 44–49. Архивировано из оригинала (PDF) 30 мая 2009 года . Проверено 3 мая 2009 г.
Высокий, Дэвид О. (1976). «Конфликты и катастрофы в изучении математики» (PDF) . Математическое образование для преподавания . 2 (4): 2–18. Архивировано из оригинала (PDF) 26 марта 2009 года . Проверено 3 мая 2009 г.
Высокий, Дэвид (2000). «Когнитивное развитие в области высшей математики с использованием технологий» (PDF) . Журнал исследований математического образования . 12 (3): 210–230. Бибкод : 2000MEdRJ..12..196T . дои : 10.1007/BF03217085 . S2CID 143438975 . Архивировано из оригинала (PDF) 30 мая 2009 года . Проверено 3 мая 2009 г.
Тао, Теренс (2012). Анализ Фурье высшего порядка (PDF) . Американское математическое общество.
Тао, Теренс (2003). «Математика 131AH: неделя 1» (PDF) . Анализ с отличием . Математика Калифорнийского университета в Лос-Анджелесе . Проверено 23 мая 2024 г.
Уоллес, Дэвид Фостер (2003). Все и даже больше: компактная история бесконечности . Нортон. ISBN 978-0-393-00338-3 .

Дальнейшее чтение [ править ]

Бесвик, Ким (2004). «Почему 0,999... = 1?: Вечный вопрос и чувство числа» . Учитель математики из Австралии . 60 (4): 7–9.
Бурков С.Е. (1987). «Одномерная модель квазикристаллического сплава». Журнал статистической физики . 47 (3/4): 409–438. Бибкод : 1987JSP....47..409B . дои : 10.1007/BF01007518 . S2CID 120281766 .
Берн, Боб (март 1997 г.). «81.15 Случай конфликта» . Математический вестник . 81 (490): 109–112. дои : 10.2307/3618786 . JSTOR 3618786 . S2CID 187823601 .
Калверт, Дж. Б.; Таттл, скорая помощь; Мартин, Майкл С.; Уоррен, Питер (февраль 1981 г.). «Эпоха Ньютона: интенсивный междисциплинарный курс» . Учитель истории . 14 (2): 167–190. дои : 10.2307/493261 . JSTOR 493261 .
Чхве, Ёнги; До, Чонхун (ноябрь 2005 г.). «Равенство участвует в 0,999... и (-8)1/3». Для изучения математики . 25 (3): 13–15, 36. JSTOR 40248503 .
Чунг, Кентукки; Дайкин, Делавэр; Рэтбоун, Чехия (апрель 1971 г.). «Рациональные приближения к π» . Математика вычислений . 25 (114): 387–392. дои : 10.2307/2004936 . JSTOR 2004936 .
Эдвардс, Б. (1997). «Понимание и использование студентами математических определений в реальном анализе». В Досси, Дж.; Сваффорд, Джо; Парментье, М.; Досси, А.Э. (ред.). Труды 19-го ежегодного собрания Североамериканского отделения Международной группы по психологии математического образования . Том. 1. Колумбус, Огайо: Информационный центр ERIC по науке, математике и экологическому образованию. стр. 17–22.
Эйзенманн, Петр (2008). «Почему это неправда, что 0,999... < 1?» (PDF) . Преподавание математики . 11 (1): 35–40 . Проверено 4 июля 2011 г.
Феррини-Манди, Дж.; Грэм, К. (1994). Капут, Дж.; Дубинский Э. (ред.). «Исследования в области математического анализа: понимание пределов, производных и интегралов». Примечания MAA: Проблемы исследования в изучении математики на бакалавриате . 33 : 31–45.
Гардинер, Тони (июнь 1985 г.). «Бесконечные процессы в элементарной математике: что нужно рассказывать детям?» . Математический вестник . 69 (448): 77–87. дои : 10.2307/3616921 . JSTOR 3616921 . S2CID 125222118 .
Монаган, Джон (декабрь 1988 г.). «Настоящая математика: один аспект будущего A-Level» . Математический вестник . 72 (462): 276–281. дои : 10.2307/3619940 . JSTOR 3619940 . S2CID 125825964 .
Нуньес, Рафаэль (2006). «Действительно ли действительные числа движутся? Язык, мысль и жест: воплощенные когнитивные основы математики» . 18 нетрадиционных очерков о природе математики . Спрингер. стр. 160–181. ISBN 978-0-387-25717-4 . Архивировано из оригинала 18 июля 2011 года . Проверено 4 июля 2011 г.
Пшениосло, Малгожата (март 2004 г.). «Образы предела функции, сложившиеся в ходе математических занятий в университете». Образовательные исследования по математике . 55 (1–3): 103–132. дои : 10.1023/B:EDUC.0000017667.70982.05 . S2CID 120453706 .
Сандефур, Джеймс Т. (февраль 1996 г.). «Использование самоподобия для определения длины, площади и размера» . Американский математический ежемесячник . 103 (2): 107–120. дои : 10.2307/2975103 . JSTOR 2975103 .
Серпинская, Анна (ноябрь 1987 г.). «Студенты-гуманитарии и эпистемологические препятствия, связанные с ограничениями». Образовательные исследования по математике . 18 (4): 371–396. дои : 10.1007/BF00240986 . JSTOR 3482354 . S2CID 144880659 .
Старберд, Майкл ; Старберд, Томас (март 1992 г.). «Требуемая избыточность в представлении действительных чисел» . Труды Американского математического общества . 114 (3): 769–774. дои : 10.1090/S0002-9939-1992-1086343-5 . JSTOR 2159403 .
Шидлик, Дженнифер Эрлз (май 2000 г.). «Математические убеждения и концептуальное понимание предела функции». Журнал исследований в области математического образования . 31 (3): 258–276. дои : 10.2307/749807 . JSTOR 749807 .
Высокий, Дэвид О. (2009). «Динамическая математика и смешение структур знаний в исчислении». ЗДМ Математическое образование . 41 (4): 481–492. дои : 10.1007/s11858-009-0192-6 . S2CID 14289039 .
Высокий, Дэвид О. (май 1981 г.). «Интуиция бесконечности» . Математика в школе . 10 (3): 30–33. JSTOR 30214290 .

Внешние ссылки [ править ]

Послушайте эту статью ( 50 минут )

Этот аудиофайл был создан на основе редакции этой статьи от 19 октября 2006 г. и не отражает последующие изменения.

[1] Это определение эквивалентно определению десятичных чисел как пределов их суммированных компонентов, что в случае 0,999... является пределом последовательности (0,9, 0,99, 0,999, ...). Эквивалентность возникает из-за ограниченных возрастающих последовательностей, предел которых всегда равен их наименьшей верхней границе .

[8] Например, это можно показать так: если $x$ любое число такое, что $0.(9)_{n}\leq x<1$ , затем $0.(9)_{n-1}\leq 10x-9<x<1$ . Таким образом, если $x$ имеет это свойство для всех $n$ , меньшее число $10x-9$ тоже делает.

[22] Предел следует, например, из Рудина (1976) , с. 57, теорема 3.20д. Более прямой подход см. также в Finney, Weir & Giordano (2001) , раздел 8.1, пример 2(a), пример 6(b).

[32] Исторический синтез заявлен Гриффитсом и Хилтоном (1970) , с. xiv и снова Пью (2002) , с. 10; оба на самом деле предпочитают сокращения Дедекинда аксиомам. Информацию об использовании сокращений в учебниках см. Pugh (2002) , с. 17 или Рудин (1976) , с. 17. Точки зрения на логику см. Pugh (2002) , с. 10, Рудин (1976) , с.ix, или Мункрес (2000) , с. 30.

[33] Эндертон (1977) , с. 113 уточняет это описание: «Идея сокращений Дедекинда состоит в том, что действительное число $x$ можно назвать, задав бесконечное множество рациональных чисел, а именно все рациональные числа, меньшие, чем $x$ . Мы фактически определим $x$ быть множеством рациональных чисел, меньших, чем $x$ . Чтобы избежать цикличности в определении, мы должны уметь характеризовать множества рациональных чисел, получаемые таким образом...»

[34] Рудин (1976) , стр. 17–20, Ричман (1999) , стр. 17–20. 399, или Эндертон (1977) , с. 119. Если быть точным, Рудин, Ричман и Эндертон называют этот разрез $1*$ , $1_{-}$ , и $1_{R}$ , соответственно; все трое отождествляют его с традиционным действительным числом 1. Обратите внимание, что то, что Рудин и Эндертон называют разрезом Дедекинда, Ричман называет «неглавным разрезом Дедекинда».

[53] Маор (1987) , с. 60 и Манкевич (2000) , с. 151 рассмотрите первый метод; Манкевич приписывает это Кантору, но первоисточник неясен. Мункрес (2000) , с. 50 упоминает последний метод.

[55] Банч (1982) , с. 119; Талл и Шварценбергер (1978) , с. 6. Последнее предложение принадлежит Барреллу (1998) , с. 28: «Возможно, самое обнадеживающее из всех чисел — это 1… Поэтому особенно тревожно, когда кто-то пытается выдать 0,9~ за 1».

[69] Полную информацию о нестандартных числах см. в Robinson (1996) .

[73] Стюарт (2009) , с. 175; полное обсуждение 0,999... распространяется на стр. 172–175.

[76] Berlekamp, Conway & Guy (1982) , стр. 79–80, 307–311, обсуждаются 1 и ${\textstyle {\frac {1}{3}}}$ и коснитесь ${\textstyle {\frac {1}{\omega }}}$ . Игра для $0.111\dots _{2}$ следует непосредственно из правила Берлекампа.

[78] Ричман (1999) , стр. 398–400. Рудин (1976) , с. 23 назначает эту альтернативную конструкцию (но без рациональных оснований) последним упражнением главы 1.

[FOOTNOTECheng2023141-2] Ченг (2023) , стр. 141.

[FOOTNOTEDiamond1955-3] Даймонд (1955) .

[FOOTNOTEBaldwinNorton2012-4] Болдуин и Нортон (2012) .

[FOOTNOTEMeierSmith2017§8.2-5] Мейер и Смит (2017) , §8.2.

[FOOTNOTEStewart2009175-6] Стюарт (2009) , с. 175.

[FOOTNOTEPropp2023-7] Пропп (2023) .

[FOOTNOTEStillwell199442-9] Стиллвелл (1994) , с. 42.

[FOOTNOTEEarlNicholson2021"bound"-10] Эрл и Николсон (2021) , «связанный».

[FOOTNOTERosenlicht198527-11] Перейти обратно: ^а ^б Розенлихт (1985) , с. 27.

[FOOTNOTEByers200739-12] Байерс (2007) , с. 39.

[FOOTNOTERichman1999-13] Перейти обратно: ^а ^б ^с Ричман (1999) .

[FOOTNOTEPeressiniPeressini2007[httpsarchiveorgdetailsperspectivesonma0000unse_f3x1page186mode1upqequalityviewtheater_186]-14] Перессини и Перессини (2007) , с. 186 .

[FOOTNOTEBaldwinNorton2012KatzKatz2010a-15] Болдуин и Нортон (2012) ; Кац и Кац (2010а) .

[FOOTNOTECheng2023136-16] Ченг (2023) , стр. 136.

[FOOTNOTETao2003-17] Люди (2003) .

[FOOTNOTERudin197661Theorem_3.26Stewart1999706-18] Рудин (1976) , с. 61, теорема 3.26; Стюарт (1999) , с. 706.

[FOOTNOTEEuler1822170-19] Эйлер (1822) , с. 170.

[FOOTNOTEGrattan-Guinness197069Bonnycastle1806177-20] Граттан-Гиннесс (1970) , с. 69; Бонникасл (1806) , с. 177.

[FOOTNOTEStewart1999706Rudin197661ProtterMorrey1991213Pugh2002180Conway197831-21] Стюарт (1999) , с. 706; Рудин (1976) , с. 61; Проттер и Морри (1991) , с. 213; Пью (2002) , с. 180; Конвей (1978) , с. 31.

[FOOTNOTEDavies1846175SmithHarrington1895115-23] Дэвис (1846) , с. 175; Смит и Харрингтон (1895) , с. 115.

[FOOTNOTETall2000221-24] Перейти обратно: ^а ^б Высокий (2000) , с. 221.

[FOOTNOTEBeals200422Stewart200934-25] Билз (2004) , с. 22; Стюарт (2009) , с. 34.

[FOOTNOTEBartleSherbert198260–62Pedrick199429Sohrab200346-26] Бартл и Шерберт (1982) . 60–62; Педрик (1994) , с. 29; Сохраб (2003) , с. 46.

[FOOTNOTEApostol19749,_11–12Beals200422Rosenlicht198527-27] Апостол (1974) , стр. 107-1. 9, 11–12; Билз (2004) , с. 22; Розенлихт (1985) , с. 27.

[FOOTNOTEApostol197412-28] Апостол (1974) , с. 12.

[FOOTNOTECheng2023153–156-29] Ченг (2023) , стр. 153–156.

[FOOTNOTEConway200125–27-30] Конвей (2001) , стр. 25–27.

[FOOTNOTERudin19763,_8-31] Рудин (1976) , стр. 3 и 8.

[FOOTNOTERichman1999399-35] Ричман (1999) , с. 399.

[FOOTNOTEO'ConnorRobertson2005-36] Перейти обратно: ^а ^б О'Коннор и Робертсон (2005) .

[37] Ричман (1999) , с. 398–399. «Зачем это делать? Именно для того, чтобы исключить существование различных чисел. ${\textstyle 0.{\overline {9}}}$ и $1$ . [...] Итак, мы видим, что в традиционном определении действительных чисел уравнение ${\textstyle 0.{\overline {9}}=1}$ встроено в начале».

[FOOTNOTEGriffithsHilton1970386§24.2_"Sequences"-38] Гриффитс и Хилтон (1970) , с. 386, §24.2 «Последовательности».

[FOOTNOTEGriffithsHilton1970388,_393-39] Гриффитс и Хилтон (1970) , стр. 388, 393.

[FOOTNOTEGriffithsHilton1970395-40] Гриффитс и Хилтон (1970) , с. 395.

[FOOTNOTEGriffithsHilton1970viii,_395-41] Гриффитс и Хилтон (1970) , стр. viii, 395.

[FOOTNOTELi2011-42] Это (2011) .

[FOOTNOTEArtigue2002212"..._the_ordering_of_the_real_numbers_is_recognized_as_a_dense_order._However,_depending_on_the_context,_students_can_reconcile_this_property_with_the_existence_of_numbers_just_before_or_after_a_given_number_(0.999..._is_thus_often_seen_as_the_predecessor_of_1)."-43] Артиг (2002) , с. 212, «...упорядочение действительных чисел признается плотным порядком. Однако, в зависимости от контекста, учащиеся могут совместить это свойство с существованием чисел непосредственно перед или после данного числа (0,999... таким образом часто рассматривается как предшественник 1).".

[FOOTNOTEPetkovšek1990408-44] Петковшек (1990) , с. 408.

[FOOTNOTEProtterMorrey1991503BartleSherbert198261-45] Проттер и Морри (1991) , с. 503; Бартл и Шерберт (1982) , с. 61.

[FOOTNOTEKomornikLoreti1998636-46] Коморник и Лорети (1998) , стр. 636.

[FOOTNOTEKempner1936611Petkovšek1990409-47] Кемпнер (1936) , с. 611; Петковшек (1990) , с. 409.

[FOOTNOTEPetkovšek1990410–411-48] Петковшек (1990) , стр. 410–411.

[FOOTNOTEGoodwyn1802Dickson1919161-49] Гудвин (1802) ; Диксон (1919) , стр. 161.

[FOOTNOTELeavitt1984301-50] Ливитт (1984) , с. 301.

[FOOTNOTEGinsberg200426–30Lewittes20061–3Leavitt1967669,_673Shrader-Frechette197896–98-51] Гинзберг (2004) , стр. 26–30; Левиттс (2006) , стр. 1–3; Ливитт (1967) , стр. 669, 673; Шрейдер-Фрешетт (1978) , стр. 96–98.

[FOOTNOTEPugh200297AlligoodSauerYorke1996150–152ProtterMorrey1991507Pedrick199429-52] Пью (2002) , с. 97; Аллигуд, Зауэр и Йорк (1996) . 150–152; Проттер и Морри (1991) , с. 507; Педрик (1994) , с. 29.

[FOOTNOTERudin197650Pugh200298-54] Рудин (1976) , с. 50; Пью (2002) , с. 98.

[FOOTNOTETallSchwarzenberger19786–7Tall2000221-56] Талл и Шварценбергер (1978) , стр. 6–7; Высокий (2000) , с. 221.

[FOOTNOTETallSchwarzenberger19786Tall2000221-57] Талл и Шварценбергер (1978) , с. 6; Высокий (2000) , с. 221.

[FOOTNOTETall197610–14-58] Высокий (1976) , стр. 10–14.

[FOOTNOTEPintoTall20015EdwardsWard2004416–417-59] Пинто и Талл (2001) , стр. 5; Эдвардс и Уорд (2004) , стр. 101–111. 416–417.

[FOOTNOTEMazur2005137–141-60] Мазур (2005) , стр. 137–141.

[FOOTNOTEDubinskyWellerMcDonaldBrown2005261–262-61] Дубинский и др. (2005) , стр. 101-1. 261–262.

[FOOTNOTERichman1999396-62] Ричман (1999) , с. 396.

[FOOTNOTEde_Vreught1994-63] Врейта (1994) .

[FOOTNOTEAdams2003-64] Адамс (2003) .

[65] Элленберг, Иордания (6 июня 2014 г.). «Разве 0,999... = 1? И являются ли расходящиеся ряды изобретением дьявола?» . Сланец . Архивировано из оригинала 8 августа 2023 года.

[66] «Blizzard Entertainment объявляет, что 0,999~ (повторяется) = 1» (пресс-релиз). Близзард Энтертейнмент . 1 апреля 2004 г. Архивировано из оригинала 4 ноября 2009 г. Проверено 16 ноября 2009 г.

[FOOTNOTERentelnDundes200527-67] Renteln & Dundes (2005) , с. 27.

[FOOTNOTEGowers200260-68] Гауэрс (2002) , с. 60.

[FOOTNOTELightstone1972245–247-70] Лайтстоун (1972) , стр. 245–247.

[FOOTNOTETao2012156–180-71] Люди (2012) , стр. 156–180.

[FOOTNOTEKatzKatz2010a-72] Кац и Кац (2010a) .

[FOOTNOTEKatzKatz2010bEly2010-74] Кац и Кац (2010b) ; Эли (2010) .

[FOOTNOTEConway20013–5,_12–13,_24–27-75] Конвей (2001) , стр. 3–5, 12–13, 24–27.

[FOOTNOTERichman1999397–399-77] Ричман (1999) , стр. 397–399.

[FOOTNOTEGardiner200398Gowers200260-79] Гардинер (2003) , с. 98; Гауэрс (2002) , с. 60.

[FOOTNOTEMascariMiola1988[httpsbooksgooglecombooksidYVKzPSseyu4CpgPA83_83&ndash;84]-80] Маскари и Миола (1988) , с. 83–84 .

[FOOTNOTEFjelstad199511-81] Перейти обратно: ^а ^б Фьелстад (1995) , стр. 11.

[FOOTNOTEFjelstad199514–15-82] Фьелстад (1995) , стр. 14–15.

[FOOTNOTEDeSua1960901-83] ДеСуа (1960) , с. 901.

[FOOTNOTEDeSua1960902&ndash;903-84] ДеСуа (1960) , с. 902–903.

[FOOTNOTEWallace200351Maor198717-85] Уоллес (2003) , с. 51; Маор (1987) , с. 17.

[FOOTNOTEMunkres200034Exercise_1(c)-86] Мункрес (2000) , с. 34, Упражнение 1(в).

[87] Кремер и Киттель (1980) , с. 462. «Типы с плавающей запятой» . MSDN Спецификация языка C# . Архивировано из оригинала 24 августа 2006 года . Проверено 29 августа 2006 г.

[а]

[1]

[2]

[3]

[4]

[5]

[6]

[б]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[с]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[д]

[Это]

[ф]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[41]

[42]

[43]

[44]

[45]

[46]

[г]

[47]

[час]

[48]

[49]

[50]

[51]

[52]

[53]

[54]

[55]

[56]

[57]

[58]

[59]

[60]

[я]

[61]

[62]

[63]

[Дж]

[64]

[65]

[к]

[66]

[л]

[67]

[68]

[69]

[70]

[71]

[72]

[73]

[74]

[75]