Тор

Не путать с Тельцом .

Эта статья о математической поверхности. Об объеме см. Полнотелый тор . Чтобы узнать о других значениях, см. Тор (значения) .

Кольцевой тор с набором окружностей на поверхности.

По мере уменьшения расстояния от оси вращения кольцевой тор становится роговым, затем веретенообразным и, наконец, вырождается в двупокрытую сферу .

Кольцевой тор с соотношением сторон 3, соотношением диаметров большего (пурпурного) круга и меньшего (красного) круга.

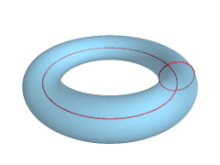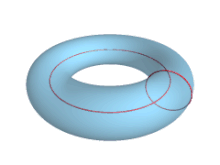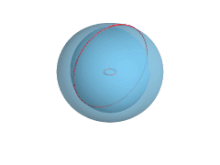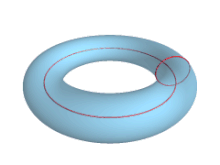
В геометрии тор трехмерном ( мн.ч.: торы или торы ) — это поверхность вращения, образованная вращением круга в пространстве на один полный оборот вокруг оси, копланарной с кругом. К основным типам торов относятся кольцевые торы, роговые торы и веретенообразные торы. Кольцевой тор иногда в просторечии называют бубликом или бубликом .

Если ось вращения не касается круга, поверхность имеет форму кольца и называется тором вращения , также известным как кольцевой тор . Если ось вращения касается окружности, поверхность представляет собой роговой тор . Если ось вращения дважды проходит через круг, поверхность представляет собой веретенообразный тор (или самопересекающийся тор , или самопересекающийся тор ). Если ось вращения проходит через центр круга, поверхность представляет собой вырожденный тор, дважды покрытую сферу . Если вращающаяся кривая не является кругом, поверхность называется тороидом , как и квадратный тороид.

Реальные объекты, которые приближаются к тору вращения, включают плавательные кольца , внутренние трубки и кольца-кольца .

Тор не следует путать с полнотелым тором , который образуется в результате вращения вокруг оси диска , а не круга. Полнотелый тор — это тор плюс объем внутри тора. Реальные объекты, которые приближаются к твердотельному тору , включают уплотнительные кольца , ненадувные спасательные круги , кольцевые пончики и бублики .

В топологии кольцевой тор гомеоморфен декартову произведению двух окружностей : $S^{1}\times S^{1}$, и последнее считается определением в этом контексте. Это компактное 2-многообразие рода 1. Кольцевой тор — это один из способов вложить это пространство в евклидово пространство , но другой способ сделать это — декартово вложения произведение $S^{1}$ в самолете сам с собой. В результате получается геометрический объект, называемый тором Клиффорда , поверхность в 4-мерном пространстве .

В области топологии тор — это любое топологическое пространство, гомеоморфное тору. Поверхность кофейной чашки и пончика являются топологическими торами рода один.

Пример тора можно построить, взяв прямоугольную полосу гибкого материала, например резины, и соединив верхний край с нижним краем, а левый край с правым, без каких-либо полуповоротов (сравните бутылку Клейна ).

Этимология

Тор — латинское слово, означающее «круглый, вздутый, возвышенный, выпуклый».

Геометрия

Нижние половины и
вертикальные сечения

R > r : кольцевой тор или якорное кольцо.

R = r : роговой тор

R < r : самопересекающийся веретенообразный тор.

Полоидальное направление (красная стрелка) и тороидальное направление (синяя стрелка)

Тор можно параметризовать как: $${\begin{aligned}x(\theta ,\varphi )&=(R+r\cos \theta )\cos {\varphi }\\y(\theta ,\varphi )&=(R+r\cos \theta )\sin {\varphi }\\z(\theta ,\varphi )&=r\sin \theta \\\end{aligned}}$$

используя угловые координаты $\theta ,\varphi \in [0,2\pi ),$ представляющее вращение вокруг трубки и вращение вокруг оси вращения тора соответственно, где большой радиус $R$ - расстояние от центра трубки до центра тора и малый радиус $r$ это радиус трубки.

Соотношение $R/r$ называется соотношением сторон тора. Типичные кондитерские пончики имеют соотношение сторон примерно 3 к 2.

уравнение Неявное в декартовых координатах для тора, радиально симметричного относительно $z$- ось есть $${\textstyle {\bigl (}{\sqrt {x^{2}+y^{2}}}-R{\bigr )}^{2}}+z^{2}=r^{2}.$$

Алгебраическое исключение квадратного корня дает уравнение четвертой степени : $$\left(x^{2}+y^{2}+z^{2}+R^{2}-r^{2}\right)^{2}=4R^{2}\left(x^{2}+y^{2}\right).$$

Три класса стандартных торов соответствуют трем возможным соотношениям сторон между R и r :

• Когда R > r , поверхность будет представлять собой знакомый кольцевой тор или якорное кольцо.
• R = r соответствует рупорному тору, который по сути представляет собой тор без «дырки».
• R < r описывает самопересекающийся веретенообразный тор; его внутренняя оболочка — лимон , а внешняя — яблоко .
• Когда R = 0 , тор вырождается до сферы радиуса r .
• Когда r = 0 тор вырождается до радиуса окружности R. ,

Когда R ≥ r , внутренняя часть $${\textstyle {\bigl (}{\sqrt {x^{2}+y^{2}}}-R{\bigr )}^{2}}+z^{2}<r^{2}$$этого тора диффеоморфен (а значит, и гомеоморфен) произведению евклидова открытого диска и окружности. Объем теоремы этого полнотора и площадь поверхности его тора легко вычисляются с помощью Паппа о центроиде , что дает: $${\begin{aligned}A&=\left(2\pi r\right)\left(2\pi R\right)=4\pi ^{2}Rr,\\[5mu]V&=\left(\pi r^{2}\right)\left(2\pi R\right)=2\pi ^{2}Rr^{2}.\end{aligned}}$$

Эти формулы такие же, как и для цилиндра длиной 2π R и радиуса r , полученного в результате разрезания трубки по плоскости малого круга и разворачивания его путем выпрямления (выпрямления) линии, огибающей центр трубки. Потери площади поверхности и объема на внутренней стороне трубки в точности сводят на нет выигрыш на внешней стороне.

Выражая площадь поверхности и объем расстоянием p от крайней точки поверхности тора до центра и расстоянием q от самой внутренней точки до центра (так что R = р + д / 2 и г = p − q / 2 ), дает $${\begin{aligned}A&=4\pi ^{2}\left({\frac {p+q}{2}}\right)\left({\frac {p-q}{2}}\right)=\pi ^{2}(p+q)(p-q),\\[5mu]V&=2\pi ^{2}\left({\frac {p+q}{2}}\right)\left({\frac {p-q}{2}}\right)^{2}={\tfrac {1}{4}}\pi ^{2}(p+q)(p-q)^{2}.\end{aligned}}$$

Поскольку тор представляет собой произведение двух окружностей, модифицированная версия сферической системы координат иногда используется .В традиционных сферических координатах есть три меры: R — расстояние от центра системы координат, а также θ и φ — углы, измеренные от центральной точки.

Поскольку тор фактически имеет две центральные точки, центры углов перемещаются; φ измеряет тот же угол, что и в сферической системе, но известен как «тороидальное» направление. Центральная точка θ перемещается в центр r и называется «полоидальным» направлением. Эти термины были впервые использованы при обсуждении магнитного поля Земли, где слово «полоидальное» использовалось для обозначения «направления к полюсам».

В современном использовании тороидальные и полоидальные чаще используются для описания термоядерных устройств с магнитным удержанием .

Топология

Топологически тор представляет собой замкнутую поверхность, определяемую как произведение двух окружностей : S ¹ × С ¹ . Это можно рассматривать как лежащее в C ² и является подмножеством 3-сферы S ³ радиуса √2. Этот топологический тор также часто называют тором Клиффорда . Фактически, С ³ семейством таким образом заполняется вложенных торов (с двумя вырожденными окружностями), что важно при изучении S ³ как расслоение над S ² ( расслоение Хопфа ).

Описанная выше поверхность с учетом относительной топологии из $\mathbb {R} ^{3}$, гомеоморфен топологическому тору до тех пор, пока он не пересекает собственную ось. Особый гомеоморфизм задается стереографическим проецированием топологического тора в $\mathbb {R} ^{3}$ от северного полюса Ю. ³ .

Тор можно также описать как фактор декартовой плоскости при отождествлениях

$(x,y)\sim (x+1,y)\sim (x,y+1),\,$

или, что то же самое, как частное единичного квадрата путем склеивания противоположных ребер вместе, что описывается как фундаментальный многоугольник ABA. ⁻¹ Б ⁻¹ .

Выворачивание проколотого тора наизнанку

Фундаментальная группа тора является прямым произведением фундаментальной группы окружности на саму себя:

$\pi _{1}(\mathbb {T} ^{2})=\pi _{1}(\mathbb {S} ^{1})\times \pi _{1}(\mathbb {S} ^{1})\cong \mathbb {Z} \times \mathbb {Z} .$

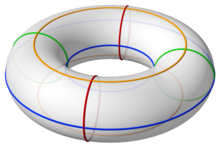
Интуитивно говоря, это означает, что замкнутый путь , который огибает «отверстие» тора (скажем, круг, очерчивающий определенную широту), а затем огибает «тело» тора (скажем, круг, очерчивающий определенную долготу) можно деформировать до траектории, огибающей тело, а затем отверстие. Таким образом, коммутируют строго «широтные» и строго «продольные» пути. Эквивалентное утверждение можно представить себе как два шнурка, проходящие друг через друга, затем разматывающиеся и затем перематывающиеся.

Если тор проколоть и вывернуть наизнанку, получится другой тор, в котором линии широты и долготы поменяются местами. Это эквивалентно построению тора из цилиндра путем соединения круглых концов вместе двумя способами: снаружи, как соединение двух концов садового шланга, или внутри, как скатывание носка (с отрезанным пальцем). Кроме того, если цилиндр был создан путем склеивания двух противоположных сторон прямоугольника, выбор двух других сторон приведет к такому же изменению ориентации.

Первая группа гомологий тора изоморфна фундаментальной группе (это следует из теоремы Гуревича, поскольку фундаментальная группа абелева ).

Двухлистовая обложка

2-тор дважды покрывает 2-сферу с четырьмя точками ветвления . Любую конформную структуру на 2-торе можно представить как двулистное покрытие 2-сферы. Точки на торе, соответствующие точкам ветвления, являются точками Вейерштрасса . Фактически конформный тип тора определяется перекрестным отношением четырех точек.

n -мерный тор

Стереографическая проекция тора Клиффорда в четырех измерениях, совершающая простое вращение через xz . плоскость

Тор имеет обобщение на более высокие размерности, n-мерный тор , часто называемый n -тором или гипертором сокращенно . (Это более типичное значение термина « n -тор», другое относится к n дыркам или роду n . ) Напоминая, что тор — это произведение двух окружностей, n -мерный тор — это произведение n окружностей. То есть:

$\mathbb {T} ^{n}=\underbrace {\mathbb {S} ^{1}\times \cdots \times \mathbb {S} ^{1}} _{n}.$

Стандартный 1-тор — это просто круг: $\mathbb {T} ^{1}=\mathbb {S} ^{1}$. Обсуждаемый выше тор является стандартным 2-тором, $\mathbb {T} ^{2}$. И подобно 2-тору, n -тор, $\mathbb {T} ^{n}$ можно описать как частное $\mathbb {R} ^{n}$ при интегральных сдвигах по любой координате. То есть n -тор $\mathbb {R} ^{n}$ по модулю действия целочисленной решетки $\mathbb {Z} ^{n}$ (при этом действие выполняется как сложение векторов). Эквивалентно, n -тор получается из n -мерного гиперкуба путем склеивания противоположных граней.

n - тор в этом смысле является примером n- мерного компактного многообразия . Это также пример компактной абелевой группы Ли . Это следует из того, что единичная окружность является компактной абелевой группой Ли (при отождествлении с единичными комплексными числами с умножением). Групповое умножение на торе тогда определяется умножением по координатам.

Тороидальные группы играют важную роль в теории компактных групп Ли . Частично это связано с тем, что в любой компактной группе Ли G всегда можно найти максимальный тор ; то есть замкнутая подгруппа , представляющая собой тор максимально возможной размерности. Такие максимальные торы T играют контролирующую роль в теории связного G . Тороидальные группы являются примерами проторов , которые (как и торы) являются компактными связными абелевыми группами, которые не обязательно должны быть многообразиями .

Автоморфизмы T легко строятся из автоморфизмов решетки $\mathbb {Z} ^{n}$, которые классифицируются обратимыми целочисленными матрицами размера n с целым обратным; это просто целочисленные матрицы с определителем ±1. Заставить их действовать $\mathbb {R} ^{n}$ обычным способом имеет место типичный торический автоморфизм фактора.

Фундаментальная группа - тора n — это свободная абелева группа ранга n . группа k -я гомологий тора n- является свободной абелевой группой ранга n, выбираем k . Отсюда следует, что эйлерова характеристика - тора n равна 0 для всех n . когомологий Кольцо H ^• ( $\mathbb {T} ^{n}$, Z ) можно отождествить с внешней алгеброй над Z - модулем $\mathbb {Z} ^{n}$ чьи генераторы являются двойственными к n нетривиальным циклам.

Смотрите также: Квазиторическое многообразие

Конфигурационное пространство

Конфигурационное пространство двух не обязательно различных точек на окружности представляет собой орбифолдный фактор 2-тора T ² / S ₂ , представляющий собой ленту Мёбиуса .

Тоннец — пример тора в теории музыки.
Тоннец действительно является тором только в том случае, если энгармоническая эквивалентность предполагается , так что сегмент (F ♯-A ♯) правого края повторяющегося параллелограмма отождествляется с сегментом (G ♭-B ♭) левого края.

Поскольку n -тор представляет собой n -кратное произведение окружности, n -тор представляет собой конфигурационное пространство из n упорядоченных, не обязательно различных точек окружности. Символически, $\mathbb {T} ^{n}=(\mathbb {S} ^{1})^{n}$. Конфигурационное пространство неупорядоченных , не обязательно различных точек, соответственно, является орбифолдом. $\mathbb {T} ^{n}/\mathbb {S} _{n}$, который является фактором тора по симметрической группе по n буквам (путем перестановки координат).

Для n = 2 фактором является полоса Мёбиуса , ребро, соответствующее точкам орбифолда, в которых две координаты совпадают. Для n = 3 это частное можно описать как полноторие с поперечным сечением равностороннего треугольника с закруткой ; эквивалентно, как треугольная призма , верхняя и нижняя грани которой соединены поворотом на 1/3 (120 °): трехмерная внутренняя часть соответствует точкам на трехмерном торе, где все три координаты различны, двухмерная грань соответствует точкам, у которых 2 координаты равны, а 3-я отличается, а одномерное ребро соответствует точкам, у которых все 3 координаты одинаковы.

Эти орбифолды нашли существенное применение в теории музыки в работах Дмитрия Тимочко и его соавторов (Фелипе Посада, Майкл Колинас и др.), Использовавшись для моделирования музыкальных триад .

Плоский тор

В трех измерениях можно согнуть прямоугольник в тор, но при этом поверхность обычно растягивается, о чем свидетельствует искажение клетчатого узора.

Если смотреть в стереографической проекции , то четырехмерный плоский тор можно проецировать в трехмерном пространстве и вращать вокруг фиксированной оси.

Простейшей мозаикой плоского тора является {4,4} _1,0 , построенная на поверхности дуоцилиндра с 1 вершиной, 2 ортогональными ребрами и одной квадратной гранью. Здесь он стереографически проецируется в трехмерное пространство в виде тора.

метрика которого унаследована от его представления в виде частного Плоский тор — это тор , $\mathbb {R} ^{2}$/ L , где L — дискретная подгруппа $\mathbb {R} ^{2}$ изоморфен $\mathbb {Z} ^{2}$. Это придает фактору структуру риманова многообразия . Возможно, самый простой пример этого — когда L = $\mathbb {Z} ^{2}$: $\mathbb {R} ^{2}/\mathbb {Z} ^{2}$, которую также можно описать как декартову плоскость при отождествлении ( x , y ) ~ ( x + 1, y ) ~ ( x , y + 1) . Этот конкретный плоский тор (и любая его версия с равномерным масштабом) известен как «квадратный» плоский тор.

Эта метрика квадратного плоского тора также может быть реализована путем конкретных вложений знакомого 2-тора в евклидово 4-мерное пространство или более высокие измерения. Его поверхность всюду имеет нулевую гауссову кривизну . Его поверхность плоская в том же смысле, в каком плоская поверхность цилиндра. В трех измерениях плоский лист бумаги можно согнуть в цилиндр, не растягивая бумагу, но этот цилиндр нельзя согнуть в тор, не растягивая бумагу (если не отказаться от некоторых условий регулярности и дифференцируемости, см. ниже).

Простое 4-мерное евклидово вложение прямоугольного плоского тора (более общего, чем квадратный) выглядит следующим образом:

$(x,y,z,w)=(R\cos u,R\sin u,P\cos v,P\sin v)$

где R и P — положительные константы, определяющие соотношение сторон. Он диффеоморфен регулярному тору, но не изометричен . Он не может быть аналитически вложен ( гладкий класса C ^к , 2 ≤ k ≤ ∞ ) в евклидово 3-пространство. Для отображения его в трехмерном пространстве необходимо его растянуть, и в этом случае он будет выглядеть как обычный тор. Например, на следующей карте:

$(x,y,z)=((R+P\sin v)\cos u,(R+P\sin v)\sin u,P\cos v).$

Если R и P в приведенной выше параметризации плоского тора образуют единичный вектор ( R , P ) = (cos( ​​η ), sin( η )) тогда u , v и 0 < η < π /2 параметризуют единичную 3-сферу. как координаты Хопфа . В частности, для некоторых весьма специфических вариантов выбора квадратного плоского тора в 3-сфере S ³ , где η = π /4 выше, тор разделит 3-сферу на два конгруэнтных подмножества полноторий с вышеупомянутой плоской поверхностью тора в качестве их общей границы . Одним из примеров является тор T, определяемый формулой

$T=\left\{(x,y,z,w)\in \mathbb {S} ^{3}\mid x^{2}+y^{2}={\frac {1}{2}},\ z^{2}+w^{2}={\frac {1}{2}}\right\}.$

Другие торы в S ³ обладающие этим свойством разделения, включают квадратные торы формы Q ⋅ T , где Q — вращение 4-мерного пространства. $\mathbb {R} ^{4}$, или, другими словами, Q является членом группы Ли SO(4).

Известно, что не существует C ² (дважды непрерывно дифференцируемое) вложение плоского тора в трехмерное пространство. (Идея доказательства состоит в том, чтобы взять большую сферу, содержащую такой плоский тор внутри, и уменьшить радиус сферы до тех пор, пока она впервые не коснется тора. Такая точка контакта должна быть точкой касания. Но это означало бы, что часть тора, поскольку она всюду имеет нулевую кривизну, должна лежать строго вне сферы, что является противоречием.) С другой стороны, согласно теореме Нэша-Койпера , доказанной в 1950-х годах, изометрический С ¹ встраивание существует. Это исключительно доказательство существования и не дает явных уравнений для такого вложения.

$C^{1}$ изометрическое вложение плоского тора в $\mathbb {R} ^{3}$, с гофрами

В апреле 2012 года явный C ¹ (непрерывно дифференцируемое) вложение плоского тора в трехмерное евклидово пространство $\mathbb {R} ^{3}$ был найден. Это плоский тор в том смысле, что, как метрические пространства, он изометричен плоскому квадратному тору. По структуре он похож на фрактал , поскольку создается путем многократного гофрирования обычного тора. Как и фракталы, он не имеет определенной гауссовой кривизны. Однако, в отличие от фракталов, он имеет определенные нормали к поверхности , что дает так называемый «гладкий фрактал». Ключом к достижению гладкости этого гофрированного тора является то, чтобы амплитуды последовательных гофров уменьшались быстрее, чем их «длины волн». (Эти бесконечно рекурсивные гофры используются только для встраивания в три измерения; они не являются внутренней особенностью плоского тора.) Впервые такое вложение было определено явными уравнениями или изображено с помощью компьютерной графики.

плоских

При изучении римановых поверхностей говорят, что любые две гладкие компактные геометрические поверхности «конформно эквивалентны», если между ними существует гладкий гомеоморфизм, сохраняющий как угол, так и ориентацию. Теорема униформизации гарантирует, что каждая риманова поверхность конформно эквивалентна поверхности, имеющей постоянную гауссову кривизну. В случае тора постоянная кривизна должна быть равна нулю. Затем определяют «пространство модулей» тора так, чтобы оно содержало по одной точке для каждого класса конформной эквивалентности с соответствующей топологией. Оказывается, это пространство модулей M можно отождествить с проколотой сферой, которая является гладкой, за исключением двух точек, угол которых вокруг них меньше 2π (радиан): одна имеет π, а другая - 2π/3.

M можно превратить в компактное пространство M*, добавив одну дополнительную точку, которая представляет предельный случай, когда прямоугольный тор приближается к соотношению сторон 0 в пределе. В результате это компактифицированное пространство модулей представляет собой сферу с тремя точками, каждая из которых имеет угол меньше 2π вокруг них. (Такие точки называются «каспами».) Эта дополнительная точка будет иметь нулевой угол вокруг себя. В силу симметрии M* можно построить путем склейки двух конгруэнтных геодезических треугольников в гиперболической плоскости вдоль их (идентичных) границ, где каждый треугольник имеет углы π/2, π/3 и 0. В результате площадь каждый треугольник можно вычислить как π - (π/2 + π/3 + 0) = π/6, откуда следует, что компактифицированное пространство модулей M* имеет площадь, равную π/3.

Два других возврата находятся в точках, соответствующих в M* а) квадратному тору (π) и б) шестиугольному тору (2π/3). Это единственные классы конформной эквивалентности плоских торов, которые имеют любые конформные автоморфизмы, кроме тех, которые порождены сдвигами и отрицанием.

Род g поверхность

Основная статья: рода g Поверхность

В теории поверхностей существует более общее семейство объектов — « род » поверхностей . Поверхность рода g — это связная сумма двухторов g . (Итак, сам тор является поверхностью рода 1.) Чтобы образовать связную сумму двух поверхностей, удалите из каждой внутренности диска и «склейте» поверхности вместе по граничным окружностям. (То есть объедините два граничных круга, чтобы они стали одним кругом.) Чтобы сформировать связную сумму более чем двух поверхностей, последовательно берите связную сумму двух из них за раз, пока они все не соединятся. В этом смысле поверхность рода g напоминает поверхность g пончиков, склеенных рядом, или 2-сферу с прикрепленными g ручками.

Например, поверхность нулевого рода (без края) представляет собой двухсферу , а поверхность рода один (без края) представляет собой обычный тор. Поверхности более высокого рода иногда называют n- дырочными торами (или, реже, n -кратными торами). термины двойной тор и тройной тор Иногда также используются .

Теорема классификации поверхностей утверждает, что каждая компактная связная поверхность топологически эквивалентна либо сфере, либо связной сумме некоторого числа торов, дисков и вещественных проективных плоскостей .

род второй

род третий

Тороидальные многогранники

Дополнительная информация: Тороидальный многогранник.

Тороидальный многогранник с 6 × 4 = 24 четырехугольными гранями.

Многогранники с топологическим типом тора называются тороидальными многогранниками и имеют эйлерову характеристику V − E + F = 0. Для любого количества дырок формула обобщается до V − E + F = 2 − 2 N , где N — количество отверстий.

Термин «тороидальный многогранник» также используется для обозначения многогранников высших родов и погружений тороидальных многогранников.

Автоморфизмы

Группа гомеоморфизмов (или подгруппа диффеоморфизмов) тора изучается в геометрической топологии . Его группа классов отображений (компоненты связности группы гомеоморфизмов) сюръективна на группу $\operatorname {GL} (n,\mathbb {Z} )$ обратимых целочисленных матриц, которые можно реализовать как линейные отображения на универсальном накрывающем пространстве $\mathbb {R} ^{n}$ сохраняющие стандартную решетку $\mathbb {Z} ^{n}$ (это соответствует целым коэффициентам) и таким образом спуститься к частному.

На уровне гомотопий и гомологий группу классов отображений можно идентифицировать как действие на первые гомологии (или, что то же самое, на первые когомологии или на фундаментальную группу , поскольку все они естественно изоморфны; также первая группа когомологий порождает когомологии алгебра:

$\operatorname {MCG} _{\operatorname {Ho} }(\mathbb {T} ^{n})=\operatorname {Aut} (\pi _{1}(X))=\operatorname {Aut} (\mathbb {Z} ^{n})=\operatorname {GL} (n,\mathbb {Z} ).$

Поскольку тор является пространством Эйленберга–Маклейна K ( G , 1), его гомотопические эквивалентности с точностью до гомотопии можно отождествить с автоморфизмами фундаментальной группы; все гомотопические эквивалентности тора могут быть реализованы посредством гомеоморфизмов - каждая гомотопическая эквивалентность гомотопна гомеоморфизму.

Таким образом, короткая точная последовательность группы классов отображений расщепляется (идентификация тора как фактора $\mathbb {R} ^{n}$ дает расщепление посредством линейных отображений, как указано выше):

$1\to \operatorname {Homeo} _{0}(\mathbb {T} ^{n})\to \operatorname {Homeo} (\mathbb {T} ^{n})\to \operatorname {MCG} _{\operatorname {TOP} }(\mathbb {T} ^{n})\to 1.$

Группа классов отображения поверхностей более высокого рода намного сложнее и является областью активных исследований.

Раскраска тора

тора Число Хивуда равно семи, что означает, что каждый граф, который можно встроить в тор, имеет хроматическое число не более семи. (Поскольку полный граф ${\mathsf {K_{7}}}$ можно вложить в тор, причем $\chi ({\mathsf {K_{7}}})=7$, верхняя граница точная.) Аналогично, в торе, разделенном на области, всегда можно раскрасить области, используя не более семи цветов, так, чтобы ни одна из соседних областей не была одного цвета. (В отличие от теоремы о четырех цветах для плоскости .)

Эта конструкция показывает тор, разделенный на семь областей, каждая из которых касается друг друга, то есть каждой должен быть присвоен уникальный цвет.

тор де Брёйна

Основная статья: тор де Брёйна

STL- модель тора де Брейна (16,32;3,3) ₂ с единицами в виде панелей и нулями в виде отверстий в сетке - при последовательной ориентации каждая матрица 3×3 появляется ровно один раз.

В комбинаторной математике тор де Брейна — это массив символов алфавита (часто только 0 и 1), который содержит каждую размером m x n матрицу ровно один раз. Это тор, потому что при поиске матриц его края считаются закругленными. Его название происходит от последовательности Де Брейна , которую можно считать частным случаем, когда n равно 1 (одно измерение).

Разрезание тора

Полнотелый тор вращения можно разрезать n (>0) плоскостями не более чем на

${\begin{pmatrix}n+2\\n-1\end{pmatrix}}+{\begin{pmatrix}n\\n-1\end{pmatrix}}={\tfrac {1}{6}}(n^{3}+3n^{2}+8n)$

части. (При этом предполагается, что части нельзя переставлять, но они должны оставаться на месте при всех разрезах.)

Первые 11 номеров частей для 0 ≤ n ≤ 10 (включая случай n = 0, не охватываемый приведенными выше формулами) следующие:

1, 2, 6, 13, 24, 40, 62, 91, 128, 174, 230, ... (последовательность A003600 в OEIS ).

См. также

• 3-тор
• Алгебраический тор
• Ангенентный тор
• Кольцевое пространство (геометрия)
• Тор Клиффорда
• Комплексный тор
• Циклида Дюпена
• Эллиптическая кривая
• Иррациональная обмотка тора
• Объединенный европейский тор
• бутылка Клейна
• Неравенство тора Лёвнера
• Максимальный тор
• Решетка периода
• Реальная проективная плоскость
• Сфера
• Спирический раздел
• Поверхность (топология)
• Торическая линза
• Торическое сечение
• Торическая разновидность
• Тороид
• Тороидальный и полоидальный
• Криптография на основе тора
• Торовый узел
• Пупочный тор
• круги Вильярсо

Примечания

• Понятия аналитической геометрии и линейной алгебры , ISBN   978-970-10-6596-9 , автор: Козак Ана Мария, Помпея Пасторелли Соня, Верданега Педро Эмилио, редакция: McGraw-Hill, издание 2007 г., 744 страницы, язык: испанский
• Аллен Хэтчер. Алгебраическая топология . Издательство Кембриджского университета, 2002. ISBN   0-521-79540-0 .
• В.В. Никулин, И.Р. Шафаревич. Геометрии и группы . Спрингер, 1987. ISBN   3-540-15281-4 , ISBN   978-3-540-15281-1 .
• «Тор (геометрическое понятие)» в Энциклопедии замечательных математических форм.

Внешние ссылки

• Создание тора при разрезании узла
• «4D тор» Пролетные сечения четырехмерного тора.
• «Карта реляционной перспективы» Визуализация многомерных данных с помощью плоского тора
• Полидо, многоугольники в форме пончика.
• Архивировано в Ghostarchive и Wayback Machine : Секен, Карло Х (27 января 2014 г.). «Топология витого тора – нумерфил» (видео) . Брэйди Харан .
• Андерс Сандберг (4 февраля 2014 г.). «Торус Земли» . Проверено 24 июля 2019 г.