Машина Тьюринга

Чтобы узнать о других значениях, см. Машина Тьюринга (значения) .

Физическая модель машины Тьюринга. Настоящая машина Тьюринга имела бы неограниченное количество ленты с обеих сторон; однако физические модели могут иметь только ограниченное количество ленты.

Классы автоматов

Машина Тьюринга — это математическая модель вычислений, описывающая абстрактную машину. который манипулирует символами на полоске ленты в соответствии с таблицей правил. Несмотря на простоту модели, она способна реализовать любой компьютерный алгоритм .

Машина работает бесконечно лента памяти разделена на дискретные ячейки, каждый из которых может содержать один символ, взятый из конечного набора символов, называемого алфавитом машины. У него есть «голова», которая в любой момент работы машины располагается над одной из этих ячеек, и «состояние», выбираемое из конечного набора состояний. На каждом этапе своей работы головка считывает символ в своей ячейке. Затем, основываясь на символе и текущем состоянии машины, машина записывает символ в ту же ячейку и перемещает головку на один шаг влево или вправо. или останавливает вычисления. Выбор того, какой символ замены записать, в каком направлении перемещать головку и остановиться ли, основан на конечной таблице, которая определяет, что делать для каждой комбинации текущего состояния и считываемого символа. Как и настоящая компьютерная программа, машина Тьюринга может войти в бесконечный цикл , который никогда не остановится.

Машина Тьюринга была изобретена в 1936 году Аланом Тьюрингом . который назвал это «а-машиной» (автоматической машиной). Именно научный руководитель Тьюринга Алонсо Чёрч позже ввел в обзоре термин «машина Тьюринга». С помощью этой модели Тьюринг смог ответить отрицательно на два вопроса:

• Существует ли машина, которая может определить, является ли любая произвольная машина на ее ленте «круговой» (например, зависает или не может продолжить выполнение своей вычислительной задачи)?
• Существует ли машина, которая может определить, напечатает ли когда-либо произвольная машина на своей ленте данный символ?

Таким образом, предоставив математическое описание очень простого устройства, способного выполнять произвольные вычисления, он смог доказать свойства вычислений в целом — и, в частности, невычислимость проблемы Entscheidungsproblem ( «проблемы принятия решений»).

Машины Тьюринга доказали существование фундаментальных ограничений мощности механических вычислений. Хотя они могут выполнять произвольные вычисления, их минималистичный дизайн делает их слишком медленными для практических вычислений: реальные компьютеры основаны на других конструкциях, которые, в отличие от машин Тьюринга, используют оперативную память .

Полнота по Тьюрингу — это способность вычислительной модели или системы инструкций моделировать машину Тьюринга. Язык программирования, полный по Тьюрингу, теоретически способен выражать все задачи, решаемые компьютерами; почти все языки программирования полны по Тьюрингу, если игнорировать ограничения ограниченной памяти.

Обзор

Машина Тьюринга — это идеализированная модель центрального процессора (ЦП), который контролирует все манипуляции с данными, выполняемые компьютером, при этом каноническая машина использует последовательную память для хранения данных. Обычно последовательная память представляет собой ленту бесконечной длины, на которой машина может выполнять операции чтения и записи.

В контексте теории формального языка машина Тьюринга ( автомат ) способна пересчитывать некоторое произвольное подмножество допустимых строк алфавита . Набор строк, которые можно перечислить таким образом, называется рекурсивно перечислимым языком . Машину Тьюринга можно эквивалентно определить как модель, которая распознает действительные входные строки, а не перечисляет выходные строки.

Учитывая машину Тьюринга M и произвольную строку s , обычно невозможно решить, будет ли M в конечном итоге создавать s . Это связано с тем, что проблема остановки неразрешима, что имеет серьезные последствия для теоретических пределов вычислений.

Машина Тьюринга способна обрабатывать неограниченную грамматику , что далее означает, что она способна надежно оценивать логику первого порядка бесконечным числом способов. Это прекрасно демонстрируется с помощью лямбда-исчисления .

Машина Тьюринга, способная моделировать любую другую машину Тьюринга, называется универсальной машиной Тьюринга (UTM или просто универсальной машиной). Другой математический формализм, лямбда-исчисление , имеющий аналогичную «универсальную» природу, был введен Алонзо Чёрчем . Работы Чёрча переплелись с работами Тьюринга и легли в основу тезиса Чёрча-Тьюринга . В этом тезисе утверждается, что машины Тьюринга, лямбда-исчисление и другие подобные формализмы вычислений действительно отражают неформальное представление об эффективных методах в логике и математике и, таким образом, предоставляют модель, с помощью которой можно рассуждать об алгоритме или «механической процедуре» в математической форме. точным способом, не привязываясь к какому-либо конкретному формализму. Изучение абстрактных свойств машин Тьюринга позволило многое понять в области информатики , теории вычислимости и теории сложности .

Физическое описание

В своем эссе 1948 года «Интеллектуальная техника» Тьюринг писал, что его машина состоит из:

...неограниченный объем памяти, полученный в виде бесконечной ленты, размеченной на квадраты, на каждом из которых можно было напечатать символ. В любой момент в машине есть один символ; это называется сканируемым символом. Машина может изменить отсканированный символ, и его поведение частично определяется этим символом, но символы на ленте в других местах не влияют на поведение машины. Однако ленту можно перемещать вперед и назад по машине, что является одной из элементарных операций машины. Таким образом, любой символ на ленте может в конечном итоге иметь подачу.

- Тьюринг 1948, с. 3

Описание

Визуализации машин Тьюринга см. в галерее машин Тьюринга .

Машина Тьюринга математически моделирует машину, которая механически работает с лентой. На этой ленте находятся символы, которые машина может читать и записывать по одному, используя ленточную головку. Операция полностью определяется конечным набором элементарных инструкций, таких как «в состоянии 42, если видимый символ равен 0, запишите 1; если видимый символ равен 1, перейдите в состояние 17; в состоянии 17, если видимый символ равен 0, запишите 1 и измените состояние на 6;" и т. д. В оригинальной статье (« О вычислимых числах с применением к Entscheidungsproblem », см. также ссылки ниже ) Тьюринг представляет не механизм, а человека, которого он называет «компьютером», который рабски выполняет эти детерминированные механические правила. (или, как выразился Тьюринг, «бессистемно»).

Голова всегда находится над определенным квадратом ленты; показан только конечный участок квадратов. Инструкция, которую необходимо выполнить (q ₄ ), отображается над отсканированным квадратом. (Рисунок по Клини (1952), стр. 375.)

Здесь внутреннее состояние (q ₁ ) показано внутри головки, а иллюстрация описывает ленту как бесконечную и предварительно заполненную «0», причем этот символ служит пустым. Полное состояние системы («полная конфигурация») состоит из внутреннего состояния, любых непустых символов на ленте (на этом рисунке «11B») и положения головки относительно этих символов, включая пробелы, т. е. «011B». ". (Рисунок по Минскому (1967), стр. 121.)

Более конкретно, машина Тьюринга состоит из:

• Лента разделена на ячейки, расположенные одна рядом с другой. В каждой ячейке содержится символ некоторого конечного алфавита. Алфавит содержит специальный пустой символ (здесь он обозначается как «0») и один или несколько других символов. Предполагается, что лента может произвольно растягиваться влево и вправо, так что машина Тьюринга всегда снабжается столько ленты, сколько ей необходимо для вычислений. Предполагается, что ячейки, которые не были записаны ранее, заполнены пустым символом. В некоторых моделях лента имеет левый конец, отмеченный специальным символом; лента простирается или бесконечно растягивается вправо.
• Головка , которая может читать и писать символы на ленте и перемещать ленту влево и вправо по одной (и только одной) ячейке за раз. В некоторых моделях головка движется, а лента неподвижна.
• Государственный регистр , в котором хранится состояние машины Тьюринга, один из конечного числа. Среди них особое начальное состояние , с помощью которого инициализируется государственный регистр. Эти состояния, пишет Тьюринг, заменяют «состояние ума», в котором обычно находится человек, выполняющий вычисления.
• Конечная таблица инструкций что, учитывая состояние (q _i ), в котором в данный момент находится машина , и символ 5- (a _j ), который она считывает на ленте (символ, который в данный момент находится под заголовком), приказывает машине выполнить следующие действия последовательно (для модели кортежей ):

1. Либо сотрите, либо напишите символ (заменив _j на _j1 ).
2. Переместите голову (описывается d _k и может иметь значения: «L» для одного шага влево , «R» для одного шага вправо или «N» для пребывания на том же месте).
3. Примите то же самое или новое состояние , как предписано (перейдите в состояние q _i1 ).

В четырехкортежных моделях стирание или запись символа (a _j1 ) и перемещение головы влево или вправо (d _k ) задаются как отдельные инструкции. Таблица предписывает машине (ia) стереть или написать символ или (ib) переместить голову влево или вправо, а затем (ii) принять то же самое или новое состояние, как предписано, но не оба действия (ia) и (ib). ) в той же инструкции. В некоторых моделях, если в таблице нет записи о текущей комбинации символа и состояния, машина остановится; другие модели требуют заполнения всех записей.

Каждая часть машины (т.е. ее состояние, наборы символов и используемая лента в любой момент времени) и ее действия (такие как печать, стирание и движение ленты) конечны , дискретны и различимы ; именно неограниченный объем ленты и время выполнения дают неограниченный объем места для хранения .

Формальное определение

Следуя Хопкрофту и Ульману (1979 , стр. 148), (одноленточную) машину Тьюринга можно формально определить как 7- кортежную машину Тьюринга. $M=\langle Q,\Gamma ,b,\Sigma ,\delta ,q_{0},F\rangle$ где

• $\Gamma$ — конечное, непустое множество символов ленточного алфавита ;
• $b\in \Gamma$ — пустой символ (единственный символ, который может появляться на ленте бесконечно часто на любом этапе вычислений);
• $\Sigma \subseteq \Gamma \setminus \{b\}$ — набор входных символов , то есть набор символов, которым разрешено появляться в исходном содержимом ленты;
• $Q$ — конечное, непустое множество состояний ;
• $q_{0}\in Q$ — исходное состояние ;
• $F\subseteq Q$ — это набор конечных состояний или принимающих состояний . Говорят, что исходное содержимое принято ленты $M$ если он в конечном итоге остановится в состоянии от $F$.
• $\delta :(Q\setminus F)\times \Gamma \not \to Q\times \Gamma \times \{L,R\}$ — это частичная функция , называемая функцией перехода , где L — сдвиг влево, R — сдвиг вправо. Если $\delta$ не определено текущее состояние и текущий символ ленты, то машина останавливается; интуитивно функция перехода определяет следующее состояние, перешедшее из текущего состояния, какой символ перезаписать текущий символ, на который указывает голова, и следующее движение головы.

Занятой бобр с 3 штатами. Черные значки обозначают местоположение и состояние головы; квадратные цвета обозначают 1 (оранжевый) и 0 (белый); время прогрессирует вертикально сверху до состояния HALT внизу.

Относительно редкий вариант допускает «отсутствие смещения», скажем N, в качестве третьего элемента набора направлений. $\{L,R\}$.

с 3 состояниями 7-кортеж для занятого бобра выглядит следующим образом (подробнее об этом занятом бобре см. в примерах машины Тьюринга ):

• $Q=\{{\mbox{A}},{\mbox{B}},{\mbox{C}},{\mbox{HALT}}\}$ (состояния);
• $\Gamma =\{0,1\}$ (символы ленточного алфавита);
• $b=0$ (пустой символ);
• $\Sigma =\{1\}$ (входные символы);
• $q_{0}={\mbox{A}}$ (исходное состояние);
• $F=\{{\mbox{HALT}}\}$ (конечные состояния);
• $\delta =$ см. таблицу состояний ниже (функция перехода).

Изначально все ячейки ленты отмечены значком $0$.

Таблица состояний для занятого бобра с 3 состояниями и 2 символами

Символ ленты	Текущее состояние А			Текущее состояние Б			Текущее состояние C
	Написать символ	Переместить ленту	Следующее состояние	Написать символ	Переместить ленту	Следующее состояние	Написать символ	Переместить ленту	Следующее состояние
0	1	Р	Б	1	л	А	1	л	Б
1	1	л	С	1	Р	Б	1	Р	ОСТАНОВКА

необходимые для визуализации или реализации машин

По словам ван Эмде Боаса (1990), с. 6: «Теоретико-множественный объект [его формальное семикортежное описание, подобное приведенному выше] предоставляет лишь частичную информацию о том, как будет вести себя машина и как будут выглядеть ее вычисления».

Например,

• Потребуется множество решений о том, как на самом деле выглядят символы, а также надежный способ чтения и записи символов на неопределенный срок.
• Операции сдвига влево и вправо могут смещать головку ленты по ленте, но при построении машины Тьюринга более практично вместо этого заставить ленту скользить вперед и назад под головкой.
• Лента может быть конечной и автоматически расширяться пробелами по мере необходимости (что наиболее близко к математическому определению), но чаще всего ее представляют как бесконечно растягивающуюся на одном или обоих концах и предварительно заполненную пробелами, за исключением явно задан конечный фрагмент, на котором находится головка ленты (это, конечно, неосуществимо на практике). Лента не может быть фиксированной по длине, поскольку это не соответствовало бы данному определению и серьезно ограничивало бы диапазон вычислений, которые машина может выполнять, до вычислений линейного ограниченного автомата, если бы лента была пропорциональна входному размеру или имела конечное состояние. машина, если бы она была строго фиксированной длины.

Альтернативные определения

Определения в литературе иногда немного различаются, чтобы сделать аргументы или доказательства проще или понятнее, но это всегда делается таким образом, чтобы полученная машина имела одинаковую вычислительную мощность. Например, набор можно изменить с $\{L,R\}$ к $\{L,R,N\}$, где N («Нет» или «Нет операций») позволит машине оставаться на той же ячейке ленты вместо перемещения влево или вправо. Это не увеличит вычислительную мощность машины.

Наиболее распространенное соглашение представляет каждую «инструкцию Тьюринга» в «таблице Тьюринга» одним из девяти кортежей из 5 частей в соответствии с соглашением Тьюринга/Дэвиса (Тьюринг (1936) в «Неразрешимом» , стр. 126–127 и Дэвис (2000). стр. 152):

(определение 1): (q _i , S _j , S _k /E/N, L/R/N, q _m )

( текущее состояние q _i , символ отсканирован S _j , символ печати S _k / стереть E / нет N , move_tape_one_square влево L / вправо R / нет N , новое состояние q _m )

Другие авторы (Минский (1967), стр. 119, Хопкрофт и Ульман (1979), стр. 158, Стоун (1972), стр. 9) принимают другое соглашение, в котором новое состояние q _m указывается сразу после отсканированного символа S _j :

(определение 2): (q _i , S _j , q _m , S _k /E/N, L/R/N)

( текущее состояние q _i , символ отсканирован S _j , новое состояние q _m , символ печати S _k / стереть E / нет N , move_tape_one_square влево L / вправо R / нет N )

В оставшейся части этой статьи будет использоваться «определение 1» (конвенция Тьюринга/Дэвиса).

Пример: таблица состояний для занятого бобра с 3 состояниями и 2 символами, уменьшенная до 5 кортежей.

Текущее состояние	Отсканированный символ	Символ печати	Переместить ленту	Конечное (т.е. следующее) состояние	5-кортежи
А	0	1	Р	Б	( А , 0, 1, Р, Б )
А	1	1	л	С	( А , 1, 1, Л, С )
Б	0	1	л	А	( Б , 0, 1, Л, А )
Б	1	1	Р	Б	( Б , 1, 1, Р, Б )
С	0	1	л	Б	( С , 0, 1, Л, Б )
С	1	1	Н	ЧАС	( С , 1, 1, Н, Ч )

В следующей таблице исходная модель Тьюринга допускала только первые три строки, которые он назвал N1, N2, N3 (ср. Тьюринг в «Неразрешимом» , стр. 126). Он разрешил стирание «отсканированного квадрата», назвав 0-й символ S ₀ = «стирание» или «пусто» и т. д. Однако он не допускал непечатания, поэтому каждая строка инструкции включает «символ печати S _k или «стирать» (ср. сноску 12 в Post (1947), The Undecidable , стр. 300). Аббревиатуры Тьюринга ( «Неразрешимые» , стр. 119). После оригинальной статьи Тьюринга в 1936–1937 годах модели машин допускали все девять возможных типов пятерок:

	Текущая м-конфигурация (состояние Тьюринга)	Символ ленты	Операция печати	Лента-движение	Окончательная m-конфигурация (состояние Тьюринга)	5-кортеж	5-кратные комментарии	4-кортеж
N1	q я	С Дж	Печать(S k )	Левый Л	q м	(q i , S j , S k , L, q m )	«пусто» = S 0 , 1=S 1 и т. д.
Н2	q я	С Дж	Печать(S k )	Правая Р	q м	(q i , S j , S k , R, q m )	«пусто» = S 0 , 1=S 1 и т. д.
N3	q я	С Дж	Печать(S k )	Нет Н	q м	(q i , S j , S k , N, q m )	«пусто» = S 0 , 1=S 1 и т. д.	(q я , S j , S k , q м )
4	q я	С Дж	Нет Н	Левый Л	q м	(q i , S j , N, L, q m )		(q i , S j , L, q m )
5	q я	С Дж	Нет Н	Правая Р	q м	(q i , S j , N, R, q m )		(q i , S j , R, q m )
6	q я	С Дж	Нет Н	Нет Н	q м	(q i , S j , N, N, q m )	Прямой «прыжок»	(q i , S j , N, q m )
7	q я	С Дж	Стереть	Левый Л	q м	(q i , S j , E, L, q m )
8	q я	С Дж	Стереть	Правая Р	q м	(q i , S j , E, R, q m )
9	q я	С Дж	Стереть	Нет Н	q м	(q i , S j , E, N, q m )		(q i , S j , E, q m )

Любая таблица Тьюринга (список инструкций) может быть построена из девяти вышеуказанных кортежей. По техническим причинам обычно можно обойтись без трех непечатаемых инструкций или инструкций «N» (4, 5, 6). Примеры см. в разделе «Примеры машин Тьюринга» .

Реже встречается использование четырехкортежей: они представляют собой дальнейшую атомизацию инструкций Тьюринга (ср. Post (1947), Boolos & Jeffrey (1974, 1999), Davis-Sigal-Weyuker (1994)); Также см. дополнительную информацию на странице «Машина Пост-Тьюринга» .

«Государство»

Слово «состояние», используемое в контексте машин Тьюринга, может вызвать путаницу, поскольку оно может означать две вещи. Большинство комментаторов после Тьюринга использовали слово «состояние» для обозначения имени/обозначения текущей выполняемой инструкции, то есть содержимого регистра состояния. Но Тьюринг (1936) провел четкое различие между записью того, что он называл «м-конфигурацией» машины, и «состоянием прогресса» машины (или человека) в вычислениях — текущим состоянием всей системы. То, что Тьюринг назвал «формулой состояния», включает в себя как текущую инструкцию, так и все символы на ленте:

Таким образом, ход вычислений на любом этапе полностью определяется записью инструкций и символами на ленте. То есть состояние системы можно описать одним выражением (последовательностью символов), состоящим из символов на ленте, за которыми следует Δ (которое не должно появляться где-либо еще), а затем записка с инструкциями. Это выражение называется «формулой состояния».

- Неразрешимое , стр. 139–140, курсив добавлен.

Ранее в своей статье Тьюринг пошел еще дальше: он приводит пример, в котором он поместил символ текущей «м-конфигурации» — метку инструкции — под отсканированный квадрат вместе со всеми символами на ленте ( «Неразрешимое» , стр. . 121); это он называет « полной конфигурацией » ( «Неразрешимое» , стр. 118). Чтобы напечатать «полную конфигурацию» в одной строке, он помещает метку состояния/m-конфигурацию слева от отсканированного символа.

Вариант этого можно увидеть у Клини (1952), где Клини показывает, как записать число Гёделя для «ситуации» машины: он помещает символ «м-конфигурации» q ₄ над отсканированным квадратом примерно в центре 6 не -пустые квадраты на ленте (см. рисунок ленты Тьюринга в этой статье) и помещает их справа от сканируемого квадрата. Но Клини называет «q ₄ » «состоянием машины» (Клин, стр. 374–375). Хопкрофт и Ульман называют это соединение «мгновенным описанием» и следуют соглашению Тьюринга, помещая «текущее состояние» (метку инструкции, m-конфигурацию) слева от отсканированного символа (стр. 149), то есть мгновенное состояние. Описание представляет собой совокупность непустых символов слева, состояния машины, текущего символа, сканируемого головкой, и непустых символов справа.

Пример: общее состояние занятого бобра с 3 состояниями и 2 символами после 3 «ходов» (взято из примера «бега» на рисунке ниже):

1 А 1

означает: после трех ходов на ленте появляется... 000110000..., головка сканирует крайнюю правую 1, а состояние - A. Это Пробелы (в данном случае обозначенные «0») могут быть частью общего состояния, как показано здесь: B 01; на ленте есть единственная 1, но головка сканирует 0 («пустой») слева от нее, и состояние равно B .

«Состояние» в контексте машин Тьюринга следует уточнять, что описывается: текущая инструкция, или список символов на ленте вместе с текущей инструкцией, или список символов на ленте вместе с текущей инструкцией. размещается слева от сканируемого символа или справа от сканируемого символа.

Биограф Тьюринга Эндрю Ходжес (1983: 107) отметил и обсудил эту путаницу.

Диаграммы «состояний»

Таблица для занятого бобра с 3 состояниями («P» = напечатать/записать «1»)

Символ ленты	Текущее состояние А			Текущее состояние Б			Текущее состояние C
	Написать символ	Переместить ленту	Следующее состояние	Написать символ	Переместить ленту	Следующее состояние	Написать символ	Переместить ленту	Следующее состояние
0	П	Р	Б	П	л	А	П	л	Б
1	П	л	С	П	Р	Б	П	Р	ОСТАНОВКА

Машина Тьюринга «занятого бобра с 3 состояниями» в представлении с конечными состояниями . Каждый круг представляет «состояние» таблицы — «m-конфигурацию» или «инструкцию». состояний «Направление» перехода показано стрелкой. Метка (например, 0/P,R ) рядом с исходящим состоянием (на «хвосте» стрелки) указывает отсканированный символ, который вызывает определенный переход (например, 0 ), за которым следует косая черта / , за которой следуют последующие «поведения». аппарата, например « P print », затем переместите ленту « R вправо ». Общепринятого формата не существует. Показанная конвенция взята из МакКласки (1965), Бута (1967), Хилла и Петерсона (1974).

Справа: приведенная выше таблица, выраженная в виде диаграммы «перехода состояний».

Обычно большие столы лучше оставить столами (Бут, стр. 74). Их легче моделировать на компьютере в табличной форме (Бут, стр. 74). Однако некоторые концепции — например, машины с состояниями «перезагрузки» и машины с повторяющимися шаблонами (ср. Хилл и Петерсон, стр. 244 и далее) — легче увидеть, если рассматривать их в виде рисунков.

Читатель должен решить, представляет ли рисунок улучшение своей таблицы в конкретном контексте.

Эволюция вычислений занятого бобра начинается сверху и продолжается вниз.

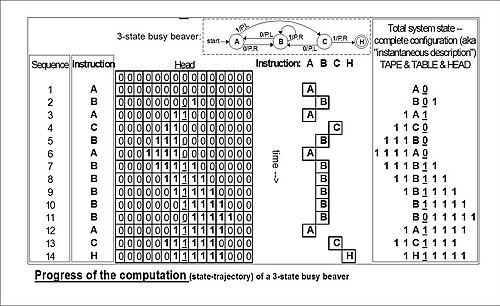
Читателя следует еще раз предупредить, что такие диаграммы представляют собой снимок таблицы, замороженной во времени, а не ход («траекторию») вычислений во времени и пространстве. Хотя каждый раз, когда занятая машина-бобр «запускается», она всегда будет следовать одной и той же траектории состояния, это не верно для «копирующей» машины, которая может быть снабжена переменными входными «параметрами».

Диаграмма «прогресс вычислений» показывает прогресс «состояния» (инструкции) занятого бобра с тремя состояниями в ходе вычислений от начала до конца. В крайнем правом углу находится «полная конфигурация» Тьюринга («ситуация» Клини, «мгновенное описание» Хопкрофта – Ульмана) на каждом этапе. Если бы машину нужно было остановить и очистить, чтобы очистить как «регистр состояния», так и всю ленту, эти «конфигурации» можно было бы использовать для возобновления вычислений в любом месте их выполнения (ср. Тьюринг (1936) «Неразрешимое », стр. 139–139). 140).

Эквивалентные модели

См. также: Эквиваленты машины Тьюринга , Регистровая машина и Машина Пост-Тьюринга.

Можно показать, что многие машины, которые, как можно подумать, обладают большей вычислительной мощностью, чем простая универсальная машина Тьюринга, не обладают большей мощностью (Хопкрофт и Ульман, стр. 159, ср. Мински (1967)). Возможно, они могут вычислять быстрее или использовать меньше памяти, или их набор команд может быть меньше, но они не могут выполнять более мощные вычисления (т. е. больше математических функций). ( Тезис Чёрча-Тьюринга предполагает, что это верно для любого типа машины: все, что можно «вычислить», может быть вычислено с помощью некоторой машины Тьюринга.)

Машина Тьюринга эквивалентна автомату с выталкивающим устройством с одним стеком (PDA), который стал более гибким и кратким за счет ослабления «последним пришел — первым вышел требования к стеку » (LIFO). Кроме того, машина Тьюринга также эквивалентна КПК с двумя стеками со стандартной семантикой LIFO, поскольку один стек используется для моделирования ленты слева от головки, а другой стек — для ленты справа.

С другой стороны, некоторые очень простые модели оказываются эквивалентными по Тьюрингу , то есть имеют ту же вычислительную мощность, что и модель машины Тьюринга.

Распространенными эквивалентными моделями являются многоленточная машина Тьюринга , многодорожечная машина Тьюринга , машины с вводом и выводом, а также недетерминированная машина Тьюринга (NDTM) в отличие от детерминированной машины Тьюринга (DTM), для которой таблица действий имеет максимум одна запись для каждой комбинации символа и состояния.

Правосторонние машины Тьюринга только для чтения эквивалентны DFA (а также NFA путем преобразования с использованием алгоритма преобразования NDFA в DFA ).

В практических и дидактических целях эквивалентную регистровую машину можно использовать как обычный ассемблер язык программирования .

Актуальный вопрос заключается в том, является ли модель вычислений, представленная конкретными языками программирования, эквивалентной Тьюрингу. Хотя вычисления реального компьютера основаны на конечных состояниях и, следовательно, не способны моделировать машину Тьюринга, сами языки программирования не обязательно имеют это ограничение. Кирнер и др., 2009 показали, что среди языков программирования общего назначения некоторые являются полными по Тьюрингу, а другие — нет. Например, ANSI C не является эквивалентом Тьюринга, поскольку все реализации ANSI C (возможны разные реализации, поскольку стандарт намеренно оставляет определенное поведение неопределенным по причинам наследия) подразумевают память с конечным пространством. Это связано с тем, что размер ссылочных типов данных памяти, называемых указателями , доступен внутри языка. Однако другие языки программирования, такие как Паскаль , не имеют этой функции, что позволяет им в принципе быть полными по Тьюрингу.В принципе, это просто Тьюринг-полнота, поскольку при выделении памяти в языке программирования допускается сбой, а это означает, что язык программирования может быть Тьюринг-полным, если игнорировать неудачные выделения памяти, но скомпилированные программы, исполняемые на реальном компьютере, не могут.

Выбор c-машин, oracle o-машин

В начале своей статьи (1936) Тьюринг проводит различие между «автоматом» — его «движением… полностью определяемым конфигурацией» и «машиной выбора»:

...движение которого лишь частично определяется конфигурацией... Когда такая машина достигает одной из этих неоднозначных конфигураций, она не может продолжать работу до тех пор, пока внешний оператор не сделает какой-то произвольный выбор. Так было бы, если бы мы использовали машины для работы с аксиоматическими системами.

— Неразрешимое , с. 118

Тьюринг (1936) не дает дальнейших подробностей, за исключением сноски, в которой он описывает, как использовать машину для «нахождения всех доказуемых формул исчисления [Гильберта]», а не использовать машину выбора. Он «предполагает, что выбор всегда делается между двумя возможностями 0 и 1. Тогда каждое доказательство будет определяться последовательностью вариантов выбора i ₁ , i ₂ , ..., i _n (i ₁ = 0 или 1, i ₂ = 0 или 1, ..., i _n = 0 или 1), и, следовательно, число 2 ^н + я ₁ 2 ^n-1 + я ₂ 2 ^n-2 + ... +i _n полностью определяет доказательство. Автомат выполняет последовательно доказательство 1, доказательство 2, доказательство 3,...» (Сноска ‡, «Неразрешимое» , стр. 138).

Это действительно метод, с помощью которого детерминированная (т. е. а-) машина Тьюринга может использоваться для имитации действия недетерминированной машины Тьюринга ; Тьюринг решил этот вопрос в сноске и, похоже, исключил его из дальнейшего рассмотрения.

Машина -оракул или о-машина — это машина Тьюринга, которая приостанавливает свои вычисления в состоянии « о », в то время как для завершения вычислений она «ожидает решения» «оракула» — сущности, не указанной Тьюрингом, «кроме высказывания что он не может быть машиной» (Тьюринг (1939), «Неразрешимое» , стр. 166–168).

машины

Основная статья: Универсальная машина Тьюринга

Реализация машины Тьюринга

Как писал Тьюринг в «Неразрешимом» , стр. 128 (курсив добавлен):

Можно изобрести одну машину , которую можно использовать для вычисления любой вычислимой последовательности. Если к этой машине U снабдить ленту, в начале которой записана строка из пятерок, разделенных точками с запятой некоторой вычислительной машины M , то U вычислит ту же последовательность, что M. и

Сейчас это открытие считается само собой разумеющимся, но в то время (1936 г.) оно считалось поразительным. Модель вычислений, которую Тьюринг назвал своей «универсальной машиной» (для краткости « U »), некоторые считают (см. Дэвис (2000)) фундаментальным теоретическим прорывом, который привел к понятию компьютера с хранимой программой .

Статья Тьюринга... содержит, по сути, изобретение современного компьютера и некоторых сопутствующих ему методов программирования.

— Минский (1967), с. 104

С точки зрения вычислительной сложности , многоленточная универсальная машина Тьюринга должна быть медленнее всего лишь в логарифмическом коэффициенте по сравнению с машинами, которые она моделирует. Этот результат был получен в 1966 году Ф.К. Хенни и Р.Э. Стернсом . (Арора и Барак, 2009, теорема 1.9)

Сравнение с реальными машинами

Реализация машины Тьюринга с использованием Lego деталей

Часто верят что машины Тьюринга, в отличие от более простых автоматов, столь же мощны, как и настоящие машины, и способны выполнять любую операцию, которую может выполнить настоящая программа. В этом утверждении игнорируется то, что, поскольку реальная машина может иметь только конечное число конфигураций , она представляет собой не что иное, как конечный автомат , тогда как машина Тьюринга имеет неограниченный объем памяти, доступной для ее вычислений.

Есть несколько способов объяснить, почему машины Тьюринга являются полезными моделями реальных компьютеров:

• Все, что может вычислить настоящий компьютер, может вычислить и машина Тьюринга. Например: «Машина Тьюринга может моделировать любой тип подпрограммы, встречающейся в языках программирования, включая рекурсивные процедуры и любой из известных механизмов передачи параметров» (Хопкрофт и Ульман, стр. 157). Достаточно большой FSA также может моделировать любой реальный компьютер, независимо от ввода-вывода. Таким образом, утверждение об ограничениях машин Тьюринга будет применимо и к реальным компьютерам.
• Разница заключается только в способности машины Тьюринга манипулировать неограниченным количеством данных. Однако за ограниченное время машина Тьюринга (как и настоящая машина) может манипулировать только ограниченным количеством данных.
• Как и машина Тьюринга, объем памяти реальной машины может быть увеличен по мере необходимости путем приобретения большего количества дисков или других носителей данных.
• Описания реальных машинных программ с использованием более простых абстрактных моделей часто намного сложнее, чем описания с использованием машин Тьюринга. Например, машина Тьюринга, описывающая алгоритм, может иметь несколько сотен состояний, в то время как эквивалентный детерминированный конечный автомат (DFA) на данной реальной машине имеет квадриллионы. Это делает представление DFA невозможным для анализа.
• Машины Тьюринга описывают алгоритмы независимо от того, сколько памяти они используют. Существует предел памяти, которой обладает любая современная машина, но этот предел может произвольно увеличиваться со временем. Машины Тьюринга позволяют нам делать заявления об алгоритмах, которые (теоретически) будут действовать вечно, независимо от достижений в традиционной архитектуре вычислительных машин.
• Машины Тьюринга упрощают формулировку алгоритмов. Алгоритмы, работающие на абстрактных машинах, эквивалентных Тьюрингу, обычно более общие, чем их аналоги, работающие на реальных машинах, поскольку им доступны типы данных произвольной точности и им никогда не приходится сталкиваться с неожиданными условиями (включая, помимо прочего, нехватку памяти ). .

Еще одна реализация машины Тьюринга

Ограничения

Теория сложности вычислений

Дополнительная информация: Теория сложности вычислений.

Ограничением машин Тьюринга является то, что они плохо моделируют сильные стороны конкретного устройства. Например, современные компьютеры с хранимыми программами на самом деле являются экземплярами более конкретной формы абстрактной машины, известной как машина с произвольным доступом к хранимой программе или модель машины RASP. Подобно универсальной машине Тьюринга, RASP хранит свою «программу» в «памяти», внешней по отношению к «инструкциям» конечного автомата. В отличие от универсальной машины Тьюринга, RASP имеет бесконечное число различимых, пронумерованных, но неограниченных «регистров» — «ячейок» памяти, которые могут содержать любое целое число (ср. Элгот и Робинсон (1964), Хартманис (1971) и, в частности, Кук). -Речоу (1973); ссылки на произвольные машины . Конечный автомат RASP оснащен возможностью косвенной адресации (например, содержимое одного регистра может использоваться в качестве адреса для указания другого регистра); таким образом, «программа» RASP может обращаться к любому регистру в последовательности регистров. Результатом этого различия является то, что существуют вычислительные оптимизации, которые можно выполнить на основе индексов памяти, что невозможно в обычной машине Тьюринга; таким образом, когда машины Тьюринга используются в качестве основы для определения времени работы, «ложная нижняя граница» может быть доказана для времени работы определенных алгоритмов (из-за ложного упрощающего предположения о машине Тьюринга). Примером этого является двоичный поиск — алгоритм, который, как можно показать, работает быстрее при использовании модели вычислений RASP, а не модели машины Тьюринга.

Взаимодействие

На заре вычислительной техники использование компьютеров обычно ограничивалось пакетной обработкой , то есть неинтерактивными задачами, каждая из которых производила выходные данные из заданных входных данных. Теория вычислимости, изучающая вычислимость функций от входных данных к выходным и для которой были изобретены машины Тьюринга, отражает эту практику.

С 1970-х годов интерактивное использование компьютеров стало гораздо более распространенным. В принципе, это можно смоделировать, заставив внешнего агента читать с ленты и писать на нее одновременно с машиной Тьюринга, но это редко соответствует тому, как на самом деле происходит взаимодействие; поэтому при описании интерактивности таким альтернативам, как автоматы ввода-вывода обычно отдаются предпочтение .

Сравнение с арифметической моделью вычислений

Арифметическая модель вычислений отличается от модели Тьюринга в двух аспектах:

• В арифметической модели каждое действительное число требует одной ячейки памяти, тогда как в модели Тьюринга размер хранилища действительного числа зависит от количества битов, необходимых для его представления.
• В арифметической модели каждая базовая арифметическая операция над действительными числами (сложение, вычитание, умножение и деление) может быть выполнена за один шаг, тогда как в модели Тьюринга время выполнения каждой арифметической операции зависит от длины операндов.

Некоторые алгоритмы работают за полиномиальное время в одной модели, но не в другой. Например:

• Алгоритм Евклида работает за полиномиальное время в модели Тьюринга, но не в арифметической модели.
• Алгоритм, который считывает n чисел, а затем вычисляет $2^{2^{n}}$ путем повторного возведения в квадрат за полиномиальное время в арифметической модели, но не в модели Тьюринга. Это связано с тем, что количество битов, необходимых для представления результата, экспоненциально зависит от размера входных данных.

Однако если в арифметической модели алгоритм работает за полиномиальное время и, кроме того, двоичная длина всех задействованных чисел полиномиальна по отношению к длине входных данных, то в модели Тьюринга это всегда полиномиальное время. Говорят, что такой алгоритм работает за сильно полиномиальное время .

История

См. Также: Алгоритм и тезис Чёрча – Тьюринга.

: вычислительная

Робин Ганди (1919–1995) — ученик Алана Тьюринга (1912–1954) и его друг на всю жизнь — прослеживает происхождение понятия «вычислительная машина» до Чарльза Бэббиджа (около 1834 г.) и фактически предлагает «Тезис Бэббиджа». :

Что все разработки и операции анализа теперь могут быть выполнены с помощью машин .

- (курсив Бэббиджа, цитируется Ганди, стр. 54)

Анализ Ганди аналитической машины Бэббиджа описывает следующие пять операций (ср. стр. 52–53):

1. Арифметические функции +, −, ×, где − указывает на «правильное» вычитание: x − y = 0, если y ≥ x .
2. Любая последовательность операций является операцией.
3. Итерация операции (повторение операции P n раз).
4. Условная итерация (повторение n раз операции P при условии «успеха» теста T).
5. Условный переход (т.е. условный « goto »).

Ганди утверждает, что «функции, которые можно вычислить с помощью (1), (2) и (4), — это именно те функции, которые вычислимы по Тьюрингу ». (с. 53). Он цитирует другие предложения по поводу «универсальных вычислительных машин», в том числе предложения Перси Ладгейта (1909 г.), Леонардо Торреса Кеведо (1914 г.), Морис д'Окань (1922), Луи Куффиньяль (1933), Ванневар Буш (1936), Ховард Эйкен (1937). Однако:

… упор делается на программирование фиксированной повторяемой последовательности арифметических операций. Не признается фундаментальное значение условной итерации и условного переноса для общей теории счетных машин…

- Ганди П. 55

Entscheidungsproblem («проблема принятия решения»): десятый вопрос Гильберта

Что касается проблем Гильберта, поставленных знаменитым математиком Дэвидом Гильбертом в 1900 году, один из аспектов проблемы № 10 обсуждался почти 30 лет, прежде чем он был четко сформулирован. Исходное выражение Гильберта для номера 10 выглядит следующим образом:

10. Определение разрешимости диофантова уравнения . Дано диофантово уравнение с любым количеством неизвестных и с рациональными целыми коэффициентами: разработать процесс, согласно которому за конечное число операций можно определить, разрешимо ли уравнение в целых рациональных числах.Проблема Entscheidungsproblem [проблема решения для логики первого порядка ] решается, когда мы знаем процедуру, которая позволяет для любого данного логического выражения с помощью конечного числа операций определить его достоверность или выполнимость ... Проблему Entscheidungsproblem следует считать основной проблемой математической логики.

- цитируется с этим переводом и оригинальным немецким языком у Дершовица и Гуревича, 2008 г.

К 1922 году понятие « Entscheidungsproblem » немного развилось, и Х. Беманн заявил, что

... наиболее общая форма проблемы Entscheidungsproblem [является] следующей:

Требуется вполне определенное общеприменимое предписание, которое позволит за конечное число шагов решить истинность или ложность данного чисто логического утверждения...

- Ганди П. 57, цитируя Бемана

Беманн отмечает, что... общая проблема эквивалентна проблеме определения того, какие математические утверждения верны.

— там же.

Если бы кто-то мог решить проблему Entscheidungs, то у него была бы «процедура решения многих (или даже всех) математических задач».

— там же. , с. 92

К международному конгрессу математиков 1928 года Гильберт «сформулировал свои вопросы весьма точно. Во-первых, была ли математика полной … Во-вторых, была ли математика непротиворечивой … И, в-третьих, была ли математика разрешима ?» (Ходжес, стр. 91, Хокинг, стр. 1121). На первые два вопроса ответил в 1930 году Курт Гёдель на том самом собрании, где Гильберт произнес свою пенсионную речь (к большому огорчению Гильберта); третью — проблему Entscheidungs ​​— пришлось ждать до середины 1930-х годов.

Проблема заключалась в том, что для ответа сначала требовалось точное определение «определенного общеприменимого предписания», которое профессор Принстона Алонзо Чёрч назвал « эффективной вычислимостью », а в 1928 году такого определения не существовало. Но в течение следующих 6–7 лет Эмиль Пост разработал свое определение рабочего, перемещающегося из комнаты в комнату и записывающего и стирающего пометки в соответствии со списком инструкций (Пост, 1936), как это сделали Черч и два его ученика Стивен Клини и Дж. Б. Россер, используя метод Гёделя Лямбда-исчисление Чёрча и теория рекурсии (1934). Статья Чёрча (опубликованная 15 апреля 1936 г.) показала, что проблема Entscheidungs ​​действительно была «неразрешимой». и опередил Тьюринга почти на год (статья Тьюринга была представлена ​​28 мая 1936 г., опубликована в январе 1937 г.). Тем временем осенью 1936 года Эмиль Пост представил краткую статью, так что Тьюринг, по крайней мере, имел приоритет над Постом. Пока Чёрч рецензировал статью Тьюринга, у Тьюринга было время изучить статью Чёрча и добавить приложение, в котором он набросал доказательство того, что лямбда-исчисление Чёрча и его машины будут вычислять одни и те же функции.

Но то, что сделал Черч, было чем-то совершенно иным и в определенном смысле более слабым. ... конструкция Тьюринга была более прямой и обеспечивала аргументацию, основанную на основных принципах, устраняя пробел в демонстрации Чёрча.

- Ходжес с. 112

А Пост лишь предложил определение вычислимости и раскритиковал «определение» Чёрча, но ничего не доказал.

Машина Алана Тьюринга

Весной 1935 года Тьюринг, будучи молодым студентом магистратуры Королевского колледжа в Кембридже , принял на себя этот вызов; его вдохновили лекции логика МХА Ньюмана «и он узнал из них о работе Гёделя и проблеме Entscheidungs… Ньюман использовал слово «механический»… В своем некрологе Тьюрингу 1955 года Ньюман пишет:

На вопрос «что такое «механический» процесс?» Тьюринг дал характерный ответ: «Что-то, что может сделать машина» и приступил к весьма подходящей задаче анализа общего понятия вычислительной машины.

- Ганди, с. 74

Ганди утверждает, что:

Я предполагаю, но не знаю, что Тьюринг с самого начала своей работы имел целью доказать неразрешимость проблемы Entscheidungs. Он рассказал мне, что «основная идея» статьи пришла к нему, когда он лежал на лугах Гранчестера летом 1935 года. «Основной идеей» мог быть либо его анализ вычислений, либо его осознание того, что существует универсальная машина. и, следовательно, диагональный аргумент для доказательства неразрешимости.

— там же. , с. 76

Хотя Ганди считал, что приведенное выше заявление Ньюмана «вводит в заблуждение», это мнение разделяют не все. Тьюринг всю жизнь интересовался машинами: «Алан в детстве мечтал изобрести пишущие машинки; у [его матери] миссис Тьюринг была пишущая машинка; и он вполне мог начать с вопроса, что означало, называя пишущую машинку «механической»» (Ходжес, стр. 96). Работая над докторской диссертацией в Принстоне, Тьюринг построил множитель булевой логики (см. ниже). Его докторская диссертация под названием « Системы логики, основанные на ординалах », содержит следующее определение «вычислимой функции»:

Выше было сказано, что «функция эффективно вычислима, если ее значения могут быть найдены с помощью некоторого чисто механического процесса». Мы можем понимать это утверждение буквально, понимая под ним чисто механический процесс, который может быть осуществлен машиной. Можно дать математическое описание в некоторой нормальной форме конструкции этих машин. Развитие этих идей приводит к авторскому определению вычислимой функции и отождествлению вычислимости с эффективной вычислимостью. Нетрудно, хотя и несколько трудоемко, доказать, что эти три определения (третье — λ-исчисление) эквивалентны.

- Тьюринг (1939) в «Неразрешимом» , с. 160

Алан Тьюринг изобрел «а-машину» (автомат) в 1936 году. Тьюринг представил свою статью 31 мая 1936 года в Лондонское математическое общество для публикации (ср. Hodges 1983:112), но она была опубликована в начале 1937 года, а ее отпечатки были доступны в феврале 1937 года (ср. Hodges 1983:129). Это была работа Тьюринга. научный руководитель Алонзо Чёрч , который позже в обзоре ввёл термин «машина Тьюринга». С помощью этой модели Тьюринг смог ответить отрицательно на два вопроса:

• Существует ли машина, которая может определить, является ли любая произвольная машина на ее ленте «круговой» (например, зависает или не может продолжить выполнение своей вычислительной задачи)?
• Существует ли машина, которая может определить, напечатает ли когда-либо произвольная машина на своей ленте данный символ?

Таким образом, предоставив математическое описание очень простого устройства, способного выполнять произвольные вычисления, он смог доказать свойства вычислений в целом — и, в частности, невычислимость проблемы Entscheidungsproblem ( «проблемы принятия решений»).

Когда Тьюринг вернулся в Великобританию, он в конечном итоге стал совместно ответственным за взлом немецких секретных кодов, созданных шифровальными машинами под названием «Энигма»; он также принял участие в разработке ACE ( автоматической вычислительной машины ), «предложение [Тьюринга] ACE было фактически самодостаточным, и его корни лежали не в EDVAC [инициативе США], а в его собственной универсальной машине» ( Ходжес, стр. 318). До сих пор продолжаются споры относительно происхождения и природы того, что Клини (1952) назвал « Тезисом Тьюринга » . Но то, что Тьюринг действительно доказал с помощью своей модели вычислительной машины, показано в его статье « О вычислимых числах с применением к проблеме Entscheidungs » (1937):

[что] проблема Гильберта Entscheidungs ​​не может иметь решения ... Поэтому я предлагаю показать, что не может быть общего процесса определения того, доказуема ли данная формула U функционального исчисления K, то есть что не может быть машины, которая, снабженный любой U из этих формул, в конечном итоге скажет, доказуемо ли U.

— из статьи Тьюринга, перепечатанной в «Неразрешимом» , стр. 145

Пример Тьюринга (его второе доказательство): Если кто-то спросит об общей процедуре, которая скажет нам: «Выводит ли эта машина когда-нибудь 0», вопрос «неразрешим».

1937–1970: «цифровой компьютер», рождение «

В 1937 году, работая в Принстоне над докторской диссертацией, Тьюринг с нуля построил цифровой умножитель (булева логика), создав собственные электромеханические реле (Ходжес, стр. 138). «Задачей Алана было воплотить логическую конструкцию машины Тьюринга в сети переключателей с релейным управлением…» (Ходжес стр. 138). Хотя Тьюринг, возможно, поначалу был просто любопытен и экспериментировал, вполне серьезная работа в том же направлении велась в Германии ( Конрад Цузе (1938)), а также в Соединенных Штатах ( Говард Эйкен ) и Джордж Стибиц (1937); плоды их труда использовались армиями как стран Оси, так и союзников во Второй мировой войне (ср. Ходжес, стр. 298–299). В начале-середине 1950-х годов Хао Ван и Марвин Мински свели машину Тьюринга к более простой форме (предшественник машины Пост-Тьюринга Мартина Дэвиса ); одновременно европейские исследователи сводили новомодный электронный компьютер к компьютероподобному теоретическому объекту, эквивалентному тому, что теперь называлось «машиной Тьюринга». В конце 1950-х и начале 1960-х годов случайно параллельные разработки Мельзака и Ламбека (1961), Мински (1961) и Шепердсона и Стерджиса (1961) продвинули европейскую работу дальше и превратили машину Тьюринга в более дружественную, компьютерную систему. абстрактная модель, называемая счетчик машина ; Элгот и Робинсон (1964), Хартманис (1971), Кук и Рекхоу (1973) продвинули эту работу еще дальше, разработав модели регистровых машин и машин с произвольным доступом , но по сути все они представляют собой просто многоленточные машины Тьюринга с арифметическими инструкциями. набор.

вычислений

Сегодня счетчики, регистры и машины с произвольным доступом, а также их предшественник, машина Тьюринга, продолжают оставаться моделями, которые выбирают теоретики, исследующие вопросы теории вычислений . В частности, теория сложности вычислений использует машину Тьюринга:

В зависимости от объектов, которыми нравится манипулировать в вычислениях (числа, такие как неотрицательные целые числа или буквенно-цифровые строки), две модели заняли доминирующее положение в теории сложности машин:

автономная многоленточная машина Тьюринга ..., которая представляет собой стандартную модель для строко-ориентированных вычислений, имашина произвольного доступа (ОЗУ) , представленная Куком и Рекхоу..., которая моделирует идеализированный компьютер в стиле фон Неймана.

- из Эмде Боас 1990:4

Лишь в смежной области анализа алгоритмов эту роль берет на себя модель RAM.

- из Эмде Боас 1990:16

См. также

• Арифметическая иерархия
• Оценка Бекенштейна , показывающая невозможность создания машин Тьюринга с бесконечной лентой конечного размера и ограниченной энергии.
• БлуП и ФлуП
• Константа Чайтина или Омега (информатика) для получения информации, касающейся проблемы остановки.
• Китайская комната
• «Игра жизни» Конвея — клеточный автомат, полный по Тьюрингу.
• Цифровая бесконечность
• Новый разум императора
• Счетчик (по теоретической информатике)
• Генетикс
• Гёдель, Эшер, Бах: Вечная золотая коса , знаменитая книга, в которой, среди прочего, обсуждается тезис Чёрча-Тьюринга.
• Проблема с остановкой , для получения дополнительных ссылок
• Гарвардская архитектура
• Императивное программирование
• Муравей Лэнгтона и Турмиты , простые двумерные аналоги машины Тьюринга
• Список вещей, названных в честь Алана Тьюринга
• Модифицированная архитектура Гарварда
• Квантовая машина Тьюринга
• Клод Шеннон , еще один ведущий мыслитель теории информации.
• Примеры машины Тьюринга
• Переключатель Тьюринга
• Тарпит Тьюринга — любая вычислительная система или язык, который, несмотря на то, что он является полным по Тьюрингу, обычно считается бесполезным для практических вычислений.
• Неорганизованная машина , для самых ранних идей Тьюринга о нейронных сетях.
• Архитектура фон Неймана

Ссылки

и

• Б. Джек Коупленд изд. (2004), «Основные работы Тьюринга: основополагающие труды по вычислительной технике, логике, философии, искусственному интеллекту и искусственной жизни плюс секреты загадки», Clarendon Press (Oxford University Press), Оксфорд, Великобритания, ISBN   0-19-825079-7 . Содержит документы Тьюринга, а также проект письма Эмилю Посту с его критикой «конвенции Тьюринга» и « Поправки Дональда В. Дэвиса к универсальной вычислительной машине Тьюринга».
• Мартин Дэвис (редактор) (1965), Неразрешимое , Raven Press, Хьюлетт, Нью-Йорк.
• Эмиль Пост (1936), «Конечные комбинаторные процессы — формула 1», Журнал символической логики , 1, 103–105, 1936. Перепечатано в The Undecidable , стр. 289 и далее.
• Эмиль Пост (1947), «Рекурсивная неразрешимость проблемы Туэ», Журнал символической логики , том. 12, стр. 1–11. Перепечатано в «Неразрешимом» , стр. 293 и далее. В Приложении к этой статье Пост комментирует и исправляет статью Тьюринга 1936–1937 годов. В частности, см. сноску 11 с поправками к кодированию универсальной вычислительной машины и сноску 14 с комментариями к первому и второму доказательствам Тьюринга .
• Тьюринг, AM (1936). «О вычислимых числах с применением к проблеме Entscheidungs». Труды Лондонского математического общества . 2. 42 (опубликовано в 1937 г.): 230–265. дои : 10.1112/plms/s2-42.1.230 . S2CID   73712 . (и Тьюринг, AM (1938). «О вычислимых числах с применением к проблеме Entscheidungs: исправление». Труды Лондонского математического общества . 2. 43 (6) (опубликовано в 1937 г.): 544–6. дои : 10.1112/plms/s2-43.6.544 . ). Перепечатано во многих сборниках, например, в The Undecidable , стр. 115–154; доступен в сети во многих местах.
• Алан Тьюринг, 1948 год, «Интеллектуальная техника». Перепечатано в «Кибернетика: ключевые статьи». Эд. Ч.Р. Эванс и А.Д. Робертсон. Балтимор: University Park Press, 1968. с. 31. Перепечатано в Тьюринг, AM (1996). «Интеллектуальная техника, еретическая теория» . Философия Математика . 4 (3): 256–260. дои : 10.1093/филмат/4.3.256 .
• ФК Хенни и RE Stearns . Двухленточное моделирование многоленточных машин Тьюринга . JACM , 13(4):533–546, 1966.

Теория вычислимости

• Булос, Джордж; Ричард Джеффри (1999) [1989]. Вычислимость и логика (3-е изд.). Кембридж, Великобритания: Издательство Кембриджского университета. ISBN  0-521-20402-Х .
• Булос, Джордж; Джон Берджесс; Ричард Джеффри (2002). Вычислимость и логика (4-е изд.). Кембридж, Великобритания: Издательство Кембриджского университета. ISBN  0-521-00758-5 . Некоторые части были существенно переписаны Берджессом. Представление машин Тьюринга в контексте «счетных машин» Ламбека (см. Регистровая машина ) и рекурсивных функций с указанием их эквивалентности.
• Тейлор Л. Бут (1967), Теория последовательных машин и автоматов , John Wiley and Sons, Inc., Нью-Йорк. Инженерный текст для высшего образования; охватывает широкий круг тем, глава IX «Машины Тьюринга» включает некоторые теории рекурсии.
• Мартин Дэвис (1958). Вычислимость и неразрешимость . McGraw-Hill Book Company, Inc, Нью-Йорк. . На страницах 12–20 он приводит примеры таблиц из 5 кортежей для сложения, функции-преемника, вычитания (x ≥ y), правильного вычитания (0, если x < y), функции тождества и различных функций тождества, а также умножения.
• Дэвис, Мартин; Рон Сигал; Элейн Дж. Вейкер (1994). Вычислимость, сложность, языки и логика: основы теоретической информатики (2-е изд.). Сан-Диего: Academic Press, Harcourt, Brace & Company. ISBN  0-12-206382-1 .
• Хенни, Фредрик (1977). Введение в вычислимость . Аддисон-Уэсли, Ридинг, Массачусетс QA248.5H4 1977. . На страницах 90–103 Хенни обсуждает UTM с примерами и блок-схемами, но без реального «кода».
• Хопкрофт, Джон ; Ульман, Джеффри (1979). Введение в теорию автоматов, языки и вычисления (1-е изд.). Аддисон-Уэсли, Reading Mass. ISBN  0-201-02988-Х . В центре внимания вопросы машинной интерпретации «языков», NP-полноты и т. д.
• Хопкрофт, Джон Э.; Раджив Мотвани; Джеффри Д. Уллман (2001). Введение в теорию автоматов, языки и вычисления (2-е изд.). Чтение мессы: Аддисон – Уэсли. ISBN  0-201-44124-1 .
• Стивен Клини (1952), «Введение в метаматематику» , издательство North-Holland Publishing Company, Амстердам, Нидерланды, 10-е издание (с исправлениями 6-го переиздания 1971 г.). Текст для выпускников; большая часть главы XIII «Вычислимые функции» посвящена машинным доказательствам вычислимости рекурсивных функций и т. д.
• Кнут, Дональд Э. (1973). Том 1 / Фундаментальные алгоритмы: Искусство компьютерного программирования (2-е изд.). Ридинг, Массачусетс: Издательство Addison-Wesley. . О роли машин Тьюринга в развитии вычислений (как аппаратного, так и программного) см. 1.4.5 История и библиография, стр. 225 и далее, и 2.6 История и библиография, стр. 456 и далее.
• Зоар Манна , 1974, Математическая теория вычислений . Перепечатано, Дувр, 2003 г. ISBN   978-0-486-43238-0
• Марвин Мински , Вычисления: конечные и бесконечные машины , Prentice-Hall, Inc., Нью-Джерси, 1967. См. главу 8, раздел 8.2 «Неразрешимость проблемы остановки».
• Христос Пападимитриу (1993). Вычислительная сложность (1-е изд.). Эддисон Уэсли. ISBN  0-201-53082-1 . Глава 2: Машины Тьюринга, стр. 19–56.
• Хартли Роджерс-младший , Теория рекурсивных функций и эффективная вычислимость , MIT Press, Кембридж, Массачусетс, издание в мягкой обложке, 1987 г., оригинальное издание McGraw-Hill, 1967 г., ISBN   0-262-68052-1 (пбк.)
• Майкл Сипсер (1997). Введение в теорию вычислений . Издательство ПВС. ISBN  0-534-94728-Х . Глава 3: Тезис Чёрча – Тьюринга, стр. 125–149.
• Стоун, Гарольд С. (1972). Введение в компьютерную организацию и структуры данных (1-е изд.). Нью-Йорк: Книжная компания McGraw – Hill. ISBN  0-07-061726-0 .
• Питер ван Эмде Боас, 1990, Машинные модели и моделирование , стр. 3–66, в издании Яна ван Леувена , Справочник по теоретической информатике, Том A: Алгоритмы и сложность , MIT Press/Elsevier, [место?], ISBN   0-444-88071-2 (Том А). QA76.H279 1990.

Чёрча

• Нахум Дершовиц; Юрий Гуревич (сентябрь 2008 г.). «Естественная аксиоматизация вычислимости и доказательство тезиса Чёрча» (PDF) . Бюллетень символической логики . 14 (3) . Проверено 15 октября 2008 г.
• Роджер Пенроуз (1990) [1989]. Новый разум императора (2-е изд.). Издательство Оксфордского университета, Нью-Йорк. ISBN  0-19-851973-7 .

машины

• Рогожин, Юрий, 1998, « Универсальная машина Тьюринга с 22 состояниями и 2 символами », Румынский журнал информационных наук и технологий , 1 (3), 259–265, 1998. (обзоры известных результатов о небольших универсальных машинах Тьюринга)
• Стивен Вольфрам , 2002, Новый вид науки , Wolfram Media, ISBN   1-57955-008-8
• Брунфилд, Джефф, Студент получает приз по математике , Nature , 24 октября 2007 г.
• Джим Джайлс (2007), Простейший «универсальный компьютер» принес студенту 25 000 долларов , New Scientist, 24 октября 2007 г.
• Алекс Смит, Универсальность машины Тьюринга Вольфрама 2, 3 , заявка на премию Вольфрама 2, 3 за исследования машин Тьюринга.
• Воган Пратт, 2007 г., « Простые машины Тьюринга, универсальность, кодирование и т. д. », список адресов электронной почты FOM. 29 октября 2007 г.
• Мартин Дэвис, 2007 г., « Самая маленькая универсальная машина » и список адресов электронной почты FOM « Определение универсальной машины Тьюринга» . 26–27 октября 2007 г.
• Аласдер Уркарт, 2007 г. « Самая маленькая универсальная машина », список адресов электронной почты FOM. 26 октября 2007 г.
• Гектор Зенил (Wolfram Research), 2007 г., « Самая маленькая универсальная машина », список адресов электронной почты FOM. 29 октября 2007 г.
• Тодд Роуленд, 2007 г., « Путаница по поводу FOM », доска объявлений Wolfram Science, 30 октября 2007 г.
• Оливье и Марк РЕЙНО, 2014 г., Программируемый прототип для создания машин Тьюринга. Архивировано 14 января 2016 г. в лаборатории Wayback Machine «LIMOS» Университета Блеза Паскаля (Клермон-Ферран, Франция).

Другое

• Мартин Дэвис (2000). Логические машины: математики и происхождение компьютера (1-е изд.). WW Norton & Company, Нью-Йорк. ISBN  978-0-393-32229-3 .
• Робин Ганди , «Слияние идей в 1936 году», стр. 51–102 в книге Рольфа Херкена , см. ниже.
• Стивен Хокинг (редактор), 2005, «Бог создал целые числа: математические прорывы, которые изменили историю» , Running Press, Филадельфия, ISBN   978-0-7624-1922-7 . Включает статью Тьюринга 1936–1937 годов с краткими комментариями и биографией Тьюринга, написанную Хокингом.
• Рольф Херкен (1995). Универсальная машина Тьюринга — обзор полувека . Спрингер Верлаг. ISBN  978-3-211-82637-9 .
• Эндрю Ходжес , Алан Тьюринг: Загадка , Саймон и Шустер , Нью-Йорк. См. Глава «Дух истины» содержит историю, ведущую к его доказательству, и обсуждение его.
• Иварс Петерсон (1988). Математический турист: снимки современной математики (1-е изд.). WH Freeman and Company, Нью-Йорк. ISBN  978-0-7167-2064-5 .
• Роджер Пенроуз , Новый разум императора: о компьютерах, разуме и законах физики , Oxford University Press , Оксфорд и Нью-Йорк, 1989 (исправления 1990 года), ISBN   0-19-851973-7 .
• Пол Стратерн (1997). Тьюринг и компьютер — большая идея . Anchor Books/Doubleday. ISBN  978-0-385-49243-0 .
• Хао Ван , «Вариант теории вычислительных машин Тьюринга», Журнал Ассоциации вычислительной техники (JACM) 4, 63–92 (1957).
• Чарльз Петцольд , Аннотированный Тьюринг , John Wiley & Sons, Inc., ISBN   0-470-22905-5
• Арора, Санджив; Барак, Боаз, «Теория сложности: современный подход» , Cambridge University Press, 2009 г., ISBN   978-0-521-42426-4 , раздел 1.4, «Машины как строки и универсальная машина Тьюринга» и 1.7, «Доказательство теоремы 1.9».
• Канторовиц, Исайя Пинхас (1 декабря 2005 г.). «Заметка о вычислимости систем, управляемых правилами, на машине Тьюринга». Новости СИГАКТ . 36 (4): 109–110. дои : 10.1145/1107523.1107525 . S2CID   31117713 .
• Кирнер, Раймунд; Циммерманн, Вольф; Рихтер, Дирк: «О результатах неразрешимости реальных языков программирования» , на 15-м коллоквиуме «Языки программирования и основы программирования» (KPS'09), Мария Таферл, Австрия, октябрь. 2009.

Внешние ссылки

• «Машина Тьюринга» , Математическая энциклопедия , EMS Press , 2001 [1994]
• Машина Тьюринга - Стэнфордская энциклопедия философии
• Причинно-следственные сети машины Тьюринга Энрике Зелени в рамках демонстрационного проекта Wolfram .
• Машины Тьюринга в Керли