Альфа-бета-обрезка

Альфа-бета-обрезка
Сорт	Алгоритм поиска
Худшая производительность
Лучшая производительность

Альфа-бета-обрезка — это алгоритм поиска , который стремится уменьшить количество узлов, которые оцениваются минимаксным алгоритмом в его дереве поиска . Это алгоритм состязательного поиска, обычно используемый для машинной игры в комбинаторные игры для двух игроков ( Крестики-нолики , Шахматы , Connect 4 и т. д.). Он прекращает оценивать ход, когда найдена хотя бы одна возможность, доказывающая, что этот ход хуже, чем ранее рассмотренный ход. Такие шаги не нуждаются в дальнейшей оценке. При применении к стандартному минимаксному дереву он возвращает тот же ход, что и минимакс, но отсекает ветви, которые не могут повлиять на окончательное решение. ^[1]

История

Джон Маккарти во время Дартмутского семинара встретил Алекса Бернштейна из IBM , который писал шахматную программу. Маккарти изобрел альфа-бета-поиск и рекомендовал его ему, но Бернштейна это «не убедило». ^[2]

Аллен Ньюэлл и Герберт А. Саймон, которые использовали то, что Джон Маккарти называет «приближением». ^[3] в 1958 году написал, что альфа-бета «похоже, изобреталась заново несколько раз». ^[4] У Артура Сэмюэля была ранняя версия симуляции шашек. Ричардс, Тимоти Харт, Майкл Левин и/или Дэниел Эдвардс также независимо изобрели альфа-бету в Соединенных Штатах . ^[5] Маккарти предложил аналогичные идеи во время семинара в Дартмуте в 1956 году и предложил их группе своих студентов, включая Алана Котока из Массачусетского технологического института в 1961 году. ^[6] Александр Брудно независимо разработал альфа-бета-алгоритм и опубликовал свои результаты в 1963 году. ^[7] Дональд Кнут и Рональд В. Мур усовершенствовали алгоритм в 1975 году. ^[8]^[9] Judea Pearl доказала свою оптимальность с точки зрения ожидаемого времени работы для деревьев со случайно назначенными значениями листьев в двух статьях. ^[10]^[11] Оптимальность рандомизированной версии альфа-бета была показана Майклом Саксом и Ави Вигдерсоном в 1986 году. ^[12]

Основная идея

Дерево игры для двух игроков может представлять множество игр с нулевой суммой , таких как шахматы, шашки и реверси. Каждый узел дерева представляет возможную ситуацию в игре. Каждому конечному узлу (исходу) ветки присваивается числовой балл, определяющий ценность результата для игрока при следующем ходе. ^[13]

Алгоритм поддерживает два значения: альфа и бета, которые соответственно представляют собой минимальное количество очков, которое гарантировано максимизирующему игроку, и максимальное количество очков, которое гарантировано минимизирующему игроку. Первоначально альфа — это отрицательная бесконечность, а бета — положительная бесконечность, т. е. оба игрока начинают с наихудшим возможным счетом. Всякий раз, когда максимальное количество очков, которое гарантировано минимизирующему игроку (т. е. «бета-игроку»), становится меньше минимального количества очков, которое гарантировано максимизирующему игроку (т. е. «альфа-игроку») (т. е. бета < альфа), максимизирующий игрок игроку не нужно рассматривать дальнейших потомков этого узла, поскольку они никогда не будут достигнуты в реальной игре.

Чтобы проиллюстрировать это примером из реальной жизни, предположим, что кто-то играет в шахматы, и настала его очередь. Ход «А» улучшит положение игрока. Игрок продолжает искать ходы, чтобы не упустить лучший ход. Ход «Б» также является хорошим ходом, но затем игрок понимает, что он позволит противнику поставить мат за два хода. Таким образом, другие результаты хода Б больше не нужно учитывать, поскольку противник может добиться победы. Максимальный счет, который противник может получить после хода «Б», равен отрицательной бесконечности: проигрыш для игрока. Это меньше минимальной позиции, которая была найдена ранее; Ход «А» не приводит к вынужденному проигрышу в два хода.

Улучшения по сравнению с наивным минимаксом

Преимущество альфа-бета-отсечения заключается в том, что можно исключить ветви дерева поиска. ^[13] Таким образом, время поиска может быть ограничено «более перспективным» поддеревом и за то же время может быть выполнен более глубокий поиск. Как и его предшественник, он принадлежит к ветвей и границ классу алгоритмов . Оптимизация уменьшает эффективную глубину до чуть более половины от простого минимакса, если узлы оцениваются в оптимальном или близком к оптимальному порядке (лучший выбор для стороны на ходу, упорядоченной первой в каждом узле).

При (среднем или постоянном) ветвления коэффициенте b и глубине поиска d plies максимальное количество оцениваемых позиций конечных узлов (когда порядок перемещения пессимален ) равно O ( b ^д) – то же, что и простой минимаксный поиск. Если порядок ходов для поиска оптимален (то есть лучшие ходы всегда ищутся первыми), количество оцениваемых позиций конечных узлов составляет около O ( b ×1× b ×1×...× b ) для нечетной глубины и O ( b ×1× b ×1×...×1) для четной глубины, или $O(b^{d/2})=O({\sqrt {b^{d}}})$ . В последнем случае, когда слой поиска четный, эффективный коэффициент ветвления уменьшается до квадратного корня или, что то же самое, поиск может идти в два раза глубже при том же объеме вычислений. ^[14] Объяснение b ×1× b ×1×... заключается в том, что все ходы первого игрока должны быть изучены, чтобы найти лучший, но для каждого из них нужен только лучший ход второго игрока, чтобы опровергнуть все, кроме первого (и лучший) ход первого игрока — альфа-бета гарантирует, что другие ходы второго игрока учитываться не будут. Когда узлы рассматриваются в случайном порядке (т. е. алгоритм рандомизируется), асимптотическиожидаемое количество узлов, оцениваемых в однородных деревьях с двоичными значениями листьев, равно $\Theta (((b-1+{\sqrt {b^{2}+14b+1}})/4)^{d})$ . ^[12]Для одних и тех же деревьев, когда значения присваиваются значениям листьев независимо друг от друга и, скажем, ноль и единица одинаково вероятны, ожидаемое количество оцениваемых узлов равно $\Theta ((b/2)^{d})$ , что намного меньше работы, выполняемой рандомизированным алгоритмом, упомянутым выше, и снова является оптимальным для таких случайных деревьев. ^[10] Когда конечные значения выбираются независимо друг от друга, но из $[0,1]$ интервал равномерно случайным образом, ожидаемое количество оцениваемых узлов увеличивается до $\Theta (b^{d/log(d)})$ в $d\to \infty$ предел, ^[11] что снова оптимально для таких случайных деревьев. Обратите внимание, что фактическая работа для «малых» значений $d$ лучше аппроксимировать с помощью $0.925d^{0.747}$ . ^[11]^[10]

Шахматная программа, которая ищет четыре слоя со средним числом 36 ветвей на узел, оценивает более миллиона конечных узлов. Оптимальная альфа-бета-обрезка позволит устранить все терминальные узлы, за исключением примерно 2000, что составляет сокращение на 99,8%. ^[13]

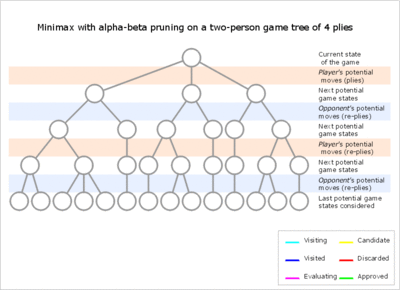
Анимированный педагогический пример, который пытается быть дружественным к человеку, заменяя пустоты исходными бесконечными (или произвольно большими) значениями и избегая использования упрощений кодирования negamax .

Обычно во время альфа-бета поддеревья временно доминируют либо из-за преимущества первого игрока (когда многие ходы первого игрока хороши, и на каждой глубине поиска первый ход, проверенный первым игроком, является адекватным, но все ответы второго игрока необходимы для попытаться найти опровержение), или наоборот. Это преимущество может многократно переходить на другую сторону во время поиска, если порядок ходов неверен, что каждый раз приводит к неэффективности. Поскольку количество искомых позиций экспоненциально уменьшается с каждым приближением к текущей позиции, стоит потратить значительные усилия на сортировку ранних ходов. Улучшенная сортировка на любой глубине экспоненциально уменьшит общее количество искомых позиций, но сортировка всех позиций на глубинах рядом с корневым узлом обходится относительно дешево, поскольку их очень мало. На практике порядок перемещения часто определяется результатами более ранних, более мелких поисков, например, посредством итеративного углубления .

Кроме того, этот алгоритм можно тривиально модифицировать, чтобы он возвращал всю основную вариацию не только оценку, но и . Некоторые более агрессивные алгоритмы, такие как MTD(f), с трудом допускают такую модификацию.

Псевдокод

Псевдокод для минимакса с ограниченной глубиной и альфа-бета-обрезкой выглядит следующим образом: ^[15]

Реализации альфа-бета-обрезки часто можно охарактеризовать по тому, являются ли они «отказоустойчивыми» или «отказоустойчивыми». При отказоустойчивом альфа-бета функция алфавита может возвращать значения (v), которые превышают (v < α или v > β) границы α и β, установленные аргументами вызова функции. Для сравнения, отказоустойчивая альфа-бета ограничивает возвращаемое значение функции инклюзивным диапазоном α и β. Основное различие между отказоустойчивой и отказоустойчивой реализациями заключается в том, обновляются ли α и β до или после проверки отсечки. Если они обновляются до проверки, то они могут превысить начальные границы и алгоритм будет отказоустойчивым.

Следующий псевдокод иллюстрирует отказоустойчивый вариант. ^[15]

функция  алфавита (узел, глубина, α, β, maximizingPlayer)  —      если  глубина == 0  или  узел является терминалом  , то          возвращает  эвристическое значение узла     если  максимизировать Player  , то         значение := −∞         для каждого  дочернего элемента узла  выполните             значение := max(значение, алфавита(ребенок, глубина - 1, α, β, ЛОЖЬ))             если  значение > β  , то                  разрыв   (*отсечение β *)             α := max(α, значение)         возвращаемое  значение     еще         значение := +∞         для каждого  дочернего элемента узла  выполните             значение := min(значение, алфавита(ребенок, глубина - 1, α, β, ИСТИНА))             если  значение < α  , то                  разрыв   (* α отсечка *)             β := мин(β, значение)         возвращаемое  значение

(*Первоначальный звонок*) алфавита (происхождение, глубина, −  ∞  , +  ∞  , ИСТИНА)

Следующий псевдокод иллюстрирует отказоустойчивую альфа-бету.

функция  алфавита (узел, глубина, α, β, maximizingPlayer)  —      если  глубина == 0  или  узел является терминалом  , то          возвращает  эвристическое значение узла     если  максимизировать Player  , то         значение := −∞         для каждого  дочернего элемента узла  выполните             значение := max(значение, алфавита(ребенок, глубина - 1, α, β, ЛОЖЬ))            α := max(α, значение)             если  значение ≥ β  , то                  разрыв   (* отсечение β *)          возвращаемое  значение     еще         значение := +∞         для каждого  дочернего элемента узла  выполните             значение := min(значение, алфавита(ребенок, глубина - 1, α, β, ИСТИНА))            β := мин(β, значение)             если  значение ≤ α  , то                  разрыв   (* отсечение α *)          возвращаемое  значение

(*Первоначальный звонок*) алфавита (происхождение, глубина, −  ∞  , +  ∞  , ИСТИНА)

Эвристические улучшения

Дальнейшего улучшения можно добиться, не жертвуя точностью, используя эвристику упорядочения для поиска в более ранних частях дерева, которые могут привести к сокращению альфа-бета. Например, в шахматах ходы, захватывающие фигуры, могут быть проверены перед ходами, которые этого не делают, а ходы, получившие высокие оценки в предыдущих проходах анализа дерева игры, могут оцениваться раньше других. Другая распространенная и очень дешевая эвристика — это эвристика-убийца , где в первую очередь всегда проверяется последний ход, вызвавший бета-обрезание на том же уровне дерева при поиске по дереву. Эту идею также можно обобщить в виде набора таблиц опровержений .

Альфа-бета-поиск можно сделать еще быстрее, если рассматривать только узкое окно поиска (обычно определяемое путем догадок, основанных на опыте). Это известно как окно стремления . В крайнем случае поиск осуществляется при равенстве альфа и бета; метод, известный как поиск с нулевым окном , поиск с нулевым окном или поисковый поиск . Это особенно полезно для поиска выигрышей/проигрышей ближе к концу игры, когда дополнительная глубина, полученная за счет узкого окна, и простая функция оценки выигрыша/проигрыша могут привести к убедительному результату. Если аспирационный поиск не удался, можно легко определить, был ли он неудачным ( верхний край окна был слишком низким) или низким (нижний край окна был слишком высоким). Это дает информацию о том, какие значения окна могут быть полезны при повторном поиске позиции.

Со временем были предложены и другие улучшения, и действительно, идея Джона Фишберна Falphabeta (мягкая альфа-бета) является почти универсальной и уже включена выше в несколько измененной форме. Фишберн также предложил комбинацию эвристики-убийцы и поиска с нулевым окном под названием Lalphabeta («последний ход с альфа-бета-поиском с минимальным окном»).

Другие алгоритмы

Поскольку минимаксный алгоритм и его варианты по своей сути ориентированы в глубину , такая стратегия, как итеративное углубление , обычно используется в сочетании с альфа-бета, чтобы можно было вернуть достаточно хороший ход, даже если алгоритм будет прерван до завершения его выполнения. Еще одним преимуществом использования итеративного углубления является то, что поиск на меньшей глубине дает подсказки по порядку ходов, а также мелкие альфа- и бета-оценки, которые могут помочь создать отсечки для поиска на большей глубине гораздо раньше, чем это было бы возможно в противном случае.

такие алгоритмы, как SSS* С другой стороны, , используют стратегию «сначала лучшее» . Потенциально это может сделать их более эффективными по времени, но, как правило, за счет высокой эффективности использования пространства. ^[16]

См. также

Ссылки

^ Рассел и Норвиг 2021 , с. 152-161.
^ Маккарти, Джон (30 октября 2006 г.). «Дартмутский семинар – как планировалось и как это произошло» . www-formal.stanford.edu . Проверено 29 октября 2023 г.
^ Маккарти, Джон (27 ноября 2006 г.). «ИИ на человеческом уровне сложнее, чем казалось в 1955 году» . Стэнфордский университет . Проверено 20 декабря 2006 г.
^ Ньюэлл, Аллен; Саймон, Герберт А. (1 марта 1976 г.). «Информатика как эмпирическое исследование: символы и поиск» . Коммуникации АКМ . 19 (3): 113–126. дои : 10.1145/360018.360022 .
^ Эдвардс, диджей; Харт, Т.П. (4 декабря 1961 г.). Альфа-бета-эвристика (Технический отчет). Массачусетский технологический институт . hdl : 1721.1/6098 . АИМ-030.
^ Коток, Алан (2004) [1962]. «Шахматная программа» . Проект искусственного интеллекта . РЛЭ и Вычислительный центр Массачусетского технологического института. Памятка 41 . Проверено 1 июля 2006 г.
^ Марсленд, штат Калифорния (май 1987 г.). «Компьютерные шахматные методы» (PDF) . В Шапиро, С. (ред.). Энциклопедия искусственного интеллекта . Уайли. стр. 159–171. ISBN 978-0-471-62974-0 . Архивировано из оригинала (PDF) 30 октября 2008 г.
^ Кнут, Дональд Э.; Мур, Рональд В. (1975). «Анализ альфа-бета-обрезки». Искусственный интеллект . 6 (4): 293–326. дои : 10.1016/0004-3702(75)90019-3 . S2CID 7894372 .
^ Абрамсон, Брюс (1 июня 1989 г.). «Стратегии управления для игр двух игроков». Обзоры вычислительной техники ACM . 21 (2): 137–161. дои : 10.1145/66443.66444 . S2CID 11526154 .
^ Jump up to: ^а ^б ^с Перл, Иудея (1980). «Асимптотические свойства минимаксных деревьев и процедуры поиска игр». Искусственный интеллект . 14 (2): 113–138. дои : 10.1016/0004-3702(80)90037-5 .
^ Jump up to: ^а ^б ^с Перл, Иудея (1982). «Решение фактора ветвления алгоритма обрезки альфа-бета и его оптимальность» . Коммуникации АКМ . 25 (8): 559–64. дои : 10.1145/358589.358616 . S2CID 8296219 .
^ Jump up to: ^а ^б Сакс, М.; Вигдерсон, А. (1986). «Вероятностные логические деревья решений и сложность оценки игровых деревьев». 27-й ежегодный симпозиум по основам информатики . стр. 29–38. дои : 10.1109/SFCS.1986.44 . ISBN 0-8186-0740-8 . S2CID 6130392 .
^ Jump up to: ^а ^б ^с Леви, Дэвид (январь 1986 г.). «Альфа-Бета-суп» . MacUser . стр. 98–102 . Проверено 19 октября 2021 г.
^ Рассел и Норвиг 2021 , с. 155.
^ Jump up to: ^а ^б Рассел и Норвиг 2021 , с. 154.
^ Перл, Иудея ; Корф, Ричард (1987), «Методы поиска», Annual Review of Computer Science , 2 : 451–467, doi : 10.1146/annurev.cs.02.060187.002315 . Как и его аналог A* для однопользовательских игр, SSS* оптимален по среднему количеству исследуемых узлов; но его превосходная мощность обрезки более чем компенсируется значительным объемом необходимого места для хранения и ведения бухгалтерского учета.

Библиография

Рассел, Стюарт Дж .; Норвиг, Питер. (2021). Искусственный интеллект: современный подход (4-е изд.). Хобокен: Пирсон. ISBN 9780134610993 . LCCN 20190474 .
Хейнеман, Джордж Т.; Поллис, Гэри; Селков, Стэнли (2008). «7. Поиск пути в ИИ». Коротко об алгоритмах . Орейли Медиа . стр. 217–223. ISBN 978-0-596-51624-6 .
Перл, Иудея (1984). Эвристика: стратегии интеллектуального поиска для решения компьютерных задач . Аддисон-Уэсли. ISBN 978-0-201-05594-8 . OCLC 1035596197 .
Фишберн, Джон П. (1984). «Приложение A: Некоторые оптимизации поиска α-β». Анализ ускорения распределенных алгоритмов (переработка кандидатской диссертации 1981 г.) . UMI Research Press. стр. 107–111. ISBN 0-8357-1527-2 .

[FOOTNOTERussellNorvig2021152-161-1] Рассел и Норвиг 2021 , с. 152-161.

[2] Маккарти, Джон (30 октября 2006 г.). «Дартмутский семинар – как планировалось и как это произошло» . www-formal.stanford.edu . Проверено 29 октября 2023 г.

[JMC-3] Маккарти, Джон (27 ноября 2006 г.). «ИИ на человеческом уровне сложнее, чем казалось в 1955 году» . Стэнфордский университет . Проверено 20 декабря 2006 г.

[NS-4] Ньюэлл, Аллен; Саймон, Герберт А. (1 марта 1976 г.). «Информатика как эмпирическое исследование: символы и поиск» . Коммуникации АКМ . 19 (3): 113–126. дои : 10.1145/360018.360022 .

[AIM30-5] Эдвардс, диджей; Харт, Т.П. (4 декабря 1961 г.). Альфа-бета-эвристика (Технический отчет). Массачусетский технологический институт . hdl : 1721.1/6098 . АИМ-030.

[AIM41-6] Коток, Алан (2004) [1962]. «Шахматная программа» . Проект искусственного интеллекта . РЛЭ и Вычислительный центр Массачусетского технологического института. Памятка 41 . Проверено 1 июля 2006 г.

[Marsland-7] Марсленд, штат Калифорния (май 1987 г.). «Компьютерные шахматные методы» (PDF) . В Шапиро, С. (ред.). Энциклопедия искусственного интеллекта . Уайли. стр. 159–171. ISBN 978-0-471-62974-0 . Архивировано из оригинала (PDF) 30 октября 2008 г.

[Knuth-Moore-8] Кнут, Дональд Э.; Мур, Рональд В. (1975). «Анализ альфа-бета-обрезки». Искусственный интеллект . 6 (4): 293–326. дои : 10.1016/0004-3702(75)90019-3 . S2CID 7894372 .

[Abramson-9] Абрамсон, Брюс (1 июня 1989 г.). «Стратегии управления для игр двух игроков». Обзоры вычислительной техники ACM . 21 (2): 137–161. дои : 10.1145/66443.66444 . S2CID 11526154 .

[Pearl1980-10] Jump up to: ^а ^б ^с Перл, Иудея (1980). «Асимптотические свойства минимаксных деревьев и процедуры поиска игр». Искусственный интеллект . 14 (2): 113–138. дои : 10.1016/0004-3702(80)90037-5 .

[Pearl1982-11] Jump up to: ^а ^б ^с Перл, Иудея (1982). «Решение фактора ветвления алгоритма обрезки альфа-бета и его оптимальность» . Коммуникации АКМ . 25 (8): 559–64. дои : 10.1145/358589.358616 . S2CID 8296219 .

[SaksWigderson-12] Jump up to: ^а ^б Сакс, М.; Вигдерсон, А. (1986). «Вероятностные логические деревья решений и сложность оценки игровых деревьев». 27-й ежегодный симпозиум по основам информатики . стр. 29–38. дои : 10.1109/SFCS.1986.44 . ISBN 0-8186-0740-8 . S2CID 6130392 .

[levy198601-13] Jump up to: ^а ^б ^с Леви, Дэвид (январь 1986 г.). «Альфа-Бета-суп» . MacUser . стр. 98–102 . Проверено 19 октября 2021 г.

[FOOTNOTERussellNorvig2021155-14] Рассел и Норвиг 2021 , с. 155.

[FOOTNOTERussellNorvig2021154-15] Jump up to: ^а ^б Рассел и Норвиг 2021 , с. 154.

[16] Перл, Иудея ; Корф, Ричард (1987), «Методы поиска», Annual Review of Computer Science , 2 : 451–467, doi : 10.1146/annurev.cs.02.060187.002315 . Как и его аналог A* для однопользовательских игр, SSS* оптимален по среднему количеству исследуемых узлов; но его превосходная мощность обрезки более чем компенсируется значительным объемом необходимого места для хранения и ведения бухгалтерского учета.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

v т и графов и деревьев Алгоритмы обхода
Search	α–β pruning A* IDA* LPA* SMA* Best-first search Beam search Bidirectional search Breadth-first search Lexicographic Parallel B* Depth-first search Iterative deepening D* Fringe search Jump point search Monte Carlo tree search SSS*
Shortest path	Bellman–Ford Dijkstra's Floyd–Warshall Johnson's Shortest path faster Yen's
Minimum spanning tree	Borůvka's Kruskal's Prim's Reverse-delete
List of graph search algorithms

v т и Темы теории игр
Definitions	Congestion game Cooperative game Determinacy Escalation of commitment Extensive-form game First-player and second-player win Game complexity Graphical game Hierarchy of beliefs Information set Normal-form game Preference Sequential game Simultaneous game Simultaneous action selection Solved game Succinct game Mechanism design
Equilibrium concepts	Bayes correlated equilibrium Bayesian Nash equilibrium Berge equilibrium Core Correlated equilibrium Coalition-proof Nash equilibrium Epsilon-equilibrium Evolutionarily stable strategy Gibbs equilibrium Mertens-stable equilibrium Markov perfect equilibrium Nash equilibrium Pareto efficiency Perfect Bayesian equilibrium Proper equilibrium Quantal response equilibrium Quasi-perfect equilibrium Risk dominance Satisfaction equilibrium Self-confirming equilibrium Sequential equilibrium Shapley value Strong Nash equilibrium Subgame perfection Trembling hand equilibrium
Strategies	Appeasement Backward induction Bid shading Collusion Cheap talk De-escalation Deterrence Escalation Forward induction Grim trigger Markov strategy Dominant strategies Pure strategy Mixed strategy Strategy-stealing argument Tit for tat
Classes of games	Auction Bargaining problem Global game Intransitive game Mean-field game n-player game Perfect information Large Poisson game Potential game Repeated game Screening game Signaling game Strictly determined game Stochastic game Symmetric game Zero-sum game
Games	Go Chess Infinite chess Checkers All-pay auction Prisoner's dilemma Gift-exchange game Optional prisoner's dilemma Traveler's dilemma Coordination game Chicken Centipede game Lewis signaling game Volunteer's dilemma Dollar auction Battle of the sexes Stag hunt Matching pennies Ultimatum game Electronic mail game Rock paper scissors Pirate game Dictator game Public goods game Blotto game War of attrition El Farol Bar problem Fair division Fair cake-cutting Bertrand competition Cournot competition Stackelberg competition Deadlock Diner's dilemma Guess 2/3 of the average Kuhn poker Nash bargaining game Induction puzzles Trust game Princess and monster game Rendezvous problem
Theorems	Aumann's agreement theorem Folk theorem Minimax theorem Nash's theorem Negamax theorem Purification theorem Revelation principle Sprague–Grundy theorem Zermelo's theorem
Key figures	Albert W. Tucker Amos Tversky Antoine Augustin Cournot Ariel Rubinstein Claude Shannon Daniel Kahneman David K. Levine David M. Kreps Donald B. Gillies Drew Fudenberg Eric Maskin Harold W. Kuhn Herbert Simon Hervé Moulin John Conway Jean Tirole Jean-François Mertens Jennifer Tour Chayes John Harsanyi John Maynard Smith John Nash John von Neumann Kenneth Arrow Kenneth Binmore Leonid Hurwicz Lloyd Shapley Melvin Dresher Merrill M. Flood Olga Bondareva Oskar Morgenstern Paul Milgrom Peyton Young Reinhard Selten Robert Axelrod Robert Aumann Robert B. Wilson Roger Myerson Samuel Bowles Suzanne Scotchmer Thomas Schelling William Vickrey
Miscellaneous	Alpha–beta pruning Bounded rationality Combinatorial game theory Confrontation analysis Coopetition Evolutionary game theory Glossary of game theory List of game theorists List of games in game theory No-win situation Topological game Tragedy of the commons