Свободная энергия Гиббса

В термодинамике ( свободная энергия Гиббса или энергия Гиббса в качестве рекомендуемого названия; символ $G$ ) — это термодинамический потенциал , который можно использовать для расчета максимального количества работы , отличной от работы давление-объем , которую может выполнить термодинамически замкнутая система при постоянных температуре и давлении . Это также обеспечивает необходимое условие для таких процессов, как химические реакции , которые могут происходить в этих условиях. Свободная энергия Гиббса выражается как $G(p,T)=U+pV-TS=H-TS$ Где:

${\textstyle U}$ это внутренняя энергия системы
${\textstyle H}$ это энтальпия системы
${\textstyle S}$ это энтропия системы
${\textstyle T}$ это температура системы
${\textstyle V}$ это объем системы
${\textstyle p}$ - давление системы (которое должно быть равно давлению окружающей среды для механического равновесия).

Изменение свободной энергии Гиббса ( $\Delta G=\Delta H-T\Delta S$ , измеряется в джоулях в системе СИ ) — это максимальное количество работы необъемного расширения, которую можно извлечь из закрытой системы (той, которая может обмениваться теплом и работать с окружающей средой, но не с веществом) при фиксированной температуре и давлении. Этот максимум может быть достигнут только в ходе вполне обратимого процесса . Когда в этих условиях система обратимо переходит из начального состояния в конечное, уменьшение свободной энергии Гиббса равно работе, совершаемой системой с окружающей средой, за вычетом работы сил давления . ^[1]

Энергия Гиббса — это термодинамический потенциал, который минимизируется, когда система достигает химического равновесия при постоянном давлении и температуре, когда она не приводится в действие приложенным электролитическим напряжением. Тогда ее производная по координате реакции системы обращается в нуль в точке равновесия. Таким образом, сокращение $G$ необходимо, чтобы реакция протекала самопроизвольно в этих условиях .

Концепция свободной энергии Гиббса, первоначально называвшаяся доступной энергией , была разработана в 1870-х годах американским учёным Джозайей Уиллардом Гиббсом . В 1873 году Гиббс описал эту «доступную энергию» как ^[2]^: 400

наибольшая сумма механической работы, которую можно получить от данного количества определенного вещества в данном исходном состоянии, не увеличивая его общий объем и не допуская перехода тепла к внешним телам или от них, за исключением случаев, когда процессы завершаются остались в исходном состоянии.

Начальное состояние тела, по мнению Гиббса, должно быть таким, что «тело можно заставить перейти из него в состояния рассеянной энергии путем обратимых процессов ». В своем выдающемся труде 1876 года «О равновесии гетерогенных веществ» , графическом анализе многофазных химических систем, он полностью изложил свои мысли о безхимической энергии.

Если все реагенты и продукты находятся в своих термодинамических стандартных состояниях , то определяющее уравнение записывается как $\Delta G^{\circ }=\Delta H^{\circ }-T\Delta S^{\circ }$ , где $H$ это энтальпия , $T$ – абсолютная температура , а $S$ это энтропия .

Обзор

Реакция C _(s)^алмаз → С _(с)^графит имеет отрицательное изменение свободной энергии Гиббса и поэтому термодинамически выгоден при 25 ° C и 1 атм. Однако реакция слишком медленная, чтобы ее можно было наблюдать из-за очень высокой энергии активации . Является ли реакция термодинамически выгодной, не определяет ее скорость.

Согласно второму закону термодинамики , для систем, реагирующих при фиксированных температуре и давлении без вклада , не связанной с давлением и объемом (пВ) работы , существует общая естественная тенденция к достижению минимума свободной энергии Гиббса.

Количественной мерой благоприятности данной реакции в этих условиях является изменение Δ G (иногда обозначаемое «дельта G » или «d G ») свободной энергии Гиббса, которое вызвано (или могло бы быть) реакцией. В качестве необходимого условия для того, чтобы реакция протекала при постоянной температуре и давлении, ΔG должно быть меньше работы без давления-объема (не- pV , например, электрической), которая часто равна нулю (тогда ΔG должна быть отрицательной). ). Δ G равна максимальному количеству не- PV работы, которое может быть совершено в результате химической реакции для случая обратимого процесса. Если анализ указывает на положительную величину ΔG для энергию в форме электрической или другой не -PV реакции, то к реагирующей системе необходимо будет добавить работы, чтобы ΔG было меньше, чем не -PV -работа, и сделать ее меньше. возможно возникновение реакции. ^[3]^{: 298–299}

Можно думать о ∆G как о количестве «свободной» или «полезной» энергии, доступной для выполнения не- PV работы при постоянной температуре и давлении. Уравнение можно также рассматривать с точки зрения системы вместе с ее окружением (остальной Вселенной). Во-первых, предполагается, что данная реакция при постоянных температуре и давлении является единственной, которая протекает. Тогда энтропия , выделяемая или поглощаемая системой, равна энтропии, которую должна поглотить или высвободить окружающая среда соответственно. Реакция будет разрешена только в том случае, если общее изменение энтропии Вселенной будет равно нулю или положительно. Это отражается в отрицательном ΔG , и реакция называется экзергоническим процессом .

Если две химические реакции связаны, то эндергоническая реакция (с положительным ΔG ) может возникнуть . Ввод тепла в эндергоническую реакцию по своей сути, такую как отщепление циклогексанола циклогексена до изменяется , можно рассматривать как соединение неблагоприятной реакции (элиминирования) с благоприятной (сжигание угля или другое получение тепла), так что общая энтропия Вселенной больше или равно нулю, что делает полное изменение свободной энергии Гиббса связанных реакций отрицательным.

В традиционном использовании термин «бесплатная» был включен в «свободную энергию Гиббса» и означает «доступную в форме полезной работы». ^[1] Характеристика станет более точной, если мы добавим уточнение, что это энергия, доступная для работы без давления и объема. ^[4] (Аналогичное, но немного другое значение слова «свободный» применяется в сочетании со свободной энергией Гельмгольца для систем с постоянной температурой). Однако все большее количество книг и журнальных статей не содержат приставки «бесплатно», называя G просто «энергией Гиббса». Это результат встречи ИЮПАК 1988 года по установлению единой терминологии для международного научного сообщества, на которой было рекомендовано удалить прилагательное «свободный». ^[5]^[6]^[7] Однако этот стандарт еще не получил всеобщего признания.

название «свободная энтальпия ». также использовалось для обозначения G В прошлом ^[6]

История

Величина, называемая «свободной энергией», является более продвинутой и точной заменой устаревшего термина « сродство », который использовался химиками в ранние годы физической химии для описания силы , вызывающей химические реакции .

В 1873 году Джозайя Уиллард Гиббс опубликовал «Метод геометрического представления термодинамических свойств веществ с помощью поверхностей» , в котором он обрисовал принципы своего нового уравнения, которое было способно предсказать или оценить тенденции различных естественных процессов, которые происходят, когда тела или системы вступают в контакт. Изучая взаимодействия однородных веществ, находящихся в контакте, то есть тел, состоящих частично из твердого тела, частично из жидкости и частично из пара, и используя трехмерный график объем - энтропия - внутренняя энергия , Гиббс смог определить три состояния равновесия: т. е. «обязательно стабильный», «нейтральный» и «нестабильный», и последуют ли изменения. Далее Гиббс заявил: ^[2]

Если мы хотим выразить в одном уравнении необходимое и достаточное условие термодинамического равновесия вещества, окруженного средой с постоянным давлением р и температурой Т , то это уравнение можно записать:
δ ( ε - Tη + pν ) знак равно 0
когда δ относится к изменению, вызванному любыми изменениями в состоянии частей тела, и (когда разные части тела находятся в разных состояниях) к пропорции, в которой тело разделено между различными состояниями. Условием устойчивого равновесия является то, что значение выражения в скобках должно быть минимальным.

В этом описании, используемом Гиббсом, ε относится к внутренней энергии тела, η относится к энтропии тела, а ν — к объему тела...

Впоследствии, в 1882 году, немецкий учёный Герман фон Гельмгольц охарактеризовал сродство как наибольшее количество работы, которое можно получить, если реакция осуществляется обратимым образом, например электрическая работа в обратимой ячейке. Таким образом, максимальная работа рассматривается как уменьшение свободной или доступной энергии системы ( свободная энергия Гиббса G при T = константа, P = константа или свободная энергия Гельмгольца F при T = константа, V = константа), в то время как Выделяемое тепло обычно является мерой уменьшения полной энергии системы ( внутренней энергии ). Таким образом, G или F — это количество энергии, «свободной» для работы в данных условиях.

До этого момента общая точка зрения была такова: «все химические реакции приводят систему к состоянию равновесия, в котором сходство реакций исчезает». В течение следующих 60 лет термин «родство» был заменен термином «свободная энергия». По словам историка химии Генри Лестера, влиятельный учебник Гилберта Н. Льюиса и Мерла Рэндалла «Термодинамика и свободная энергия химических веществ» 1923 года « привел к замене термина сродство» термином «свободная энергия» в большей части английского языка. говорящий мир. ^[8]^: 206

Определения

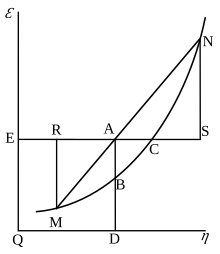
Свободная энергия Гиббса определяется как $G(p,T)=U+pV-TS,$

что то же самое, что $G(p,T)=H-TS,$

где:

U — внутренняя энергия (единица СИ: джоуль ),
p — давление (единица СИ: паскаль ),
V is volume (SI unit: m ³),
T — температура (единица СИ: кельвин ),
S — энтропия (единица СИ: джоуль на кельвин),
H — энтальпия (единица СИ: джоуль).

Выражение бесконечно малого обратимого изменения свободной энергии Гиббса как функции ее «естественных переменных» p и T для открытой системы , подверженной действию внешних сил (например, электрических или магнитных) X _i , которые вызывают Если внешние параметры системы a _i изменятся на величину d a _i , можно получить из первого закона для обратимых процессов следующим образом:

${\begin{aligned}T\,\mathrm {d} S&=\mathrm {d} U+p\,\mathrm {d} V-\sum _{i=1}^{k}\mu _{i}\,\mathrm {d} N_{i}+\sum _{i=1}^{n}X_{i}\,\mathrm {d} a_{i}+\cdots \\\mathrm {d} (TS)-S\,\mathrm {d} T&=\mathrm {d} U+\mathrm {d} (pV)-V\,\mathrm {d} p-\sum _{i=1}^{k}\mu _{i}\,\mathrm {d} N_{i}+\sum _{i=1}^{n}X_{i}\,\mathrm {d} a_{i}+\cdots \\\mathrm {d} (U-TS+pV)&=V\,\mathrm {d} p-S\,\mathrm {d} T+\sum _{i=1}^{k}\mu _{i}\,\mathrm {d} N_{i}-\sum _{i=1}^{n}X_{i}\,\mathrm {d} a_{i}+\cdots \\\mathrm {d} G&=V\,\mathrm {d} p-S\,\mathrm {d} T+\sum _{i=1}^{k}\mu _{i}\,\mathrm {d} N_{i}-\sum _{i=1}^{n}X_{i}\,\mathrm {d} a_{i}+\cdots \end{aligned}}$

где:

µ _i – химический потенциал го i - химического компонента . (Единица СИ: джоули на частицу ^[9] или джоули на моль ^[1])
N _i — количество частиц (или количество молей), составляющих i -й химический компонент.

Это одна из форм фундаментального уравнения Гиббса . ^[10] В бесконечно малом выражении термин, включающий химический потенциал, учитывает изменения свободной энергии Гиббса в результате притока или оттока частиц. Другими словами, это справедливо для открытой системы или для закрытой химически реагирующей системы, где N _i изменяются. Для закрытой, нереагирующей системы этот термин можно опустить.

В зависимости от конкретной рассматриваемой системы может быть добавлено любое количество дополнительных терминов. Помимо механической работы , система может выполнять множество других видов работы. Например, в бесконечно малом выражении энергия работы сокращения, связанная с термодинамической системой, которая представляет собой сократительное волокно, которое укорачивается на величину -d l под действием силы f, приведет к члена f d l добавлению . Если некоторое количество заряда −d e приобретается системой при электрическом потенциале Ψ, связанная с этим электрическая работа равна −Ψ d e , которая будет включена в бесконечно малое выражение. Остальные условия работы добавляются согласно системным требованиям. ^[11]

Каждую величину в приведенных выше уравнениях можно разделить на количество вещества, измеренное в молях , чтобы образовать молярную свободную энергию Гиббса . Свободная энергия Гиббса — одна из наиболее важных термодинамических функций для характеристики системы. Это фактор, определяющий такие результаты, как напряжение и электрохимической ячейки константа равновесия реакции обратимой . В изотермических изобарических системах свободную энергию Гиббса можно рассматривать как «динамическую» величину, поскольку она является репрезентативной мерой конкурирующих эффектов энтальпийной энергии. ^{[ нужны разъяснения ]} и энтропийные движущие силы, участвующие в термодинамическом процессе.

Температурная зависимость энергии Гиббса для идеального газа дается уравнением Гиббса–Гельмгольца , а ее зависимость от давления – формулой ^[12] ${\frac {G}{N}}={\frac {G^{\circ }}{N}}+kT\ln {\frac {p}{p^{\circ }}}.$

или, что более удобно, его химический потенциал : ${\frac {G}{N}}=\mu =\mu ^{\circ }+kT\ln {\frac {p}{p^{\circ }}}.$

В неидеальных системах летучесть в игру вступает .

Вывод

свободной энергии Гиббса Полный дифференциал относительно натуральных переменных может быть получен с помощью преобразований Лежандра внутренней энергии .

\mathrm {d} U=T\,\mathrm {d} S-p\,\mathrm {d} V+\sum _{i}\mu _{i}\,\mathrm {d} N_{i}.

Определение G сверху:

G=U+pV-TS

.

Беря полный дифференциал, имеем

\mathrm {d} G=\mathrm {d} U+p\,\mathrm {d} V+V\,\mathrm {d} p-T\,\mathrm {d} S-S\,\mathrm {d} T.

Замена d U результатом первого закона дает ^[13]

{\begin{aligned}\mathrm {d} G&=T\,\mathrm {d} S-p\,\mathrm {d} V+\sum _{i}\mu _{i}\,\mathrm {d} N_{i}+p\,\mathrm {d} V+V\,\mathrm {d} p-T\,\mathrm {d} S-S\,\mathrm {d} T\\&=V\,\mathrm {d} p-S\,\mathrm {d} T+\sum _{i}\mu _{i}\,\mathrm {d} N_{i}.\end{aligned}}

естественными переменными группы G Тогда будут p , T и { N _i }.

Гомогенные системы

Поскольку S , V и Ni _: являются обширными переменными , соотношение Эйлера d U позволяет легко интегрировать ^[13]

U=TS-pV+\sum _{i}\mu _{i}N_{i}.

Поскольку некоторые из естественных переменных G являются интенсивными, d G нельзя интегрировать с использованием соотношений Эйлера, как в случае с внутренней энергией. Однако простая подстановка приведенного выше интегрированного результата для U в определение G дает стандартное выражение для G : ^[13]

{\begin{aligned}G&=U+pV-TS\\&=\left(TS-pV+\sum _{i}\mu _{i}N_{i}\right)+pV-TS\\&=\sum _{i}\mu _{i}N_{i}.\end{aligned}}

Этот результат показывает, что химический потенциал вещества $i$ - его (парциальная) молярная свободная энергия Гиббса. Это применимо к однородным макроскопическим системам, но не ко всем термодинамическим системам. ^[14]

Свободная энергия реакций Гиббса.

Рассматриваемая система поддерживается при постоянной температуре и давлении и является закрытой (вещество не может войти или выйти). Энергия Гиббса любой системы равна ⁠ $G=U+pV-TS$ ⁠ и бесконечно малое изменение G при постоянной температуре и давлении дает

dG=dU+pdV-TdS

.

По первому закону термодинамики изменение внутренней энергии U определяется выражением

dU=\delta Q+\delta W

где $δQ$ — энергия, добавленная в виде тепла, а $δW$ — энергия, добавленная в виде работы. Работу, совершаемую над системой, можно записать как $δW = - pdV + δW x$ , где $- pdV$ — механическая работа сжатия/расширения, совершаемая системой или системой, а $δW x$ — все другие формы работы, которые могут включать в себя электрическую, магнитный и т. д. Тогда

dU=\delta Q-pdV+\delta W_{x}

и бесконечно малое изменение в G равно

dG=\delta Q-TdS+\delta W_{x}

.

Второй закон термодинамики гласит, что для закрытой системы при постоянной температуре (в тепловой бане) $TdS\geq \delta Q$ , и отсюда следует, что

dG\leq \delta W_{x}

Если предположить, что совершается только механическая работа, то это упрощается.

dG\leq 0

Это означает, что для такой системы, когда она не находится в равновесии, энергия Гиббса всегда будет убывать, а в равновесии бесконечно малое изменение dG будет равно нулю. В частности, это будет верно, если на пути к равновесию система испытывает любое количество внутренних химических реакций.

В электрохимической термодинамике

При прохождении электрического заряда dQ _ele между электродами электрохимической ячейки возникает ЭДС ${\mathcal {E}}$ , в выражении для изменения энергии Гиббса появляется член электрической работы: $dG=-SdT+Vdp+{\mathcal {E}}dQ_{ele},$ где S — энтропия , V — объем системы, p — ее давление, а T — ее абсолютная температура .

Комбинация ( ${\mathcal {E}}$ , Q _ele ) является примером сопряженной пары переменных . При постоянном давлении приведенное выше уравнение дает соотношение Максвелла , которое связывает изменение напряжения открытой ячейки с температурой T (измеримая величина) с изменением энтропии S прохождении заряда при изотермическом и изобарном . Последнее тесно связано с реакционной энтропией электрохимической реакции, которая придает батарее энергию. Это соотношение Максвелла: ^[15]

\left({\frac {\partial {\mathcal {E}}}{\partial T}}\right)_{Q_{ele},p}=-\left({\frac {\partial S}{\partial Q_{ele}}}\right)_{T,p}

Если моль ионов переходит в раствор (например, в ячейке Даниэля, как обсуждается ниже), заряд во внешней цепи равен

\Delta Q_{ele}=-n_{0}F_{0}\,,

где n ₀ — число электронов на ион, а F ₀ — постоянная Фарадея , а знак минус указывает на разряд ячейки. Предполагая постоянные давление и объем, термодинамические свойства ячейки строго связаны с поведением ее ЭДС соотношением

\Delta H=-n_{0}F_{0}\left({\mathcal {E}}-T{\frac {d{\mathcal {E}}}{dT}}\right),

где ΔH – энтальпия реакции . Все величины справа поддаются непосредственному измерению.

Полезные тождества для вывода уравнения Нернста

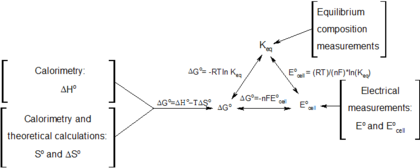
Во время обратимой электрохимической реакции при постоянной температуре и давлении выполняются следующие уравнения, включающие свободную энергию Гиббса:

$\Delta _{\text{r}}G=\Delta _{\text{r}}G^{\circ }+RT\ln Q_{\text{r}}$ (см. химическое равновесие ),
$\Delta _{\text{r}}G^{\circ }=-RT\ln K_{\text{eq}}$ (для системы, находящейся в химическом равновесии),
$\Delta _{\text{r}}G=w_{\text{elec,rev}}=-nF{\mathcal {E}}$ (для обратимого электрохимического процесса при постоянной температуре и давлении),
$\Delta _{\text{r}}G^{\circ }=-nF{\mathcal {E}}^{\circ }$ (определение ${\mathcal {E}}^{\circ }$ ),

и перестановка дает ${\begin{aligned}nF{\mathcal {E}}^{\circ }&=RT\ln K_{\text{eq}},\\nF{\mathcal {E}}&=nF{\mathcal {E}}^{\circ }-RT\ln Q_{\text{r}},\\{\mathcal {E}}&={\mathcal {E}}^{\circ }-{\frac {RT}{nF}}\ln Q_{\text{r}},\end{aligned}}$

которое связывает потенциал клетки, возникающий в результате реакции, с константой равновесия и коэффициентом реакции для этой реакции ( уравнение Нернста ),

где

$Δ r G$ , изменение свободной энергии Гиббса на моль реакции,
$Δ r G°$ , изменение свободной энергии Гиббса на моль реакции для несмешанных реагентов и продуктов в стандартных условиях (т. е. 298 К, 100 кПа, 1 М каждого реагента и продукта),
$R$ , газовая постоянная ,
$Т$ , абсолютная температура ,
$ln$ , натуральный логарифм ,
$Q r$ , коэффициент реакции (безразмерный),
$K eq$ , константа равновесия (безразмерная),
$w elec,rev$ , электрическая работа в обратимом процессе (химическое соглашение о знаках),
$n$ , число молей электронов , перешедших в реакции,
$F = N A e \approx 96485 Кл/моль$ , постоянная Фарадея (заряд на моль электронов),
${\mathcal {E}}$ , клеточный потенциал ,
${\mathcal {E}}^{\circ }$ , стандартный клеточный потенциал .

Более того, у нас также есть ${\begin{aligned}K_{\text{eq}}&=e^{-{\frac {\Delta _{\text{r}}G^{\circ }}{RT}}},\\\Delta _{\text{r}}G^{\circ }&=-RT\left(\ln K_{\text{eq}}\right)=-2.303\,RT\left(\log _{10}K_{\text{eq}}\right),\end{aligned}}$

которое связывает константу равновесия со свободной энергией Гиббса. Это означает, что в равновесии $Q_{\text{r}}=K_{\text{eq}}$ и $\Delta _{\text{r}}G=0.$

Стандартное изменение энергии Гиббса в формации

Таблица выбранных веществ ^[16]
Вещество (состояние)	Δ _f G°
Вещество (состояние)	( кДж / моль )	( ккал / моль )
НЕТ(г)	87.6	20.9
НЕТ ₂ (г)	51.3	12.3
Н ₂ О(г)	103.7	24.78
Н ₂ О(г)	−228.6	−54.64
Н ₂ О(л)	−237.1	−56.67
СО ₂ (г)	−394.4	−94.26
CO(г)	−137.2	−32.79
СН ₄ (г)	−50.5	−12.1
С ₂ Н ₆ (г)	−32.0	−7.65
С ₃ Н ₈ (г)	−23.4	−5.59
С ₆ Н ₆ (г)	129.7	29.76
С ₆ Н ₆ (л)	124.5	31.00

Стандартная свободная энергия Гиббса образования соединения — это изменение свободной энергии Гиббса, сопровождающее образование 1 моля этого вещества из составляющих его элементов в их стандартных состояниях (наиболее стабильная форма элемента при 25 °С и 100 °С). кПа ). Его символ — Δ _f G ˚.

Все элементы в своих стандартных состояниях (двухатомный кислород , графит и т. д.) имеют стандартное изменение свободной энергии Гиббса, равное нулю, поскольку никаких изменений не происходит.

Δ _f G = Δ _f G ˚ + RT ln Q _f ,

где Q _f – коэффициент реакции .

В состоянии равновесия Δ _f G = 0 и Q _f = K , поэтому уравнение принимает вид

Δ _ж G ˚ знак равно - RT ln K ,

где К — константа равновесия реакции образования вещества из элементов в их стандартных состояниях.

Графическая интерпретация Гиббса

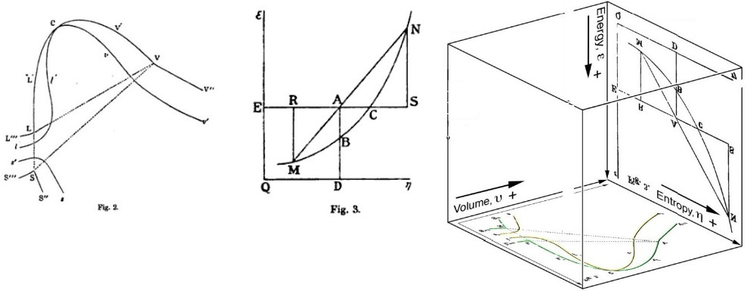
Свободная энергия Гиббса первоначально определялась графически. В 1873 году американский учёный Уиллард Гиббс опубликовал свою первую статью по термодинамике «Графические методы в термодинамике жидкостей», в которой Гиббс использовал две координаты: энтропию и объём для представления состояния тела. В своей второй последующей статье «Метод геометрического представления термодинамических свойств веществ с помощью поверхностей», опубликованной позже в том же году, Гиббс добавил третью координату энергии тела, определенную на трех фигурах. В 1874 году шотландский физик Джеймс Клерк Максвелл использовал фигуры Гиббса, чтобы создать трехмерную термодинамическую поверхность энергии-энтропии-объема вымышленного водоподобного вещества. ^[17] Таким образом, чтобы понять концепцию свободной энергии Гиббса, может быть полезно понять ее интерпретацию Гиббсом как сечения AB на его рисунке 3 и то, как Максвелл вылепил это сечение на своей трехмерной поверхности .

См. также

Биоэнергетика
Кальфад (РАСЧЕТ ФАЗНЫХ диаграмм)
Критическая точка (термодинамика)
Электронный эквивалент
Энтальпийно-энтропийная компенсация
Свободная энтропия
Уравнение Гиббса – Гельмгольца
Большой потенциал
Неслучайная модель двух жидкостей (модель NRTL) - расчет энергии Гиббса избытка и смешивания, а также коэффициенты активности.
Спинодаль – Спинодальные кривые (матрица Гессе)
Стандартная молярная энтропия
Термодинамическая свободная энергия
Модель UNIQUAC – расчет энергии избытка Гиббса и смешивания, а также коэффициенты активности

Примечания и ссылки

^ Jump up to: ^а ^б ^с Перро, Пьер (1998). Термодинамика от А до Я. Издательство Оксфордского университета. ISBN 0-19-856552-6 .
^ Jump up to: ^а ^б Гиббс, Джозайя Уиллард (декабрь 1873 г.). «Метод геометрического представления термодинамических свойств веществ с помощью поверхностей» (PDF) . Труды Академии искусств и наук Коннектикута . 2 : 382–404.
^ Питер Аткинс; Лоретта Джонс (1 августа 2007 г.). Химические принципы: В поисках понимания . У. Х. Фриман. ISBN 978-1-4292-0965-6 .
^ Рейсс, Ховард (1965). Методы термодинамики . Дуврские публикации. ISBN 0-486-69445-3 .
^ Калверт, Дж. Г. (1 января 1990 г.). «Глоссарий терминов по химии атмосферы (Рекомендации 1990 г.)» . Чистая и прикладная химия . 62 (11): 2167–2219. дои : 10.1351/pac199062112167 .
^ Jump up to: ^а ^б «Энергия (функция) Гиббса, Г» . Золотая книга ИЮПАК (Сборник химических технологий) . ИЮПАК (Международный союз теоретической и прикладной химии). 2008. doi : 10.1351/goldbook.G02629 . Проверено 24 декабря 2020 г. Раньше ее называли свободной энергией или свободной энтальпией.
^ Леманн, HP; Фуэнтес-Ардериу, X.; Бертелло, LF (1 января 1996 г.). «Глоссарий терминов в количествах и единицах клинической химии (Рекомендации IUPAC-IFCC 1996)» . Чистая и прикладная химия . 68 (4): 957–1000. дои : 10.1351/pac199668040957 . S2CID 95196393 .
^ Генри Маршалл Лестер (1971). Историческая основа химии . Курьерская компания. ISBN 978-0-486-61053-5 .
^ Химический потенциал , Золотая книга ИЮПАК.
^ Мюллер, Инго (2007). История термодинамики – учение об энергии и энтропии . Спрингер. ISBN 978-3-540-46226-2 .
^ Качальский А.; Карран, Питер Ф. (1965). Неравновесная термодинамика в биофизике . Издательство Гарвардского университета . КСН 65-22045.
^ Аткинс, Питер; де Паула, Хулио (2006). Физическая химия Аткинса (8-е изд.). У. Х. Фриман. п. 109. ИСБН 0-7167-8759-8 .
^ Jump up to: ^а ^б ^с Зальцман, Уильям Р. (21 августа 2001 г.). «Открытые системы» . Химическая термодинамика . Университет Аризоны . Архивировано из оригинала 7 июля 2007 г. Проверено 11 октября 2007 г.
^ Брахман, МК (1954). «Уровень Ферми, химический потенциал и свободная энергия Гиббса». Журнал химической физики . 22 (6): 1152. Бибкод : 1954ЖЧФ..22.1152Б . дои : 10.1063/1.1740312 .
^ Х.С. Харнед, Б.Б. Оуэн, Физическая химия электролитических растворов, третье издание, Reinhold Publishing Corporation, Нью-Йорк, 1958, стр. 2-6
^ Справочник CRC по химии и физике, 2009, стр. 5-4–5-42, 90-е изд., Lide.
^ Джеймс Клерк Максвелл, Элизабет Гарбер , Стивен Г. Браш и К.В. Фрэнсис Эверитт (1995), Максвелл о теплоте и статистической механике: о «избежании всех личных вопросов» о молекулах , Lehigh University Press, ISBN 0-934223-34-3 , с. 248.

Внешние ссылки

Определение ИЮПАК (энергия Гиббса)
Свободная энергия Гиббса – Университет штата Джорджия

[Perrot-1] Jump up to: ^а ^б ^с Перро, Пьер (1998). Термодинамика от А до Я. Издательство Оксфордского университета. ISBN 0-19-856552-6 .

[Gibbs1873-2] Jump up to: ^а ^б Гиббс, Джозайя Уиллард (декабрь 1873 г.). «Метод геометрического представления термодинамических свойств веществ с помощью поверхностей» (PDF) . Труды Академии искусств и наук Коннектикута . 2 : 382–404.

[AtkinsJones2007-3] Питер Аткинс; Лоретта Джонс (1 августа 2007 г.). Химические принципы: В поисках понимания . У. Х. Фриман. ISBN 978-1-4292-0965-6 .

[4] Рейсс, Ховард (1965). Методы термодинамики . Дуврские публикации. ISBN 0-486-69445-3 .

[5] Калверт, Дж. Г. (1 января 1990 г.). «Глоссарий терминов по химии атмосферы (Рекомендации 1990 г.)» . Чистая и прикладная химия . 62 (11): 2167–2219. дои : 10.1351/pac199062112167 .

[GoldBook-6] Jump up to: ^а ^б «Энергия (функция) Гиббса, Г» . Золотая книга ИЮПАК (Сборник химических технологий) . ИЮПАК (Международный союз теоретической и прикладной химии). 2008. doi : 10.1351/goldbook.G02629 . Проверено 24 декабря 2020 г. Раньше ее называли свободной энергией или свободной энтальпией.

[7] Леманн, HP; Фуэнтес-Ардериу, X.; Бертелло, LF (1 января 1996 г.). «Глоссарий терминов в количествах и единицах клинической химии (Рекомендации IUPAC-IFCC 1996)» . Чистая и прикладная химия . 68 (4): 957–1000. дои : 10.1351/pac199668040957 . S2CID 95196393 .

[Leicester1971-8] Генри Маршалл Лестер (1971). Историческая основа химии . Курьерская компания. ISBN 978-0-486-61053-5 .

[9] Химический потенциал , Золотая книга ИЮПАК.

[10] Мюллер, Инго (2007). История термодинамики – учение об энергии и энтропии . Спрингер. ISBN 978-3-540-46226-2 .

[11] Качальский А.; Карран, Питер Ф. (1965). Неравновесная термодинамика в биофизике . Издательство Гарвардского университета . КСН 65-22045.

[12] Аткинс, Питер; де Паула, Хулио (2006). Физическая химия Аткинса (8-е изд.). У. Х. Фриман. п. 109. ИСБН 0-7167-8759-8 .

[Salzman2001-13] Jump up to: ^а ^б ^с Зальцман, Уильям Р. (21 августа 2001 г.). «Открытые системы» . Химическая термодинамика . Университет Аризоны . Архивировано из оригинала 7 июля 2007 г. Проверено 11 октября 2007 г.

[14] Брахман, МК (1954). «Уровень Ферми, химический потенциал и свободная энергия Гиббса». Журнал химической физики . 22 (6): 1152. Бибкод : 1954ЖЧФ..22.1152Б . дои : 10.1063/1.1740312 .

[15] Х.С. Харнед, Б.Б. Оуэн, Физическая химия электролитических растворов, третье издание, Reinhold Publishing Corporation, Нью-Йорк, 1958, стр. 2-6

[16] Справочник CRC по химии и физике, 2009, стр. 5-4–5-42, 90-е изд., Lide.

[17] Джеймс Клерк Максвелл, Элизабет Гарбер , Стивен Г. Браш и К.В. Фрэнсис Эверитт (1995), Максвелл о теплоте и статистической механике: о «избежании всех личных вопросов» о молекулах , Lehigh University Press, ISBN 0-934223-34-3 , с. 248.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

v т и Статистическая механика
Theory	Principle of maximum entropy ergodic theory
Statistical thermodynamics	Ensembles partition functions equations of state thermodynamic potential: U H F G Maxwell relations
Models	Ferromagnetism models Ising Potts Heisenberg percolation Particles with force field depletion force Lennard-Jones potential
Mathematical approaches	Boltzmann equation H-theorem Vlasov equation BBGKY hierarchy stochastic process mean-field theory and conformal field theory
Critical phenomena	Phase transition Critical exponents correlation length size scaling
Entropy	Boltzmann Shannon Tsallis Rényi von Neumann
Applications	Statistical field theory elementary particle superfluidity Condensed matter physics Complex system chaos information theory Boltzmann machine