Синус и косинус
| Синус и косинус | |
|---|---|
 | |
| Общая информация | |
| Общее определение | |
| Области применения | Тригонометрия , ряды Фурье и т. д. |
| Тригонометрия |
|---|
 |
| Ссылка |
| Законы и теоремы |
| Исчисление |
| Математики |
В математике синус и косинус являются тригонометрическими угла функциями . Синус и косинус острого угла определяются в контексте прямоугольного треугольника : для указанного угла его синус — это отношение длины стороны, противоположной этому углу, к длине самой длинной стороны треугольника ( гипотенуза . ), а косинус — это отношение длины прилежащего катета к гипотенузы длине Для угла , функции синуса и косинуса обозначаются как и . [1]
Определения синуса и косинуса были расширены до любого реального значения в терминах длин определенных отрезков в единичном круге . Более современные определения выражают синус и косинус как бесконечные ряды или как решения некоторых дифференциальных уравнений , позволяя расширять их до произвольных положительных и отрицательных значений и даже до комплексных чисел .
Функции синуса и косинуса обычно используются для моделирования периодических явлений, таких как звуковые и световые волны , положение и скорость гармонических осцилляторов, интенсивность солнечного света и продолжительность дня, а также изменения средней температуры в течение года. Их можно проследить до функций джья и коти-джья, которые использовались в индийской астрономии в период Гуптов .
Обозначения
[ редактировать ]Синус и косинус записываются с использованием функциональной записи с сокращениями sin и cos .
Часто, если аргумент достаточно простой, значение функции будет записано без круглых скобок, как sin θ , а не как sin( θ ) .
Синус и косинус являются функцией угла, который обычно выражается в радианах или градусах . Если явно не указано иное, в этой статье предполагается, что угол измеряется в радианах.
Определения
[ редактировать ]Определения прямоугольного треугольника.
[ редактировать ]
Чтобы определить синус и косинус острого угла α , начните с прямоугольного треугольника , содержащего угол меры α ; на прилагаемом рисунке угол α в треугольнике ABC представляет собой интересующий угол. Три стороны треугольника называются следующим образом: [2]
- Противоположная сторона — это сторона, противоположная интересующему углу; в данном случае это .
- Гипотенуза — это сторона , противолежащая прямому углу; в данном случае это h . Гипотенуза всегда является самой длинной стороной прямоугольного треугольника.
- Прилегающая сторона является оставшейся стороной; в данном случае это б . Он образует сторону (и примыкает к нему) как к интересующему углу (углу A ), так и к прямому углу.
Если такой треугольник выбран, синус угла равен длине противоположной стороны, деленной на длину гипотенузы, а косинус угла равен длине прилежащей стороны, разделенной на длину гипотенузы. гипотенуза: [2] Аналогично определяются и другие тригонометрические функции угла; например, касательная — это соотношение между противоположной и прилегающей сторонами. [2]
Как было сказано, значения и по-видимому, зависят от выбора прямоугольного треугольника, содержащего угол меры α . Однако это не так: все такие треугольники подобны , а значит, и соотношения для каждого из них одинаковы.
Определения единичного круга
[ редактировать ]
Функции синуса и косинуса также можно определить с помощью единичного круга , круга радиуса один с центром в начале координат (0, 0) в декартовой системе координат .
Пусть линия, проходящая через начало координат, пересекает единичную окружность, образуя угол θ с положительной половиной x оси . Координаты x и y θ точки пересечения равны cos( этой ) и sin( θ ) соответственно. Это определение согласуется с определением синуса и косинуса в прямоугольном треугольнике, когда 0 < θ < π / 2, поскольку длина гипотенузы единичной окружности всегда равна 1; Говоря математическим языком, синус угла равен противоположной стороне треугольника, которая представляет собой просто y координату . Аналогичный аргумент можно привести в пользу функции косинуса, чтобы показать, что косинус угла является косинусом угла, когда 0 < θ < π /2 , даже в соответствии с новым определением, использующим единичный круг. Затем функция тангенса tan( θ ) определяется как соотношение между синусом и косинусом угла или как наклон отрезка прямой.
Преимущество использования определения единичного круга заключается в расширении угла до любого реального аргумента. Этого также можно достичь, потребовав определенной симметрии и того, чтобы синус был периодической функцией .
Определения сложных экспоненциальных функций
[ редактировать ]Показательная функция определяется во всей области определения комплексных чисел . Определение синуса и косинуса можно распространить на все комплексные числа с помощью
Их можно перевернуть, чтобы получить формулу Эйлера.
При построении графика на комплексной плоскости функция для реальных значений чертит единичную окружность в комплексной плоскости.
Когда - действительное число, синус и косинус упрощаются до мнимой и действительной частей или , как:
Когда за реальные ценности и , синус и косинус можно выразить через действительные синусы, косинусы и гиперболические функции как
Определение дифференциального уравнения
[ редактировать ]это решение к двумерной системе дифференциальных уравнений и с начальными условиями и . Можно интерпретировать единичную окружность в приведенных выше определениях как определение траектории фазового пространства дифференциального уравнения с заданными начальными условиями.
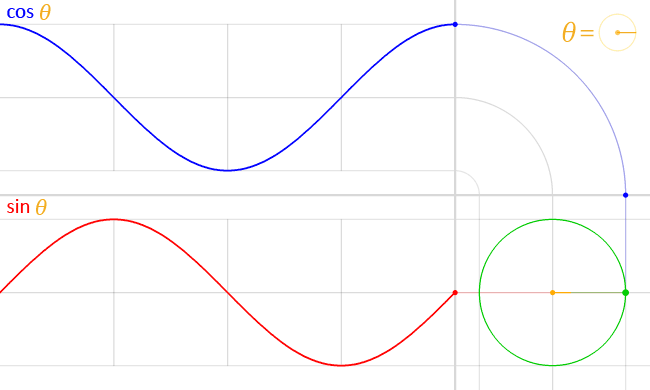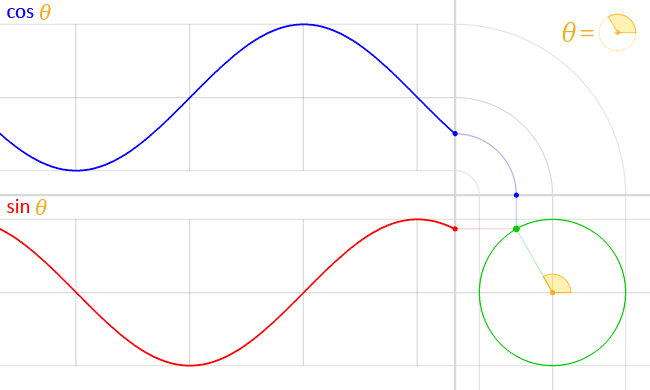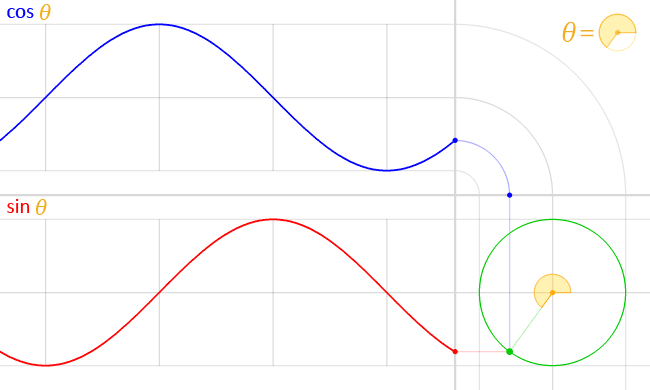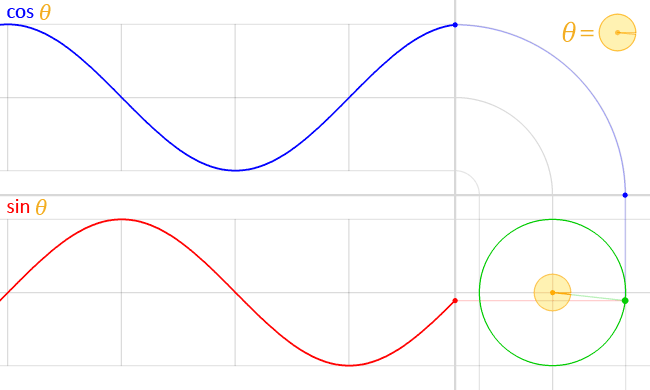
- Анимация, демонстрирующая, как синусоидальная функция (красный цвет) строится по координате y (красная точка) точки единичного круга (зеленый цвет) под углом θ . Косинус (синий) — это координата x .
Ее можно интерпретировать как траекторию в фазовом пространстве системы дифференциальных уравнений. и начиная с начальных условий и .
Определения серий
[ редактировать ]

Последовательные производные синуса, оцененные как ноль, можно использовать для определения его ряда Тейлора. Используя только геометрию и свойства пределов , можно показать, что производная синуса — это косинус, а производная косинуса — это минус синуса. Это означает, что последовательные производные от sin(x) — это cos(x), -sin(x), -cos(x), sin(x), продолжая повторять эти четыре функции. -я производная (4 n + k ) , оцененная в точке 0:
где верхний индекс представляет собой повторное дифференцирование. Это подразумевает следующее разложение в ряд Тейлора при x = 0 . Затем можно использовать теорию рядов Тейлора, чтобы показать, что следующие тождества справедливы для всех действительных чисел x (где x — угол в радианах) и, в более общем плане, для всех комплексных чисел : [3]
Взяв производную каждого члена, получим ряд Тейлора для косинуса:
Эти ряды Тейлора дают явные, вычислимые определения синуса и косинуса в терминах элементарных арифметических операций.
Определения непрерывных дробей
[ редактировать ]Функцию синуса также можно представить в виде обобщенной цепной дроби :
Представления цепной дроби могут быть получены из формулы непрерывной дроби Эйлера и выражать значения действительных чисел , как рациональные , так и иррациональные , функций синуса и косинуса.
Личности
[ редактировать ]Точные тождества (в радианах ):
Они применимы ко всем значениям .
Взаимные
[ редактировать ]Обратная величина синуса является косекансом, т. е. обратная величина синуса. является . Косеканс дает отношение длины гипотенузы к длине противоположной стороны. Точно так же обратная величина косинуса является секущей, которая дает отношение длины гипотенузы к длине прилежащей стороны.
Реверсы
[ редактировать ]
Обратная функция синуса — это арксинус (arcsin или asin) или обратный синус ( sin −1 ). Обратная функция косинуса — арккосинус (arccos, acos или cos −1 ). (Верхний индекс −1 в грехе −1 и потому что −1 обозначает обратную функцию, а не возведение в степень .) Поскольку синус и косинус не инъективны , их обратные функции не являются точными обратными функциями, а являются частичными обратными функциями. Например, sin(0) = 0 , но также sin( π ) = 0 , sin(2 π ) = 0 и т. д. Отсюда следует, что функция арксинус многозначна: arcsin(0) = 0 , но также arcsin(0) = π , arcsin(0) = 2 π и т. д. Если требуется только одно значение, функция может быть ограничена своей главной ветвью . С этим ограничением для каждого x в домене выражение arcsin( x ) будет оценивать только одно значение, называемое его главным значением . Стандартный диапазон главных значений для arcsin составляет от − π /2 до π /2 , а стандартный диапазон для arccos — от 0 до π .
где (для некоторого целого числа k ):
По определению, arcsin и arccos удовлетворяют уравнениям:
и
Пифагорейское тригонометрическое тождество
[ редактировать ]Основное соотношение между синусом и косинусом представляет собой тригонометрическое тождество Пифагора : [1]
где грех 2 ( x ) означает (грех ( x )) 2 .
Формулы двойного угла
[ редактировать ]Синус и косинус удовлетворяют следующим формулам двойного угла:

Формула косинуса двойного угла подразумевает, что sin 2 и потому что 2 сами по себе являются смещенными и масштабированными синусоидальными волнами. Конкретно, [4]
На графике показаны как функция синуса, так и функция синус-квадрат : синус выделен синим цветом, а синус-квадрат красным. Оба графика имеют одинаковую форму, но с разными диапазонами значений и разными периодами. Синус-квадрат имеет только положительные значения, но количество периодов в два раза больше.
Производная и интегралы
[ редактировать ]Производные синуса и косинуса:
и их первообразные:
где C обозначает константу интегрирования . [1]
Свойства, относящиеся к квадрантам
[ редактировать ]
В таблице ниже показаны многие ключевые свойства функции синуса (знак, монотонность, выпуклость), упорядоченные по квадранту аргумента. Для аргументов, не входящих в таблицу, можно вычислить соответствующую информацию, используя периодичность функции синуса.
| Квадрант | Угол | Его | Косинус | |||||
|---|---|---|---|---|---|---|---|---|
| Степени | радианы | Знак | Монотонность | Выпуклость | Знак | Монотонность | Выпуклость | |
| 1-й квадрант, я | увеличение | вогнутый | уменьшение | вогнутый | ||||
| 2-й квадрант, II | уменьшение | вогнутый | уменьшение | выпуклый | ||||
| 3-й квадрант, III | уменьшение | выпуклый | увеличение | выпуклый | ||||
| 4-й квадрант, IV | увеличение | выпуклый | увеличение | вогнутый | ||||

В следующей таблице представлена основная информация о границах квадрантов.
| Степени | радианы | ||||
|---|---|---|---|---|---|
| Ценить | Тип точки | Ценить | Тип точки | ||
| Корень , перегиб | Максимум | ||||
| Максимум | Корень , перегиб | ||||
| Корень , перегиб | Минимум | ||||
| Минимум | Корень , перегиб | ||||
Фиксированные точки
[ редактировать ]
Ноль — единственная реальная фиксированная точка синусоидальной функции; другими словами, единственное пересечение функции синуса и тождественной функции - это . Единственная действительная неподвижная точка косинуса называется числом Дотти . То есть число Дотти является единственным вещественным корнем уравнения. Десятичное разложение числа Дотти: . [5]
Длина дуги
[ редактировать ]Длина дуги синусоиды между и это
где — неполный эллиптический интеграл второго рода с модулем . Его невозможно выразить с помощью элементарных функций .
Длина дуги за полный период равна [6]
где и функция гамма - — константа лемнискаты . [6] [7]
Законы
[ редактировать ]Закон синусов гласит, что для произвольного треугольника со сторонами a , b и c и углами, противоположными сторонам A , B и C :
Это эквивалентно равенству первых трех выражений ниже:
где R треугольника — радиус описанной окружности .
Это можно доказать, разделив треугольник на два прямоугольных и воспользовавшись приведенным выше определением синуса. Закон синусов полезен для вычисления длин неизвестных сторон треугольника, если известны два угла и одна сторона. Это обычная ситуация, возникающая при триангуляции — методе определения неизвестных расстояний путем измерения двух углов и доступного замкнутого расстояния.
Закон косинусов гласит, что для произвольного треугольника со сторонами a , b и c и углами, противоположными этим сторонам A , B и C :
В случае, когда , и это становится теоремой Пифагора : для прямоугольного треугольника где с — гипотенуза.
Особые значения
[ редактировать ]
Для целых чисел, кратных 15° (т.е. радианы), значения sin( x ) и cos( x ) особенно просты и могут быть выражены через только. Таблица этих углов приведена ниже. Более сложные выражения углов см. в разделе Точные тригонометрические значения § Общие углы .
| Угол, х | грех( х ) | потому что ( х ) | |||||
|---|---|---|---|---|---|---|---|
| Степени | радианы | Градианы | Повороты | Точный | Десятичный | Точный | Десятичный |
| 0° | 0 | 0 г | 0 | 0 | 0 | 1 | 1 |
| 15° | 1 / 12 π | 16 + 2 / 3 г | 1 / 24 | 0.2588 | 0.9659 | ||
| 30° | 1 / 6 π | 33 + 1 / 3 г | 1 / 12 | 1 / 2 | 0.5 | 0.8660 | |
| 45° | 1 / 4 π | 50 г | 1 / 8 | 0.7071 | 0.7071 | ||
| 60° | 1 / 3 π | 66 + 2 / 3 г | 1 / 6 | 0.8660 | 1 / 2 | 0.5 | |
| 75° | 5 / 12 π | 83 + 1 / 3 г | 5 / 24 | 0.9659 | 0.2588 | ||
| 90° | 1 / 2 π | 100 г | 1 / 4 | 1 | 1 | 0 | 0 |
Шаг 90 градусов:
| х в градусах | 0° | 90° | 180° | 270° | 360° |
|---|---|---|---|---|---|
| х в радианах | 0 | п /2 | п | 3 р /2 | 14:00 |
| х в гонах | 0 | 100 г | 200 г | 300 г | 400 г |
| х по очереди | 0 | 1/4 | 1/2 | 3/4 | 1 |
| без х | 0 | 1 | 0 | −1 | 0 |
| потому что х | 1 | 0 | −1 | 0 | 1 |
Связь с комплексными числами
[ редактировать ]
Синус и косинус используются для соединения действительной и мнимой частей комплексного числа с его полярными координатами ( r , φ ) :
Действительная и мнимая части:
где r и φ представляют собой величину и угол комплексного числа z .
Для любого действительного числа θ : формула Эйлера гласит, что
Следовательно, если полярные координаты z равны ( r , φ ) ,
Сложные аргументы
[ редактировать ]

Применение определения синуса и косинуса в виде ряда к комплексному аргументу z дает:
где sinh и cosh — гиперболические синус и косинус . Это целые функции .
Также иногда полезно выразить сложные функции синуса и косинуса через действительную и мнимую части аргумента:
Частные дроби и разложения по произведениям комплексного синуса
[ редактировать ]Используя технику разложения в частные дроби в комплексном анализе , можно обнаружить, что бесконечный ряд
оба сходятся и равны . Аналогично можно показать, что
Используя технику расширения продукта, можно получить
Альтернативно, бесконечное произведение синуса можно доказать с помощью комплексного ряда Фурье .
Доказательство бесконечного произведения синуса |
|---|
Использование комплексного синуса
[ редактировать ]sin( z ) находится в функциональном уравнении для гамма-функции ,
что, в свою очередь, находится в функциональном уравнении для дзета-функции Римана ,
Как голоморфная функция , sin z является двумерным решением уравнения Лапласа :
Комплексная синусоидальная функция также связана с кривыми уровня маятников . [ как? ] [9] [ нужен лучший источник ]
Сложные графики
[ редактировать ] |  |  |
| реальный компонент | мнимая компонента | величина |
 |  |  |
| реальный компонент | мнимая компонента | величина |
История
[ редактировать ]
Хотя раннее изучение тригонометрии восходит к древности, тригонометрические функции , используемые сегодня, были разработаны в средневековый период. Функция аккорда была открыта Гиппархом из Никеи (180–125 гг. До н.э.) и Птолемеем из Римского Египта (90–165 гг. н.э.). [10]
Функции синуса и косинуса можно проследить до функций джья и коти-джья, которые использовались в индийской астрономии в период Гуптов ( Арьябхатия и Сурья Сиддханта ), посредством перевода с санскрита на арабский, а затем с арабского на латынь. [11]
Все шесть тригонометрических функций, используемых в настоящее время, были известны в исламской математике к 9 веку, как и закон синусов , используемый при решении треугольников . [12] За исключением синуса (который был заимствован из индийской математики), остальные пять современных тригонометрических функций были открыты арабскими математиками, включая косинус, тангенс, котангенс, секанс и косеканс. [12] Аль-Хваризми (ок. 780–850) составил таблицы синусов, косинусов и тангенсов. [13] [14] Мухаммад ибн Джабир аль-Харрани аль-Баттани (853–929) открыл взаимные функции секущего и косеканса и составил первую таблицу косекансов для каждой степени от 1 ° до 90 °. [14]
Первое опубликованное использование аббревиатур sin , cos и tan принадлежит французскому математику XVI века Альберту Жирару ; в дальнейшем они были обнародованы Эйлером (см. ниже). Opus palatinum de triangulis Георга Иоахима Ретикуса , ученика Коперника , был, вероятно, первым в Европе, который определил тригонометрические функции непосредственно в терминах прямоугольных треугольников вместо кругов, с таблицами для всех шести тригонометрических функций; эта работа была завершена учеником Ретикуса Валентином Отоном в 1596 году.
В статье, опубликованной в 1682 году, Лейбниц доказал, что sin x не является алгебраической функцией от x . [15] Роджер Коутс вычислил производную синуса в своей «Harmonia Mensurarum» (1722 г.). [16] Работа Леонарда Эйлера Introductio in analysin infinitorum (1748 г.) в основном способствовала созданию аналитической трактовки тригонометрических функций в Европе, а также определила их как бесконечные ряды и представила « формулу Эйлера », а также почти современные сокращения греха. , потому что. , Тан. , детская кроватка. , сек. , и косек. [11]
Этимология
[ редактировать ]Слово синус косвенно происходит от санскритского слова jyā «тетива лука». [17] [18] или, точнее, его синоним джива (оба заимствованы из древнегреческого χορδή «струна»). [19] ), из-за визуального сходства дуги круга с соответствующей ей хордой и луком с его тетивой (см. джья, коти-джья и уткрама-джья ). это слово было транслитерировано На арабском языке как jība , что на этом языке бессмысленно, и записано как jb ( جب ). Поскольку в арабском языке нет кратких гласных, jb интерпретировался как гомограф jayb ( جيب ), что означает «грудь», «карман» или «складка». Когда арабские тексты Аль-Баттани и аль-Хорезми были переведены на средневековую латынь в XII веке Герардом Кремонским , он использовал латинский эквивалент sinus (который также означает «залив» или «складка», а точнее «висячий»). складка тоги на груди»). [11] [20] [21] Джерард, вероятно, был не первым ученым, использовавшим этот перевод; Роберт Честерский, по-видимому, предшествовал ему, и есть свидетельства еще более раннего использования. [22] [23] Английская форма sine была введена в 1590-х годах. [24]
Слово косинус происходит от аббревиатуры латинского комплементи синус «синус дополнительного угла » как косинус в Эдмунда Гюнтера » «Каноне треугольника (1620), который также включает аналогичное определение котангена . [25] [26] [27]
Реализации программного обеспечения
[ редактировать ]Стандартного алгоритма вычисления синуса и косинуса не существует. IEEE 754 , наиболее широко используемый стандарт для спецификации надежных вычислений с плавающей запятой, не рассматривает вычисление тригонометрических функций, таких как синус. Причина в том, что не известен эффективный алгоритм вычисления синуса и косинуса с заданной точностью, особенно для больших входных данных. [28]
Алгоритмы расчета синуса могут быть сбалансированы с учетом таких ограничений, как скорость, точность, портативность или диапазон принимаемых входных значений. Это может привести к разным результатам для разных алгоритмов, особенно для особых обстоятельств, таких как очень большие входные данные, например sin(1022).
Общая оптимизация программирования, особенно используемая в 3D-графике, заключается в предварительном расчете таблицы значений синуса, например, одного значения на градус, затем для промежуточных значений выбирают ближайшее предварительно рассчитанное значение или линейно интерполируют между двумя ближайшими значениями. значения для его аппроксимации. Это позволяет искать результаты в таблице, а не рассчитывать их в реальном времени. При использовании современных архитектур ЦП этот метод может не дать никаких преимуществ. [ нужна ссылка ]
Алгоритм CORDIC обычно используется в научных калькуляторах.
Функции синуса и косинуса, а также другие тригонометрические функции широко доступны на разных языках программирования и платформах. В вычислительной технике их обычно сокращают до sin и cos.
Некоторые архитектуры ЦП имеют встроенную инструкцию для синуса, включая FPU Intel x87, начиная с 80387.
В языках программирования, sin и cos обычно являются либо встроенной функцией, либо находятся в стандартной математической библиотеке языка.
Например, стандартная библиотека C определяет функции синуса в math.h : sin(double), sinf(float), и sinl(long double). Параметр каждого из них представляет собой значение с плавающей запятой , определяющее угол в радианах. Каждая функция возвращает тот же тип данных , который она принимает. Многие другие тригонометрические функции также определены в math.h , например, для косинуса, арксинуса и гиперболического синуса (sinh).
Аналогично, Python определяет math.sin(x) и math.cos(x) внутри встроенного math модуль. В программе также доступны сложные функции синуса и косинуса. cmath модуль, например cmath.sin(z). CPython Математические функции вызывают C math библиотеку и использовать формат чисел с плавающей запятой двойной точности .
Пошаговые реализации
[ редактировать ]Некоторые библиотеки программного обеспечения предоставляют реализации синуса и косинуса с использованием входного угла в пол- оборота , причем полуоборот представляет собой угол 180 градусов или радианы. Представление углов в виде поворотов или полуповоротов в некоторых случаях дает преимущества в точности и эффективности. [29] [30] В MATLAB, OpenCL, R, Julia, CUDA и ARM эти функции называются sinpi и cospi. [29] [31] [30] [32] [33] [34] Например, sinpi(x) оценил бы где x выражается в полуоборотах, и, следовательно, окончательный вход в функцию, πx можно интерпретировать в радианах как sin .
Преимущество в точности обусловлено способностью идеально отображать ключевые углы, такие как полный оборот, полуоборот и четверть оборота, без потерь в двоичном формате с плавающей запятой или с фиксированной запятой. Напротив, представляя , , и в двоичном формате с плавающей запятой или в двоичном масштабе с фиксированной запятой всегда происходит потеря точности, поскольку иррациональные числа не могут быть представлены конечным числом двоичных цифр.
Повороты также имеют преимущество в точности и эффективности при вычислении по модулю до одного периода. Вычисления по модулю 1 оборота или по модулю 2 полуоборотов могут быть выполнены без потерь и эффективно как с плавающей, так и с фиксированной запятой. Например, вычисление по модулю 1 или по модулю 2 для значения с фиксированной точкой в двоичном масштабе требует только побитового сдвига или побитовой операции И. Напротив, вычисление по модулю предполагает неточности в представлении .
В приложениях, в которых используются датчики угла, датчик обычно обеспечивает измерение угла в форме, непосредственно совместимой с поворотами или полуповоротами. Например, датчик угла может считать от 0 до 4096 за один полный оборот. [35] Если в качестве единицы измерения угла используются полуобороты, то значение, предоставляемое датчиком, напрямую и без потерь отображается в тип данных с фиксированной точкой с 11 битами справа от двоичной точки. Напротив, если в качестве единицы хранения угла используются радианы, то неточности и стоимость умножения необработанного целого числа датчика на приближение к было бы понесено.
См. также
[ редактировать ]- Таблица синусов Арьябхаты
- Формула аппроксимации синуса Бхаскары I
- Дискретное синусоидальное преобразование
- Эллиптические функции Диксона
- Формула Эйлера
- Обобщенная тригонометрия
- Гиперболическая функция
- Лемнискатные эллиптические функции
- Закон синусов
- Список периодических функций
- Список тригонометрических тождеств
- Серия Мадхава
- Таблица синусов Мадхавы
- Теорема оптического синуса
- Полярный синус - обобщение углов при вершинах.
- Доказательства тригонометрических тождеств.
- Функция Sinc
- Синусные и косинусные преобразования
- Синусоидальный интеграл
- Синусоидальный квадрант
- Синусоидальная волна
- Уравнение Синус – Гордон
- Синусоидальная модель
- СОХ-КА-ТОА
- Тригонометрические функции
- Тригонометрический интеграл
Цитаты
[ редактировать ]- ^ Jump up to: а б с Вайсштейн, Эрик В. «Синус» . mathworld.wolfram.com . Проверено 29 августа 2020 г.
- ^ Jump up to: а б с Янг, Синтия (2017). Тригонометрия . Джон Уайли и сыновья. п. 27. ISBN 978-1-119-32113-2 .
- ^ Альфорс, Ларс (1 января 1979 г.). Комплексный анализ (3-е изд.). стр. 43–44.
- ^ «Функция синус-квадрат» . Проверено 9 августа 2019 г.
- ^ «ОЭИС А003957» . oeis.org . Проверено 26 мая 2019 г.
- ^ Jump up to: а б «А105419 — Оайс» .
- ^ Адлай, Семен (2012). «Красноречивая формула периметра эллипса» (PDF) . Американское математическое общество . п. 1097.
- ^ Рудин, Уолтер (1987). Реальный и комплексный анализ (Третье изд.). Книжная компания МакГроу-Хилл. ISBN 0-07-100276-6 . п. 299, Теорема 15.4.
- ^ «Почему фазовый портрет простого плоского маятника и доменная раскраска sin(z) так похожи?» . math.stackexchange.com . Проверено 12 августа 2019 г.
- ^ Брендан, Т. (февраль 1965 г.). «Как Птолемей построил таблицы тригонометрии». Учитель математики . 58 (2): 141–149. дои : 10.5951/MT.58.2.0141 . JSTOR 27967990 – через JSTOR.
- ^ Jump up to: а б с Мерцбах, Ута К. ; Бойер, Карл Б. (2011), История математики (3-е изд.), John Wiley & Sons : Именно перевод Роберта Честера с арабского языка привел к появлению нашего слова «синус». Индусы дали полухорде название джива в тригонометрии, а арабы переняли его как джиба. В арабском языке также есть слово джаиб, означающее «залив» или «залив». Когда Роберт Честерский начал переводить техническое слово джиба, он, похоже, перепутал его со словом джаиб (возможно, потому, что были опущены гласные); следовательно, он использовал слово sinus, латинское слово, означающее «залив» или «входное отверстие».
- ^ Jump up to: а б Джинджерич, Оуэн (1986). «Исламская астрономия» . Научный американец . Том. 254. с. 74. Архивировано из оригинала 19 октября 2013 г. Проверено 13 июля 2010 г.
- ^ Жак Сезиано, «Исламская математика», с. 157, в Селин, Хелейн ; Д'Амброзио, Убиратан , ред. (2000). Математика в разных культурах: история незападной математики . Springer Science+Business Media . ISBN 978-1-4020-0260-1 .
- ^ Jump up to: а б «тригонометрия» . Британская энциклопедия. 17 июня 2024 г.
- ^ Николас Бурбаки (1994). Элементы истории математики . Спрингер. ISBN 9783540647676 .
- ^ « Почему у синуса есть простая производная. Архивировано 20 июля 2011 г. в Wayback Machine », в «Исторических заметках для учителей исчисления». Архивировано 20 июля 2011 г. в Wayback Machine В. Фредериком Рики. Архивировано 20 июля 2011 г. в Вейбэк-машина
- ^ «Как триггерные функции получили свои названия» . Спросите доктора Математика . Дрексельский университет . Проверено 2 марта 2010 г.
- ^ Джей Джей О'Коннор и Э. Ф. Робертсон (июнь 1996 г.). «Тригонометрические функции» . Проверено 2 марта 2010 г.
- ^ См. Плофкер, Математика в Индии , Princeton University Press, 2009, стр. 257
Видеть «Университет Кларка» . Архивировано из оригинала 15 июня 2008 года.
См. Maor (1998), главу 3, относительно этимологии. - ^ Эли Маор (1998), Тригонометрические наслаждения , Принстон: Princeton University Press, стр. 35-36.
- ^ Виктор Дж. Кац (2008), История математики , Бостон: Аддисон-Уэсли, 3-е место. ред., с. 253, врезка 8.1. «История математики» (PDF) . Архивировано (PDF) из оригинала 14 апреля 2015 г. Проверено 9 апреля 2015 г. : Английское слово «синус» происходит от серии неправильных переводов санскритского джья-ардха (половина аккорда). Арьябхата часто сокращал этот термин до джья или его синонима джива . Когда некоторые из индуистских произведений были позже переведены на арабский язык, это слово было просто фонетически транскрибировано в бессмысленное арабское слово джиба . Но поскольку арабский язык пишется без гласных, более поздние авторы интерпретировали согласные jb как jaib , что означает грудь или грудь. В двенадцатом веке, когда работа по арабской тригонометрии была переведена на латынь, переводчик использовал эквивалентное латинское слово sinus , которое также означало грудь и, в более широком смысле, складку (как в тоге на груди), залив или залив.
- ^ Смит, Д.Э. (1958) [1925], История математики , том. Я, Дувр, с. 202, ISBN 0-486-20429-4
- ^ Различные источники приписывают первое использование пазухи либо
- Перевод Платона Тибуртина « 1116 года. Астрономии Аль -Баттани»
- Герарда Кремонского Перевод «Алгебры аль -Хорезми»
- Робертом Честерским в 1145 году. Перевод таблиц аль-Хорезми
См. Maor (1998), глава 3, где приведена более ранняя этимология, в которой упоминается Джерард.
Видеть Каткс, Виктор (июль 2008 г.). История математики (3-е изд.). Бостон: Пирсон . п. 210 (боковая панель). ISBN 978-0321387004 . - ↑ Англизированная форма впервые упоминается в 1593 году в Томаса Фэйла «Часографии, искусстве набора номера» .
- ^ Гюнтер, Эдмунд (1620). Канон треугольников
- ^ Рогель, Денис, изд. (6 декабря 2010 г.). «Реконструкция Треугольного канона Гюнтера (1620 г.)» (отчет об исследовании). ХЭЛ. инрия-00543938. Архивировано из оригинала 28 июля 2017 года . Проверено 28 июля 2017 года .
- ^ «косинус» .
- ^ Циммерманн, Пол (2006), «Можем ли мы доверять числам с плавающей запятой?», «Большие проблемы информатики» (PDF) , стр. 31 ноября, заархивировано (PDF) из оригинала 16 июля 2011 г. , получено 11 сентября 2010 г.
- ^ Jump up to: а б " Документация MATLAB sinpi
- ^ Jump up to: а б " Документация R sinpi
- ^ " Документация OpenCL sinpi
- ^ " Документация Джулии sinpi
- ^ " Документация CUDA sinpi
- ^ " Документация ARM sinpi
- ^ " Техническое описание датчика угла ALLEGRO , заархивировано 17 апреля 2019 г. на Wayback Machine.
Ссылки
[ редактировать ]- Траупман, доктор философии, Джон К. (1966), Латинский и английский словарь Нового колледжа , Торонто: Bantam, ISBN 0-553-27619-0
- Седьмой новый университетский словарь Вебстера , Спрингфилд: G. & C. Merriam Company, 1969.
Внешние ссылки
[ редактировать ] СМИ, связанные с функцией синуса, на Викискладе?
СМИ, связанные с функцией синуса, на Викискладе?
![{\displaystyle {\begin{aligned}&\sin(\alpha)={\frac {\textrm {противоположность}}{\textrm {гипотенуза}}}\\[8pt]&\cos(\alpha)={\ frac {\textrm {adjacent}}{\textrm {гипотенуза}}}\\[8pt]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea2762f231f5fdc1dcfacd59c303106f596ab2e1)


















![{\displaystyle {\begin{aligned}\sin z&=\sin x\cosh y+i\cos x\sinh y\\[5pt]\cos z&=\cos x\cosh yi\sin x\sinh y\end {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c1646655eab602e234f42df85cae241ffbb867cf)







![{\displaystyle {\begin{aligned}\sin(x)&=x- {\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}- {\frac {x^{7}}{7!}}+\cdots \\[5mu]&=\sum _{n=0}^{\infty }{\frac {(-1)^{n} }{(2n+1)!}}x^{2n+1}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d9e556638e5bae76e7f002d24327023007673221)
![{\displaystyle {\begin{aligned}\cos(x)&=1- {\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}- {\frac {x^{6}}{6!}}+\cdots \\[5mu]&=\sum _{n=0}^{\infty }{\frac {(-1)^{n} }{(2n)!}}x^{2n}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/09c2868a6d99b6f581a5d53b177b7b108570c301)















































































![{\displaystyle \cos(zx)={\frac {z\sin(\pi z)}{\pi }}\displaystyle \sum _{n=-\infty }^{\infty }{\frac {(-1)^{n}\,e^{inx}}{z^{2}-n^{2}}},\,z\in \mathbb {C} \setminus \mathbb {Z} ,\,x\in [-\pi ,\pi ].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4344e0e79e6b3e4af5cabc1ae8ac71054f88e915)


























