Стандартный счет

В статистике стандартной оценкой является количество стандартных отклонений , с помощью которых значение необработанного балла (то есть наблюдаемого значения или точки данных) выше или ниже среднего значения того, что наблюдается или измеряется. Необработанные оценки выше среднего имеют положительные стандартные оценки, в то время как те, кто ниже среднего, имеют отрицательные стандартные оценки.

Он рассчитывается путем вычитания среднего значения населения из индивидуального необработанного балла, а затем деления разницы на стандартное отклонение населения . Этот процесс преобразования необработанного балла в стандартную оценку называется стандартизацией или нормализацией (однако, «нормализация» может относиться ко многим типам соотношений; см. Нормализацию для большего).

Стандартные оценки чаще всего называются z -шрифтами ; Два термина могут использоваться взаимозаменяемо, как они есть в этой статье. Другие эквивалентные используемые термины включают Z-значение , Z-статистику , нормальную оценку , стандартизированную переменную и привлечение физики с высокой энергией . ^{[ 1 ]}^{[ 2 ]}

Вычисление Z-показателя требует знания среднего и стандартного отклонения полной популяции, к которой принадлежит точка данных; Если у человека есть только выборка наблюдений из популяции, то аналогичное вычисление с использованием среднего среднего и стандартного отклонения выборки дает T -статистику .

Расчет

Если известно среднее население и стандартное отклонение населения, необработанный балл x преобразуется в стандартную оценку ^{[ 3 ]}

z={x-\mu  \over \sigma }

где:

μ - среднее населения,

σ - стандартное отклонение населения.

Абсолютное значение z представляет собой расстояние между этой необработанной оценкой x и средним значением населения в единицах стандартного отклонения. z является отрицательным, когда необработанный балл ниже среднего, положительного, когда выше.

Расчет Z Использование этой формулы требует использования среднего значения популяции и стандартного отклонения населения, а не среднего значения выборки или отклонения выборки. Однако знание истинного среднего и стандартного отклонения населения часто является нереалистичным ожиданием, за исключением таких случаев, как стандартизированное тестирование , где измеряется вся популяция.

Когда среднее значение населения и стандартное отклонение населения неизвестны, стандартная оценка может быть оценена с использованием среднего среднего и стандартного отклонения выборки в качестве оценок значений населения. ^{[ 4 ]}^{[ 5 ]}^{[ 6 ]}^{[ 7 ]}

В этих случаях z -Score дается

z={x-{\bar {x}} \over S}

где:

{\bar {x}}

это среднее из образца,

S - стандартное отклонение образца.

Хотя это всегда должно быть заявлено, различие между использованием популяции и статистикой выборки часто не проводится. В любом случае числитель и знаменатель уравнений имеют одинаковые единицы измерения, так что единицы отмены через разделение, а z оставляют в качестве безразмерного количества .

Приложения

Z-тест

Z-показатель часто используется в z-тесте в стандартизированном тестировании-аналогом T-критерия студента для популяции, параметры которых известны, а не оценены. Поскольку очень необычно знать всю популяцию, t-критерий гораздо более широко используется.

Интервалы прогнозирования

Стандартный балл может быть использован при расчете интервалов прогнозирования . Интервал прогнозирования [ l , u ], состоящий из нижней конечной точки, обозначенной L и верхней конечной точки U , является интервалом, так что будущее наблюдение x будет лежать в интервале с высокой вероятностью $\gamma$ IE

P(L<X<U)=\gamma ,

стандартной оценки z x Для дает: ^{[ 8 ]}

P\left({\frac {L-\mu }{\sigma }}<Z<{\frac {U-\mu }{\sigma }}\right)=\gamma .

Определяя квантильный Z, такой, что

P\left(-z<Z<z\right)=\gamma

Это следует:

L=\mu -z\sigma ,\ U=\mu +z\sigma

Управление процессом

В приложениях управления процессами значение Z обеспечивает оценку степени, в которой процесс работает вне цели.

Сравнение баллов, измеренных в разных масштабах: ACT и SAT

Когда оценки измеряются в разных масштабах, они могут быть преобразованы в Z-оценки для сравнения. Dietz et al. ^{[ 9 ]} Приведите следующий пример, сравнивая оценки учащихся на (старых) SAT и ACT School Spects. В таблице показано среднее и стандартное отклонение для общих баллов по SAT и ACT. Предположим, что этот студент забил 1800 на SAT, а студент B забил 24 по акту. Какой студент показал лучшее по сравнению с другими тестирующими?

	Сидящий	ДЕЙСТВОВАТЬ
Иметь в виду	1500	21
Стандартное отклонение	300	5

Z-оценка для студента A $z={x-\mu \over \sigma }={1800-1500 \over 300}=1$

Z-оценка для студента B $z={x-\mu \over \sigma }={24-21 \over 5}=0.6$

Поскольку у студента А есть более высокий Z-показатель, чем у студента B, студент A выступил лучше по сравнению с другими тестирующими, чем ученик B.

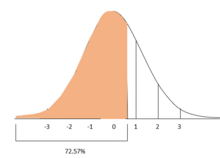
Процент наблюдений ниже z-показателя

Продолжение примера баллов ACT и SAT, если можно дополнительно предположить, что оценки ACT и SAT обычно распределены (что приблизительно правильно), то оценки Z могут использоваться для расчета процента испытателей, которые получали более низкие результаты, чем студенты A и B.

Кластерный анализ и многомерное масштабирование

«Для некоторых многомерных методов, таких как многомерное масштабирование и кластерный анализ, концепция расстояния между единицами в данных часто представляет значительный интерес и важность… Когда переменные в многомерном наборе данных находятся в разных масштабах, имеет смысл расчет Расстояния после некоторой формы стандартизации ». ^{[ 10 ]}

Анализ основных компонентов

В анализе основных компонентов «переменные, измеренные в разных шкалах или по общей шкале с широко разными диапазонами, часто стандартизируются». ^{[ 11 ]}

Относительная важность переменных в множественной регрессии: стандартизированные коэффициенты регрессии

Стандартизация переменных до множественного регрессионного анализа иногда используется в качестве помощи для интерпретации. ^{[ 12 ]} (стр. 95) Укажите следующее.

«Стандартизированный наклон регрессии - это наклон в уравнении регрессии, если x и y стандартизированы… стандартизация x и y выполняется путем вычитания соответствующих средств из каждого набора наблюдений и деления на соответствующие стандартные отклонения… в множественных регрессии, где несколько Используются переменные x, стандартизированные коэффициенты регрессии определяют относительный вклад каждой переменной x.

Однако Kutner et al. ^{[ 13 ]} (стр. 278) Дайте следующее предостережение: «… Нужно быть осторожным в интерпретации каких -либо коэффициентов регрессии, стандартизированных или нет. Причина в том, что когда переменные предиктора коррелированы между собой,… коэффициенты регрессии влияют другие переменные предиктора В модели… величины стандартизированных коэффициентов регрессии влияют не только наличие корреляций между переменными предикторов, но также и различными наблюдениями на каждой из этих переменных Обычно не разумно интерпретировать величины стандартизированных коэффициентов регрессии как отражение сравнительной важности переменных предиктора ».

Стандартизация в математической статистике

В математической статистике случайная величина x стандартизируется ожидаемого путем вычитания его значения $\operatorname {E} [X]$ и делить разницу на его стандартное отклонение $\sigma (X)={\sqrt {\operatorname {Var} (X)}}:$

Z={X-\operatorname {E} [X] \over \sigma (X)}

Если рассматриваемой случайной величиной является среднее значение случайной выборки $\ X_{1},\dots ,X_{n}$ X :

{\bar {X}}={1 \over n}\sum _{i=1}^{n}X_{i}

тогда стандартизированная версия

Z={\frac {{\bar {X}}-\operatorname {E} [{\bar {X}}]}{\sigma (X)/{\sqrt {n}}}}

Где дисперсия стандартизированного среднего значения была рассчитана следующим образом:

{\begin{array}{l}\operatorname {Var} \left(\sum x_{i}\right)=\sum \operatorname {Var} (x_{i})=n\operatorname {Var} (x_{i})=n\sigma ^{2}\\\operatorname {Var} ({\overline {X}})=\operatorname {Var} \left({\frac {\sum x_{i}}{n}}\right)={\frac {1}{n^{2}}}\operatorname {Var} \left(\sum x_{i}\right)={\frac {n\sigma ^{2}}{n^{2}}}={\frac {\sigma ^{2}}{n}}\end{array}}

T-Score

При оценке образования T-показатель является стандартной оценкой Z, сдвинутой и масштабированным, чтобы иметь среднее значение 50 и стандартное отклонение 10. ^{[ 14 ]}^{[ 15 ]}^{[ 16 ]} Он также известен как Хенсоши на японском языке, где эта концепция гораздо более широко известна и используется в контексте поступлений в старшую школу и университета.

При измерениях плотности костей T-показатель является стандартной оценкой измерения по сравнению с популяцией здоровых 30-летних взрослых, и имеет обычное среднее значение 0 и стандартное отклонение 1. ^{[ 17 ]}

Смотрите также

Ссылки

^ Малдерс, Мартиян; Зандерги, Джулия, ред. (2017). Европейская школа высокоэнергетической физики 2015 года: Банско, Болгария 02 - 15 сентября 2015 года . Cern Yellow Reports: Школьное разбирательство. Женева: Церн. ISBN 978-92-9083-472-4 .
^ Гросс, Эйлам (2017-11-06). «Практическая статистика для физики высокой энергии» . Cern Yellow Reports: Школьное разбирательство . 4/2017: 165–186. doi : 10.23730/cyrsp-2017-004.165 .
^ E. Kreyszig (1979). Усовершенствованная инженерная математика (четвертое изд.). Уайли. п. 880, уравнение 5. ISBN 0-471-02140-7 .
^ Spiegel, Murray R.; Стивенс, Ларри Дж. (2008), Статистика Шаума (четвертое изд.), McGraw Hill, ISBN 978-0-07-148584-5
^ Менденхолл, Уильям; Sincich, Terry (2007), Статистика инженерии и наук (пятое изд.), Pearson / Prentice Hall, ISBN 978-0131877061
^ Гланц, Стентон А.; Слинкер, Брайан К.; Neilands, Torsten B. (2016), праймер прикладной регрессии и дисперсии (третье изд.), McGraw Hill, ISBN 978-0071824118
^ Ахо, Кен А. (2014), Основополагающая и прикладная статистика для биологов (первое изд.), Chapman & Hall / Crc Press, ISBN 978-1439873380
^ E. Kreyszig (1979). Усовершенствованная инженерная математика (четвертое изд.). Уайли. п. 880, уравнение 6. ISBN 0-471-02140-7 .
^ Диз, Дэвид; Барр, Кристофер; Çetinkaya-rundel, Mine (2012), OpenIntro Statistics (второе изд.), OpenIntro.org
^ Эверитт, Брайан; Hothorn, Torsten J (2011), введение в прикладное многовариантное анализ с R , Springer, ISBN 978-1441996497
^ Джонсон, Ричард; Wichern, Wichern (2007), Applied Multivariate Statistical Analysis , Pearson / Prentice Hall
^ Afifi, Abdelmonem; Май, Сюзанна К.; Кларк, Вирджиния А. (2012), Практический многомерный анализ (пятое изд.), Chapman & Hall/Crc, ISBN 978-1439816806
^ Кутнер, Майкл; Нахтсхайм, Кристофер; Neter, John (204), прикладные модели линейной регрессии (четвертое изд.), McGraw Hill, ISBN 978-0073014661
^ Джон Сальвия; Джеймс Иссельдике; Сара Витмер (29 января 2009 г.). Оценка: в специальном и инклюзивном образовании . Cengage Learning. С. 43–. ISBN 978-0-547-13437-6 .
^ Эдвард С. Нейкруг; Р. Чарльз Фосетт (1 января 2014 г.). Основы тестирования и оценки: практическое руководство для консультантов, социальных работников и психологов . Cengage Learning. С. 133–. ISBN 978-1-305-16183-2 .
^ Рэнди В. Кампхаус (16 августа 2005 г.). Клиническая оценка разведки детей и подростков . Спрингер. С. 123–. ISBN 978-0-387-26299-4 .
^ «Измерение костной массы: что означают цифры» . NIH остеопороз и связанные с ними заболевания костей Национальный центр ресурсов . Национальный институт здравоохранения . Получено 5 августа 2017 года .

Дальнейшее чтение

Кэрролл, Сьюзен Ровецци; Кэрролл, Дэвид Дж. (2002). Статистика сделана простыми для школьных лидеров (иллюстрировано изд.). Роуман и Литтлфилд. ISBN 978-0-8108-4322-6 Полем Получено 7 июня 2009 года .
Ларсен, Ричард Дж.; Маркс, Моррис Л. (2000). Введение в математическую статистику и ее приложения (третье изд.). п. 282. ISBN 0-13-922303-7 .

Внешние ссылки

z-балковой калькулятор

[1] Малдерс, Мартиян; Зандерги, Джулия, ред. (2017). Европейская школа высокоэнергетической физики 2015 года: Банско, Болгария 02 - 15 сентября 2015 года . Cern Yellow Reports: Школьное разбирательство. Женева: Церн. ISBN 978-92-9083-472-4 .

[2] Гросс, Эйлам (2017-11-06). «Практическая статистика для физики высокой энергии» . Cern Yellow Reports: Школьное разбирательство . 4/2017: 165–186. doi : 10.23730/cyrsp-2017-004.165 .

[3] E. Kreyszig (1979). Усовершенствованная инженерная математика (четвертое изд.). Уайли. п. 880, уравнение 5. ISBN 0-471-02140-7 .

[SpiegelStephens2008-4] Spiegel, Murray R.; Стивенс, Ларри Дж. (2008), Статистика Шаума (четвертое изд.), McGraw Hill, ISBN 978-0-07-148584-5

[Mendenhall2007-5] Менденхолл, Уильям; Sincich, Terry (2007), Статистика инженерии и наук (пятое изд.), Pearson / Prentice Hall, ISBN 978-0131877061

[GlantzSlinker2016-6] Гланц, Стентон А.; Слинкер, Брайан К.; Neilands, Torsten B. (2016), праймер прикладной регрессии и дисперсии (третье изд.), McGraw Hill, ISBN 978-0071824118

[Aho2014-7] Ахо, Кен А. (2014), Основополагающая и прикладная статистика для биологов (первое изд.), Chapman & Hall / Crc Press, ISBN 978-1439873380

[8] E. Kreyszig (1979). Усовершенствованная инженерная математика (четвертое изд.). Уайли. п. 880, уравнение 6. ISBN 0-471-02140-7 .

[Diez2012-9] Диз, Дэвид; Барр, Кристофер; Çetinkaya-rundel, Mine (2012), OpenIntro Statistics (второе изд.), OpenIntro.org

[EverittHothorn2011-10] Эверитт, Брайан; Hothorn, Torsten J (2011), введение в прикладное многовариантное анализ с R , Springer, ISBN 978-1441996497

[JohnsonWichern2007-11] Джонсон, Ричард; Wichern, Wichern (2007), Applied Multivariate Statistical Analysis , Pearson / Prentice Hall

[AfifiMayClark2012-12] Afifi, Abdelmonem; Май, Сюзанна К.; Кларк, Вирджиния А. (2012), Практический многомерный анализ (пятое изд.), Chapman & Hall/Crc, ISBN 978-1439816806

[KutnerNachtsheim2004-13] Кутнер, Майкл; Нахтсхайм, Кристофер; Neter, John (204), прикладные модели линейной регрессии (четвертое изд.), McGraw Hill, ISBN 978-0073014661

[14] Джон Сальвия; Джеймс Иссельдике; Сара Витмер (29 января 2009 г.). Оценка: в специальном и инклюзивном образовании . Cengage Learning. С. 43–. ISBN 978-0-547-13437-6 .

[15] Эдвард С. Нейкруг; Р. Чарльз Фосетт (1 января 2014 г.). Основы тестирования и оценки: практическое руководство для консультантов, социальных работников и психологов . Cengage Learning. С. 133–. ISBN 978-1-305-16183-2 .

[16] Рэнди В. Кампхаус (16 августа 2005 г.). Клиническая оценка разведки детей и подростков . Спрингер. С. 123–. ISBN 978-0-387-26299-4 .

[17] «Измерение костной массы: что означают цифры» . NIH остеопороз и связанные с ними заболевания костей Национальный центр ресурсов . Национальный институт здравоохранения . Получено 5 августа 2017 года .

[ 1 ]

[ 2 ]

[ 3 ]

[ 4 ]

[ 5 ]

[ 6 ]

[ 7 ]

[ 8 ]

[ 9 ]

[ 10 ]

[ 11 ]

[ 12 ]

[ 13 ]

[ 14 ]

[ 15 ]

[ 16 ]

[ 17 ]