Van der Pol oscillator

При изучении динамических систем генератор Ван дер Поля (названный в честь голландского физика ван дер Поля ) представляет собой неконсервативную колебательную систему Бальтазара с нелинейным затуханием . Оно развивается во времени согласно дифференциальному уравнению второго порядка ${d^{2}x \over dt^{2}}-\mu (1-x^{2}){dx \over dt}+x=0,$ где $x$ положения — координата , которая является функцией времени $t$ , а $μ$ — скалярный параметр, указывающий нелинейность и силу демпфирования.

осциллятора Ван дер Поля Фазовый график , где

значение μ

варьируется от 0,1 до 3,0. Зеленые линии — это линии

x

- nullclines .

Тот же фазовый график осциллятора, но с преобразованием Льенара .

Эволюция предельного цикла на фазовой плоскости . Предельный цикл начинается с круга и с изменением $ц$ становится все более острым. Пример релаксационного генератора .

История

Генератор Ван дер Поля был первоначально предложен голландским инженером-электриком и физиком Бальтазаром ван дер Полем, когда он работал в компании Philips . ^[2] Ван дер Поль обнаружил устойчивые колебания. ^[3] которые он впоследствии назвал релаксационными колебаниями ^[4] и теперь известны как тип предельного цикла в электрических цепях, использующих электронные лампы . Когда эти цепи работают вблизи предельного цикла , они увлекаются , то есть управляющий сигнал тянет за собой ток. Ван дер Поль и его коллега ван дер Марк сообщили в сентябрьском номере журнала Nature привода за 1927 год, что на определенных частотах был слышен нерегулярный шум : ^[5] который позже был признан результатом детерминированного хаоса . ^[6]

Уравнение Ван дер Поля имеет долгую историю использования как в физических , так и в биологических науках . Например, в биологии Фитцхью ^[7] и Нагумо ^[8] уравнение плоского поля как модель потенциалов действия нейронов расширил . Уравнение также использовалось в сейсмологии для моделирования двух плит в геологическом разломе . ^[9] и в исследованиях фонации для моделирования генераторов правой и левой голосовых связок . ^[10]

Двумерная форма

Теорему Льенара можно использовать для доказательства того, что система имеет предельный цикл. Применение преобразования Льенара $y=x-x^{3}/3-{\dot {x}}/\mu$ , где точка указывает производную по времени, генератор Ван дер Поля можно записать в двумерной форме: ^[11]

{\dot {x}}=\mu \left(x-{\tfrac {1}{3}}x^{3}-y\right)

{\dot {y}}={\frac {1}{\mu }}x

.

Другая часто используемая форма, основанная на преобразовании $y={\dot {x}}$ приводит к:

{\dot {x}}=y

{\dot {y}}=\mu (1-x^{2})y-x

.

Результаты для невынужденного осциллятора

Релаксационные колебания в генераторе Ван дер Поля без внешнего воздействия. Параметр нелинейного демпфирования равен

µ = 5

.

^[12]

Когда $µ = 0$ , т.е. функция демпфирования отсутствует, уравнение принимает вид ${\frac {d^{2}x}{dt^{2}}}+x=0.$ Это разновидность простого гармонического осциллятора , в котором всегда сохраняется энергия .

Когда $µ > 0$ , все начальные условия сходятся к глобально уникальному предельному циклу. Рядом с источником $x={\tfrac {dx}{dt}}=0,$ система неустойчива и вдали от начала координат система затухает.
Осциллятор Ван дер Поля не имеет точного аналитического решения. ^[13] Однако такое решение существует для предельного цикла, если $f (x)$ в уравнении Льенара является постоянной кусочной функцией.
Период при малых $μ$ имеет серийное разложение $T={\frac {2\pi }{1-\mu ^{2}/16+17\mu ^{4}/3072+O(\mu ^{6})}}.$ См . главу 10 книги. метод Пуанкаре – Линдстедта. Для вывода до порядка 2 см. ^[14] для вывода до порядка 3, и ^[15] для численного вывода до порядка 164.
При больших ц поведение осциллятора имеет цикл медленного нарастания и быстрого ослабления (цикл нарастания и снятия напряжения, то есть релаксационные колебания ). Это легче всего увидеть в виде ${\dot {x}}=\mu \left(x-{\frac {1}{3}}x^{3}-y\right)\!,\quad {\dot {y}}={\frac {1}{\mu }}x.$ ${\dot {x}}=\mu \left(x- {\frac {1}{3}}x^{3}-y\right)\!,\quad {\dot {y}} = {\frac {1}{\mu }}x.$ В этой форме осциллятор завершает один цикл следующим образом:
- Медленно поднимаясь по правой ветви кубической кривой. $y=x-{\tfrac {x^{3}}{3}},$ от $(2, -2/3)$ до $(1, 2/3)$ .
- Быстрое движение к левой ветви кубической кривой от $(1, 2/3)$ к $(-2, 2/3)$ .
- Повторите два шага на левой ветке.
Ведущий член периода цикла обусловлен медленными восходящими и нисходящими темпами, которые можно рассчитать как: $T=2\int dt=2\int \mu {\frac {dy}{x}}=2\mu \int _{2}^{1}{\frac {dy}{dx}}{\frac {dx}{x}}=(3-2\ln 2)\mu$ Высшие порядки периода цикла $T=(3-2\ln 2)\mu +3\alpha \mu ^{-1/3}-{\frac {22}{9\mu }}\ln \mu +{\frac {0.0087\cdots }{\mu }}+O(\mu ^{-4/3}).$ где $α \approx 2,338$ — наименьший корень из $Ai(- α) = 0$ , где $Ai$ — функция Эйри . (раздел 9.7 ^[16]) ( ^[17] содержит вывод, но имеет опечатку от $3 α$ до $2 α$ .) Это вывел Анатолий Дородницын . ^[18]^[19]
Амплитуда цикла ^[20] $2+{\frac {\alpha }{3}}\mu ^{-4/3}-{\frac {16}{27}}\mu ^{-2}\ln \mu +O(\mu ^{-2})$

бифуркация Хопфа

Когда $μ$ перемещается от меньшего нуля к большему нуля, спиральный сток в начале становится спиральным источником, и «неожиданно» появляется предельный цикл с радиусом два. Это связано с тем, что переход не является общим: когда $ε = 0$ , дифференциальное уравнение становится линейным, а начало координат становится круговым узлом.

Зная, что при бифуркации Хопфа предельный цикл должен иметь размер $\propto \varepsilon ^{1/2},$ мы можем попытаться преобразовать это в бифуркацию Хопфа, используя замену переменных $u=\varepsilon ^{1/2}x,$ что дает ${\ddot {u}}+u+u^{2}{\dot {u}}-\varepsilon {\dot {u}}=0$ Это действительно бифуркация Хопфа. ^[21]

Гамильтониан для осциллятора Ван дер Поля

Случайно выбранные начальные условия притягиваются к устойчивой орбите.

Можно также написать независимый от времени гамильтонов формализм для осциллятора Ван дер Поля, дополнив его до четырехмерной автономной динамической системы с использованием вспомогательного нелинейного дифференциального уравнения второго порядка следующим образом:

{\ddot {x}}-\mu (1-x^{2}){\dot {x}}+x=0,

{\ddot {y}}+\mu (1-x^{2}){\dot {y}}+y=0.

Обратите внимание, что на динамику исходного осциллятора Ван дер Поля не влияет односторонняя связь между временными изменениями переменных x и y . гамильтониан H для этой системы уравнений равен Можно показать, что ^[22]

H(x,y,p_{x},p_{y})=p_{x}p_{y}+xy-\mu (1-x^{2})yp_{y},

где $p_{x}={\dot {y}}+\mu (1-x^{2})y$ и $p_{y}={\dot {x}}$ — сопряженные импульсы , соответствующие x и y соответственно. В принципе это может привести к квантованию генератора Ван дер Поля. Такой гамильтониан также связывает ^[23] геометрическая фаза системы предельного цикла, имеющая параметры, зависящие от времени, с углом Ханнея соответствующей гамильтоновой системы.

Квантовый осциллятор

Квантовый осциллятор Ван дер Поля, который является квантовомеханической версией классического осциллятора Ван дер Поля, был предложен с использованием уравнения Линдблада для изучения его квантовой динамики и квантовой синхронизации . ^[24] Обратите внимание, что приведенный выше гамильтонов подход со вспомогательным уравнением второго порядка дает неограниченные траектории в фазовом пространстве и, следовательно, не может использоваться для квантования осциллятора Ван дер Поля. В пределе слабой нелинейности (т.е. µ→ 0) осциллятор Ван дер Поля сводится к уравнению Стюарта – Ландау . Уравнение Стюарта–Ландау фактически описывает целый класс осцилляторов предельного цикла в слабонелинейном пределе. Форма классического уравнения Стюарта – Ландау намного проще и, что, возможно, неудивительно, может быть квантована с помощью уравнения Линдблада, которое также проще, чем уравнение Линдблада для осциллятора Ван дер Поля. Квантовая модель Стюарта – Ландау сыграла важную роль в изучении квантовой синхронизации. ^[25]^[26] (где его часто называют осциллятором Ван дер Поля, хотя его нельзя однозначно связать с осциллятором Ван дер Поля). Связь между классической моделью Стюарта – Ландау ( ц → 0) и более общими осцилляторами предельного цикла (произвольный ц ) также была продемонстрирована численно в соответствующих квантовых моделях. ^[24]

Forced Van der Pol oscillator

Хаотическое поведение генератора Ван дер Поля с синусоидальным воздействием. Параметр нелинейного демпфирования равен

µ = 8,53

, а воздействие имеет амплитуду

A = 1,2

и угловую частоту

ω = 2π/10

.

Вынужденный или управляемый генератор Ван дер Поля берет «исходную» функцию и добавляет движущую функцию $A sin(ωt),$ чтобы получить дифференциальное уравнение вида:

{d^{2}x \over dt^{2}}-\mu (1-x^{2}){dx \over dt}+x-A\sin(\omega t)=0,

где $A$ — амплитуда или смещение волновой функции , а $ω$ — ее угловая скорость .

См. также

Мэри Картрайт , британский математик, одна из первых, кто изучил теорию детерминированного хаоса, в частности, применительно к этому осциллятору. ^[30]

Ссылки

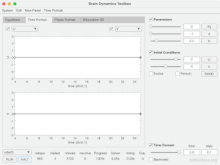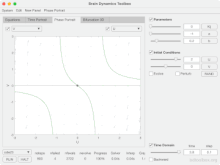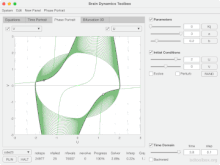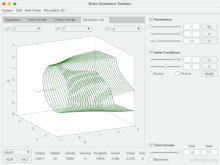
^ Хейтманн, С., Брейкспир, М (2017–2022) Набор инструментов для динамики мозга. bdtoolbox.org doi.org/10.5281/zenodo.5625923
^ Картрайт, ML (1960). «Бальтазар Ван Дер Поль» . Журнал Лондонского математического общества . с1-35(3). Уайли: 367–376. дои : 10.1112/jlms/s1-35.3.367 . ISSN 0024-6107 .
^ Б. ван дер Пол: «Теория амплитуды свободных и вынужденных колебаний триода», Radio Review (позже Wireless World) 1 701–710 (1920)
^ ван дер Пол, Балт. (1926). «О «релаксации-колебаниях» ». Лондонский, Эдинбургский и Дублинский философский журнал и научный журнал . 2 (11). Информа UK Limited: 978–992. дои : 10.1080/14786442608564127 . ISSN 1941-5982 .
^ ВАН ДЕР ПОЛ, БАЛТ; ВАН ДЕР МАРК, Дж. (1927). «Деммножение частоты». Природа . 120 (3019). ООО «Спрингер Сайенс энд Бизнес Медиа»: 363–364. Бибкод : 1927Natur.120..363V . дои : 10.1038/120363a0 . ISSN 0028-0836 . S2CID 186244992 .
^ Канамару, Т., «Осциллятор Ван дер Поля» , Scholarpedia , 2 (1), 2202, (2007).
^ ФитцХью, Ричард (1961). «Импульсы и физиологические состояния в теоретических моделях нервной мембраны» . Биофизический журнал . 1 (6). Эльзевир Б.В.: 445–466. Бибкод : 1961BpJ.....1..445F . дои : 10.1016/s0006-3495(61)86902-6 . ISSN 0006-3495 . ПМЦ 1366333 . ПМИД 19431309 .
^ Нагумо, Дж.; Аримото, С.; Ёсидзава, С. (1962). «Активная линия передачи импульсов, имитирующая нервный аксон». Труды ИРЭ . 50 (10). Институт инженеров по электротехнике и электронике (IEEE): 2061–2070. дои : 10.1109/jrproc.1962.288235 . ISSN 0096-8390 . S2CID 51648050 .
^ Картрайт, Джулиан HE ; Эгилуз, Виктор М.; Эрнандес-Гарсия, Эмилио; Пиро, Оресте (1999). «Динамика упругих возбудимых сред». Международный журнал бифуркации и хаоса . 09 (11): 2197–2202. arXiv : чао-дин/9905035 . Бибкод : 1999IJBC....9.2197C . дои : 10.1142/s0218127499001620 . ISSN 0218-1274 . S2CID 9120223 .
^ Лусеро, Хорхе К.; Шентген, Жан (2013). Моделирование асимметрии голосовых связок с помощью связанных осцилляторов Ван дер Поля . Материалы совещаний по акустике. Том. 19. с. 060165. дои : 10.1121/1.4798467 . ISSN 1939-800Х .
^ Каплан Д. и Гласс Л., Понимание нелинейной динамики , Springer, 240–244, (1995).
^ Гримшоу, Р., Нелинейные обыкновенные дифференциальные уравнения , CRC Press , 153–163, (1993), ISBN 0-8493-8607-1 .
^ Панайотунакос, Делавэр; Панайотунаку, Северная Дакота; Вакакис, А.Ф. (1 сентября 2003 г.). «Об отсутствии аналитического решения осциллятора Ван дер Поля». ЗАММ . 83 (9). Уайли: 611–615. Бибкод : 2003ЗаММ...83..611П . дои : 10.1002/zamm.200310040 . ISSN 0044-2267 . S2CID 120504403 .
^ Ферхюльст, Фердинанд (1996). Нелинейные дифференциальные уравнения и динамические системы . Университеттекст. Берлин, Гейдельберг: Springer Berlin Heidelberg. дои : 10.1007/978-3-642-61453-8 . ISBN 978-3-540-60934-6 .
^ Андерсен, CM; Гир, Джеймс Ф. (июнь 1982 г.). «Разложение в степенной ряд для частоты и периода предельного цикла уравнения Ван дер Поля» . SIAM Journal по прикладной математике . 42 (3): 678–693. дои : 10.1137/0142047 . ISSN 0036-1399 .
^ Бендер, Карл М. (1999). Перспективные математические методы для ученых и инженеров I: асимптотические методы и теория возмущений . Стивен А. Орзаг. Нью-Йорк, штат Нью-Йорк. ISBN 978-1-4757-3069-2 . ОСЛК 851704808 . {{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка )
^ Гримшоу, Р. (1993). Нелинейные обыкновенные дифференциальные уравнения . Бока-Ратон, Флорида: CRC Press. стр. 161–163. ISBN 0-8493-8607-1 . OCLC 28275539 .
^ А, Дородницын А. (1947). «Асимптотическое решение уравнения Ван дер Поля» . Прикл. Мат. Мех. (на русском языке). 11 : 313–328.
^ Дородницын А.А. Асимптотическое решение уравнения Ван дер Поля . Исследовательская библиотека НИСТ. Национальное бюро стандартов.
^ Зонневельд, Дж. А. (1966). «Периодические решения уравнения Ван дер Поля» . Indagationes Mathematicae (Труды) . 69 : 620–622. дои : 10.1016/s1385-7258(69)50068-x . ISSN 1385-7258 .
^ Строгац, Стивен (2019). «Пример 8.4.1». Нелинейная динамика и хаос: с приложениями к физике, биологии, химии и технике (2-е изд.). Бока Ратон. ISBN 978-0-367-09206-1 . OCLC 1112373147 . {{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка )
^ Шах, Тирт; Чаттопадхьяй, Рохиташва; Вайдья, Кедар; Чакраборти, Сагар (2015). «Консервативная теория возмущений для неконсервативных систем» . Физический обзор E . 92 (6): 062927. arXiv : 1512.06758 . Бибкод : 2015PhRvE..92f2927S . дои : 10.1103/physreve.92.062927 . ПМИД 26764794 . S2CID 14930486 .
^ Чаттопадхьяй, Рохиташва; Шах, Тирт; Чакраборти, Сагар (2018). «Нахождение угла Ханнея в диссипативных колебательных системах с помощью консервативной теории возмущений» . Физический обзор E . 97 (6): 062209. arXiv : 1610.05218 . Бибкод : 2018PhRvE..97f2209C . дои : 10.1103/PhysRevE.97.062209 . ПМИД 30011548 . S2CID 51635019 .
^ Jump up to: ^а ^б Чиа, А.; Квек, LC; Но, К. (16 октября 2020 г.). «Релаксационные колебания и унос частоты в квантовой механике». Физический обзор E . 102 (4): 042213. arXiv : 1711.07376 . Бибкод : 2020PhRvE.102d2213C . дои : 10.1103/physreve.102.042213 . ISSN 2470-0045 . ПМИД 33212685 . S2CID 224801468 .
^ Уолтер, Стефан; Нунненкамп, Андреас; Брудер, Кристоф (6 марта 2014 г.). «Квантовая синхронизация ведомого автогенератора». Письма о физических отзывах . 112 (9): 094102. arXiv : 1307.7044 . Бибкод : 2014PhRvL.112i4102W . дои : 10.1103/physrevlett.112.094102 . ISSN 0031-9007 . ПМИД 24655255 . S2CID 7950471 .
^ Ли, Тони Э.; Садегпур, HR (4 декабря 2013 г.). «Квантовая синхронизация квантовых осцилляторов Ван дер Поля с захваченными ионами». Письма о физических отзывах . 111 (23): 234101. arXiv : 1306.6359 . Бибкод : 2013PhRvL.111w4101L . дои : 10.1103/physrevlett.111.234101 . ISSN 0031-9007 . ПМИД 24476274 . S2CID 33622111 .
^ К. Томита (1986): «Периодически вынужденные нелинейные генераторы». В: Хаос , Ред. Арун В. Холден. Издательство Манчестерского университета, ISBN 0719018110 , стр. 213–214.
^ Глейк, Джеймс (1987). Хаос: создание новой науки . Нью-Йорк: Книги Пингвина. стр. 41–43. ISBN 0-14-009250-1 .
^ Колман, Дэвид (11 июля 2011 г.). «Нет тишины без шума» . Нью-Йорк Таймс . Проверено 11 июля 2011 г.
^ Картрайт, ML ; Литтлвуд, Дж. Э. (1945). «О нелинейных дифференциальных уравнениях второго порядка: I. Уравнение y¨ − k (1-y 2 )y˙ + y = b λk cos(λl + α), k Large». Журнал Лондонского математического общества . с1-20 (3). Уайли: 180–189. дои : 10.1112/jlms/s1-20.3.180 . ISSN 0024-6107 .

Внешние ссылки

«Уравнение Ван дер Поля» , Математическая энциклопедия , EMS Press , 2001 [1994]
Осциллятор Ван дер Поля в Scholarpedia
Интерактивные демонстрации осциллятора Ван дер Поля, заархивированные 14 февраля 2017 г. на Wayback Machine

[1] Хейтманн, С., Брейкспир, М (2017–2022) Набор инструментов для динамики мозга. bdtoolbox.org doi.org/10.5281/zenodo.5625923

[Biography-2] Картрайт, ML (1960). «Бальтазар Ван Дер Поль» . Журнал Лондонского математического общества . с1-35(3). Уайли: 367–376. дои : 10.1112/jlms/s1-35.3.367 . ISSN 0024-6107 .

[3] Б. ван дер Пол: «Теория амплитуды свободных и вынужденных колебаний триода», Radio Review (позже Wireless World) 1 701–710 (1920)

[relax-4] ван дер Пол, Балт. (1926). «О «релаксации-колебаниях» ». Лондонский, Эдинбургский и Дублинский философский журнал и научный журнал . 2 (11). Информа UK Limited: 978–992. дои : 10.1080/14786442608564127 . ISSN 1941-5982 .

[Nature-5] ВАН ДЕР ПОЛ, БАЛТ; ВАН ДЕР МАРК, Дж. (1927). «Деммножение частоты». Природа . 120 (3019). ООО «Спрингер Сайенс энд Бизнес Медиа»: 363–364. Бибкод : 1927Natur.120..363V . дои : 10.1038/120363a0 . ISSN 0028-0836 . S2CID 186244992 .

[6] Канамару, Т., «Осциллятор Ван дер Поля» , Scholarpedia , 2 (1), 2202, (2007).

[fitz-7] ФитцХью, Ричард (1961). «Импульсы и физиологические состояния в теоретических моделях нервной мембраны» . Биофизический журнал . 1 (6). Эльзевир Б.В.: 445–466. Бибкод : 1961BpJ.....1..445F . дои : 10.1016/s0006-3495(61)86902-6 . ISSN 0006-3495 . ПМЦ 1366333 . ПМИД 19431309 .

[nag-8] Нагумо, Дж.; Аримото, С.; Ёсидзава, С. (1962). «Активная линия передачи импульсов, имитирующая нервный аксон». Труды ИРЭ . 50 (10). Институт инженеров по электротехнике и электронике (IEEE): 2061–2070. дои : 10.1109/jrproc.1962.288235 . ISSN 0096-8390 . S2CID 51648050 .

[9] Картрайт, Джулиан HE ; Эгилуз, Виктор М.; Эрнандес-Гарсия, Эмилио; Пиро, Оресте (1999). «Динамика упругих возбудимых сред». Международный журнал бифуркации и хаоса . 09 (11): 2197–2202. arXiv : чао-дин/9905035 . Бибкод : 1999IJBC....9.2197C . дои : 10.1142/s0218127499001620 . ISSN 0218-1274 . S2CID 9120223 .

[10] Лусеро, Хорхе К.; Шентген, Жан (2013). Моделирование асимметрии голосовых связок с помощью связанных осцилляторов Ван дер Поля . Материалы совещаний по акустике. Том. 19. с. 060165. дои : 10.1121/1.4798467 . ISSN 1939-800Х .

[11] Каплан Д. и Гласс Л., Понимание нелинейной динамики , Springer, 240–244, (1995).

[12] Гримшоу, Р., Нелинейные обыкновенные дифференциальные уравнения , CRC Press , 153–163, (1993), ISBN 0-8493-8607-1 .

[13] Панайотунакос, Делавэр; Панайотунаку, Северная Дакота; Вакакис, А.Ф. (1 сентября 2003 г.). «Об отсутствии аналитического решения осциллятора Ван дер Поля». ЗАММ . 83 (9). Уайли: 611–615. Бибкод : 2003ЗаММ...83..611П . дои : 10.1002/zamm.200310040 . ISSN 0044-2267 . S2CID 120504403 .

[:0-14] Ферхюльст, Фердинанд (1996). Нелинейные дифференциальные уравнения и динамические системы . Университеттекст. Берлин, Гейдельберг: Springer Berlin Heidelberg. дои : 10.1007/978-3-642-61453-8 . ISBN 978-3-540-60934-6 .

[15] Андерсен, CM; Гир, Джеймс Ф. (июнь 1982 г.). «Разложение в степенной ряд для частоты и периода предельного цикла уравнения Ван дер Поля» . SIAM Journal по прикладной математике . 42 (3): 678–693. дои : 10.1137/0142047 . ISSN 0036-1399 .

[:02-16] Бендер, Карл М. (1999). Перспективные математические методы для ученых и инженеров I: асимптотические методы и теория возмущений . Стивен А. Орзаг. Нью-Йорк, штат Нью-Йорк. ISBN 978-1-4757-3069-2 . ОСЛК 851704808 . {{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка )

[17] Гримшоу, Р. (1993). Нелинейные обыкновенные дифференциальные уравнения . Бока-Ратон, Флорида: CRC Press. стр. 161–163. ISBN 0-8493-8607-1 . OCLC 28275539 .

[18] А, Дородницын А. (1947). «Асимптотическое решение уравнения Ван дер Поля» . Прикл. Мат. Мех. (на русском языке). 11 : 313–328.

[19] Дородницын А.А. Асимптотическое решение уравнения Ван дер Поля . Исследовательская библиотека НИСТ. Национальное бюро стандартов.

[20] Зонневельд, Дж. А. (1966). «Периодические решения уравнения Ван дер Поля» . Indagationes Mathematicae (Труды) . 69 : 620–622. дои : 10.1016/s1385-7258(69)50068-x . ISSN 1385-7258 .

[21] Строгац, Стивен (2019). «Пример 8.4.1». Нелинейная динамика и хаос: с приложениями к физике, биологии, химии и технике (2-е изд.). Бока Ратон. ISBN 978-0-367-09206-1 . OCLC 1112373147 . {{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка )

[22] Шах, Тирт; Чаттопадхьяй, Рохиташва; Вайдья, Кедар; Чакраборти, Сагар (2015). «Консервативная теория возмущений для неконсервативных систем» . Физический обзор E . 92 (6): 062927. arXiv : 1512.06758 . Бибкод : 2015PhRvE..92f2927S . дои : 10.1103/physreve.92.062927 . ПМИД 26764794 . S2CID 14930486 .

[23] Чаттопадхьяй, Рохиташва; Шах, Тирт; Чакраборти, Сагар (2018). «Нахождение угла Ханнея в диссипативных колебательных системах с помощью консервативной теории возмущений» . Физический обзор E . 97 (6): 062209. arXiv : 1610.05218 . Бибкод : 2018PhRvE..97f2209C . дои : 10.1103/PhysRevE.97.062209 . ПМИД 30011548 . S2CID 51635019 .

[CKN20-24] Jump up to: ^а ^б Чиа, А.; Квек, LC; Но, К. (16 октября 2020 г.). «Релаксационные колебания и унос частоты в квантовой механике». Физический обзор E . 102 (4): 042213. arXiv : 1711.07376 . Бибкод : 2020PhRvE.102d2213C . дои : 10.1103/physreve.102.042213 . ISSN 2470-0045 . ПМИД 33212685 . S2CID 224801468 .

[25] Уолтер, Стефан; Нунненкамп, Андреас; Брудер, Кристоф (6 марта 2014 г.). «Квантовая синхронизация ведомого автогенератора». Письма о физических отзывах . 112 (9): 094102. arXiv : 1307.7044 . Бибкод : 2014PhRvL.112i4102W . дои : 10.1103/physrevlett.112.094102 . ISSN 0031-9007 . ПМИД 24655255 . S2CID 7950471 .

[26] Ли, Тони Э.; Садегпур, HR (4 декабря 2013 г.). «Квантовая синхронизация квантовых осцилляторов Ван дер Поля с захваченными ионами». Письма о физических отзывах . 111 (23): 234101. arXiv : 1306.6359 . Бибкод : 2013PhRvL.111w4101L . дои : 10.1103/physrevlett.111.234101 . ISSN 0031-9007 . ПМИД 24476274 . S2CID 33622111 .

[Tomita-27] К. Томита (1986): «Периодически вынужденные нелинейные генераторы». В: Хаос , Ред. Арун В. Холден. Издательство Манчестерского университета, ISBN 0719018110 , стр. 213–214.

[gleick-chaos-28] Глейк, Джеймс (1987). Хаос: создание новой науки . Нью-Йорк: Книги Пингвина. стр. 41–43. ISBN 0-14-009250-1 .

[colman-nyt-29] Колман, Дэвид (11 июля 2011 г.). «Нет тишины без шума» . Нью-Йорк Таймс . Проверено 11 июля 2011 г.

[30] Картрайт, ML ; Литтлвуд, Дж. Э. (1945). «О нелинейных дифференциальных уравнениях второго порядка: I. Уравнение y¨ − k (1-y 2 )y˙ + y = b λk cos(λl + α), k Large». Журнал Лондонского математического общества . с1-20 (3). Уайли: 180–189. дои : 10.1112/jlms/s1-20.3.180 . ISSN 0024-6107 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]