✖


Jump to content

Кубик Рубика

Страница полузащищена
(Перенаправлено из нотации Singmaster )

Кубик Рубика
Другие имена Волшебный куб, Скоростной куб, Куб-головоломка, Куб
Тип Комбинированная головоломка
Изобретатель(и) Эрно Рубик
Компания Бренд Рубика, ООО ( Спин Мастер ) [1]
Страна Венгрия
Доступность 1977: Венгерский Magic Cube, первые тестовые партии выпущены в Будапеште.
В роли кубика Рубика, во всем мире, с 1980 г. по настоящее время.
Официальный сайт
Иллюстрация неразгаданного кубика Рубика.

— Кубик Рубика это 3D- головоломка, изобретенная в 1974 году. [2] [3] венгерский Эрне скульптор и профессор архитектуры Рубик . Первоначально назывался « Волшебный куб» . [4] Рубик лицензировал головоломку для продажи компанией Pentangle Puzzles в Великобритании в 1978 году . [5] а затем компанией Ideal Toy Corp в 1980 году. [6] через бизнесмена Тибора Лачи и основателя Seven Towns Тома Кремера . [7] Куб был выпущен на международном уровне в 1980 году и стал одним из самых узнаваемых символов массовой культуры. В 1980 году она получила специальную награду «Игра года в Германии» в категории «Лучшая головоломка». По состоянию на январь 2024 г. , по всему миру было продано около 500 миллионов кубов, [8] [9] [10] сделав ее самой продаваемой игрой-головоломкой в ​​мире [11] [12] и самая продаваемая игрушка. [13] Кубик Рубика был занесен в Национальный зал славы игрушек США в 2014 году. [14]

В оригинальном классическом кубике Рубика каждая из шести граней была покрыта девятью наклейками, каждая из шести однотонных цветов: белого, красного, синего, оранжевого, зеленого и желтого. Некоторые более поздние версии куба были обновлены и теперь используют цветные пластиковые панели, что предотвращает шелушение и выцветание. [15] С 1988 года расположение цветов было стандартизировано: белый напротив желтого, синий напротив зеленого и оранжевый напротив красного, а красный, белый и синий расположены по часовой стрелке в этом порядке. [16] На ранних кубиках положение цветов менялось от куба к кубу. [17]

Служащий . пытается собрать кубик Рубика в изакая после работы в Японии , 2008 год

Внутренний поворотный механизм позволяет каждой грани поворачиваться независимо, смешивая цвета. Чтобы головоломка была решена, каждая грань должна иметь только один цвет. Это вдохновило других дизайнеров на создание ряда подобных головоломок с разным количеством сторон, размеров и механизмов.

Хотя кубик Рубика достиг пика популярности в 1980-х годах, он до сих пор широко известен и используется. Многие спидкуберы продолжают практиковать эту и подобные головоломки и соревнуются за лучшее время в различных категориях. С 2003 года Всемирная ассоциация кубиков (WCA), международный руководящий орган по сборке кубика Рубика, организует соревнования по всему миру и признает мировые рекорды.

История

Прекурсоры

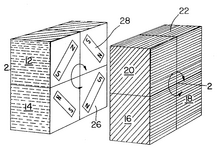
Схема из патента Николса, показывающая куб, скрепленный магнитами.

В марте 1970 года Ларри Д. Николс изобрел «головоломку 2x2x2 с деталями, вращающимися группами» и подал на нее заявку на патент в Канаде. Куб Николса удерживался магнитами. Николс получил патент США № 3 655 201 11 апреля 1972 года, за два года до того, как Рубик изобрел свой кубик.

9 апреля 1970 года Фрэнк Фокс подал заявку на патент на «устройство для развлечения», тип скользящей головоломки на сферической поверхности с «по крайней мере двумя массивами 3×3», предназначенной для использования в игре в крестики-нолики . Он получил патент Великобритании (1344259) 16 января 1974 года. [18]

изобретение Рубика

В середине 1970-х годов Эрне Рубик работал на кафедре дизайна интерьера Академии прикладных искусств и ремесел в Будапеште. [19] Хотя широко известно, что Куб был создан как обучающий инструмент, чтобы помочь ученикам понять трехмерные объекты, его настоящей целью было решение структурной проблемы независимого перемещения частей без разрушения всего механизма. Он не осознавал, что создал головоломку, пока впервые не собрал свой новый Куб, а затем не попытался восстановить его. [20] Рубик подал заявку на патент в Венгрии на свой «Волшебный кубик» ( венгерский : bűvös kocka ) 30 января 1975 года. [4] и HU170062 был предоставлен позже в том же году.

Первые пробные партии Magic Cube были произведены в конце 1977 года и проданы в магазинах игрушек Будапешта . Magic Cube скреплялся с помощью взаимосвязанных пластиковых деталей, которые не позволяли легко разобрать головоломку, в отличие от магнитов в конструкции Николса. С разрешения Эрне Рубика бизнесмен Тибор Лачи взял кубик на Нюрнбергскую ярмарку игрушек в Германии в феврале 1979 года, пытаясь популяризировать его. [21] Это заметил основатель Seven Towns Том Кремер, и в сентябре 1979 года они подписали соглашение с Ideal Toys о выпуске Magic Cube по всему миру. [21] Компания Ideal хотела, чтобы в качестве товарного знака было хотя бы узнаваемое название; Благодаря такому расположению Рубик оказался в центре внимания, поскольку в 1980 году Magic Cube был переименован в честь его изобретателя.

Оригинальный кубик Рубика — Ideal Toy Corp., производство Венгрия, 1980 г.

Международный дебют головоломки состоялся на ярмарках игрушек в Лондоне, Париже, Нюрнберге и Нью-Йорке в январе и феврале 1980 года. [22]

После международного дебюта продвижение Cube на полки магазинов игрушек Запада было ненадолго остановлено, чтобы его можно было производить в соответствии с западными спецификациями безопасности и упаковки. Был выпущен более легкий Cube, и Ideal решил переименовать его. « Гордиев узел » и «Золото инков», но в конце концов компания остановила свой выбор на «Кубике Рубика», и первая партия была экспортирована из Венгрии в мае 1980 года. Рассматривались [23]

Упаковка имела несколько вариантов в зависимости от страны, наиболее популярным из которых был прозрачный пластиковый цилиндр, но использовались и картонные версии. Сам куб имел несколько разные вариации порядка цветов (западная и японская цветовая схема, где переключаются синий и желтый), а на некоторых кубиках не было логотипа белой фигуры.

Увлечение кубами 1980-х годов

Самый большой в мире кубик Рубика был построен для Всемирной выставки 1982 года в Ноксвилле, штат Теннесси .

После того, как в мае 1980 года были выпущены первые партии кубиков Рубика, первоначальные продажи были скромными, но в середине года Ideal начал телевизионную рекламную кампанию, которую дополнил рекламой в газетах. [24] В конце 1980 года кубик Рубика получил специальную награду «Игра года в Германии». [25] и получил аналогичные награды за лучшую игрушку в Великобритании, Франции и США. [26] К 1981 году кубик Рубика стал повальным увлечением, и, по оценкам, в период с 1980 по 1983 год по всему миру было продано около 200 миллионов кубиков Рубика. [27] В марте 1981 года чемпионат по спидкубингу , организованный Книгой рекордов Гиннеса прошел в Мюнхене . [25] а кубик Рубика был изображен на обложке журнала Scientific American в том же месяце. [28] В июне 1981 года газета The Washington Post сообщила, что кубик Рубика — это «головоломка, которая прямо сейчас движется, как фаст-фуд… в этом году обруч Hoola или доска для бонго ». [29] а к сентябрю 1981 года журнал New Scientist отметил, что этим летом куб «привлек внимание детей в возрасте от 7 до 70 лет во всем мире». [30]

Поскольку большинство людей могли решить только одну или две стороны, было опубликовано множество книг, в том числе « Заметки Дэвида Сингмастера о «Волшебном кубике» Рубика» Патрика Боссерта (1980) и «Вы можете собрать кубик» (1981). [25] На каком-то этапе в 1981 году три из десяти самых продаваемых книг в США были книгами по сборке кубика Рубика. [31] а самой продаваемой книгой 1981 года стала книга Джеймса Г. Норса «Простое решение кубика Рубика» , которая была продана тиражом более 6 миллионов экземпляров. [32] В 1981 году в Музее современного искусства в Нью-Йорке был выставлен кубик Рубика, а на Всемирной выставке 1982 года в Ноксвилле , штат Теннесси, был выставлен шестифутовый кубик. [25] Телевидение ABC даже разработало мультсериал под названием « Удивительный кубик Рубика» . [33] В июне 1982 года первый чемпионат мира по сборке кубика Рубика состоялся в Будапеште , который стал единственным соревнованием, признанным официальным, до возобновления чемпионата в 2003 году. [34]

В октябре 1982 года газета The New York Times сообщила, что продажи упали и что «увлечение ушло». [35] и к 1983 году стало ясно, что продажи резко упали. [25] Однако в некоторых странах, таких как Китай и СССР, увлечение началось позже, и спрос все еще был высоким из-за нехватки кубов. [36] [37]

Возрождение 21 века

Кубики Рубика продолжали продаваться на протяжении 1980-х и 1990-х годов. [25] но только в начале 2000-х годов интерес к Кубу снова начал расти. [38] В США продажи удвоились в период с 2001 по 2003 год, и The Boston Globe отметила, что «становится круто снова владеть Cube». [39] Чемпионат мира по играм Рубика 2003 года стал первым турниром по спидкубингу с 1982 года. [38] Он проходил в Торонто , и в нем приняли участие 83 участника. [38] Турнир привел к созданию Всемирной ассоциации кубов в 2004 году. [38] Сообщается, что в 2008 году годовые продажи кубиков Рубика по всему миру достигли 15 миллионов штук. [40] Частично новая привлекательность была связана с появлением видеосайтов в Интернете, таких как YouTube, которые позволяли фанатам делиться своими стратегиями решения. [40] После истечения срока действия патента Рубика в 2000 году появились кубики других марок, особенно китайских компаний. [41] Многие из этих кубиков китайской марки созданы для скорости и пользуются популярностью среди спидкуберов. [41] 27 октября 2020 года Spin Master заявила, что заплатит 50 миллионов долларов за покупку бренда «Кубик Рубика». [1]

Имитации

Воспользовавшись первоначальным дефицитом кубиков, появилось множество имитаций и вариаций, многие из которых, возможно, нарушали один или несколько патентов. В 2000 году срок действия патентов истек, и с тех пор многие китайские компании выпустили копии, модификации и улучшения конструкций Рубика и V-Cube . [41]

Патентная история

Николс передал свой патент своему работодателю Moleculon Research Corp., которая подала в суд на Ideal в 1982 году. В 1984 году Ideal проиграла иск о нарушении патентных прав и подала апелляцию. В 1986 году апелляционный суд подтвердил решение о том, что карманный кубик Рубика 2×2×2 нарушает патент Николса, но отменил решение по кубику Рубика 3×3×3. [42]

Пока обрабатывалась заявка на патент Рубика, Терутоши Исиги, инженер-самоучка и владелец металлургического завода недалеко от Токио, подал заявку на японский патент на почти идентичный механизм, который был выдан в 1976 году (публикация японского патента JP55-008192). До 1999 года, когда вступили в силу измененные японские патентные законы , патентное ведомство Японии выдавало японские патенты на нераскрытые технологии внутри Японии, не требуя новизны во всем мире . [43] [44] Таким образом, патент Исиги в то время обычно воспринимался как независимое изобретение. [45] [46] [47] Рубик подал заявку на получение новых патентов в 1980 году, включая еще один венгерский патент 28 октября. В Соединенных Штатах 29 марта 1983 года Рубику был выдан патент США № 4 378 116 на кубик. Срок действия этого патента истек в 2000 году.

Товарные знаки

Rubik's Brand Ltd. также владеет зарегистрированными товарными знаками на слова «Rubik» и «Rubik's», а также на 2D- и 3D-визуализации головоломки. Товарные знаки были оставлены в силе постановлением Генерального суда Европейского Союза от 25 ноября 2014 года в результате успешной защиты против немецкого производителя игрушек, пытавшегося признать их недействительными. Тем не менее, европейским производителям игрушек разрешено создавать головоломки различной формы, которые имеют схожие функции вращения или скручивания составных частей, такие как, например, Skewb , Pyraminx или Imposossiball . [48]

10 ноября 2016 года кубик Рубика проиграл десятилетнюю битву по ключевому вопросу о товарном знаке. Высший суд Европейского Союза , Суд ООН , постановил, что форма головоломки недостаточна для предоставления ей защиты товарного знака. [49]

Механика

Компоненты кубика Рубика с этикеткой
Кубик Рубика в перевернутом состоянии

Стандартные размеры кубика Рубика. 5,6 сантиметра ( + 1/4 дюйма ) 2 с каждой стороны. [50] Пазл состоит из 26 уникальных миниатюрных кубиков, также известных как «кубики» или «кулететы». Каждый из них включает в себя скрытое внутреннее расширение, которое соединяется с другими кубами, позволяя им перемещаться в разные места. Однако центральный куб каждой из шести граней представляет собой всего лишь один квадратный фасад; все шесть прикреплены к основному механизму. Они обеспечивают структуру, в которую другие части могут вставляться и вращаться. Таким образом, получается 21 деталь: одна основная деталь, состоящая из трех пересекающихся осей, удерживающих шесть центральных квадратов на месте, но позволяющих им вращаться, и 20 пластиковых деталей меньшего размера, которые вписываются в нее, образуя собранную головоломку. [51]

Каждая из шести центральных частей поворачивается на застежке, удерживаемой центральной частью, в виде «3D-креста». Пружина между каждым крепежом и соответствующей деталью натягивает деталь внутрь, так что в целом вся сборка остается компактной, но ею по-прежнему можно легко манипулировать. В более старых версиях официального Cube использовался винт, который можно затягивать или ослаблять, чтобы изменить «ощущение» Cube. Новые официальные кубики Рубика имеют заклепки вместо винтов и не подлежат регулировке. Недорогие клоны не имеют винтов или пружин, у них есть только пластиковый зажим, удерживающий центральную часть на месте и свободно вращающийся.

Куб можно разобрать без особого труда, обычно повернув верхний слой на 45°, а затем отделив один из его краевых кубиков от двух других слоев. Следовательно, «решить» Куб — это простой процесс, разобрав его и снова собрав в решенном состоянии.

Есть шесть центральных частей, на которых изображена одна цветная грань, двенадцать краевых частей, на которых изображены две цветные грани, и восемь угловых частей, на которых изображены три цветные грани. На каждой части изображена уникальная цветовая комбинация, но присутствуют не все комбинации (например, если красный и оранжевый находятся на противоположных сторонах собранного Куба, не существует реберной части с красной и оранжевой сторонами). Расположение этих кубиков относительно друг друга можно изменить, повернув внешнюю треть куба с шагом 90 градусов, но расположение цветных сторон относительно друг друга в завершенном состоянии головоломки изменить нельзя; это фиксируется относительным положением центральных квадратов. Однако существуют также кубы с альтернативным цветовым расположением; например, желтая грань напротив зеленой, синяя грань напротив белой, а красная и оранжевая остаются напротив друг друга.

Дуглас Хофштадтер в июльском номере журнала Scientific American за 1982 год отметил, что кубы можно раскрасить таким образом, чтобы подчеркнуть углы или края, а не грани, как это делает стандартная раскраска; но ни одна из этих альтернативных расцветок так и не стала популярной. [45]

Математика

Первоначально головоломка рекламировалась как имеющая «более 3 000 000 000 (три миллиарда ) комбинаций, но только одно решение». [52] В зависимости от того, как подсчитываются комбинации, фактическое количество значительно выше.

Перестановки

Основная статья: Группа «Кубик Рубика»
Текущая цветовая схема кубика Рубика: желтый против белого, синий против зеленого, оранжевый против красного, а белый, зеленый и красный расположены вокруг угла против часовой стрелки.

Оригинальный кубик Рубика (3×3×3) имеет восемь углов и двенадцать граней. Их 8! (40 320) способов расположить угловые кубики. Каждый угол имеет три возможных направления, хотя только семь (из восьми) можно ориентировать независимо; ориентация восьмого (последнего) угла зависит от предыдущих семи, что дает 3 7 (2187) возможностей. Существует 12!/2 (239 500 800) способов расположения ребер, ограниченное числом 12! потому что края должны находиться в четной перестановке ровно тогда, когда находятся углы. (Когда также разрешено расположение центров, как описано ниже, правило состоит в том, что комбинированное расположение углов, ребер и центров должно быть четной перестановкой.) Одиннадцать ребер можно перевернуть независимо, при этом переворот двенадцатого зависит от предыдущие, давая 2 11 (2048) возможностей. [53]

что составляет примерно 43 квинтиллиона . [54] [ нужен лучший источник ] Для сравнения: если бы у вас был один кубик Рубика стандартного размера для каждой перестановки , можно было бы покрыть поверхность Земли 275 раз или сложить их в башне высотой 261 световой год .

Предыдущий рисунок ограничен перестановками, которых можно достичь, просто поворачивая стороны куба. Если учесть перестановки, полученные в результате разборки куба, это число станет в двенадцать раз больше:

что составляет примерно 519 квинтиллионов [54] возможные расположения частей, составляющих куб, но только одна двенадцатая из них действительно разрешима. Это связано с тем, что не существует последовательности ходов, которая меняет местами одну пару фигур или вращает один угол или ребро куба. Таким образом, существует 12 возможных наборов достижимых конфигураций, иногда называемых «вселенными» или « орбитами », в которые куб можно поместить, разобрав и собрав его заново.

Предыдущие числа предполагают, что центральные грани находятся в фиксированном положении. Если считать поворот всего куба другой перестановкой, то каждое из предыдущих чисел следует умножить на 24. Выбранный цвет может находиться на одной из шести сторон, и тогда один из соседних цветов может находиться в одной из четырех позиций. ; это определяет позиции всех остальных цветов.

Центральные грани

Оригинальный кубик Рубика не имел отметок ориентации на центральных гранях (хотя некоторые имели знак «Кубик Рубика» на центральном квадрате белой грани), и поэтому для его решения не требуется никакого внимания к правильной ориентации этих граней. Однако с помощью маркеров можно, например, пометить центральные квадраты расшифрованного Куба четырьмя цветными метками на каждом ребре, каждая из которых соответствует цвету соседней грани; куб, отмеченный таким образом, называется «суперкубом». Некоторые кубики также производятся в коммерческих целях с маркировкой на всех квадратах, например, Ло Шу магический квадрат или игральных карт масти . Также производятся кубики, в которых девять наклеек на грани используются для создания одной более крупной картинки, и для них также имеет значение ориентация по центру. Таким образом, номинально можно собрать куб, но повернуть отметки в центрах; тогда это становится дополнительным испытанием для решения центров.

Маркировка центров кубика Рубика усложняет задачу, поскольку расширяет набор различимых возможных конфигураций. Есть 4 6 /2 (2048) способов ориентации центров, поскольку четная перестановка углов предполагает и четное число четвертей оборота центров. В частности, когда Куб расшифрован, независимо от ориентации центральных квадратов, всегда будет четное количество центральных квадратов, требующих четверти оборота. Таким образом, ориентация центров увеличивает общее количество возможных перестановок Куба с 43 252 003 274 489 856 000 (4,3×10 19 ) до 88 580 102 706 155 225 088 000 (8,9 × 10 22 ). [55]

Если переворот куба считается изменением перестановки, мы также должны учитывать расположение центральных граней. Номинально их 6! способы расположения шести центральных граней куба, но только 24 из них достижимы без разборки куба. Когда также подсчитываются ориентации центров, как указано выше, это увеличивает общее количество возможных перестановок Куба с 88 580 102 706 155 225 088 000 (8,9×10 22 ) до 2 125 922 464 947 725 402 112 000 (2,1×10 24 ).

Алгоритмы

На языке кубикистов Рубика запомненная последовательность ходов, оказывающих желаемое воздействие на кубик, называется «алгоритмом». Эта терминология происходит от математического использования алгоритма , означающего список четко определенных инструкций для выполнения задачи от заданного начального состояния через четко определенные последовательные состояния до желаемого конечного состояния. Каждый метод решения куба использует свой собственный набор алгоритмов вместе с описаниями того, какой эффект имеет алгоритм и когда его можно использовать, чтобы приблизить куб к решению.

Многие алгоритмы предназначены для преобразования только небольшой части куба, не мешая другим частям, которые уже решены, поэтому их можно многократно применять к различным частям куба, пока не будет решено все. Например, существуют хорошо известные алгоритмы циклического прохождения трех углов без изменения остальной части головоломки или изменения ориентации пары ребер, оставляя остальные нетронутыми.

Некоторые алгоритмы оказывают определенное желаемое воздействие на куб (например, меняют местами два угла), но могут также иметь побочный эффект, заключающийся в изменении других частей куба (например, перестановке некоторых ребер). Такие алгоритмы часто проще, чем алгоритмы без побочных эффектов, и используются на ранних этапах решения, когда большая часть головоломки еще не решена и побочные эффекты не важны. Ближе к концу решения вместо этого используются более конкретные (и обычно более сложные) алгоритмы.

Актуальность и применение математической теории групп.

Кубик Рубика пригоден для применения математической теории групп , которая помогла вывести некоторые алгоритмы, в частности те, которые имеют структуру коммутатора , а именно XYX. −1 И −1 (где X и Y — конкретные ходы или последовательности ходов, а X −1 и Ю −1 являются их обратными), или сопряженной структуры, а именно XYX −1 , который спидкуберы в просторечии часто называют «подготовочным ходом». [56] Кроме того, тот факт, что внутри группы кубика Рубика есть четко определенные подгруппы, позволяет изучить и освоить головоломку, продвигаясь вверх по различным автономным «уровням сложности». Например, один из таких «уровней» может включать в себя сборку кубиков, перемешанных с помощью поворотов только на 180 градусов. Эти подгруппы являются принципом, лежащим в основе компьютерных методов кубирования Тистлтуэйта и Косиембы , которые решают куб путем дальнейшего сведения его к другой подгруппе.

Унитарное представительство

Группу Рубика можно наделить унитарным представлением : такое описание позволяет отобразить кубик Рубика в квантовую систему из нескольких частиц, где повороты его граней реализуются унитарными операторами. Вращения граней действуют как генераторы группы Ли . [57]

Решения

В Wikibooks есть книга на тему: Как собрать кубик Рубика.

Обозначение Сингмастера

Многие энтузиасты кубика Рубика 3 × 3 × 3 используют систему обозначений, разработанную Дэвидом Сингмастером для обозначения последовательности ходов, называемую «нотацией Сингмастера» или простой «нотацией куба». [58] Его относительный характер позволяет писать алгоритмы таким образом, чтобы их можно было применять независимо от того, какая сторона обозначена вершиной или как цвета организованы на конкретном кубе.

  • F (Спереди): сторона, обращенная в данный момент к решателю.
  • B (задняя сторона): сторона, противоположная передней.
  • U (вверх): сторона выше или сверху передней стороны.
  • D (Вниз): сторона, противоположная верху, под кубом.
  • L (слева): сторона непосредственно слева от передней части.
  • R (справа): сторона прямо справа от передней части.
  • f (два передних слоя): сторона, обращенная к решателю, и соответствующий средний слой.
  • б (два задних слоя): сторона, противоположная переднему, и соответствующий средний слой.
  • u (два слоя вверх): верхняя сторона и соответствующий средний слой.
  • d (два нижних слоя): нижний слой и соответствующий средний слой.
  • l (два слоя слева): сторона слева от переда и соответствующий средний слой.
  • r (два правых слоя): сторона справа от переднего и соответствующий средний слой.
  • x (повернуть): повернуть весь куб на R
  • y (повернуть): повернуть весь куб на U.
  • z (повернуть): повернуть весь куб на F

Когда штриховой символ ( ′ ) следует за буквой, это указывает на поворот лица против часовой стрелки; а буква без штриха обозначает поворот по часовой стрелке. Эти направления соответствуют взгляду на определенное лицо. Буква, за которой следует цифра 2 (иногда верхний индекс). 2 ) обозначает два поворота или поворот на 180 градусов. Например, R означает поворот правой стороны по часовой стрелке, а R' означает поворот правой стороны против часовой стрелки. Буквы x , y и z используются для обозначения того, что весь куб следует повернуть вокруг одной из своих осей, что соответствует поворотам R, U и F соответственно. Если x , y или z отмечены штрихом, это означает, что куб необходимо повернуть в противоположном направлении. Когда x , y или z возведены в квадрат, куб необходимо повернуть на 180 градусов.

Одним из наиболее распространенных отклонений от нотации Singmaster и, по сути, текущего официального стандарта, является использование буквы «w», обозначающей «широкий», вместо строчных букв для обозначения ходов двух слоев; таким образом, перемещение Rw эквивалентно перемещению r . [59]

Для методов, использующих повороты среднего уровня (особенно методы «сначала углы»), существует общепринятое расширение обозначения «MES», где буквы M , E и S обозначают повороты среднего уровня. Он использовался, например, в алгоритме Марка Уотермана. [60]

  • M (Средний): слой между L и R, направление поворота L (сверху вниз).
  • E (Экватор): слой между U и D, направление поворота как D (слева-направо).
  • S (Стоячий): слой между F и B, направление поворота как F.

Кубы 4×4×4 и более используют расширенное обозначение для обозначения дополнительных средних слоев. Вообще говоря, заглавные буквы ( FBUDLR ) относятся к самым внешним частям куба (называемым гранями). Строчные буквы ( fbudlr ) относятся к внутренним частям куба (называемым срезами). Звездочка (L*), число перед ней (2L) или два слоя в круглых скобках (Ll) означают одновременный поворот двух слоев (как внутренней, так и внешней левой грани). Например: ( Rr )' l 2 f ' означает поворот двух крайних правых слоев против часовой стрелки, затем дважды левый внутренний слой, а затем внутренний передний слой против часовой стрелки. В более широком смысле, для кубиков 6×6×6 и больше ходы трех слоев обозначаются цифрой 3, например, 3L.

Альтернативное обозначение, обозначение Вольстенхолма, [61] разработан, чтобы облегчить запоминание последовательности движений новичкам. В этом обозначении для лиц используются те же буквы, за исключением того, что U заменяется на T (вверху), так что все буквы являются согласными. Ключевым отличием является использование гласных O, A и I для поворотов по часовой стрелке, против часовой стрелки и двойного поворота (на 180 градусов), что приводит к образованию словесных последовательностей, таких как LOTA RATO LATA ROTI (эквивалентно LU' R' UL' U' R U2 в обозначениях Сингмастера). Добавление буквы C подразумевает вращение всего куба, поэтому ROC — это вращение куба по часовой стрелке вокруг его правой грани. Движения среднего слоя обозначаются добавлением буквы M к соответствующему перемещению грани, поэтому RIM означает поворот на 180 градусов среднего слоя, примыкающего к грани R.

Еще одно обозначение появилось в книге 1981 года «Простое решение кубика Рубика» . Нотация Singmaster не была широко известна на момент публикации. Грани были названы Верх (T), Нижний (B), Левый (L), Правый (R), Передний (F) и Задний (P), с + для вращения по часовой стрелке, – для против часовой стрелки и 2 для угла на 180 градусов. поворачивается.

Еще одно обозначение появилось в книге «Идеальное решение» 1982 года для «Мести Рубика». Горизонтальные плоскости обозначались как таблицы, причем таблица 1 или Т1 начиналась сверху. Вертикальные плоскости спереди назад были отмечены как книги, причем книга 1 или B1 начиналась слева. Вертикальные плоскости слева направо были отмечены как окна, причем окно 1 или W1 начиналось спереди. При использовании лицевой панели в качестве эталонного вида перемещение стола осуществлялось влево или вправо, перемещение книги вверх или вниз, а перемещение окна — по часовой стрелке или против часовой стрелки.

Период последовательностей ходов

Повторение любой заданной последовательности ходов на кубе, который изначально находится в решенном состоянии, в конечном итоге вернет куб обратно в решенное состояние: наименьшее необходимое количество итераций - это период последовательности. Например, поворот любой стороны на 180 градусов имеет период 2 (например, {U 2 } 2 ); поворот любой стороны на 90 градусов имеет период 4 (например, {R} 4 ). Максимальный период последовательности ходов — 1260: [58] например, учитывая полный оборот, {F x} 1260 или {R y} 1260 или {U z} 1260 ; не учитывая вращения, {D R' U 2 М} 1260 , или {BE L' F 2 } 1260 , или {S'U'BD 2 } 1260 ; допускается только четверть оборота по часовой стрелке, {URSUL} 1260 , или {ФЛЕБЛ} 1260 , или {RURDS} 1260 ; допускается только боковые четверть оборота по часовой стрелке, {FBLFBRFU} 1260 , или {UDRUDLUF} 1260 или {RLDRLURF} 1260 .

Оптимальные решения

Основная статья: Оптимальные решения для кубика Рубика

Хотя существует значительное количество возможных перестановок кубика Рубика, был разработан ряд решений, которые позволяют собрать кубик менее чем за 100 ходов.

Многие общие решения для Куба были найдены независимо. Дэвид Сингмастер впервые опубликовал свое решение в книге «Заметки о «Волшебном кубике» Рубика» в 1981 году. [56] Это решение включает в себя послойное решение куба, при котором сначала решается один слой (обозначенный верхним), затем средний слой, а затем последний и нижний слой. После достаточной практики решение куба слой за слоем можно выполнить менее чем за одну минуту. Другие общие решения включают методы «сначала углы» или комбинации нескольких других методов. В 1982 году Дэвид Сингмастер и Александр Фрей выдвинули гипотезу, что количество ходов, необходимое для решения куба при наличии идеального алгоритма, может быть «около двадцати». [62] В 2007 году Дэниел Канкл и Джин Куперман использовали методы компьютерного поиска, чтобы продемонстрировать, что любую конфигурацию кубика Рубика 3×3×3 можно собрать за 26 ходов или меньше. [63] [64] [65] В 2008 году Томаш Рокицкий снизил это число до 22 ходов. [66] [67] [68] а в июле 2010 года группа исследователей, в том числе Рокицки, работая с компьютерами, предоставленными Google , доказала, что так называемое « число Бога » для кубика Рубика равно 20. [69] [70] [71] Это означает, что все начальные конфигурации можно решить за 20 ходов или меньше, а некоторые (фактически миллионы) требуют 20. [69] В более общем плане было показано, что кубик Рубика размером n × n × n можно оптимально решить за Θ( n 2 / log( n )) перемещается. [72]

Методы спидкубинга

Решение, обычно используемое спидкуберами, было разработано Джессикой Фридрих . Этот метод называется CFOP , что означает «Cross, F2L, OLL, PLL». Он похож на послойный метод, но использует большое количество алгоритмов, особенно для ориентации и перестановки последнего слоя. Сначала собирается крест, затем одновременно создаются углы первого слоя и края второго слоя, причем каждый угол соединяется с кромкой второго слоя, таким образом завершая первые два слоя (F2L). Затем следует ориентация последнего слоя, а затем перестановка последнего слоя (OLL и PLL соответственно). Всего существует 120 алгоритмов метода Фридриха, однако не все они необходимы для использования метода CFOP . Большинство преданных кубистов изучат как можно больше из этих алгоритмов, а самые продвинутые куберы знают их все. Если кубер знает каждый алгоритм для OLL, его можно назвать знающим полный OLL. То же самое касается PLL и F2L.

Известный ныне метод разработал Ларс Петрус . В этом методе сначала решается участок 2×2×2, затем 2×2×3, а затем неправильные ребра решаются с использованием трехходового алгоритма, что устраняет необходимость в возможном 32-ходовом алгоритме позже. . Принцип заключается в том, что слой за слоем необходимо постоянно ломать и фиксировать готовый слой(и); Секции 2×2×2 и 2×2×3 позволяют поворачивать три или два слоя (соответственно), не разрушая прогресс. Одним из преимуществ этого метода является то, что он дает решение за меньшее количество ходов. По этой причине этот метод также популярен в соревнованиях с наименьшим количеством ходов. [73]

Метод Ру, разработанный Жилем Ру , похож на метод Петрюса тем, что он основан на построении блоков, а не на слоях, но основан на методе «сначала углы». В Ру решается блок 3×2×1, за которым следует еще один блок 3×2×1 на противоположной стороне. Далее решаются углы верхнего слоя. Затем куб можно решить, используя только ходы слоя U и среза M. [74]

Методы для начинающих

Большинство методов решения для начинающих включают решение куба по одному слою за раз («метод послойно» или «метод новичка») с использованием алгоритмов, которые сохраняют то, что уже было решено. Самые простые послойные методы требуют всего 3–8 алгоритмов. [75] [76]

В 1981 году тринадцатилетний Патрик Боссерт разработал решение для решения куба вместе с графическими обозначениями, предназначенными для легкого понимания новичками. [77] Впоследствии он был опубликован под названием You Can Do The Cube и стал бестселлером. [78]

В 1997 году Денни Дедмор опубликовал решение, описанное с использованием схематических значков, обозначающих ходы, которые необходимо сделать, вместо обычных обозначений. [79]

В книге Филипа Маршалла «Окончательное решение кубика Рубика» используется другой подход: в среднем требуется всего 65 поворотов, но требуется запоминание только двух алгоритмов. Сначала собирается крест, затем остальные края (с использованием серии Edge Piece FR'F'R), затем пять углов (с использованием серии угловых частей URU'L'UR'U'L, которая аналогична типичной алгоритм перестановки углов последнего слоя) и, наконец, последние три угла. [80]

Программы для решения кубика Рубика

В наиболее оптимальных по ходу онлайн-программах для решения кубика Рубика используется двухфазный алгоритм Герберта Коциембы , который обычно может определить решение за 20 ходов или меньше. Пользователь должен установить цветовую конфигурацию зашифрованного куба, и программа возвращает шаги, необходимые для его решения. [81]

Соревнования и рекорды

Соревнования по спидкубингу

Основные статьи: Спидкубинг и Всемирная ассоциация кубов
Продолжительность: 26 секунд.
Speedsolve на соревнованиях по спидкубингу

Спидкубинг (или спидсолвинг) — это попытка собрать кубик Рубика за максимально короткое время. По всему миру проводится ряд соревнований по спидкубингу.

прошел чемпионат по спидкубингу, организованный Книгой рекордов Гиннеса 13 марта 1981 года в Мюнхене . [82] В соревновании использовались стандартизированное скремблирование и фиксированное время проверки, и победителями стали Рональд Бринкманн и Юри Фрёшль со временем 38,0 секунды. [82] Первым чемпионатом мира стал чемпионат мира по сборке кубика Рубика 1982 года, проходивший в Будапеште 5 июня 1982 года, который выиграл Минь Тай , вьетнамский студент из Лос-Анджелеса, со временем 22,95 секунды. [83]

С 2003 года победитель соревнований определяется по среднему времени средних трёх попыток из пяти. Однако также фиксируется лучшее время из всех попыток. Всемирная ассоциация кубов ведет историю мировых рекордов. [84] В 2004 году WCA обязала использовать специальное устройство для измерения времени, называемое таймером Stackmat.

Помимо основного мероприятия 3х3х3, WCA также проводит мероприятия, где кубик решается разными способами: [85]

  • Решение вслепую [86]
  • Множественное решение с завязанными глазами, или «мульти-слепое», при котором участник собирает любое количество кубиков с завязанными глазами подряд. [87]
  • Сборка куба одной рукой или решение одной рукой [88]
  • Решение куба за наименьшее количество ходов [89]

При решении с завязанными глазами участник сначала изучает перемешанный куб (т. е. смотрит на него как обычно, без повязки на глаза), а затем ему завязывают глаза, прежде чем он начинает поворачивать грани куба. Записанное время этого события включает в себя как время, потраченное на запоминание куба, так и время, потраченное на манипулирование им.

При многократном решении с завязанными глазами все кубики запоминаются, а затем все кубики собираются с завязанными глазами; таким образом, основная задача — запомнить множество — часто десять и более — отдельных кубиков. Событие оценивается не по времени, а по количеству очков, набранных по истечении часового лимита. Количество набранных очков равно количеству правильно решенных кубиков за вычетом количества неразгаданных кубиков после окончания попытки, причем чем больше очков, тем лучше. Если несколько участников набирают одинаковое количество очков, рейтинги оцениваются на основе общего времени попытки, причем чем меньше время, тем лучше.

За наименьшее количество ходов участнику дается один час на то, чтобы найти решение, и он должен его записать.

Рекорды

Рекорды соревнований

  • Одиночное время: мировой рекорд по сборке кубика Рубика 3×3×3 составляет 3,13 секунды, установлен Максом Парком из США и побит 11 июня 2023 года на стадионе Pride в Лонг-Бич . [90]
  • Среднее время: средний мировой рекорд среднего времени решения трех из пяти (без учета самого быстрого и самого медленного) составляет 4,48 секунды, установленный Ихэн Ваном (王艺衡) из Китая 20 июня 2023 года на круизном турнире Mofunland Cruise Open из Сингапура на Пхукет. Таиланд . [91]
  • Решение одной рукой: мировой рекорд по скорости решения одной рукой составляет 6,20 секунды, установлен Максом Парком из США 27 августа 2022 года в Marshall Middle Slice в Сан-Диего, Калифорния . Мировой рекорд по быстрому решению пяти задач одной рукой составляет 8,62 секунды, установлен Максом Парком из США 3 декабря 2023 года на турнире Nub Open Mission Viejo 2023. [92] [93]
  • Сборка ногами: мировой рекорд по скорости сборки кубика Рубика ногами — 15,56 секунды, установлен Мохаммедом Айманом Коли из Индии 27 декабря 2019 года на турнире VJTI Mumbai Cube Open . Средний мировой рекорд по решению пяти футов составляет 19,90 секунды, установленный Лим Хунгом (林弘) из Малайзии 21 декабря 2019 года на Медана праздновании 10-летия . [94] С 1 января 2020 года решение 3x3x3 футов больше не является соревнованием, признанным WCA, и никакие результаты не принимаются. [95]
  • Сборка вслепую: мировой рекорд по скорости сборки кубика Рубика вслепую составляет 12,00 секунд (включая запоминание), установленный Томми Черри из США 11 февраля 2024 года на соревнованиях Triton Tricubealon 2024 в Сан-Диего, Калифорния . Средний мировой рекорд по сборке кубиков вслепую, равный трем, составляет 14,15 секунды и установлен Томми Черри 15 августа 2023 года на чемпионате мира по Рубику WCA в Инчхоне, Южная Корея . [96]
  • Многократное сборка кубика Рубика вслепую: мировой рекорд по многократному сбору кубика Рубика вслепую — 62 кубика из 65 за 57 минут и 47 секунд, установлен Грэмом Сиггинсом из США 26 июня 2022 года в Blind Is Back, Лос-Анджелес . Сиггинс изучил 65 кубиков, надел повязку на глаза и успешно решил 62 из них, и все это за время, равное одному часу. [97]
  • Решение наименьшего количества ходов: мировой рекорд по наименьшему количеству ходов для решения куба за один час на определение решения составляет 16, что было достигнуто Себастьяно Тронто из Италии 15 июня 2019 года на FMC 2019 . Средний мировой рекорд из трех для испытания с наименьшим количеством ходов (с различными схватками) - 20,00, установлен Вонг Чонг Вен (黄崇文) из Сингапура 17 сентября 2023 года в FMC Джохор-Бару . [98]

Другие записи

  • Нечеловеческое решение: самое быстрое нечеловеческое решение кубика Рубика было выполнено изобретением Рубика, роботом, созданным Беном Кацем и Джаредом Ди Карло. Видео на YouTube показывает время решения 0,38 секунды с использованием Nucleo с алгоритмом min2phase . [99]
  • физического куба высшего порядка размера n×n×n : Джереми Смит решил задачу 21x21x21 за 95 минут и 55,52 секунды. Решение [100] [101] [ самостоятельно опубликованный источник? ]
  • Групповое решение (12 минут): Рекорд большинства людей, решивших кубик Рубика одновременно за двенадцать минут, - 134, установленный 17 марта 2010 года школьниками из гимназии доктора Чаллонера в Амершаме, Англия, побив предыдущий мировой рекорд Гиннеса - 96 человек. сразу. [102]
  • Групповое решение (30 минут): 21 ноября 2012 года на арене O2 в Лондоне 1414 человек, в основном ученики школ со всего Лондона, собрали кубик Рубика менее чем за 30 минут, побив предыдущий мировой рекорд Гиннеса - 937 человек. Мероприятие проводилось от Depaul UK. [103]
4 ноября 2012 года 3248 человек, в основном студенты Инженерного колледжа Пуны , успешно собрали кубик Рубика за 30 минут на территории колледжа. Успешная попытка занесена в Книгу рекордов Лимки . Колледж предоставит соответствующие данные, показания свидетелей и видеозапись события в органы Книги Гиннесса. [104]

10 лучших решателей по одному решению [105]

Позиция Имя Результат Национальность Соревнование
1 Макс Парк 3.13 Соединенные Штаты Соединенные Штаты Соединенные Штаты Гордость в Лонг-Бич 2023
2 Люк Гарретт 3.44 Соединенные Штаты Соединенные Штаты Соединенные Штаты Флаг города Лето 2023
3 Ихэн Ван (王伊хэн) 3.47 Китай Китай Сингапур Чемпионат Сингапура MYHM 2024
Юшэн Ду (Du Yusheng) Китай Китай Китай Уху Опен 2018
5 Таймон Коласински 3.66 Польша Польша Норвегия Флатасен Опен 2024
6 Клаудио Матиас Кансино Бруна 3.74 Чили Чили Чили Вина Мастерс 2024
7 Джоуд Брюстер 3.88 Австралия Австралия Австралия Тэсси, лето 2023 г.
8 Ашер Ким-Магиерек 3.89 Соединенные Штаты Соединенные Штаты Соединенные Штаты Город роз 2022
9 Жуйхан Сюй (Xu Ruihang) 4.01 Китай Китай Вьетнам Чемпионат Вьетнама 2023
10 Наттапхат Махтани (Наттапхат Г. Матани) 4.02 Таиланд Таиланд Таиланд День куба в Бангкоке, зима 2024 г.

Вариации

Варианты кубика РубикаКарманный кубКубик РубикаМесть РубикаПрофессорский кубV-Cube 6V-Cube 7
Вариации кубиков Рубика. Верхний ряд: V-Cube 7 , Профессорский куб , V-Cube 6 . Нижний ряд: Месть Рубика , оригинальный кубик Рубика, Карманный кубик . Нажатие на куб на картинке приведет к перенаправлению на страницу соответствующего куба. (Примечание: зашифрованные состояния)
Куб 17×17×17.

Существует множество различных вариаций кубиков Рубика. Самый распространенный класс вариантов меняет «порядок» куба, определяемый количеством слоев в каждом измерении или, что то же самое, количеством частей вдоль каждого края (включая углы). Наиболее распространенными являются кубики 2×2×2 ( карманный/мини-куб ), стандартные кубики 3×3×3, 4×4×4 (куб «Месть Рубика»/мастер-куб) и 5×5×5 (куб профессора). хорошо известны, поскольку все они доступны под официальным брендом Rubik. WCA санкционирует соревнования по скоростному решению кубиков размером до 7×7×7. Эти «большие кубики» представляют собой предел практичности для целей соревновательного скоростного решения, поскольку кубики становятся все более неуклюжими и склонными к механическим повреждениям (например, «выскакиванию», когда одна или несколько частей выпадают из головоломки) и в среднем время решения увеличивается квадратично с каждым большим порядком, пропорционально количеству общих «граней» куба.

Кубы еще большего размера на основе патентов V-Cube [106] коммерчески доступны для массового рынка от нелицензированных производителей, большинство из которых — китайские фирмы, которые также производят популярные кубики, предназначенные для быстрого решения задач. Куб «Over the Top» размером 17 × 17 × 17 (доступный в конце 2011 года) до декабря 2017 года был самым большим коммерчески продаваемым кубом и самым дорогим, его стоимость превышала 2000 долларов США. Массовое производство 17×17×17 позже было представлено китайским производителем YuXin. Рабочий проект куба 22×22×22 существует и был продемонстрирован в январе 2016 года. [107] и 33×33×33 в декабре 2017 года, [108] хотя конструкции такого размера в настоящее время не производятся массово. Китайский производитель ShengShou производит кубики всех размеров от 2×2×2 до 15×15×15 (по состоянию на май 2020 года), а также выпустил кубики 17×17×17. [109] Самый большой куб, выпускаемый в настоящее время серийно, размером 21×21×21, производится MoYu начиная с 2021 года и стоит от 1100 до 1600 долларов. [110]

Есть много вариаций [111] оригинального кубика, некоторые из которых сделаны Рубиком. Механические продукты включают Rubik's Magic, 360 и Twist. Кроме того, такие электронные устройства, как Rubik's Revolution и Slide, также были вдохновлены оригиналом. Одним из вариантов кубика 3×3×3 является TouchCube Рубика. Если провести пальцем по его граням, узоры цветных огней начнут вращаться так же, как на механическом кубе. TouchCube также имеет кнопки для подсказок и самостоятельного решения, а также подставку для зарядки. TouchCube был представлен на Американской международной выставке игрушек в Нью-Йорке 15 февраля 2009 года. [112] [113]

Куб вдохновил на создание целой категории подобных головоломок, обычно называемых извилистыми головоломками , в которую входят упомянутые выше кубики разных размеров, а также различные другие геометрические фигуры. Некоторые из таких форм включают тетраэдр ( Пираминкс ), октаэдр ( Скевб Алмаз ), додекаэдр ( Мегаминкс ) и икосаэдр ( Догик ). Есть также головоломки, меняющие форму, такие как «Змейка Рубика» и « Квадрат» .

В 2011 году Книга рекордов Гиннеса присудила «волшебный кубик Рубика крупнейшего порядка» кубику 17×17×17, изготовленному Оскаром ван Девентером . [114] [115] 2 декабря 2017 года Грегуар Пфенниг объявил, что он побил этот рекорд с помощью куба 33×33×33, и что его заявление было отправлено в Книгу рекордов Гиннесса для проверки. [108] 8 апреля 2018 года Грегуар Пфенниг объявил об еще одном мировом рекорде — кубике 2х2х50. [116] Будет ли это замена пластинки 33×33×33 или дополнительная запись, еще неизвестно.

Все пять платоновых тел представлены в виде запутанных головоломок.

Некоторые головоломки также были созданы в форме многогранников Кеплера-Пуансо , например Звезда Александра ( большой додекаэдр ). Грегуар Пфенниг также создал по крайней мере одну головоломку в форме небольшого звездчатого додекаэдра .

Пазлы на заказ

Новинка брелок

Головоломки были построены как кубик Рубика или на основе его внутреннего устройства. Например, кубоид — это головоломка, основанная на кубике Рубика, но с разными функциональными размерами, например 2×2×4, 2×3×4 и 3×3×5. [117]

Другие модификации кубика Рубика включают «модификации формы», кубики, которые были расширены или усечены для формирования новой формы. Примером этого является октаэдр Трабьера, который можно построить путем усечения и удлинения частей обычного 3×3×3. Большинство модификаций формы можно адаптировать к кубам более высокого порядка. В случае с ромбическим додекаэдром Тони Фишера существуют версии головоломки 3×3×3, 4×4×4, 5×5×5 и 6×6×6.

Программа Кубик Рубика

Головоломки , такие как кубик Рубика, могут быть смоделированы с помощью компьютерного программного обеспечения , чтобы создать очень большие головоломки, которые непрактично собирать, а также виртуальные головоломки, которые невозможно построить физически, такие как многие аналоги кубика Рубика в более высоких измерениях. [118] [119]

  • 2×2×2×2 в MagicCube4D
    2×2×2×2 в MagicCube4D
  • 3×3×3×3 в MagicCube4D
    3×3×3×3 в MagicCube4D
  • 4×4×4×4 в MagicCube4D
    4×4×4×4 в MagicCube4D
  • 3×3×3×3×3 в MagicCube5D.
    3×3×3×3×3 в MagicCube5D.

Лаборатория Chrome Cube

Google запустил Chrome Cube Lab совместно с [120] Эрне Рубик . На сайте представлены различные интерактивные объекты на основе кубика Рубика. Можно создавать и загружать индивидуальные версии кубика Рубика. [121]

Экспонаты и искусство

Большой кубик Рубика, построенный в северном кампусе Мичиганского университета.

Центр Liberty Science в Джерси-Сити, штат Нью-Джерси , и Google разработали интерактивную выставку на основе кубика Рубика. [122] Он открылся в апреле 2014 года в честь 40-летия изобретения Куба, а затем семь лет путешествовал по всему миру. [123] Элементы выставки включают в себя куб высотой 35 футов, сделанный из огней, которым люди могут управлять с помощью своих мобильных телефонов, куб из бриллиантов стоимостью 2,5 миллиона долларов, гигантский куб, демонстрирующий внутреннюю работу головоломки, и роботов, решающих кубы. [124]

Вероятно, с самых первых дней увлечения кубиком Рубика в 1980-х годах люди собирали кубики, образуя простые произведения искусства. Несколько первых «народных художников» известны своими работами. [125] [126] Кубики Рубика также стали предметом нескольких инсталляций в стиле поп-арт. Благодаря популярности кубиков Рубика в качестве детской игрушки, несколько художников и групп создали большие кубики Рубика.

Тони Розенталя Аламо ( Куб Астор Плейс ) — вращающаяся статуя Куба, стоящая в Нью-Йорке . Когда-то кубик покрыли цветными панелями так, что он напоминал кубик Рубика. [127] [128] Точно так же студенты Мичиганского университета освещали Эндовер, создав большой кубик Рубика в центральном кампусе Мичиганского университета ко Дню дурака в 2008 году. [129]

Кубизм Рубика

Помимо народного искусства 1980-х и 1990-х годов и простого копирования кубика Рубика в увеличенной форме, художники разработали стиль пуантилистского искусства с использованием кубиков. В искусстве кубика Рубика, также известном как кубизм Рубика или RubikCubism, используется стандартный кубик Рубика, популярная игрушка-головоломка 1980-х годов. [130]

Самые ранние зарегистрированные произведения искусства, судя по всему, были созданы Фредом Холли, юридически слепым мужчиной в возрасте 60 лет в середине 1980-х годов. [125] Эти ранние произведения сосредоточены на геометрических и цветовых узорах. Похоже, что до середины 1990-х годов не было других записанных произведений искусства, созданных поклонниками кубов, вовлеченными в индустрию головоломок и игр. [126]

Работа Пита Фекто «Dream Big» в разработке

Форма народного искусства достигла нового уровня своей эволюции с развитием и зрелостью в форму поп-арта, состоящую из изображений пуантилистского кубического искусства. Уличный художник, использующий псевдоним « Захватчик » или «Космический захватчик», начал выставлять произведения пуантилизма, в том числе изображение человека за столом и братьев Марио, использующих кубик Рубика, в июне 2005 года на выставке под названием «Кубизм Рубика» в Sixspace в Лос-Анджелесе. Анджелес. [131] До этой выставки художник использовал кубики Рубика для создания гигантских космических захватчиков. [132] Еще один художник - Робби Маккиннон из Торонто, Канада. [133] с самой ранней опубликованной работой в 2007 году [134] который утверждает, что разработал свое пуантилистское искусство куба несколько лет назад, когда работал учителем в Китае. Работы Робби Маккиннона были выставлены в музее Ripley's «Хотите верьте, хотите нет» и посвящены использованию поп-арта, а Space Invader выставлял свое Cube Art вместе с мозаичными Space Invaders в коммерческих и общественных галереях. [135]

В 2010 году художник Пит Фекто создал «Dream Big». [136] дань уважения Мартину Лютеру Кингу-младшему с использованием 4242 официально лицензированных кубиков Рубика. Фекто также работал с организацией You Can Do The Rubik's Cube. [137] создать два отдельных руководства, предназначенных для обучения школьников созданию мозаики из кубика Рубика по шаблонам, которые он также создал.

Музыка

Итальянский композитор Мария Манноне создала куб под названием «CubeHarmonic», на гранях которого есть названия музыкальных нот, создавая различные структуры аккордов в зависимости от его конфигурации. [138]

Отзывы

См. также

Ссылки

  1. ^ Перейти обратно: а б Эванс, Пит (27 октября 2020 г.). «Канадская компания, владеющая классическими игрушками Etch A Sketch и Aerobie, покупает кубик Рубика за 50 миллионов долларов» . Новости ЦБК .
  2. ^ Фотерингем, Уильям (2007). Спортивные развлечения Фотерингема . Книги Анова. п. 50 . ISBN  978-1-86105-953-6 .
  3. ^ де Кастелла, Том (28 апреля 2014 г.). «Люди, которые до сих пор увлекаются кубиком Рубика» . Журнал BBC News . Би-би-си . Проверено 28 апреля 2014 г.
  4. ^ Перейти обратно: а б «30 января 1975 года: Рубик подает заявку на патент на волшебный кубик» . Проводной . 30 января 2009 года . Проверено 24 января 2019 г.
  5. ^ «25-летие Волшебного кубика Эрно Рубика. Впервые представлен западному миру компанией Pentangle Puzzles в 1978 году» . сайт Puzzlemuseum.com . Проверено 29 ноября 2020 г. .
  6. ^ Дэйнтит, Джон (1994). Биографическая энциклопедия учёных . Бристоль: Паб Института физики. п. 771. ИСБН  0-7503-0287-9 .
  7. ^ Майкл Шэнкс (8 мая 2005 г.). «История Куба» . Стэнфордский университет. Архивировано из оригинала 20 января 2013 года . Проверено 26 июля 2012 года .
  8. ^ Пракаш, Прартхана. «Как кубик Рубика прожил 50 лет и продолжает вызывать ярость среди поколения Z и за его пределами» . Фортуна Европа . Проверено 3 апреля 2024 г.
  9. ^ Адамс, Уильям Ли (28 января 2009 г.). «Кубик Рубика: загадочный успех» . Время . Архивировано из оригинала 1 февраля 2009 года . Проверено 5 февраля 2009 г.
  10. ^ Джеймисон, Аластер (31 января 2009 г.). «Изобретатель кубика Рубика вернулся с Рубиком 360» . «Дейли телеграф» . Лондон. Архивировано из оригинала 11 января 2022 года . Проверено 5 февраля 2009 г.
  11. ^ «eGames, Mindscape привнесли международный поворот в компьютерную игру «Кубик Рубика»» . Рейтер . 6 февраля 2008 г. Архивировано из оригинала 12 февраля 2009 г. Проверено 6 февраля 2009 г.
  12. ^ Маршалл, Рэй. «Приготовьтесь к Rubchallenge» . Архивировано из оригинала 20 января 2013 года . Проверено 15 августа 2005 г.
  13. ^ «Кубик Рубика 25 лет спустя: сумасшедшие игрушки, сумасшедшие времена» . Независимый . Лондон. 16 августа 2007 года . Проверено 6 февраля 2009 г.
  14. ^ «Национальный зал славы игрушек 2014 — Новости CBS» . Новости CBS . 6 ноября 2014 г.
  15. ^ «Рубик 3х3х3» . Проверено 12 апреля 2018 г. [ постоянная мертвая ссылка ]
  16. ^ Демпси, Майкл В. (1988). Растем вместе с наукой: Иллюстрированная энциклопедия изобретений . Лондон: Маршалл Кавендиш. п. 1245. ИСБН  0-87475-841-6 .
  17. ^ Юинг, Джон; Чес Косневский (1982). Puzzle It Out: кубики, группы и головоломки . Кембридж: Пресс-синдикат Кембриджского университета. п. 4. ISBN  0-521-28924-6 . Проверено 19 мая 2014 г.
  18. ^ «Описание патента 1344259» (PDF) . Проверено 15 июня 2012 г.
  19. ^ Сагерт, Келли Бойер (2007). 1970-е годы (Американская популярная культура через историю) . Вестпорт, Коннектикут: Greenwood Press. п. 130 . ISBN  978-0-313-33919-6 .
  20. ^ «Кубик Рубика» . Головоломка. 1 декабря 2006 года . Проверено 20 июня 2012 г.
  21. ^ Перейти обратно: а б Холпер, Пол (2006). Изобретение миллионов . Восток. стр. 64–65. ISBN  8122204589 .
  22. ^ «История» . Рубикс. 19 мая 2008 г. Архивировано из оригинала 26 января 2019 г. . Проверено 25 января 2019 г.
  23. ^ "О" . Рубикс. 25 января 2019 года. Архивировано из оригинала 14 августа 2018 года . Проверено 25 января 2019 г.
  24. ^ Догерти, Филип Х. (30 июля 1981 г.). «Реклама идеальной игрушки-сына кубика Рубика» . Нью-Йорк Таймс .
  25. ^ Перейти обратно: а б с д и ж Карлайл, Родни П. (2009). Энциклопедия игр в современном обществе . Мудрец. п. 612 . ISBN  978-1452266107 .
  26. ^ «Интервью с Эрне Рубиком» . Европа. Архивировано из оригинала 27 мая 2018 года . Проверено 26 октября 2016 г.
  27. ^ Сингмастер, Дэвид (1994). «Полезность развлекательной математики» . В Гае, Ричард К.; Вудро, Роберт Э. (ред.). Светлая сторона математики: материалы конференции памяти Эжена Стренса по занимательной математике и ее истории . Издательство Кембриджского университета. п. 340 . ISBN  088385516X . Сингмастера По оценкам , было продано от 100 до 300 миллионов экземпляров. Его оценка основана на продажах от 50 до 100 миллионов настоящих кубиков и, возможно, на большем количестве имитаций.
  28. ^ Бэтчелор, Боб; Стоддарт, Скотт (2007). 1980-е годы . Гринвуд. п. 97 . ISBN  978-0313330001 .
  29. ^ Аллен, Генри (10 июня 1981 г.). «Куб» . Вашингтон Пост .
  30. ^ Герман, Рос (10 сентября 1981 г.). «Кубическое мастерство» . Новый учёный . Архивировано из оригинала 19 августа 2020 года.
  31. ^ Сингмастер, Дэвид (1994). «Полезность развлекательной математики» . В Гае, Ричард К.; Вудро, Роберт Э. (ред.). Светлая сторона математики: материалы конференции памяти Эжена Стренса по занимательной математике и ее истории . Издательство Кембриджского университета. п. 340 . ISBN  088385516X .
  32. ^ Ханауэр, Джоан (5 января 1982 г.). «Человек, написавший самую продаваемую книгу 1981 года» . Юнайтед Пресс Интернэшнл .
  33. ^ Терраса, Винсент (2008). Энциклопедия телешоу с 1925 по 2010 год . МакФарланд. п. 915. ИСБН  978-0786486410 .
  34. ^ Шеффлер, Ян (2016). Взлом Куба . Саймон и Шустер. п. 88. ИСБН  978-1501121944 .
  35. ^ «Кубик Рубика: Безумие заканчивается» . Нью-Йорк Таймс . 30 октября 1982 года.
  36. ^ «Китай сталкивается с нехваткой кубика Рубика» . Юнайтед Пресс Интернэшнл . 22 февраля 1982 года.
  37. ^ Рид, Стивен Р. (8 декабря 1982 г.). «Русские в очереди за кубиком Рубика» . Юнайтед Пресс Интернэшнл .
  38. ^ Перейти обратно: а б с д Харрис, Дэн (2008). Быстрое решение куба . Стерлинг. п. 3. ISBN  978-1402753138 .
  39. ^ Нунан, Эрика (8 ноября 2003 г.). «Давай еще раз покрутим» . Бостон Глобус .
  40. ^ Перейти обратно: а б Кенкуа, Дуглас (6 августа 2012 г.). «Кубик Рубика снова в центре внимания» . Нью-Йорк Таймс .
  41. ^ Перейти обратно: а б с Хукуэй, Джеймс (14 декабря 2011 г.). «Один куб, много подделок, квинтиллионы возможностей» . Уолл Стрит Джорнал .
  42. ^ «Moleculon Research Corporation против CBS, Inc» . Digital-law-online.info . Проверено 20 июня 2012 г.
  43. ^ «Япония: Патенты» . 26 апреля 1978 года. Архивировано из оригинала 12 февраля 2009 года.
  44. ^ «Основные поправки к Патентному закону Японии (с 1985 г.)» (PDF) . Архивировано из оригинала (PDF) 16 февраля 2012 года . Проверено 20 июня 2012 г.
  45. ^ Перейти обратно: а б Хофштадтер, Дуглас Р. (1985). Метамагические темы: поиск сущности разума и закономерностей . Нью-Йорк: Основные книги. ISBN  0-465-04566-9 . Хофштадтер дает название «Исигэ».
  46. ^ Лонгридж, Марк (2004). «Хронология кубика Рубика» .
  47. ^ «История кубика Рубика – Эрно Рубик» . Inventors.about.com. 9 апреля 2012 г. Архивировано из оригинала 23 мая 2020 г. . Проверено 20 июня 2012 г.
  48. ^ Бодони (25 ноября 2014 г.). «Кубик Рубика выиграл историю игрушек по торговой марке в суде ЕС» . Bloomberg LP Проверено 13 декабря 2014 г.
  49. ^ Смитерс, Ребекка (10 ноября 2016 г.). «Кубик Рубика озадачен после поражения в битве за товарный знак в ЕС» . Хранитель . Проверено 8 декабря 2016 г.
  50. ^ Банделов, К. (6 декабря 2012 г.). Внутри кубика Рубика и за его пределами . Springer Science & Business Media. п. 2. ISBN  978-1-4684-7779-5 .
  51. ^ Цзэн, Да-Син; Ли, Мин; Ван, Хуан-Хуан; Хоу, Ю-Лэй; Лу, Вэнь-Цзюань; Хуан, Чжэнь (27 августа 2018 г.). «Обзор кубика Рубика и размышления о его применении в механизме» . Китайский журнал машиностроения . 31 (1): 77. Бибкод : 2018ЧЮМЭ..31...77З . дои : 10.1186/s10033-018-0269-7 . ISSN   2192-8258 .
  52. ^ Реклама кубика Рубика, 1981 год . 23 октября 2008 г. Архивировано из оригинала 11 декабря 2021 г. Проверено 10 октября 2017 г. - через YouTube.
  53. ^ Шёнерт, Мартин. «Анализ кубика Рубика с помощью GAP» . Gap-system.org . Проверено 30 декабря 2022 г.
  54. ^ Перейти обратно: а б Скотт Вон. «Подсчет перестановок кубика Рубика» . Общественный колледж округа Монтгомери . Архивировано из оригинала 19 июля 2011 года . Проверено 19 января 2011 г.
  55. ^ «Научный американец» . 246 . 1982: 28 . Проверено 29 января 2009 г. {{cite journal}}: Для цитирования журнала требуется |journal= ( помощь )
  56. ^ Перейти обратно: а б Сингмастер, Дэвид (1981). Заметки о волшебном кубике Рубика . Хармондсворт, Англия: Penguin Books. ISBN  0-907395-00-7 .
  57. ^ С. Корли; Л. Моро; Д.Е. Галли; Э. Прати (2021). «Решение кубика Рубика с помощью квантовой механики и глубокого обучения с подкреплением». Физический журнал A: Математический и теоретический . 54 (5): 425302. arXiv : 2109.07199 . Бибкод : 2021JPhA...54P5302C . дои : 10.1088/1751-8121/ac2596 . ISSN   1751-8113 . S2CID   237513509 .
  58. ^ Перейти обратно: а б Джойнер, Дэвид (2002). Приключения в теории групп: кубик Рубика, машина Мерлина и другие математические игрушки . Балтимор: Издательство Университета Джонса Хопкинса. п. 7 . ISBN  0-8018-6947-1 .
  59. ^ «Положение о соревнованиях Всемирной ассоциации кубов» . Всемирная ассоциация кубов . Проверено 5 мая 2012 г.
  60. ^ Трип, Аннеке; Уотерман, Марк (1987). Алгоритм Марка Уотермана, часть 2 . Кубизм для развлечения 15. Nederlandse Kubus Club. п. 10.
  61. ^ «Кубик Рубика — решение и обозначения Вольстенхолма» . topaccolades.com . Проверено 19 февраля 2022 г.
  62. ^ Фрей, Александр Х. младший; Сингмастер, Дэвид (1982). Справочник по математике Кубика . Хиллсайд, Нью-Джерси: Издательство Enslow Publishers. ISBN  0-89490-058-7 .
  63. ^ Канкл, Д.; Куперман, К. (2007). «Для кубика Рубика достаточно двадцати шести ходов» (PDF) . Труды Международного симпозиума по символьным и алгебраическим вычислениям (ISSAC '07) . АКМ Пресс.
  64. ^ Сборка кубика Рубика сократилась до 25 ходов . 2008.
  65. ^ Джули Дж. Ремейер. «Взлом куба» . МатТрек. Архивировано из оригинала 11 октября 2007 года . Проверено 9 августа 2007 г.
  66. ^ Том Рокики (2008). «Для кубика Рубика достаточно двадцати пяти ходов». arXiv : 0803.3435 [ cs.SC ].
  67. ^ «Алгоритм кубика Рубика снова сокращен до 23 ходов» . [Слэшдот]. 5 июня 2008 года . Проверено 5 июня 2008 г.
  68. ^ Рокики, Том. «Двадцати двух ходов достаточно» . Проверено 20 августа 2008 г.
  69. ^ Перейти обратно: а б Филдс, Джонатан (11 августа 2010 г.). «Поиски быстрого решения кубика Рубика подходят к концу» . Новости Би-би-си .
  70. ^ Флэтли, Джозеф Ф. (9 августа 2010 г.). «Кубик Рубика собран за двадцать ходов, 35 лет процессорного времени» . Engadget . Проверено 10 августа 2010 г.
  71. ^ Дэвидсон, Морли; Детридж, Джон; Коцемба, Герберт; Рокицки, Томас. «Число Бога — 20» . Cube20.org . Проверено 10 августа 2010 г.
  72. ^ Демейн, Эрик Д.; Демейн, Мартин Л.; Эйзенштат, Сара; Любив, Анна ; Уинслоу, Эндрю (2011). «Алгоритмы решения кубиков Рубика». arXiv : 1106.5736v1 [ cs.DS ].
  73. ^ «Решение кубика Рубика — метод Петруса» . lar5.com . Проверено 8 ноября 2018 г.
  74. ^ "Введение" . Grrroux.free.fr . Проверено 20 июня 2012 г.
  75. ^ «Как собрать кубик Рубика» . как-решить-a-rubix- cube.com. Проверено 28 июня 2016 г.
  76. ^ «Решение кубика Рубика для начинающих (доступно на нескольких языках)» . Жасмин Ли . Проверено 17 июля 2017 г.
  77. ^ Эванс, Роб (24 сентября 1981 г.). «Восстанови свой куб» . New Scientist : 802. Архивировано из оригинала 18 августа 2020 года.
  78. ^ «Кубик Рубика» . Newsweek . 99 : 16. 1982.
  79. ^ «Веб-сайт с решениями, созданными Денни Дедмором» . Хелм.лу. ​Проверено 20 июня 2012 г.
  80. ^ Маршалл, Филип (2005). «Оптимальное решение кубика Рубика» . helm.lu . Проверено 30 декабря 2022 г.
  81. ^ «Решатель кубика Рубика» . Rubiks-cube-solver.com . Проверено 28 июня 2016 г.
  82. ^ Перейти обратно: а б МакВиртер, Норрис, изд. (1983). «Кубизм» . Книга рекордов Гиннесса . Издательство Гиннесс. п. 85. ИСБН  9780851122519 .
  83. ^ Ханауэр, Джоан (26 мая 1982 г.). «Конкурс кубиков» . Юнайтед Пресс Интернэшнл .
  84. ^ «Официальные результаты Всемирной ассоциации кубов» . Всемирная ассоциация кубов. Архивировано из оригинала 7 июня 2019 года . Проверено 16 февраля 2008 г.
  85. ^ «Положение о соревнованиях, статья 9: Мероприятия» . Всемирная ассоциация кубов. 9 апреля 2008 года . Проверено 16 апреля 2008 г.
  86. ^ «Кубик Рубика 3х3х3: пластинки с завязанными глазами» . WorldCubeAssociation.org . Архивировано из оригинала 10 декабря 2015 года . Проверено 20 июня 2012 г.
  87. ^ «Правила WCA – Всемирная ассоциация кубов» . worldcubeassociation.org . Проверено 5 апреля 2018 г.
  88. ^ «Кубик Рубика 3х3х3: Одной рукой» . Worldcubeassociation.org. Архивировано из оригинала 10 декабря 2015 года . Проверено 20 июня 2012 г.
  89. ^ «Рейтинги | Всемирная ассоциация кубов» . worldcubeassociation.org .
  90. ^ «ВКА Live» . live.worldcubeassociation.org . Проверено 12 июня 2023 г.
  91. ^ «Всемирная ассоциация кубов – официальные результаты» . worldcubeassociation.org . Архивировано из оригинала 12 июня 2018 года . Проверено 25 июня 2023 г.
  92. ^ «Рекорды | Всемирная ассоциация кубов» . www.worldcubeassociation.org .
  93. ^ «Nub Open Mission Viejo 2023 | Всемирная ассоциация кубов» . www.worldcubeassociation.org . Проверено 10 декабря 2023 г.
  94. ^ «Всемирная ассоциация кубов – официальные результаты» . worldcubeassociation.org .
  95. ^ «Правила WCA – январь 2020 г. | Всемирная ассоциация кубов» . www.worldcubeassociation.org . Проверено 4 января 2021 г.
  96. ^ «Рекорды WCA 3x3x3 с завязанными глазами» . Всемирная ассоциация кубов . Проверено 17 марта 2019 г. [ постоянная мертвая ссылка ]
  97. ^ «3x3x3 записи WCA с несколькими завязанными глазами» . Всемирная ассоциация кубов . Проверено 21 июля 2018 г. [ постоянная мертвая ссылка ]
  98. ^ «Всемирная ассоциация кубов – официальные результаты» . worldcubeassociation.org . Архивировано из оригинала 2 июля 2018 года . Проверено 28 марта 2018 г.
  99. ^ «Робот Рубика решает головоломку за 0,38 секунды» . Новости Би-би-си . 8 марта 2018 года . Проверено 8 марта 2018 г.
  100. ^ MoYu 21x21x21 M solve - 1:35:55.52 , 22 February 2022 , retrieved 12 March 2023
  101. ^ «Список неофициальных мировых рекордов» . Speedsolve.com — Вики . Проверено 12 марта 2023 г.
  102. ^ «Ученики побили рекорд кубика Рубика» . Новости Би-би-си . 17 марта 2010 г. Проверено 20 июня 2012 г.
  103. ^ «Школы бьют мировой рекорд» . Деполь Великобритания. 21 ноября 2012 года. Архивировано из оригинала 20 января 2013 года . Проверено 21 ноября 2012 г.
  104. ^ «CoEP устанавливает очередной рекорд: более 3000 человек собрали кубик Рубика за 30 минут» . Индийский экспресс . 5 ноября 2012 года . Проверено 5 ноября 2012 г.
  105. ^ «Рейтинги | Всемирная ассоциация кубов» . worldcubeassociation.org . Проверено 30 декабря 2022 г.
  106. ^ «Патент US7600756B2» . Гугл Патенты . Проверено 14 апреля 2022 г.
  107. ^ «Вероятно, вы не проживете достаточно долго, чтобы собрать самый большой в мире кубик Рубика 22х22» . 15 января 2016 года. Архивировано из оригинала 10 февраля 2016 года . Проверено 10 февраля 2016 г.
  108. ^ Перейти обратно: а б «Мировой рекорд 33х33х33 Кубик Рубика!!!!!» . 2 декабря 2017 г. Архивировано из оригинала 11 декабря 2021 г. Проверено 10 февраля 2018 г. - через YouTube.
  109. ^ «ШэнШоу» . Кабичка . Проверено 23 мая 2020 г.
  110. ^ "MoYu 21x21 Cube Stickerless → MasterCubeStore" . MasterCubeStore.com .
  111. ^ «Вариации» . Рубик . Проверено 30 декабря 2012 г.
  112. ^ «Нью-Йоркская ярмарка игрушек открывается новыми предложениями по кубику Рубика и Lego» . Рейтер. 16 февраля 2009 года . Проверено 23 марта 2009 г.
  113. ^ «Ярмарка игрушек стартует в Джавитс-центре» . Архивировано из оригинала 22 апреля 2009 года . Проверено 23 марта 2009 г.
  114. ^ «Крупнейший заказ Рубика/Волшебный кубик» . Книги рекордов Гиннесса . Проверено 4 января 2013 г.
  115. ^ Ван Девентер, Оскар. «Сверху – 17х17х17» .
  116. ^ «Мировой рекорд 2х2х50 Кубик Рубика!!! :D» . 8 апреля 2018 г. Архивировано из оригинала 11 декабря 2021 г. Проверено 13 апреля 2018 г. - через YouTube.
  117. ^ Мартин, В. Эрик (апрель 2004 г.). «Gamebits: Кубик Рубика... в кубике». Игры . Том. 28, нет. 3. п. 4.
  118. ^ Грин, Мелинда (25 июня 2009 г.). «Волшебный Куб 4D» . Superliminal.com . Проверено 20 июня 2012 г.
  119. ^ «Волшебный Куб 5D» . Gravitation3d.com . Проверено 20 июня 2012 г.
  120. ^ Армстронг, Кальвин; Голдстайн, Сьюзен (сентябрь 2014 г.). «Обзор: выставка за пределами кубика Рубика». Математический журнал колледжа . 45 : 254–256. дои : 10.4169/college.math.j.45.4.254 . JSTOR   10.4169/college.math.j.45.4.254 . S2CID   218549192 .
  121. ^ «Лаборатория Chrome Cube» . Проверено 19 мая 2014 г.
  122. ^ «Научный центр Свободы» . Архивировано из оригинала 20 июня 2012 года . Проверено 15 ноября 2012 г.
  123. ^ Шаффри, Тед (27 апреля 2012 г.). «Кубизм? Рубик помогает с юбилейной выставкой игрушки» . Нью-Йорк. Ассошиэйтед Пресс.
  124. ^ Кенкуа, Дуглас (6 августа 2012 г.). «Кубик Рубика снова в центре внимания» . Нью-Йорк Таймс . Нью-Йорк.
  125. ^ Перейти обратно: а б Конструкции кубика Рубика Фреда Холли. Архивировано 31 августа 2009 года в Wayback Machine.
  126. ^ Перейти обратно: а б «Джейкоб Давенпорт » Искусство кубика Рубика» . www.playagaingames.com .
  127. ^ Мойнихан, Колин (19 ноября 2005 г.). «Восстановленный куб вернулся и поворачивает на Астор-плейс» . Нью-Йорк Таймс . Проверено 18 марта 2009 г.
  128. ^ «Все слишком плоско: Пранки: Куб» . Проверено 29 мая 2009 г.
  129. ^ МакКинни, Тодд (7 апреля 2008 г.). «Фото: Куб Блю-бика» . Университетская запись онлайн . Регенты Мичиганского университета. Архивировано из оригинала 24 февраля 2021 года . Проверено 3 декабря 2010 г.
  130. ^ «Рубиккубизм» . Архивировано из оригинала 7 марта 2012 года.
  131. ^ «РУБИККУБИЗМ/ЛОГИЧЕСКАЯ ВЫСТАВКА INVADER В SIXSPACE/LA. 2005» . Архивировано из оригинала 3 марта 2012 года.
  132. ^ «Пространство Рубика от Invader» . Архивировано из оригинала 13 марта 2012 года.
  133. ^ "Дом" . Кубворкс . Архивировано из оригинала 3 апреля 2011 года.
  134. ^ «Twoguysfromtoronto.com» . www.twoguysfromtoronto.com . Архивировано из оригинала 23 апреля 2021 года . Проверено 27 августа 2023 г.
  135. ^ «Выставки» . Архивировано из оригинала 23 февраля 2012 года.
  136. ^ «Мечтайте по-крупному, Пит Фекто» . Архивировано из оригинала 5 марта 2012 года.
  137. ^ «Официальный сайт You Can Do The Cube» . Архивировано из оригинала 26 января 2012 года . Проверено 22 января 2012 г.
  138. ^ Робертс, Шивон (1 июля 2024 г.). «Кубику Рубика исполняется 50 лет» . Нью-Йорк Таймс . Проверено 4 июля 2024 г.
  139. ^ РМК (1 ноября 1979 г.). «Волшебный куб» . Журнал ИГРЫ . № 14. с. 78.
  140. ^ «Журнал ИГРЫ №20» . Ноябрь 1980 года.

Дальнейшее чтение

Retrieved from "https://en.wikipedia.org/w/index.php?title=Rubik%27s_Cube&oldid=1239248254#Singmaster_notation"
Arc.Ask3.Ru: конец переведенного документа.
Arc.Ask3.Ru
Номер скриншота №: ca653d4e3649ecc322e4be8aa3c96583__1723083420
URL1:https://arc.ask3.ru/arc/aa/ca/83/ca653d4e3649ecc322e4be8aa3c96583.html
Заголовок, (Title) документа по адресу, URL1:
Rubik's Cube - Wikipedia
Данный printscreen веб страницы (снимок веб страницы, скриншот веб страницы), визуально-программная копия документа расположенного по адресу URL1 и сохраненная в файл, имеет: квалифицированную, усовершенствованную (подтверждены: метки времени, валидность сертификата), открепленную ЭЦП (приложена к данному файлу), что может быть использовано для подтверждения содержания и факта существования документа в этот момент времени. Права на данный скриншот принадлежат администрации Ask3.ru, использование в качестве доказательства только с письменного разрешения правообладателя скриншота. Администрация Ask3.ru не несет ответственности за информацию размещенную на данном скриншоте. Права на прочие зарегистрированные элементы любого права, изображенные на снимках принадлежат их владельцам. Качество перевода предоставляется как есть. Любые претензии, иски не могут быть предъявлены. Если вы не согласны с любым пунктом перечисленным выше, вы не можете использовать данный сайт и информация размещенную на нем (сайте/странице), немедленно покиньте данный сайт. В случае нарушения любого пункта перечисленного выше, штраф 55! (Пятьдесят пять факториал, Денежную единицу (имеющую самостоятельную стоимость) можете выбрать самостоятельно, выплаичвается товарами в течение 7 дней с момента нарушения.)