Энтальпия
| Энтальпия | |
|---|---|
Общие символы | ЧАС |
| И объединились | джоули |
| В базовых единицах СИ | kg⋅m 2 ⋅s −2 |
| Термодинамика |
|---|
 |
Энтальпия ( / ˈ ɛ n θ əl p i / ) представляет собой сумму термодинамической системы и внутренней энергии произведения ее давления на объем . [1] Это функция состояния в термодинамике, используемая во многих измерениях в химических, биологических и физических системах при постоянном внешнем давлении, которое удобно обеспечивается большой окружающей атмосферой. Член давление-объем выражает работу это было сделано вопреки постоянному внешнему давлению установить физические размеры системы из до какого-то окончательного тома (как ), т.е. освободить для него место, вытеснив его окружение. [2] [3] Соотношение давление-объем очень мало для твердых тел и жидкостей в обычных условиях и довольно мало для газов. Следовательно, энтальпия является заменой энергии в химических системах; связь , решетка , сольватация и другие химические «энергии» на самом деле представляют собой разницу энтальпий. Как функция состояния, энтальпия зависит только от окончательной конфигурации внутренней энергии, давления и объема, а не от пути, пройденного для ее достижения.
В Международной системе единиц (СИ) единицей измерения энтальпии является джоуль . Другие исторические условные единицы, которые до сих пор используются, включают калорию и британскую тепловую единицу (БТЕ).
Полную энтальпию системы невозможно измерить напрямую, поскольку внутренняя энергия содержит компоненты, которые неизвестны, труднодоступны или не представляют интереса для рассматриваемой термодинамической задачи. На практике изменение энтальпии является предпочтительным выражением для измерений при постоянном давлении, поскольку оно упрощает описание переноса энергии . Когда перенос вещества в систему или из нее также предотвращается и не совершается никакая электрическая или механическая работа (перемешивающий вал или подъемный насос), при постоянном давлении изменение энтальпии равняется энергии, которой обмениваются с окружающей средой теплом .
В химии стандартная энтальпия реакции — это изменение энтальпии, когда реагенты в их стандартных состояниях ( р = 1 бар ; обычно Т = 298 К ) превращаются в продукты в их стандартных состояниях. [4] Эта величина представляет собой стандартную теплоту реакции при постоянных давлении и температуре, но ее можно измерить калориметрическими методами, даже если температура в процессе измерения меняется, при условии, что начальное и конечное давление и температура соответствуют стандартному состоянию. Величина не зависит от пути от начального состояния к конечному, поскольку энтальпия является функцией состояния .
Энтальпии химических веществ обычно указываются для давления 1 бар (100 кПа) в качестве стандартного состояния. Энтальпии и изменения энтальпии реакций изменяются в зависимости от температуры. [5] но в таблицах обычно указаны стандартные теплоты образования веществ при 25 ° C (298 К). Для эндотермических (теплопоглощающих) процессов изменение ΔH имеет положительную величину; для экзотермических (тепловыделительных) процессов он отрицателен.
Энтальпия идеального газа не зависит от его давления или объема и зависит только от его температуры, которая коррелирует с его тепловой энергией. Реальные газы при обычных температурах и давлениях часто очень близки к такому поведению, что упрощает практическое термодинамическое проектирование и анализ.
Слово «энтальпия» происходит от греческого слова enthalpein , что означает «тепло». [6] [7]
Определение
[ редактировать ]Энтальпия H термодинамической системы определяется как сумма ее внутренней энергии и произведения ее давления на объем: [1]
- ЧАС знак равно U + п V ,
где U — внутренняя энергия , p — давление , V — объём системы; p V иногда называют энергией давления Ɛ p . [8]
Энтальпия — обширное свойство ; он пропорционален размеру системы (для однородных систем). В качестве интенсивных свойств удельная энтальпия h = H / m молярная единице массы m системы, а энтальпия m H относится к = H / n , где n — количество молей . Для неоднородных систем энтальпия представляет собой сумму энтальпий составляющих подсистем: где
- H – суммарная энтальпия всех подсистем,
- k относится к различным подсистемам,
- H k относится к энтальпии каждой подсистемы.
Закрытая система может находиться в термодинамическом равновесии в статическом гравитационном поле , так что ее давление p непрерывно меняется с высотой , в то время как из-за требования равновесия ее температура T инвариантна с высотой. системы (Соответственно, плотность потенциальной гравитационной энергии также меняется с высотой.) Тогда сумма энтальпий становится интегралом : где
- ρ (« ро ») — плотность (масса единицы объема),
- h – удельная энтальпия (энтальпия на единицу массы),
- ( ρh ) представляет собой плотность энтальпии (энтальпия на единицу объема),
- d V обозначает бесконечно малый элемент объема внутри системы, например, объем бесконечно тонкого горизонтального слоя.
Таким образом, интеграл представляет собой сумму энтальпий всех элементов объема.
Энтальпия замкнутой однородной системы — это ее энергетическая функция H ( S , p ) , с ее энтропией S [ p ] и давлением p как естественными переменными состояния , которые обеспечивают дифференциальное соотношение для d H простейшей формы, полученное следующим образом. Начнем с первого закона термодинамики для закрытых систем для бесконечно малого процесса:
где
- δ Q — небольшое количество тепла, добавленное в систему,
- δ W – малый объем работы, совершаемый системой.
В однородной системе, в которой рассматриваются только обратимые процессы или чистая теплопередача, второй закон термодинамики дает δ Q = T d S , где T - абсолютная температура , а d S - бесконечно малое изменение энтропии S системы. Более того, если только p V совершается работы, δ W = p d V . Как результат,
Добавление d( p V ) к обеим частям этого выражения дает
или
Так
а коэффициенты дифференциалов натуральных переменных d S и d p представляют собой всего лишь отдельные переменные T и V .
Другие выражения
[ редактировать ]Вышеприведенное выражение d H через энтропию и давление может быть незнакомо некоторым читателям. Существуют также выражения в терминах более непосредственно измеримых переменных, таких как температура и давление: [9] (стр. 88) [10]
Здесь C p — теплоемкость при постоянном давлении , а α — коэффициент (кубического) теплового расширения :
С помощью этого выражения в принципе можно определить энтальпию, если C p и V известны как функции p и T . Однако выражение сложнее, чем потому что не является естественной переменной для энтальпии H. T
При постоянном давлении, так что Для идеального газа сводится к этой форме, даже если процесс включает изменение давления, поскольку α T = 1 . [примечание 1]
В более общей форме первый закон описывает внутреннюю энергию с дополнительными членами, включающими химический потенциал и количество частиц различных типов. Дифференциальное утверждение для d H тогда становится
где μ i — химический потенциал на одну частицу для частицы типа i , а N i — количество таких частиц. Последний член также можно записать как μ i d n i (где d n i 0 — количество молей компонента i, добавленного в систему, и, в данном случае, μ i — молярный химический потенциал) или как μ i d m i (где d m i — масса компонента i, добавленного в систему, и, в данном случае, μ i — удельный химический потенциал).
Характеристические функции и естественные переменные состояния
[ редактировать ]Энтальпия H ( S [ p ], p , { N i }) выражает термодинамику системы в энергетическом представлении . Как функция состояния , его аргументы включают как одну интенсивную, так и несколько экстенсивных переменных состояния . Переменные состояния S [ p ] , p и { N i } называются естественными переменными состояния в этом представлении. Они подходят для описания процессов, в которых они определяются факторами окружающей среды. Например, когда виртуальный пакет атмосферного воздуха перемещается на другую высоту, давление вокруг него меняется, и процесс часто настолько быстрый, что времени для передачи тепла остается слишком мало. На этом основано так называемое адиабатическое приближение , которое используется в метеорологии . [11]
Сопряженная с энтальпией, с этими аргументами, другая характеристическая функция состояния термодинамической системы - это ее энтропия как функция S [ p ]( H , p , {N i } ) того же списка переменных состояния , за исключением того, что энтропия S [ p ] заменяется в списке энтальпией H . Оно выражает представление энтропии . Переменные состояния H , p и { N i } называются естественными переменными состояния в этом представлении. Они подходят для описания процессов, в которых контролируются экспериментально. Например, H и p можно контролировать, допуская передачу тепла и изменяя только внешнее давление на поршень, который устанавливает объем системы. [12] [13] [14]
Физическая интерпретация
[ редактировать ]Член U представляет собой энергию системы, а член p V можно интерпретировать как работу , которая потребовалась бы, чтобы «освободить место» для системы, если бы давление окружающей среды оставалось постоянным. Когда система, например, n молей газа объемом V при давлении p и температуре T , создается или приводится в текущее состояние от абсолютного нуля , необходимо подвести энергию, равную ее внутренней энергии U плюс pV , где p V — работа , совершаемая при толкании против окружающего (атмосферного) давления.
В физике и статистической механике может быть более интересно изучать внутренние свойства системы постоянного объема, поэтому используется внутренняя энергия. [15] [16] В химии эксперименты часто проводятся при постоянном атмосферном давлении , а работа давление-объем представляет собой небольшой, четко определенный обмен энергией с атмосферой, так что Δ H является подходящим выражением для теплоты реакции . Для теплового двигателя изменение его энтальпии после полного цикла равно нулю, поскольку конечное и начальное состояние равны.
Отношение к теплу
[ редактировать ]Чтобы обсудить связь между увеличением энтальпии и подводом тепла, мы вернемся к первому закону для закрытых систем с физическим соглашением о знаках: d U = δ Q − δ W , где тепло δ Q передается за счет проводимости, излучения , Джоулево нагрев . Применим его к частному случаю с постоянным давлением на поверхности. В этом случае работа определяется как p d V (где p — давление на поверхности, d V — увеличение объема системы). Случаи дальнодействующего электромагнитного взаимодействия требуют дополнительных переменных состояния в их формулировке и здесь не рассматриваются. В этом случае первый закон гласит:
Сейчас,
Так
Если система находится под постоянным давлением , d p = 0 и, следовательно, прирост энтальпии системы равен подведенному теплу :
Вот почему ныне устаревший термин теплосодержание использовался для обозначения энтальпии в 19 веке.
Приложения
[ редактировать ]В термодинамике можно вычислить энтальпию, определив требования для создания системы из «ничто»; требуемая механическая работа p V различается в зависимости от условий, возникающих при создании термодинамической системы .
Энергия должна быть подана для удаления частиц из окружающей среды, чтобы освободить место для создания системы, при условии, что давление p остается постоянным; это p V. термин Подаваемая энергия должна также обеспечивать изменение внутренней энергии U , которая включает в себя энергии активации , энергии ионизации, энергии смешивания, энергии испарения, энергии химической связи и т. д. Вместе они составляют изменение энтальпии U + p V . Для систем с постоянным давлением, в которых не совершается никакая внешняя работа, кроме работы p V , изменение энтальпии представляет собой тепло, полученное системой.
Для простой системы с постоянным числом частиц при постоянном давлении разница в энтальпии представляет собой максимальное количество тепловой энергии, получаемой в результате изобарного термодинамического процесса. [17]
Теплота реакции
[ редактировать ]Полную энтальпию системы невозможно измерить напрямую; изменение энтальпии системы Вместо этого измеряется . Изменение энтальпии определяется следующим уравнением: где
- Δ H - «изменение энтальпии»,
- H f – конечная энтальпия системы (в химической реакции энтальпия продуктов или системы, находящейся в равновесии),
- H i — начальная энтальпия системы (в химической реакции — энтальпия реагирующих веществ).
Для экзотермической реакции при постоянном давлении изменение энтальпии системы Δ H отрицательно, поскольку продукты реакции имеют меньшую энтальпию, чем реагенты, и равняется теплу, выделяемому в реакции, если не совершается электрическая работа или работа вала. . Другими словами, общее снижение энтальпии достигается за счет выделения тепла. [18] при постоянном давлении И наоборот, для эндотермической реакции Δ H положительна и равна теплу, поглощенному в реакции.
Из определения энтальпии как H = U + p V , изменение энтальпии при постоянном давлении равно Δ H = Δ U + p Δ V . Однако для большинства химических реакций рабочий член p Δ V намного меньше изменения внутренней энергии Δ U , которое примерно равно Δ H . Например, для сгорания угарного газа 2 CO(г) + O 2 (г) → 2 CO 2 (г) Δ H = −566,0 кДж и Δ U = −563,5 кДж. [19] Поскольку различия настолько малы, энтальпии реакции часто описываются как энергии реакции и анализируются с точки зрения энергий связи .
Удельная энтальпия
[ редактировать ]Удельная энтальпия однородной системы определяется как h = H / m где m — масса системы. Единицей в системе СИ удельной энтальпии является джоуль на килограмм. В других конкретных величинах ее можно выразить как h = u + pv , где u — удельная внутренняя энергия , p — давление, а v — удельный объем , равный 1 / ρ , где ρ — плотность .
Изменения энтальпии
[ редактировать ]Изменение энтальпии описывает изменение энтальпии, наблюдаемое в компонентах термодинамической системы при превращении или химической реакции. Это разница между энтальпией после завершения процесса, т. е. энтальпией продуктов при условии, что реакция дошла до завершения, и начальной энтальпией системы, а именно реагентов. Эти процессы определяются исключительно их начальным и конечным состояниями, так что изменение энтальпии для обратного процесса является отрицательным, чем для прямого процесса.
Обычным стандартным изменением энтальпии является энтальпия образования , которая определена для большого числа веществ. Изменения энтальпии регулярно измеряются и обобщаются в химических и физических справочных изданиях, таких как Справочник CRC по химии и физике . Ниже приводится подборка изменений энтальпии, обычно признаваемых в термодинамике.
При использовании этих общепризнанных терминов изменение квалификатора обычно опускается и свойство называется просто энтальпией «процесса» . Поскольку эти свойства часто используются в качестве эталонных значений, их очень часто называют для стандартизированного набора параметров окружающей среды или стандартных условий , в том числе:
- Давление в одну атмосферу (1 атм или 1013,25 гПа) или 1 бар.
- Температура К. 25 °C или 298,15
- Концентрация 1,0 М , когда элемент или соединение присутствует в растворе.
- Элементы или соединения в их нормальном физическом состоянии, т.е. стандартном состоянии.
Для таких стандартизированных значений к названию энтальпии обычно добавляется термин «стандарт» , например, стандартная энтальпия образования .
Химические свойства
[ редактировать ]Энтальпия реакции – определяется как изменение энтальпии, наблюдаемое в компоненте термодинамической системы, когда один моль вещества вступает в реакцию полностью.
Энтальпия образования - определяется как изменение энтальпии, наблюдаемое в компоненте термодинамической системы, когда один моль соединения образуется из его элементарных предшественников.
Энтальпия сгорания – определяется как изменение энтальпии, наблюдаемое в компоненте термодинамической системы, когда один моль вещества полностью сгорает с кислородом.
Энтальпия гидрирования — определяется как изменение энтальпии, наблюдаемое в компоненте термодинамической системы, когда один моль ненасыщенного соединения полностью реагирует с избытком водорода с образованием насыщенного соединения .
Энтальпия распыления – определяется как изменение энтальпии, необходимое для полного разделения одного моля вещества на составляющие его атомы .
Энтальпия нейтрализации - определяется как изменение энтальпии, наблюдаемое в компоненте термодинамической системы, когда при реакции кислоты и основания образуется один моль воды.
Стандартная энтальпия раствора – определяется как изменение энтальпии, наблюдаемое в компоненте термодинамической системы, когда один моль растворенного вещества полностью растворяется в избытке растворителя, так что раствор находится в бесконечном разбавлении.
Стандартная энтальпия денатурации (биохимия) – определяется как изменение энтальпии, необходимое для денатурации одного моля соединения.
Энтальпия гидратации – определяется как изменение энтальпии, наблюдаемое при полном растворении одного моля газообразных ионов в воде с образованием одного моля водных ионов.
Физические свойства
[ редактировать ]Энтальпия плавления – определяется как изменение энтальпии, необходимое для полного изменения состояния одного моля вещества из твердого в жидкое.
Энтальпия парообразования – определяется как изменение энтальпии, необходимое для полного перехода одного моля вещества из жидкого в газообразное.
Энтальпия сублимации – определяется как изменение энтальпии, необходимое для полного перехода одного моля вещества из твердого состояния в газообразное.
Энтальпия решетки - определяется как энергия, необходимая для разделения одного моля ионного соединения на отдельные газообразные ионы на бесконечное расстояние друг от друга (что означает отсутствие силы притяжения).
Энтальпия смешения – определяется как изменение энтальпии при смешивании двух (нереагирующих) химических веществ.
Открытые системы
[ редактировать ]В термодинамических открытых системах масса (веществ) может втекать и выходить из границ системы. Первый закон термодинамики для открытых систем гласит: увеличение внутренней энергии системы равно количеству энергии, добавленной к системе за счет притока массы и нагревания, за вычетом количества, потерянного за счет вытекания массы и в виде работы, выполненной системой:
где U in — средняя внутренняя энергия, поступающая в систему, а U out — средняя внутренняя энергия, покидающая систему.

Область пространства, ограниченная границами открытой системы, обычно называется контрольным объемом и может соответствовать, а может и не соответствовать физическим стенам. Если мы выберем форму управляющего объема так, чтобы весь приток и выход происходил перпендикулярно его поверхности, то приток массы в систему совершает работу так, как если бы это был поршень с жидкостью, толкающий массу в систему, и система совершает работайте над вытеканием массы так, как если бы она приводила в движение поршень с жидкостью. Тогда выполняются два типа работы: работа потока , описанная выше, которая выполняется над жидкостью (ее также часто называют p V работой ), и механическая работа ( работа вала ), которая может быть выполнена каким-либо механическим устройством, таким как турбина или насос.
Эти два вида работы выражаются уравнением
Подстановка контрольного объема (cv) в приведенное выше уравнение дает:
Определение энтальпии H позволяет нам использовать этот термодинамический потенциал для учета как внутренней энергии, так и работы pV в жидкостях для открытых систем:
Если мы допустим также перемещение границы системы (например, за счет перемещения поршней), мы получим довольно общую форму первого закона для открытых систем. [20] Что касается производных по времени, используя точечную запись Ньютона для производных по времени, это звучит так:
с суммами по различным местам k, куда поступает тепло, масса поступает в систему и границы перемещаются. . k представляют потоки энтальпии, которые можно записать как
с k массовый расход и k молярный поток в положении k соответственно. Термин d V k / d t представляет скорость изменения объема системы в положении k , что приводит к мощности p V, создаваемой системой. Параметр P представляет все другие формы мощности, вырабатываемые системой, такие как мощность на валу, но это также может быть, скажем, электроэнергия, производимая электростанцией.
Обратите внимание, что предыдущее выражение справедливо только в том случае, если скорость потока кинетической энергии сохраняется между входом и выходом системы. [ нужны разъяснения ] В противном случае его приходится включать в баланс энтальпии. При установившейся работе устройства ( см. турбина , насос , двигатель ) среднее значение d U / d t можно положить равным нулю. Это дает полезное выражение для средней выработки мощности этими устройствами в отсутствие химических реакций:
где угловые скобки обозначают средние значения по времени. Техническое значение энтальпии напрямую связано с ее наличием в первом законе открытых систем, сформулированном выше.
Диаграммы
[ редактировать ]
Значения энтальпии важных веществ можно получить с помощью коммерческого программного обеспечения. Практически все соответствующие свойства материалов можно получить либо в табличной, либо в графической форме. Существует много типов диаграмм, таких как диаграммы h – T , которые показывают удельную энтальпию как функцию температуры для различных давлений, и диаграммы h – p , которые показывают h как функцию p для различных T . Одной из наиболее распространенных диаграмм является диаграмма энтропии, зависящая от температуры ( диаграмма T – s ). Он дает кривую плавления и значения насыщенной жидкости и пара вместе с изобарами и изентальпами. Эти диаграммы являются мощным инструментом в руках инженера-теплотехника.
Некоторые базовые приложения
[ редактировать ]Точки от a до h на рисунке играют роль в обсуждении в этом разделе.
Точка Т п с час К бар кДж / кг К кДж / кг а 300 1 6.85 461 б 380 2 6.85 530 с 300 200 5.16 430 д 270 1 6.79 430 и 108 13 3.55 100 ж 77.2 1 3.75 100 г 77.2 1 2.83 28 час 77.2 1 5.41 230
Точки е и g — насыщенные жидкости, а точка h — насыщенный газ.
Регулирование
[ редактировать ]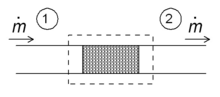
Одним из простых применений понятия энтальпии является так называемый процесс дросселирования, также известный как расширение Джоуля-Томсона . Речь идет об устойчивом адиабатическом течении жидкости через гидравлическое сопротивление (клапан, пористую пробку или любой другой тип гидравлического сопротивления), как показано на рисунке. Этот процесс очень важен, поскольку он лежит в основе бытовых холодильников и отвечает за перепад температур между температурой окружающей среды и внутренней частью холодильника. Это также последняя стадия во многих типах ожижителей .
Для установившегося режима течения энтальпия системы (пунктирный прямоугольник) должна быть постоянной. Следовательно
Поскольку массовый расход постоянен, удельные энтальпии по обе стороны сопротивления потоку одинаковы:
то есть энтальпия на единицу массы при дросселировании не меняется. Последствия этого соотношения можно продемонстрировать с помощью диаграммы T - s, приведенной выше.
Пример 1
[ редактировать ]Точка c соответствует давлению 200 бар и комнатной температуре (300 К). Расширение Джоуля-Томсона от 200 бар до 1 бар следует кривой постоянной энтальпии примерно 425. кДж / кг (на схеме не показан) лежит между 400 и 450 кДж / кг изэнтальп и заканчивается в точке d , которая находится при температуре около 270 К. Следовательно, расширение с 200 бар до 1 бар охлаждает азот с 300 К до 270 К. В клапане возникает большое трение и выделяется много энтропии, но конечная температура все равно ниже стартового значения.
Пример 2
[ редактировать ]Точка е выбрана так, чтобы она находилась на линии насыщенной жидкости с h = 100. кДж / кг . Это примерно соответствует p = 13 бар и T = 108 К. Дросселирование от этой точки до давления 1 бар заканчивается в двухфазной области (точка f ). Это означает, что смесь газа и жидкости выходит из дроссельного клапана. Поскольку энтальпия является расширенным параметром, энтальпия в f ( h f ) равна энтальпии в g ( h g ), умноженной на долю жидкости в f ( x f ), плюс энтальпия в h ( h h ), умноженная на доля газа в ж (1 - Икс ж ) . Так
С цифрами:
- 100 знак равно Икс ж × 28 + ( 1 - Икс ж ) × 230 , поэтому Икс ж знак равно 0,64 .
Это означает, что массовая доля жидкости в газожидкостной смеси, выходящей из дроссельного клапана, составляет 64%.
Компрессоры
[ редактировать ]
Мощность P применяется, например, как электрическая мощность. Если сжатие адиабатическое , температура газа повышается. В обратимом случае это будет постоянная энтропия, что соответствует вертикальной линии на диаграмме T – s . Например, сжатие азота с 1 бар (точка а ) до 2 бар (точка б ) приведет к повышению температуры с 300 К до 380 К. Чтобы позволить сжатому газу выйти при температуре окружающей среды Т а , необходимо осуществить теплообмен, например необходимо охлаждающей водой. В идеальном случае сжатие изотермическое. Средний тепловой поток в окружающую среду равен Q̇ . Поскольку система находится в установившемся состоянии, первый закон дает
Минимальная мощность, необходимая для сжатия, достигается, если сжатие обратимо. В этом случае второй закон термодинамики для открытых систем дает
Устранение Q̇ дает минимальную мощность
Например, сжатие 1 кг азота с давления 1 бар до 200 бар стоит как минимум: ( час c - час a ) - T a ( s c - s a ) . По данным, полученным с помощью диаграммы T – s , находим значение (430 – 461) – 300 × (5,16 – 6,85) = 476. кДж / кг .
Отношение для мощности можно еще упростить, записав его в виде
С
- d час знак равно Т d s + v d п ,
это приводит к окончательному соотношению
История и этимология
[ редактировать ]Термин энтальпия появился относительно поздно в истории термодинамики, в начале 20 века. Энергия была введена в современном смысле Томасом Янгом в 1802 году, а энтропия - Рудольфом Клаузиусом в 1865 году. Энергия использует корень греческого слова ἔργον ( эргон ), что означает «работа», [22] выражать идею способности выполнять работу. Энтропия использует греческое слово τροπή ( тропе ), означающее трансформацию или поворот . [23] Энтальпия использует корень греческого слова θάλπος ( thalpos ) «тепло, тепло». [24]
Термин выражает устаревшее понятие теплосодержания , [примечание 2] поскольку d H относится к количеству тепла, полученному в процессе только при постоянном давлении, [25] но не в общем случае, когда давление является переменным. [18] Дж. Гиббс для ясности использовал термин «тепловая функция при постоянном давлении». [примечание 3]
Введение понятия «теплосодержание» H связано с Бенуа-Полем Эмилем Клапейроном и Рудольфом Клаузиусом ( соотношение Клаузиуса-Клапейрона , 1850).
Термин энтальпия впервые появился в печати в 1909 году. [28] Его приписывают Хайке Камерлинг-Оннесу , который, скорее всего, представил его устно годом ранее, на первом заседании Института холода в Париже. [29] Он получил распространение только в 1920-х годах, особенно с « Таблицами и диаграммами Молье Стима» , опубликованными в 1927 году.
До 1920-х годов символ H использовался несколько непоследовательно для обозначения «тепла» в целом. Определение H как строго ограниченного энтальпией или «теплосодержанием при постоянном давлении» было официально предложено А. В. Портером в 1922 году. [30] [31]
Примечания
[ редактировать ]- ^
- ^ Ховард (2002) цитирует Дж. Р. Партингтона в «Расширенном трактате по физической химии» (1949), который говорит, что функция H «обычно называлась теплосодержанием».
- ^ Гиббса Том I Собрания сочинений [26] не содержит слова «энтальпия» используется фраза «тепловая функция при постоянном давлении» . , вместо этого для той же величины [27]
См. также
[ редактировать ]Ссылки
[ редактировать ]- ^ Jump up to: а б ИЮПАК , Сборник химической терминологии , 2-е изд. («Золотая книга») (1997). Исправленная онлайн-версия: (2006–) « Энтальпия ». дои : 10.1351/goldbook.E02141
- ^ Земанский, Марк В. (1968). Тепло и термодинамика (5-е изд.). Нью-Йорк, штат Нью-Йорк: МакГроу-Хилл. глава 11 стр 275 .
- ^ ван Вайлен, Дж.Дж.; Зоннтаг, RE (1985). Основы классической термодинамики (3-е изд.). Нью-Йорк, штат Нью-Йорк: Джон Уайли и сыновья. раздел 5.5. ISBN 978-0-471-82933-1 .
- ^ Аткинс, Питер; де Паула, Хулио (2006). Физическая химия Аткинса (8-е изд.). У.Х.Фриман. п. 51. ИСБН 0-7167-8759-8 .
- ^ Лейдлер, Кейт Дж.; Мейзер, Джон Х. (1999). Физическая химия (3-е изд.). Бостон, Массачусетс: Хоутон Миффлин. п. 66. ИСБН 0-395-91848-0 .
- ^ Ченгель, Юнус А.; Болес, Майкл А.; Каноглу, Мехмет (2019). Термодинамика: инженерный подход (Девятое изд.). Нью-Йорк, штат Нью-Йорк: McGraw-Hill Education. п. 123. ИСБН 978-1-259-82267-4 .
- ^ ἐνθαλπειν , ἐν , θαλπειν . Лидделл, Генри Джордж ; Скотт, Роберт ; Греко-английский лексикон в проекте «Персей» .
- ^ «1-й закон термодинамики» . Химия LibreTexts . 02.10.2013 . Проверено 17 октября 2023 г.
- ^ Гуггенхайм, Э.А. (1959). Термодинамика . Амстердам, Нидерланды: Издательская компания Северной Голландии.
- ^ Моран, MJ; Шапиро, Х.Н. (2006). Основы инженерной термодинамики (5-е изд.). Джон Уайли и сыновья. п. 511 . ISBN 9780470030370 .
- ^ Ирибарн, СП; Годсон, WL (1981). Атмосферная термодинамика (2-е изд.). Дордрехт, Нидерланды: Издательство Kluwer Academic Publishers. стр. 235–236. ISBN 90-277-1297-2 .
- ^ Чогль, Северо-Запад (2000). Основы равновесной и стационарной термодинамики . Амстердам, Нидерланды: Elsevier. п. 17. ISBN 0-444-50426-5 .
- ^ Каллен, Х.Б. (1985) [1960]. Термодинамика и введение в термостатистику (1-е (1960 г.), 2-е (1985 г.) изд.). Нью-Йорк, штат Нью-Йорк: Джон Уайли и сыновья. Глава 5. ISBN 0-471-86256-8 .
- ^ Мюнстер, А. (1970). Классическая термодинамика . Перевод Хальберштадта, ES Лондон, Великобритания: Wiley – Interscience. п. 6. ISBN 0-471-62430-6 .
- ^ Рейф, Ф. (1967). Статистическая физика . Лондон, Великобритания: МакГроу-Хилл.
- ^ Киттель, К.; Кремер, Х. (1980). Теплофизика . Лондон, Великобритания: Фриман.
- ^ Ратакришнан (2015). Высокоэнтальпийная газодинамика . Джон Уайли и сыновья Сингапур Pte. ООО ISBN 978-1118821893 .
- ^ Jump up to: а б Лейдлер, Кей Джей ; Мейзер, Джон Х. (1982). Физическая химия . Бенджамин/Каммингс. п. 53. ИСБН 978-0-8053-5682-3 .
- ^ Петруччи, Ральф Х.; Харвуд, Уильям С.; Херринг, Ф. Джеффри (2002). Общая химия (8-е изд.). Прентис Холл. стр. 237–238 . ISBN 978-0-13-014329-7 .
- ^ Моран, MJ; Шапиро, Х.Н. (2006). Основы инженерной термодинамики (5-е изд.). Джон Уайли и сыновья. п. 129 . ISBN 9780470030370 .
- ^ Рисунок составлен на основе данных, полученных с помощью RefProp , стандартной справочной базы данных NIST 23.
- ^ работа в Лидделле и Скотте .
- ^ сдайте Лидделла и Скотта .
- ^ θάλπος у Лидделла и Скотта .
- ^ Тиноко, Игнасио младший; Зауэр, Кеннет; Ван, Джеймс С. (1995). Физическая химия (3-е изд.). Прентис-Холл. п. 41. ИСБН 978-0-13-186545-7 .
- ^ Гиббс (1948)
- ^ Хендерсон, Дуглас; Айринг, Генри; Йост, Вильгельм (1967). Физическая химия: продвинутый трактат . Академическая пресса. п. 29.
- ^ Далтон (1909) , с. 864, сноска (1).
- ^ Лайдлер (1995) , с. 110; ван Несс (2003) , с. 486.
- ^ Портер, Альфред В. (1922). «Получение и использование холода. Общая дискуссия» . Труды Фарадеевского общества . 18 : 139–143 особенно. п. 140. дои : 10.1039/tf9221800139 .
- ^ Ховард (2002) , с. 697.
Библиография
[ редактировать ]- Далтон, JP (1909). «Исследования эффекта Джоуля-Кельвина, особенно при низких температурах. I. Расчеты для водорода» (PDF) . Koninklijke Akademie van Wetenschappen te Amsterdam [Труды Королевской академии наук в Амстердаме, Секция наук] . 11 : 863–873. Бибкод : 1908KNAB...11..863D .
- Гиббс, JW (1948). Собрание сочинений Дж. Уилларда Гиббса . Том. Я. Нью-Хейвен, Коннектикут: Издательство Йельского университета. п. 88.
- Хаазе, Р. (1971). Йост, В. (ред.). Физическая химия: продвинутый трактат . Нью-Йорк, штат Нью-Йорк: Академический. п. 29.
- де Хофф, Р. (2006). Термодинамика в материаловедении . Бока-Ратон, Флорида: CRC Press. ISBN 9780849340659 .
- Ховард, Ирмгард К. (2002). « H означает энтальпию, спасибо Хайке Камерлинг-Оннесу и Альфреду В. Портеру». Журнал химического образования . 79 (6): 697–698. Бибкод : 2002JChEd..79..697H . дои : 10.1021/ed079p697 .
- Киттель, К.; Кремер, Х. (1980). Теплофизика . Нью-Йорк, штат Нью-Йорк: SR Furphy & Co., с. 246.
- Лейдлер, К.Дж. (1995). Мир физической химии . Оксфорд, Великобритания: Издательство Оксфордского университета. п. 110 . ISBN 978-0-19-855597-1 – через archive.org.
- ван Несс, Хендрик К. (2003). « H означает энтальпию». Журнал химического образования . 80 (6): 486. Бибкод : 2003ЖЧЭд..80..486В . дои : 10.1021/ed080p486.1 .
Внешние ссылки
[ редактировать ]- Вайсштейн, Эрик. «Энтальпия» . Мир физики Эрика Вайсштейна – через scienceworld.wolfram.com.
- « Энтальпия » . Гипертекст термодинамики. Кафедра физики и астрономии. Государственный университет Джорджии .
- «Пример расчета энтальпии» (примечания к учебнику). Химический факультет. Техасский университет A&M . Архивировано из оригинала 10 октября 2006 года.






















































