Закон идеального газа

Изотермы для идеального газа разных температур. Кривые линии представляют собой прямоугольные гиперболы вида y = a/x. Они представляют соотношение между давлением (по вертикальной оси) и объемом (по горизонтальной оси) для идеального газа при различных температурах : линии, которые находятся дальше от начала координат (то есть линии, которые ближе к верхнему правому углу). угол диаграммы) соответствуют более высоким температурам.

Закон идеального газа , также называемый общим уравнением газа , представляет собой уравнение состояния гипотетического идеального газа . Это хорошее приближение поведения многих газов во многих условиях, хотя оно имеет несколько ограничений. Впервые он был сформулирован Бенуа Полем Эмилем Клапейроном в 1834 году как комбинация эмпирического закона Бойля , закона Шарля , закона Авогадро и закона Гей-Люссака . Закон идеального газа часто записывают в эмпирической форме:

$$pV=nRT$$ где $p$, $V$ и $T$ – давление , объем и температура соответственно; $n$ — количество вещества ; и $R$ — идеальная газовая постоянная . Его также можно вывести из микроскопической кинетической теории , как это было достигнуто (по-видимому, независимо) Августом Крёнигом в 1856 году. и Рудольф Клаузиус в 1857 году.

Уравнение

Молекулярные столкновения внутри закрытого контейнера (пропанового баллона) показаны (справа). Стрелки представляют случайные движения и столкновения этих молекул. Давление и температура газа прямо пропорциональны: при повышении температуры давление пропана увеличивается в тот же раз. Простым следствием этой пропорциональности является то, что в жаркий летний день давление в баллонах с пропаном будет повышенным, и, следовательно, баллоны с пропаном должны быть рассчитаны на то, чтобы выдерживать такое увеличение давления.

Состояние газа некоторого количества определяется его давлением, объемом и температурой. Современная форма уравнения связывает их просто в двух основных формах. Температура, используемая в уравнении состояния, является абсолютной температурой: подходящей единицей СИ является кельвин .

Общие формы

Наиболее часто встречающиеся формы: $$pV=nRT=nk_{\text{B}}N_{\text{A}}T=Nk_{\text{B}}T$$где:

• $p$ абсолютное давление газа,
• $V$ - объем газа,
• $n$ количество вещества газа (также известное как количество молей),
• $R$ — идеальная, или универсальная, газовая постоянная , равная произведению постоянной Больцмана и постоянной Авогадро ,
• $k_{\text{B}}$ — постоянная Больцмана ,
• $N_{A}$ – постоянная Авогадро ,
• $T$ – абсолютная температура газа,
• $N$ количество частиц (обычно атомов или молекул) газа.

В СИ единицах p измеряется в паскалях , V измеряется в кубических метрах , n измеряется в молях , а T в кельвинах ( шкала Кельвина представляет собой сдвинутую шкалу Цельсия , где 0,00 К = −273,15 °C, самая низкая возможная температура). ). R имеет значение 8,314 Дж /( моль · К ) = 1,989 ≈ 2 кал /(моль·К), или 0,0821 л⋅ атм /(моль⋅К).

Молярная форма

Сколько газа присутствует, можно указать, указав массу вместо химического количества газа. Следовательно, может оказаться полезной альтернативная форма закона идеального газа. Химическое количество n (в молях) равно общей массе газа ( m килограммах), деленной на молярную массу ) ( в M (в килограммах на моль):

$n={\frac {m}{M}}.$

Заменив n на m / M и введя затем плотность ρ = m / V , получим:

$pV={\frac {m}{M}}RT$

$p={\frac {m}{V}}{\frac {RT}{M}}$

$p=\rho {\frac {R}{M}}T$

Определяя удельную газовую постоянную R, _{специфичную} как отношение R / M ,

$p=\rho R_{\text{specific}}T$

Эта форма закона идеального газа очень полезна, поскольку она связывает давление, плотность и температуру в уникальную формулу, независимую от количества рассматриваемого газа. Альтернативно, закон может быть записан в терминах удельного объема v , обратной плотности, как

$pv=R_{\text{specific}}T.$

Обычно, особенно в инженерных и метеорологических приложениях, газовую постоянную обозначают символом R. удельную В таких случаях универсальной газовой постоянной обычно присваивают другой символ, например: ${\bar {R}}$ или $R^{*}$ чтобы отличить его. В любом случае контекст и/или единицы измерения газовой постоянной должны ясно указывать, используется ли универсальная или специальная газовая постоянная.

Статистическая механика

В статистической механике следующее молекулярное уравнение выведено из первых принципов:

$P=nk_{\text{B}}T,$

где P — абсолютное давление газа, n — плотность числа молекул (задается соотношением n = N / V , в отличие от предыдущей формулировки, в которой n — число молей ), T — абсолютная температура , а k _B — постоянная Больцмана, связывающая температуру и энергию, определяемая формулой:

$k_{\text{B}}={\frac {R}{N_{\text{A}}}}$

где N _A — постоянная Авогадро .

Отсюда мы замечаем, что для газа массы m со средней массой частицы, умноженной на массы атомную константу m _u (т. е. масса равна μ   Da ), число молекул будет определяться выражением

$N={\frac {m}{\mu m_{\text{u}}}},$

и поскольку ρ = m / V = nμm _u , мы находим, что закон идеального газа можно переписать как

$P={\frac {1}{V}}{\frac {m}{\mu m_{\text{u}}}}k_{\text{B}}T={\frac {k_{\text{B}}}{\mu m_{\text{u}}}}\rho T.$

В единицах СИ P измеряется в паскалях , V в кубических метрах, T в кельвинах и k _B = 1,38 × 10. ⁻²³  J⋅K ⁻¹ в единицах СИ .

Комбинированный газовый закон

Объединение законов Шарля, Бойля и Гей-Люссака дает объединенный газовый закон , который принимает ту же функциональную форму, что и закон идеального газа, говорящий о том, что число молей не указано, а соотношение $PV$ к $T$ просто принимается как константа:

${\frac {PV}{T}}=k,$

где $P$ давление газа , $V$ - объем газа, $T$ - абсолютная температура газа, а $k$ является константой. При сравнении одного и того же вещества в двух разных условиях закон можно записать как

${\frac {P_{1}V_{1}}{T_{1}}}={\frac {P_{2}V_{2}}{T_{2}}}.$

Энергия, связанная с газом

Согласно положениям кинетической теории идеальных газов, можно считать, что между молекулами или атомами идеального газа нет межмолекулярного притяжения. Другими словами, его потенциальная энергия равна нулю. Следовательно, вся энергия, которой обладает газ, представляет собой кинетическую энергию молекул или атомов газа.

$E={\frac {3}{2}}nRT$

Это соответствует кинетической энергии п молей одноатомного газа, имеющего 3 степени свободы ; х , у , z . В таблице ниже показано это соотношение для различных количеств одноатомного газа.

Энергия одноатомного газа	Математическое выражение
Энергия, связанная с одним молем	$E={\frac {3}{2}}RT$
Энергия, связанная с одним граммом	$E={\frac {3}{2}}rT$
Энергия, связанная с одним атомом	$E={\frac {3}{2}}k_{B}T$

Приложения к термодинамическим процессам

Приведенная ниже таблица существенно упрощает уравнение идеального газа для конкретных процессов, что упрощает решение этого уравнения с использованием численных методов.

Термодинамический процесс определяется как система, которая переходит из состояния 1 в состояние 2, где номер состояния обозначается нижним индексом. Как показано в первом столбце таблицы, основные термодинамические процессы определяются так, что одно из свойств газа ( P , V , T , S или H ) остается постоянным на протяжении всего процесса.

Для данного термодинамического процесса, чтобы указать степень конкретного процесса, необходимо указать одно из соотношений свойств (которые перечислены в столбце с надписью «известное соотношение») (прямо или косвенно). Кроме того, свойство, для которого известно соотношение, должно отличаться от свойства, сохраняемого постоянным в предыдущем столбце (в противном случае соотношение будет равно единице, и будет недостаточно информации для упрощения уравнения газового закона).

В последних трех столбцах свойства ( p , V или T ) в состоянии 2 могут быть рассчитаны на основе свойств в состоянии 1 с использованием перечисленных уравнений.

Процесс	Постоянный	Известное соотношение или дельта	п 2	VV2	TТ2
Изобарный процесс	Давление	В2 / В1	п 2 = п 1	В 2 = В 1 (В 2 /В 1 )	Т 2 = Т 1 (В 2 /В 1 )
		Т 2 /Т 1	п 2 = п 1	В 2 = В 1 (Т 2 /Т 1 )	Т 2 = Т 1 (Т 2 /Т 1 )
Изохорный процесс (Изоволюметрический процесс) (Изометрический процесс)	Объем	п 2 /п 1	п 2 = п 1 (п 2 /п 1 )	В2 = В1	Т 2 = Т 1 (п 2 /р 1 )
		Т 2 /Т 1	п 2 = р 1 (Т 2 /Т 1 )	В2 = В1	Т 2 = Т 1 (Т 2 /Т 1 )
Изотермический процесс	Температура	п 2 /п 1	п 2 = п 1 (п 2 /п 1 )	В 2 = В 1 (п 1 /р 2 )	Т 2 = Т 1
		В2 / В1	р 2 = р 1 (V 1 /V 2 )	В 2 = В 1 (В 2 /В 1 )	Т 2 = Т 1
Изэнтропический процесс (Обратимый адиабатический процесс )	Энтропия [а]	п 2 /п 1	п 2 = п 1 (п 2 /п 1 )	В 2 = В 1 (п 2 /р 1 ) (−1/с)	Т 2 = Т 1 (п 2 /р 1 ) (γ − 1)/γ
		В2 / В1	р 2 = р 1 (V 2 /V 1 ) -с	В 2 = В 1 (В 2 /В 1 )	Т 2 = Т 1 (В 2 /В 1 ) (1 - в)
		Т 2 /Т 1	п 2 = р 1 (Т 2 /Т 1 ) γ/(γ − 1)	В 2 = В 1 (Т 2 /Т 1 ) 1/(1 - с)	Т 2 = Т 1 (Т 2 /Т 1 )
Политропный процесс	P V н	п 2 /п 1	п 2 = п 1 (п 2 /п 1 )	В 2 = В 1 (п 2 /р 1 ) (−1/ п )	Т 2 = Т 1 (п 2 /р 1 ) ( п - 1)/ п
		В2 / В1	р 2 = р 1 (V 2 /V 1 ) − п	В 2 = В 1 (В 2 /В 1 )	Т 2 = Т 1 (В 2 /В 1 ) (1 - п )
		Т 2 /Т 1	п 2 = р 1 (Т 2 /Т 1 ) п /( п - 1)	В 2 = В 1 (Т 2 /Т 1 ) 1/(1 - п )	Т 2 = Т 1 (Т 2 /Т 1 )
Изентальпический процесс (Необратимый адиабатический процесс )	Энтальпия [б]	п 2 - п 1	п 2 знак равно п 1 + (п 2 - п 1 )		Т 2 знак равно Т 1 + μ JT (п 2 - п 1 )
		Т 2 - Т 1	п 2 знак равно п 1 + (Т 2 - Т 1 )/μ JT		Т 2 знак равно Т 1 + ( Т 2 - Т 1 )

^{^} а. В изэнтропическом процессе энтропия системы ( S ) постоянна. В этих условиях p ₁ V ₁ ^с = р ₂ В ₂ ^с , где γ определяется как коэффициент теплоемкости , который является постоянным для калорически совершенного газа . Значение, используемое для γ, обычно составляет 1,4 для двухатомных газов, таких как азот (N ₂ ) и кислород (O ₂ ) (и воздух, который на 99% состоит из двухатомных газов). Кроме того, γ обычно составляет 1,6 для одноатомных газов, таких как благородные газы гелий (He) и аргон (Ar). В двигателях внутреннего сгорания γ варьируется от 1,35 до 1,15 в зависимости от состава газов и температуры.

^{^} б. В изоэнтальпическом процессе энтальпия системы ( H ) постоянна. В случае свободного расширения идеального газа молекулярные взаимодействия отсутствуют и температура остается постоянной. В реальных газах молекулы взаимодействуют посредством притяжения или отталкивания в зависимости от температуры и давления, при этом происходит нагревание или охлаждение. Это известно как эффект Джоуля-Томсона . Для справки: коэффициент Джоуля-Томсона μ _JT для воздуха при комнатной температуре и уровне моря составляет 0,22 °C/ бар .

Отклонения от идеального поведения реальных газов

Приведенное здесь уравнение состояния ( PV = nRT ) применимо только к идеальному газу или как приближение к реальному газу, который ведет себя достаточно похоже на идеальный газ. На самом деле существует множество различных форм уравнения состояния. Поскольку закон идеального газа не учитывает как размер молекул , так и межмолекулярное притяжение, он наиболее точен для одноатомных газов при высоких температурах и низких давлениях. Пренебрежение размером молекул становится менее важным для более низких плотностей, т. е. для больших объемов при более низких давлениях, поскольку среднее расстояние между соседними молекулами становится намного больше, чем размер молекулы. Относительная значимость межмолекулярного притяжения уменьшается с увеличением тепловой кинетической энергии , т. е. с повышением температуры. Более подробные уравнения состояния , такие как уравнение Ван-дер-Ваальса , учитывают отклонения от идеальности, вызванные размером молекул и межмолекулярными силами.

Выводы

Эмпирический

Эмпирические законы, которые привели к выводу закона идеального газа, были открыты с помощью экспериментов, в которых изменялись только две переменные состояния газа и сохранялись все остальные постоянными.

Все возможные газовые законы, которые можно было бы открыть с помощью такой установки, таковы:

• Закон Бойля ( уравнение 1 ) $$PV=C_{1}\quad {\text{or}}\quad P_{1}V_{1}=P_{2}V_{2}$$
• Закон Чарльза ( уравнение 2 ) $${\frac {V}{T}}=C_{2}\quad {\text{or}}\quad {\frac {V_{1}}{T_{1}}}={\frac {V_{2}}{T_{2}}}$$
• Закон Авогадро ( уравнение 3 ) $${\frac {V}{N}}=C_{3}\quad {\text{or}}\quad {\frac {V_{1}}{N_{1}}}={\frac {V_{2}}{N_{2}}}$$
• Закон Гей-Люссака ( уравнение 4 ) $${\frac {P}{T}}=C_{4}\quad {\text{or}}\quad {\frac {P_{1}}{T_{1}}}={\frac {P_{2}}{T_{2}}}$$
• Уравнение 5 $$NT=C_{5}\quad {\text{or}}\quad N_{1}T_{1}=N_{2}T_{2}$$
• Уравнение 6 $${\frac {P}{N}}=C_{6}\quad {\text{or}}\quad {\frac {P_{1}}{N_{1}}}={\frac {P_{2}}{N_{2}}}$$

Связь между законами Бойля , Шарля , Гей-Люссака , Авогадро , комбинированного и идеального газа с постоянной Больцмана k = ⁠ R / N _A ⁠ = ⁠ n   R / N ⁠ (в каждом законе свойства , обведенные кружком, являются переменными, а свойства, не обведенные кружком, остаются постоянными)

где P означает давление , V – объем , N – число частиц в газе и T – температуру ; где $C_{1},C_{2},C_{3},C_{4},C_{5},C_{6}$ являются константами в этом контексте, поскольку каждое уравнение требует изменения только параметров, явно указанных в них.

Чтобы вывести закон идеального газа, не обязательно знать все 6 формул, можно просто знать 3 и с их помощью вывести остальные или еще одну, чтобы получить закон идеального газа, для которого нужны 4.

Поскольку каждая формула справедлива только тогда, когда изменяются только переменные состояния, включенные в указанную формулу, в то время как другие (которые являются свойством газа, но не указаны явно в указанной формуле) остаются постоянными, мы не можем просто использовать алгебру и напрямую объединить их все. Вот почему: Бойль проводил свои эксперименты, сохраняя постоянные N и T , и это необходимо учитывать (точно так же в каждом эксперименте сохранялся какой-то параметр постоянным, и это необходимо учитывать при выводе).

Имея это в виду, чтобы правильно провести вывод, нужно представить себе, что газ изменяется в результате одного процесса за раз (как это было сделано в экспериментах). Вывод по 4 формулам может выглядеть так:

сначала газ имеет параметры $P_{1},V_{1},N_{1},T_{1}$

Скажем, начав изменять только давление и объем, согласно закону Бойля ( Уравнение 1 ), тогда:

$$P_{1}V_{1}=P_{2}V_{2}$$ ( 7 )

После этого процесса газ имеет параметры $P_{2},V_{2},N_{1},T_{1}$

Используя затем уравнение ( 5 ), чтобы изменить количество частиц в газе и температуру,

$$N_{1}T_{1}=N_{2}T_{2}$$ ( 8 )

После этого процесса газ имеет параметры $P_{2},V_{2},N_{2},T_{2}$

Используя затем уравнение ( 6 ), чтобы изменить давление и количество частиц,

$${\frac {P_{2}}{N_{2}}}={\frac {P_{3}}{N_{3}}}$$ ( 9 )

После этого процесса газ имеет параметры $P_{3},V_{2},N_{3},T_{2}$

Используя затем закон Чарльза (уравнение 2) для изменения объема и температуры газа,

$${\frac {V_{2}}{T_{2}}}={\frac {V_{3}}{T_{3}}}$$ ( 10 )

После этого процесса газ имеет параметры $P_{3},V_{3},N_{3},T_{3}$

Использование простой алгебры для уравнений ( 7 ), ( 8 ), ( 9 ) и ( 10 ) дает результат: $${\frac {P_{1}V_{1}}{N_{1}T_{1}}}={\frac {P_{3}V_{3}}{N_{3}T_{3}}}$$ или $${\frac {PV}{NT}}=k_{\text{B}},$$ где $k_{\text{B}}$ обозначает постоянную Больцмана .

Другой эквивалентный результат, использующий тот факт, что $nR=Nk_{\text{B}}$, где n — количество молей в газе, а R — универсальная газовая постоянная , равна: $$PV=nRT,$$ который известен как закон идеального газа.

Если известны три из шести уравнений, оставшиеся три можно вывести тем же методом. Однако, поскольку каждая формула имеет две переменные, это возможно только для определенных групп из трех. Например, если бы у вас были уравнения ( 1 ), ( 2 ) и ( 4 ), вы не смогли бы получить больше, потому что объединение любых двух из них даст вам только третье. Однако, если бы у вас были уравнения ( 1 ), ( 2 ) и ( 3 ), вы смогли бы получить все шесть уравнений, поскольку объединение ( 1 ) и ( 2 ) даст ( 4 ), тогда ( 1 ) и ( 3 ) будут выход ( 6 ), затем ( 4 ) и ( 6 ) дадут ( 5 ), а также комбинация ( 2 ) и ( 3 ), как объяснено в следующем визуальном отношении:

Связь между шестью газовыми законами

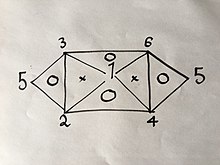
где цифры обозначают газовые законы, пронумерованные выше.

Если бы вы использовали тот же метод, что и выше, для двух из трех законов в вершинах одного треугольника, внутри которого есть буква «О», вы бы получили третий.

Например:

Сначала измените только давление и объем:

$$P_{1}V_{1}=P_{2}V_{2}$$ ( 1' )

тогда только объём и температура:

$${\frac {V_{2}}{T_{1}}}={\frac {V_{3}}{T_{2}}}$$ ( 2' )

тогда, поскольку мы можем выбрать любое значение для $V_{3}$, если мы установим $V_{1}=V_{3}$, уравнение ( 2' ) принимает вид:

$${\frac {V_{2}}{T_{1}}}={\frac {V_{1}}{T_{2}}}$$ ( 3' )

объединение уравнений ( 1' ) и ( 3' ) дает ${\frac {P_{1}}{T_{1}}}={\frac {P_{2}}{T_{2}}}$, которое представляет собой уравнение ( 4 ), о котором мы не знали до этого вывода.

Теоретический

Кинетическая теория

Основная статья: Кинетическая теория газов

Закон идеального газа также может быть выведен из первых принципов с использованием кинетической теории газов , в которой делается несколько упрощающих предположений, главным из которых является то, что молекулы или атомы газа представляют собой точечные массы, обладающие массой, но не имеющие значительного объема. , и испытывают только упругие столкновения друг с другом и со стенками контейнера, в которых сохраняются как линейный импульс, так и кинетическая энергия.

Сначала мы покажем, что из основных предположений кинетической теории газов следует, что

$PV={\frac {1}{3}}Nmv_{\text{rms}}^{2}.$

Рассмотрим контейнер в $xyz$ Декартова система координат. Для простоты будем считать, что треть молекул движется параллельно $x$-оси, третья движется параллельно $y$-ось, а третья движется параллельно $z$-ось. Если все молекулы движутся с одинаковой скоростью $v$, обозначим соответствующее давление через $P_{0}$. Выбираем район $S$ на стенке контейнера, перпендикулярной $x$-ось. Когда время $t$ истекает, все молекулы в объеме $vtS$ двигаться в положительном направлении $x$-ось попадет в эту область. Есть $NvtS/V$ молекулы в части объема $vtS$ контейнера, но только одна шестая (т.е. половина трети) из них движется в положительном направлении $x$-ось. Следовательно, число молекул $N'$ это поразит область $S$ когда время $t$ истекает $NvtS/(6V)$.

Когда молекула отскакивает от стенки сосуда, она меняет свой импульс. $\mathbf {p} _{1}$ к $\mathbf {p} _{2}=-\mathbf {p} _{1}$. Следовательно, величина изменения импульса одной молекулы равна $|\mathbf {p} _{2}-\mathbf {p} _{1}|=2mv$. Величина изменения импульса всех молекул, отскакивающих от площадки $S$ когда время $t$ истекает. тогда $|\Delta \mathbf {p} |=2mvN'=NtSmv^{2}/(3V)$. От $F=|\Delta \mathbf {p} |/t$ и $P_{0}=F/S$ мы получаем

$P_{0}={\frac {1}{3}}Nm{\frac {v^{2}}{V}}.$

Мы рассмотрели ситуацию, когда все молекулы движутся с одинаковой скоростью. $v$. Теперь мы рассматриваем ситуацию, когда они могут двигаться с разными скоростями, поэтому мы применяем «преобразование усреднения» к приведенному выше уравнению, эффективно заменяя $P_{0}$ под новым давлением $P$ и $v^{2}$ средним арифметическим всех квадратов всех скоростей молекул, т.е. $v_{\text{rms}}^{2}.$ Поэтому

$P={\frac {1}{3}}Nm{\frac {v_{\text{rms}}^{2}}{V}}$

что дает искомую формулу.

Используя распределение Максвелла – Больцмана , определите долю молекул, скорость которых находится в диапазоне $v$ к $v+dv$ является $f(v)\,dv$, где

$f(v)=4\pi \left({\frac {m}{2\pi kT}}\right)^{\!{\frac {3}{2}}}v^{2}e^{-{\frac {mv^{2}}{2kT}}}$

и $k$ обозначает постоянную Больцмана. Среднеквадратическую скорость можно рассчитать по формуле

$v_{\text{rms}}^{2}=\int _{0}^{\infty }v^{2}f(v)\,dv=4\pi \left({\frac {m}{2\pi kT}}\right)^{\frac {3}{2}}\int _{0}^{\infty }v^{4}e^{-{\frac {mv^{2}}{2kT}}}\,dv.$

Используя формулу интегрирования

$\int _{0}^{\infty }x^{2n}e^{-{\frac {x^{2}}{a^{2}}}}\,dx={\sqrt {\pi }}\,{\frac {(2n)!}{n!}}\left({\frac {a}{2}}\right)^{2n+1},\quad n\in \mathbb {N} ,\,a\in \mathbb {R} ^{+},$

отсюда следует, что

$v_{\text{rms}}^{2}=4\pi \left({\frac {m}{2\pi kT}}\right)^{\!{\frac {3}{2}}}{\sqrt {\pi }}\,{\frac {4!}{2!}}\left({\frac {\sqrt {\frac {2kT}{m}}}{2}}\right)^{\!5}={\frac {3kT}{m}},$

откуда мы получаем закон идеального газа:

$PV={\frac {1}{3}}Nm\left({\frac {3kT}{m}}\right)=NkT.$

Статистическая механика

Основная статья: Статистическая механика

Пусть q = ( q _x , q _y , q _z ) и p = ( p _x , p _y , p _z ) обозначают вектор положения и вектор импульса частицы идеального газа соответственно. Пусть F обозначает результирующую силу, действующую на эту частицу. Тогда (дважды) усредненная по времени кинетическая энергия частицы равна:

${\begin{aligned}\langle \mathbf {q} \cdot \mathbf {F} \rangle &=\left\langle q_{x}{\frac {dp_{x}}{dt}}\right\rangle +\left\langle q_{y}{\frac {dp_{y}}{dt}}\right\rangle +\left\langle q_{z}{\frac {dp_{z}}{dt}}\right\rangle \\&=-\left\langle q_{x}{\frac {\partial H}{\partial q_{x}}}\right\rangle -\left\langle q_{y}{\frac {\partial H}{\partial q_{y}}}\right\rangle -\left\langle q_{z}{\frac {\partial H}{\partial q_{z}}}\right\rangle =-3k_{\text{B}}T,\end{aligned}}$

где первое равенство — это второй закон Ньютона , а вторая строка использует уравнения Гамильтона и теорему о равнораспределении . Суммирование по системе из N частиц дает

$3Nk_{B}T=-\left\langle \sum _{k=1}^{N}\mathbf {q} _{k}\cdot \mathbf {F} _{k}\right\rangle .$

Согласно третьему закону Ньютона и предположению об идеальном газе, результирующая сила системы — это сила, приложенная стенками контейнера, и эта сила определяется давлением P газа. Следовательно

$-\left\langle \sum _{k=1}^{N}\mathbf {q} _{k}\cdot \mathbf {F} _{k}\right\rangle =P\oint _{\text{surface}}\mathbf {q} \cdot d\mathbf {S} ,$

где d S — бесконечно малый элемент площади вдоль стенок контейнера. Поскольку дивергенция вектора положения q равна

$\nabla \cdot \mathbf {q} ={\frac {\partial q_{x}}{\partial q_{x}}}+{\frac {\partial q_{y}}{\partial q_{y}}}+{\frac {\partial q_{z}}{\partial q_{z}}}=3,$

из теоремы о дивергенции следует, что

$P\oint _{\text{surface}}\mathbf {q} \cdot d\mathbf {S} =P\int _{\text{volume}}\left(\nabla \cdot \mathbf {q} \right)dV=3PV,$

где dV — бесконечно малый объем внутри контейнера, а V — общий объем контейнера.

Сложив эти равенства вместе, получим

$3Nk_{\text{B}}T=-\left\langle \sum _{k=1}^{N}\mathbf {q} _{k}\cdot \mathbf {F} _{k}\right\rangle =3PV,$

откуда сразу следует закон идеального газа для N частиц:

$PV=Nk_{B}T=nRT,$

где n = N / N _A — число молей газа, а R = N _A k _B — газовая постоянная .

Другие размеры

Для d -мерной системы идеальное давление газа равно:

$P^{(d)}={\frac {Nk_{B}T}{L^{d}}},$

где $L^{d}$ — объем d -мерной области, в которой существует газ. Размеры давления изменяются с размерностью.

См. также

• Константа Больцмана - физическая константа, связывающая кинетическую энергию частицы с температурой.
• Интеграл конфигурации - функция в термодинамике и статистической физике
• Динамическое давление - кинетическая энергия единицы объема жидкости.
• Газовые законы
• Внутренняя энергия - энергия, содержащаяся в системе.
• Уравнение Ван дер Ваальса - уравнение состояния газа, которое объясняет неидеальное поведение газа.

Дальнейшее чтение

• Дэвис; Мастен (2002). Принципы экологической инженерии и науки . Нью-Йорк: МакГроу-Хилл. ISBN  0-07-235053-9 .

Внешние ссылки

• «Веб-сайт, посвященный Бенуа Полю Эмилю Клапейрону (1799–1864) в 1834 году» . Архивировано из оригинала 5 июля 2007 года.
• Конфигурационный интеграл (статистическая механика), в котором представлен альтернативный статистический механический вывод закона идеального газа с использованием соотношения между свободной энергией Гельмгольца и статистической суммой , но без использования теоремы о равнораспределении. Ву-Куок, Л., Конфигурационный интеграл (статистическая механика) , 2008. Этот вики-сайт недоступен; эту статью смотрите в веб-архиве от 28 апреля 2012 года .
• Уравнения газа в деталях