Октонион

Октонионы
Символ	$\mathbb {O}$
Тип	Гиперкомплексная алгебра
Единицы	е 0 , ..., е 7
Мультипликативная идентичность	е 0
Основные свойства	Некоммутативный Неассоциативный
Общие системы
$\mathbb {N}$ Натуральные числа $\mathbb {Z}$ Целые числа $\mathbb {Q}$ Рациональные числа $\mathbb {R}$ Реальные числа $\mathbb {C}$ Комплексные числа $\mathbb {H}$ Кватернионы show Менее распространенные системы Octonions ($\mathbb {O}$) Sedenions ($\mathbb {S}$)

В математике октонионы нормированную представляют собой алгебру с делением действительных чисел , своего рода гиперкомплексную систему счисления . Октонионы обычно обозначаются заглавной буквой О, используя жирный шрифт О или жирный шрифт на доске. $\mathbb {O}$. Октонионы имеют восемь измерений ; в два раза больше измерений кватернионов , расширением которых они являются. Они некоммутативны и неассоциативны , но удовлетворяют более слабой форме ассоциативности; а именно, они альтернативны . Они также являются силовыми ассоциативными .

Октонионы не так известны, как кватернионы и комплексные числа , которые гораздо более широко изучаются и используются. Октонионы относятся к исключительным структурам в математике, в том числе к исключительным группам Ли . Октонионы находят применение в таких областях, как теория струн , специальная теория относительности и квантовая логика . Применение конструкции Кэли-Диксона к октонионам дает седенионы .

История

Октонионы были открыты в 1843 году Джоном Т. Грейвсом , вдохновленным его другом Уильямом Роуэном Гамильтоном открытием кватернионов . Грейвс назвал свое открытие «октавами» и упомянул о них в письме Гамильтону от 26 декабря 1843 года. Впервые он опубликовал свой результат несколько позже Артура Кэли . статьи Октонионы были открыты независимо Кэли. и иногда их называют «числами Кэли» или «алгеброй Кэли». Гамильтон описал раннюю историю открытия Грейвса.

Определение

Октонионы можно рассматривать как октеты (или восьмерки) действительных чисел. Каждый октонион представляет собой реальную линейную комбинацию единичных октонионов :

$\{e_{0},e_{1},e_{2},e_{3},e_{4},e_{5},e_{6},e_{7}\},$

где e ₀ – скалярный или вещественный элемент; его можно отождествить с действительным числом 1. То есть каждый октонион x можно записать в виде

$x=x_{0}e_{0}+x_{1}e_{1}+x_{2}e_{2}+x_{3}e_{3}+x_{4}e_{4}+x_{5}e_{5}+x_{6}e_{6}+x_{7}e_{7},\,$

с действительными коэффициентами x _i .

Сложение и вычитание октонионов осуществляется путем добавления и вычитания соответствующих членов и, следовательно, их коэффициентов, например, кватернионов. Умножение более сложное. Умножение является распределительным по сравнению с сложением, поэтому произведение двух октонионов можно вычислить путем суммирования произведений всех членов, опять же, как кватернионы. Произведение каждой пары членов можно получить путем умножения коэффициентов и таблицы умножения единичных октонионов, например этой (благодаря Кэли, 1845 г. и Грейвсу, 1843 г.):

$e_{i}e_{j}$		$e_{j}$
		$e_{0}$	$e_{1}$	$e_{2}$	$e_{3}$	$e_{4}$	$e_{5}$	$e_{6}$	$e_{7}$
$e_{i}$	$e_{0}$	$e_{0}$	$e_{1}$	$e_{2}$	$e_{3}$	$e_{4}$	$e_{5}$	$e_{6}$	$e_{7}$
	$e_{1}$	$e_{1}$	$-e_{0}$	$e_{3}$	$-e_{2}$	$e_{5}$	$-e_{4}$	$-e_{7}$	$e_{6}$
	$e_{2}$	$e_{2}$	$-e_{3}$	$-e_{0}$	$e_{1}$	$e_{6}$	$e_{7}$	$-e_{4}$	$-e_{5}$
	$e_{3}$	$e_{3}$	$e_{2}$	$-e_{1}$	$-e_{0}$	$e_{7}$	$-e_{6}$	$e_{5}$	$-e_{4}$
	$e_{4}$	$e_{4}$	$-e_{5}$	$-e_{6}$	$-e_{7}$	$-e_{0}$	$e_{1}$	$e_{2}$	$e_{3}$
	$e_{5}$	$e_{5}$	$e_{4}$	$-e_{7}$	$e_{6}$	$-e_{1}$	$-e_{0}$	$-e_{3}$	$e_{2}$
	$e_{6}$	$e_{6}$	$e_{7}$	$e_{4}$	$-e_{5}$	$-e_{2}$	$e_{3}$	$-e_{0}$	$-e_{1}$
	$e_{7}$	$e_{7}$	$-e_{6}$	$e_{5}$	$e_{4}$	$-e_{3}$	$-e_{2}$	$e_{1}$	$-e_{0}$

Большинство недиагональных элементов таблицы антисимметричны, что делает ее почти кососимметричной матрицей, за исключением элементов на главной диагонали, а также строки и столбца, для которых e ₀ является операндом.

Таблицу можно резюмировать следующим образом:

$e_{i}e_{j}={\begin{cases}e_{j},&{\text{if }}i=0\\e_{i},&{\text{if }}j=0\\-\delta _{ij}e_{0}+\varepsilon _{ijk}e_{k},&{\text{otherwise}}\end{cases}}$

где δ _ij — дельта Кронекера (равная 1 тогда и только тогда, когда i = j ), а ε _ijk — полностью антисимметричный тензор со значением 1, когда ijk = 123, 145, 176, 246, 257, 347, 365 .

Однако приведенное выше определение не уникально; это только одно из 480 возможных определений умножения октонионов с e ₀ = 1 . Остальные можно получить перестановкой и изменением знаков нескалярных базисных элементов { e ₁ , e ₂ , e ₃ , e ₄ , e ₅ , e ₆ , e ₇ } . 480 различных алгебр изоморфны , и редко возникает необходимость учитывать, какое конкретное правило умножения используется.

Каждое из этих 480 определений инвариантно с точностью до знаков относительно некоторого 7-цикла точек (1234567), причем для каждого 7-цикла существует четыре определения, различающиеся знаками и обращением порядка. Распространенным выбором является использование определения, инвариантного относительно 7-цикла (1234567) с e ₁ e ₂ = e _4, используя треугольную диаграмму умножения или плоскость Фано ниже, которая также показывает отсортированный список 7-цикловых триад на основе 124 и связанные с ним матрицы умножения как в en _, так и в $\mathrm {IJKL}$ формат.

Иногда используемый вариант - это пометка элементов базиса элементами ∞ , 0, 1, 2, ..., 6 проективной прямой над конечным полем порядка 7. Тогда умножение задается выражением e _∞ = 1 и e ₁ e ₂ = e ₄ , и все выражения, полученные из этого путем добавления константы ( по модулю 7) ко всем индексам: другими словами, используя семь троек (124) (235) (346) (450) ( 561) (602) (013). Это ненулевые кодовые слова квадратичного вычетного кода длины 7 над полем Галуа из двух элементов, GF (2) . Существует симметрия порядка 7, определяемая добавлением константы по модулю 7 ко всем индексам, а также симметрия порядка 3, определяемая умножением всех индексов на один из квадратичных остатков 1, 2, 4 по модулю 7. Эти семь троек также можно рассматривать как семь трансляций набора {1,2,4} ненулевых квадратов. образующее циклическое (7,3,1) -разностное множество в конечном поле GF(7) из семи элементов.

Таблицу умножения для геометрической алгебры сигнатуры (----) можно представить в виде следующих 7 кватернионных троек (без единичного элемента):

( I , j , k ), ( я , J , k ), ( я , j , K ), ( I , J , K ), ( * I , я , м ), (* J , j , м ), (* К , к , м )

в котором элементы нижнего регистра являются векторами , а элементы верхнего регистра — бивекторами и ∗ = mijk (который является звездным оператором Ходжа ). Если * принудительно приравнять к единице, то умножение перестает быть ассоциативным, но * можно удалить из таблицы умножения, в результате чего получится таблица умножения октонионов.

Сохраняя ассоциативность ∗ = mijk и, таким образом, не сводя 4-мерную геометрическую алгебру к октонионной, вся таблица умножения может быть получена из уравнения для ∗ . Рассмотрим гамма-матрицы . Формула, определяющая пятую гамма-матрицу, показывает, что это * четырехмерной геометрической алгебры гамма-матриц.

Строительство Кэли – Диксона

Основная статья: конструкция Кэли-Диксона

Более систематический способ определения октонионов - это конструкция Кэли-Диксона. Точно так же, как кватернионы можно определить как пары комплексных чисел, октонионы можно определить как пары кватернионов. Сложение определяется попарно. Произведение двух пар кватернионов ( a , b ) и ( c , d ) определяется формулой

$(a,b)(c,d)=(ac-d^{*}b,da+bc^{*}),$

где z * обозначает сопряженный кватернион z . Это определение эквивалентно приведенному выше, когда восемь единичных октонионов отождествляются с парами

(1, 0), ( i , 0), ( j , 0), ( k , 0), (0, 1), (0, i ), (0, j ), (0, k )

Мнемоника плоскости Фано

Мнемоника произведений единичных октонионов

Трехмерная мнемоническая визуализация, показывающая 7 триад как гиперплоскости, проходящие через действительную ( e ₀ ) вершину примера октониона, приведенного выше.

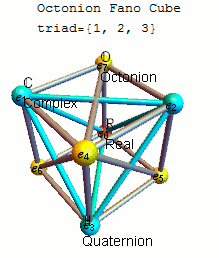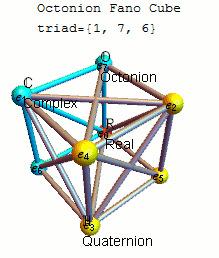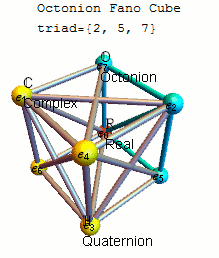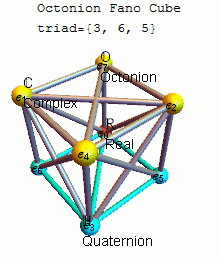
Удобную мнемосхему для запоминания произведений единичных октонионов дает схема, представляющая собой таблицу умножения Кэли и Грейвса. Эта диаграмма с семью точками и семью линиями (круг, проходящий через точки 1, 2 и 3, считается линией) называется плоскостью Фано . Линии направленные. Семь точек соответствуют семи стандартным базисным элементам Im( O ) (см. определение ниже ). Каждая пара различных точек лежит на уникальной прямой, и каждая прямая проходит ровно через три точки.

Пусть ( a , b , c ) — упорядоченная тройка точек, лежащих на заданной прямой в порядке, указанном направлением стрелки. Тогда умножение определяется выражением

ab = c и ba = − c

вместе с циклическими перестановками . Эти правила вместе с

• 1 – мультипликативное тождество,
• ${e_{i}}^{2}=-1$ для каждой точки на диаграмме

полностью определяет мультипликативную структуру октонионов. Каждая из семи строк порождает подалгебру O , изоморфную кватернионам H .

Сопряженное, нормальное и обратное

Конъюгат ​ октониона

$x=x_{0}\,e_{0}+x_{1}\,e_{1}+x_{2}\,e_{2}+x_{3}\,e_{3}+x_{4}\,e_{4}+x_{5}\,e_{5}+x_{6}\,e_{6}+x_{7}\,e_{7}$

дается

$x^{*}=x_{0}\,e_{0}-x_{1}\,e_{1}-x_{2}\,e_{2}-x_{3}\,e_{3}-x_{4}\,e_{4}-x_{5}\,e_{5}-x_{6}\,e_{6}-x_{7}\,e_{7}.$

Сопряжение является инволюцией O ( и удовлетворяет условию ( xy )* = y * x * обратите внимание на изменение порядка).

Действительная часть x определяется выражением

${\frac {x+x^{*}}{2}}=x_{0}\,e_{0}$

и часть мнимая

${\frac {x-x^{*}}{2}}=x_{1}\,e_{1}+x_{2}\,e_{2}+x_{3}\,e_{3}+x_{4}\,e_{4}+x_{5}\,e_{5}+x_{6}\,e_{6}+x_{7}\,e_{7}.$

Набор всех чисто мнимых октонионов охватывает 7- мерное подпространство O Im , обозначенное ( O ) .

Сопряжение октонионов удовлетворяет уравнению

$-6x^{*}=x+(e_{1}x)e_{1}+(e_{2}x)e_{2}+(e_{3}x)e_{3}+(e_{4}x)e_{4}+(e_{5}x)e_{5}+(e_{6}x)e_{6}+(e_{7}x)e_{7}.$

Произведение октониона на сопряженное ему x * x = xx * всегда является неотрицательным действительным числом:

$x^{*}x=x_{0}^{2}+x_{1}^{2}+x_{2}^{2}+x_{3}^{2}+x_{4}^{2}+x_{5}^{2}+x_{6}^{2}+x_{7}^{2}.$

Используя это, норму октониона можно определить как

$\|x\|={\sqrt {x^{*}x}}.$

Эта норма согласуется со стандартной 8-мерной евклидовой нормой на R ⁸ .

Существование нормы на O подразумевает существование обратных для каждого ненулевого элемента O . Обратный к x ≠ 0 , который является уникальным октонионом x ⁻¹ удовлетворение хх ⁻¹ = х ⁻¹ x = 1 , определяется выражением

$x^{-1}={\frac {x^{*}}{\|x\|^{2}}}.$

Характеристики

Октонионное умножение не является коммутативным :

e _i e _j = - e _j e _i ≠ e _j e _i, если i , j различны и не равны нулю,

ни ассоциативный :

( е _я е _j ) е _k знак равно - я ₍ е j _е k ₎ ≠ е я ₍ е j _е k ₎ если я , j различны , е ненулевые и е я _е j _≠ ± е _k .

Октонионы удовлетворяют более слабой форме ассоциативности: они альтернативны. Это означает, что подалгебра, порожденная любыми двумя элементами, ассоциативна. что подалгебра, порожденная любыми двумя элементами из , C На самом деле можно показать , или O, изоморфна R H , все из которых ассоциативны. Из-за своей неассоциативности октонионы не могут быть представлены подалгеброй матричного кольца над $\mathbb {R}$, в отличие от действительных чисел, комплексных чисел и кватернионов.

Октонионы сохраняют одно важное свойство, общее для R , C и H : норма O удовлетворяет

$\|xy\|=\|x\|\|y\|.$

Это уравнение означает, что октонионы образуют композиционную алгебру . Алгебры более высокой размерности, определенные конструкцией Кэли-Диксона (начиная с седенионов ) , не удовлетворяют этому свойству. Все они имеют делители нуля .

Существуют более широкие системы счисления, которые имеют мультипликативный модуль (например, 16-мерные конические седенионы). Их модуль определяется иначе, чем их норма, и они также содержат делители нуля.

Как показал Гурвиц , R , C , H и O являются единственными нормированными алгебрами с делением над действительными числами. Эти четыре алгебры также образуют единственные альтернативные конечномерные алгебры с делением над действительными числами ( с точностью до изоморфизма).

Не будучи ассоциативными, ненулевые элементы O не образуют группу . Однако они образуют петлю , в частности петлю Муфанг .

Коммутатор и векторное произведение

Коммутатор x двух октонионов и y имеет вид

$[x,y]=xy-yx.$

Это антисимметрично и воображаемо. Если его рассматривать только как произведение в мнимом подпространстве Im( O ), оно определяет произведение в этом пространстве, семимерное векторное произведение , определяемое формулой

$x\times y={\tfrac {1}{2}}(xy-yx).$

Как и векторное произведение в трех измерениях, это вектор, ортогональный x и y с величиной

$\|x\times y\|=\|x\|\|y\|\sin \theta .$

Но, как и продукт октониона, он не имеет однозначного определения. Вместо этого существует множество различных перекрестных произведений, каждое из которых зависит от выбора произведения октониона.

Автоморфизмы

Автоморфизм A октонионов , является обратимым линейным преобразованием которое O удовлетворяет условию

$A(xy)=A(x)A(y).$

Множество всех автоморфизмов O образует группу под названием G ₂ . Группа G2 _{односвязную} представляет собой компактную , вещественную группу Ли размерности 14. Эта группа является наименьшей из исключительных групп Ли и изоморфна подгруппе Spin ( 7) которая сохраняет любой выбранный конкретный вектор в своем 8-мерном пространстве. реальное спинорное представление. Группа Spin(7), в свою очередь, является подгруппой группы изотопий, описанной ниже.

См. также : PSL(2,7) – группа автоморфизмов плоскости Фано.

Изотопии

Изотопия алгебры — это тройка биективных линейных отображений a , b , c такая, что если xy = z , то a ( x ) b ( y ) = c ( z ) . Для a = b = c это то же самое, что автоморфизм. Изотопическая группа алгебры — это группа всех изотопий, которая содержит группу автоморфизмов в качестве подгруппы.

Изотопическая группа октонионов — это группа Spin ₈ ( R ) , где a , b , c действуют как три 8-мерных представления. Подгруппа элементов, где c фиксирует тождество, - это подгруппа Spin ₇ ( R ) , а подгруппа, где a , b , c все фиксируют тождество, - это группа автоморфизмов G ₂ .

Приложения

Октонионы играют значительную роль в классификации и построении других математических объектов. Например, исключительная группа Ли G ₂ является группой автоморфизмов октонионов, а другие исключительные группы Ли F ₄ , E ₆ , E ₇ и E ₈ можно понимать как изометрии некоторых проективных плоскостей, определенных с помощью октонионов. Набор самосопряженных размера 3 × 3 октононных матриц , снабженных симметризованным матричным произведением, определяет алгебру Альберта . В дискретной математике октонионы представляют собой элементарное образование решетки Лича и, таким образом, тесно связаны со спорадическими простыми группами .

Применение октонионов в физике во многом было предположительным. Например, в 1970-е годы были предприняты попытки понять кварки посредством октонионного гильбертова пространства . Известно, что октонионы и тот факт, что могут существовать только четыре нормированные алгебры с делением, относятся к измерениям пространства-времени , в которых суперсимметричные квантовые теории поля . могут быть построены Также предпринимались попытки получить Стандартную модель физики элементарных частиц из октонионных конструкций, например, с помощью «алгебры Диксона C ⊗ H ⊗ O. »

Октонионы также возникли при изучении энтропии черных дыр , квантовой информатике , теория струн , и обработка изображений.

Октонионы использовались для решения проблемы калибровки руки и глаза в робототехнике .

Сети глубоких октонионов предоставляют средства эффективного и компактного выражения в приложениях машинного обучения.

Целые октонионы

Существует несколько естественных способов выбора целой формы октонионов. Самый простой — просто взять октонионы, координаты которых — целые числа . Это дает неассоциативную алгебру целых чисел, называемую грейвсовскими октонионами. Однако это не максимальный порядок (в смысле теории колец); существует ровно семь максимальных порядков, содержащих его. Все эти семь максимальных порядков эквивалентны относительно автоморфизмов. Фраза «целые октонионы» обычно относится к фиксированному выбору одного из этих семи порядков.

Эти максимальные порядки были построены Кирмсом (1924) , Диксоном и Бруком следующим образом. Обозначьте восемь базисных векторов точками проективной прямой над полем с семью элементами. Сначала сформируйте «целые числа Кирмсе»: они состоят из октонионов, координаты которых являются целыми или полуцелыми числами, и которые являются полуцелыми числами (то есть половинами нечетных целых чисел) в одном из 16 наборов.

∅ (∞124) (∞235) (∞346) (∞450) (∞561) (∞602) (∞013) (∞0123456) (0356) (1460) (2501) (3612) (4023) (5134) (6245)

расширенного квадратичного кода-вычета длины 8 над полем из двух элементов, заданным ∅ , (∞124), и его образами при добавлении константы по модулю 7, а также дополнениями к этим восьми наборам. Затем поменяйте местами бесконечность и любую другую координату; эта операция создает биекцию целых чисел Кирмса в другой набор, который является максимальным порядком. Есть семь способов сделать это, давая семь максимальных порядков, которые все эквивалентны при циклических перестановках семи координат 0123456. (Кирмсе ошибочно утверждал, что целые числа Кирмсе также образуют максимальный порядок, поэтому он думал, что существует восемь максимальных порядков, а не семь, но, как Коксетер (1946) указал , они не замкнуты при умножении, эта ошибка встречается в нескольких опубликованных статьях.)

Целые числа Кирмзе и семь максимальных порядков изометричны E _8, решетке масштабированной в коэффициент 1 ⁄ √ 2 . В частности, в каждом из этих порядков имеется 240 элементов с минимальной ненулевой нормой 1, образующих петлю Муфанг порядка 240.

Целые октонионы обладают свойством «деление с остатком»: учитывая целые октонионы a и b ≠ 0 , мы можем найти q и r с a = qb + r , где остаток r имеет норму меньше, чем норма b .

В целочисленных октонионах все левые и правые идеалы являются двусторонними идеалами, а единственными двусторонними идеалами являются главные идеалы nO , где n — неотрицательное целое число.

Целочисленные октонионы имеют версию факторизации в простые числа, хотя это не так просто сформулировать, поскольку октонионы не ассоциативны, поэтому произведение октонионов зависит от порядка, в котором они производятся. Неприводимые целочисленные октонионы — это в точности октонионы простой нормы, и каждый целочисленный октонион можно записать как произведение неприводимых октонионов. Точнее, целый октонион нормы mn можно записать как произведение целых октонионов норм m и n .

Группой автоморфизмов целых октонионов является группа G ₂ ( F ₂ ) порядка 12 096, имеющая простую подгруппу индекса 2, изоморфную унитарной группе ² А ₂ (3 ² ) . Изотопическая группа целых октонионов представляет собой идеальное двойное покрытие группы вращений решетки Е ₈ .

См. также

• G ₂ Коллектор
• Алгебра октониона
• Алгебра путей
• Спин(7) коллектор
• Спин(8)
• Сплит-октонионы
• Триальность

Ссылки

• Баэз, Джон К. (2002). «Октонионы» . Бюллетень Американского математического общества . 39 (2): 145–205. arXiv : math/0105155 . дои : 10.1090/S0273-0979-01-00934-X . ISSN   0273-0979 . МР   1886087 . S2CID   586512 .
• Баэз, Джон К. (2005). «Ошибки для Октонионов » (PDF) . Бюллетень Американского математического общества . 42 (2): 213–214. дои : 10.1090/S0273-0979-05-01052-9 .
• Конвей, Джон Хортон ; Смит, Дерек А. (2003), О кватернионах и октонионах: их геометрия, арифметика и симметрия , AK Peters, Ltd., ISBN  1-56881-134-9 , Збл   1098.17001 . ( Обзор ).
• Коксетер, HSM (1946), «Целочисленные числа Кэли», Duke Math. J. , 13 (4): 561–578, doi : 10.1215/s0012-7094-46-01347-6 , MR   0019111
• Диксон, Джеффри М. (1994), Алгебры деления: октонионы, кватернионы, комплексные числа и алгебраический дизайн физики , Kluvwer Academic Publishers, ISBN  0-7923-2890-6
• Фрейденталь, Ганс (1985) [1951], «Октавы, группы исключений и геометрия октав», Geom. Dedicata , 19 (1): 7–63, doi : 10.1007/BF00233101 , MR   0797151 , S2CID   121496094
• Грейвс (1845 г.), «О связи между общей теорией нормальных пар и теорией полных квадратичных функций двух переменных» , Phil. Маг. , 26 : 315–320, дои : 10.1080/14786444508645136
• Кирмзе (1924), «О представимости натуральных целых чисел в виде сумм восьми квадратов и о некоммутативной и неассоциативной системе счисления, связанной с этой проблемой», Бер. Женатый саксонец Академическая наука Лейпциг. Матем. Кл. , 76 : 63–82.
• Лахти, Уско (2015), проф. Корвус Адамас: Цифры и методы доказательства. Знакомство с основами математики в компании увлеченных студентов. , Хельсинки: Книги по запросу, ISBN  978-952-318-558-6
• Зальцманн, Гельмут; Беттен, Дитер; Грундхёфер, Тео; Хель, Герман; Лёвен, Райнер; Строппель, Маркус (1995), Компактные проективные плоскости, с введением в геометрию октонионов , Изложения Де Грютера по математике, Уолтер де Грюйтер, ISBN  3-11-011480-1 , ISSN   0938-6572 , OCLC   748698685
• ван дер Блий, Ф. (1961), «История октав», Саймон Стевин , 34 : 106–125, MR   0130283

Внешние ссылки

• Куцуку-Аргираки, Анжелики. Октонионы (разработка формальных доказательств в Isabelle/HOL, Архив формальных доказательств)
• «Числа Кэли» , Математическая энциклопедия , EMS Press , 2001 [1994]
• Уилсон, Р.А. (2008), Octonions (PDF) , заметки семинара по чистой математике