Коробочный сюжет

Рисунок 1. Ящик с данными эксперимента Майкельсона.

В описательной статистике или ящичная диаграмма коробчатая диаграмма — это метод графической демонстрации групп локальности, разброса и асимметрии числовых данных через их квартили . ^[1] Помимо прямоугольника на коробчатом графике могут быть линии (которые называются «усами »), отходящие от прямоугольника, обозначающие изменчивость за пределами верхнего и нижнего квартилей, таким образом, график еще называют коробчатым графиком и коробчатым графиком. диаграмма -и-усы . Выбросы , которые значительно отличаются от остального набора данных ^[2] могут быть изображены в виде отдельных точек за усами на коробчатой диаграмме.Ящичные диаграммы непараметричны : они отображают вариации выборок статистической совокупности без каких-либо предположений об основном статистическом распределении. ^[3] (хотя коробчатая диаграмма Тьюки предполагает симметрию усов и нормальность их длины). Интервалы в каждом подразделе диаграммы указывают на степень дисперсии (разброса) и асимметрии данных, которые обычно описываются с помощью пятизначной сводки . Кроме того, коробчатая диаграмма позволяет визуально оценить различные L-оценки , в частности межквартильный размах , средний шарнир , размах , средний диапазон и тримедиан . Ящичные диаграммы можно рисовать как горизонтально, так и вертикально.

История

Метод диапазонных баров был впервые представлен Мэри Элеонорой Спир в ее книге «Статистика диаграмм» в 1952 году. ^[4] и снова в ее книге «Практические методы построения графиков» в 1969 году. ^[5] График «коробка с усами» был впервые представлен в 1970 году Джоном Тьюки , который позже опубликовал эту тему в своей книге «Исследовательский анализ данных» в 1977 году. ^[6]

Элементы

Ящичная диаграмма — это стандартизированный способ отображения набора данных на основе пятизначной сводки : минимум, максимум, выборочная медиана, а также первый и третий квартили.

Минимум ( Q ₀ или 0-й процентиль ) : самая низкая точка данных в наборе данных, исключая любые выбросы.
Максимум ( Q ₄ или 100-й процентиль) : самая высокая точка данных в наборе данных, исключая любые выбросы.
Медиана ( Q ₂ или 50-й процентиль) : среднее значение в наборе данных.
Первый квартиль ( Q ₁ или 25-й процентиль) : также известный как нижний квартиль q _n (0,25), это медиана нижней половины набора данных.
Третий квартиль ( Q ₃ или 75-й процентиль) : также известный как верхний квартиль q _n (0,75), это медиана верхней половины набора данных. ^[7]

В дополнение к минимальным и максимальным значениям, используемым для построения коробчатой диаграммы, еще одним важным элементом, который также можно использовать для получения коробчатой диаграммы, является межквартильный размах (IQR), как указано ниже:

Межквартильный размах (IQR) : расстояние между верхним и нижним квартилем.

{\text{IQR}}=Q_{3}-Q_{1}=q_{n}(0.75)-q_{n}(0.25)

Ящик-график обычно состоит из двух частей: ящика и набора усов, как показано на рисунке 2.

Коробка

Рамка нарисована от Q ₁ до Q ₃ с горизонтальной линией, проведенной внутри нее, чтобы обозначить медиану. Некоторые коробчатые диаграммы включают дополнительный символ, обозначающий среднее значение данных. ^[8]^[9]

Бакенбарды

Усы должны заканчиваться в наблюдаемой точке данных, но их можно определить различными способами. В самом прямом методе граница нижнего «уса» — это минимальное значение набора данных, а граница верхнего «уса» — максимальное значение набора данных. Из-за этой изменчивости уместно описать соглашение, которое используется для «усов» и выбросов в заголовке коробчатой диаграммы.

Другой популярный выбор границ усов основан на значении IQR 1,5. Сверху верхнего квартиля ( Q ₃ ) измеряется расстояние, в 1,5 раза превышающее IQR, и проводится усик до самой большой наблюдаемой точки данных из набора данных, которая попадает в пределах этого расстояния. Аналогичным образом, расстояние, в 1,5 раза превышающее IQR, измеряется ниже нижнего квартиля ( Q ₁ ), и черта рисуется до самой низкой наблюдаемой точки данных из набора данных, которая попадает в пределы этого расстояния. Поскольку усы должны заканчиваться в наблюдаемой точке данных, длина усов может выглядеть неодинаковой, хотя 1,5 IQR одинаково для обеих сторон. Все остальные наблюдаемые точки данных за пределами границ усов отображаются как выбросы . ^[10] Выбросы можно нанести на коробчатую диаграмму в виде точки, маленького круга, звезды и т. д. (см. пример ниже).

Существуют и другие представления, в которых усы могут обозначать и другие вещи, например:

Одно стандартное отклонение выше и ниже среднего значения набора данных
9-й процентиль и 91-й процентиль набора данных
2-й процентиль и 98-й процентиль набора данных

Редко коробчатый график можно построить без усов. Это может быть целесообразно для конфиденциальной информации, чтобы избежать появления «усов» (и выбросов), раскрывающих фактические наблюдаемые значения. ^[11]

Необычные процентили 2%, 9%, 91%, 98% иногда используются для штриховки усами и концов усиков для изображения сводки из семи цифр . Если данные распределены нормально , местоположения семи меток на коробчатой диаграмме будут расположены на одинаковом расстоянии. На некоторых коробчатых диаграммах перед концом каждого «уса» ставится штриховка.

Вариации

Рисунок 4. Четыре прямоугольные диаграммы с вырезами и без них и переменной шириной.

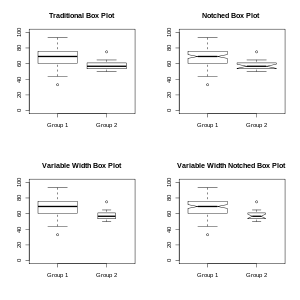
С тех пор, как математик Джон В. Тьюки впервые популяризировал этот тип отображения визуальных данных в 1969 году, было разработано несколько вариаций классической коробчатой диаграммы, и двумя наиболее часто встречающимися вариациями являются коробчатые диаграммы переменной ширины и коробчатые диаграммы с надрезом, показанные на рисунке. 4.

Диаграммы переменной ширины иллюстрируют размер каждой группы, данные которой отображаются, делая ширину прямоугольника пропорциональной размеру группы. Популярное соглашение заключается в том, чтобы ширина поля была пропорциональна квадратному корню из размера группы. ^[12]

На диаграммах с надрезом применяется «выемка» или сужение рамки вокруг медианы. Отсечки полезны, поскольку дают приблизительное представление о значимости разницы медиан; если вырезы двух прямоугольников не перекрываются, это будет свидетельствовать о статистически значимой разнице между медианами. ^[12] Высота насечек пропорциональна межквартильному размаху (IQR) образца и обратно пропорциональна квадратному корню из размера образца. Однако существует неопределенность в отношении наиболее подходящего множителя (поскольку он может варьироваться в зависимости от сходства дисперсий выборок). ^[12] Ширина выреза выбирается произвольно, чтобы она была визуально приятной и должна быть одинаковой для всех коробчатых диаграмм, отображаемых на одной странице.

Одним из правил получения границ этих вырезов является использование расстояния $\pm {\frac {1.58{\text{ IQR}}}{\sqrt {n}}}$ вокруг медианы. ^[13]

Скорректированные коробчатые диаграммы предназначены для описания асимметричного распределения и основаны на медпарами . статистике асимметрии, полученной ^[14] Для значения MC для медицинской пары длины верхних и нижних усов на коробчатой диаграмме соответственно определяются как:

{\begin{matrix}1.5{\text{IQR}}\cdot e^{3{\text{MC}}},&1.5{\text{ IQR}}\cdot e^{-4{\text{MC}}}{\text{ if }}{\text{MC}}\geq 0,\\1.5{\text{IQR}}\cdot e^{4{\text{MC}}},&1.5{\text{ IQR}}\cdot e^{-3{\text{MC}}}{\text{ if }}{\text{MC}}\leq 0.\end{matrix}}

Для симметричного распределения данных медпара будет равна нулю, и это сводит скорректированную коробчатую диаграмму к коробчатой диаграмме Тьюки с равными длинами усов $1.5{\text{ IQR}}$ для обоих усов.

Другие виды коробчатых диаграмм , такие как скрипичные диаграммы и бобовые диаграммы, могут показать разницу между одномодальными и мультимодальными распределениями, которую невозможно наблюдать на исходной классической коробчатой диаграмме. ^[6]

Примеры

Пример без выбросов

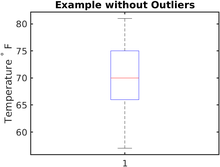
В течение дня измерялась серия почасовых температур в градусах по Фаренгейту. Записанные значения перечислены в следующем порядке (°F): 57, 57, 57, 58, 63, 66, 66, 67, 67, 68, 69, 70, 70, 70, 70, 72, 73, 75, 75, 76, 76, 78, 79, 81.

Ящичковую диаграмму набора данных можно создать, сначала вычислив пять соответствующих значений этого набора данных: минимум, максимум, медиану ( Q ₂ ), первый квартиль ( Q ₁ ) и третий квартиль ( Q ₃ ).

Минимум — это наименьшее число набора данных. В этом случае минимальная зарегистрированная дневная температура составляет 57°F.

Максимум — это наибольшее число набора данных. В этом случае максимальная зарегистрированная дневная температура составляет 81°F.

Медиана — это «среднее» число упорядоченного набора данных. Это означает, что ровно 50% элементов находятся ниже медианы и 50% элементов больше медианы. Медиана этого упорядоченного набора данных составляет 70°F.

Значение первого квартиля ( Q ₁ или 25-й процентиль) — это число, обозначающее одну четверть упорядоченного набора данных. Другими словами, существует ровно 25% элементов, которые меньше первого квартиля, и ровно 75% элементов, которые больше его. Значение первого квартиля можно легко определить, найдя «среднее» число между минимумом и медианой. Для почасовых температур «среднее» число между 57°F и 70°F составляет 66°F.

Значение третьего квартиля ( Q ₃ или 75-й процентиль) — это число, обозначающее три четверти упорядоченного набора данных. Другими словами, существует ровно 75% элементов, которые меньше третьего квартиля, и 25% элементов, которые больше его. Значение третьего квартиля можно легко получить, найдя «среднее» число между медианой и максимумом. Для часовых температур «среднее» число между 70°F и 81°F составляет 75°F.

Межквартильный размах, или IQR, можно рассчитать путем вычитания значения первого квартиля ( Q ₁ ) из значения третьего квартиля ( Q ₃ ):

{\text{IQR}}=Q_{3}-Q_{1}=75^{\circ }F-66^{\circ }F=9^{\circ }F.

Следовательно, $1.5{\text{IQR}}=1.5\cdot 9^{\circ }F=13.5^{\circ }F.$

1,5 IQR выше третьего квартиля составляет:

Q_{3}+1.5{\text{ IQR}}=75^{\circ }F+13.5^{\circ }F=88.5^{\circ }F.

На 1,5 IQR ниже первого квартиля это:

Q_{1}-1.5{\text{ IQR}}=66^{\circ }F-13.5^{\circ }F=52.5^{\circ }F.

Верхняя граница усов коробчатой диаграммы — это наибольшее значение данных, которое находится в пределах 1,5 IQR выше третьего квартиля. Здесь 1,5 IQR выше третьего квартиля составляет 88,5°F, а максимум — 81°F. Поэтому верхний «ус» рисуется при значении максимума, равном 81°F.

Аналогично, нижняя граница «усов» прямоугольной диаграммы — это наименьшее значение данных, которое находится в пределах 1,5 IQR ниже первого квартиля. Здесь 1,5 IQR ниже первого квартиля составляет 52,5°F, а минимум — 57°F. Поэтому нижний ус рисуется при значении минимума, равном 57°F.

Пример с выбросами

Выше приведен пример без выбросов. Вот последующий пример создания коробчатой диаграммы с выбросами:

Упорядоченный набор регистрируемых температур составляет (°F): 52, 57, 57, 58, 63, 66, 66, 67, 67, 68, 69, 70, 70, 70, 70, 72, 73, 75, 75. , 76, 76, 78, 79, 89.

В этом примере изменяются только первое и последнее число. Медиана, третий и первый квартиль остаются прежними.

В этом случае максимальное значение в этом наборе данных составляет 89°F, а 1,5 IQR выше третьего квартиля составляет 88,5°F. Максимум превышает 1,5 IQR плюс третий квартиль, поэтому максимум является выбросом. Таким образом, верхний «ус» рисуется при максимальном значении менее 1,5 IQR выше третьего квартиля, что составляет 79°F.

Аналогично, минимальное значение в этом наборе данных составляет 52°F, а IQR на 1,5 ниже первого квартиля составляет 52,5°F. Минимум меньше 1,5 IQR минус первый квартиль, поэтому минимум также является выбросом. Таким образом, нижний «ус» рисуется при наименьшем значении, превышающем 1,5 IQR ниже первого квартиля, что составляет 57°F.

В случае больших наборов данных

Дополнительный пример получения коробчатой диаграммы из набора данных, содержащего большое количество точек данных:

Общее уравнение для расчета эмпирических квантилей

q_{n}(p)=x_{(k)}+\alpha (x_{(k+1)}-x_{(k)})

{\text{with }}k=[p(n+1)]{\text{ and }}\alpha =p(n+1)-k

Здесь

x_{(k)}

означает общий порядок точек данных (т.е. если

i<k

, затем

x_{(i)}<x_{(k)}

)

Используя приведенный выше пример с 24 точками данных ( n = 24), можно вычислить медиану, первый и третий квартиль математически или визуально.

Медиана : $q_{n}(0.5)=x_{(12)}+(0.5\cdot 25-12)\cdot (x_{(13)}-x_{(12)})=70+(0.5\cdot 25-12)\cdot (70-70)=70^{\circ }F$

Первый квартиль : $q_{n}(0.25)=x_{(6)}+(0.25\cdot 25-6)\cdot (x_{(7)}-x_{(6)})=66+(0.25\cdot 25-6)\cdot (66-66)=66^{\circ }F$

Третий квартиль : $q_{n}(0.75)=x_{(18)}+(0.75\cdot 25-18)\cdot (x_{(19)}-x_{(18)})=75+(0.75\cdot 25-18)\cdot (75-75)=75^{\circ }F$

Визуализация

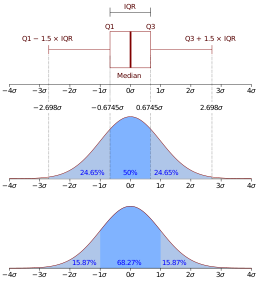
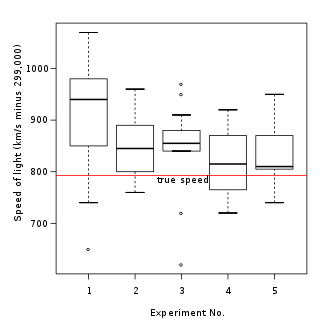
Хотя коробчатые диаграммы могут показаться более примитивными, чем гистограммы или оценки плотности ядра , они имеют ряд преимуществ. Во-первых, ящичная диаграмма позволяет статистикам провести быстрое графическое исследование одного или нескольких наборов данных. Ящичные диаграммы также занимают меньше места и поэтому особенно полезны для параллельного сравнения распределений между несколькими группами или наборами данных (пример см. на рисунке 1). Наконец, на общую структуру гистограмм и оценку плотности ядра может сильно влиять выбор метода количества и ширины интервалов и выбор полосы пропускания соответственно.

Хотя просмотр статистического распределения более распространен, чем просмотр коробчатой диаграммы, может быть полезно сравнить коробчатую диаграмму с функцией плотности вероятности (теоретической гистограммой) для нормального N(0, σ ²) распределение и непосредственно наблюдать за их характеристиками (как показано на рисунке 7).

См. также

Ссылки

^ К., Дютуа, С.Х. (2012). Графический разведочный анализ данных . Спрингер. ISBN 978-1-4612-9371-2 . OCLC 1019645745 . {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка )
^ Граббс, Фрэнк Э. (февраль 1969 г.). «Процедуры обнаружения посторонних наблюдений в выборках» . Технометрика . 11 (1): 1–21. дои : 10.1080/00401706.1969.10490657 . ISSN 0040-1706 .
^ Ричард., Бодди (2009). Статистические методы на практике: для ученых и технологов . Джон Уайли и сыновья. ISBN 978-0-470-74664-6 . OCLC 940679163 .
^ Копье, Мэри Элеонора (2024). График статистики . МакГроу Хилл. п. 166.
^ Спир, Мэри Элеонора. (1969). Практические методы построения графиков . Нью-Йорк: МакГроу-Хилл. ISBN 0070600104 . OCLC 924909765 .
^ Jump up to: ^а ^б Уикхэм, Хэдли; Стриевский, Лиза. «40 лет коробочных сюжетов» (PDF) . Проверено 24 декабря 2020 г.
^ Холмс, Александр; Илловски, Барбара; Дин, Сьюзен (31 марта 2015 г.). «Вводная статистика бизнеса» . ОпенСтакс . Архивировано из оригинала 27 июля 2020 года . Проверено 29 апреля 2020 г.
^ Фригг, Майкл; Хоглин, Дэвид К.; Иглевич, Борис (февраль 1989 г.). «Некоторые реализации коробочного сюжета». Американский статистик . 43 (1): 50–54. дои : 10.2307/2685173 . JSTOR 2685173 .
^ Мармолехо-Рамос, Ф.; Тиан, С. (2010). «Смещающаяся коробчатая диаграмма. Ящичковая диаграмма, основанная на важной сводной статистике вокруг среднего значения» . Международный журнал психологических исследований . 3 (1): 37–46. дои : 10.21500/20112084.823 . hdl : 10819/6492 .
^ Деккинг, FM (2005). Современное введение в вероятность и статистику . Спрингер. стр. 234–238 . ISBN 1-85233-896-2 .
^ Деррик, Бен; Грин, Элизабет; Ричи, Феликс; Уайт, Пол (сентябрь 2022 г.). «Риск раскрытия информации при сообщении широко используемой одномерной статистики». Конфиденциальность в статистических базах данных . Конспекты лекций по информатике. Том. 13463. стр. 119–129. дои : 10.1007/978-3-031-13945-1_9 . ISBN 978-3-031-13944-4 .
^ Jump up to: ^а ^б ^с МакГилл, Роберт; Тьюки, Джон В .; Ларсен, Уэйн А. (февраль 1978 г.). «Вариации коробчатых сюжетов». Американский статистик . 32 (1): 12–16. дои : 10.2307/2683468 . JSTOR 2683468 .
^ «R: Статистика коробчатой диаграммы» . Р инструкция . Проверено 26 июня 2011 г.
^ Юбер, М .; Вандервирен, Э. (2008). «Скорректированная коробчатая диаграмма для асимметричного распределения». Вычислительная статистика и анализ данных . 52 (12): 5186–5201. CiteSeerX 10.1.1.90.9812 . дои : 10.1016/j.csda.2007.11.008 .

Дальнейшее чтение

Тьюки, Джон В. (1977). Исследовательский анализ данных . Аддисон-Уэсли . ISBN 9780201076165 .
Бенджамини, Ю. (1988). «Открытие коробки коробочного сюжета». Американский статистик . 42 (4): 257–262. дои : 10.2307/2685133 . JSTOR 2685133 .
Руссиу, П.Дж. ; Рутс, И.; Тьюки, JW (1999). «Бэг-сюжет: двумерный коробчатый сюжет». Американский статистик . 53 (4): 382–387. дои : 10.2307/2686061 . JSTOR 2686061 .

Внешние ссылки

Beeswarm Boxplot — наложение ленточной диаграммы с дрожанием частоты поверх коробчатой диаграммы.

[1] К., Дютуа, С.Х. (2012). Графический разведочный анализ данных . Спрингер. ISBN 978-1-4612-9371-2 . OCLC 1019645745 . {{cite book}}: CS1 maint: несколько имен: список авторов ( ссылка )

[2] Граббс, Фрэнк Э. (февраль 1969 г.). «Процедуры обнаружения посторонних наблюдений в выборках» . Технометрика . 11 (1): 1–21. дои : 10.1080/00401706.1969.10490657 . ISSN 0040-1706 .

[3] Ричард., Бодди (2009). Статистические методы на практике: для ученых и технологов . Джон Уайли и сыновья. ISBN 978-0-470-74664-6 . OCLC 940679163 .

[4] Копье, Мэри Элеонора (2024). График статистики . МакГроу Хилл. п. 166.

[5] Спир, Мэри Элеонора. (1969). Практические методы построения графиков . Нью-Йорк: МакГроу-Хилл. ISBN 0070600104 . OCLC 924909765 .

[:0-6] Jump up to: ^а ^б Уикхэм, Хэдли; Стриевский, Лиза. «40 лет коробочных сюжетов» (PDF) . Проверено 24 декабря 2020 г.

[7] Холмс, Александр; Илловски, Барбара; Дин, Сьюзен (31 марта 2015 г.). «Вводная статистика бизнеса» . ОпенСтакс . Архивировано из оригинала 27 июля 2020 года . Проверено 29 апреля 2020 г.

[frigge_hoaglin_iglewicz2-8] Фригг, Майкл; Хоглин, Дэвид К.; Иглевич, Борис (февраль 1989 г.). «Некоторые реализации коробочного сюжета». Американский статистик . 43 (1): 50–54. дои : 10.2307/2685173 . JSTOR 2685173 .

[9] Мармолехо-Рамос, Ф.; Тиан, С. (2010). «Смещающаяся коробчатая диаграмма. Ящичковая диаграмма, основанная на важной сводной статистике вокруг среднего значения» . Международный журнал психологических исследований . 3 (1): 37–46. дои : 10.21500/20112084.823 . hdl : 10819/6492 .

[10] Деккинг, FM (2005). Современное введение в вероятность и статистику . Спрингер. стр. 234–238 . ISBN 1-85233-896-2 .

[DGRW-11] Деррик, Бен; Грин, Элизабет; Ричи, Феликс; Уайт, Пол (сентябрь 2022 г.). «Риск раскрытия информации при сообщении широко используемой одномерной статистики». Конфиденциальность в статистических базах данных . Конспекты лекций по информатике. Том. 13463. стр. 119–129. дои : 10.1007/978-3-031-13945-1_9 . ISBN 978-3-031-13944-4 .

[mcgill_tukey_larsen-12] Jump up to: ^а ^б ^с МакГилл, Роберт; Тьюки, Джон В .; Ларсен, Уэйн А. (февраль 1978 г.). «Вариации коробчатых сюжетов». Американский статистик . 32 (1): 12–16. дои : 10.2307/2683468 . JSTOR 2683468 .

[Rboxplotstats-13] «R: Статистика коробчатой диаграммы» . Р инструкция . Проверено 26 июня 2011 г.

[Hubert2008-14] Юбер, М .; Вандервирен, Э. (2008). «Скорректированная коробчатая диаграмма для асимметричного распределения». Вычислительная статистика и анализ данных . 52 (12): 5186–5201. CiteSeerX 10.1.1.90.9812 . дои : 10.1016/j.csda.2007.11.008 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]