Сопряженные функторы

О конструкциях в теории поля см. Присоединение (теория поля) . Для построения топологии см. Пространство присоединения .

В математике , особенно в теории категорий , присоединение — это отношение, которое могут проявлять два функтора , интуитивно соответствующее слабой форме эквивалентности между двумя связанными категориями. Два функтора, которые находятся в этом отношении, известны как сопряженные функторы , один из которых является сопряженным слева , а другой - сопряженным справа . Пары сопряженных функторов повсеместно распространены в математике и часто возникают в результате конструкций «оптимальных решений» определенных задач (т. е. конструкций объектов, обладающих определенным универсальным свойством ), таких как построение свободной группы на множестве в алгебре или построение компактификации Стоуна–Чеха топологического пространства в топологии.

По определению, примыкание между категориями ${\mathcal {C}}$ и ${\mathcal {D}}$ представляет собой пару функторов (предполагаемых ковариантными )

$F:{\mathcal {D}}\rightarrow {\mathcal {C}}$ и $G:{\mathcal {C}}\rightarrow {\mathcal {D}}$

и для всех объектов $X$ в ${\mathcal {C}}$ и $Y$ в ${\mathcal {D}}$, биекция между соответствующими множествами морфизмов

$\mathrm {hom} _{\mathcal {C}}(FY,X)\cong \mathrm {hom} _{\mathcal {D}}(Y,GX)$

такая, что это семейство биекций естественно в $X$ и $Y$. Естественность здесь означает наличие естественных изоморфизмов между парой функторов ${\mathcal {C}}(F-,X):{\mathcal {D}}\to \mathrm {Set^{\text{op}}}$ и ${\mathcal {D}}(-,GX):{\mathcal {D}}\to \mathrm {Set^{\text{op}}}$ за фиксированную $X$ в ${\mathcal {C}}$, а также пару функторов ${\mathcal {C}}(FY,-):{\mathcal {C}}\to \mathrm {Set}$ и ${\mathcal {D}}(Y,G-):{\mathcal {C}}\to \mathrm {Set}$ за фиксированную $Y$ в ${\mathcal {D}}$.

Функтор $F$ называется левым сопряженным функтором или левым сопряженным к $G$, пока $G$ называется правосопряженным функтором или правосопряженным функтором. $F$. Мы пишем $F\dashv G$.

Соединение между категориями ${\mathcal {C}}$ и ${\mathcal {D}}$ в некоторой степени сродни «слабой форме» эквивалентности между ${\mathcal {C}}$ и ${\mathcal {D}}$, и действительно, всякая эквивалентность является присоединением. Во многих ситуациях дополнение можно «повысить» до эквивалентности путем подходящей естественной модификации задействованных категорий и функторов.

Терминология и обозначения

Термины «дополнительный» и «дополнительный» оба используются и являются родственными : один взят непосредственно из латыни, другой — из латыни через французский язык. В классическом тексте «Категории для работающего математика » Мак Лейн проводит различие между ними. Учитывая семью

$\varphi _{XY}:\mathrm {hom} _{\mathcal {C}}(FY,X)\cong \mathrm {hom} _{\mathcal {D}}(Y,GX)$

биекций hom-множества мы называем $\varphi$ присоединение или присоединение между $F$ и $G$. Если $f$ это стрелка в $\mathrm {hom} _{\mathcal {C}}(FY,X)$, $\varphi f$ правильным дополнением является $f$(с. 81). Функтор $F$ остается присоединенным к $G$, и $G$ является правосопряженным к $F$. (Обратите внимание, что $G$ может иметь право сопряженное, совершенно отличное от $F$; см. пример ниже.)

В общем, фразы " $F$ является левым сопряженным» и « $F$ имеет правый сопряженный» эквивалентны. Мы называем $F$ левый сопряженный, поскольку он применяется к левому аргументу $\mathrm {hom} _{\mathcal {C}}$, и $G$ правый сопряженный, поскольку он применяется к правому аргументу $\mathrm {hom} _{\mathcal {D}}$.

Если F сопряжено слева с G , мы также пишем

$F\dashv G.$

Терминология происходит от гильбертова пространства идеи сопряженных операторов. $T$, $U$ с $\langle Ty,x\rangle =\langle y,Ux\rangle$, что формально аналогично приведенному выше соотношению между hom-множествами. Аналогию с присоединенными отображениями гильбертовых пространств можно уточнить в определенных контекстах.

и

Лозунг: «Сопряженные функторы возникают повсюду».

- Сондерс Мак Лейн, Категории для работающего математика

Обычными математическими конструкциями очень часто являются сопряженные функторы. Следовательно, общие теоремы о левых/правых сопряженных функторах содержат детали многих полезных и в других отношениях нетривиальных результатов. К таким общим теоремам относятся эквивалентность различных определений сопряженных функторов, уникальность правого сопряженного для данного левого сопряженного, тот факт, что левые/правые сопряженные функторы соответственно сохраняют копределы/пределы (которые также встречаются во всех областях математики). и общие теоремы о сопряженных функторах, определяющие условия, при которых данный функтор является сопряженным слева/справа.

Решения проблем оптимизации

В некотором смысле сопряженный функтор — это способ дать наиболее эффективное метода решение некоторой проблемы с помощью шаблонного . Например, элементарная проблема теории колец состоит в том, как превратить кольцо (похожее на кольцо, которое может не иметь мультипликативной идентичности) в кольцо . Самый эффективный способ — присоединить элемент «1» к группе, присоединить все (и только) элементы, которые необходимы для удовлетворения аксиом кольца (например, r +1 для каждого r в кольце), и не налагать никаких отношений в вновь сформированное кольцо, не обусловленное аксиомами. Более того, эта конструкция является шаблонной в том смысле, что она работает по существу одинаково для любого кольца.

Это довольно расплывчато, хотя и наводит на размышления, и его можно уточнить на языке теории категорий: конструкция наиболее эффективна, если она удовлетворяет универсальному свойству , и является шаблонной, если она определяет функтор . Универсальные свойства бывают двух типов: начальные свойства и конечные свойства. Поскольку это двойственные понятия, необходимо обсудить только одно из них.

Идея использования начального свойства состоит в том, чтобы поставить задачу в терминах некоторой вспомогательной категории так , чтобы рассматриваемая проблема соответствовала поиску исходного объекта E. E Преимущество этого метода заключается в том, что оптимизация — ощущение, что процесс находит наиболее эффективное решение — означает нечто строгое и узнаваемое, скорее похожее на достижение супремума . Категория E также является шаблонной в этой конструкции, поскольку это всегда категория элементов функтора, к которому строится сопряженное.

Вернёмся к нашему примеру: возьмём заданную группу R и создадим категорию E которой , объектами являются гомоморфизмы rng R → S , где S — кольцо, имеющее мультипликативную единицу. Морфизмы где в E между R → S1 _, и R → S2 _R представляют собой вида ( → S1 S2 _{коммутативные} R → S2 , _{сохраняет} S1 → _→ S2 ) _— S1 _{треугольники} кольцевое _, отображение (которое личность). (Обратите внимание, что это в точности определение запятой категории R над включением унитарных колец в rng.) Существование морфизма между R → S ₁ и R → S ₂ означает, что S ₁ является, по крайней мере, столь же эффективным решением как S ₂ к нашей проблеме: S ₂ может иметь больше присоединенных элементов и/или больше отношений, не налагаемых аксиомами, чем S ₁ . Поэтому утверждение о том, что объект R → R* является начальным в E , т. е. что существует морфизм от него к любому другому элементу E , означает, что кольцо R * является наиболее эффективным решением нашей задачи.

Два факта, заключающиеся в том, что этот метод превращения чисел в кольца является наиболее эффективным и шаблонным, можно выразить одновременно, сказав, что он определяет сопряженный функтор . Более подробно: пусть F обозначает описанный выше процесс присоединения единицы к rng, поэтому F ( R )= R* . Пусть G обозначает процесс «забывания» того, имеет ли кольцо S единицу, и рассмотрения его просто как кольца, так что, по сути, ( S ) = S. G Тогда F — функтор группы G. левый сопряженный

Однако обратите внимание, что на самом деле мы еще не построили R* ; важным и не совсем тривиальным алгебраическим фактом является то, что такой левый сопряженный функтор R → R* действительно существует.

Симметрия

Также можно начать с функтора F и задать следующий (неопределенный) вопрос: существует ли проблема, для которой F является наиболее эффективным решением?

Представление о том, что F является наиболее эффективным решением проблемы, поставленной G , в определенном строгом смысле эквивалентно представлению о том, что G представляет собой наиболее сложную проблему , которую F. решает

дает интуитивное представление о том, что сопряженные функторы встречаются парами: если F сопряжен слева с G , то G сопряжен справа с F. Это

Формальные определения

Существуют различные эквивалентные определения сопряженных функторов:

• Определения с помощью универсальных морфизмов легко сформулировать и требуют минимальных проверок при построении сопряженного функтора или доказательстве сопряженности двух функторов. Они также наиболее похожи на нашу интуицию, связанную с оптимизацией.
• Определение через hom-множества делает симметрию наиболее очевидной и является причиной использования слова «сопряженный» .
• Определение через присоединение единица-единица удобно для доказательства функторов, которые, как известно, являются сопряженными, поскольку они предоставляют формулы, которыми можно напрямую манипулировать.

Эквивалентность этих определений весьма полезна. Сопряженные функторы возникают повсюду, во всех областях математики. Поскольку структура любого из этих определений порождает структуры других, переключение между ними приводит к неявному использованию многих деталей, которые в противном случае пришлось бы повторять отдельно в каждой предметной области.

Соглашения

теории сопряженных лежат термины «лево» и «право» В основе категорий C и D. , и существует множество компонентов, относящихся к одной из двух рассматриваемых Поэтому может оказаться полезным выбирать буквы в алфавитном порядке в зависимости от того, относятся ли они к «левой» категории C или к «правой» категории D , а также по возможности записывать их в этом порядке.

Например, в этой статье буквы X , F , f , ε будут последовательно обозначать вещи, которые живут в категории C , буквы Y , G , g , η будут последовательно обозначать вещи, которые живут в категории D , и, когда это возможно, такие вещи будут упоминаться в порядке слева направо (функтор F : D → C можно рассматривать как «живущий» там, где находятся его выходные данные, в C ). Если бы стрелки левого сопряженного функтора F были нарисованы, они бы указывали влево; если бы стрелки для правого сопряженного функтора G были нарисованы, они бы указывали вправо.

универсальные

По определению функтор $F:D\to C$ является левым сопряженным функтором , если для каждого объекта $X$ в $C$существует универсальный морфизм от $F$ к $X$. Прописано, что это означает, что для каждого объекта $X$ в $C$ существует объект $G(X)$ в $D$ и морфизм $\epsilon _{X}:F(G(X))\to X$ такой, что для каждого объекта $Y$ в $D$ и каждый морфизм $f:F(Y)\to X$ существует единственный морфизм $g:Y\to G(X)$ с $\epsilon _{X}\circ F(g)=f$.

Последнее уравнение выражается следующей коммутативной диаграммой :

Here the counit is a universal morphism.

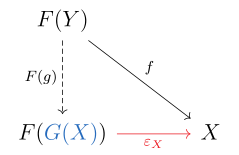
В этой ситуации можно показать, что $G$ можно превратить в функтор $G:C\to D$ уникальным способом, таким образом, что $\epsilon _{X}\circ F(G(f))=f\circ \epsilon _{X'}$ для всех морфизмов $f:X'\to X$ в $C$; $F$ тогда называется левым сопряженным к $G$.

Аналогично мы можем определить правосопряженные функторы. Функтор $G:C\to D$ является правосопряженным функтором , если для каждого объекта $Y$ в $D$, существует универсальный морфизм из $Y$ к $G$. Прописано, что это означает, что для каждого объекта $Y$ в $D$, существует объект $F(Y)$ в $C$ и морфизм $\eta _{Y}:Y\to G(F(Y))$ такой, что для каждого объекта $X$ в $C$ и каждый морфизм $g:Y\to G(X)$ существует единственный морфизм $f:F(Y)\to X$ с $G(f)\circ \eta _{Y}=g$.

The existence of the unit, a universal morphism, can prove the existence of an adjunction.

Опять же, это $F$ можно однозначно превратить в функтор $F:D\to C$ такой, что $G(F(g))\circ \eta _{Y}=\eta _{Y'}\circ g$ для $g:Y\to Y'$ морфизм в $D$; $G$ тогда называется правым сопряженным к $F$.

Верно, как следует из терминологии, что $F$ остается присоединенным к $G$ если и только если $G$ является правосопряженным к $F$.

Эти определения через универсальные морфизмы часто полезны для установления того, что данный функтор является сопряженным слева или справа, поскольку они минималистичны в своих требованиях. Они также интуитивно значимы, поскольку поиск универсального морфизма аналогичен решению задачи оптимизации.

Определение через дополнение Hom-set

Присоединение гомомножества → между двумя категориями C и D состоит из двух функторов F : C → D и G : D и C изоморфизма естественного

$\Phi :\mathrm {hom} _{C}(F-,-)\to \mathrm {hom} _{D}(-,G-)$.

Это задает семейство биекций

$\Phi _{Y,X}:\mathrm {hom} _{C}(FY,X)\to \mathrm {hom} _{D}(Y,GX)$

всех объектов X в C и Y в D. для

В этой ситуации F сопряжена слева с G , а G сопряжена справа с F .

Это определение является логическим компромиссом, поскольку его труднее удовлетворить, чем определения универсального морфизма, и оно имеет меньше непосредственных последствий, чем определение «единица-единица». Оно полезно из-за своей очевидной симметрии и в качестве трамплина между другими определениями.

Чтобы интерпретировать Φ как естественный изоморфизм , необходимо признать hom _C ( F –, –) и hom _D (–, G –) функторами. Фактически, они оба являются бифункторами из D ^на × C к Set ( категория множеств ). Подробности смотрите в статье о hom функторах . Явно естественность Φ означает, что для всех морфизмов f : X → X′ в C и всех морфизмов g : Y ′ → Y в D следующая диаграмма коммутирует :

Naturality of Φ

Вертикальные стрелки на этой диаграмме — это стрелки, вызванные составом. Формально Hom( Fg , f ) : Hom _C ( FY , X ) → Hom _C ( FY , X ) задается формулой h → f o h o Fg для каждого h в Hom _C ( FY , X ). Hom( g , Gf ) аналогично.

Определение через присоединение единиц к единицам

Соединение «единица» между двумя категориями C и D состоит из двух функторов F : D → C и G : C → D и двух естественных преобразований.

${\begin{aligned}\varepsilon &:FG\to 1_{\mathcal {C}}\\\eta &:1_{\mathcal {D}}\to GF\end{aligned}}$

называются соответственно единицей и единицей присоединения (терминология универсальной алгебры ), такие, что композиции

$F{\xrightarrow {\;F\eta \;}}FGF{\xrightarrow {\;\varepsilon F\,}}F$

$G{\xrightarrow {\;\eta G\;}}GFG{\xrightarrow {\;G\varepsilon \,}}G$

являются тождественными преобразованиями 1 _F и 1 _G на F и G соответственно.

В этой ситуации мы говорим, что F сопряжено слева с G , а G сопряжено справа с F , и можем указать это соотношение, написав $(\varepsilon ,\eta ):F\dashv G$ или просто $F\dashv G$ .

В форме уравнения приведенные выше условия на ( ε , η ) представляют собой уравнения с единичными единицами.

${\begin{aligned}1_{F}&=\varepsilon F\circ F\eta \\1_{G}&=G\varepsilon \circ \eta G\end{aligned}}$

это означает, что для каждого X в C и каждого Y в D ,

${\begin{aligned}1_{FY}&=\varepsilon _{FY}\circ F(\eta _{Y})\\1_{GX}&=G(\varepsilon _{X})\circ \eta _{GX}\end{aligned}}$.

Обратите внимание, что $1_{\mathcal {C}}$ обозначает идентификационный функтор категории ${\mathcal {C}}$, $1_{F}$ обозначает тождественное естественное преобразование функтора F в самого себя, а $1_{FY}$ обозначает тождественный морфизм объекта FY .

Струнная диаграмма для присоединения.

Эти уравнения полезны для сведения доказательств сопряженных функторов к алгебраическим манипуляциям. Их иногда называют тождествами треугольников , а иногда и уравнениями зигзага из-за появления соответствующих струнных диаграмм . Чтобы их запомнить, нужно сначала записать бессмысленное уравнение $1=\varepsilon \circ \eta$ а затем заполните букву F или G одним из двух простых способов, которые определяют составы.

Примечание. Использование здесь префикса «co» в counit не согласуется с терминологией пределов и копределов, поскольку копредел удовлетворяет начальному свойству, тогда как морфизмы counit будут удовлетворять терминальным свойствам, причем двойственно. Термин единица здесь заимствован из теории монад , где он выглядит как вставка тождества 1 в моноид.

История

Идея сопряженных функторов была предложена Дэниелом Каном в 1958 году. Как и многие концепции теории категорий, оно было предложено потребностями гомологической алгебры , которая в то время была посвящена вычислениям. Те, кто столкнулся с необходимостью аккуратного и систематического изложения предмета, заметили бы такие связи, как

hom( F ( X ), Y ) = hom( X , G ( Y ))

в категории абелевых групп , где F — функтор $-\otimes A$(т.е. возьмем тензорное произведение с A ), а G был функтором hom( A ,–) (теперь это известно как присоединение тензора к hom ). Использование знака равенства является злоупотреблением обозначениями ; способ их идентификации эти две группы на самом деле не идентичны, но существует естественный . Это можно видеть естественным, исходя, во-первых, из того, что это два альтернативных описания билинейных отображений из X × A в Y . Однако это нечто особенное в случае тензорного произведения. В теории категорий «естественность» биекции включается в понятие естественного изоморфизма .

Примеры

Бесплатные группы

Построение свободных групп является распространенным и показательным примером.

Пусть F : Set → Grp — функтор, присваивающий каждому множеству Y , свободную группу порожденную элементами Y , и пусть G : Grp → Set — функтор забывания , который присваивает каждой группе X ее базовый набор. Тогда F левосопряжён к G :

Начальные морфизмы. Для каждого набора Y набор GFY является просто базовым набором свободной группы FY порожденной Y. , Позволять $\eta _{Y}:Y\to GFY$быть отображением множества, заданным «включением генераторов». Это начальный морфизм из Y в G , потому что любое отображение множества из Y в базовое множество GW некоторой группы W будет факторизоваться через $\eta _{Y}:Y\to GFY$посредством единственного группового гомоморфизма из FY в W . Это и есть универсальное свойство свободной группы на Y .

Терминальные морфизмы. Для каждой группы X группа FGX свободно порожденной GX , элементами X. является свободной группой , Позволять $\varepsilon _{X}:FGX\to X$— групповой гомоморфизм, который переводит генераторы FGX в элементы X , которым они соответствуют, что существует в силу универсального свойства свободных групп. Затем каждый $(GX,\varepsilon _{X})$ является терминальным морфизмом из F в X , поскольку любой групповой гомоморфизм из свободной группы FZ в X будет факторизоваться через $\varepsilon _{X}:FGX\to X$через уникальную карту множества от Z до GX . Это означает, что ( F , G ) — сопряженная пара.

Присоединение Hom-set. Групповые гомоморфизмы свободной группы FY в группу X соответствуют в точности отображениям множества Y в множество GX : каждый гомоморфизм из FY в X полностью определяется его действием на образующие, что является еще одним подтверждением универсального свойства свободных групп. Можно непосредственно проверить, что это соответствие является естественным преобразованием, а это означает, что оно является присоединением гомомножества для пары ( F , G ).

присоединение единица-единица. Можно также непосредственно проверить, что ε и η естественны. Затем прямая проверка того, что они образуют соединение единица. $(\varepsilon ,\eta ):F\dashv G$ как следует:

Первое частно-единичное уравнение  $1_{F}=\varepsilon F\circ F\eta$ говорит, что для каждого множества Y композиция

$FY{\xrightarrow {\;F(\eta _{Y})\;}}FGFY{\xrightarrow {\;\varepsilon _{FY}\,}}FY$

должна быть личность. Промежуточная группа FGFY — это свободная группа, свободно порожденная словами свободной группы FY . (Подумайте об этих словах, заключенных в круглые скобки, чтобы указать, что они являются независимыми генераторами.) Стрелка $F(\eta _{Y})$— групповой гомоморфизм из FY в FGFY , переводящий каждый генератор y из FY в соответствующее слово длины один ( y ) в качестве генератора FGFY . Стрелка $\varepsilon _{FY}$- это групповой гомоморфизм из FGFY в FY , отправляющий каждый генератор в слово FY , которому он соответствует (поэтому это отображение является «опусканием круглых скобок»). Состав этих карт действительно идентичен ФГ .

Второе счетно-единичное уравнение  $1_{G}=G\varepsilon \circ \eta G$ говорит, что для каждой группы X композиция

 $GX{\xrightarrow {\;\eta _{GX}\;}}GFGX{\xrightarrow {\;G(\varepsilon _{X})\,}}GX$ 

должна быть личность. Промежуточный набор GGFX — это всего лишь базовый набор FGX . Стрелка $\eta _{GX}$— это отображение множества «включения генераторов» из множества GX в множество GFGX . Стрелка $G(\varepsilon _{X})$- это отображение множества из GFGX в GX , которое лежит в основе группового гомоморфизма, отправляющего каждый генератор FGX в элемент X , которому он соответствует («опускание скобок»). Композиция этих отображений действительно тождественна на GX .

Свободные конструкции и забывчивые функторы

Все свободные объекты являются примерами левого сопряжения к забывчивому функтору , который присваивает алгебраическому объекту его базовый набор. Эти алгебраические свободные функторы обычно имеют то же описание, что и в подробном описании ситуации со свободной группой выше.

функторы

Произведения , расслоенные произведения , эквалайзеры и ядра — все это примеры категориального понятия предела . Любой предельный функтор сопряжен справа с соответствующим диагональным функтором (при условии, что категория имеет рассматриваемый тип пределов), а единица присоединения обеспечивает определяющие отображения предельного объекта (т. е. диагонального функтора на пределе в категория функтора). Ниже приведены некоторые конкретные примеры.

• Продукты Let Π: Grp ² → Grp — функтор, который присваивает каждой паре ( X ₁ , X ₂ ) группу произведений X ₁ × X ₂ , и пусть ∆: Grp → Grp ² — диагональный функтор , который присваивает каждой группе X пару ( X , X ) в категории продуктов Grp ² . Универсальное свойство группы произведений показывает, что Π правосопряжено к Δ. Единицей этого присоединения является определяющая пара отображений проекции X ₁ × X ₂ на X ₁ и X ₂ , определяющие предел, а единицей — диагональное включение группы X в X × X (отображение x в (x ,Икс)).

Декартово произведение множеств и , произведение колец, произведение топологических пространств т. д. следуют той же схеме; его также можно напрямую распространить на более чем два фактора. В более общем смысле любой тип предела правосопряжен с диагональным функтором.

• Ядра. Рассмотрим категорию D гомоморфизмов абелевых групп. Если f ₁ : A ₁ → B ₁ и f ₂ : A ₂ → B ₂ — два объекта D , то морфизм из f ₁ в f ₂ — это пара ( g _A , g _B ) таких морфизмов, что g _B f ₁ знак равно ж ₂ г _А . Пусть G : D → Ab — функтор, который сопоставляет каждому гомоморфизму его ядро , и пусть F : Ab → D — функтор, который отображает группу A в гомоморфизм A → 0. Тогда G правосопряжен к F , который выражает универсальный свойство ядер. Единицей этого присоединения является определяющее вложение ядра гомоморфизма в область определения гомоморфизма, а единицей — морфизм, отождествляющий группу A с ядром гомоморфизма A → 0.

Подходящий вариант этого примера также показывает, что функторы ядра для векторных пространств и модулей являются правосопряженными. Аналогично можно показать, что функторы коядра абелевых групп, векторных пространств и модулей являются левыми сопряженными.

диагональные

Копроизведения , расслоенные копродукции , коэквалайзеры и коядра — все это примеры категориального понятия копредела . Любой функтор копредела остается сопряженным с соответствующим диагональным функтором (при условии, что категория имеет рассматриваемый тип копредела), а единица присоединения обеспечивает определяющие отображения в объект копредела. Ниже приведены некоторые конкретные примеры.

• Сопродукты. Если F : Ab ² → Ab сопоставляет каждой паре ( X2 ₎ X1, абелевых _групп их прямую сумму , и если G : Ab → Ab ² является функтором, который сопоставляет каждой абелевой группе Y пару ( Y , Y ), тогда F сопряжена слева к G , что опять-таки является следствием универсального свойства прямых сумм. Единицей этой сопряженной пары является определяющая пара отображений включения из X ₁ и X ₂ в прямую сумму, а единицей является аддитивная карта из прямой суммы ( X , X ) обратно в X (отправка элемента ( a , b ) прямой суммы к элементу a + b из X ).

Аналогичные примеры дают прямая сумма векторных пространств и модулей , свободное произведение групп и несвязное объединение множеств.

Дальнейшие примеры

Алгебра

• Присоединение идентификатора к rng . Этот пример обсуждался в разделе мотивации выше. Учитывая rng R , мультипликативный единичный элемент можно добавить, взяв R x Z и определив Z -билинейное произведение с (r,0)(0,1) = (0,1)(r,0) = (r, 0), (r,0)(s,0) = (rs,0), ​​(0,1)(0,1) = (0,1). Это создает левый сопряженный функтор, переводящий кольцо в базовую цепь.
• Присоединение единицы к полугруппе . Аналогично, учитывая полугруппу S , мы можем добавить единичный элемент и получить моноид , взяв дизъюнктное объединение S $\sqcup${1} и определение над ним бинарной операции, расширяющей операцию над S , а 1 является единичным элементом. Эта конструкция дает функтор, который является левым сопряженным функтором, переводящим моноид в базовую полугруппу.
• Удлинители колец. Предположим, что R и S — кольца, а ρ : R → S — гомоморфизм колец . Тогда S можно рассматривать как (левый) R -модуль, а тензорное произведение с S дает функтор F : R - Mod → S - Mod . Тогда F левосопряжён к функтору забвения G : S - Mod → R - Mod .
• Тензорные произведения . Если R — кольцо и M — правый R -модуль, то тензорное произведение с M дает функтор F : R — Mod → Ab . Функтор G : Ab → R - Mod , определенный формулой G ( A ) = hom _Z ( M , A ) для любой абелевой группы A является правосопряженным к F. ,
• От моноидов и групп к кольцам. Целочисленная конструкция моноидного кольца дает функтор от моноидов к кольцам. Этот функтор сопряжен слева с функтором, который сопоставляет данному кольцу лежащий в его основе мультипликативный моноид. Аналогично, конструкция целого группового кольца дает функтор от групп к кольцам, сопряженный слева с функтором, который ставит в соответствие данному кольцу его группу единиц . Можно также начать с поля K и рассмотреть категорию K - алгебр вместо категории колец, чтобы получить моноид и групповые кольца K. над
• Поле дробей. Рассмотрим категорию Dom _m областей целостности с инъективными морфизмами. Функтор забывчивости Field → Dom _m из полей имеет левый сопряженный — он ставит в соответствие каждой области целостности свое поле дробей .
• Полиномиальные кольца . Пусть Ring _* — категория точечных коммутативных колец с единицей (пары (A,a), где A — кольцо, a ∈ A и морфизмы сохраняют выделенные элементы). Функтор забывания G: Ring _* → Ring имеет левый сопряженный – он ставит в соответствие каждому кольцу R пару (R[x],x), где R[x] – кольцо полиномов с коэффициентами из R.
• Абелианизация . Рассмотрим функтор включения G : Ab → Grp из категории абелевых групп в категорию групп . Он имеет левый сопряженный элемент, называемый абелианизацией , который присваивает каждой группе G факторгруппу G. ^аб = G /[ G , G ].
• Группа Гротендика . В K-теории отправной точкой является наблюдение, что категория векторных расслоений в топологическом пространстве имеет коммутативную структуру моноида при прямой сумме . можно сделать абелеву группу Из этого моноида , группу Гротендика , формально добавив аддитивную обратную группу для каждого расслоения (или класса эквивалентности). В качестве альтернативы можно заметить, что функтор, который для каждой группы принимает основной моноид (игнорируя обратные), имеет левый сопряженный. Это универсальная конструкция, что соответствует обсуждению третьего раздела выше. То есть можно имитировать построение отрицательных чисел ; но есть и другой вариант теоремы существования . В случае финитарных алгебраических структур существование само по себе может быть отнесено к универсальной алгебре или теории моделей ; естественно, существует и доказательство, адаптированное к теории категорий.
• Взаимность Фробениуса в теории представлений групп : см. индуцированное представление . Этот пример предвосхитил общую теорию примерно на полвека.

Топология

• Функтор с левым и правым сопряженными. Пусть G — функтор из топологических пространств в множества , который сопоставляет каждому топологическому пространству его базовый набор (то есть забывая о топологии). G имеет левый сопряженный F , создающий дискретное пространство на множестве Y , и правый сопряженный H создающий тривиальную топологию на Y. ,
• Подвески и петлевые пространства. Учитывая топологические пространства X и Y , пространство [ SX , Y ] гомотопических классов отображений из надстройки SX в X . Y естественно изоморфно пространству [ X , Ω Y ] гомотопических классов отображений из X в пространство петель Ом Y из Y . Таким образом, функтор подвески слева сопряжен с функтором пространства петель в гомотопической категории , что является важным фактом в теории гомотопии .
• Компактификация Стоуна-Чеха. Пусть KHaus — категория компактных хаусдорфовых пространств и G : KHaus → Top — функтор включения в категорию топологических пространств . Тогда G имеет левое сопряженное F : Top → KHaus , компактификацию Стоуна–Чеха . Единица этой сопряженной пары дает непрерывное отображение любого топологического пространства X в его компактификацию Стоуна – Чеха.
• Прямые и обратные образы пучков. Каждое непрерывное отображение f : X → Y между топологическими пространствами индуцирует функтор f _∗ из категории пучков (множеств, абелевых групп или колец...) на X в соответствующую категорию пучков на Y , функтор прямого образа . Это также индуцирует функтор f ⁻¹ из категории пучков абелевых групп на Y в категорию пучков абелевых групп на X — функтор обратного образа . ж ⁻¹ слева сопряжено с f _∗ . Здесь более тонкий момент заключается в том, что левый сопряженный для когерентных пучков будет отличаться от сопряженного для пучков (множеств).
• Трезвение. В статье о двойственности Стоуна описывается соединение между категорией топологических пространств и категорией трезвых пространств , известное как трезвость. Примечательно, что в статье также содержится подробное описание еще одного дополнения, которое готовит почву для знаменитой двойственности трезвых пространств и пространственных локалей, эксплуатируемой в бессмысленной топологии .

Позы

Каждое частично упорядоченное множество можно рассматривать как категорию (где элементы частично упорядоченного множества становятся объектами категории, и у нас есть единственный морфизм от x до y тогда и только тогда, когда x ≤ y ). Пара сопряженных функторов между двумя частично упорядоченными множествами называется связностью Галуа (или, если она контравариантна, антитонной связностью Галуа). См. эту статью для ряда примеров: случай теории Галуа, конечно, является ведущим. Любая связность Галуа порождает операторы замыкания и обратные, сохраняющие порядок биекции между соответствующими замкнутыми элементами.

Как и в случае с группами Галуа, реальный интерес часто заключается в уточнении соответствия двойственности ( т. е. изоморфизму антитонного порядка). Трактовка Капланским теории Галуа в этом направлении сыграла важную роль в признании здесь общей структуры.

Случай частичного порядка весьма заметно сворачивает определения присоединения, но может обеспечить несколько тем:

• присоединения не могут быть двойственностями или изоморфизмами, но являются кандидатами на повышение до этого статуса.
• Операторы замыкания могут указывать на наличие присоединений как соответствующих монад (ср. аксиомы замыкания Куратовского ).
• очень общий комментарий Уильяма Ловера заключается в том, что синтаксис и семантика сопряжены: возьмите C за множество всех логических теорий (аксиоматизаций), а D за степенное множество множества всех математических структур. Для теории T в C пусть G ( T ) будет множеством всех структур, которые удовлетворяют аксиомам T ; набора математических структур S пусть F ( S ) — минимальная аксиоматизация S. для Тогда мы можем сказать, что S является подмножеством G ( T ) тогда и только тогда, когда F ( S ) логически следует T : «семантический функтор» G правосопряжен к «синтаксическому функтору» F. из
• деление — это (вообще) попытка обратить умножение, но в ситуациях, когда это невозможно, мы часто пытаемся вместо этого построить сопряженное : идеальное частное сопряжено с умножением на кольцевые идеалы , а импликация в логике высказываний сопряжена. к логическому соединению .

Теория категорий

• Эквиваленты. Если F : D → C — эквивалентность категорий , то мы имеем обратную эквивалентность G : C → D , и два функтора F и G образуют присоединенную пару. В этом случае единица и единица являются естественными изоморфизмами.
• Серия дополнений. Функтор π ₀ , сопоставляющий категории ее множество компонентов связности, левосопряжен с функтором D , сопоставляющим множеству дискретную категорию на этом множестве. Более того, D левосопряжен с объектным функтором U , который присваивает каждой категории свой набор объектов, и, наконец, U сопряжен слева с A , который присваивает каждому множеству недискретную категорию. на этом наборе.
• Экспоненциальный объект . В декартовой замкнутой категории эндофунктор C → C , заданный формулой –× A, имеет правый сопряженный – ^А . Эту пару часто называют каррирующей и некаринговой; во многих частных случаях они также непрерывны и образуют гомеоморфизм.

Категориальная логика

• Количественная оценка. Если $\phi _{Y}$ является унарным предикатом, выражающим некоторое свойство, то достаточно сильная теория множеств может доказать существование множества $Y=\{y\mid \phi _{Y}(y)\}$условий, которые реализуют свойство. Правильное подмножество $T\subset Y$ и связанное с этим введение $T$ в $Y$ характеризуется предикатом $\phi _{T}(y)=\phi _{Y}(y)\land \varphi (y)$ выражающее строго более ограничительное свойство.

Роль кванторов в логике предикатов заключается в формировании предложений, а также в выражении сложных предикатов путем замыкания формул с возможным большим количеством переменных. Например, рассмотрим предикат $\psi _{f}$ с двумя открытыми переменными типа $X$ и $Y$. Использование квантификатора для закрытия $X$, мы можем сформировать набор

$\{y\in Y\mid \exists x.\,\psi _{f}(x,y)\land \phi _{S}(x)\}$

всех элементов $y$ из $Y$ для чего существует $x$ к чему это $\psi _{f}$-относящиеся и которые сами по себе характеризуются свойством $\phi _{S}$. Теоретические операции над множествами, такие как пересечение $\cap$ из двух наборов непосредственно соответствует союзу $\land$предикатов. В категориальной логике , подразделе теории топоса , кванторы отождествляются с сопряженными функтору обратного преобразования. Такую реализацию можно увидеть по аналогии с обсуждением логики высказываний с использованием теории множеств, но общее определение обеспечивает более богатый диапазон логик.

Итак, рассмотрим объект $Y$в категории с откатами. Любой морфизм $f:X\to Y$ вы представите функционера

$f^{*}:{\text{Sub}}(Y)\longrightarrow {\text{Sub}}(X)$

по категории, которая является предзаказом подобъектов . Он отображает подобъекты $T$ из $Y$ (технически: классы мономорфизма $T\to Y$) к откату $X\times _{Y}T$. Если этот функтор имеет левый или правый сопряженный, они называются $\exists _{f}$ и $\forall _{f}$, соответственно. Они оба отображают ${\text{Sub}}(X)$ вернуться к ${\text{Sub}}(Y)$. Очень грубо, учитывая домен $S\subset X$ количественно оценить отношение, выраженное через $f$ окончено, функтор/квантификатор закрывается $X$ в $X\times _{Y}T$ и возвращает указанное таким образом подмножество $Y$.

Пример : В $\operatorname {Set}$, категория множеств и функций, канонические подобъекты являются подмножеством (вернее, их каноническими инъекциями). Откат $f^{*}T=X\times _{Y}T$ инъекции подмножества $T$ в $Y$ вдоль $f$ характеризуется как самый большой набор, который знает все о $f$ и инъекции $T$ в $Y$. Следовательно, это оказывается (в биекции) прообразом $f^{-1}[T]\subseteq X$.

Для $S\subseteq X$, выясним левый сопряженный, который определяется через

${\operatorname {Hom} }(\exists _{f}S,T)\cong {\operatorname {Hom} }(S,f^{*}T),$

что здесь просто означает

$\exists _{f}S\subseteq T\leftrightarrow S\subseteq f^{-1}[T]$.

Учитывать $f[S]\subseteq T$. Мы видим $S\subseteq f^{-1}[f[S]]\subseteq f^{-1}[T]$. И наоборот, если для $x\in S$ у нас также есть $x\in f^{-1}[T]$, то ясно $f(x)\in T$. Так $S\subseteq f^{-1}[T]$ подразумевает $f[S]\subseteq T$. Делаем вывод, что левосопряженный к функтору обратного образа $f^{*}$задается прямым изображением. Вот характеристика этого результата, которая больше соответствует логической интерпретации: Образ $S$ под $\exists _{f}$ это полный набор $y$s, такой, что $f^{-1}[\{y\}]\cap S$непусто. Это работает, потому что игнорирует именно те $y\in Y$ которые входят в состав $f[S]$. Так

$\exists _{f}S=\{y\in Y\mid \exists (x\in f^{-1}[\{y\}]).\,x\in S\;\}=f[S].$

Поставьте это по аналогии с нашей мотивацией. $\{y\in Y\mid \exists x.\,\psi _{f}(x,y)\land \phi _{S}(x)\}$.

Правый сопряженный функтору обратного образа задается (без выполнения здесь вычислений) выражением

$\forall _{f}S=\{y\in Y\mid \forall (x\in f^{-1}[\{y\}]).\,x\in S\;\}.$

Подмножество $\forall _{f}S$ из $Y$ характеризуется как полный набор $y$обладает тем свойством, что прообраз $\{y\}$ относительно $f$ полностью содержится внутри $S$. Обратите внимание, что предикат, определяющий набор, такой же, как и выше, за исключением того, что $\exists$ заменяется на $\forall$.

См. также powerset .

Вероятность

Двойной факт в вероятности можно понимать как дополнение: ожидание коммутирует с аффинным преобразованием и что ожидание в некотором смысле является лучшим решением проблемы нахождения вещественного приближения к распределению действительных чисел.

Определите категорию на основе $\mathbb {R}$, где объекты представляют собой действительные числа, а морфизмы представляют собой «аффинные функции, вычисляемые в точке». То есть для любой аффинной функции $f(x)=ax+b$ и любое действительное число $r$, определим морфизм $(r,f):r\to f(r)$.

Определите категорию на основе $M(\mathbb {R} )$, набор распределения вероятностей на $\mathbb {R}$с конечным ожиданием. Определить морфизмы на $M(\mathbb {R} )$как «аффинные функции, оцениваемые по распределению». То есть для любой аффинной функции $f(x)=ax+b$ и любой $\mu \in M(\mathbb {R} )$, определим морфизм $(\mu ,f):\mu \to \mu \circ f^{-1}$.

Тогда дельта-мера Дирака определяет функтор: $\delta :x\mapsto \delta _{x}$, а математическое ожидание определяет другой функтор $\mathbb {E} :\mu \mapsto \mathbb {E} [\mu ]$, и они сопряжены: $\mathbb {E} \dashv \delta$. (Несколько смущенно, $\mathbb {E}$ является левым сопряженным, хотя $\mathbb {E}$ является «забывчивым» и $\delta$ бесплатно".)

Дополнения полностью

Следовательно, с каждым присоединением связано множество функторов и естественных преобразований, и лишь небольшой части достаточно, чтобы определить остальные.

Присоединение категорий C и D состоит из

• Функтор , F : D → C называемый левым сопряженным
• Функтор G : C → D , называемый правым сопряженным
• Естественный изоморфизм Φ : hom _C ( F –,–) → hom _D (–, G –)
• ε Естественное преобразование : FG → 1 _C , называемое счетчиком
• Естественное преобразование η : 1 _D → GF , называемое единицей

Эквивалентная формулировка, где X обозначает любой объект C , а Y обозначает любой объект D , выглядит следующим образом:

Для каждого C -морфизма f : FY → X существует единственный D -морфизм Φ _{Y , X} ( f ) = g : Y → GX что приведенные ниже диаграммы коммутируют, и для каждого D -морфизма g : Y → GX такой , существует единственный C -морфизм Φ ⁻¹ _{Y , X} ( g ) = f : FY → X в C такие, что диаграммы ниже коммутируют:

Из этого утверждения можно понять, что:

• Преобразования ε, η и Φ связаны уравнениями

${\begin{aligned}f=\Phi _{Y,X}^{-1}(g)&=\varepsilon _{X}\circ F(g)&\in &\,\,\mathrm {hom} _{C}(F(Y),X)\\g=\Phi _{Y,X}(f)&=G(f)\circ \eta _{Y}&\in &\,\,\mathrm {hom} _{D}(Y,G(X))\\\Phi _{GX,X}^{-1}(1_{GX})&=\varepsilon _{X}&\in &\,\,\mathrm {hom} _{C}(FG(X),X)\\\Phi _{Y,FY}(1_{FY})&=\eta _{Y}&\in &\,\,\mathrm {hom} _{D}(Y,GF(Y))\\\end{aligned}}$

• Преобразования ε, η удовлетворяют счетно-единичным уравнениям

${\begin{aligned}1_{FY}&=\varepsilon _{FY}\circ F(\eta _{Y})\\1_{GX}&=G(\varepsilon _{X})\circ \eta _{GX}\end{aligned}}$

• Каждая пара ( GX , ε _X ) представляет собой терминальный морфизм из F в X в C
• Каждая пара ( FY , η _Y ) представляет собой начальный морфизм из Y в G в D

В частности, приведенные выше уравнения позволяют определить Φ, ε и η через любой из трех. Однако одних только сопряженных функторов F и G , как правило, недостаточно для определения присоединения. Эквивалентность этих ситуаций продемонстрирована ниже.

множества

Дан правосопряженный функтор G : C → D ; в смысле начальных морфизмов можно построить индуцированное присоединение hom-множества, выполнив следующие шаги.

• Построим функтор F : D → C и естественное преобразование η.
  • Для каждого объекта Y в D выберите начальный морфизм ( F ( Y ), η _Y ) из Y в G , так что η _Y : Y → G ( F ( Y )). У нас есть отображение F на объектах и ​​семейство морфизмов η.
  • Для каждого f : Y ₀ → Y ₁ , поскольку ( F ( Y ₀ ), η _{Y 0} ) является исходным морфизмом, затем факторизуйте η _{Y 1} o f с η _{Y 0} и получите F ( f ) : F ( Y ₀ ) → Ж ( Y ₁ ). Это отображение F на морфизмах.
  • Коммутационная диаграмма этой факторизации подразумевает коммутационную диаграмму естественных преобразований, поэтому η : 1 _D → G o F является естественным преобразованием .
  • Единственность этой факторизации и то, что G является функтором, означает, что отображение F на морфизмах сохраняет композиции и тождества.
• Построим естественный изоморфизм Φ : hom _C ( F -,-) → hom _D (-, G -).
  • Для каждого объекта X в C каждый объект Y в D , поскольку ( F ( Y ), η _Y ) является исходным морфизмом, то Φ _{Y , X} является биекцией, где Φ _{Y , X} ( f : F ( Y ) → Икс ) знак равно грамм ( ж ) о η _Y .
  • η — естественное преобразование, G — функтор, тогда для любых объектов X ₀ , X ₁ в C , любых объектов Y ₀ , Y ₁ в D , любого x : X ₀ → X ₁ , любого y : Y ₁ → Y ₀ , у нас есть Φ _{Y 1 , X 1} ( x o f o F ( y )) = G(x) o G ( f ) o G ( F ( y )) o η _{Y 1} = G ( x ) o G ( f ) o η _{Y 0} o y = G ( x ) o Φ _{Y 0 , X 0} ( f ) o y , и тогда Φ является натуральным по обоим аргументам.

Аналогичный аргумент позволяет построить присоединение гомомножества терминальных морфизмов к левому сопряженному функтору. (Конструкция, начинающаяся с правого сопряженного, встречается несколько чаще, поскольку правый сопряженный во многих сопряженных парах представляет собой тривиально определенное включение или забывчивый функтор.)

Соединение единица-единица вызывает соединение hom-множества

Даны функторы F : D → C , G : C → D и присоединение единица-единица (ε, η) : F $\dashv$ G мы можем построить присоединение hom-множества, найдя естественное преобразование Φ : hom _C ( F -,-) → hom _D (-, G -) в следующих шагах:

• Для каждого f : FY → X и каждого g : Y → GX определите

${\begin{aligned}\Phi _{Y,X}(f)=G(f)\circ \eta _{Y}\\\Psi _{Y,X}(g)=\varepsilon _{X}\circ F(g)\end{aligned}}$

Преобразования Φ и Ψ естественны, поскольку η и ε естественны.

• Используя по порядку, что F является функтором, что ε является натуральным, и уравнение с единичной единицей 1 _FY = ε _FY o F (η _Y ), получаем

${\begin{aligned}\Psi \Phi f&=\varepsilon _{X}\circ FG(f)\circ F(\eta _{Y})\\&=f\circ \varepsilon _{FY}\circ F(\eta _{Y})\\&=f\circ 1_{FY}=f\end{aligned}}$

следовательно, ΨΦ — тождественное преобразование.

• Двойственным образом, используя тот факт, что G является функтором, что η естественно, и уравнение с единицей 1 _GX = G (ε _X ) o η _GX , мы получаем

${\begin{aligned}\Phi \Psi g&=G(\varepsilon _{X})\circ GF(g)\circ \eta _{Y}\\&=G(\varepsilon _{X})\circ \eta _{GX}\circ g\\&=1_{GX}\circ g=g\end{aligned}}$

следовательно, ΦΨ — тождественное преобразование. Таким образом, Φ является естественным изоморфизмом с обратным Φ ⁻¹ = Пс.

Присоединение Hom-set вызывает все вышеперечисленное

Учитывая функторы F : D → C , G : C → D и присоединение к hom-множеству Φ : hom _C ( F -,-) → hom _D (-, G -), можно построить присоединение единица-единица

$(\varepsilon ,\eta ):F\dashv G$ ,

который определяет семейства начальных и терминальных морфизмов, на следующих этапах:

• Позволять $\varepsilon _{X}=\Phi _{GX,X}^{-1}(1_{GX})\in \mathrm {hom} _{C}(FGX,X)$ для каждого X в C , где $1_{GX}\in \mathrm {hom} _{D}(GX,GX)$ является тождественным морфизмом.
• Позволять $\eta _{Y}=\Phi _{Y,FY}(1_{FY})\in \mathrm {hom} _{D}(Y,GFY)$ для каждого Y в D , где $1_{FY}\in \mathrm {hom} _{C}(FY,FY)$ является тождественным морфизмом.
• Из биективности и естественности Φ следует, что каждый ( , ε _X ) является терминальным морфизмом из F в X в C , а каждый ( FY , η _Y ) является начальным морфизмом из Y в G в D. GX
• Из естественности Φ следует естественность ε и η, а две формулы

${\begin{aligned}\Phi _{Y,X}(f)=G(f)\circ \eta _{Y}\\\Phi _{Y,X}^{-1}(g)=\varepsilon _{X}\circ F(g)\end{aligned}}$

для каждого f : FY → X и g : Y → GX (которые полностью определяют Φ).

• Подстановка FY вместо X и η _Y = Φ _{Y , FY} (1 _FY ) вместо g во второй формуле дает первое двуединичное уравнение.

$1_{FY}=\varepsilon _{FY}\circ F(\eta _{Y})$,

и заменив Y на GX и ε _X = Φ ⁻¹ _{GX, X} (1 _GX ) для f в первой формуле дает второе единичное уравнение

$1_{GX}=G(\varepsilon _{X})\circ \eta _{GX}$.

Свойства

Существование

См. Также: Формальные критерии для сопряженных функторов.

Не каждый функтор G : C → D допускает левый сопряженный. Если C — полная категория , то функторы с левыми сопряженными можно охарактеризовать о сопряженных функторах теоремой Питера Дж. Фрейда : G имеет левый сопряженный тогда и только тогда, когда он непрерывен и выполняется определенное условие малости: для каждого объекта Y из D существует семейство морфизмов

ж _я : Y → грамм ( Икс _я )

где индексы i происходят из множества I , а не из собственного класса , такого, что каждый морфизм

час : Y → г ( Икс )

можно записать как

час знак равно грамм ( т ) ∘ ж _я

для некоторого i в I и некоторого морфизма

т : Икс _я → Икс ∈ C .

Аналогичное утверждение характеризует функторы с правым сопряженным.

Важным частным случаем являются локально представимые категории . Если $F:C\to D$ является функтором между локально представимыми категориями, тогда

• F имеет правый сопряженный тогда и только тогда, когда F сохраняет малые копределы
• F имеет левый сопряженный тогда и только тогда, когда F сохраняет малые пределы и является доступным функтором.

Уникальность

Если функтор F : D → C имеет два правых сопряженных G и G ′, то G и G ′ естественно изоморфны . То же самое справедливо и для левых сопряженных.

И наоборот, если F сопряжена слева с G и G естественно изоморфна G , то F также сопряжена слева с G . В более общем смысле, если 〈 F , G , ε, η〉 является присоединением (со единицей-единицей (ε,η)) и

σ : F → F ′

τ : G → G ′

являются естественными изоморфизмами, то 〈 F ′, G ′, ε′, η′〉 является присоединением, где

${\begin{aligned}\eta '&=(\tau \ast \sigma )\circ \eta \\\varepsilon '&=\varepsilon \circ (\sigma ^{-1}\ast \tau ^{-1}).\end{aligned}}$

Здесь $\circ$ обозначает вертикальную композицию естественных преобразований, а $\ast$ обозначает горизонтальную композицию.

Состав

Присоединения могут составляться естественным образом. В частности, если 〈 F , G , ε, η〉 является присоединением между C и D и 〈 F ′, G ′, ε′, η′〉 является присоединением между D и E , то функтор

$F\circ F':E\rightarrow C$

остается присоединенным к

$G'\circ G:C\to E.$

существует соединение Точнее, между F F' и G' G с единицей и единицей, заданными соответственно композициями:

${\begin{aligned}&1_{\mathcal {E}}{\xrightarrow {\eta '}}G'F'{\xrightarrow {G'\eta F'}}G'GFF'\\&FF'G'G{\xrightarrow {F\varepsilon 'G}}FG{\xrightarrow {\varepsilon }}1_{\mathcal {C}}.\end{aligned}}$

Это новое присоединение называется композицией двух данных присоединения.

Поскольку существует также естественный способ определить тождественное присоединение между категорией C и самой собой, можно затем сформировать категорию, все объекты которой являются малыми категориями , а морфизмы которой являются присоединениями.

Ограничить сохранение

Важнейшим свойством сопряженных является их непрерывность: каждый функтор, имеющий сопряженный слева (и, следовательно, являющийся сопряженным справа), непрерывен (т.е. коммутирует с пределами в теоретическом смысле категорий); каждый функтор, который имеет правый сопряженный (и, следовательно, является левым сопряженным), конепрерывен (т. е. коммутирует с копределами ).

Поскольку многие распространенные конструкции в математике являются пределами или копределами, это дает богатую информацию. Например:

• применение правосопряженного функтора к произведению объектов дает произведение изображений;
• применение левого сопряженного функтора к копроизведению объектов дает копроизведение изображений;
• каждый правосопряженный функтор между двумя абелевыми категориями точен слева ;
• каждый сопряженный слева функтор между двумя абелевыми категориями точен справа .

Аддитивность

Если C и D — преаддитивные категории и F : D → C — аддитивный функтор с правым сопряженным G : C → D , то G также является аддитивным функтором и биекции гомомножества

$\Phi _{Y,X}:\mathrm {hom} _{\mathcal {C}}(FY,X)\cong \mathrm {hom} _{\mathcal {D}}(Y,GX)$

фактически являются изоморфизмами абелевых групп. Двойственным образом, если G аддитивен с левым сопряженным F , то F также аддитивен.

Более того, если и C , и D являются аддитивными категориями (т.е. предаддитивными категориями со всеми конечными бипроизведениями ), то любая пара сопряженных функторов между ними автоматически аддитивна.

Отношения

Универсальные конструкции

Как говорилось ранее, соединение категорий C и D порождает семейство универсальных морфизмов , по одному для каждого объекта в C и по одному для каждого объекта D. в Обратно, если существует универсальный морфизм функтора G : C → D из каждого объекта D , то G имеет левый сопряженный.

Однако универсальные конструкции более общие, чем сопряженные функторы: универсальная конструкция подобна задаче оптимизации; она порождает сопряженную пару тогда и только тогда, когда эта проблема имеет решение для каждого объекта из D (т. е. для каждого объекта из C ).

Эквиваленты категорий

Если функтор F : D → C является половиной эквивалентности категорий , то он является левым сопряженным в присоединенной эквивалентности категорий, т.е. присоединением, единица и единица которого являются изоморфизмами.

Каждое присоединение 〈 F , G , ε, η〉 расширяет эквивалентность определенных подкатегорий. Определим C ₁ как полную подкатегорию C , состоящую из тех объектов X из C , для которых ε _X является изоморфизмом, и определим D ₁ как полную подкатегорию D, состоящую из тех объектов Y из D , для которых η _Y является изоморфизмом. Тогда F и G могут быть ограничены до D ₁ и C ₁ и давать обратные эквивалентности этих подкатегорий.

В некотором смысле сопряженные являются «обобщенными» обратными. Обратите внимание, однако, что правый инверсный к F (т.е. функтор G такой, что FG естественно изоморфен 1 _D ) не обязательно должен быть правым (или левым) сопряженным к F . Сопряженные обобщают двусторонние обратные.

Монады

Каждое присоединение 〈 F , G , ε, η〉 порождает ассоциированную монаду 〈 T , η, µ〉 в категории D . Функтор

$T:{\mathcal {D}}\to {\mathcal {D}}$

определяется как T = GF . Единица монады

$\eta :1_{\mathcal {D}}\to T$

есть всего лишь единица η присоединения и преобразования умножения

$\mu :T^{2}\to T\,$

задается выражением µ знак равно грамм ε F . Двойственным образом тройка 〈 FG , ε, F η G 〉 определяет комонаду в C .

Каждая монада возникает из некоторого присоединения — фактически, обычно из многих присоединений — указанным выше способом. Две конструкции, называемые категорией алгебр Эйленберга–Мура и категорией Клейсли, представляют собой два экстремальных решения проблемы построения присоединения, порождающего данную монаду.

Ссылки

• Адамек, Иржи; Херрлих, Хорст; Стрекер, Джордж Э. (1990). Абстрактные и конкретные категории. Кошачья радость (PDF) . Джон Уайли и сыновья. ISBN  0-471-60922-6 . Збл   0695.18001 .
• Мак Лейн, Сондерс (1998). Категории для работающего математика . Тексты для аспирантов по математике . Том. 5 (2-е изд.). Спрингер-Верлаг. ISBN  0-387-98403-8 . Збл   0906.18001 .

Внешние ссылки

• Плейлист «Дополнения» на YouTube — семь коротких лекций о дополнениях от Евгении Ченг из The Catsters.
• WildCats — это пакет теории категорий для Mathematica . Манипулирование и визуализация объектов, морфизмов , категорий, функторов , естественных преобразований , универсальных свойств .