Одно- и двусторонние тесты

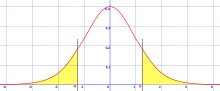
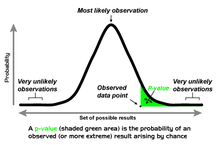
Двусторонний **тест,** применяемый к нормальному распределению .

При тестировании статистической значимости односторонний тест и двусторонний тест являются альтернативными способами вычисления статистической значимости параметра, выведенного из набора данных, с точки зрения статистики теста . Двусторонний тест подходит, если оценочное значение больше или меньше определенного диапазона значений, например, может ли испытуемый набрать балл выше или ниже определенного диапазона баллов. Этот метод используется для проверки нулевой гипотезы , и если оценочное значение существует в критических областях, альтернативная гипотеза принимается вместо нулевой гипотезы. Односторонний тест подходит, если расчетное значение может отклоняться от эталонного значения только в одном направлении, влево или вправо, но не в обоих направлениях. Примером может служить ситуация, когда машина производит более одного процента дефектной продукции. В этой ситуации, если оценочное значение существует в одной из односторонних критических областей, в зависимости от направления интереса (больше или меньше), альтернативная гипотеза принимается вместо нулевой гипотезы. Альтернативные названия: односторонние и двусторонние тесты; терминология «хвост» используется потому, что крайние части распределений, где наблюдения приводят к отклонению нулевой гипотезы, малы и часто «склоняются» к нулю, как в нормальном распределении , окрашенном в желтый цвет, или «колокольчатой кривой», изображено справа и окрашено в зеленый цвет.

Приложения

Односторонние тесты используются для асимметричных распределений с одним хвостом, таких как распределение хи-квадрат , которое часто используется при измерении согласия , или для одной стороны распределения, имеющего два хвоста, например нормального. распределение , которое часто используется при оценке местоположения; это соответствует указанию направления. Двусторонние тесты применимы только при наличии двух хвостов, например, в нормальном распределении, и соответствуют рассмотрению значимого любого направления. ^[1]^[2]

В подходе Рональда Фишера нулевая гипотеза H ₀ будет отвергнута, когда p -значение тестовой статистики является достаточно экстремальным (по сравнению с выборочным распределением тестовой статистики ) и, таким образом, считается маловероятным как результат случайности. Обычно это делается путем сравнения полученного значения p с заданным уровнем значимости, обозначаемым $\alpha$ , при вычислении статистической значимости параметра . В одностороннем тесте «крайний» определяется заранее как означающий «достаточно маленький» или «достаточно большой» — значения в другом направлении считаются незначимыми. Можно сообщить, что вероятность левого или правого хвоста представляет собой одностороннее значение p, которое в конечном итоге соответствует направлению, в котором статистика теста отклоняется от H _0.^[3] В двустороннем тесте «крайний» означает «достаточно малый или достаточно большой», и значения в любом направлении считаются значимыми. ^[4] Для данной тестовой статистики существует один двусторонний тест и два односторонних теста, по одному для каждого направления. При условии уровня значимости $\alpha$ , критические области будут существовать на двух хвостовых концах распределения с площадью $\alpha /2$ каждый для двустороннего теста. Альтернативно, критическая область могла бы существовать только на одном хвостовом конце с площадью $\alpha$ для одностороннего теста. Для данного уровня значимости в двустороннем тесте для статистики теста соответствующие односторонние тесты для той же статистики теста будут считаться либо в два раза более значимыми (половина значения p ), если данные находятся в направлении, указанном тесте или вообще незначимо ( значение p выше $\alpha$ ), если данные находятся в направлении, противоположном критической области, указанной в тесте.

Например, если подбросить монету , проверка того, смещена ли она в сторону орла, является односторонним тестом, и получение данных о «всех орлах» будет рассматриваться как очень значимое, в то время как получение данных о «всех решках» будет незначимым при все ( р = 1). Напротив, проверка того, смещена ли она в том или ином направлении, является двусторонним тестом, и оба варианта «все орлы» или «все решки» будут рассматриваться как весьма значимые данные. При медицинском тестировании обычно интересуются, приводит ли лечение к результатам, которые лучше , чем случайность, что предполагает односторонний тест; результат худший также интересен для научной области, поэтому вместо этого следует использовать двусторонний тест, который соответствует проверке того, приводит ли лечение к результатам, отличным от случайных, лучше или хуже. ^[5] В эксперименте с архетипической женщиной, дегустирующей чай , Фишер проверял, смогла ли рассматриваемая женщина лучше , чем случайно, различать два типа приготовления чая, а не отличались ли ее способности от случайности, и поэтому он использовал односторонний тест.

Пример подбрасывания монеты

При подбрасывании монеты нулевая гипотеза представляет собой последовательность испытаний Бернулли с вероятностью 0,5, дающую случайную величину X, которая равна 1 для орла и 0 для решки, а общая тестовая статистика представляет собой выборочное среднее (количества орлов). ${\bar {X}}.$ При проверке того, смещена ли монета в сторону орла, будет использоваться односторонний тест – значимым будет только большое количество орлов. В этом случае набор данных из пяти голов (HHHHH) со средним значением выборки, равным 1, имеет $1/32=0.03125\approx 0.03$ вероятность появления (5 последовательных бросков с 2 исходами - ((1/2)^5 =1/32). Это имело бы $p\approx 0.03$ и был бы значимым (отклоняя нулевую гипотезу), если бы тест был проанализирован на уровне значимости $\alpha =0.05$ (уровень значимости, соответствующий границе отсечения). Однако при проверке того, смещена ли монета в сторону орла или решки, будет использоваться двусторонний тест, а набор данных из пяти орлов (выборочное среднее 1) является таким же экстремальным, как и набор данных из пяти решек (выборочное среднее 0). ). В результате значение p будет равно $2/32=0.0625\approx 0.06$ и это не было бы существенным (не отвергая нулевую гипотезу), если бы тест анализировался на уровне значимости $\alpha =0.05$ .

История

Значение p было введено Карлом Пирсоном. ^[6] в тесте хи-квадрат Пирсона , где он определил P (исходное обозначение) как вероятность того, что статистика будет на заданном уровне или выше него. Это одностороннее определение, а распределение хи-квадрат асимметрично, принимает только положительные или нулевые значения и имеет только один хвост, верхний. Он измеряет степень соответствия данных теоретическому распределению, при этом ноль соответствует точному согласию с теоретическим распределением; Таким образом, значение p измеряет, насколько вероятно, что соответствие будет таким плохим или еще хуже.

Различие между односторонним и двусторонним тестом было популяризировано Рональдом Фишером во влиятельной книге «Статистические методы для научных работников» . ^[7] где он применил это, в частности, к нормальному распределению , которое представляет собой симметричное распределение с двумя равными хвостами. Нормальное распределение является общепринятой мерой местоположения, а не степени согласия, и имеет два хвоста, соответствующие оценке местоположения выше или ниже теоретического местоположения (например, выборочное среднее по сравнению с теоретическим средним). В случае симметричного распределения, такого как нормальное распределение, одностороннее значение p составляет ровно половину двустороннего значения p : ^[7]

Некоторую путаницу иногда вносит тот факт, что в некоторых случаях мы хотим знать вероятность того, что отклонение, заведомо положительное, превысит наблюдаемое значение, тогда как в других случаях требуемая вероятность состоит в том, что отклонение, которое одинаково часто бывает положительным. и отрицательный, должен превышать наблюдаемое значение; последняя вероятность всегда вдвое меньше первой.
— Рональд Фишер , Статистические методы для научных работников

Фишер подчеркнул важность измерения «хвоста» – наблюдаемого значения статистики теста, причем более экстремального, – а не просто вероятности конкретного результата как такового. В своей книге «План экспериментов» (1935) ^[8] Он объясняет это тем, что конкретный набор данных может быть маловероятным (в нулевой гипотезе), но более вероятны более экстремальные результаты, поэтому в этом свете конкретные, но не крайне маловероятные данные не следует считать значимыми.

Специальные тесты

Если статистика теста соответствует Стьюдента t -распределению в нулевой гипотезе – что часто встречается, когда базовая переменная следует нормальному распределению с неизвестным масштабным коэффициентом, то тест называется односторонним или двусторонним t -критерием . Если тест выполняется с использованием фактического среднего значения генеральной совокупности и дисперсии, а не оценки выборки, его можно назвать односторонним или двусторонним Z -тестом .

Статистические таблицы для t и Z предоставляют критические значения как для одно-, так и для двусторонних тестов. То есть они предоставляют критические значения, которые отсекают всю область на одном или другом конце выборочного распределения, а также критические значения, которые отсекают регионы (половины размера) на обоих концах выборочного распределения.

См. также

Тест парной разницы , когда сравниваются два образца.

Ссылки

^ Мандри, Р.; Фишер, Дж. (1998). «Использование статистических программ для непараметрических тестов небольших выборок часто приводит к неправильным значениям P: примеры из поведения животных». Поведение животных . 56 (1): 256–259. дои : 10.1006/anbe.1998.0756 . ПМИД 9710485 . S2CID 40169869 .
^ Пиллемер, Д.Б. (1991). «Односторонние и двусторонние тесты гипотез в современных исследованиях в области образования». Исследователь образования . 20 (9): 13–17. дои : 10.3102/0013189X020009013 . S2CID 145478007 .
^ Современное введение в вероятность и статистику: понимание почему и как . Деккинг, Мишель (1946 г.р.). Лондон: Спрингер. 2005. С. 389–390 . ISBN 9781852338961 . OCLC 262680588 . {{cite book}}: CS1 maint: другие ( ссылка )
^ Джон Э. Фройнд , (1984) Современная элементарная статистика , шестое издание. Прентис Холл. ISBN 0-13-593525-3 (Раздел «Выводы о средних», глава «Тесты значимости», стр. 289.)
^ Дж. М. Бланд, Д. Г. Бланд (BMJ, 1994). Статистические примечания: одно- и двусторонние тесты значимости.
^ Пирсон, Карл (1900). «О том критерии, что данная система отклонений от вероятного в случае коррелированной системы переменных такова, что можно разумно предположить, что она возникла в результате случайной выборки» (PDF) . Философский журнал . Серия 5. 50 (302): 157–175. дои : 10.1080/14786440009463897 .
^ Перейти обратно: ^а ^б Фишер, Рональд (1925). Статистические методы для научных работников . Эдинбург: Оливер и Бойд. ISBN 0-05-002170-2 .
^ Фишер, Рональд А. (1971) [1935]. План экспериментов (9-е изд.). Макмиллан. ISBN 0-02-844690-9 .

[1] Мандри, Р.; Фишер, Дж. (1998). «Использование статистических программ для непараметрических тестов небольших выборок часто приводит к неправильным значениям P: примеры из поведения животных». Поведение животных . 56 (1): 256–259. дои : 10.1006/anbe.1998.0756 . ПМИД 9710485 . S2CID 40169869 .

[2] Пиллемер, Д.Б. (1991). «Односторонние и двусторонние тесты гипотез в современных исследованиях в области образования». Исследователь образования . 20 (9): 13–17. дои : 10.3102/0013189X020009013 . S2CID 145478007 .

[3] Современное введение в вероятность и статистику: понимание почему и как . Деккинг, Мишель (1946 г.р.). Лондон: Спрингер. 2005. С. 389–390 . ISBN 9781852338961 . OCLC 262680588 . {{cite book}}: CS1 maint: другие ( ссылка )

[4] Джон Э. Фройнд , (1984) Современная элементарная статистика , шестое издание. Прентис Холл. ISBN 0-13-593525-3 (Раздел «Выводы о средних», глава «Тесты значимости», стр. 289.)

[5] Дж. М. Бланд, Д. Г. Бланд (BMJ, 1994). Статистические примечания: одно- и двусторонние тесты значимости.

[6] Пирсон, Карл (1900). «О том критерии, что данная система отклонений от вероятного в случае коррелированной системы переменных такова, что можно разумно предположить, что она возникла в результате случайной выборки» (PDF) . Философский журнал . Серия 5. 50 (302): 157–175. дои : 10.1080/14786440009463897 .

[fisher-7] Перейти обратно: ^а ^б Фишер, Рональд (1925). Статистические методы для научных работников . Эдинбург: Оливер и Бойд. ISBN 0-05-002170-2 .

[8] Фишер, Рональд А. (1971) [1935]. План экспериментов (9-е изд.). Макмиллан. ISBN 0-02-844690-9 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]