Статистическая проверка гипотез

Проверка статистической гипотезы — это метод статистического вывода, используемый для определения того, достаточно ли данные подтверждают конкретную гипотезу. Проверка статистической гипотезы обычно включает в себя расчет тестовой статистики . Затем принимается решение либо путем сравнения тестовой статистики с критическим значением , либо, что то же самое, путем оценки p значения , вычисленного на основе тестовой статистики. около 100 специализированных статистических тестов . Было определено ^[1]^[2]

История [ править ]

Хотя проверка гипотез была популяризирована в начале 20-го века, ранние формы использовались в 1700-х годах. Первое использование приписывается Джону Арбутноту (1710 г.). ^[3]за ним последовал Пьер-Симон Лаплас (1770-е годы) при анализе соотношения полов у человека при рождении; см. § Соотношение полов у человека .

Выбор нулевой гипотезы [ править ]

Пол Мил утверждал, что эпистемологическая важность выбора нулевой гипотезы осталась в значительной степени непризнанной. Когда нулевая гипотеза предсказывается теорией, более точный эксперимент станет более серьезной проверкой лежащей в ее основе теории. Когда нулевая гипотеза по умолчанию равна «нет разницы» или «нет эффекта», более точный эксперимент является менее серьезной проверкой теории, которая мотивировала проведение эксперимента. ^[4] Поэтому изучение истоков последней практики может оказаться полезным:

1778: Пьер Лаплас сравнивает рождаемость мальчиков и девочек в нескольких европейских городах. Он утверждает: «естественно заключить, что эти возможности находятся примерно в одном и том же соотношении». Таким образом, нулевая гипотеза в данном случае о том, что рождаемость мальчиков и девочек должна быть равна, принимается «общепринятым мнением». ^[5]

1900: Карл Пирсон разрабатывает критерий хи-квадрат, чтобы определить, «будет ли данная форма частотной кривой эффективно описывать выборки, взятые из данной совокупности». Таким образом, нулевая гипотеза состоит в том, что популяция описывается некоторым распределением, предсказанным теорией. В качестве примера он использует числа пять и шестерки в данных о бросках игральных костей Уэлдона . ^[6]

1904: Карл Пирсон разрабатывает концепцию « непредвиденных обстоятельств », чтобы определить, независимы ли результаты от данного категориального фактора. Здесь нулевая гипотеза по умолчанию заключается в том, что две вещи не связаны друг с другом (например, образование рубцов и уровень смертности от оспы). ^[7] Нулевая гипотеза в этом случае больше не предсказывается теорией или общепринятым мнением, а вместо этого представляет собой принцип безразличия , который побудил Фишера и других отказаться от использования «обратных вероятностей». ^[8]

Современное происхождение споры ранние и

Современное тестирование значимости во многом является продуктом Карла Пирсона ( p -значение , критерий хи-квадрат Пирсона ), Уильяма Сили Госсета ( t-распределение Стьюдента ) и Рональда Фишера (« нулевая гипотеза », дисперсионный анализ , « критерий значимости »). , а проверку гипотез разработали Ежи Нейман и Эгон Пирсон (сын Карла). Рональд Фишер начал свою карьеру в статистике как байесианец (Zabell 1992), но вскоре Фишер разочаровался в связанной с этим субъективности (а именно, в использовании принципа безразличия при определении априорных вероятностей) и стремился предложить более «объективный» подход к индуктивным вычислениям. вывод. ^[9]

Фишер подчеркнул строгий план эксперимента и методы извлечения результата из нескольких выборок, предполагая распределение Гаусса . Нейман (который сотрудничал с Пирсоном-младшим) подчеркивал математическую строгость и методы, позволяющие получить больше результатов из множества выборок и более широкого диапазона распределений. Современная проверка гипотез представляет собой противоречивый гибрид формулировок Фишера и Неймана/Пирсона, методов и терминологии, разработанных в начале 20 века.

Фишер популяризировал «тест значимости». Ему потребовалась нулевая гипотеза (соответствующая частотному распределению населения) и выборка. Его (теперь знакомые) расчеты определяли, следует ли отвергать нулевую гипотезу или нет. При проверке значимости не использовалась альтернативная гипотеза, поэтому не существовало понятия ошибки II рода (ложноотрицательный результат).

Значение p было разработано как неформальный, но объективный индекс, призванный помочь исследователю определить (на основе других знаний), следует ли модифицировать будущие эксперименты или укрепить веру в нулевую гипотезу. ^[10] -значению Фишера Проверка гипотез (и ошибки типа I/II) была разработана Нейманом и Пирсоном как более объективная альтернатива p , также предназначенная для определения поведения исследователя, но не требующая каких-либо индуктивных выводов . от исследователя ^[11]^[12]

Нейман и Пирсон рассматривали другую проблему, чем Фишер (которую они назвали «проверкой гипотез»). Первоначально они рассматривали две простые гипотезы (обе с частотными распределениями). Они рассчитали две вероятности и обычно выбирали гипотезу, связанную с более высокой вероятностью (гипотеза, которая с большей вероятностью создала выборку). Их метод всегда выбирал гипотезу. Это также позволило рассчитать вероятности ошибок обоих типов.

Фишер и Нейман/Пирсон сильно поссорились. Нейман/Пирсон считали свою формулировку улучшенным обобщением проверки значимости (определяющая статья ^[11]был абстрактным ; Математики десятилетиями обобщали и уточняли теорию. ^[13]). Фишер считал, что она неприменима к научным исследованиям, поскольку часто в ходе эксперимента обнаруживается, что первоначальные предположения о нулевой гипотезе сомнительны из-за неожиданных источников ошибок. Он считал, что использование жестких решений «отклонить/принять», основанных на моделях, сформулированных до сбора данных, несовместимо с этим распространенным сценарием, с которым сталкиваются ученые, и попытки применить этот метод к научным исследованиям приведут к массовой путанице. ^[14]

Спор между Фишером и Нейманом-Пирсоном велся на философских основаниях, охарактеризованный философом как спор о надлежащей роли моделей в статистическом выводе. ^[15]

Вмешались события: Нейман принял должность в Калифорнийском университете в Беркли в 1938 году, разорвав партнерство с Пирсоном и разделив участников спора (которые занимали одно и то же здание). Вторая мировая война дала перерыв в дебатах. Спор между Фишером и Нейманом завершился (неразрешенный спустя 27 лет) со смертью Фишера в 1962 году. Нейман написал уважаемую панегирик. ^[16] В некоторых из более поздних публикаций Неймана сообщалось о p -значениях и уровнях значимости. ^[17]

Современная версия проверки гипотез представляет собой гибрид двух подходов, возникший в результате путаницы авторов статистических учебников (как и предсказывал Фишер) начиная с 1940-х годов. ^[18](но , например, обнаружение сигнала по-прежнему использует формулировку Неймана/Пирсона). Большие концептуальные различия и многие предостережения помимо упомянутых выше были проигнорированы. Нейман и Пирсон предоставили более строгую терминологию, более строгую математику и более последовательную философию, но предмет, преподаваемый сегодня во вводной статистике, имеет больше сходства с методом Фишера, чем с их методом. ^[19]

Где-то около 1940 г. ^[18] авторы статистических учебников начали комбинировать два подхода, используя значение p вместо тестовой статистики (или данных) для проверки «уровня значимости» Неймана-Пирсона.

Сравнение между Фишерианским и частотным (Нейман-Пирсон)
#	Проверка нулевой гипотезы Фишера	Теория принятия решений Неймана – Пирсона
1	Установите статистическую нулевую гипотезу. Нулевая гипотеза не обязательно должна быть нулевой гипотезой (т. е. нулевой разницей).	Создайте две статистические гипотезы, H1 и H2, и примите решение об α, β и размере выборки перед экспериментом, исходя из субъективных соображений затрат и выгод. Они определяют область отклонения для каждой гипотезы.
2	Укажите точный уровень значимости (например, p = 0,051 или p = 0,049). Не ссылайтесь на «принятие» или «отвержение» гипотез. Если результат «незначителен», не делайте выводов и не принимайте решений, а отложите суждение до тех пор, пока не появятся дополнительные данные.	Если данные попадают в область отклонения H1, примите H2; в противном случае примите H1. Принятие гипотезы не означает, что вы в нее верите, а лишь то, что вы действуете так, как если бы она была верной.
3	Используйте эту процедуру только в том случае, если о рассматриваемой проблеме мало что известно, и только для того, чтобы сделать предварительные выводы в контексте попытки понять экспериментальную ситуацию.	Полезность процедуры ограничена, среди прочего, ситуациями, когда у вас есть расхождение гипотез (например, либо µ1 = 8, либо µ2 = 10 верно) и когда вы можете сделать значимый компромисс между затратами и выгодами для выбора альфа и бета.

Философия [ править ]

Проверка гипотез и философия пересекаются. Инференциальная статистика , включающая проверку гипотез, представляет собой прикладную вероятность. И вероятность, и ее применение переплетаются с философией. Философ Дэвид Юм писал: «Все знания вырождаются в вероятность». Конкурирующие практические определения вероятности отражают философские различия. Наиболее распространенным применением проверки гипотез является научная интерпретация экспериментальных данных, которая, естественно, изучается философией науки .

Фишер и Нейман выступили против субъективности вероятности. Их взгляды способствовали объективным определениям. Суть их исторических разногласий была философской.

Многие философские критические замечания по проверке гипотез обсуждаются статистиками в других контекстах, в частности, корреляция не подразумевает причинно-следственную связь и планирование экспериментов . Проверка гипотез представляет постоянный интерес для философов. ^[15]^[20]

Образование [ править ]

Статистика все чаще преподается в школах, причем проверка гипотез является одним из преподаваемых элементов. ^[21]^[22]Многие выводы, публикуемые в популярной прессе (от опросов политического мнения до медицинских исследований), основаны на статистике. Некоторые авторы заявляют, что статистический анализ такого рода позволяет ясно думать о проблемах, связанных с массовыми данными, а также эффективно сообщать о тенденциях и выводах из этих данных, но предупреждают, что авторы, представляющие широкую публику, должны иметь четкое понимание этой области. для того, чтобы правильно использовать термины и понятия. ^[23]^[24]На вводном курсе статистики в колледже большое внимание уделяется проверке гипотез – возможно, это половина курса. Такие области, как литература и богословие, теперь включают результаты, основанные на статистическом анализе (см. «Анализатор Библии» ). На вводном курсе статистики проверка гипотез рассматривается как процесс кулинарной книги. Проверка гипотез также преподается на уровне аспирантуры. Статистики учатся создавать хорошие статистические тестовые процедуры (такие как z Стьюдента , t , F и хи-квадрат). Проверка статистических гипотез считается зрелой областью статистики. ^[25] но ограниченное количество разработок продолжается.

В одном академическом исследовании говорится, что метод обучения вводной статистике, основанный на кулинарных книгах, не оставляет времени для истории, философии или полемики. Проверка гипотез преподавалась как общепринятый единый метод. Опросы показали, что выпускники этого класса были полны философских заблуждений (по всем аспектам статистических выводов), которые сохранялись среди преподавателей. ^[26] Хотя проблема была решена более десяти лет назад, ^[27] и призывы к реформе образования продолжаются, ^[28] Студенты по-прежнему заканчивают курсы по статистике, придерживаясь фундаментальных заблуждений о проверке гипотез. ^[29] Идеи по улучшению преподавания проверки гипотез включают в себя поощрение студентов к поиску статистических ошибок в опубликованных статьях, преподавание истории статистики и подчеркивание противоречий в обычно сухом предмете. ^[30]

частотной гипотезы на практике Выполнение проверки

Типичные этапы практической проверки частотной гипотезы:

Определите гипотезу (утверждение, которое можно проверить с использованием данных).
Выберите соответствующий статистический тест со связанной тестовой статистикой T .
Выведите распределение тестовой статистики при нулевой гипотезе из допущений. В стандартных случаях это будет хорошо известный результат. Например, статистика теста может следовать t-распределению Стьюдента с известными степенями свободы или нормальному распределению с известными средним значением и дисперсией.
Выберите уровень значимости ( α ), максимально допустимый уровень ложных срабатываний . Общие значения — 5% и 1%.
Вычислите на основе наблюдений наблюдаемое значение t _obs тестовой статистики T .
Решите либо отвергнуть нулевую гипотезу в пользу альтернативы, либо не отвергать ее. Правило принятия решения Неймана -Пирсона состоит в том, чтобы отвергнуть нулевую гипотезу H ₀ , если наблюдаемое значение t _obs находится в критической области, и не отвергать нулевую гипотезу в противном случае. ^[31]

Практический пример [ править ]

Разница в двух процессах применительно к примеру с радиоактивным чемоданом (ниже):

«Показания счетчика Гейгера — 10. Предел — 9. Проверьте чемодан».
«Показания счетчика Гейгера высокие; 97% безопасных чемоданов имеют более низкие показания. Предел — 95%. Проверьте чемодан».

Первый отчет является адекватным, второй дает более подробное объяснение данных и причины проверки чемодана.

Неопровержение нулевой гипотезы не означает, что нулевая гипотеза «принята» как таковая (хотя Нейман и Пирсон использовали это слово в своих оригинальных работах; см. «Интерпретация» раздел ).

Описанные здесь процессы вполне подходят для вычислений. Они серьезно пренебрегают соображениями планирования экспериментов . ^[32]^[33]

Особенно важно оценить соответствующие размеры выборки перед проведением эксперимента.

Фразу «тест значимости» придумал статистик Рональд Фишер . ^[34]

Интерпретация [ править ]

Когда нулевая гипотеза верна и статистические предположения выполняются, вероятность того, что значение p будет меньше или равно уровню значимости $\alpha$ самое большее $\alpha$ . Это гарантирует, что проверка гипотезы сохранит заданный уровень ложных срабатываний (при условии, что статистические предположения выполняются). ^[35]

Значение p — это вероятность того, что при нулевой гипотезе будет получена тестовая статистика, которая, по крайней мере, столь же экстремальна, как и полученная. При уровне значимости 0,05 можно ожидать, что честная монета (ошибочно) отвергнет нулевую гипотезу (о том, что она честна) в среднем в 1 из 20 тестов. Значение p не обеспечивает вероятность того, что нулевая гипотеза или ее противоположность верны (частый источник путаницы). ^[36]

Если значение p меньше выбранного порога значимости (что эквивалентно, если наблюдаемая статистика теста находится в критической области), то мы говорим, что нулевая гипотеза отклонена на выбранном уровне значимости. Если p значение не меньше выбранного порога значимости (т. е. если наблюдаемая статистика теста находится за пределами критической области), то нулевая гипотеза не отклоняется на выбранном уровне значимости.

В примере с «дамой, дегустирующей чай» (ниже) Фишер потребовал, чтобы дама правильно классифицировала все чашки чая, чтобы оправдать вывод о том, что результат вряд ли является случайным. Его тест показал, что если женщина фактически угадывала наугад (нулевая гипотеза), вероятность получения наблюдаемого результата (идеально заказанного чая) составляла 1,4%.

Использование и важность [ править ]

Статистика полезна при анализе большинства коллекций данных. Это в равной степени справедливо и для проверки гипотез, которая может обосновать выводы, даже если научной теории не существует. В примере с дамой, дегустирующей чай, было «очевидно», что не существует никакой разницы между (молоко, налитое в чай) и (чай, налитое в молоко). Данные противоречили «очевидному».

Реальные применения проверки гипотез включают в себя: ^[37]

Тестирование: мужчины страдают от кошмаров чаще, чем женщины
Установление авторства документов
Оценка влияния полнолуния на поведение
Определение расстояния, на котором летучая мышь может обнаружить насекомое по эху.
Решение о том, приводит ли больничное ковровое покрытие к большему количеству инфекций
Выбор лучших средств, чтобы бросить курить
Проверяем, отражают ли наклейки на бампере поведение владельца автомобиля
Проверка утверждений почерковедческих аналитиков

Статистическая проверка гипотез играет важную роль во всей статистике и в статистических выводах . Например, Леманн (1992) в обзоре фундаментальной работы Неймана и Пирсона (1933) говорит: «Тем не менее, несмотря на свои недостатки, новая парадигма, сформулированная в статье 1933 года, и многие разработки, выполненные в ее рамках, продолжают играют центральную роль как в теории, так и в практике статистики, и можно ожидать, что это произойдет в обозримом будущем».

Тестирование значимости было излюбленным статистическим инструментом в некоторых экспериментальных социальных науках (более 90% статей в Журнале прикладной психологии в начале 1990-х годов). ^[38]Другие области отдают предпочтение оценке параметров (например, размера эффекта ). Проверка значимости используется вместо традиционного сравнения прогнозируемого значения и экспериментального результата, лежащего в основе научного метода . Когда теория способна предсказать только знак взаимосвязи, направленную (одностороннюю) проверку гипотезы можно сконфигурировать так, чтобы только статистически значимый результат поддерживал теорию. Эта форма оценки теории является наиболее подвергаемым критике применением проверки гипотез.

Предостережения [ править ]

«Если бы правительство требовало, чтобы статистические процедуры имели предупреждающие надписи, подобные тем, что есть на лекарствах, большинство методов вывода действительно имели бы длинные надписи». ^[39] Это предостережение относится к проверке гипотез и альтернативам им.

Успешная проверка гипотезы связана с вероятностью и частотой ошибок I рода. Вывод может быть неверным.

Выводы теста столь же надежны, как и образец, на котором они основаны. Дизайн эксперимента имеет решающее значение. Был обнаружен ряд неожиданных эффектов, в том числе:

Умный эффект Ганса . Лошадь, казалось, была способна выполнять простые арифметические действия.
Эффект Хоторна . Промышленные рабочие были более продуктивны при лучшем освещении и наиболее продуктивны при худшем.
плацебо Эффект . Таблетки, не содержащие активных ингредиентов, оказались чрезвычайно эффективными.

Статистический анализ вводящих в заблуждение данных приводит к ошибочным выводам. Вопрос качества данных может быть более тонким. Например, в прогнозировании не существует единого мнения относительно меры точности прогноза. В отсутствие консенсусного измерения ни одно решение, основанное на измерениях, не будет бесспорным.

Предвзятость публикации: статистически незначимые результаты могут быть опубликованы с меньшей вероятностью, что может привести к искажению литературы.

Множественное тестирование: когда несколько тестов истинной нулевой гипотезы проводятся одновременно без корректировки, общая вероятность ошибки типа I выше номинального альфа-уровня. ^[40]

Те, кто принимает критические решения на основе результатов проверки гипотез, благоразумно обращают внимание на детали, а не только на выводы. В физических науках большинство результатов полностью принимаются только в том случае, если они подтверждены независимо. Общий совет относительно статистики таков: «Цифры никогда не лгут, а лжецы верят» (анонимно).

Определение терминов [ править ]

Следующие определения в основном основаны на изложении книги Лемана и Романо: ^[35]

Статистическая гипотеза : утверждение о параметрах, описывающих популяцию (а не выборку ).
Статистика теста: значение, рассчитанное на основе выборки без каких-либо неизвестных параметров, часто для обобщения выборки в целях сравнения.
Простая гипотеза : любая гипотеза, которая полностью определяет распределение населения.
Составная гипотеза: любая гипотеза, которая не полностью определяет распределение населения.
Нулевая гипотеза (H ₀ )
Положительные данные: данные, которые позволяют исследователю отвергнуть нулевую гипотезу.
Альтернативная гипотеза (H ₁ )

Критические значения s статистического теста — это границы приемлемой области теста. ^[41]Область приемлемости — это набор значений тестовой статистики, для которых нулевая гипотеза не отвергается. В зависимости от формы приемной области может быть одно или несколько критических значений.
- Область отторжения / Критическая область : набор значений тестовой статистики, для которых нулевая гипотеза отклоняется.
Мощность теста (1 - β )
Размер отклонения теста : для простых гипотез это вероятность неправильного нулевой гипотезы. Уровень ложноположительных результатов . Для составных гипотез это верхняя граница вероятности отклонения нулевой гипотезы во всех случаях, охватываемых нулевой гипотезой. Дополнение ложноположительных результатов называется специфичностью в биостатистике . («Это специфический тест. Поскольку результат положительный, мы можем с уверенностью сказать, что у пациента есть это заболевание».) См. чувствительность и специфичность , а также ошибки типа I и типа II для получения исчерпывающих определений.
Уровень значимости теста ( α)
р -значение
Тест статистической значимости : предшественник теста статистической гипотезы (см. раздел «Происхождение»). Экспериментальный результат считался статистически значимым, если выборка в достаточной степени не соответствовала (нулевой) гипотезе. По-разному это считалось здравым смыслом, прагматической эвристикой для выявления значимых экспериментальных результатов, соглашением, устанавливающим порог статистических данных или методом получения выводов на основе данных. Проверка статистической гипотезы добавила концепции математическую строгость и философскую последовательность, сделав альтернативную гипотезу явной. Этот термин широко используется для обозначения современной версии, которая сейчас является частью проверки статистических гипотез.
Консервативный тест: тест является консервативным, если при его построении для данного номинального уровня значимости истинная вероятность неправильного отклонения нулевой гипотезы никогда не превышает номинальный уровень.
Точный тест

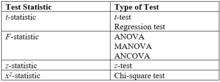
Проверка статистической гипотезы сравнивает статистику теста ( z или t для примеров) с пороговым значением. Статистика теста (формула приведена в таблице ниже) основана на оптимальности. Для фиксированного уровня частоты ошибок типа I использование этой статистики минимизирует частоту ошибок типа II (эквивалентно максимизации мощности). Следующие термины описывают тесты с точки зрения такой оптимальности:

Самый мощный тест: для данного размера или уровня значимости тест с наибольшей мощностью (вероятностью отклонения) для данного значения проверяемого параметра(ов), содержащегося в альтернативной гипотезе.
Равномерно самый мощный тест (UMP)

бутстрепа Непараметрическая проверка гипотез

на основе бутстрапа Методы повторной выборки можно использовать для проверки нулевой гипотезы. Бутстрап создает множество смоделированных выборок путем случайной повторной выборки (с заменой) исходных объединенных выборочных данных, предполагая, что нулевая гипотеза верна. Бутстрап очень универсален, поскольку он не имеет распределения и не опирается на ограничительные параметрические предположения, а скорее на эмпирические приближенные методы с асимптотическими гарантиями. Традиционные параметрические тесты гипотез более эффективны в вычислительном отношении, но делают более строгие структурные предположения. В ситуациях, когда вычисление вероятности тестовой статистики при нулевой гипотезе затруднено или невозможно (возможно, из-за неудобства или отсутствия знания основного распределения), бутстрап предлагает жизнеспособный метод статистического вывода. ^[42]^[43]^[44]^[45]

Примеры [ править ]

Соотношение полов человека [ править ]

Самое раннее использование проверки статистических гипотез обычно связано с вопросом о том, одинаково ли вероятны рождения мальчиков и девочек (нулевая гипотеза), который был рассмотрен в 1700-х годах Джоном Арбутнотом (1710). ^[46] а позже Пьер-Симон Лаплас (1770-е). ^[47]

Арбутнот изучил записи о рождении в Лондоне за каждый из 82 лет с 1629 по 1710 год и применил знаковый тест — простой непараметрический критерий . ^[48]^[49]^[50]Ежегодно количество мужчин, рожденных в Лондоне, превышало количество женщин. Учитывая, что большее количество рождений мальчиков и девочек одинаково вероятно, вероятность наблюдаемого исхода равна 0,5. ⁸², или примерно 1 из 4 836 000 000 000 000 000 000 000; говоря современным языком, это p -значение. Арбутнот пришел к выводу, что это слишком мало, чтобы быть результатом случайности, и вместо этого должно быть связано с божественным провидением: «Отсюда следует, что правит Искусство, а не Случай». Говоря современным языком, он отверг нулевую гипотезу о равной вероятности рождения мальчиков и девочек при p = 1/2. ⁸² уровень значимости.

Лаплас рассмотрел статистику почти полумиллиона рождений. Статистика показала преобладание мальчиков над девочками. ^[5]^[51] Путем расчета значения p он пришел к выводу , что превышение было реальным, но необъяснимым эффектом. ^[52]

Леди дегустирует чай [ править ]

В известном примере проверки гипотез, известном как « Леди, дегустирующая чай» , ^[53]Доктор Мюриэл Бристоль , коллега Фишера, утверждала, что может определить, чай или молоко было добавлено в чашку первым. Фишер предложил подарить ей восемь чашек, по четыре каждого сорта, в случайном порядке. Тогда можно было бы спросить, какова вероятность того, что она назовет правильное число, но это просто случайно. Нулевая гипотеза заключалась в том, что у Леди не было такой способности. Статистика теста представляла собой простой подсчет количества успешных попыток выбрать 4 чашки. Критическая область представляла собой единственный случай 4 успехов из 4 возможных, основанных на общепринятом критерии вероятности (< 5%). Паттерн из 4 успехов соответствует 1 из 70 возможных комбинаций (р≈ 1,4%). Фишер утверждал, что никакая альтернативная гипотеза (никогда) не требовалась. Дама правильно определила каждую чашку, ^[54] что можно было бы считать статистически значимым результатом.

Судебный процесс [ править ]

Процедура статистического тестирования сравнима с уголовным судом ; Подсудимый считается невиновным, пока его вина не доказана. Прокурор пытается доказать вину подсудимого. Только тогда, когда имеется достаточно доказательств для обвинения, обвиняемый признается виновным.

В начале процедуры есть две гипотезы. $H_{0}$ : «подсудимый не виновен», и $H_{1}$ : «Подсудимый виновен». Первый, $H_{0}$ , называется нулевой гипотезой . Второй, $H_{1}$ , называется альтернативной гипотезой . Это альтернативная гипотеза, которую мы надеемся поддержать.

Гипотеза о невиновности отвергается только тогда, когда ошибка очень маловероятна, поскольку нежелательно осуждать невиновного обвиняемого. Такая ошибка называется ошибкой первого рода (т. е. осуждением невиновного лица), и возникновение этой ошибки контролируется, чтобы быть редким. Вследствие такого асимметричного поведения чаще встречается ошибка второго рода (оправдание лица, совершившего преступление).

	H ₀ верно Действительно не виноват	H ₁ верно Действительно виновен
Не отвергайте нулевую гипотезу Оправдание	Верное решение	Неправильное решение Ошибка типа II
Отклонить нулевую гипотезу Убеждение	Неправильное решение Ошибка типа I	Верное решение

Уголовный процесс можно рассматривать как один или оба из двух процессов принятия решений: виновен против невиновности или доказательства против порога («вне разумного сомнения»). С одной точки зрения, обвиняемого судят; с другой точки зрения, оценивается деятельность обвинения (которое несет бремя доказывания). Проверка гипотезы может рассматриваться либо как оценка гипотезы, либо как оценка доказательств.

Философские бобы [ править ]

Следующий пример был приведен философом, описывающим научные методы за несколько поколений до того, как появилась проверка гипотез. формализована и популяризирована. ^[55]

Лишь немногие зерна из этой горстки белые.
Большинство зерен в этом мешке белые.
Следовательно: Вероятно, эти бобы были взяты из другого мешка.
Это гипотетический вывод.

Бобы в мешке — это население. Горстка — это образец. Нулевая гипотеза состоит в том, что выборка возникла из генеральной совокупности. Критерием отклонения нулевой гипотезы является «очевидная» разница во внешнем виде (неформальная разница в среднем). Интересный результат заключается в том, что при рассмотрении реальной популяции и реальной выборки получился воображаемый мешок. Философ рассматривал логику, а не вероятность. Чтобы быть настоящей статистической проверкой гипотезы, этот пример требует формальностей расчета вероятности и сравнения этой вероятности со стандартом.

Простое обобщение примера рассматривает смешанный мешок фасоли и горстку, содержащую либо очень мало, либо очень много белой фасоли. Обобщение учитывает обе крайности. Для получения формального ответа требуется больше расчетов и сравнений, но основная философия остается неизменной; Если состав горсти сильно отличается от состава мешка, то, вероятно, образец был взят из другого мешка. Исходный пример называется односторонним или односторонним тестом, а обобщение называется двусторонним или двусторонним тестом.

Это утверждение также основано на выводе о том, что выборка была случайной. Если бы кто-то рылся в мешке в поисках белой фасоли, это объяснило бы, почему в горстке было так много белой фасоли, а также объяснило бы, почему количество белой фасоли в мешке исчерпалось (хотя предполагается, что мешок, вероятно, намного больше ладони).

Карточная игра «Ясновидение» [ править ]

Человек (субъект) проверяется на ясновидение . Им 25 раз показывают обратную сторону случайно выбранной игральной карты и спрашивают, к какой из четырех мастей она принадлежит. Количество попаданий или правильных ответов X. называется

Пока мы пытаемся найти доказательства их ясновидения, на данный момент нулевая гипотеза состоит в том, что этот человек не является ясновидящим. ^[56] Альтернатива такова: человек (более или менее) ясновидящий.

Если нулевая гипотеза верна, единственное, что может сделать испытуемый, — это гадать. Для каждой карты вероятность (относительная частота) появления одной масти равна 1/4. Если альтернатива верна, испытуемый правильно предскажет масть с вероятностью больше 1/4. Вероятность правильного угадывания будем называть p . Итак, гипотезы таковы:

нулевая гипотеза ${\text{:}}\qquad H_{0}:p={\tfrac {1}{4}}$ (просто предполагаю)

и

Альтернативная гипотеза ${\text{:}}H_{1}:p>{\tfrac {1}{4}}$ (истинный ясновидящий).

Когда испытуемый правильно предскажет все 25 карт, мы будем считать его ясновидящим и отвергнем нулевую гипотезу. Таким образом, также с 24 или 23 попаданиями. С другой стороны, при наличии всего лишь 5 или 6 попаданий нет оснований считать их таковыми. А как насчет 12 или 17 попаданий? Каково критическое число попаданий c , при котором мы считаем субъекта ясновидящим? Как определить критическое значение c ? При выборе c =25 (т.е. мы принимаем ясновидение только тогда, когда все карты предсказаны правильно) мы более критичны, чем при c =10. В первом случае почти никто из испытуемых не будет признан ясновидящим, во втором случае определенное количество пройдет тест. На практике каждый решает, насколько критичным он будет. То есть каждый решает, как часто он допускает ошибку первого рода – ложное срабатывание или ошибку I рода. При c = 25 вероятность такой ошибки равна:

P({\text{reject }}H_{0}\mid H_{0}{\text{ is valid}})=P\left(X=25\mid p={\frac {1}{4}}\right)=\left({\frac {1}{4}}\right)^{25}\approx 10^{-15}

,

и, следовательно, очень мал. Вероятность ложного срабатывания — это вероятность случайного угадывания правильно все 25 раз.

Менее критичный вариант с c = 10 дает:

P({\text{reject }}H_{0}\mid H_{0}{\text{ is valid}})=P\left(X\geq 10\mid p={\frac {1}{4}}\right)=\sum _{k=10}^{25}P\left(X=k\mid p={\frac {1}{4}}\right)=\sum _{k=10}^{25}{\binom {25}{k}}\left(1-{\frac {1}{4}}\right)^{25-k}\left({\frac {1}{4}}\right)^{k}\approx 0.0713

.

Таким образом, c = 10 дает гораздо большую вероятность ложного срабатывания.

Перед фактическим проведением испытания максимально допустимая вероятность ошибки I рода ( α определяется ). Обычно выбираются значения в диапазоне от 1% до 5%. (Если максимально допустимая частота ошибок равна нулю, требуется бесконечное количество правильных предположений.) В зависимости от этой частоты ошибок типа 1 критическое значение c рассчитывается . Например, если мы выберем коэффициент ошибок 1%, c рассчитывается следующим образом:

P({\text{reject }}H_{0}\mid H_{0}{\text{ is valid}})=P\left(X\geq c\mid p={\frac {1}{4}}\right)\leq 0.01

.

Из всех чисел с, обладающих этим свойством, выбираем наименьшее, чтобы минимизировать вероятность ошибки II рода, ложноотрицательный результат . Для приведенного выше примера мы выбираем: $c=13$ .

Вариации и подклассы [ править ]

Статистическая проверка гипотез является ключевым методом как частотного вывода, так и байесовского вывода , хотя эти два типа вывода имеют заметные различия. Статистические проверки гипотез определяют процедуру, которая контролирует (исправляет) вероятность неправильного решения о том, что позиция по умолчанию ( нулевая гипотеза ) неверна. Процедура основана на том, насколько вероятно было бы появление набора наблюдений, если бы нулевая гипотеза была верной. Эта вероятность принятия неправильного решения не является вероятностью того, что нулевая гипотеза верна или верна какая-либо конкретная альтернативная гипотеза. Это контрастирует с другими возможными методами теории принятия решений , в которых нулевая и альтернативная гипотезы рассматриваются на более равной основе.

Один из наивных байесовских подходов к проверке гипотез состоит в том, чтобы основывать решения на апостериорной вероятности . ^[57]^[58]но это не удается при сравнении точечных и непрерывных гипотез. Другие подходы к принятию решений, такие как байесовская теория принятия решений , пытаются сбалансировать последствия неправильных решений по всем возможностям, а не концентрироваться на одной нулевой гипотезе. Ряд других подходов к принятию решения на основе данных доступен через теорию принятия решений и оптимальные решения , некоторые из которых обладают желаемыми свойствами. Однако проверка гипотез является доминирующим подходом к анализу данных во многих областях науки. Расширение теории проверки гипотез включает изучение силы тестов, т.е. вероятности правильного отклонения нулевой гипотезы при условии, что она ложна. Такие соображения можно использовать для определения размера выборки до сбора данных.

гипотезы Неймана Проверка Пирсона -

Пример проверки гипотезы Неймана-Пирсона (или проверки статистической значимости нулевой гипотезы) можно представить, изменив пример с радиоактивным чемоданом. Если «чемодан» на самом деле представляет собой экранированный контейнер для перевозки радиоактивного материала, то можно использовать тест для выбора одной из трех гипотез: радиоактивный источник отсутствует, присутствует один, присутствуют два (все). Испытание может потребоваться в целях безопасности, при этом действия необходимы в каждом случае. Лемма Неймана -Пирсона о проверке гипотез гласит, что хорошим критерием выбора гипотез является отношение их вероятностей ( отношение правдоподобия ). Простой метод решения — выбрать гипотезу с наибольшей вероятностью наблюдаемых чисел Гейгера. Типичный результат соответствует интуиции: небольшое количество подсчетов подразумевает отсутствие источника, большое количество подсчетов предполагает наличие двух источников, а промежуточные подсчеты подразумевают один источник. Обратите также внимание, что обычно возникают проблемы с доказательством отрицательного результата . Нулевые гипотезы должны быть как минимум фальсифицируемы .

Теория Неймана-Пирсона может учитывать как априорные вероятности, так и стоимость действий, следующих из решений. ^[59]Первый позволяет каждому тесту учитывать результаты предыдущих тестов (в отличие от тестов значимости Фишера). Последнее позволяет учитывать экономические вопросы (например), а также вероятности. Отношение правдоподобия остается хорошим критерием выбора гипотез.

Две формы проверки гипотез основаны на разных формулировках задач. Исходный тест аналогичен вопросу «верно/неверно»; тест Неймана-Пирсона больше похож на множественный выбор. По мнению Тьюки ^[60]первый делает вывод только на основе веских доказательств, а второй принимает решение на основе имеющихся доказательств. Хотя эти два теста кажутся совершенно разными как с математической, так и с философской точки зрения, более поздние разработки привели к противоположному утверждению. Рассмотрим множество крошечных радиоактивных источников. Гипотезы становятся 0,1,2,3... песчинками радиоактивного песка. Существует небольшая разница между отсутствием радиации или некоторым количеством радиации (Фишер) и нулевым количеством песчинок радиоактивного песка по сравнению со всеми альтернативами (Нейман-Пирсон). Основная статья Неймана – Пирсона 1933 года. ^[11]также рассматриваются составные гипотезы (те, распределение которых включает неизвестный параметр). На примере доказана оптимальность t - критерия (Студента), «лучшего теста для рассматриваемой гипотезы не может быть» (стр. 321). Теория Неймана-Пирсона с самого начала доказывала оптимальность методов Фишера.

Проверка значимости Фишера оказалась популярным гибким статистическим инструментом с небольшим математическим потенциалом роста. Проверка гипотез Неймана-Пирсона считается основой математической статистики. ^[61]создание новой парадигмы в этой области. Это также стимулировало новые применения в статистическом управлении процессами , теории обнаружения , теории принятия решений и теории игр . Обе формулировки оказались успешными, но успехи носили разный характер.

Спор по формулировкам не разрешен. Наука в основном использует формулировку Фишера (слегка измененную), как она преподается во вводной статистике. Статистики изучают теорию Неймана-Пирсона в аспирантуре. Математики гордятся объединением формулировок. Философы рассматривают их отдельно. Ученые считают, что эти формулировки по-разному конкурируют (Фишер против Неймана), несовместимы. ^[9] или дополняющий. ^[13] Спор стал более сложным, поскольку байесовский вывод приобрел респектабельность.

Терминология противоречива. Проверка гипотезы может означать любую смесь двух формулировок, каждая из которых изменилась со временем. Любое обсуждение проверки значимости и проверки гипотез вдвойне подвержено путанице.

Фишер считал, что проверка гипотез является полезной стратегией для осуществления промышленного контроля качества, однако он категорически не соглашался с тем, что проверка гипотез может быть полезна для ученых. ^[10] Проверка гипотез обеспечивает средства поиска статистики тестирования, используемой при проверке значимости. ^[13]Концепция мощности полезна для объяснения последствий корректировки уровня значимости и широко используется при определении размера выборки . Эти два метода остаются философски разными. ^[15]Обычно (но не всегда ) они дают один и тот же математический ответ. Предпочтительный ответ зависит от контекста. ^[13] Хотя существующее слияние теорий Фишера и Неймана-Пирсона подверглось резкой критике, рассматривалась возможность изменения слияния для достижения байесовских целей. ^[62]

Критика [ править ]

Критика проверки статистических гипотез заполняет тома. ^[63]^[64]^[65]^[66]^[67]^[68] Большую часть критики можно резюмировать следующими вопросами:

Интерпретация значения p зависит от правила остановки и определения множественного сравнения. Первое часто меняется в ходе исследования, а второе неизбежно неоднозначно. (т.е. «значения p зависят как от наблюдаемых (данных), так и от других возможных (данных), которые могли бы наблюдаться, но не наблюдались»). ^[69]
Путаница, возникающая (частично) из-за объединения концептуально различных методов Фишера и Неймана-Пирсона. ^[60]
Акцент на статистической значимости, исключая оценку и подтверждение повторными экспериментами. ^[70]
Жесткое требование статистической значимости в качестве критерия публикации, что приводит к предвзятости публикации . ^[71]Большая часть критики носит косвенный характер. Вместо того, чтобы быть ошибочным, проверка статистической гипотезы неправильно понимается, злоупотребляется и используется неправильно.
При использовании для определения наличия различий между группами возникает парадокс. По мере усовершенствования плана эксперимента (например, повышения точности измерений и размера выборки) тест становится более мягким. Если не принять абсурдное предположение, что все источники шума в данных полностью компенсируются, вероятность найти статистическую значимость в любом направлении приближается к 100%. ^[72]Однако это абсурдное предположение о том, что средняя разница между двумя группами не может быть нулевой, подразумевает, что данные не могут быть независимыми и одинаково распределенными (iid), поскольку ожидаемая разница между любыми двумя подгруппами iid случайных величин равна нулю; следовательно, предположение iid также абсурдно.
Слои философских проблем. Вероятность статистической значимости является функцией решений, принятых экспериментаторами/аналитиками. ^[73] Если решения основаны на условностях, их называют произвольными или бессмысленными. ^[74]в то время как те, которые не основаны на этом, можно назвать субъективными. Чтобы свести к минимуму ошибки второго рода, рекомендуется использовать большие выборки. В психологии практически все нулевые гипотезы считаются ложными для достаточно больших выборок, поэтому «... обычно бессмысленно проводить эксперимент с единственной целью отвергнуть нулевую гипотезу». ^[75] «Статистически значимые результаты часто вводят в заблуждение» в психологии. ^[76]Статистическая значимость не подразумевает практическую значимость, а корреляция не подразумевает причинно-следственную связь . Ставить под сомнение нулевую гипотезу, таким образом, далеко от прямого подтверждения исследовательской гипотезы.
«[Я] не говорит нам того, что мы хотим знать». ^[77] Доступны списки из десятков жалоб. ^[67]^[78]^[79]

Критики и сторонники в основном сходятся во мнении относительно характеристик проверки значимости нулевой гипотезы (NHST): хотя она может предоставить критическую информацию, она неадекватна в качестве единственного инструмента статистического анализа . Успешное отклонение нулевой гипотезы может не поддержать исследовательскую гипотезу. Продолжающиеся споры касаются выбора лучших статистических практик на ближайшую перспективу с учетом существующих практик. Однако адекватный дизайн исследования может свести к минимуму эту проблему. Критики предпочли бы полностью запретить NHST, вынудив полностью отказаться от этой практики. ^[80] в то время как сторонники предлагают менее абсолютные изменения. ^{[ нужна цитата ]}

Споры по поводу проверки значимости и, в частности, ее влияния на предвзятость публикаций привели к нескольким результатам. Американская психологическая ассоциация ужесточила свои требования к статистической отчетности после проверки. ^[81] издатели медицинских журналов признали обязанность публиковать некоторые результаты, которые не являются статистически значимыми, для борьбы с предвзятостью публикаций, ^[82] журнал ( Журнал статей в поддержку нулевой гипотезы ) исключительно для публикации таких результатов. и был создан ^[83] В учебники добавлены некоторые предостережения, ^[84]и более широкий охват инструментов, необходимых для оценки размера выборки, необходимой для получения значимых результатов. Лишь немногие крупные организации отказались от использования тестов значимости, хотя некоторые обсуждали это. ^[81] Например, в 2023 году редакторы журнала « Физиология » «настоятельно рекомендуют использовать методы оценки тем, кто публикуется в журнале» (имеется в виду величина эффекта ( чтобы позволить читателям судить, имеет ли вывод практическое, физиологическое, или клиническая значимость) и доверительные интервалы , чтобы передать точность этой оценки), говоря: «В конечном счете, тех, кто публикует в «Журнале физиологии», должна больше всего интересовать физиологическая важность данных, а не статистическая значимость». ^[85]

Альтернативы [ править ]

Объединяющая позиция критиков заключается в том, что статистика должна приводить не к выводу или решению «принять-отклонить», а к оценочному значению с интервальной оценкой ; Эта философия анализа данных широко называется оценочной статистикой . Статистика оценки может быть получена с помощью частотного [1] или байесовского метода. ^[86]^[87]

Критики проверки значимости выступают за то, чтобы выводы основывались не столько на p-значениях, сколько на доверительных интервалах для размеров эффекта по важности, интервалах прогнозирования для уверенности, повторениях и расширениях для воспроизводимости, метаанализе для общности: ^[88]Но ни одна из этих предложенных альтернатив по своей сути не приводит к решению. Леманн сказал, что теория проверки гипотез может быть представлена в терминах выводов/решений, вероятностей или доверительных интервалов: «Различие между... подходами во многом заключается в сообщении и интерпретации». ^[25]

Байесовский вывод является одной из предлагаемых альтернатив проверке значимости. (Никерсон процитировал 10 источников, предполагающих это, включая Розебума (1960)). ^[78]Например, оценка байесовских параметров может предоставить обширную информацию о данных, из которой исследователи могут сделать выводы, используя при этом неопределенные априорные данные , которые оказывают лишь минимальное влияние на результаты, когда доступно достаточно данных. Психолог Джон К. Крушке предложил байесовскую оценку в качестве альтернативы t -тесту. ^[86] а также сравнил байесовскую оценку для оценки нулевых значений со сравнением байесовской модели для проверки гипотез. ^[87] Две конкурирующие модели/гипотезы можно сравнить с использованием факторов Байеса . ^[89]Байесовские методы можно критиковать за то, что они требуют информации, которая редко доступна в тех случаях, когда проверка значимости используется наиболее интенсивно. Ни априорные вероятности, ни распределение вероятностей тестовой статистики согласно альтернативной гипотезе часто недоступны в социальных науках. ^[78]

Сторонники байесовского подхода иногда утверждают, что целью исследователя чаще всего является объективная оценка вероятности того, что гипотеза верна, на основе собранных им данных. ^[90]^[91]Ни проверка проверка значимости Фишера, ни гипотезы Неймана-Пирсона не могут предоставить эту информацию и не претендуют на нее. Вероятность того, что гипотеза верна, может быть получена только на основе использования теоремы Байеса , которая была неудовлетворительной как для лагеря Фишера, так и для лагеря Неймана-Пирсона из-за явного использования субъективности в форме априорной вероятности . ^[11]^[92] Стратегия Фишера состоит в том, чтобы обойти это с помощью p -значения (объективного индекса , основанного только на данных) с последующим индуктивным выводом , в то время как Нейман-Пирсон разработали свой подход индуктивного поведения .

См. также [ править ]

Ссылки [ править ]

^ Льюис, Нэнси Д.; Льюис, Найджел Да Коста; Льюис, Северная Дакота (2013). 100 статистических тестов в R: что выбрать, как легко посчитать, с более чем 300 иллюстрациями и примерами . Хизер Хиллз Пресс. ISBN 978-1-4840-5299-0 .
^ Канджи, Гопал К. (18 июля 2006 г.). 100 статистических тестов . МУДРЕЦ. ISBN 978-1-4462-2250-8 .
^ Беллхаус, П. (2001), «Джон Арбутнот», в книге «Статистики столетий» К. К. Хейда и Э. Сенеты , Springer, стр. 39–42, ISBN 978-0-387-95329-8
^ Мил, П. (1990). «Оценка и изменение теорий: стратегия защиты Лакатоса и два принципа, которые ее оправдывают» (PDF) . Психологический опрос . 1 (2): 108–141. дои : 10.1207/s15327965pli0102_1 .
^ Перейти обратно: ^а ^б Лаплас, П. (1778). «Вероятностная диссертация» (PDF) . Мемуары Парижской королевской академии наук . 9 : 227–332. Архивировано из оригинала (PDF) 27 апреля 2015 г. Проверено 5 сентября 2013 г.
^ Пирсон, К. (1900). «О том критерии, что данная система отклонений от вероятного в случае коррелированной системы переменных такова, что можно разумно предположить, что она возникла в результате случайной выборки» (PDF) . Лондонский, Эдинбургский и Дублинский философский журнал и научный журнал . 5 (50): 157–175. дои : 10.1080/14786440009463897 .
^ Пирсон, К. (1904). «О теории непредвиденных обстоятельств и ее связи с ассоциацией и нормальной корреляцией» . Серия биометрических мемуаров об исследованиях компании Drapers . 1 :1–35.
^ Забелл, С. (1989). «РА Фишер по истории обратной вероятности» . Статистическая наука . 4 (3): 247–256. дои : 10.1214/ss/1177012488 . JSTOR 2245634 .
^ Перейти обратно: ^а ^б Рэймонд Хаббард, М. Дж. Баярри , Значения P не являются вероятностью ошибки. Архивировано 4 сентября 2013 г. в Wayback Machine . Фишера Рабочий документ, объясняющий разницу между доказательным значением p и частотой ошибок Неймана-Пирсона типа I. $\alpha$ .
^ Перейти обратно: ^а ^б Фишер, Р. (1955). «Статистические методы и научная индукция» (PDF) . Журнал Королевского статистического общества, серия B. 17 (1): 69–78.
^ Перейти обратно: ^а ^б ^с ^д Нейман, Дж; Пирсон, Э.С. (1 января 1933 г.). «К проблеме наиболее эффективной проверки статистических гипотез» . Философские труды Королевского общества А. 231 (694–706): 289–337. Бибкод : 1933RSPTA.231..289N . дои : 10.1098/rsta.1933.0009 .
^ Гудман, С.Н. (15 июня 1999 г.). «К медицинской статистике, основанной на фактических данных. 1: Ошибка значения P». Энн, интерн, мед . 130 (12): 995–1004. дои : 10.7326/0003-4819-130-12-199906150-00008 . ПМИД 10383371 . S2CID 7534212 .
^ Перейти обратно: ^а ^б ^с ^д Леманн, Э.Л. (декабрь 1993 г.). «Теории проверки гипотез Фишера, Неймана-Пирсона: одна теория или две?». Журнал Американской статистической ассоциации . 88 (424): 1242–1249. дои : 10.1080/01621459.1993.10476404 .
^ Фишер, Р.Н. (1958). «Природа вероятности» (PDF) . Столетний обзор . 2 : 261–274. Мы рискуем отправить в мир высококвалифицированных и очень умных молодых людей с таблицами ошибочных чисел под мышкой и с густым туманом в том месте, где должны быть их мозги. В этом столетии, конечно, они будут работать над управляемыми ракетами и консультировать медиков по вопросам борьбы с болезнями, и нет предела тому, до какой степени они могут препятствовать любым национальным усилиям.
^ Перейти обратно: ^а ^б ^с Ленхард, Йоханнес (2006). «Модели и статистические выводы: противоречие между Фишером и Нейманом-Пирсоном». Бр. Дж. Филос. Наука . 57 : 69–91. дои : 10.1093/bjps/axi152 . S2CID 14136146 .
^ Нейман, Ежи (1967). «РА Фишер (1890–1962): Признательность». Наука . 156 (3781): 1456–1460. Бибкод : 1967Sci...156.1456N . дои : 10.1126/science.156.3781.1456 . ПМИД 17741062 . S2CID 44708120 .
^ Лосавич, Дж.Л.; Нейман, Дж.; Скотт, Эл.; Уэллс, Массачусетс (1971). «Гипотетические объяснения очевидных негативных последствий засева облаков в эксперименте с Белой вершиной» . Труды Национальной академии наук Соединенных Штатов Америки . 68 (11): 2643–2646. Бибкод : 1971PNAS...68.2643L . дои : 10.1073/pnas.68.11.2643 . ПМК 389491 . ПМИД 16591951 .
^ Перейти обратно: ^а ^б Халпин, П.Ф.; Стам, HJ (зима 2006 г.). «Индуктивный вывод или индуктивное поведение: Фишер и Нейман: подходы Пирсона к статистическому тестированию в психологических исследованиях (1940–1960)». Американский журнал психологии . 119 (4): 625–653. дои : 10.2307/20445367 . JSTOR 20445367 . ПМИД 17286092 .
^ Гигеренцер, Герд; Зено Свитинк; Теодор Портер; Лоррейн Дастон; Джон Битти; Лоренц Крюгер (1989). «Часть 3: Эксперты по выводам». Империя случая: как вероятность изменила науку и повседневную жизнь . Издательство Кембриджского университета. стр. 70–122. ISBN 978-0-521-39838-1 .
^ Мэйо, генеральный директор; Спанос, А. (2006). «Строгое тестирование как основная концепция индукционной философии Неймана-Пирсона». Британский журнал философии науки . 57 (2): 323–357. CiteSeerX 10.1.1.130.8131 . дои : 10.1093/bjps/axl003 . S2CID 7176653 .
^ Математика > Средняя школа: статистика и вероятность > Введение. Архивировано 28 июля 2012 г., в archive.today Инициатива по общим основным государственным стандартам (касается студентов из США).
^ Тесты Совета колледжа > AP: Предметы > Статистика Совет колледжа (относится к студентам из США)
^ Хафф, Даррелл (1993). Как лгать со статистикой . Нью-Йорк: Нортон. п. 8 . ISBN 978-0-393-31072-6 . «Статистические методы и статистические термины необходимы при сообщении массовых данных о социальных и экономических тенденциях, условиях предпринимательской деятельности, опросах общественного мнения, переписи населения. Но без писателей, которые честно используют эти слова, и читателей, которые знают, что они означают, результатом может стать лишь смысловая чепуха».
^ Снедекор, Джордж В.; Кокран, Уильям Г. (1967). Статистические методы (6-е изд.). Эймс, Айова: Издательство Университета штата Айова. п. 3. «...основные идеи статистики помогают нам ясно размышлять над проблемой, дают некоторые указания относительно условий, которые должны быть удовлетворены, чтобы можно было сделать правильные выводы, и позволяют нам обнаруживать многие выводы, которые не имеют хорошей логики. фундамент."
^ Перейти обратно: ^а ^б Э. Л. Леманн (1997). «Проверка статистических гипотез: история книги» . Статистическая наука . 12 (1): 48–52. дои : 10.1214/сс/1029963261 .
^ Сотос, Ана Элиза Кастро; Ванхоф, Стейн; Ноортгейт, Вим Ван ден; Онгена, Патрик (2007). «Заблуждения студентов о статистических выводах: обзор эмпирических данных исследований в области статистического образования» (PDF) . Обзор образовательных исследований . 2 (2): 98–113. дои : 10.1016/j.edurev.2007.04.001 .
^ Мур, Дэвид С. (1997). «Новая педагогика и новый контент: пример статистики» (PDF) . Международный статистический обзор . 65 (2): 123–165. дои : 10.2307/1403333 . JSTOR 1403333 .
^ Хаббард, Раймонд; Армстронг, Дж. Скотт (2006). «Почему мы на самом деле не знаем, что означает статистическая значимость: последствия для преподавателей». Журнал маркетингового образования . 28 (2): 114–120. дои : 10.1177/0273475306288399 . hdl : 2092/413 . S2CID 34729227 .
^ Сотос, Ана Элиза Кастро; Ванхоф, Стейн; Ноортгейт, Вим Ван ден; Онгена, Патрик (2009). «Насколько студенты уверены в своих заблуждениях о проверке гипотез?» . Журнал статистического образования . 17 (2). дои : 10.1080/10691898.2009.11889514 .
^ Гигеренцер, Г. (2004). «Нулевой ритуал. Что вы всегда хотели знать о серьезных тестах, но боялись спросить» (PDF) . Справочник SAGE по количественной методологии для социальных наук . стр. 391–408. дои : 10.4135/9781412986311 . ISBN 9780761923596 .
^ «Проверка статистических гипотез» . Тексты Спрингера в статистике . 2005. doi : 10.1007/0-387-27605-x . ISBN 978-0-387-98864-1 . ISSN 1431-875X .
^ Хинкельманн, Клаус; Кемпторн, Оскар (2008). Планирование и анализ экспериментов . Том. I и II (Второе изд.). Уайли. ISBN 978-0-470-38551-7 .
^ Монтгомери, Дуглас (2009). Планирование и анализ экспериментов . Хобокен, Нью-Джерси: Уайли. ISBN 978-0-470-12866-4 .
^ Р. А. Фишер (1925). Статистические методы для научных работников , Эдинбург: Оливер и Бойд, 1925, стр. 43.
^ Перейти обратно: ^а ^б Леманн, Эль; Романо, Джозеф П. (2005). Проверка статистических гипотез (3E-изд.). Нью-Йорк: Спрингер. ISBN 978-0-387-98864-1 .
^ Нуццо, Регина (2014). «Научный метод: Статистические ошибки» . Природа . 506 (7487): 150–152. Бибкод : 2014Natur.506..150N . дои : 10.1038/506150a . ПМИД 24522584 .
^ Ричард Дж. Ларсен; Донна Фокс Строуп (1976). Статистика в реальном мире: книга примеров . Макмиллан. ISBN 978-0023677205 .
^ Хаббард, Р.; Парса, Арканзас; Люти, MR (1997). «Распространение тестирования статистической значимости в психологии: на примере журнала прикладной психологии». Теория и психология . 7 (4): 545–554. дои : 10.1177/0959354397074006 . S2CID 145576828 .
^ Мур, Дэвид (2003). Введение в практику статистики . Нью-Йорк: WH Freeman and Co., с. 426. ИСБН 9780716796572 .
^ Ранганатан, Прия; Прамеш, К.С.; Буйс, Марк (апрель – июнь 2016 г.). «Распространенные ошибки статистического анализа: опасности множественного тестирования» . Перспектива Клин Рес . 7 (2): 106–107. дои : 10.4103/2229-3485.179436 . ПМЦ 4840791 . ПМИД 27141478 .
^ Хьюз, Энн Дж.; Гравойг, Деннис Э. (1971). Статистика: основа анализа . Ридинг, Массачусетс: Аддисон-Уэсли. п. 191 . ISBN 0-201-03021-7 .
^ Холл, П. и Уилсон, С.Р., 1991. Два руководства по проверке гипотез начальной загрузки. Биометрия, стр.757-762.
^ Тибширани, Р.Дж. и Эфрон, Б., 1993. Введение в бутстрап. Монографии по статистике и прикладной вероятности, 57(1).
^ Мартин, Массачусетс, 2007. Проверка гипотезы начальной загрузки для некоторых распространенных статистических проблем: критическая оценка свойств размера и мощности. Вычислительная статистика и анализ данных, 51 (12), стр. 6321-6342.
^ Горовиц, Дж. Л., 2019. Бутстрап-методы в эконометрике. Ежегодный обзор экономики, 11, стр. 193–224. Я
^ Джон Арбутнот (1710). «Аргумент в пользу Божественного Провидения, основанный на постоянной регулярности рождаемости у представителей обоих полов» (PDF) . Философские труды Лондонского королевского общества . 27 (325–336): 186–190. дои : 10.1098/rstl.1710.0011 . S2CID 186209819 .
^ Брайан, Эрик; Джейссон, Мари (2007). «Физико-теология и математика (1710–1794)». Изменение соотношения полов при рождении . Springer Science & Business Media. стр. 1–25 . ISBN 978-1-4020-6036-6 .
^ Коновер, WJ (1999), «Глава 3.4: Знаковый тест», Практическая непараметрическая статистика (Третье изд.), Wiley, стр. 157–176, ISBN 978-0-471-16068-7
^ Срент, П. (1989), Прикладные непараметрические статистические методы (второе изд.), Chapman & Hall, ISBN 978-0-412-44980-2
^ Стиглер, Стивен М. (1986). История статистики: измерение неопределенности до 1900 года . Издательство Гарвардского университета. стр. 225–226 . ISBN 978-0-67440341-3 .
^ Лаплас, П. (1778). «Память о вероятности (XIX, XX)» . Полное собрание сочинений Лапласа . Полет. 9.стр. 429–438. {{cite book}}: |journal= игнорируется ( помогите )
^ Стиглер, Стивен М. (1986). История статистики: измерение неопределенности до 1900 года . Кембридж, Массачусетс: Belknap Press издательства Гарвардского университета. п. 134 . ISBN 978-0-674-40340-6 .
^ Фишер, сэр Рональд А. (1956) [1935]. «Математика дамы, дегустирующей чай» . В Джеймсе Рое Ньюмане (ред.). Мир математики, том 3 [ Планирование экспериментов ]. Публикации Курьера Дувра. ISBN 978-0-486-41151-4 . Первоначально из книги Фишера « Планирование экспериментов» .
^ Коробка, Джоан Фишер (1978). Р. А. Фишер, Жизнь учёного . Нью-Йорк: Уайли. п. 134. ИСБН 978-0-471-09300-8 .
^ К.С. Пирс (август 1878 г.). «Иллюстрации логики науки VI: дедукция, индукция и гипотеза» . Научно-популярный ежемесячник . 13 . Проверено 30 марта 2012 г.
^ Джейнс, ET (2007). Теория вероятностей: логика науки (5-е печатное изд.). Кембридж [ua]: Cambridge Univ. Нажимать. ISBN 978-0-521-59271-0 .
^ Шервиш, М. (1996) Теория статистики , с. 218. Спрингер ISBN 0-387-94546-6
^ Кэй, Дэвид Х.; Фридман, Дэвид А. (2011). «Справочник по статистике» . Справочное руководство по научным данным (3-е изд.). Иган, Миннесота Вашингтон, округ Колумбия: Издательство Западных национальных академий. п. 259. ИСБН 978-0-309-21421-6 .
^ Эш, Роберт (1970). Основная теория вероятностей . Нью-Йорк: Уайли. ISBN 978-0471034506 . Раздел 8.2
^ Перейти обратно: ^а ^б Тьюки, Джон В. (1960). «Выводы против решений». Технометрика . 26 (4): 423–433. дои : 10.1080/00401706.1960.10489909 . «Пока мы не пройдемся по отчетам о проверке гипотез, отделяя элементы решения [Неймана-Пирсона] от элементов заключения [Фишера], тесная смесь несопоставимых элементов будет постоянным источником путаницы». ... «Есть место и для того, чтобы «делать все, что в твоих силах», и для того, чтобы «говорить только то, что несомненно», но важно знать в каждом случае и то, что делается, и то, что следует делать. "
^ Стиглер, Стивен М. (август 1996 г.). «История статистики в 1933 году» . Статистическая наука . 11 (3): 244–252. дои : 10.1214/ss/1032280216 . JSTOR 2246117 .
^ Бергер, Джеймс О. (2003). «Могли ли Фишер, Джеффрис и Нейман договориться о тестировании?» . Статистическая наука . 18 (1): 1–32. дои : 10.1214/ss/1056397485 .
^ Моррисон, Дентон; Хенкель, Рамон, ред. (2006) [1970]. Споры о тесте значимости . Альдинская сделка. ISBN 978-0-202-30879-1 .
^ Оукс, Майкл (1986). Статистический вывод: комментарий для социальных и поведенческих наук . Чичестер, Нью-Йорк: Уайли. ISBN 978-0471104438 .
^ Чоу, Сиу Л. (1997). Статистическая значимость: обоснование, достоверность и полезность . Публикации SAGE. ISBN 978-0-7619-5205-3 .
^ Харлоу, Лиза Лавуа; Стэнли А. Мулайк; Джеймс Х. Стайгер, ред. (1997). Что, если бы не было никаких тестов значимости? . Лоуренс Эрлбаум Ассошиэйтс. ISBN 978-0-8058-2634-0 .
^ Перейти обратно: ^а ^б Клайн, Рекс (2004). За пределами тестирования значимости: реформирование методов анализа данных в поведенческих исследованиях . Вашингтон, округ Колумбия: Американская психологическая ассоциация. ISBN 9781591471189 .
^ Макклоски, Дейдра Н.; Стивен Т. Зилиак (2008). Культ статистической значимости: как стандартная ошибка стоит нам рабочих мест, правосудия и жизней . Издательство Мичиганского университета. ISBN 978-0-472-05007-9 .
^ Корнфилд, Джером (1976). «Последний методологический вклад в клинические исследования» (PDF) . Американский журнал эпидемиологии . 104 (4): 408–421. doi : 10.1093/oxfordjournals.aje.a112313 . ПМИД 788503 .
^ Йейтс, Фрэнк (1951). «Влияние статистических методов для научных работников на развитие статистической науки». Журнал Американской статистической ассоциации . 46 (253): 19–34. дои : 10.1080/01621459.1951.10500764 . «Акцент, уделяемый формальным тестам значимости в «Статистических методах» [Р.А. Фишера]... заставил научно-исследовательских работников уделять чрезмерное внимание результатам тестов значимости, которые они выполняют над своими данными, особенно данными, полученными в результате экспериментов, а также мало что соответствует оценкам масштабов эффектов, которые они исследуют». ... «Акцент на проверках значимости и рассмотрение результатов каждого эксперимента в отдельности имели печальные последствия: научные работники часто считали выполнение проверки значимости эксперимента конечной целью».
^ Бегг, Колин Б.; Берлин, Джесси А. (1988). «Предвзятость публикации: проблема интерпретации медицинских данных». Журнал Королевского статистического общества, серия A. 151 (3): 419–463. дои : 10.2307/2982993 . JSTOR 2982993 . S2CID 121054702 .
^ Мил, Пол Э. (1967). «Проверка теории в психологии и физике: методологический парадокс» (PDF) . Философия науки . 34 (2): 103–115. дои : 10.1086/288135 . S2CID 96422880 . Архивировано из оригинала (PDF) 3 декабря 2013 года. Тридцать лет спустя Мил признал теорию статистической значимости математически обоснованной, продолжая при этом подвергать сомнению выбор нулевой гипотезы по умолчанию, обвиняя вместо этого «плохое понимание логических отношений учеными-социологами». между теорией и фактом» в «Проблема в эпистемологии, а не в статистике: заменить критерии значимости доверительными интервалами и количественно оценить точность рискованных числовых прогнозов» (глава 14 в Harlow (1997)).
^ Бакан, Дэвид (1966). «Тест значимости в психологических исследованиях». Психологический вестник . 66 (6): 423–437. дои : 10.1037/h0020412 . ПМИД 5974619 .
^ Гигеренцер, Г. (ноябрь 2004 г.). «Бессмысленная статистика». Журнал социально-экономики . 33 (5): 587–606. doi : 10.1016/j.socec.2004.09.033 .
^ Нанналли, Джам (1960). «Место статистики в психологии». Образовательные и психологические измерения . 20 (4): 641–650. дои : 10.1177/001316446002000401 . S2CID 144813784 .
^ Ликкен, Дэвид Т. (1991). «А что не так с психологией?». Ясно думая о психологии . 1 :3–39.
^ Джейкоб Коэн (декабрь 1994 г.). «Земля круглая (p < 0,05)». Американский психолог . 49 (12): 997–1003. дои : 10.1037/0003-066X.49.12.997 . S2CID 380942 . Этот документ представляет собой обзор статистической практики, проведенный APA. Коэн был членом оперативной группы, проводившей проверку.
^ Перейти обратно: ^а ^б ^с Никерсон, Раймонд С. (2000). «Проверка значимости нулевой гипотезы: обзор старого и продолжающегося спора». Психологические методы . 5 (2): 241–301. дои : 10.1037/1082-989X.5.2.241 . ПМИД 10937333 . S2CID 28340967 .
^ Бранч, Марк (2014). «Злокачественные побочные эффекты проверки значимости нулевой гипотезы». Теория и психология . 24 (2): 256–277. дои : 10.1177/0959354314525282 . S2CID 40712136 .
^ Хантер, Джон Э. (январь 1997 г.). «Необходимо: запрет на тест на значимость». Психологическая наука . 8 (1): 3–7. дои : 10.1111/j.1467-9280.1997.tb00534.x . S2CID 145422959 .
^ Перейти обратно: ^а ^б Уилкинсон, Лиланд (1999). «Статистические методы в психологических журналах: рекомендации и пояснения». Американский психолог . 54 (8): 594–604. дои : 10.1037/0003-066X.54.8.594 . S2CID 428023 . «Проверка гипотез. Трудно представить ситуацию, в которой дихотомическое решение принять-отклонить лучше, чем сообщать фактическое значение p или, еще лучше, доверительный интервал». (стр. 599). Комитет использовал предостерегающий термин «терпимость», описывая свое решение против запрета проверки гипотез в психологических репортажах. (стр. 603)
^ «ICMJE: Обязательство публиковать отрицательные исследования» . Архивировано из оригинала 16 июля 2012 года . Проверено 3 сентября 2012 г. Редакторы должны серьезно рассматривать возможность публикации любого тщательно проведенного исследования важного вопроса, интересующего читателей, независимо от того, являются ли результаты основного или любого дополнительного результата статистически значимыми. Неспособность представить или опубликовать результаты из-за отсутствия статистической значимости является важной причиной предвзятости публикации.
^ Веб- сайт журнала статей в поддержку нулевой гипотезы : домашняя страница JASNH . Том 1 номер 1 был опубликован в 2002 году, и все статьи посвящены темам, связанным с психологией.
^ Хауэлл, Дэвид (2002). Статистические методы психологии (5-е изд.). Даксбери. п. 94 . ISBN 978-0-534-37770-0 .
^ Уильямс С., Карсон Р., Тот К. (10 октября 2023 г.). «Выход за рамки значений P в Журнале физиологии: введение в значение величины эффекта и доверительных интервалов» . Дж Физиол . 601 (23): 5131–5133. дои : 10.1113/JP285575 . ПМИД 37815959 . S2CID 263827430 . {{cite journal}}: CS1 maint: несколько имен: список авторов ( ссылка )
^ Перейти обратно: ^а ^б Крушке, Ю.К. (9 июля 2012 г.). «Байесовская оценка заменяет T-тест» (PDF) . Журнал экспериментальной психологии: Общие сведения . 142 (2): 573–603. дои : 10.1037/a0029146 . ПМИД 22774788 . S2CID 5610231 .
^ Перейти обратно: ^а ^б Крушке, Ю.К. (8 мая 2018 г.). «Отклонение или принятие значений параметров в байесовской оценке» (PDF) . Достижения в методах и практике психологической науки . 1 (2): 270–280. дои : 10.1177/2515245918771304 . S2CID 125788648 .
^ Армстронг, Дж. Скотт (2007). «Проверка значимости вредит прогрессу в прогнозировании» . Международный журнал прогнозирования . 23 (2): 321–327. CiteSeerX 10.1.1.343.9516 . doi : 10.1016/j.ijforecast.2007.03.004 . S2CID 1550979 .
^ Касс, Р.Э. (1993). Факторы Байеса и неопределенность модели (PDF) (Отчет). Департамент статистики Вашингтонского университета.
^ Розбум, Уильям В. (1960). «Ошибочность теста значимости нулевой гипотезы» (PDF) . Психологический вестник . 57 (5): 416–428. CiteSeerX 10.1.1.398.9002 . дои : 10.1037/h0042040 . ПМИД 13744252 . «... правильное применение статистики для научных выводов неизбежно связано с широким рассмотрением обратных [так называемых байесовских] вероятностей...» Было с сожалением признано, что априорные распределения вероятностей были доступны «только как субъективное ощущение, отличаться от одного человека к другому, «по крайней мере, в ближайшем будущем».
^ Бергер, Джеймс (2006). «Аргументы в пользу объективного байесовского анализа» . Байесовский анализ . 1 (3): 385–402. дои : 10.1214/06-ba115 . Перечисляя конкурирующие определения «объективного» байесовского анализа, «Основная цель статистики (на самом деле науки) состоит в том, чтобы найти полностью последовательную объективную байесовскую методологию обучения на данных». Автор выразил мнение, что эта цель «недостижима».
^ Олдрич, Дж (2008). «РА Фишер о Байесе и теореме Байеса» . Байесовский анализ . 3 (1): 161–170. дои : 10.1214/08-BA306 .

Дальнейшее чтение [ править ]

Леманн Э.Л. (1992) «Введение в работу Неймана и Пирсона (1933) о проблеме наиболее эффективных проверок статистических гипотез». В: Прорывы в статистике, Том 1 , (Эдс Коц, С., Джонсон, Н.Л.), Springer-Verlag. ISBN 0-387-94037-5 (с последующим переизданием статьи)
Нейман, Дж.; Пирсон, ES (1933). «К проблеме наиболее эффективной проверки статистических гипотез» . Философские труды Королевского общества А. 231 (694–706): 289–337. Бибкод : 1933RSPTA.231..289N . дои : 10.1098/rsta.1933.0009 .

Внешние ссылки [ править ]

«Статистические гипотезы, проверка» , Энциклопедия математики , EMS Press , 2001 [1994]
Уилсон Гонсалес, Джорджина; Кей Шанкаран (10 сентября 1997 г.). "Проверка гипотезы" . Учебное пособие по отбору проб и мониторингу окружающей среды . Вирджинский технологический институт.
Байесовская критика проверки классической гипотезы
Критика проверки классической гипотезы, подчеркивающая давние сомнения статистиков
Даллал GE (2007) Маленький справочник статистической практики (хорошее учебное пособие)
Ссылки на аргументы за и против проверки гипотез.
Обзор статистических тестов: как выбрать правильный статистический тест
[2] Метод проверки гипотез на основе статистического анализа при открытии биологических знаний; Доктор Насиф-Ур-Рахман Чоудхури, Суванкар Пол, Кази Закиа Султана

Онлайн калькуляторы [ править ]

[1] Льюис, Нэнси Д.; Льюис, Найджел Да Коста; Льюис, Северная Дакота (2013). 100 статистических тестов в R: что выбрать, как легко посчитать, с более чем 300 иллюстрациями и примерами . Хизер Хиллз Пресс. ISBN 978-1-4840-5299-0 .

[2] Канджи, Гопал К. (18 июля 2006 г.). 100 статистических тестов . МУДРЕЦ. ISBN 978-1-4462-2250-8 .

[Bellhouse2001-3] Беллхаус, П. (2001), «Джон Арбутнот», в книге «Статистики столетий» К. К. Хейда и Э. Сенеты , Springer, стр. 39–42, ISBN 978-0-387-95329-8

[4] Мил, П. (1990). «Оценка и изменение теорий: стратегия защиты Лакатоса и два принципа, которые ее оправдывают» (PDF) . Психологический опрос . 1 (2): 108–141. дои : 10.1207/s15327965pli0102_1 .

[Laplace_1778-5] Перейти обратно: ^а ^б Лаплас, П. (1778). «Вероятностная диссертация» (PDF) . Мемуары Парижской королевской академии наук . 9 : 227–332. Архивировано из оригинала (PDF) 27 апреля 2015 г. Проверено 5 сентября 2013 г.

[Pearson_1900-6] Пирсон, К. (1900). «О том критерии, что данная система отклонений от вероятного в случае коррелированной системы переменных такова, что можно разумно предположить, что она возникла в результате случайной выборки» (PDF) . Лондонский, Эдинбургский и Дублинский философский журнал и научный журнал . 5 (50): 157–175. дои : 10.1080/14786440009463897 .

[Pearson_1904-7] Пирсон, К. (1904). «О теории непредвиденных обстоятельств и ее связи с ассоциацией и нормальной корреляцией» . Серия биометрических мемуаров об исследованиях компании Drapers . 1 :1–35.

[8] Забелл, С. (1989). «РА Фишер по истории обратной вероятности» . Статистическая наука . 4 (3): 247–256. дои : 10.1214/ss/1177012488 . JSTOR 2245634 .

[ftp.isds.duke-9] Перейти обратно: ^а ^б Рэймонд Хаббард, М. Дж. Баярри , Значения P не являются вероятностью ошибки. Архивировано 4 сентября 2013 г. в Wayback Machine . Фишера Рабочий документ, объясняющий разницу между доказательным значением p и частотой ошибок Неймана-Пирсона типа I. $\alpha$ .

[Fisher_1955_69–78-10] Перейти обратно: ^а ^б Фишер, Р. (1955). «Статистические методы и научная индукция» (PDF) . Журнал Королевского статистического общества, серия B. 17 (1): 69–78.

[Neyman_289–337-11] Перейти обратно: ^а ^б ^с ^д Нейман, Дж; Пирсон, Э.С. (1 января 1933 г.). «К проблеме наиболее эффективной проверки статистических гипотез» . Философские труды Королевского общества А. 231 (694–706): 289–337. Бибкод : 1933RSPTA.231..289N . дои : 10.1098/rsta.1933.0009 .

[12] Гудман, С.Н. (15 июня 1999 г.). «К медицинской статистике, основанной на фактических данных. 1: Ошибка значения P». Энн, интерн, мед . 130 (12): 995–1004. дои : 10.7326/0003-4819-130-12-199906150-00008 . ПМИД 10383371 . S2CID 7534212 .

[Lehmann93-13] Перейти обратно: ^а ^б ^с ^д Леманн, Э.Л. (декабрь 1993 г.). «Теории проверки гипотез Фишера, Неймана-Пирсона: одна теория или две?». Журнал Американской статистической ассоциации . 88 (424): 1242–1249. дои : 10.1080/01621459.1993.10476404 .

[14] Фишер, Р.Н. (1958). «Природа вероятности» (PDF) . Столетний обзор . 2 : 261–274. Мы рискуем отправить в мир высококвалифицированных и очень умных молодых людей с таблицами ошибочных чисел под мышкой и с густым туманом в том месте, где должны быть их мозги. В этом столетии, конечно, они будут работать над управляемыми ракетами и консультировать медиков по вопросам борьбы с болезнями, и нет предела тому, до какой степени они могут препятствовать любым национальным усилиям.

[Lenhard-15] Перейти обратно: ^а ^б ^с Ленхард, Йоханнес (2006). «Модели и статистические выводы: противоречие между Фишером и Нейманом-Пирсоном». Бр. Дж. Филос. Наука . 57 : 69–91. дои : 10.1093/bjps/axi152 . S2CID 14136146 .

[16] Нейман, Ежи (1967). «РА Фишер (1890–1962): Признательность». Наука . 156 (3781): 1456–1460. Бибкод : 1967Sci...156.1456N . дои : 10.1126/science.156.3781.1456 . ПМИД 17741062 . S2CID 44708120 .

[17] Лосавич, Дж.Л.; Нейман, Дж.; Скотт, Эл.; Уэллс, Массачусетс (1971). «Гипотетические объяснения очевидных негативных последствий засева облаков в эксперименте с Белой вершиной» . Труды Национальной академии наук Соединенных Штатов Америки . 68 (11): 2643–2646. Бибкод : 1971PNAS...68.2643L . дои : 10.1073/pnas.68.11.2643 . ПМК 389491 . ПМИД 16591951 .

[Halpin_625–653-18] Перейти обратно: ^а ^б Халпин, П.Ф.; Стам, HJ (зима 2006 г.). «Индуктивный вывод или индуктивное поведение: Фишер и Нейман: подходы Пирсона к статистическому тестированию в психологических исследованиях (1940–1960)». Американский журнал психологии . 119 (4): 625–653. дои : 10.2307/20445367 . JSTOR 20445367 . ПМИД 17286092 .

[Gigerenzer-19] Гигеренцер, Герд; Зено Свитинк; Теодор Портер; Лоррейн Дастон; Джон Битти; Лоренц Крюгер (1989). «Часть 3: Эксперты по выводам». Империя случая: как вероятность изменила науку и повседневную жизнь . Издательство Кембриджского университета. стр. 70–122. ISBN 978-0-521-39838-1 .

[doi10.1093/bjps/axl003-20] Мэйо, генеральный директор; Спанос, А. (2006). «Строгое тестирование как основная концепция индукционной философии Неймана-Пирсона». Британский журнал философии науки . 57 (2): 323–357. CiteSeerX 10.1.1.130.8131 . дои : 10.1093/bjps/axl003 . S2CID 7176653 .

[21] Математика > Средняя школа: статистика и вероятность > Введение. Архивировано 28 июля 2012 г., в archive.today Инициатива по общим основным государственным стандартам (касается студентов из США).

[22] Тесты Совета колледжа > AP: Предметы > Статистика Совет колледжа (относится к студентам из США)

[Huff8-23] Хафф, Даррелл (1993). Как лгать со статистикой . Нью-Йорк: Нортон. п. 8 . ISBN 978-0-393-31072-6 . «Статистические методы и статистические термины необходимы при сообщении массовых данных о социальных и экономических тенденциях, условиях предпринимательской деятельности, опросах общественного мнения, переписи населения. Но без писателей, которые честно используют эти слова, и читателей, которые знают, что они означают, результатом может стать лишь смысловая чепуха».

[S&C-24] Снедекор, Джордж В.; Кокран, Уильям Г. (1967). Статистические методы (6-е изд.). Эймс, Айова: Издательство Университета штата Айова. п. 3. «...основные идеи статистики помогают нам ясно размышлять над проблемой, дают некоторые указания относительно условий, которые должны быть удовлетворены, чтобы можно было сделать правильные выводы, и позволяют нам обнаруживать многие выводы, которые не имеют хорошей логики. фундамент."

[Lehmann97-25] Перейти обратно: ^а ^б Э. Л. Леманн (1997). «Проверка статистических гипотез: история книги» . Статистическая наука . 12 (1): 48–52. дои : 10.1214/сс/1029963261 .

[26] Сотос, Ана Элиза Кастро; Ванхоф, Стейн; Ноортгейт, Вим Ван ден; Онгена, Патрик (2007). «Заблуждения студентов о статистических выводах: обзор эмпирических данных исследований в области статистического образования» (PDF) . Обзор образовательных исследований . 2 (2): 98–113. дои : 10.1016/j.edurev.2007.04.001 .

[27] Мур, Дэвид С. (1997). «Новая педагогика и новый контент: пример статистики» (PDF) . Международный статистический обзор . 65 (2): 123–165. дои : 10.2307/1403333 . JSTOR 1403333 .

[28] Хаббард, Раймонд; Армстронг, Дж. Скотт (2006). «Почему мы на самом деле не знаем, что означает статистическая значимость: последствия для преподавателей». Журнал маркетингового образования . 28 (2): 114–120. дои : 10.1177/0273475306288399 . hdl : 2092/413 . S2CID 34729227 .

[29] Сотос, Ана Элиза Кастро; Ванхоф, Стейн; Ноортгейт, Вим Ван ден; Онгена, Патрик (2009). «Насколько студенты уверены в своих заблуждениях о проверке гипотез?» . Журнал статистического образования . 17 (2). дои : 10.1080/10691898.2009.11889514 .

[Gigerenzer_2004_391–408-30] Гигеренцер, Г. (2004). «Нулевой ритуал. Что вы всегда хотели знать о серьезных тестах, но боялись спросить» (PDF) . Справочник SAGE по количественной методологии для социальных наук . стр. 391–408. дои : 10.4135/9781412986311 . ISBN 9780761923596 .

[31] «Проверка статистических гипотез» . Тексты Спрингера в статистике . 2005. doi : 10.1007/0-387-27605-x . ISBN 978-0-387-98864-1 . ISSN 1431-875X .

[32] Хинкельманн, Клаус; Кемпторн, Оскар (2008). Планирование и анализ экспериментов . Том. I и II (Второе изд.). Уайли. ISBN 978-0-470-38551-7 .

[33] Монтгомери, Дуглас (2009). Планирование и анализ экспериментов . Хобокен, Нью-Джерси: Уайли. ISBN 978-0-470-12866-4 .

[Fisher1925-34] Р. А. Фишер (1925). Статистические методы для научных работников , Эдинбург: Оливер и Бойд, 1925, стр. 43.

[LR-35] Перейти обратно: ^а ^б Леманн, Эль; Романо, Джозеф П. (2005). Проверка статистических гипотез (3E-изд.). Нью-Йорк: Спрингер. ISBN 978-0-387-98864-1 .

[36] Нуццо, Регина (2014). «Научный метод: Статистические ошибки» . Природа . 506 (7487): 150–152. Бибкод : 2014Natur.506..150N . дои : 10.1038/506150a . ПМИД 24522584 .

[larsen-37] Ричард Дж. Ларсен; Донна Фокс Строуп (1976). Статистика в реальном мире: книга примеров . Макмиллан. ISBN 978-0023677205 .

[hubbard-38] Хаббард, Р.; Парса, Арканзас; Люти, MR (1997). «Распространение тестирования статистической значимости в психологии: на примере журнала прикладной психологии». Теория и психология . 7 (4): 545–554. дои : 10.1177/0959354397074006 . S2CID 145576828 .

[moore-39] Мур, Дэвид (2003). Введение в практику статистики . Нью-Йорк: WH Freeman and Co., с. 426. ИСБН 9780716796572 .

[40] Ранганатан, Прия; Прамеш, К.С.; Буйс, Марк (апрель – июнь 2016 г.). «Распространенные ошибки статистического анализа: опасности множественного тестирования» . Перспектива Клин Рес . 7 (2): 106–107. дои : 10.4103/2229-3485.179436 . ПМЦ 4840791 . ПМИД 27141478 .

[41] Хьюз, Энн Дж.; Гравойг, Деннис Э. (1971). Статистика: основа анализа . Ридинг, Массачусетс: Аддисон-Уэсли. п. 191 . ISBN 0-201-03021-7 .

[42] Холл, П. и Уилсон, С.Р., 1991. Два руководства по проверке гипотез начальной загрузки. Биометрия, стр.757-762.

[43] Тибширани, Р.Дж. и Эфрон, Б., 1993. Введение в бутстрап. Монографии по статистике и прикладной вероятности, 57(1).

[44] Мартин, Массачусетс, 2007. Проверка гипотезы начальной загрузки для некоторых распространенных статистических проблем: критическая оценка свойств размера и мощности. Вычислительная статистика и анализ данных, 51 (12), стр. 6321-6342.

[45] Горовиц, Дж. Л., 2019. Бутстрап-методы в эконометрике. Ежегодный обзор экономики, 11, стр. 193–224. Я

[46] Джон Арбутнот (1710). «Аргумент в пользу Божественного Провидения, основанный на постоянной регулярности рождаемости у представителей обоих полов» (PDF) . Философские труды Лондонского королевского общества . 27 (325–336): 186–190. дои : 10.1098/rstl.1710.0011 . S2CID 186209819 .

[47] Брайан, Эрик; Джейссон, Мари (2007). «Физико-теология и математика (1710–1794)». Изменение соотношения полов при рождении . Springer Science & Business Media. стр. 1–25 . ISBN 978-1-4020-6036-6 .

[Conover1999-48] Коновер, WJ (1999), «Глава 3.4: Знаковый тест», Практическая непараметрическая статистика (Третье изд.), Wiley, стр. 157–176, ISBN 978-0-471-16068-7

[Sprent1989-49] Срент, П. (1989), Прикладные непараметрические статистические методы (второе изд.), Chapman & Hall, ISBN 978-0-412-44980-2

[50] Стиглер, Стивен М. (1986). История статистики: измерение неопределенности до 1900 года . Издательство Гарвардского университета. стр. 225–226 . ISBN 978-0-67440341-3 .

[Laplace_1878-51] Лаплас, П. (1778). «Память о вероятности (XIX, XX)» . Полное собрание сочинений Лапласа . Полет. 9.стр. 429–438. {{cite book}}: |journal= игнорируется ( помогите )

[52] Стиглер, Стивен М. (1986). История статистики: измерение неопределенности до 1900 года . Кембридж, Массачусетс: Belknap Press издательства Гарвардского университета. п. 134 . ISBN 978-0-674-40340-6 .

[fisher-53] Фишер, сэр Рональд А. (1956) [1935]. «Математика дамы, дегустирующей чай» . В Джеймсе Рое Ньюмане (ред.). Мир математики, том 3 [ Планирование экспериментов ]. Публикации Курьера Дувра. ISBN 978-0-486-41151-4 . Первоначально из книги Фишера « Планирование экспериментов» .

[54] Коробка, Джоан Фишер (1978). Р. А. Фишер, Жизнь учёного . Нью-Йорк: Уайли. п. 134. ИСБН 978-0-471-09300-8 .

[55] К.С. Пирс (август 1878 г.). «Иллюстрации логики науки VI: дедукция, индукция и гипотеза» . Научно-популярный ежемесячник . 13 . Проверено 30 марта 2012 г.

[56] Джейнс, ET (2007). Теория вероятностей: логика науки (5-е печатное изд.). Кембридж [ua]: Cambridge Univ. Нажимать. ISBN 978-0-521-59271-0 .

[57] Шервиш, М. (1996) Теория статистики , с. 218. Спрингер ISBN 0-387-94546-6

[58] Кэй, Дэвид Х.; Фридман, Дэвид А. (2011). «Справочник по статистике» . Справочное руководство по научным данным (3-е изд.). Иган, Миннесота Вашингтон, округ Колумбия: Издательство Западных национальных академий. п. 259. ИСБН 978-0-309-21421-6 .

[Ash-59] Эш, Роберт (1970). Основная теория вероятностей . Нью-Йорк: Уайли. ISBN 978-0471034506 . Раздел 8.2

[Tukey60-60] Перейти обратно: ^а ^б Тьюки, Джон В. (1960). «Выводы против решений». Технометрика . 26 (4): 423–433. дои : 10.1080/00401706.1960.10489909 . «Пока мы не пройдемся по отчетам о проверке гипотез, отделяя элементы решения [Неймана-Пирсона] от элементов заключения [Фишера], тесная смесь несопоставимых элементов будет постоянным источником путаницы». ... «Есть место и для того, чтобы «делать все, что в твоих силах», и для того, чтобы «говорить только то, что несомненно», но важно знать в каждом случае и то, что делается, и то, что следует делать. "

[61] Стиглер, Стивен М. (август 1996 г.). «История статистики в 1933 году» . Статистическая наука . 11 (3): 244–252. дои : 10.1214/ss/1032280216 . JSTOR 2246117 .

[62] Бергер, Джеймс О. (2003). «Могли ли Фишер, Джеффрис и Нейман договориться о тестировании?» . Статистическая наука . 18 (1): 1–32. дои : 10.1214/ss/1056397485 .

[morrison-63] Моррисон, Дентон; Хенкель, Рамон, ред. (2006) [1970]. Споры о тесте значимости . Альдинская сделка. ISBN 978-0-202-30879-1 .

[64] Оукс, Майкл (1986). Статистический вывод: комментарий для социальных и поведенческих наук . Чичестер, Нью-Йорк: Уайли. ISBN 978-0471104438 .

[chow-65] Чоу, Сиу Л. (1997). Статистическая значимость: обоснование, достоверность и полезность . Публикации SAGE. ISBN 978-0-7619-5205-3 .

[harlow-66] Харлоу, Лиза Лавуа; Стэнли А. Мулайк; Джеймс Х. Стайгер, ред. (1997). Что, если бы не было никаких тестов значимости? . Лоуренс Эрлбаум Ассошиэйтс. ISBN 978-0-8058-2634-0 .

[kline-67] Перейти обратно: ^а ^б Клайн, Рекс (2004). За пределами тестирования значимости: реформирование методов анализа данных в поведенческих исследованиях . Вашингтон, округ Колумбия: Американская психологическая ассоциация. ISBN 9781591471189 .

[mccloskey-68] Макклоски, Дейдра Н.; Стивен Т. Зилиак (2008). Культ статистической значимости: как стандартная ошибка стоит нам рабочих мест, правосудия и жизней . Издательство Мичиганского университета. ISBN 978-0-472-05007-9 .

[69] Корнфилд, Джером (1976). «Последний методологический вклад в клинические исследования» (PDF) . Американский журнал эпидемиологии . 104 (4): 408–421. doi : 10.1093/oxfordjournals.aje.a112313 . ПМИД 788503 .

[70] Йейтс, Фрэнк (1951). «Влияние статистических методов для научных работников на развитие статистической науки». Журнал Американской статистической ассоциации . 46 (253): 19–34. дои : 10.1080/01621459.1951.10500764 . «Акцент, уделяемый формальным тестам значимости в «Статистических методах» [Р.А. Фишера]... заставил научно-исследовательских работников уделять чрезмерное внимание результатам тестов значимости, которые они выполняют над своими данными, особенно данными, полученными в результате экспериментов, а также мало что соответствует оценкам масштабов эффектов, которые они исследуют». ... «Акцент на проверках значимости и рассмотрение результатов каждого эксперимента в отдельности имели печальные последствия: научные работники часто считали выполнение проверки значимости эксперимента конечной целью».

[71] Бегг, Колин Б.; Берлин, Джесси А. (1988). «Предвзятость публикации: проблема интерпретации медицинских данных». Журнал Королевского статистического общества, серия A. 151 (3): 419–463. дои : 10.2307/2982993 . JSTOR 2982993 . S2CID 121054702 .

[72] Мил, Пол Э. (1967). «Проверка теории в психологии и физике: методологический парадокс» (PDF) . Философия науки . 34 (2): 103–115. дои : 10.1086/288135 . S2CID 96422880 . Архивировано из оригинала (PDF) 3 декабря 2013 года. Тридцать лет спустя Мил признал теорию статистической значимости математически обоснованной, продолжая при этом подвергать сомнению выбор нулевой гипотезы по умолчанию, обвиняя вместо этого «плохое понимание логических отношений учеными-социологами». между теорией и фактом» в «Проблема в эпистемологии, а не в статистике: заменить критерии значимости доверительными интервалами и количественно оценить точность рискованных числовых прогнозов» (глава 14 в Harlow (1997)).

[bakan66-73] Бакан, Дэвид (1966). «Тест значимости в психологических исследованиях». Психологический вестник . 66 (6): 423–437. дои : 10.1037/h0020412 . ПМИД 5974619 .

[Gigerenzer_587–606-74] Гигеренцер, Г. (ноябрь 2004 г.). «Бессмысленная статистика». Журнал социально-экономики . 33 (5): 587–606. doi : 10.1016/j.socec.2004.09.033 .

[75] Нанналли, Джам (1960). «Место статистики в психологии». Образовательные и психологические измерения . 20 (4): 641–650. дои : 10.1177/001316446002000401 . S2CID 144813784 .

[76] Ликкен, Дэвид Т. (1991). «А что не так с психологией?». Ясно думая о психологии . 1 :3–39.

[cohen94-77] Джейкоб Коэн (декабрь 1994 г.). «Земля круглая (p < 0,05)». Американский психолог . 49 (12): 997–1003. дои : 10.1037/0003-066X.49.12.997 . S2CID 380942 . Этот документ представляет собой обзор статистической практики, проведенный APA. Коэн был членом оперативной группы, проводившей проверку.

[nickerson-78] Перейти обратно: ^а ^б ^с Никерсон, Раймонд С. (2000). «Проверка значимости нулевой гипотезы: обзор старого и продолжающегося спора». Психологические методы . 5 (2): 241–301. дои : 10.1037/1082-989X.5.2.241 . ПМИД 10937333 . S2CID 28340967 .

[branch-79] Бранч, Марк (2014). «Злокачественные побочные эффекты проверки значимости нулевой гипотезы». Теория и психология . 24 (2): 256–277. дои : 10.1177/0959354314525282 . S2CID 40712136 .

[80] Хантер, Джон Э. (январь 1997 г.). «Необходимо: запрет на тест на значимость». Психологическая наука . 8 (1): 3–7. дои : 10.1111/j.1467-9280.1997.tb00534.x . S2CID 145422959 .

[wilkinson-81] Перейти обратно: ^а ^б Уилкинсон, Лиланд (1999). «Статистические методы в психологических журналах: рекомендации и пояснения». Американский психолог . 54 (8): 594–604. дои : 10.1037/0003-066X.54.8.594 . S2CID 428023 . «Проверка гипотез. Трудно представить ситуацию, в которой дихотомическое решение принять-отклонить лучше, чем сообщать фактическое значение p или, еще лучше, доверительный интервал». (стр. 599). Комитет использовал предостерегающий термин «терпимость», описывая свое решение против запрета проверки гипотез в психологических репортажах. (стр. 603)

[82] «ICMJE: Обязательство публиковать отрицательные исследования» . Архивировано из оригинала 16 июля 2012 года . Проверено 3 сентября 2012 г. Редакторы должны серьезно рассматривать возможность публикации любого тщательно проведенного исследования важного вопроса, интересующего читателей, независимо от того, являются ли результаты основного или любого дополнительного результата статистически значимыми. Неспособность представить или опубликовать результаты из-за отсутствия статистической значимости является важной причиной предвзятости публикации.

[JASNH-83] Веб- сайт журнала статей в поддержку нулевой гипотезы : домашняя страница JASNH . Том 1 номер 1 был опубликован в 2002 году, и все статьи посвящены темам, связанным с психологией.

[84] Хауэлл, Дэвид (2002). Статистические методы психологии (5-е изд.). Даксбери. п. 94 . ISBN 978-0-534-37770-0 .

[WilliamsToth2023-85] Уильямс С., Карсон Р., Тот К. (10 октября 2023 г.). «Выход за рамки значений P в Журнале физиологии: введение в значение величины эффекта и доверительных интервалов» . Дж Физиол . 601 (23): 5131–5133. дои : 10.1113/JP285575 . ПМИД 37815959 . S2CID 263827430 . {{cite journal}}: CS1 maint: несколько имен: список авторов ( ссылка )

[Kruschke_2012-86] Перейти обратно: ^а ^б Крушке, Ю.К. (9 июля 2012 г.). «Байесовская оценка заменяет T-тест» (PDF) . Журнал экспериментальной психологии: Общие сведения . 142 (2): 573–603. дои : 10.1037/a0029146 . ПМИД 22774788 . S2CID 5610231 .

[Kruschke_2018-87] Перейти обратно: ^а ^б Крушке, Ю.К. (8 мая 2018 г.). «Отклонение или принятие значений параметров в байесовской оценке» (PDF) . Достижения в методах и практике психологической науки . 1 (2): 270–280. дои : 10.1177/2515245918771304 . S2CID 125788648 .

[Armstrong1-88] Армстронг, Дж. Скотт (2007). «Проверка значимости вредит прогрессу в прогнозировании» . Международный журнал прогнозирования . 23 (2): 321–327. CiteSeerX 10.1.1.343.9516 . doi : 10.1016/j.ijforecast.2007.03.004 . S2CID 1550979 .

[89] Касс, Р.Э. (1993). Факторы Байеса и неопределенность модели (PDF) (Отчет). Департамент статистики Вашингтонского университета.

[90] Розбум, Уильям В. (1960). «Ошибочность теста значимости нулевой гипотезы» (PDF) . Психологический вестник . 57 (5): 416–428. CiteSeerX 10.1.1.398.9002 . дои : 10.1037/h0042040 . ПМИД 13744252 . «... правильное применение статистики для научных выводов неизбежно связано с широким рассмотрением обратных [так называемых байесовских] вероятностей...» Было с сожалением признано, что априорные распределения вероятностей были доступны «только как субъективное ощущение, отличаться от одного человека к другому, «по крайней мере, в ближайшем будущем».

[91] Бергер, Джеймс (2006). «Аргументы в пользу объективного байесовского анализа» . Байесовский анализ . 1 (3): 385–402. дои : 10.1214/06-ba115 . Перечисляя конкурирующие определения «объективного» байесовского анализа, «Основная цель статистики (на самом деле науки) состоит в том, чтобы найти полностью последовательную объективную байесовскую методологию обучения на данных». Автор выразил мнение, что эта цель «недостижима».

[92] Олдрич, Дж (2008). «РА Фишер о Байесе и теореме Байеса» . Байесовский анализ . 3 (1): 161–170. дои : 10.1214/08-BA306 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[41]

[42]

[43]

[44]

[45]

[46]

[47]

[48]

[49]

[50]

[51]

[52]

[53]

[54]

[55]

[56]

[57]

[58]

[59]

[60]

[61]

[62]

[63]

[64]

[65]

[66]

[67]

[68]

[69]

[70]

[71]

[72]

[73]

[74]

[75]

[76]

[77]

[78]

[79]

[80]

[81]

[82]

[83]

[84]

[85]

[86]

[87]

[88]

[89]

[90]

[91]

[92]