Рассеяние

В физике рассеяние — это широкий спектр физических процессов, при которых движущиеся частицы или излучение той или иной формы, например свет или звук , вынуждены отклоняться от прямой траектории из-за локализованных неоднородностей (включая частицы и излучение) в среде, через которую они проходят. В обычном использовании сюда также входит отклонение отраженного излучения от угла, предсказанного законом отражения . Отражения излучения, подвергающегося рассеянию, часто называют диффузными отражениями , а нерассеянные отражения — зеркальными (зеркальными) отражениями. Первоначально этот термин ограничивался рассеянием света (по крайней мере, начиная с Исаака Ньютона в 17 веке). ^{[ 1 ]}). По мере открытия большего количества «лучевых» явлений идея рассеяния была распространена и на них, так что Уильям Гершель в 1800 году мог сослаться на рассеяние «тепловых лучей» (тогда не признававшихся электромагнитными по своей природе). ^{[ 2 ]} Джон Тиндалл , пионер исследований светорассеяния, отметил связь между светорассеянием и акустическим рассеянием в 1870-х годах. ^{[ 3 ]} Ближе к концу XIX века рассеяние катодных лучей (электронных пучков) ^{[ 4 ]} и рентген ^{[ 5 ]} наблюдалось и обсуждалось. С открытием субатомных частиц (например, Эрнестом Резерфордом в 1911 г. ) ^{[ 6 ]}) и развитие квантовой теории в 20-м веке смысл этого термина стал шире, поскольку было признано, что те же математические основы, которые используются в рассеянии света, могут быть применены ко многим другим явлениям.

Рассеяние может относиться к последствиям столкновений частиц между молекулами, атомами, электронами , фотонами и другими частицами. Примеры включают: рассеяние космических лучей в верхних слоях атмосферы Земли; столкновения частиц внутри ускорителей частиц ; рассеяние электронов атомами газа в люминесцентных лампах; и рассеяние нейтронов внутри ядерных реакторов . ^{[ 7 ]}

Типы неоднородностей, которые могут вызывать рассеяние, иногда называемые рассеивателями или рассеивающими центрами , слишком многочисленны, чтобы их перечислять, но небольшая выборка включает частицы , пузырьки , капли , плотности флуктуации в жидкостях , кристаллиты в поликристаллических твердых телах, дефекты в монокристаллических твердых телах. , шероховатость поверхности , клетки организмов и текстильные волокна в одежде. Влияние таких особенностей на путь практически любого типа распространяющейся волны или движущейся частицы можно описать в рамках теории рассеяния .

Некоторые области, где рассеяние и теория рассеяния имеют важное значение, включают радиолокационное зондирование, медицинский ультразвук , проверку полупроводниковых пластин , мониторинг процесса полимеризации , акустическую мозаику, связь в свободном пространстве и компьютерные изображения . ^{[ 8 ]} Теория рассеяния частиц важна в таких областях, как физика элементарных частиц , атомная, молекулярная и оптическая физика , ядерная физика и астрофизика . В физике элементарных частиц квантовое взаимодействие и рассеяние фундаментальных частиц описывается матрицей рассеяния или S-матрицей , введенной и разработанной Джоном Арчибальдом Уилером и Вернером Гейзенбергом . ^{[ 9 ]}

Рассеяние количественно оценивается с использованием множества различных концепций, включая сечение рассеяния (σ), коэффициенты затухания , функцию распределения двунаправленного рассеяния (BSDF), S-матрицы и среднюю длину свободного пробега .

Однократное и многократное рассеяние

Когда излучение рассеивается только одним локализованным рассеивающим центром, это называется однократным рассеянием . Чаще всего рассеивающие центры группируются вместе; в таких случаях излучение может рассеиваться многократно, что известно как многократное рассеяние . ^{[ 11 ]} Основное различие между эффектами однократного и многократного рассеяния заключается в том, что однократное рассеяние обычно можно рассматривать как случайное явление, тогда как многократное рассеяние, что несколько противоречит интуиции, можно моделировать как более детерминированный процесс, поскольку совокупные результаты большого количества событий рассеяния имеют тенденцию к усреднению. Таким образом, многократное рассеяние часто можно хорошо смоделировать с помощью теории диффузии . ^{[ 12 ]}

Поскольку местоположение отдельного рассеивающего центра относительно пути излучения обычно не известно, результат, который имеет тенденцию сильно зависеть от точной падающей траектории, кажется наблюдателю случайным. Примером такого типа рассеяния может служить электрон, попадающий в атомное ядро. В этом случае точное положение атома относительно пути электрона неизвестно и не поддается измерению, поэтому точную траекторию электрона после столкновения невозможно предсказать. Поэтому однократное рассеяние часто описывается распределениями вероятностей.

При многократном рассеянии случайность взаимодействия имеет тенденцию усредняться большим количеством событий рассеяния, так что конечный путь излучения оказывается детерминированным распределением интенсивности. Примером этого может служить луч света, проходящий сквозь густой туман . Многократное рассеяние во многом аналогично диффузии , а термины многократное рассеяние и диффузия взаимозаменяемы во многих контекстах. Оптические элементы, предназначенные для создания многократного рассеяния, известны как диффузоры . ^{[ 13 ]} Когерентное обратное рассеяние — усиление обратного рассеяния , возникающее при многократном рассеянии когерентного излучения случайной средой, — обычно связывают со слабой локализацией .

Однако не все однократные рассеяния являются случайными. Например, хорошо контролируемый лазерный луч можно точно расположить, чтобы рассеять микроскопическую частицу с детерминированным результатом. Подобные ситуации также встречаются при рассеянии радиолокационных сигналов , когда целями обычно являются макроскопические объекты, такие как люди или самолеты.

Точно так же многократное рассеяние иногда может иметь несколько случайные результаты, особенно при когерентном излучении. Случайные флуктуации многократно рассеянной интенсивности когерентного излучения называются спеклами . Спекл также возникает, если несколько частей когерентной волны рассеиваются из разных центров. В некоторых редких случаях многократное рассеяние может включать лишь небольшое количество взаимодействий, так что случайность не усредняется полностью. Эти системы считаются одними из самых сложных для точного моделирования.

Описание рассеяния и различие между однократным и многократным рассеянием тесно связаны с корпускулярно-волновым дуализмом .

Теория

Теория рассеяния является основой для изучения и понимания рассеяния волн и частиц . Прозаически рассеяние волн соответствует столкновению и рассеянию волны с каким-либо материальным объектом, например (солнечным светом), рассеянным каплями дождя с образованием радуги . К рассеянию относятся также взаимодействие бильярдных шаров на столе, резерфордовское рассеяние (или изменение угла) альфа-частиц на золота ядрах , брэгговское рассеяние (или дифракция) электронов и рентгеновских лучей на кластере атомов, а также неупругое рассеяние. осколка деления при его прохождении через тонкую фольгу. Точнее, рассеяние состоит в исследовании того, как решения уравнений в частных производных , свободно распространяющиеся «в далеком прошлом», собираются вместе и взаимодействуют друг с другом или с граничным условием , а затем распространяются «в далекое будущее».

Задача прямого рассеяния – это задача определения распределения рассеянного излучения/потока частиц на основе характеристик рассеивателя. Обратная задача рассеяния — это задача определения характеристик объекта (например, его формы, внутреннего строения) по данным измерений излучения или частиц, рассеянных от объекта.

Затухание из-за рассеяния

Эквивалентные величины, используемые в теории рассеяния на составных образцах, но с различными единицами измерения.

Когда целью является совокупность множества центров рассеяния, относительное положение которых меняется непредсказуемо, принято думать об уравнении дальности, аргументы которого принимают разные формы в разных областях применения. В простейшем случае рассмотрим взаимодействие, при котором частицы удаляются из «нерассеянного луча» с равномерной скоростью, пропорциональной числу падающих частиц на единицу площади в единицу времени ( $I$ ), то есть что

{\frac {dI}{dx}}=-QI\,\!

где Q — коэффициент взаимодействия, а x — расстояние, пройденное в цели.

Вышеупомянутое обыкновенное дифференциальное уравнение первого порядка имеет решения вида:

I=I_{o}e^{-Q\Delta x}=I_{o}e^{-{\frac {\Delta x}{\lambda }}}=I_{o}e^{-\sigma (\eta \Delta x)}=I_{o}e^{-{\frac {\rho \Delta x}{\tau }}},

где I _o - начальный поток, длина пути Δx ≡ x - x _o , второе равенство определяет длину свободного пробега взаимодействия λ, третье использует количество целей на единицу объема η для определения площади поперечного сечения σ, а последний использует целевую массовую плотность ρ для определения средней длины свободного пробега τ. Следовательно, между этими величинами осуществляется преобразование через Q = 1/ λ = ησ = ρ/τ , как показано на рисунке слева.

В спектроскопии электромагнитного поглощения, например, коэффициент взаимодействия (например, Q в см ⁻¹) по-разному называется непрозрачностью , коэффициентом поглощения и коэффициентом ослабления . В ядерной физике сечения площадей (например, σ в амбарах или единицах по 10 ⁻²⁴ см ²), плотность среднего свободного пробега (например, τ в граммах/см ²), и обратный ему массовый коэффициент затухания (например, в см ²/грамм) или площадь на нуклон — все они популярны, тогда как в электронной микроскопии неупругий средний свободный пробег ^{[ 14 ]} (например, λ в нанометрах) часто обсуждается ^{[ 15 ]} вместо.

Упругое и неупругое рассеяние

Термин «упругое рассеяние» подразумевает, что внутренние состояния рассеивающих частиц не изменяются и, следовательно, они выходят из процесса рассеяния неизмененными. При неупругом рассеянии, напротив, внутреннее состояние частиц изменяется, что может означать возбуждение части электронов рассеивающего атома или полное уничтожение рассеивающей частицы и рождение совершенно новых частиц.

Пример рассеяния в квантовой химии особенно поучителен, поскольку теория достаточно сложна, но при этом имеет хорошую основу для интуитивного понимания. Когда два атома рассеиваются друг от друга, их можно понимать как в связанном состоянии решения некоторого дифференциального уравнения . Так, например, атом водорода соответствует решению уравнения Шрёдингера с отрицательным обратным степенным (т. е. притягивающим кулоновским) центральным потенциалом . Рассеяние двух атомов водорода нарушит состояние каждого атома, в результате чего один или оба станут возбужденными или даже ионизированными , что представляет собой процесс неупругого рассеяния.

Термин « глубоконеупругое рассеяние » относится к особому типу экспериментов по рассеянию в физике элементарных частиц.

Математическая основа

В математике теория рассеяния имеет дело с более абстрактной формулировкой того же набора понятий. Например, если известно, что дифференциальное уравнение имеет несколько простых локализованных решений, и эти решения являются функцией одного параметра, этот параметр может взять на себя концептуальную роль времени . Затем возникает вопрос, что может произойти, если два таких решения будут установлены далеко друг от друга, в «далеком прошлом», и их заставят двигаться навстречу друг другу, взаимодействовать (под ограничениями дифференциального уравнения), а затем разойтись в разные стороны. «будущее». Затем матрица рассеяния объединяет решения из «далекого прошлого» с решениями из «далекого будущего».

Решения дифференциальных уравнений часто задаются на многообразиях . средство решения требует изучения спектра оператора на Часто многообразии. В результате решения часто имеют спектр, который можно отождествить с гильбертовым пространством , а рассеяние описывается неким отображением — матрицей S — на гильбертовых пространствах. Решения с дискретным спектром соответствуют связанным состояниям в квантовой механике, а непрерывный спектр — состояниям рассеяния. Тогда при изучении неупругого рассеяния возникает вопрос, как смешиваются дискретные и непрерывные спектры.

Важным и заметным достижением является обратное преобразование рассеяния , занимающее центральное место в решении многих точно решаемых моделей .

Теоретическая физика

В математической физике теория рассеяния является основой для изучения и понимания взаимодействия или рассеяния решений уравнений в частных производных . В акустике дифференциальное уравнение — это волновое уравнение , а рассеяние изучает, как его решения — звуковые волны — рассеиваются от твердых объектов или распространяются через неоднородные среды (например, звуковые волны, в морской воде , исходящие с подводной лодки ). В случае классической электродинамики рассеяние света или радиоволн дифференциальное уравнение снова является волновым уравнением, и изучается . В физике элементарных частиц используются уравнения квантовой электродинамики , квантовой хромодинамики и стандартной модели , решения которых соответствуют фундаментальным частицам .

В обычной квантовой механике , которая включает в себя квантовую химию , соответствующим уравнением является уравнение Шрёдингера , хотя эквивалентные формулировки, такие как уравнение Липпмана-Швингера и уравнения Фаддеева , также широко используются. Интересующие решения описывают долговременное движение свободных атомов, молекул, фотонов, электронов и протонов. Сценарий таков: несколько частиц собираются вместе на бесконечном расстоянии. Затем эти реагенты сталкиваются, при необходимости вступая в реакцию, разрушаясь или создавая новые частицы. Продукты и неиспользованные реагенты затем снова улетают в бесконечность. (Атомы и молекулы для наших целей фактически являются частицами. Кроме того, в повседневных обстоятельствах создаются и уничтожаются только фотоны.) Решения показывают, в каких направлениях продукты с наибольшей вероятностью улетят и как быстро. Они также раскрывают вероятность различных реакций, творений и распадов. Существует два преобладающих метода поиска решений проблем рассеяния: парциальный волновой анализ и борновское приближение .

Электромагнетизм

Диаграмма Фейнмана рассеяния между двумя электронами при испускании виртуального фотона

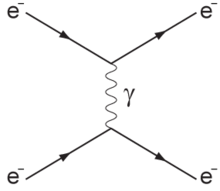
Электромагнитные волны являются одной из наиболее известных и наиболее часто встречающихся форм излучения, подвергающегося рассеянию. ^{[ 16 ]} Рассеяние света и радиоволн (особенно в радиолокации ) имеет особое значение. Некоторые различные аспекты электромагнитного рассеяния достаточно различны, чтобы иметь условные названия. Основными формами упругого рассеяния света (с незначительной передачей энергии) являются рассеяние Рэлея и рассеяние Ми . Неупругое рассеяние включает рассеяние Бриллюэна , комбинационное рассеяние , неупругое рентгеновское рассеяние и рассеяние Комптона .

Рассеяние света — один из двух основных физических процессов, которые способствуют видимому появлению большинства объектов, второй — поглощение. Поверхности, описываемые как белые, обязаны своим появлением многократному рассеянию света внутренними или поверхностными неоднородностями объекта, например границами прозрачных микроскопических кристаллов, из которых состоит камень, или микроскопическими волокнами в листе бумаги. В более общем смысле блеск (или блеск , или сияние ) поверхности определяется рассеянием. Поверхности с высокой степенью рассеивания описываются как матовые или матовые, тогда как отсутствие рассеяния на поверхности приводит к глянцевому виду, как в случае с полированным металлом или камнем.

Спектральное поглощение, избирательное поглощение определенных цветов, определяет цвет большинства объектов с некоторой модификацией за счет упругого рассеяния . Очевидный синий цвет вен кожи является типичным примером того, как спектральное поглощение и рассеяние играют важную и сложную роль в окраске. Рассеяние света также может создавать цвета без поглощения, часто оттенки синего, как в случае с небом ( рэлеевское рассеяние человека ), голубой радужной оболочкой и перьями некоторых птиц (Prum et al. 1998). Однако резонансное рассеяние света в наночастицах может давать множество различных насыщенных и ярких оттенков, особенно когда поверхностный плазмонный резонанс (Roqué et al. 2006). задействован ^{[ 17 ]}^{[ 18 ]}

Модели рассеяния света можно разделить на три области на основе безразмерного параметра размера α , который определяется как: $\alpha =\pi D_{\text{p}}/\lambda ,$ где πD _p — длина окружности частицы, λ — длина волны падающего излучения в среду. В зависимости от значения α эти домены следующие:

α ≪ 1: рэлеевское рассеяние (маленькая частица по сравнению с длиной волны света);
α ≈ 1: рассеяние Ми (размер частиц примерно равен длине волны света, справедливо только для сфер);
α ≫ 1: геометрическое рассеяние (частица намного больше длины волны света).

Рэлеевское рассеяние — это процесс, при котором электромагнитное излучение (включая свет) рассеивается небольшим сферическим объемом с разными показателями преломления, таким как частица, пузырек, капля или даже флуктуация плотности. Этот эффект был впервые успешно смоделирован лордом Рэлеем , от которого он и получил свое название. Чтобы применить модель Рэлея, диаметр сферы должен быть намного меньше длины волны ( λ ) рассеянной волны; обычно верхний предел принимается равным примерно 1/10 длины волны. В этом размерном режиме точная форма рассеивающего центра обычно не имеет большого значения и часто может рассматриваться как сфера эквивалентного объема. Собственное рассеяние, которому подвергается излучение при прохождении через чистый газ, обусловлено микроскопическими флуктуациями плотности при движении молекул газа, которые обычно достаточно малы по масштабу, чтобы можно было применить модель Рэлея. Этот механизм рассеяния является основной причиной синего цвета земного неба в ясный день, поскольку более короткие синие волны солнечного света, проходящего над головой, рассеиваются сильнее, чем более длинные красные волны, согласно знаменитому закону Рэлея 1/. л ⁴ связь. Наряду с поглощением такое рассеяние является основной причиной ослабления излучения атмосферой . ^{[ 19 ]} Степень рассеяния варьируется в зависимости от отношения диаметра частицы к длине волны излучения, а также от многих других факторов, включая поляризацию , угол и когерентность . ^{[ 20 ]}

Для больших диаметров проблема электромагнитного рассеяния сферами была впервые решена Густавом Ми , и поэтому рассеяние сферами, размер которых превышает диапазон Рэлея, обычно называют рассеянием Ми . В режиме Ми форма рассеивающего центра становится гораздо более значимой, и теория хорошо применима только к сферам и, с некоторыми модификациями, сфероидам и эллипсоидам . Решения в замкнутой форме для рассеяния на некоторых других простых формах существуют, но для произвольных форм не известно общего решения в замкнутой форме.

Рассеяние Ми и Рэлея считаются процессами упругого рассеяния, при которых энергия (и, следовательно, длина волны и частота) света существенно не изменяется. Однако электромагнитное излучение, рассеянное движущимися рассеивающими центрами, претерпевает доплеровский сдвиг , который можно обнаружить и использовать для измерения скорости рассеивающего центра(ов) с помощью таких методов, как лидар и радар . Этот сдвиг предполагает небольшое изменение энергии.

При значениях отношения диаметра частицы к длине волны более примерно 10 законов геометрической оптики в большинстве случаев достаточно для описания взаимодействия света с частицей. Теорию Ми все еще можно использовать для этих более крупных сфер, но решение часто становится громоздким в числовом отношении.

Для моделирования рассеяния в тех случаях, когда модели Рэлея и Ми неприменимы, например, для более крупных частиц неправильной формы, можно использовать множество численных методов. Наиболее распространенными являются методы конечных элементов , которые решают уравнения Максвелла для определения распределения рассеянного электромагнитного поля. Существуют сложные пакеты программного обеспечения, которые позволяют пользователю указывать показатель преломления или показатели характеристики рассеяния в пространстве, создавая двух-, а иногда и трехмерную модель структуры. Для относительно больших и сложных структур эти модели обычно требуют значительного времени выполнения на компьютере.

Электрофорез предполагает миграцию макромолекул под действием электрического поля. ^{[ 21 ]} Электрофоретическое рассеяние света предполагает пропускание электрического поля через жидкость, которое заставляет частицы двигаться. Чем больше заряд частиц, тем быстрее они могут двигаться. ^{[ 22 ]}

См. также

Ссылки

^ Ньютон, Исаак (1665). «Письмо г-на Исаака Ньютона, содержащее его новую теорию света и цвета». Философские труды . 6 . Лондонское королевское общество: 3087.
^ Гершель, Уильям (1800). «Опыты с солнечными и земными лучами, вызывающими тепло». Философские труды . ХС . Лондонское королевское общество: 770.
^ Тиндаль, Джон (1874). «Об атмосфере как носителе звука» . Философские труды Лондонского королевского общества . 164 : 221. Бибкод : 1874RSPT..164..183T . JSTOR 109101 .
^ Мерритт, Эрнест (5 октября 1898 г.). «Магнитное отклонение диффузно отраженных катодных лучей» . Электрический обзор . 33 (14): 217.
^ «Недавние работы с рентгеновскими лучами» . Природа . 53 (1383): 613–616. 30 апреля 1896 г. Бибкод : 1896Natur..53..613. . дои : 10.1038/053613a0 . S2CID 4023635 .
^ Резерфорд, Э. (1911). «Рассеяние α- и β-лучей материей и строение атома». Философский журнал . 6:21 .
^ Сейнфельд , Джон Х.; Пандис, Спирос Н. (2006). Химия и физика атмосферы - от загрязнения воздуха до изменения климата (2-е изд.). Джон Уайли и сыновья, Inc. ISBN 0-471-82857-2
^ Колтон, Дэвид; Райнер Кресс (1998). Обратная акустическая и электромагнитная теория рассеяния . Спрингер . ISBN 978-3-540-62838-5 .
^ Нахтманн, Отто (1990). Физика элементарных частиц: понятия и явления . Спрингер Верлаг. стр. 80–93. ISBN 3-540-50496-6 .
^ «Зодиакальное сияние освещает паранальное небо» . Картинка недели ESO . Европейская южная обсерватория . Проверено 2 декабря 2013 г.
^ Гонис, Антониос; Уильям Х. Батлер (1999). Множественное рассеяние в твердых телах . Спрингер . ISBN 978-0-387-98853-5 .
^ Гонис, Антониос; Уильям Х. Батлер (1999). Множественное рассеяние в твердых телах . Спрингер . ISBN 978-0-387-98853-5 .
^ Стовер, Джон К. (1995). Оптическое рассеяние: измерение и анализ . SPIE Оптическая инженерия. ISBN 978-0-8194-1934-7 .
^ РФ Эгертон (1996) Спектроскопия потерь энергии электронов в электронном микроскопе (второе издание, Plenum Press, Нью-Йорк) ISBN 0-306-45223-5
^ Людвиг Реймер (1997) Просвечивающая электронная микроскопия: физика формирования изображений и микроанализ (четвертое издание, Springer, Берлин) ISBN 3-540-62568-2
^ Колтон, Дэвид; Райнер Кресс (1998). Обратная акустическая и электромагнитная теория рассеяния . Спрингер . ISBN 978-3-540-62838-5 .
^ Борен, Крейг Ф.; Дональд Р. Хаффман (1983). Поглощение и рассеяние света малыми частицами . Уайли . ISBN 978-0-471-29340-8 .
^ Роке, Жозеф; Дж. Молера; П. Шау; Э. Пантос; М. Вендрелл-Саз (2006). «Нанокристаллы меди и серебра в глянцевых свинцовых глазурях: развитие и оптические свойства». Журнал Европейского керамического общества . 26 (16): 3813–3824. doi : 10.1016/j.jeurceramsoc.2005.12.024 .
^ Сейнфельд , Джон Х.; Пандис, Спирос Н. (2006). Химия и физика атмосферы - от загрязнения воздуха до изменения климата (2-е изд.). Джон Уайли и сыновья, Inc. ISBN 0-471-82857-2
^ Прум, Ричард О.; Родольфо Х. Торрес ; Скотт Уильямсон; Ян Дейк (1998). «Когерентное рассеяние света голубыми перьями». Природа . 396 (6706): 28–29. Бибкод : 1998Natur.396...28P . дои : 10.1038/23838 . S2CID 4393904 .
^ «Понимание электрофоретического рассеяния света» . Технология Уайатт .
^ «Светорассеяние» . Малверн Паналитикал .

Внешние ссылки

[1] Ньютон, Исаак (1665). «Письмо г-на Исаака Ньютона, содержащее его новую теорию света и цвета». Философские труды . 6 . Лондонское королевское общество: 3087.

[2] Гершель, Уильям (1800). «Опыты с солнечными и земными лучами, вызывающими тепло». Философские труды . ХС . Лондонское королевское общество: 770.

[3] Тиндаль, Джон (1874). «Об атмосфере как носителе звука» . Философские труды Лондонского королевского общества . 164 : 221. Бибкод : 1874RSPT..164..183T . JSTOR 109101 .

[4] Мерритт, Эрнест (5 октября 1898 г.). «Магнитное отклонение диффузно отраженных катодных лучей» . Электрический обзор . 33 (14): 217.

[5] «Недавние работы с рентгеновскими лучами» . Природа . 53 (1383): 613–616. 30 апреля 1896 г. Бибкод : 1896Natur..53..613. . дои : 10.1038/053613a0 . S2CID 4023635 .

[6] Резерфорд, Э. (1911). «Рассеяние α- и β-лучей материей и строение атома». Философский журнал . 6:21 .

[7] Сейнфельд , Джон Х.; Пандис, Спирос Н. (2006). Химия и физика атмосферы - от загрязнения воздуха до изменения климата (2-е изд.). Джон Уайли и сыновья, Inc. ISBN 0-471-82857-2

[8] Колтон, Дэвид; Райнер Кресс (1998). Обратная акустическая и электромагнитная теория рассеяния . Спрингер . ISBN 978-3-540-62838-5 .

[9] Нахтманн, Отто (1990). Физика элементарных частиц: понятия и явления . Спрингер Верлаг. стр. 80–93. ISBN 3-540-50496-6 .

[10] «Зодиакальное сияние освещает паранальное небо» . Картинка недели ESO . Европейская южная обсерватория . Проверено 2 декабря 2013 г.

[11] Гонис, Антониос; Уильям Х. Батлер (1999). Множественное рассеяние в твердых телах . Спрингер . ISBN 978-0-387-98853-5 .

[12] Гонис, Антониос; Уильям Х. Батлер (1999). Множественное рассеяние в твердых телах . Спрингер . ISBN 978-0-387-98853-5 .

[13] Стовер, Джон К. (1995). Оптическое рассеяние: измерение и анализ . SPIE Оптическая инженерия. ISBN 978-0-8194-1934-7 .

[14] РФ Эгертон (1996) Спектроскопия потерь энергии электронов в электронном микроскопе (второе издание, Plenum Press, Нью-Йорк) ISBN 0-306-45223-5

[15] Людвиг Реймер (1997) Просвечивающая электронная микроскопия: физика формирования изображений и микроанализ (четвертое издание, Springer, Берлин) ISBN 3-540-62568-2

[16] Колтон, Дэвид; Райнер Кресс (1998). Обратная акустическая и электромагнитная теория рассеяния . Спрингер . ISBN 978-3-540-62838-5 .

[17] Борен, Крейг Ф.; Дональд Р. Хаффман (1983). Поглощение и рассеяние света малыми частицами . Уайли . ISBN 978-0-471-29340-8 .

[18] Роке, Жозеф; Дж. Молера; П. Шау; Э. Пантос; М. Вендрелл-Саз (2006). «Нанокристаллы меди и серебра в глянцевых свинцовых глазурях: развитие и оптические свойства». Журнал Европейского керамического общества . 26 (16): 3813–3824. doi : 10.1016/j.jeurceramsoc.2005.12.024 .

[19] Сейнфельд , Джон Х.; Пандис, Спирос Н. (2006). Химия и физика атмосферы - от загрязнения воздуха до изменения климата (2-е изд.). Джон Уайли и сыновья, Inc. ISBN 0-471-82857-2

[20] Прум, Ричард О.; Родольфо Х. Торрес ; Скотт Уильямсон; Ян Дейк (1998). «Когерентное рассеяние света голубыми перьями». Природа . 396 (6706): 28–29. Бибкод : 1998Natur.396...28P . дои : 10.1038/23838 . S2CID 4393904 .

[ElectrophoresisWyatt-21] «Понимание электрофоретического рассеяния света» . Технология Уайатт .

[ElectrophoreticMalvPan-22] «Светорассеяние» . Малверн Паналитикал .

[ 1 ]

[ 2 ]

[ 3 ]

[ 4 ]

[ 5 ]

[ 6 ]

[ 7 ]

[ 8 ]

[ 9 ]

[ 10 ]

[ 11 ]

[ 12 ]

[ 13 ]

[ 14 ]

[ 15 ]

[ 16 ]

[ 17 ]

[ 18 ]

[ 19 ]

[ 20 ]

[ 21 ]

[ 22 ]

v т и Квантовая механика
Background	Introduction History Timeline Classical mechanics Old quantum theory Glossary
Fundamentals	Born rule Bra–ket notation Complementarity Density matrix Energy level Ground state Excited state Degenerate levels Zero-point energy Entanglement Hamiltonian Interference Decoherence Measurement Nonlocality Quantum state Superposition Tunnelling Scattering theory Symmetry in quantum mechanics Uncertainty Wave function Collapse Wave–particle duality
Formulations	Formulations Heisenberg Interaction Matrix mechanics Schrödinger Path integral formulation Phase space
Equations	Dirac Klein–Gordon Pauli Rydberg Schrödinger
Interpretations	Bayesian Consistent histories Copenhagen de Broglie–Bohm Ensemble Hidden-variable Local Superdeterminism Many-worlds Objective collapse Quantum logic Relational Transactional Von Neumann–Wigner
Experiments	Bell test Davisson–Germer Delayed-choice quantum eraser Double-slit Franck–Hertz Mach–Zehnder interferometer Elitzur–Vaidman Popper Quantum eraser Stern–Gerlach Wheeler's delayed choice
Science	Quantum biology Quantum chemistry Quantum chaos Quantum cosmology Quantum differential calculus Quantum dynamics Quantum geometry Quantum measurement problem Quantum mind Quantum stochastic calculus Quantum spacetime
Technology	Quantum algorithms Quantum amplifier Quantum bus Quantum cellular automata Quantum finite automata Quantum channel Quantum circuit Quantum complexity theory Quantum computing Timeline Quantum cryptography Quantum electronics Quantum error correction Quantum imaging Quantum image processing Quantum information Quantum key distribution Quantum logic Quantum logic gates Quantum machine Quantum machine learning Quantum metamaterial Quantum metrology Quantum network Quantum neural network Quantum optics Quantum programming Quantum sensing Quantum simulator Quantum teleportation
Extensions	Quantum fluctuation Casimir effect Quantum statistical mechanics Quantum field theory History Quantum gravity Relativistic quantum mechanics
Related	Schrödinger's cat in popular culture Wigner's friend EPR paradox Quantum mysticism
Category