Валидность (логика)

В логике , особенно в дедуктивном рассуждении , аргумент действителен посылки тогда и только тогда, когда он принимает форму, которая делает невозможным, чтобы были истинными , а заключение, тем не менее, было ложным . ^[1] Для валидного аргумента не требуется наличие действительно истинных посылок. ^[2] но иметь предпосылки, которые, если бы они были истинными, гарантировали бы истинность вывода аргумента. Действительные аргументы должны быть четко выражены с помощью предложений, называемых правильно построенными формулами (также называемыми wffs или просто формулами ).

Обоснованность логической аргумента может быть проверена, доказана или опровергнута и зависит от его формы . ^[3]

Аргументы

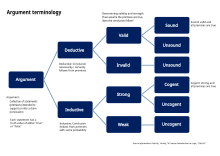
В логике аргумент — это набор утверждений, выражающих предпосылки (все, что состоит из эмпирических свидетельств и аксиоматических истин) и вывод, основанный на фактах.

Аргумент действителен тогда и только тогда, когда ложный вывод был бы противоречивым, если все посылки истинны. ^[3] Обоснованность не требует истинности посылок, а просто требует, чтобы вывод следовал из первых, не нарушая правильности логической формы . Если также доказано, что посылки действительного аргумента верны, его называют здравым . ^[3]

Соответствующее условное выражение действительному аргументу является логической истиной , а отрицание соответствующего условного выражения является противоречием . Заключение является логическим следствием его предпосылок.

Аргумент, который недействителен, называется «недействительным».

Примером валидного (и здравого ) аргумента может служить следующий известный силлогизм :

Все люди смертны. ( Истинный )

Сократ – мужчина. ( Истинный )

Следовательно, Сократ смертен. ( Истинный )

Что делает этот аргумент действительным, так это не то, что он имеет истинные посылки и истинный вывод, а логическая необходимость заключения, учитывая две посылки. Аргумент был бы столь же веским, если бы посылки и вывод были ложными. Следующий аргумент имеет ту же логическую форму , но с ложными предпосылками и ложным выводом, и он одинаково действителен:

Все чашки зеленые. ( ЛОЖЬ )

Сократ – это чаша. ( ЛОЖЬ )

Следовательно, Сократ зеленый. ( ЛОЖЬ )

Независимо от того, как могла бы быть устроена Вселенная, никогда не может быть так, чтобы эти аргументы одновременно имели истинные предпосылки и ложный вывод. Приведенным выше аргументам можно противопоставить следующий неверный аргумент:

Все люди бессмертны. ( ЛОЖЬ )

Сократ – мужчина. ( Истинный )

Следовательно, Сократ смертен. ( Истинный )

В этом случае вывод противоречит дедуктивной логике предыдущих посылок, а не вытекает из нее. Следовательно, этот аргумент логически «недействителен», хотя в общих чертах вывод можно считать «истинным». Посылка «Все люди бессмертны» также будет считаться ложной вне рамок классической логики. Однако внутри этой системы «истина» и «ложь» по существу функционируют скорее как математические состояния, такие как двоичные 1 и 0, чем как философские концепции, обычно связанные с этими терминами.

Стандартная точка зрения состоит в том, что достоверность аргумента зависит от его логической формы. Логики используют множество методов для представления логической формы аргумента. Простой пример, примененный к двум из приведенных выше иллюстраций, таков: пусть буквы «P», «Q» и «S» обозначают соответственно группу людей, группу смертных и Сократа. Используя эти символы, первый аргумент можно сократить как:

Все P суть Q.

С — это П.

Следовательно, S является Q.

Аналогично, третий аргумент становится:

Не все P являются Q.

С — это П.

Следовательно, S является Q.

Аргумент называется формально действительным, если он обладает структурной самосогласованностью, т. е. если все операнды между посылками истинны, полученное заключение также всегда истинно. В третьем примере исходные посылки не могут логически привести к заключению и поэтому классифицируются как недействительный аргумент.

Действительная формула

Формула формального языка является допустимой формулой тогда и только тогда, когда она истинна при любой возможной интерпретации языка. В логике высказываний они являются тавтологиями .

Заявления

Утверждение можно назвать валидным, то есть логической истиной, если оно истинно во всех интерпретациях.

разумность

На достоверность вывода не влияет истинность посылки или истинность заключения. Следующий вывод совершенно справедлив:

Все животные живут на Марсе. ( ЛОЖЬ )

Все люди — животные. ( Истинный )

Следовательно, все люди живут на Марсе. ( ЛОЖЬ )

Проблема с аргументом в том, что он несостоятелен . Чтобы дедуктивный аргумент был обоснованным, он должен быть действительным и все посылки должны быть истинными. ^[3]

Удовлетворенность

Теория моделей анализирует формулы относительно определенных классов интерпретации в подходящих математических структурах. В таком прочтении формула действительна, если все подобные интерпретации делают ее истинной. Вывод является действительным, если все интерпретации, подтверждающие посылки, подтверждают вывод. Это известно как семантическая достоверность . ^[4]

Сохранение

При валидности , сохраняющей истину , интерпретация, при которой всем переменным присваивается значение истинности «истина», дает значение истинности «истина».

В валидности с сохранением ложных значений интерпретация, при которой всем переменным присваивается значение истинности «ложь», дает значение истинности «ложь». ^[5]

Свойства консервации	Логические связочные предложения
Истинное и ложное сохранение:	Предложение • Логический союз (И, $\land$ ) • Логическая дизъюнкция (ИЛИ, $\lor$ )
Только истинное сохранение:	Тавтология ( $\top$ ) • Двуусловный (XNOR, $\leftrightarrow$ ) • Импликация ( $\rightarrow$ ) • Обратная импликация ( $\leftarrow$ )
Только ложное сохранение:	Противоречие ( $\bot$ ) • Исключительная дизъюнкция (XOR, $\oplus$ ) • Непричастность ( $\nrightarrow$ ) • Обратная неимпликация ( $\nleftarrow$ )
Несохраняющиеся:	Отрицание ( $\neg$ ) • Альтернативное отрицание (NAND, $\uparrow$ ) • Совместное отрицание (NOR, $\downarrow$ )

См. также

Ссылки

^ Валидность и обоснованность - Интернет-энциклопедия философии
^ Дж. Си Билл и Грег Рестолл, «Логическое следствие» , Стэнфордская энциклопедия философии (выпуск осенью 2014 г.).
↑ Перейти обратно: Перейти обратно: ^а ^б ^с ^д Генслер, Гарри Дж. (6 января 2017 г.). Введение в логику (Третье изд.). Нью-Йорк: Рутледж. ISBN 978-1-138-91058-4 . OCLC 957680480 .
^ Гамма LTF , Логика, язык и значение: Введение в логику , University of Chicago Press, 1991, стр. 115.
^ Роберт Коган, Критическое мышление: шаг за шагом , University Press of America, 1998, стр. 48 .

Дальнейшее чтение

Барвайз, Джон ; Этчеменди, Джон . Язык, доказательства и логика (1999): 42.
Бир, Фрэнсис А. « Обоснованность: взгляд на политологию », Social Epistemology 7, 1 (1993): 85-105.

[1] Валидность и обоснованность - Интернет-энциклопедия философии

[2] Дж. Си Билл и Грег Рестолл, «Логическое следствие» , Стэнфордская энциклопедия философии (выпуск осенью 2014 г.).

[:0-3] Перейти обратно: Перейти обратно: ^а ^б ^с ^д Генслер, Гарри Дж. (6 января 2017 г.). Введение в логику (Третье изд.). Нью-Йорк: Рутледж. ISBN 978-1-138-91058-4 . OCLC 957680480 .

[4] Гамма LTF , Логика, язык и значение: Введение в логику , University of Chicago Press, 1991, стр. 115.

[5] Роберт Коган, Критическое мышление: шаг за шагом , University Press of America, 1998, стр. 48 .

[1]

[2]

[3]

[4]

[5]