Частота (статистика)

В статистике частота . или абсолютная события частота $i$ это число $n_{i}$ сколько раз наблюдение произошло/зафиксировано в ходе эксперимента или исследования. ^[1]^: 12–19 Эти частоты часто изображаются графически или в табличной форме.

Типы

Кумулятивная частота — это сумма абсолютных частот всех событий в определенной точке или ниже в упорядоченном списке событий. ^[1]^: 17–19

( Относительная частота или эмпирическая вероятность ) события — это абсолютная частота, нормированная на общее количество событий:

f_{i}={\frac {n_{i}}{N}}={\frac {n_{i}}{\sum _{j}n_{j}}}.

Значения $f_{i}$ на все мероприятия $i$ можно построить график для получения частотного распределения.

В случае, когда $n_{i}=0$ наверняка $i$ , псевдосчетчики можно добавить .

Изображение частотных распределений

Гистограмма времени в пути (на работу), перепись населения США 2000 г.

Гистограмма с категориальной переменной «Страна» для дискретного набора данных.

Horizontal 3D bar chart

Круговая диаграмма населения мира по странам

Различные способы изображения частотных распределений

Распределение частот показывает обобщенную группировку данных, разделенных на взаимоисключающие классы и количество вхождений в класс. Это способ отображения неорганизованных данных, в частности, для отображения результатов выборов, доходов людей в определенном регионе, продаж продукта за определенный период, сумм студенческих кредитов выпускников и т. д. Некоторые графики, которые можно использовать с Распределения частот представляют собой гистограммы , линейные диаграммы , гистограммы и круговые диаграммы . Распределения частот используются как для качественных, так и для количественных данных.

Строительство

Определитесь с количеством занятий. Слишком много классов или слишком мало классов могут не раскрыть основную форму набора данных, а также будет сложно интерпретировать такое частотное распределение. Идеальное количество классов можно определить или оценить по формуле: ${\text{number of classes}}=C=1+3.3\log n$ (логарифм по основанию 10) или по выбора квадратного корня формуле $C={\sqrt {n}}$ где n — общее количество наблюдений в данных. (Последнее будет слишком большим для больших наборов данных, таких как статистика населения.) Однако эти формулы не являются жестким правилом, и результирующее количество классов, определяемое формулой, не всегда может точно соответствовать обрабатываемым данным.
Рассчитайте диапазон данных (Диапазон = Макс – Мин), найдя минимальное и максимальное значения данных. Диапазон будет использоваться для определения интервала класса или ширины класса.
Определите ширину классов, обозначенную h и полученную как $h={\frac {\text{range}}{\text{number of classes}}}$ (при условии, что интервалы между занятиями одинаковы для всех занятий).

Обычно интервал между классами или ширина класса одинакова для всех классов. Все классы вместе взятые должны охватывать как минимум расстояние от наименьшего (минимального) значения в данных до самого высокого (максимального) значения. Равные интервалы классов являются предпочтительными при распределении частот, в то время как неравные интервалы классов (например, логарифмические интервалы) могут быть необходимы в определенных ситуациях, чтобы обеспечить хороший разброс наблюдений между классами и избежать большого количества пустых или почти пустых классов. ^[2]

Определите пределы отдельного класса и выберите подходящую отправную точку первого класса, который является произвольным; оно может быть меньше или равно минимальному значению. Обычно его начинают перед минимальным значением таким образом, чтобы средняя точка (среднее значение нижнего и верхнего пределов первого класса) была правильно установлена. ^{[ нужны разъяснения ]} размещен.
Возьмите наблюдение и отметьте вертикальной чертой (|) класс, к которому оно принадлежит. Текущий подсчет ведется до последнего наблюдения.
Найдите частоты, относительную частоту, совокупную частоту и т. д. по мере необходимости.

Ниже приведены некоторые часто используемые методы изображения частоты: ^[3]

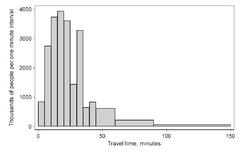
Гистограммы

Гистограмма представляет собой представление табличных частот, показанных в виде соседних прямоугольников или квадратов (в некоторых ситуациях), расположенных на дискретных интервалах (диапазонах), с площадью, пропорциональной частоте наблюдений в интервале. Высота прямоугольника также равна плотности частоты интервала, т. е. частоте, деленной на ширину интервала. Общая площадь гистограммы равна количеству данных. Гистограмму также можно нормализовать, отображая относительные частоты. Затем он показывает долю случаев, попадающих в каждую из нескольких категорий с общей площадью, равной 1. Категории обычно указываются как последовательные, непересекающиеся интервалы переменной. Категории (интервалы) должны быть смежными и часто выбираются одинакового размера. ^[4] Прямоугольники гистограммы рисуются так, чтобы они касались друг друга, что указывает на непрерывность исходной переменной. ^[5]

Гистограммы

Гистограмма пропорциональна или гистограмма — это диаграмма с прямоугольными столбцами, длина которых значениям , которые они представляют. Столбцы могут быть построены вертикально или горизонтально. Вертикальную гистограмму иногда называют гистограммой.

Таблица распределения частот

Таблица распределения частот — это совокупность значений, которые одна или несколько переменных принимают в выборке . Каждая запись в таблице содержит частоту или количество появлений значений в определенной группе или интервале, и, таким образом, таблица суммирует распределение значений в выборке.

Это пример одномерной (= одной переменной ) таблицы частот. Показана частота каждого ответа на вопрос опроса.

Классифицировать	Степень согласия	Число
1	Полностью согласен	22
2	Согласен в некоторой степени	30
3	Не уверен	20
4	Не согласен несколько	15
5	Категорически не согласен	15

Другая схема табуляции объединяет значения в ячейки, так что каждая ячейка охватывает диапазон значений. Например, рост учеников в классе можно свести в следующую таблицу частот.

Диапазон высот	Количество студентов	Совокупное число
менее 5,0 футов	25	25
5,0–5,5 футов	35	60
5,5–6,0 футов	20	80
6,0–6,5 футов	20	100

Совместные распределения частот

Двумерные совместные распределения частот часто представляются в виде (двусторонних) таблиц непредвиденных обстоятельств :

*Двусторонняя таблица непредвиденных обстоятельств с предельными частотами*
	Танец	Спорт	ТВ	Общий
Мужчины	2	10	8	20
Женщины	16	6	8	30
Общий	18	16	16	50

В строке итогов и столбце итогов указаны предельные частоты или предельное распределение , а в основной части таблицы — совместные частоты. ^[6]

Интерпретация

При частотной интерпретации вероятности предполагается, что по мере неограниченного увеличения длины серии испытаний доля экспериментов, в которых происходит данное событие, будет приближаться к фиксированному значению, известному как предельная относительная частота . ^[7]^[8]

Эту интерпретацию часто противопоставляют байесовской вероятности . Фактически, термин «частотный» впервые был использован М.Г. Кендаллом в 1949 году, чтобы противопоставить байесовцам , которых он называл «нечастотными». ^[9]^[10] Он заметил

3....мы можем в общих чертах выделить два основных подхода. Один принимает вероятность как «степень рационального убеждения» или какую-то подобную идею... второй определяет вероятность с точки зрения частоты возникновения событий или относительных пропорций в «популяциях» или «коллективах»; (стр. 101)

...

12. Можно подумать, что различия между частыми и нечастыми пользователями (если я могу их так назвать) во многом обусловлены различиями в областях, которые они призваны охватить. (стр. 104)

...

Я утверждаю, что это не так ... Существенное различие между частыми и нечастыми сторонниками, я думаю, состоит в том, что первые, стремясь избежать чего-либо, отдающего привкусом мнений, стремятся определить вероятность в терминах объективные свойства популяции, реальные или гипотетические, тогда как последние этого не делают. [курсив в оригинале]

Приложения

Управлять данными, представленными в таблицах частот, и работать с ними намного проще, чем с необработанными данными. Существуют простые алгоритмы для расчета медианы, среднего, стандартного отклонения и т. д. на основе этих таблиц.

Статистическая проверка гипотез основана на оценке различий и сходств между частотными распределениями. Эта оценка включает в себя измерения центральной тенденции или средних показателей , таких как среднее значение и медиана , а также меры изменчивости или статистической дисперсии , такие как стандартное отклонение или дисперсия .

Распределение частот называется искаженным , когда его среднее значение и медиана значительно различаются или, в более общем смысле, когда оно асимметрично . Эксцесс распределения частот — это мера доли крайних значений (выбросов), которые появляются на обоих концах гистограммы . Если распределение более склонно к выбросам, чем нормальное, его называют лептокуртическим; если он менее склонен к выбросам, его называют платикуртическим.

Распределение частот букв также используется в частотном анализе для взлома шифров и используется для сравнения относительных частот букв в разных языках, а также часто используются другие языки, такие как греческий, латынь и т. Д.

См. также

Апериодическая частота

Ссылки

^ Перейти обратно: ^а ^б Кенни, Дж. Ф.; Хранение, Е.С. (1962). Математика статистики, Часть 1 (3-е изд.). Принстон, Нью-Джерси: Ван Ностранд Рейнхольд .
^ Маникандан, С. (1 января 2011 г.). «Распределение частот» . Журнал фармакологии и фармакотерапии . 2 (1): 54–55. дои : 10.4103/0976-500X.77120 . ISSN 0976-500X . ПМК 3117575 . ПМИД 21701652 .
^ Карлсон К. и Винквист Дж. (2014) Введение в статистику . SAGE Publications, Inc. Глава 1: Введение в статистику и частотное распределение
^ Ховитт, Д. и Крамер, Д. (2008) Статистика в психологии . Прентис Холл
^ Чарльз Стангор (2011) «Методы исследования поведенческих наук». Уодсворт, Cengage Learning. ISBN 9780840031976 .
^ Stat Trek, Глоссарий статистики и вероятностей, sv Совместная частота
^ фон Мизес, Ричард (1939) Вероятность, статистика и истина (на немецком языке) (английский перевод, 1981: Dover Publications; 2 исправленное издание. ISBN 0486242145 ) (стр. 14)
^ Теория частот, глава 5; обсуждается в Дональде Жиле, «Философские теории вероятности» (2000), Psychology Press. ISBN 9780415182751 , с. 88.
^ Самые ранние известные варианты использования некоторых слов вероятности и статистики
^ Кендалл, Морис Джордж (1949). «О согласовании теорий вероятности». Биометрика . 36 (1/2). Биометрика Траст: 101–116. дои : 10.1093/biomet/36.1-2.101 . JSTOR 2332534 .

[Kenney-1] Перейти обратно: ^а ^б Кенни, Дж. Ф.; Хранение, Е.С. (1962). Математика статистики, Часть 1 (3-е изд.). Принстон, Нью-Джерси: Ван Ностранд Рейнхольд .

[2] Маникандан, С. (1 января 2011 г.). «Распределение частот» . Журнал фармакологии и фармакотерапии . 2 (1): 54–55. дои : 10.4103/0976-500X.77120 . ISSN 0976-500X . ПМК 3117575 . ПМИД 21701652 .

[3] Карлсон К. и Винквист Дж. (2014) Введение в статистику . SAGE Publications, Inc. Глава 1: Введение в статистику и частотное распределение

[4] Ховитт, Д. и Крамер, Д. (2008) Статистика в психологии . Прентис Холл

[5] Чарльз Стангор (2011) «Методы исследования поведенческих наук». Уодсворт, Cengage Learning. ISBN 9780840031976 .

[6] Stat Trek, Глоссарий статистики и вероятностей, sv Совместная частота

[Mises-7] фон Мизес, Ричард (1939) Вероятность, статистика и истина (на немецком языке) (английский перевод, 1981: Dover Publications; 2 исправленное издание. ISBN 0486242145 ) (стр. 14)

[Gilles-8] Теория частот, глава 5; обсуждается в Дональде Жиле, «Философские теории вероятности» (2000), Psychology Press. ISBN 9780415182751 , с. 88.

[9] Самые ранние известные варианты использования некоторых слов вероятности и статистики

[10] Кендалл, Морис Джордж (1949). «О согласовании теорий вероятности». Биометрика . 36 (1/2). Биометрика Траст: 101–116. дои : 10.1093/biomet/36.1-2.101 . JSTOR 2332534 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]