Радарная диаграмма
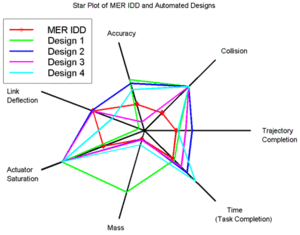
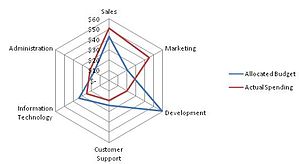
— Радарная диаграмма это графический метод отображения многомерных данных в виде двумерной диаграммы трех или более количественных переменных, представленных на осях, начиная с одной и той же точки. Относительное положение и угол осей обычно неинформативны, но различные эвристики, такие как алгоритмы, отображающие данные как максимальную общую площадь, могут применяться для сортировки переменных (осей) по относительным позициям, которые выявляют четкие корреляции, компромиссы, и множество других сравнительных показателей. [1]
Радарная диаграмма также известна как веб-диаграмма , диаграмма-паук , диаграмма-паук , диаграмма-паутина , звездная карта , [2] звездный график , паутинная диаграмма , неправильный многоугольник , полярная карта или диаграмма Кивиата . [3] [4] Это эквивалентно графику параллельных координат с радиальным расположением осей.
Обзор
[ редактировать ]Радарная диаграмма представляет собой диаграмму и/или график , состоящий из последовательности равноугольных спиц, называемых радиусами, где каждая спица представляет одну из переменных. Длина спицы пропорциональна величине переменной для точки данных относительно максимальной величины переменной во всех точках данных. Рисуется линия, соединяющая значения данных для каждой спицы. Это придает сюжету звездный вид и происхождение одного из популярных названий этого сюжета. Звездный график можно использовать для ответа на следующие вопросы: [5]
- Какие наблюдения наиболее похожи, т.е. существуют ли кластеры наблюдений? (Радиолокационные диаграммы используются для проверки относительных значений для одной точки данных (например, точка 3 большая для переменных 2 и 4, маленькая для переменных 1, 3, 5 и 6) и для поиска похожих или разных точек.) [5]
- Есть ли выбросы?
Радиолокационные диаграммы — полезный способ отображения многомерных наблюдений с произвольным количеством переменных. [6] Каждая звезда представляет собой одно наблюдение. Обычно радиолокационные диаграммы создаются в формате с несколькими графиками, где на каждой странице много звезд, и каждая звезда представляет одно наблюдение. [5] Звездный сюжет впервые был использован Георгом фон Майром в 1877 году. [7] [8] Радиолокационные диаграммы отличаются от графиков с глифами тем, что для построения построенной фигуры звезды используются все переменные. фона нет переднего плана и Разделения на переменные . Вместо этого звездообразные фигуры обычно располагаются на странице в виде прямоугольного массива. Несколько легче увидеть закономерности в данных, если наблюдения расположены в каком-то непроизвольном порядке (если переменные присвоены лучам звезды в каком-то значимом порядке). [9]
Приложения
[ редактировать ]
Радарные диаграммы можно использовать в спорте для выявления сильных и слабых сторон игроков. [10] путем расчета различных статистических данных, связанных с игроком, которые можно отслеживать по центральной оси диаграммы. Примеры включают в себя броски, подборы, передачи и т. д. баскетболистов, а также статистику отбивания или подачи бейсболиста. Это создает централизованную визуализацию сильных и слабых сторон игрока и, если она перекрывается со статистикой других игроков или средними показателями по лиге, может показать, в чем игрок преуспевает и где он может улучшиться. [11] Такое понимание сильных и слабых сторон игроков может оказаться решающим для развития игроков, поскольку оно позволяет тренерам и тренерам корректировать тренировочный режим игроков, чтобы помочь улучшить их слабые стороны. Результаты радарной диаграммы также могут быть полезны в ситуационной игре. Если показано, что отбивающий плохо бьет при подаче левой рукой, то его команда знает, что следует ограничить количество его выступлений против питчеров-левшей, в то время как команда противника может попытаться создать ситуацию, в которой отбивающий будет вынужден наносить удары по питчеру.

Еще одним применением радиолокационных диаграмм является контроль улучшения качества для отображения показателей производительности различных объектов, включая компьютерные программы, [12] компьютеры, телефоны, транспортные средства и многое другое. Программисты часто используют аналитику для проверки производительности своих программ по сравнению с другими. Примером того, где могут быть полезны радиолокационные диаграммы, является анализ производительности различных алгоритмов сортировки. Программист может собрать несколько различных алгоритмов сортировки, таких как выбор, пузырьковый и быстрый, затем проанализировать производительность этих алгоритмов, измеряя их скорость, использование памяти и энергопотребление, а затем отобразить их на радиолокационной диаграмме, чтобы увидеть, как работает каждая сортировка. под различные размеры данных. Еще одно приложение для измерения производительности — измерение производительности аналогичных автомобилей друг против друга. Потребитель может оценить такие переменные, как максимальная скорость автомобиля, количество миль на галлон, мощность и крутящий момент. Затем, используя радиолокационную диаграмму для визуализации данных, они могли на основе результатов решить, какой автомобиль им подходит лучше всего.

Радарные диаграммы можно использовать в науках о жизни для отображения сильных и слабых сторон лекарств и других лекарств. [13] На примере двух антидепрессантов исследователь может ранжировать такие переменные, как эффективность, побочные эффекты, стоимость и т. д., по шкале от одного до десяти. Затем они могли бы отобразить результаты с помощью радиолокационной диаграммы, чтобы увидеть разброс переменных и определить, чем они отличаются, например, один антидепрессант дешевле и быстрее действует, но не оказывает большого облегчения с течением времени. Между тем, другой антидепрессант обеспечивает более сильное облегчение и лучше сохраняется с течением времени, но стоит дороже. Еще одно применение в науке о жизни – анализ пациентов. Радарные диаграммы можно использовать для отображения переменных жизни, влияющих на самочувствие человека, а затем анализировать их, чтобы помочь ему. Более конкретный пример – спортсмены, чьи различные привычки в отношении здоровья, такие как сон, диета и стресс, контролируются, чтобы гарантировать, что они остаются в отличной физической форме. [14] Если какие-либо области будут показаны проваливающимися, врачи и тренеры могут вмешаться, чтобы помочь спортсмену и улучшить его самочувствие.
Ограничения
[ редактировать ]Радарные диаграммы в первую очередь подходят для яркого отображения выбросов и общности или когда одна диаграмма больше по каждой переменной, чем другая, и в основном используются для порядковых измерений - где каждая переменная соответствует «лучшему» в некотором отношении, а все переменные находятся в одном масштабе. .
И наоборот, лепестковые диаграммы подвергались критике как плохо подходящие для принятия компромиссных решений – когда одна диаграмма превосходит другую по одним переменным, но меньше по другим. [15]
Кроме того, трудно визуально сравнить длину разных спиц, поскольку трудно оценить радиальные расстояния, хотя концентрические круги помогают в качестве линий сетки. Вместо этого можно использовать простой линейный график, особенно для временных рядов. [16]
Радиолокационные диаграммы могут в некоторой степени искажать данные, особенно если области заполнены, поскольку содержащаяся в них площадь становится пропорциональной квадрату линейных мер. Например, на диаграмме с 5 переменными в диапазоне от 1 до 100 площадь, содержащаяся многоугольником, ограниченным 5 точками, когда все меры равны 90, более чем на 10 % больше, чем та же площадь для диаграммы со всеми значениями 82.
Радарные диаграммы также могут стать трудными для визуального сравнения различных образцов на диаграмме, если их значения близки, поскольку их линии или области переходят друг в друга, как показано на рисунке 5.
Искусственное сооружение
[ редактировать ]Радарные диаграммы накладывают на данные несколько структур, которые часто являются искусственными:
- Родственность соседей. Радарные диаграммы часто используются, когда соседние переменные не связаны между собой, создавая ложные связи.
- Циклическая структура – первая и последняя переменные располагаются рядом друг с другом.
- Длина – переменные часто имеют естественный порядковый номер: лучше или хуже, хотя степень различия может быть искусственной.
- Площадь: площадь масштабируется как квадрат значений, что усиливает эффект больших чисел. Например, 2, 2 занимает в 4 раза больше площади, чем 1, 1. Это общая проблема с графиками площадей, и площадь трудно оценить - см. «Иерархия Кливленда». [17] [18]
Например, чередующиеся данные 9, 1, 9, 1, 9, 1 дают пиковую радиолокационную диаграмму (которая появляется и исчезает), а переупорядочение данных как 9, 9, 9, 1, 1, 1 вместо этого дает два различных клинья (сектора).
В некоторых случаях существует естественная структура, и радиолокационные карты могут хорошо подойти. Например, для диаграмм данных, которые изменяются в течение 24-часового цикла, почасовые данные естественным образом связаны со своими соседями и имеют циклическую структуру, поэтому их естественным образом можно отобразить в виде радиолокационной диаграммы. [16] [19] [20]
Один набор рекомендаций по использованию радиолокационных карт (или, скорее, тесно связанного с ними «графика полярной зоны») таков: [20]
- вы не против читать сложенные области вместо положения по общей шкале (см. Иерархию Кливленда),
- набор данных действительно циклический, а не линейный, и
- есть две серии для сравнения, одна намного меньше другой
Размер набора данных
[ редактировать ]небольшого и среднего размера Радарные диаграммы полезны для многомерных наборов данных . Их основная слабость заключается в том, что их эффективность ограничена наборами данных с числом менее нескольких сотен точек. После этого они имеют тенденцию быть подавляющими. [5]
Кроме того, при использовании радиолокационных диаграмм с несколькими измерениями или выборками диаграмма может стать загроможденной, и ее будет сложнее интерпретировать по мере роста количества выборок.
Например, возьмем таблицу статистики ударов, в которой сравнивается MVP MLB 2021 года Шохей Отани со статистикой средних назначенных нападающих лиги и некоторых игроков Зала славы. Эта статистика представляет собой процент попаданий, хоум-ранов, аутов и т. д. на биту игрока. Для получения дополнительной информации о том, что представляет собой каждая статистика, используемая в таблице, вы можете обратиться к этой ссылке MLB. [21] Мы будем использовать эту таблицу ниже для создания радарных диаграмм, сравнивающих статистику ударов MVP 2021 года со средними показателями по лиге для назначенных нападающих и обычных игроков, пытаясь визуализировать показатели производительности и визуально прийти к выводу, что Шохей превосходит среднего игрока. Затем мы добавим дополнительные образцы в радарную диаграмму, используя игроков Зала славы Джеки Робинсона, Джима Тома и Фрэнка Томаса, чтобы сравнить Шохея с некоторыми из величайших отбивающих всех времен. Эта радарная диаграмма не только может дать нам представление о том, как Шохей сравнивается с ведущими историческими игроками, но также поможет показать ограничения, связанные с наличием слишком большого количества выборок в радарной диаграмме.
| Цель | НЕТ | ОБП | СЛГ | ОПС | HR% | ТАК% | ББ% |
|---|---|---|---|---|---|---|---|
| МЛБ | 0.244 | 0.317 | 0.411 | 0.728 | 0.037 | 0.232 | 0.087 |
| ДХ | 0.239 | 0.316 | 0.434 | 0.75 | 0.047 | 0.256 | 0.093 |
| Шохей Отани | 0.257 | 0.372 | 0.592 | 0.965 | 0.086 | 0.296 | 0.15 |
| Джеки Робинсон | 0.313 | 0.41 | 0.477 | 0.887 | 0.0282 | 0.0582 | 0.151 |
| Джим Том | 0.276 | 0.402 | 0.554 | 0.956 | 0.072 | 0.302 | 0.207 |
| Фрэнк Томас | 0.301 | 0.419 | 0.555 | 0.974 | 0.063 | 0.17 | 0.203 |
На рисунке 10 мы можем видеть, как можно легко интерпретировать лепестковую диаграмму, когда количество спиц и выборок относительно невелико. Когда мы сравниваем больше выборок на рисунке 11, даже без заполнения области на радиолокационной диаграмме, становится очевидным, насколько сложно может стать интерпретация или принятие компромиссных решений.
Пример
[ редактировать ]

График справа [5] содержит звездные сюжеты 15 автомобилей . Список переменных для примера звездного графика:
- Цена
- Пробег (миль на галлон)
- Рекорд ремонтов 1978 года (1 = худший, 5 = лучший)
- Рекорд ремонта 1977 года (1 = худший, 5 = лучший)
- Высота над головой
- Комната на заднем сиденье
- Багажник
- Масса
- Длина
Мы можем рассматривать эти графики по отдельности или использовать их для выявления групп автомобилей со схожими характеристиками. Например, мы можем посмотреть на звездный график Cadillac Seville (последний на изображении) и увидеть, что это один из самых дорогих автомобилей, расход бензина ниже среднего (но не худший), средний расход бензина. запись в ремонте, вместительность и размер от среднего до среднего. Затем мы можем сравнить модели Cadillac (последние три графика) с моделями AMC (первые три графика). Это сравнение показывает различные закономерности. Модели AMC, как правило, недороги, имеют расход топлива ниже среднего, имеют небольшие размеры и высоту, вес и вместительность. Модели Cadillac дороги, имеют небольшой расход бензина и большие по размеру и вместительности. [5]
Альтернативы
[ редактировать ]Можно использовать линейные графики для временных рядов и других данных. [16] в виде параллельных координат .
Для графического качественного сравнения двумерных табличных данных по нескольким переменным распространенной альтернативой являются шары Харви , которые широко используются Consumer Reports . [22] Сравнению в шарах Харви (и радиолокационных диаграммах) можно значительно облегчить алгоритмическое упорядочение переменных для добавления порядка. [23]
Отличный способ визуализации структур в многомерных данных предлагает анализ главных компонент (PCA).
Другой альтернативой является использование небольших линейных гистограмм, которые можно сравнить со спарклайнами . [23]
Хотя радиолокационные и полярные карты часто называют одним и тем же типом карт, [4] некоторые источники делают между ними разницу и даже считают радиолокационную карту разновидностью полярной карты, которая не отображает данные в терминах полярных координат. [24]
См. также
[ редактировать ]- Индикатор положения плана
- Сюжет (графика)
- Диаграмма полярной области
- Параллельные координаты
- Радиальное дерево
Ссылки
[ редактировать ]![]() Эта статья включает общедоступные материалы Национального института стандартов и технологий.
Эта статья включает общедоступные материалы Национального института стандартов и технологий.
- ^ Портер, Майкл М; Никсяр, Пуя (2018). «Многомерная механика: картирование характеристик природных биологических систем с использованием перестановочных радиолокационных диаграмм» . ПЛОС ОДИН . 13 (9): e0204309. Бибкод : 2018PLoSO..1304309P . дои : 10.1371/journal.pone.0204309 . ПМК 6161877 . ПМИД 30265707 .
- ^ Нэнси Р. Тейг (2005) Набор инструментов для обеспечения качества . страница 437.
- ^ Коленс, Кеннет В. (1973). «Эмпирик программного обеспечения» . Обзор оценки производительности ACM SIGMETRICS . 2 (2): 31–36. дои : 10.1145/1113644.1113647 . S2CID 18600391 .
Доктор Филип Дж. Кивиат на недавнем семинаре NBS/ACM по измерению производительности предположил, что полезной формой может быть круговой график, использующий радиусы в качестве переменных осей. […] Я рекомендую называть их «Графики Кивиата» или «Графики Кивиата», чтобы признать его понимание их важности.
- ^ Jump up to: а б «Найдите пробелы в контенте с помощью радиолокационных диаграмм» . Семинары по контент-стратегии. 3 марта 2015 года . Проверено 17 декабря 2015 г.
- ^ Jump up to: а б с д и ж НИСТ/СЕМАТЕХ (2003). Звездный сюжет в: Электронном справочнике по статистическим методам . 01.06.2003 (Дата создания)
- ^ Чемберс, Джон, Уильям Кливленд, Бит Кляйнер и Пол Тьюки (1983). Графические методы анализа данных . Уодсворт. стр. 158–162.
- ^ Майр, Георг фон (1877), Закон в общественной жизни (на немецком языке), Мюнхен: Ольденбург, OL 23294909M , стр.78. Линейные графики в кругах: Линейные графики в кругах.
- ^ Майкл Френдли (2008). «Вехи в истории тематической картографии, статистической графики и визуализации данных». Архивировано 26 сентября 2018 г. на Wayback Machine .
- ^ Майкл Френдли (1991). «Статистическая графика для многомерных данных» . Доклад, представленный на 16-й конференции SAS SUGI, апрель 1991 г.
- ^ Паучьи графики: диаграммы баскетбольной статистики
- ^ Видя данные. «Осмысление визуализации данных» . Видя данные.
- ^ Рон Басу (2004). Внедрение качества: Практическое руководство по инструментам и методам . стр.131.
- ^ Центр перевода знаний модельных систем. «Эффективное использование радиолокационных диаграмм» (PDF) . Центр перевода знаний модельных систем.
- ^ Джон Магуайр. «Денормализованные паучьи и радарные графики» . Китман Лабс.
- ^ Вы НЕ человек-паук, так почему вы используете радиолокационные карты? , Чанду, 18 сентября 2008 г.
- ^ Jump up to: а б с Пельтье, Джон (14 августа 2008 г.). «Рок круглосуточно — технический блог Пельтье» . Peltiertech.com . Проверено 11 сентября 2013 г.
- ^ Кливленд, Уильям; МакГилл, Роберт (1984). «Графическое восприятие: теория, экспериментирование и применение к разработке графических методов». Журнал Американской статистической ассоциации . 79 (387): 531–554. JSTOR 2288400 . Краткое изложение иерархии Кливленда
- ^ Кливленд и МакГилл, 1984 ( краткое изложение )
- ^ «Круглые графики в блоге Excel Charts» . Excelcharts.com. 15 августа 2008 г. Проверено 11 сентября 2013 г.
- ^ Jump up to: а б Часы это
- ^ «Стандартная статистика» . www.mlb.com . Проверено 26 апреля 2022 г.
- ^ «Качественное сравнение» . Поддержка блога аналитики . 11 декабря 2007 г. Архивировано из оригинала 8 апреля 2012 г.
- ^ Jump up to: а б «Информационный океан: Переупорядочиваемые таблицы II: Бертен против пауков» . Я-ocean.blogspot.com. 24 сентября 2008 г. Проверено 11 сентября 2013 г.
- ^ «Полярные диаграммы (построитель отчетов и службы SSRS)» . Сеть разработчиков Microsoft . Проверено 17 декабря 2015 г.
Внешние ссылки
[ редактировать ]- Звездный график - NIST / SEMATECH по статистическим методам Электронный справочник