Круговая диаграмма
Круговая диаграмма (или круговая диаграмма ) представляет собой круговой статистический график , разделенный на фрагменты для иллюстрации числовых пропорций. В круговой диаграмме длина дуги каждого среза (и, следовательно, его центральный угол и площадь ) пропорциональна величине, которую он представляет. Хотя он назван в честь своего сходства с пирогом разрезанным , существуют разные варианты его подачи. Самая ранняя известная круговая диаграмма обычно приписывается Плейфэра Уильяма Статистическому Бревиарию 1801 года. [1] [2]
Круговые диаграммы очень широко используются в деловом мире и средствах массовой информации. [3] Однако их подвергли критике, [4] и многие эксперты рекомендуют избегать их, [5] [6] [7] [8] как показали исследования, сложно сравнивать различные разделы одной круговой диаграммы или сравнивать данные на разных круговых диаграммах. Круговые диаграммы в большинстве случаев можно заменить другими графиками, такими как гистограмма , ящичная диаграмма , точечная диаграмма и т. д.
История
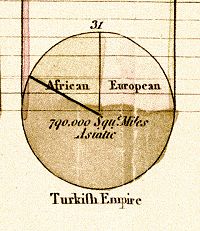
[ редактировать ]Самая ранняя известная круговая диаграмма обычно приписывается Плейфэра Уильяма Статистическому Бревиарию 1801 года, в котором используются два таких графика. [1] [2] [9] Playfair представил иллюстрацию, содержащую серию круговых диаграмм. На одной из этих диаграмм были изображены пропорции Турецкой империи, расположенной в Азии , Европе и Африке до 1789 года. Поначалу это изобретение не получило широкого распространения. [1]
В Playfair считали, что круговым диаграммам необходимо третье измерение, чтобы добавить дополнительную информацию. [10]
Флоренс Найтингейл, возможно, не изобрела круговую диаграмму, но она адаптировала ее, чтобы сделать ее более читабельной, что способствовало ее широкому использованию до сих пор. Найтингейл изменил конфигурацию круговой диаграммы, сделав переменной длину клиньев вместо их ширины. Тогда график напоминал петушиный гребешок. [11] Позже предполагалось, что она создала его из-за безвестности и непрактичности творения Playfair. [12] Найтингейла Диаграмма полярной области , [13] : 107 или иногда диаграмма розы Найтингейла , эквивалентная современной круговой гистограмме , чтобы проиллюстрировать сезонные источники смертности пациентов в военно-полевом госпитале, которым она руководила, была опубликована в «Заметках о вопросах, влияющих на здоровье, эффективность и управление больницами британской армии» и отправлена королеве Виктории в 1858 году. По словам историка Хью Смолла, «она, возможно, была первой, кто использовал [круговые диаграммы], чтобы убедить людей в необходимости перемен». [11]
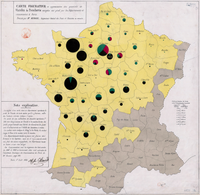
Французский инженер Шарль Жозеф Минар также использовал круговые диаграммы в 1858 году. На его карте 1858 года круговые диаграммы изображали скот, отправленный со всей Франции для потребления в Париже .
- Круговые диаграммы из «Статистического бревиария» Уильяма Плейфэра, 1801 г.
- Одна из первых круговых диаграмм, 1801 год.
- Карта Минара, 1858 г.
- Полярная карта Флоренс Найтингейл , 1858 год.
Варианты и подобные диаграммы
[ редактировать ]3D-круговая диаграмма и перспективный пирог
[ редактировать ]Круговая 3D-диаграмма или круговая диаграмма в перспективе используется для придания диаграмме трехмерного вида. Третье измерение, часто используемое по эстетическим соображениям, не улучшает считывание данных; напротив, эти сюжеты трудно интерпретировать из-за искаженного эффекта перспективы , связанного с третьим измерением. Использование лишних измерений, не используемых для отображения интересующих данных, не рекомендуется для диаграмм в целом, а не только для круговых диаграмм. [7] [14]
Кольцевая диаграмма
[ редактировать ]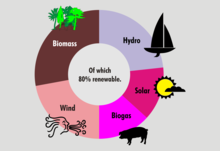
Кольцевая диаграмма (также пишется как пончик) — это вариант круговой диаграммы с пустым центром, позволяющий включать дополнительную информацию о данных в целом. [15] [16] Кольцевые диаграммы похожи на круговые диаграммы, поскольку их цель — проиллюстрировать пропорции. [ нужна ссылка ] Этот тип круговой диаграммы может поддерживать несколько статистических данных одновременно и обеспечивает лучшее соотношение интенсивности данных по сравнению со стандартными круговыми диаграммами. [16] Он не обязательно должен содержать информацию в центре.
Взорванная круговая диаграмма
[ редактировать ]
Диаграмма, в которой один или несколько секторов отделены от остальной части диска, называется развернутой круговой диаграммой . Этот эффект используется либо для выделения сектора, либо для выделения более мелких сегментов диаграммы с небольшими пропорциями.
Диаграмма полярной области
[ редактировать ]
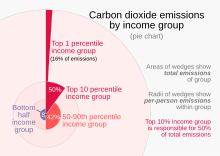
Диаграмма полярных площадей похожа на обычную круговую диаграмму, за исключением того, что сектора имеют равные углы и отличаются скорее тем, насколько далеко каждый сектор простирается от центра круга.Диаграмма полярной области используется для построения циклических явлений (например, количества смертей по месяцам).Например, если необходимо отобразить количество смертей за каждый месяц в течение года, то будет 12 секторов (по одному в месяц) с одинаковым углом 30 градусов каждый. Радиус каждого сектора будет пропорционален квадратному корню из уровня смертности за месяц, поэтому площадь сектора представляет уровень смертности за месяц.Если уровень смертности в каждом месяце подразделить по причине смерти, можно провести несколько сравнений на одной диаграмме, как это видно на диаграмме полярных зон, разработанной Флоренс Найтингейл .
Первое известное использование диаграмм полярных зон было осуществлено Андре-Мишелем Герри , который он назвал courbes circulaires (круговые кривые), в статье 1829 года, показывающей сезонные и ежедневные изменения направления ветра в течение года, а также рождаемость и смертность по часам дня. [17] Леон Лаланн позже использовал полярную диаграмму, чтобы показать частоту направлений ветра вокруг точек компаса в 1843 году. Роза ветров до сих пор используется метеорологами . Найтингейл опубликовала свою диаграмму «роза» в 1858 году. Хотя название «фатох» стало ассоциироваться с этим типом диаграмм, Найтингейл первоначально использовала этот термин для обозначения публикации, в которой эта диаграмма впервые появилась — привлекающей внимание книги диаграмм и диаграмм. таблицы, а не диаграммы этого конкретного типа. [18]
Кольцевая диаграмма, диаграмма солнечных лучей и многоуровневая круговая диаграмма
[ редактировать ]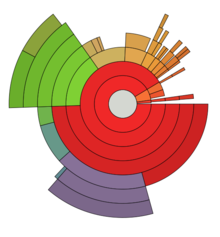
Кольцевая диаграмма, также известная как диаграмма солнечных лучей или многоуровневая круговая диаграмма, используется для визуализации иерархических данных, изображаемых концентрическими кругами. [19] Круг в центре представляет корневой узел, а иерархия движется наружу от центра. Сегмент внутреннего круга имеет иерархическую связь с теми сегментами внешнего круга, которые лежат в пределах угловой развертки родительского сегмента. [20]
Шпионская диаграмма
[ редактировать ]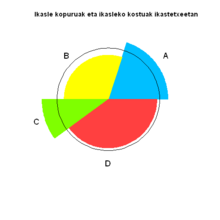
Вариантом карты полярных зон является шпионская карта, разработанная Дрором Фейтельсоном. [21] В проекте обычная круговая диаграмма накладывается на модифицированную диаграмму полярных зон, что позволяет сравнивать два набора связанных данных. Базовая круговая диаграмма представляет первый набор данных обычным способом с разными размерами срезов. Второй набор представлен наложенной диаграммой полярных площадей, в которой используются те же углы, что и в основании, и корректируются радиусы в соответствии с данными. Например, базовая круговая диаграмма может показать распределение возрастных и гендерных групп населения и наложить их представленность среди дорожно-транспортных происшествий. Возрастные и гендерные группы, которые особенно подвержены несчастным случаям, выделяются в виде срезов, выходящих за рамки исходной круговой диаграммы.
Квадратная диаграмма/Вафельная диаграмма
[ редактировать ]
Квадратные диаграммы, также называемые вафельными диаграммами, представляют собой разновидность круговых диаграмм, в которых вместо кругов для обозначения процентов используются квадраты. Подобно обычным круговым диаграммам, квадратные круговые диаграммы берут каждый процент из 100%. Часто они представляют собой сетки 10 на 10, где каждая ячейка представляет 1%. Несмотря на название, вместо квадратов можно использовать круги, пиктограммы (например, людей) и другие фигуры. Одним из основных преимуществ квадратных диаграмм является то, что можно легко отобразить меньшие проценты, которые трудно увидеть на традиционных круговых диаграммах. [22]
Пример
[ редактировать ]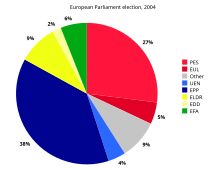
Следующий пример диаграммы основан на предварительных результатах выборов в Европейский парламент в 2004 году . В таблице указано количество мест, выделенных каждой партийной группе, а также полученный процент от общего числа мест, которые каждая из них составляет. Значения в последнем столбце — производный центральный угол каждого сектора — определяются путем принятия этого процента за 360.
| Группа | Сиденья | Процент (%) | Центральный угол (°) |
|---|---|---|---|
| ЕСУЛ | 39 | 5.3 | 19.2 |
| ПЭС | 200 | 27.3 | 98.4 |
| ЭФФ | 42 | 5.7 | 20.7 |
| ЭДД | 15 | 2.0 | 7.4 |
| СТАРШЕ | 67 | 9.2 | 33.0 |
| ЕПП | 276 | 37.7 | 135.7 |
| УЭН | 27 | 3.7 | 13.3 |
| Другой | 66 | 9.0 | 32.5 |
| Общий | 732 | 99.9* | 360.2* |
*Из-за округления эти суммы не составляют в сумме 100 и 360.
Размер каждого центрального угла пропорционален размеру соответствующего количества мест, в данном случае количества мест. Поскольку сумма центральных углов должна составлять 360°, центральный угол для величины, составляющей долю Q от общей суммы, равен 360 Q градусов.В этом примере центральный угол для самой большой группы (Европейская народная партия (ЕНП)) составляет 135,7°, поскольку 0,377 умножить на 360, округлив до одного десятичного знака, равно 135,7.
Использование и эффективность
[ редактировать ]
Недостаток круговых диаграмм заключается в том, что они не могут отображать более нескольких значений, не отделяя визуальное кодирование («срезы») от данных, которые они представляют (обычно проценты). Когда срезы становятся слишком маленькими, круговые диаграммы вынуждены полагаться на цвета, текстуры или стрелки, чтобы читатель мог их понять. Это делает их непригодными для использования с большими объемами данных. Круговые диаграммы также занимают больше места на странице по сравнению с более гибкими гистограммами, которым не нужны отдельные легенды и которые могут одновременно отображать другие значения, такие как средние или целевые значения. [7]
Статистики обычно считают круговые диаграммы плохим методом отображения информации, и они редко встречаются в научной литературе. Одна из причин заключается в том, что сравнивать размеры элементов на диаграмме сложнее , когда вместо длины используется площадь и когда разные элементы отображаются в виде разных фигур. [23]
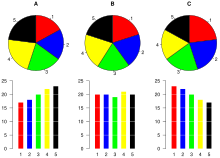
Далее, в исследованиях, проведенных в AT&T Bell Laboratories , было показано, что сравнение по углу было менее точным, чем сравнение по длине. Большинству испытуемых трудно упорядочить кусочки на круговой диаграмме по размеру; когда используется эквивалентная гистограмма, сравнение становится намного проще. [24] Аналогично, сравнение между наборами данных упрощается с помощью гистограммы. Однако если цель состоит в том, чтобы сравнить данную категорию (кусок пирога) с общим количеством (весь круг) на одной диаграмме, а кратное значение близко к 25 или 50 процентам, тогда круговая диаграмма часто может быть более эффективной. чем гистограмма. [25] [26]
На круговой диаграмме с множеством разделов несколько значений могут быть представлены одинаковыми или похожими цветами, что затрудняет интерпретацию.

В нескольких исследованиях, представленных на Европейской конференции по визуализации, анализировалась относительная точность нескольких форматов круговых диаграмм. [27] [28] [22] пришел к выводу, что круговые и кольцевые диаграммы дают одинаковые уровни ошибок при их чтении, а квадратные круговые диаграммы обеспечивают наиболее точные показания. [29]
См. также
[ редактировать ]Ссылки
[ редактировать ]- ^ Перейти обратно: а б с Спенс (2005)
- ^ Перейти обратно: а б Тафте, стр. 44.
- ^ Кливленд, с. 262
- ^ Уилкинсон, с. 23.
- ^ Тафте, стр. 178.
- ^ ван Белль, с. 160–162.
- ^ Перейти обратно: а б с Стивен Фью. «Сохраните пироги на десерт» , август 2007 г., дата обращения 2 февраля 2010 г.
- ^ Стив Фентон «Круговые диаграммы плохие»
- ^ «Вехи в истории тематической картографии, статистической графики и визуализации данных» . www.datavis.ca .
- ^ Пальский, с. 144–145
- ^ Перейти обратно: а б Гринбаум, Хилари; Рубинштейн, Дана (20 апреля 2012 г.). «Кто сделал эту круговую диаграмму?» . Нью-Йорк Таймс .
- ^ Статья Дэйва об этой информации о QI.
- ^ Коэн, И. Бернард (март 1984 г.). «Флоренс Найтингейл». Научный американец . 250 (3): 128–137. Бибкод : 1984SciAm.250c.128C . doi : 10.1038/scientificamerican0384-128 . ПМИД 6367033 . (альтернативная нумерация страниц в зависимости от страны продажи: 98–107, библиография на стр. 114) онлайн-статья – см. ссылку на документы слева.
- ^ Гуд и Хардин, глава 8.
- ^ Харрис, Роберт Л. (1999). Информационная графика: обширный иллюстрированный справочник (изд. [Начдр.]). Оксфорд: Издательство Оксфордского университета. п. 143. ИСБН 9780195135329 .
- ^ Перейти обратно: а б Дизайн данных Юргена Кай-Уве Брока на iBooks . Проверено 10 июня 2017 г.
{{cite book}}:|website=игнорируется ( помогите ) - ^ Дружелюбный, с. 509
- ^ «Статистические диаграммы Флоренс Найтингейл» . Проверено 22 ноября 2010 г.
- ^ «Многоуровневые круговые диаграммы» . www.neoformix.com .
- ^ Уэббер Ричард, Герберт Рик, Цзянбк Вел. «Методы заполнения пространства при визуализации результатов компьютерных экономических моделей»
- ^ «Фейтельсон, Дрор (2003) Сравнение разделов со шпионскими диаграммами» (PDF) . 2003 . Проверено 31 августа 2010 г.
- ^ Перейти обратно: а б Косара, Роберт; Скау, Дрю (2016). «Ошибка суждения в вариантах круговой диаграммы» . ЕвроВис .
- ^ Кригер, Джон (28 августа 2007 г.). «Перцептивное масштабирование символов карты» . Makingmaps.net . Проверено 3 мая 2015 г.
- ^ Кливленд, с. 86–87
- ^ Симкин Д. и Хасти Р. (1987). Анализ обработки информации восприятия графа. Журнал Американской статистической ассоциации, 82 (398), 454. дои : 10.2307/2289447 . Косара, Роберт (13 апреля 2011 г.). «В защиту круговых диаграмм» . Проверено 13 апреля 2011 г.
- ^ Спенс, Ян; Левандовски, Стефан (1 января 1991 г.). «Отображение пропорций и процентов». Прикладная когнитивная психология . 5 (1): 61–77. дои : 10.1002/acp.2350050106 .
- ^ «Иллюстрированный обзор результатов исследования круговой диаграммы» . нетерпеливые глаза . 28 июня 2016 г. Проверено 28 ноября 2016 г.
- ^ Скау, Дрю; Косара, Роберт (2016). «Дуги, углы или площади: кодирование отдельных данных в круговых и кольцевых диаграммах» . ЕвроВис .
- ^ «Повторный анализ исследования (квадратных) круговых диаграмм 2009 года» . нетерпеливые глаза . 11 июля 2016 г. Проверено 28 ноября 2016 г.
Дальнейшее чтение
[ редактировать ]- Кливленд, Уильям С. (1985). Элементы графических данных . Пасифик Гроув, Калифорния: Программа Уодсворт и продвинутая книга. ISBN 0-534-03730-5 .
- Дружелюбный, Майкл . « Золотой век статистической графики », Статистическая наука, том 23, номер 4 (2008), 502–535.
- Гуд, Филип И. и Хардин, Джеймс В. Распространенные ошибки в статистике (и как их избежать) . Уайли. 2003. ISBN 0-471-46068-0 .
- Герри, А.-М. (1829). Таблица метеорологических изменений по сравнению с физиологическими явлениями, согласно наблюдениям, сделанным в королевской обсерватории, и новейшим статистическим исследованиям. Анналы общественной гигиены и юридической медицины , 1:228-.
- Харрис, Роберт Л. (1999). Информационная графика: подробный иллюстрированный справочник . Издательство Оксфордского университета . ISBN 0-19-513532-6 .
- Лима, Мануэль . « Почему люди любят круговые диаграммы: историческая и эволюционная перспектива », «Примечательно» , 23 июля 2018 г.
- Пальский Жиль . Числа и карты: количественная картография в XIX веке . Париж: Комитет исторических и научных работ, 1996. ISBN 2-7355-0336-4 .
- Плейфэр, Уильям, Коммерческий и политический атлас и статистический бревиарий , издательство Кембриджского университета (2005) ISBN 0-521-85554-3 .
- Спенс, Ян . Никакого скромного пирога: происхождение и использование статистической диаграммы . Журнал образовательной и поведенческой статистики . Зима 2005 г., 30 (4), 353–368.
- Тафте, Эдвард . Визуальное отображение количественной информации . Графика Пресс, 2001. ISBN 0-9613921-4-2 .
- Ван Белль, Джеральд. Практические статистические правила . Уайли, 2002. ISBN 0-471-40227-3 .
- Уилкинсон, Леланд . Грамматика графики , 2-е издание. Спрингер, 2005. ISBN 0-387-24544-8 .