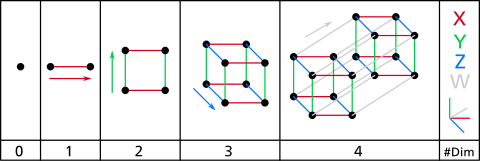Тессеракт

Эта статья о геометрической форме. Чтобы узнать о других значениях, см. Тессеракт (значения) .

Тессеракт 8-ячеечный (4-куб.)
Тип	Выпуклый правильный 4-многогранник
Символ Шлефли	{4,3,3} t 0,3 {4,3,2} или {4,3}×{ } т 0,2 {4,2,4} или {4}×{4} t 0,2,3 {4,2,2} или {4}×{ }×{ } t 0,1,2,3 {2,2,2} или { }×{ }×{ }×{ }
Диаграмма Кокстера
Клетки	8 {4,3}
Лица	24 {4}
Края	32
Вершины	16
Вершинная фигура	Тетраэдр
Полигон Петри	восьмиугольник
Группа Коксетера	Б 4 , [3,3,4]
Двойной	16-ячеечный
Характеристики	выпуклый , изогональный , изотоксальный , изоэдральный , многогранник Ханнера
Единый индекс	10

Крест Дали , сетка тессеракта.

Тессеракт можно развернуть на восемь кубов в трехмерном пространстве, так же как куб можно развернуть на шесть квадратов в двухмерном пространстве.

В геометрии тессеракт — или 4-куб ​​это четырёхмерный гиперкуб , аналог двумерного квадрата и трёхмерного куба . Подобно тому, как периметр квадрата состоит из четырех ребер, а поверхность куба — из шести квадратных граней , гиперповерхность тессеракта состоит из восьми кубических ячеек , сходящихся под прямым углом . Тессеракт — один из шести выпуклых правильных 4-многогранников .

Тессеракт также называют 8-клеточным , C ₈ , (правильным) октахороном или кубической призмой . Это четырехмерный многогранник меры , принятый за единицу гиперобъема. Коксетер называет его многогранником γ ₄ . Термин «гиперкуб» без ссылки на измерение часто рассматривается как синоним этого конкретного многогранника .

Оксфордский словарь английского языка относит слово «тессеракт» к книге Чарльза Говарда Хинтона 1888 года «Новая эра мысли» . Этот термин происходит от греческого tessara ( τέσσαρα «четыре») и aktis ( ἀκτίς «луч»), обозначая четыре ребра, идущие от каждой вершины к другим вершинам. Хинтон первоначально написал это слово как тессаракт .

Геометрия

Как правильный многогранник с тремя сложенными вместе вокруг каждого ребра кубами , он имеет символ Шлефли {4,3,3} с гипероктаэдрической симметрией порядка 384. Построенный как 4D- гиперпризма, состоящая из двух параллельных кубов, он может быть назван составным Шлефли. символ {4,3} × {} с порядком симметрии 96. Как дуопризма 4-4 , декартово произведение двух квадратов , его можно назвать составным символом Шлефли {4}×{4} с порядком симметрии 64. В качестве ортотопа его можно представить составным символом Шлефли { } × { } × { } × { } или { }. ⁴ , с порядком симметрии 16.

Поскольку к каждой вершине тессеракта примыкают четыре ребра, вершинная фигура тессеракта представляет собой правильный тетраэдр . Двойной многогранник тессеракта представляет собой 16-ячеечный символ Шлефли {3,3,4}, с которым его можно объединить, образуя соединение тессеракта и 16-ячеечного .

Все ребра правильного тессеракта имеют одинаковую длину. Это представляет интерес при использовании тессерактов в качестве основы топологии сети для соединения нескольких процессоров в параллельных вычислениях : расстояние между двумя узлами не превышает 4, и существует множество различных путей, позволяющих балансировать вес.

Тессеракт ограничен восемью трехмерными гиперплоскостями . Каждая пара непараллельных гиперплоскостей пересекается, образуя 24 квадратных грани. Три куба и три квадрата пересекаются по каждому ребру. В каждой вершине сходятся четыре куба, шесть квадратов и четыре ребра. Всего тессеракт состоит из 8 кубов, 24 квадратов, 32 ребер и 16 вершин.

Единичный тессеракт имеет длину стороны 1 и обычно считается базовой единицей гиперобъема в 4-мерном пространстве. Единичный тессеракт в декартовой системе координат для 4-мерного пространства имеет две противоположные вершины с координатами [0, 0, 0, 0] и [1, 1, 1, 1] и другие вершины с координатами во всех возможных комбинациях 0. с и 1 с. Это декартово произведение замкнутого единичного интервала [0, 1] по каждой оси.

Иногда единичный тессеракт центрируется в начале координат, поэтому его координаты более симметричны. ${\bigl (}{\pm {\tfrac {1}{2}}},\pm {\tfrac {1}{2}},\pm {\tfrac {1}{2}},\pm {\tfrac {1}{2}}{\bigr )}.$ Это декартово произведение замкнутого интервала ${\bigl [}{-{\tfrac {1}{2}}},{\tfrac {1}{2}}{\bigr ]}$ в каждой оси.

Другой обычно удобный тессеракт — это декартово произведение замкнутого интервала [−1, 1] по каждой оси с вершинами в координатах (±1, ±1, ±1, ±1) . Этот тессеракт имеет длину стороны 2 и гиперобъем 2. ⁴ = 16 .

Сеть

Развертка многогранника называется сетью . Существует 261 отдельная сеть тессеракта. Развертки тессеракта можно подсчитать, сопоставив сети с парными деревьями ( дерево вместе с идеальным паросочетанием в его дополнении ).

Строительство

Анимация изменения размеров

Построение гиперкубов можно представить следующим образом:

• Одномерное: две точки A и B могут быть соединены в линию, образуя новый отрезок AB.
• Двумерный: два параллельных отрезка AB и CD, разделенные расстоянием AB, можно соединить и образовать квадрат с углами, отмеченными как ABCD.
• Трехмерное изображение: два параллельных квадрата ABCD и EFGH, разделенные расстоянием AB, можно соединить в куб с углами, отмеченными как ABCDEFGH.
• 4-мерное: два параллельных куба ABCDEFGH и IJKLMNOP, разделенные расстоянием AB, можно соединить, образуя тессеракт с углами, отмеченными как ABCDEFGHIJKLMNOP. Однако такое параллельное расположение двух кубов, при котором каждая из восьми соответствующих пар вершин находится на расстоянии AB, может быть достигнуто только в пространстве с четырьмя или более измерениями.

Восемь ячеек тессеракта можно рассматривать (три разных способа) как два переплетенных кольца из четырех кубов.

Тессеракт можно разложить на меньшие 4-многогранники. Это выпуклая оболочка соединения двух полутессерактов ( 16-клеток ). Его также можно триангулировать в 4-мерные симплексы ( неправильные 5-ячейки ), которые имеют общие вершины с тессерактом. Известно, что 92 487 256. таких триангуляций и что наименьшее количество 4-мерных симплексов в любом из них равно 16.

Разложение тессеракта на экземпляры его характерного симплекса (частная ортосхема с диаграммой Коксетера). ) — это самая простая возможная прямая конструкция тессеракта. Характеристическая 5-ячейка 4-куба является фундаментальной областью тессеракта определяющей группы симметрии , группы, которая порождает B ₄ многогранники . Характерный симплекс тессеракта непосредственно порождает тессеракт посредством действий группы, отражаясь в собственных ограничивающих гранях ( зеркальных стенках ).

Радиальная равносторонняя симметрия

Радиус гиперсферы , описанной вокруг правильного многогранника, — это расстояние от центра многогранника до одной из вершин, а для тессеракта этот радиус равен длине его ребра; диаметр сферы, длина диагонали между противоположными вершинами тессеракта, в два раза превышает длину ребра. Лишь немногие однородные многогранники обладают этим свойством, включая четырехмерный тессеракт и 24-клеточный , трехмерный кубооктаэдр и двумерный шестиугольник . В частности, тессеракт — единственный гиперкуб (кроме нульмерной точки), который является радиально равносторонним . Самая длинная диагональ между вершинами $n$-мерный гиперкуб с единичной длиной ребра равен ${\sqrt {n{\vphantom {t}}}},$ что для квадрата ${\sqrt {2}},$ потому что куб ${\sqrt {3}},$ и только для тессеракта ${\sqrt {4}}=2$ длины ребер.

Тессеракт, ориентированный по оси, вписанный в трехмерную сферу единичного радиуса, имеет вершины с координатами. ${\bigl (}{\pm {\tfrac {1}{2}}},\pm {\tfrac {1}{2}},\pm {\tfrac {1}{2}},\pm {\tfrac {1}{2}}{\bigr )}.$

Характеристики

Доказательство без слов того, что граф гиперкуба неплоский , с использованием теорем Куратовского или Вагнера и нахождением либо K ₅ (вверху), либо K _3,3 (внизу) подграфов.

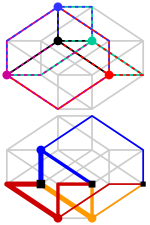
Для тессеракта с длиной стороны s :

• Гиперобъем (4D): $H=s^{4}$
• Поверхностный «объем» (3D): $SV=8s^{3}$
• Диагональ лица : $d_{\mathrm {2} }={\sqrt {2}}s$
• Диагональ ячейки : $d_{\mathrm {3} }={\sqrt {3}}s$
• 4-мерная диагональ: $d_{\mathrm {4} }=2s$

В качестве конфигурации

Эта матрица конфигурации представляет собой тессеракт. Строки и столбцы соответствуют вершинам, ребрам, граням и ячейкам. Диагональные числа показывают, сколько каждого элемента встречается во всем тессеракте. Недиагональные числа показывают, сколько элементов столбца встречается в элементе строки или рядом с ним. Например, цифра 2 в первом столбце второй строки указывает на то, что на каждом ребре (т. е. на крайних точках) имеется по две вершины; цифра 4 во втором столбце первой строки означает, что в каждой вершине сходятся 4 ребра.

${\begin{bmatrix}{\begin{matrix}16&4&6&4\\2&32&3&3\\4&4&24&2\\8&12&6&8\end{matrix}}\end{bmatrix}}$

Прогнозы

Тессеракты можно проецировать в трехмерное и двумерное пространство аналогично проектированию куба в двумерное пространство.

Параллельные проекционные оболочки тессеракта (каждая ячейка рисуется гранями разного цвета, перевернутые ячейки не рисуются)

Ромбический додекаэдр образует выпуклую оболочку параллельной проекции тессеракта с первой вершиной. Число вершин в слоях этой проекции равно 1 4 6 4 1 — четвёртая строка в треугольнике Паскаля .

Параллельная ячейку . проекция тессеракта на в трехмерное пространство имеет кубическую оболочку Ближайшая и самая дальняя ячейки проецируются на куб, а оставшиеся шесть ячеек проецируются на шесть квадратных граней куба.

Параллельная проекция тессеракта лицевой стороной вперед в трехмерное пространство имеет кубовидную оболочку. Две пары ячеек выступают на верхнюю и нижнюю половины этой оболочки, а четыре оставшиеся ячейки выступают на боковые грани.

Параллельная параллельная с края, проекция тессеракта в трехмерное пространство, имеет оболочку в форме шестиугольной призмы . Шесть ячеек проецируются на ромбические призмы, которые расположены в шестиугольной призме аналогично тому, как грани трехмерного куба проецируются на шесть ромбов в шестиугольной оболочке при проекции «сначала вершина». Две оставшиеся ячейки выступают на основания призм.

имеет параллельная сначала вершине, Параллельная проекция тессеракта в трехмерное пространство, ромбическую додекаэдрическую оболочку. Две вершины тессеракта проецируются в начало координат. Существует ровно два способа разрезать ромбдодекаэдр на четыре конгруэнтных ромбоэдра , что дает в общей сложности восемь возможных ромбоэдров, каждый из которых представляет собой проецируемый куб тессеракта. Эта проекция также имеет максимальный объем. Одним набором векторов проекции являются u = (1,1,−1,−1) , v = (−1,1,−1,1) , w = (1,−1,−1,1) .

Анимация, показывающая каждый отдельный куб в _{B 4 Кокстера.} проекции тессеракта на плоскость

Орфографические проекции

Самолет Коксетера	Б 4	Б 4 --> А 3	AА3
График
Двугранная симметрия	[8]	[4]	[4]
Самолет Коксетера	Другой	Б 3 / Д 4 / А 2	Б2 / Д3
График
Двугранная симметрия	[2]	[6]	[4]

График ортографической проекции плоскости Кокстера B ₄ со скрытыми линиями в виде пунктирных линий и тессеракт без скрытых линий.

Трехмерная проекция тессеракта, выполняющая простое вращение вокруг плоскости в четырехмерном пространстве. Плоскость делит фигуру пополам спереди слева, сзади справа и сверху вниз.

Трехмерная проекция тессеракта, совершающая двойное вращение вокруг двух ортогональных плоскостей в четырехмерном пространстве.

Продолжительность: 5 секунд. 0:05 3D-проекция трех тессерактов с гранями и без них

Перспектива с устранением скрытого объема . Красный угол является ближайшим в 4D , вокруг него встречаются 4 кубические ячейки.

Тетраэдр . образует выпуклую оболочку центральной проекции тессеракта, центрированной по вершинам Показаны четыре из 8 кубических ячеек. 16-я вершина проецируется на бесконечность и четыре ребра к ней не показаны.

Стереографическая проекция (Ребра проецируются на 3-сферу )

Стереоскопическая 3D-проекция тессеракта (параллельный вид)

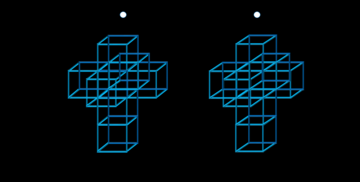Стереоскопический 3D обезвреженный гиперкуб

Тесселяция

Тессеракт, как и все гиперкубы , замощает евклидово пространство . Самодвойственная тессерактическая сота, состоящая из 4 тессерактов вокруг каждой грани, имеет Шлефли символ {4,3,3,4} . Следовательно, тессеракт имеет двугранный угол 90°.

тессеракта Радиальная равносторонняя симметрия делает его мозаику уникальной регулярной объемноцентрированной кубической решеткой из сфер одинакового размера в любом количестве измерений.

Связанные многогранники и соты

Тессеракт является четвертым в серии гиперкубов :

многоугольника Петри Ортогональные проекции

Отрезок линии	Квадрат	Куб	4-кубовый	5-куб	6-куб.	7-куб	8-кубовый

Тессеракт (8-клеточный) является третьим в последовательности из 6 выпуклых правильных 4-многогранников (в порядке размера и сложности).

показывать Правильные выпуклые 4-многогранники
Symmetry group	A4	B4		F4	H4
Name	5-cell Hyper-tetrahedron 5-point	16-cell Hyper-octahedron 8-point	8-cell Hyper-cube 16-point	24-cell 24-point	600-cell Hyper-icosahedron 120-point	120-cell Hyper-dodecahedron 600-point
Schläfli symbol	{3, 3, 3}	{3, 3, 4}	{4, 3, 3}	{3, 4, 3}	{3, 3, 5}	{5, 3, 3}
Coxeter mirrors
Mirror dihedrals	⁠𝝅/3⁠ ⁠𝝅/3⁠ ⁠𝝅/3⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠	⁠𝝅/3⁠ ⁠𝝅/3⁠ ⁠𝝅/4⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠	⁠𝝅/4⁠ ⁠𝝅/3⁠ ⁠𝝅/3⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠	⁠𝝅/3⁠ ⁠𝝅/4⁠ ⁠𝝅/3⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠	⁠𝝅/3⁠ ⁠𝝅/3⁠ ⁠𝝅/5⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠	⁠𝝅/5⁠ ⁠𝝅/3⁠ ⁠𝝅/3⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠
Graph
Vertices	5 tetrahedral	8 octahedral	16 tetrahedral	24 cubical	120 icosahedral	600 tetrahedral
Edges	10 triangular	24 square	32 triangular	96 triangular	720 pentagonal	1200 triangular
Faces	10 triangles	32 triangles	24 squares	96 triangles	1200 triangles	720 pentagons
Cells	5 tetrahedra	16 tetrahedra	8 cubes	24 octahedra	600 tetrahedra	120 dodecahedra
Tori	1 5-tetrahedron	2 8-tetrahedron	2 4-cube	4 6-octahedron	20 30-tetrahedron	12 10-dodecahedron
Inscribed	120 in 120-cell	675 in 120-cell	2 16-cells	3 8-cells	25 24-cells	10 600-cells
Great polygons		2 squares x 3	4 rectangles x 4	4 hexagons x 4	12 decagons x 6	100 irregular hexagons x 4
Petrie polygons	1 pentagon x 2	1 octagon x 3	2 octagons x 4	2 dodecagons x 4	4 30-gons x 6	20 30-gons x 4
Long radius	$1$	$1$	$1$	$1$	$1$	$1$
Edge length	${\sqrt {\tfrac {5}{2}}}\approx 1.581$	${\sqrt {2}}\approx 1.414$	$1$	$1$	${\tfrac {1}{\phi }}\approx 0.618$	${\tfrac {1}{\phi ^{2}{\sqrt {2}}}}\approx 0.270$
Short radius	${\tfrac {1}{4}}$	${\tfrac {1}{2}}$	${\tfrac {1}{2}}$	${\sqrt {\tfrac {1}{2}}}\approx 0.707$	${\sqrt {\tfrac {\phi ^{4}}{8}}}\approx 0.926$	${\sqrt {\tfrac {\phi ^{4}}{8}}}\approx 0.926$
Area	$10\left({\tfrac {5{\sqrt {3}}}{8}}\right)\approx 10.825$	$32\left({\sqrt {\tfrac {3}{4}}}\right)\approx 27.713$	$24$	$96\left({\sqrt {\tfrac {3}{16}}}\right)\approx 41.569$	$1200\left({\tfrac {\sqrt {3}}{4\phi ^{2}}}\right)\approx 198.48$	$720\left({\tfrac {\sqrt {25+10{\sqrt {5}}}}{8\phi ^{4}}}\right)\approx 90.366$
Volume	$5\left({\tfrac {5{\sqrt {5}}}{24}}\right)\approx 2.329$	$16\left({\tfrac {1}{3}}\right)\approx 5.333$	$8$	$24\left({\tfrac {\sqrt {2}}{3}}\right)\approx 11.314$	$600\left({\tfrac {\sqrt {2}}{12\phi ^{3}}}\right)\approx 16.693$	$120\left({\tfrac {15+7{\sqrt {5}}}{4\phi ^{6}{\sqrt {8}}}}\right)\approx 18.118$
4-Content	${\tfrac {\sqrt {5}}{24}}\left({\tfrac {\sqrt {5}}{2}}\right)^{4}\approx 0.146$	${\tfrac {2}{3}}\approx 0.667$	$1$	$2$	${\tfrac {{\text{Short}}\times {\text{Vol}}}{4}}\approx 3.863$	${\tfrac {{\text{Short}}\times {\text{Vol}}}{4}}\approx 4.193$

Как однородная дуопризма , тессеракт существует в последовательности однородных дуопризм : { p }×{4}.

Правильный тессеракт, наряду с 16-клеточным , существует в наборе из 15 однородных 4-многогранников с одинаковой симметрией . Тессеракт {4,3,3} существует в последовательности правильных 4-многогранников и сот { p ,3,3} с тетраэдрическими вершинными фигурами , {3,3}. Тессеракт также представляет собой последовательность правильных 4-многогранников и сот {4,3, p } с кубическими ячейками .

Ортогональный	Перспектива
4 {4} 2 , с 16 вершинами и 8 4-ребрами, причем 8 4-ребер показаны здесь как 4 красных и 4 синих квадрата

Правильный комплексный многогранник ₄ {4} ₂ , , в $\mathbb {C} ^{2}$ имеет реальное представление в виде тессеракта или 4-4- дуопризмы в 4-мерном пространстве. ₄ {4} ₂ имеет 16 вершин и 8 4-ребер. Его симметрия равна ₄ [4] ₂ , порядок 32. Он также имеет конструкцию более низкой симметрии, , или ₄ {}× ₄ {}, с симметрией ₄ [2] ₄ , порядок 16. Это симметрия, если красные и синие 4-ребра считаются различными.

В популярной культуре

С момента своего открытия четырехмерные гиперкубы стали популярной темой в искусстве, архитектуре и научной фантастике. Яркие примеры включают:

• « И он построил кривой дом » — научно-фантастический рассказ Роберта Хайнлайна 1940 года, в котором показано здание в форме четырехмерного гиперкуба. Эта книга, а также книга Мартина Гарднера «Несторонний профессор», опубликованная в 1946 году, являются одними из первых произведений научной фантастики, знакомящих читателей с лентой Мебиуса , бутылкой Клейна и гиперкубом (тессерактом).
• Распятие (Corpus Hypercubus) , картина маслом Сальвадора Дали 1954 года, изображающая четырехмерный гиперкуб, развернутый в трехмерный латинский крест .
• Большая Арка , памятник и здание недалеко от Парижа, Франция, завершенное в 1989 году. По словам инженера памятника Эрика Райтцеля , Большая Арка была спроектирована так, чтобы напоминать проекцию гиперкуба.
• Fez , видеоигра, в которой вы играете за персонажа, который может видеть за пределами двух измерений, которые видят другие персонажи, и должен использовать эту способность для решения платформерных головоломок. Включает «Точку», тессеракт, который помогает игроку ориентироваться в мире и рассказывает, как использовать способности, что соответствует теме видения за пределами человеческого восприятия известного многомерного пространства.

Слово «тессеракт» использовалось во многих других целях в популярной культуре, в том числе в качестве сюжета в произведениях научной фантастики, часто практически не связанных с четырехмерным гиперкубом; см. Тессеракт (значения) .

См. также

• Математика и искусство

Ссылки

• Коксетер, HSM (1973). Правильные многогранники (3-е изд.). Нью-Йорк: Дувр. стр. 122–123 .
• Ф. Артур Шерк, Питер МакМаллен, Энтони К. Томпсон, Азия Ивик Вайс (1995) Калейдоскопы: избранные сочинения HSM Coxeter , Wiley-Interscience Publication ISBN   978-0-471-01003-6 [1]
  • (Документ 22) HSM Coxeter, Правильные и полуправильные многогранники I , Mathematical Journal 46 (1940) 380–407, MR 2.10]
  • (Документ 23) HSM Коксетер, Правильные и полуправильные многогранники II , [Math. Зейт. 188 (1985) 559-591]
  • (Документ 24) HSM Коксетер, Правильные и полуправильные многогранники III , [Math. Зейт. 200 (1988) 3-45]
• Коксетер, HSM (1970), «Витые соты», Совет конференции серии региональных конференций математических наук по математике , 4 , Провиденс, Род-Айленд: Американское математическое общество
• Джон Х. Конвей , Хайди Бургель, Хаим Гудман-Штраус (2008) Симметрии вещей , ISBN   978-1-56881-220-5 (Глава 26. стр. 409: Гемикубы: 1 _n1 )
• Т. Госсет (1900) О правильных и полуправильных фигурах в пространстве n измерений , Вестник математики , Макмиллан.
• Холл, Т. Проктор (1893). «Проекция четверной фигуры на трехмерную». Американский журнал математики . 15 : 179–189. JSTOR   2369565 .
• Нормана Джонсона Равномерные многогранники , Рукопись (1991)
  • Н. В. Джонсон: Теория однородных многогранников и сот , доктор философии. (1966)
• Виктор Шлегель (1886) О проекционных моделях правильных четырехмерных тел , Варен.

Внешние ссылки

• Клитцинг, Ричард. «4D однородные многогранники (полихора) x4o3o3o - tes» .
• Домашняя страница Кена Перлина «Способ визуализации гиперкубов», Кен Перлин
• «Некоторые заметки о четвертом измерении» по нескольким различным аспектам тессеракта. включают анимированные уроки Давида П. Червоне
• Анимация Тессеракта с устранением скрытого объема