Излучение Хокинга

Излучение Хокинга — это теоретическое тепловое излучение черного тела , испускаемое за пределами дыры черной горизонта событий . Это противоречит здравому смыслу, поскольку, обычное электромагнитное излучение оказавшись внутри горизонта событий, не может выйти за его пределы. Он назван в честь физика Стивена Хокинга , который разработал теоретическое обоснование его существования в 1974 году. По прогнозам, излучение Хокинга будет чрезвычайно слабым и на много порядков ниже обнаруживающей способности лучших современных телескопов.

Излучение Хокинга уменьшает массу и энергию вращения черных дыр и, следовательно, теоретически вызывает испарение черных дыр. Из-за этого ожидается, что черные дыры, которые не набирают массу другими способами, будут сжиматься и в конечном итоге исчезнут.

Для всех, кроме самых маленьких черных дыр, это происходит крайне медленно. Температура излучения, называемая температурой Хокинга , обратно пропорциональна массе черной дыры, поэтому микрочерные дыры прогнозируется, что являются более крупными излучателями, чем более крупные черные дыры, и должны рассеиваться быстрее в зависимости от их массы. Таким образом, если существуют небольшие черные дыры, допускаемые гипотезой о первичных черных дырах , они должны терять массу быстрее по мере сжатия, что приведет к окончательному катаклизму только радиации высокой энергии. Такие радиационные всплески пока не обнаружены.

Обзор

Современные черные дыры были впервые предсказаны Эйнштейна в 1915 году общей теорией относительности . Доказательства существования астрофизических объектов, называемых черными дырами, начали накапливаться полвека спустя. и эти объекты представляют современный интерес прежде всего из-за их компактных размеров и огромного гравитационного притяжения . Ранние исследования черных дыр проводились такими людьми, как Карл Шварцшильд и Джон Уилер, которые моделировали черные дыры как имеющие нулевую энтропию.

Черная дыра может образоваться, когда достаточное количество материи или энергии сжимается в объем, достаточно малый, чтобы скорость убегания превышала скорость света. Ничто не может двигаться так быстро, поэтому ничто на определенном расстоянии, пропорциональном массе черной дыры, не может выйти за пределы этого расстояния. Область, за пределы которой не может выйти даже свет, — это горизонт событий ; наблюдатель вне его не может наблюдать, осознавать или подвергаться влиянию событий в пределах горизонта событий.

Изображение космоса , падающего в черную дыру Шварцшильда на ньютоновской скорости убегания . За пределами/внутри горизонта (красный) скорость падения меньше/больше скорости света. На горизонте событий скорость падения равна скорости света. Авторы и права : Эндрю Хэмилтон, JILA

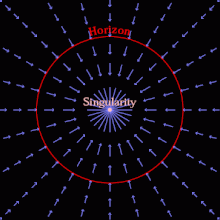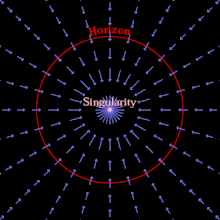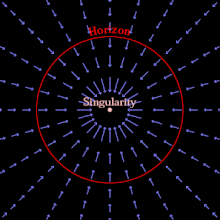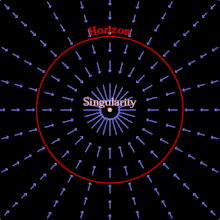
В качестве альтернативы, используя набор падающих координат в общей теории относительности, можно представить горизонт событий как область, за пределами которой пространство падает со скоростью, превышающей скорость света. (Хотя ничто не может двигаться в пространстве быстрее света, само пространство может падать с любой скоростью.) Как только материя оказывается внутри горизонта событий, вся материя внутри неизбежно попадает в гравитационную сингулярность , место бесконечной кривизны и нулевого размера, оставляя после себя искривленное пространство-время, лишенное какой-либо материи; Классическая черная дыра — это чистое пустое пространство-время , а простейшая (невращающаяся и незаряженная) характеризуется только своей массой и горизонтом событий.

Наше нынешнее понимание квантовой физики можно использовать для исследования того, что может произойти в области вокруг горизонта событий. В 1974 году британский физик Стивен Хокинг использовал квантовую теорию поля в искривленном пространстве-времени, чтобы показать, что теоретически вместо того, чтобы обычно уравновешивать друг друга, поля антиматерии и материи разрушаются черной дырой, в результате чего частицы антиматерии и материи «перескакивают» в существование в результате несбалансированных полей материи и получение энергии от самого разрушителя: черных дыр (чтобы сбежать), эффективно истощая энергию из черной дыры. Кроме того, не все частицы оказались близко к горизонту событий, а те, что были, не смогли ускользнуть. По сути, эта энергия действовала так, как будто сама черная дыра медленно испарялась (хотя на самом деле она исходила извне).

Однако, согласно предполагаемой дуальности калибровочно-гравитационной теории (также известной как соответствие AdS/CFT ), черные дыры в определенных случаях (а возможно, и в целом) эквивалентны решениям квантовой теории поля при ненулевой температуре . Это означает, что в черных дырах не ожидается никакой потери информации (поскольку теория не допускает такой потери) и излучение, испускаемое черной дырой, вероятно, является обычным тепловым излучением. Если это верно, то первоначальный расчет Хокинга следует скорректировать, хотя и неизвестно каким образом (см. ниже ).

Черная дыра массой в одну солнечную ( M _☉ ) имеет температуру всего 60 нанокельвинов (60 миллиардных долей кельвина ); на самом деле, такая черная дыра поглощала бы гораздо больше космического микроволнового фонового излучения, чем излучала. Черная дыра размером 4,5 × 10 ²² кг (около массы Луны или около 133 мкм в поперечнике) находился бы в равновесии при температуре 2,7 К, поглощая столько же радиации, сколько излучает.

Формулировка

В 1972 году Джейкоб Бекенштейн разработал теорию и сообщил, что черные дыры должны обладать энтропией. Теория и доклад Бекенштейна привлекли внимание Стивена Хокинга . из-за этого формализма заставил его задуматься об радиации. Последующая теория и доклад Хокинга последовали за визитом в Москву в 1973 году, где советские учёные Яков Зельдович и Алексей Старобинский убедили его, что вращающиеся чёрные дыры должны создавать и испускать частицы. Хокинг счел бы аспекты обоих этих аргументов верными, если бы сам провёл расчеты. Благодаря вкладу Бекенштейна в энтропию черной дыры, оно также известно как излучение Бекенштейна-Хокинга.

Процесс эмиссии

Излучение Хокинга зависит от эффекта Унру и принципа эквивалентности, применяемого к горизонтам черных дыр. Вблизи горизонта событий черной дыры локальный наблюдатель должен ускоряться, чтобы не упасть. Ускоряющийся наблюдатель видит тепловую ванну из частиц, которые выскакивают из местного горизонта ускорения, разворачиваются и свободно падают обратно. условие локального теплового равновесия подразумевает, что последовательное расширение этой локальной тепловой ванны имеет конечную температуру на бесконечности, а это означает, что некоторые из этих частиц, испускаемых горизонтом, не реабсорбируются и становятся уходящим излучением Хокинга.

Черная дыра Шварцшильда имеет метрику

$(\mathrm {d} s)^{2}=-\left(1-{\frac {2M}{r}}\right)\,(\mathrm {d} t)^{2}+{\frac {1}{\left(1-{\frac {2M}{r}}\right)}}\,(\mathrm {d} r)^{2}+r^{2}\,(\mathrm {d} \Omega )^{2}.$

Черная дыра — это фоновое пространство-время для квантовой теории поля.

Теория поля определяется локальным интегралом по траекториям, поэтому, если определены граничные условия на горизонте, будет указано состояние поля снаружи. Чтобы найти подходящие граничные условия, рассмотрим стационарного наблюдателя недалеко от горизонта в позиции

$r=2M+{\frac {\rho ^{2}}{8M}}.$

Локальная метрика низшего порядка равна

$(\mathrm {d} s)^{2}=-\left({\frac {\rho }{4M}}\right)^{2}\,(\mathrm {d} t)^{2}+(\mathrm {d} \rho )^{2}+(\mathrm {d} X_{\perp })^{2}=-\rho ^{2}\,(\mathrm {d} \tau )^{2}+(\mathrm {d} \rho )^{2}+(\mathrm {d} X_{\perp })^{2},$

что является Риндлером с точки зрения τ = ⁠ т / 4 М ⁠ . Метрика описывает кадр, который ускоряется, чтобы не упасть в черную дыру. Местное ускорение α = ⁠ 1 / ρ ⁠ , расходится при ρ → 0 .

Горизонт не является особой границей, и объекты могут падать внутрь. Поэтому локальный наблюдатель должен чувствовать ускорение в обычном пространстве Минковского по принципу эквивалентности. Близгоризонтный наблюдатель должен видеть поле, возбужденное при локальной температуре.

$T={\frac {\alpha }{2\pi }}={\frac {1}{2\pi \rho }}={\frac {1}{4\pi {\sqrt {2Mr\left(1-{\frac {2M}{r}}\right)}}}},$

это эффект Унру .

Гравитационное красное смещение определяется квадратным корнем временной составляющей метрики. Таким образом, чтобы состояние теории поля последовательно расширялось, повсюду должен существовать тепловой фон с локальным красным смещением температуры, согласованным с температурой вблизи горизонта:

$T(r')={\frac {1}{4\pi {\sqrt {2Mr\left(1-{\frac {2M}{r}}\right)}}}}{\sqrt {\frac {1-{\frac {2M}{r}}}{1-{\frac {2M}{r'}}}}}={\frac {1}{4\pi {\sqrt {2Mr\left(1-{\frac {2M}{r'}}\right)}}}}.$

Обратная температура, смещенная в красную сторону к r' на бесконечности, равна

$T(\infty )={\frac {1}{4\pi {\sqrt {2Mr}}}},$

а r — положение около горизонта, около 2 M , так что это действительно

$T(\infty )={\frac {1}{8\pi M}}.$

Таким образом, теория поля, определенная на фоне черной дыры, находится в тепловом состоянии, температура которого на бесконечности равна

$T_{\text{H}}={\frac {1}{8\pi M}}.$

По температуре черной дыры несложно вычислить энтропию черной S. дыры количества тепла dQ Изменение энтропии при добавлении равно

$\mathrm {d} S={\frac {\mathrm {d} Q}{T}}=8\pi M\,\mathrm {d} Q.$

Поступившая тепловая энергия служит увеличению общей массы, поэтому

$\mathrm {d} S=8\pi M\,\mathrm {d} M=\mathrm {d} (4\pi M^{2}).$

Радиус черной дыры в два раза превышает ее массу в планковских единицах , поэтому энтропия черной дыры пропорциональна площади ее поверхности:

$S=\pi R^{2}={\frac {A}{4}}.$

Если предположить, что маленькая черная дыра имеет нулевую энтропию, константа интегрирования равна нулю. Формирование черной дыры — наиболее эффективный способ сжатия массы в определенной области, и эта энтропия также является границей информационного содержания любой сферы в пространстве-времени. Форма результата убедительно свидетельствует о том, что физическое описание теории гравитации может быть каким-то образом закодировано на ограничивающей поверхности.

Испарение черной дыры

Когда частицы улетают, черная дыра теряет небольшое количество своей энергии и, следовательно, часть своей массы (масса и энергия связаны уравнением Эйнштейна E = mc ² ). Следовательно, испаряющаяся черная дыра будет иметь конечный срок жизни. С помощью анализа размерностей можно показать, что продолжительность жизни черной дыры равна кубу ее начальной массы: и Хокинг подсчитали, что в ранней Вселенной образовалась любая черная дыра с массой менее примерно 10 ¹² кг к настоящему времени полностью испарился бы.

В 1976 году Дон Пейдж уточнил эту оценку, рассчитав производимую мощность и время испарения невращающейся, незаряженной дыры Шварцшильда с массой M. черной Время, в течение которого горизонт событий или энтропия черной дыры уменьшается вдвое, известно как время Пейджа. Расчеты осложняются тем, что черная дыра, имея конечный размер, не является идеальным черным телом; сечение поглощения убывает сложным, спин -зависимым образом с уменьшением частоты, особенно когда длина волны становится сравнимой с размером горизонта событий. Пейдж пришел к выводу, что первичные черные дыры могли бы выжить до наших дней только в том случае, если бы их первоначальная масса составляла примерно 4 × 10 ¹¹ кг или больше. В 1976 году Пейдж, используя тогдашнее понимание нейтрино, ошибочно исходил из предположения, что нейтрино не имеют массы и что существуют только два аромата нейтрино, и поэтому его результаты о времени жизни черных дыр не соответствуют современным результатам, учитывающим 3 ароматы нейтрино с ненулевыми массами . Расчеты 2008 года с использованием содержания частиц Стандартной модели и числа WMAP для возраста Вселенной дали границу массы (5,00 ± 0,04) × 10. ¹¹ кг .

Некоторые расчеты, проведенные до 1998 года с использованием устаревших предположений о нейтрино, были следующими: если черные дыры испаряются под действием излучения Хокинга, черная дыра солнечной массы испарится за 10 ⁶⁴ лет, что значительно превышает возраст Вселенной. Сверхмассивная черная дыра с массой 10 ¹¹ (100 миллиардов) M _☉ испарится примерно за 2 × 10 ¹⁰⁰ годы . По прогнозам, некоторые чудовищные черные дыры во Вселенной будут продолжать расти, возможно, до 10 ¹⁴ M _☉ при коллапсе сверхскоплений галактик. Даже они испарились бы за время до 2 × 10 ¹⁰⁶ годы. Наука, появившаяся после 1998 года, немного изменила эти результаты; например, современная оценка времени жизни черной дыры солнечной массы составляет 10 ⁶⁷ годы.

Мощность , можно оценить для простейшего случая невращающейся незаряженной черной дыры Шварцшильда массы M. излучаемую черной дырой в виде излучения Хокинга , Объединив формулы для радиуса Шварцшильда черной дыры, закон Стефана-Больцмана для излучения черного тела, приведенную выше формулу для температуры излучения и формулу для площади поверхности сферы ( горизонта событий черной дыры), несколько уравнения можно вывести.

Температура излучения Хокинга равна:

$T_{\mathrm {H} }={\frac {\hbar c^{3}}{8\pi GMk_{\mathrm {B} }}}$

Светимость Бекенштейна – Хокинга черной дыры в предположении чистого излучения фотонов (т. е. что никакие другие частицы не испускаются) и в предположении, что горизонт является излучающей поверхностью, равна:

$P={\frac {\hbar c^{6}}{15360\pi G^{2}M^{2}}}$

где P — светимость, т. е. излучаемая мощность, ħ — приведенная постоянная Планка , c — скорость света , G — гравитационная постоянная и M — масса черной дыры. Стоит отметить, что приведенная выше формула еще не была выведена в рамках квазиклассической гравитации .

Время, необходимое черной дыре для рассеяния, равно:

$t_{\mathrm {ev} }={\frac {5120\pi G^{2}M^{3}}{\hbar c^{4}}}={\frac {480c^{2}V}{\hbar G}}=5120\pi \,t_{\text{P}}\left({\frac {M}{m_{\text{P}}}}\right)^{3}\approx 3.396\times 10^{-16}\,\mathrm {s} \ \left({M \over \mathrm {kg} }\right)^{3}\approx 2.140\times 10^{67}\,{\text{years}}\ \left({\frac {M}{M_{\odot }}}\right)^{3},$

где M и V — масса и (шварцшильдовский) объем черной дыры, m _P и t _P — планковская масса и планковское время. Черная дыра массой в одну солнечную ( M _☉ = 2,0 × 10 ³⁰ кг ) занимает более 10 ⁶⁷ лет на испарение — намного дольше, чем нынешний возраст Вселенной ( 1,4 × 10) . ¹⁰ годы . Но для черной дыры 10 ¹¹ кг , время испарения 2,6 × 10 ⁹ годы . Вот почему некоторые астрономы ищут признаки взрыва первичных черных дыр .

Однако, поскольку Вселенная содержит космическое микроволновое фоновое излучение , для того, чтобы черная дыра рассеялась, черная дыра должна иметь температуру, превышающую температуру современного излучения черного тела Вселенной, составляющую 2,7 К. Исследование предполагает, что M должна составлять менее 0,8% массы Земли – примерно масса Луны.

Испарение черной дыры имеет несколько существенных последствий:

• Испарение черных дыр дает более последовательное представление о термодинамике черных дыр , показывая, как черные дыры термически взаимодействуют с остальной частью Вселенной.
• В отличие от большинства объектов, температура черной дыры увеличивается по мере того, как она излучает массу. Скорость повышения температуры экспоненциальна, и наиболее вероятной конечной точкой является растворение черной дыры в результате сильной вспышки гамма-лучей . Полное описание этого растворения требует модели квантовой гравитации , однако, поскольку это происходит, когда масса черной дыры приближается к 1 планковской массе , ее радиус также приближается к двум планковским длинам .
• Простейшие модели испарения черной дыры приводят к информационному парадоксу черной дыры . Информационное содержание черной дыры, по-видимому, теряется при ее рассеивании, поскольку согласно этим моделям излучение Хокинга является случайным (оно не имеет никакого отношения к исходной информации). Был предложен ряд решений этой проблемы, в том числе предположения о том, что излучение Хокинга содержит недостающую информацию, что испарение Хокинга оставляет некоторую форму остаточных частиц, содержащих недостающую информацию, и что при этих условиях информация может быть потеряна. .

Проблемы и расширения

Транспланковская проблема

Транспланковская проблема заключается в том, что первоначальные расчеты Хокинга включают квантовые частицы, длина волны которых становится короче планковской длины вблизи горизонта черной дыры. Это связано со своеобразным поведением там, где время останавливается, измеренное издалека. Частица, испускаемая черной дырой с конечной частотой , если ее проследить до горизонта, должна была иметь бесконечную частоту и, следовательно, транспланковскую длину волны.

Эффект Унру и эффект Хокинга говорят о модах поля в поверхностно стационарном пространстве-времени , которые меняют частоту относительно других координат, регулярных по горизонту. Это обязательно так, поскольку для того, чтобы оставаться за горизонтом, требуется ускорение, которое постоянно доплеровски меняет моды.

Уходящий фотон излучения Хокинга, если проследить моду назад во времени, имеет частоту, отличающуюся от той, которую он имеет на большом расстоянии, по мере приближения к горизонту, что требует, чтобы длина волны фотона «сжималась вверх» бесконечно на горизонте черной дыры. В максимально расширенном внешнем решении Шварцшильда частота этого фотона остается регулярной только в том случае, если мода распространяется обратно в область прошлого, куда не может попасть ни один наблюдатель. Эта область кажется ненаблюдаемой и физически подозрительной, поэтому Хокинг использовал решение в виде черной дыры без прошлой области, которая формируется в конечное время в прошлом. В этом случае можно определить источник всех исходящих фотонов: микроскопическую точку как раз в тот момент, когда черная дыра впервые образовалась.

Квантовые флуктуации в этой крошечной точке, согласно первоначальным расчетам Хокинга, содержат все исходящее излучение. Моды, которые в конечном итоге содержат исходящее излучение в течение длительного времени, из-за длительного пребывания рядом с горизонтом событий смещаются в красную величину на такую ​​огромную величину, что начинаются как моды с длиной волны, намного меньшей планковской длины. Поскольку законы физики на таких коротких расстояниях неизвестны, некоторые считают первоначальный расчет Хокинга неубедительным.

Транспланковская проблема в настоящее время в основном считается математическим артефактом расчета горизонта. Тот же эффект происходит и при падении обычной материи на раствор белой дыры . Материя, попавшая на белую дыру, скапливается на ней, но не имеет будущей области, в которую она могла бы перейти. Прослеживая будущее этой материи, мы сжимаем ее до конечной сингулярной конечной точки эволюции белой дыры, в транспланковскую область. Причина подобных расхождений в том, что моды, заканчивающиеся на горизонте с точки зрения внешних координат, там сингулярны по частоте. Единственный способ определить, что происходит классически, — это продолжить в каких-то других координатах, пересекающих горизонт.

Существуют альтернативные физические картины, которые дают излучение Хокинга, в котором решается транспланковская проблема. Ключевым моментом является то, что аналогичные транспланковские проблемы возникают, когда моды, занятые излучением Унру, прослеживаются во времени. В эффекте Унру величина температуры может быть рассчитана с помощью обычной Минковского теории поля , и это не является спорным.

Большие дополнительные размеры

Формулы из предыдущего раздела применимы только в том случае, если законы гравитации приблизительно справедливы вплоть до масштаба Планка. В частности, для черных дыр с массами ниже планковской (~ 10 ⁻⁸ кг ), они приводят к невозможному времени жизни ниже планковского времени (~ 10 ⁻⁴³ с ). Обычно это рассматривается как указание на то, что планковская масса является нижним пределом массы черной дыры.

В модели с большими дополнительными измерениями (10 или 11) значения констант Планка могут радикально отличаться, и формулы для излучения Хокинга также придется модифицировать. В частности, время жизни микрочерной дыры с радиусом ниже шкалы дополнительных измерений определяется уравнением 9 в Cheung (2002). и уравнения 25 и 26 в Carr (2005).

$\tau \sim {\frac {1}{M_{*}}}\left({\frac {M_{\text{BH}}}{M_{*}}}\right)^{\frac {n+3}{n+1}},$

где M _∗ — масштаб низких энергий, который может составлять всего несколько ТэВ, а n — количество больших дополнительных измерений. Эта формула теперь согласуется с черными дырами с весом в несколько ТэВ и временем жизни порядка «нового планковского времени» ~ 10. ⁻²⁶ с .

Циклическая квантовая гравитация

Детальное исследование квантовой геометрии горизонта событий черной дыры было проведено с использованием петлевой квантовой гравитации . Петлевое квантование не воспроизводит результат для энтропии черной дыры, первоначально обнаруженной Бекенштейном и Хокингом , если только значение свободного параметра не установлено для компенсации различных констант, так что воспроизводится формула энтропии Бекенштейна-Хокинга. Однако на основе теории были вычислены квантовые гравитационные поправки к энтропии и излучению черных дыр.

Из-за флуктуаций площади горизонта квантовая черная дыра демонстрирует отклонения от спектра излучения Хокинга, которые можно было бы наблюдать, если бы рентгеновские лучи от излучения Хокинга испаряющихся первичных черных дыр . наблюдались Квантовые эффекты сосредоточены на наборе дискретных и несмешанных частот, ярко выраженных на вершине спектра Хокинга.

Экспериментальное наблюдение

Астрономический поиск

В июне 2008 года НАСА запустило космический телескоп Ферми , который ищет конечные вспышки гамма-излучения, ожидаемые от испаряющихся первичных черных дыр . По состоянию на 1 января 2023 года ни одного обнаружено не было.

Физика коллайдера тяжелых ионов

Если спекулятивные теории больших дополнительных измерений верны, то сможет ЦЕРН Большой адронный коллайдер создавать микрочерные дыры и наблюдать за их испарением. В ЦЕРНе такой микро-черной дыры не наблюдалось.

Экспериментальный

В экспериментально достижимых условиях для гравитационных систем этот эффект слишком мал, чтобы его можно было наблюдать напрямую. Было предсказано, что излучение Хокинга можно изучать по аналогии с использованием звуковых черных дыр , в которых звуковые возмущения аналогичны свету в гравитационной черной дыре, а течение примерно идеальной жидкости аналогично гравитации (см. Аналоговые модели гравитации ). Сообщалось о наблюдениях излучения Хокинга в звуковых черных дырах с использованием конденсатов Бозе-Эйнштейна .

В сентябре 2010 года экспериментальная установка создала лабораторный «горизонт событий белой дыры», который, как утверждали экспериментаторы, излучает оптический аналог излучения Хокинга. Однако результаты остаются непроверенными и дискуссионными. и его статус как подлинного подтверждения остается под вопросом.

См. также

• Информационный парадокс черной дыры
• Термодинамика черной дыры
• Звездолет черной дыры
• Процесс Бландфорда – Знаека и процесс Пенроуза , другие способы извлечения энергии черной дыры
• Эффект Гиббонса-Хокинга
• Ставка Торна-Хокинга-Прескилла
• Эффект Унру

Дальнейшее чтение

• Хокинг, Стивен В. (1974). «Взрывы черных дыр?». Природа . 248 (5443): 30–31. Бибкод : 1974Natur.248...30H . дои : 10.1038/248030a0 . S2CID   4290107 . → Первая статья Хокинга на эту тему
• Пейдж, Дон Н. (1976). «Скорость выбросов частиц из черной дыры: безмассовые частицы из незаряженной невращающейся дыры». Физический обзор D . 13 (2): 198–206. Бибкод : 1976PhRvD..13..198P . дои : 10.1103/PhysRevD.13.198 . → первые детальные исследования механизма испарения
• Карр, Бернард Дж.; Хокинг, Стивен В. (1974). «Черные дыры в ранней Вселенной» . Ежемесячные уведомления Королевского астрономического общества . 168 (2): 399–415. arXiv : 1209.2243 . Бибкод : 1974MNRAS.168..399C . дои : 10.1093/mnras/168.2.399 . → связи между первичными черными дырами и ранней Вселенной
• Барро, Орельен; и др. (2002). «Антипротоны из первичных черных дыр». Астрономия и астрофизика . 388 (2): 676–687. arXiv : astro-ph/0112486 . Бибкод : 2002A&A...388..676B . дои : 10.1051/0004-6361:20020313 . S2CID   17033284 .
• Барро, Орельен; и др. (2003). «Андейтроны как зонд первичных черных дыр». Астрономия и астрофизика . 398 (2): 403–410. arXiv : astro-ph/0207395 . Бибкод : 2003A&A...398..403B . дои : 10.1051/0004-6361:20021588 . S2CID   5727582 .
• Барро, Орельен; Ферон, Хлоя; Грейн, Жюльен (2005). «Астрофизическое производство микроскопических черных дыр в мире низкого планковского масштаба». Астрофизический журнал . 630 (2): 1015–1019. arXiv : astro-ph/0505436 . Бибкод : 2005ApJ...630.1015B . дои : 10.1086/432033 . S2CID   6411086 . → экспериментальные поиски первичных черных дыр благодаря испускаемой антиматерии
• Барро, Орельен; Будул, Гаэль (2002). «Некоторые аспекты физики первичных черных дыр». arXiv : astro-ph/0212225 . → космология с первичными черными дырами
• Барро, Орельен; Зерно, Жюльен; Алексеев, Станислав О. (2004). «Черные дыры Гаусса – Бонне на БАК: за пределами размерности пространства». Буквы по физике Б. 584 (1–2): 114–122. arXiv : hep-ph/0311238 . Бибкод : 2004PhLB..584..114B . дои : 10.1016/j.physletb.2004.01.019 . S2CID   14275281 . → поиски новой физики (квантовой гравитации) с первичными чёрными дырами
• Канти, Панайота (2004). «Черные дыры в теориях с большими дополнительными измерениями: обзор». Международный журнал современной физики А. 19 (29): 4899–4951. arXiv : hep-ph/0402168 . Бибкод : 2004IJMPA..19.4899K . дои : 10.1142/S0217751X04018324 . S2CID   11863375 . → Испаряющиеся черные дыры и дополнительные измерения
• Ида, Дайсуке; Ода, Кинья; Пак, Сон Чан (2003). «Вращающиеся черные дыры на будущих коллайдерах: факторы серого тела для полей бран». Физический обзор D . 67 (6): 064025. arXiv : hep-th/0212108 . Бибкод : 2003PhRvD..67f4025I . дои : 10.1103/PhysRevD.67.064025 .
• Ида, Дайсуке; Ода, Кинья; Пак, Сон Чан (2005). «Вращающиеся черные дыры на коллайдерах будущего. II. Анизотропная скалярная полевая эмиссия». Физический обзор D . 71 (12): 124039. arXiv : hep-th/0503052 . Бибкод : 2005PhRvD..71l4039I . дои : 10.1103/PhysRevD.71.124039 . S2CID   28276606 .
• Ида, Дайсуке; Ода, Кинья; Пак, Сон Чан (2006). «Вращающиеся черные дыры на будущих коллайдерах. III. Определение эволюции черных дыр». Физический обзор D . 73 (12): 124022. arXiv : hep-th/0602188 . Бибкод : 2006PhRvD..73l4022I . дои : 10.1103/PhysRevD.73.124022 . S2CID   6702415 . → определение жизни черной дыры и дополнительных измерений
• Николаевич, Нистор (2003). «Спектр черного тела от ускоренных зеркал с асимптотически инерционными траекториями». Журнал физики А. 36 (27): 7667–7677. Бибкод : 2003JPhA...36.7667N . дои : 10.1088/0305-4470/36/27/317 . S2CID   121117052 . → последовательный вывод излучения Хокинга в модели зеркала Фуллинга – Дэвиса.
• Смолин, Ли (ноябрь 2006 г.). «Квантовая гравитация сталкивается с реальностью» (PDF) . Физика сегодня . 59 (11): 44–48. Бибкод : 2006ФТ....59к..44С . дои : 10.1063/1.2435646 . Архивировано из оригинала (PDF) 10 сентября 2008 года. Содержит недавние разработки и предсказания петлевой квантовой гравитации относительно гравитации в малых масштабах, включая отклонение от эффекта излучения Хокинга Ансари .
• Ансари, Мохаммад Х. (2007). «Спектроскопия канонически квантованного горизонта». Ядерная физика Б . 783 (3): 179–212. arXiv : hep-th/0607081 . Бибкод : 2007НуФБ.783..179А . doi : 10.1016/j.nuclphysb.2007.01.009 . S2CID   9966483 . → изучает отклонение петлевой квантованной черной дыры от излучения Хокинга. Представлен новый наблюдаемый квантовый эффект квантования черной дыры.
• Шапиро, Стюарт Л.; Теукольский, Саул А. (1983). Черные дыры, белые карлики и нейтронные звезды: физика компактных объектов . Уайли-Интерсайенс. п. 366 . ISBN  978-0-471-87316-7 . → Вывод формулы испарения радиации Хокинга.
• Леонхардт, Ульф; Майя, Хлодвиг; Шуцхольд, Ральф (2010). «Сосредоточьтесь на классических и квантовых аналогах гравитационных явлений и связанных с ними эффектов» . Новый журнал физики . 14 (10): 105032. Бибкод : 2012NJPh...14j5032L . дои : 10.1088/1367-2630/14/10/105032 . hdl : 10023/4760 .

Внешние ссылки

• Инструмент калькулятора радиации Хокинга
• Случай с мини-черными дырами А. Барро и Дж. Грэйн объясняют, как излучение Хокинга можно было обнаружить на коллайдерах