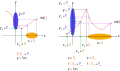Сюръективная функция

В математике ( сюръективная функция также известная как сюръекция или на функцию / ˈ ɒ n . t uː / ) — это функция $f$ такая, что для каждого элемента $y$ функции кодомена существует хотя бы один элемент $x$ в функции область такая, что $f (x) = y$ . Другими словами, для функции $f : X \to Y$ кодобласть $Y$ является образом области определения функции $X$ . ^[1]^[2] Не требуется, чтобы $x$ был уникальным ; функция $f$ может отображать один или несколько элементов $X$ и тот же элемент $Y.$ в один

Термин «сюръективный» и связанные с ним термины «инъективный» и «биективный» были введены Николя Бурбаки . ^[3]^[4] группа в основном французских 20-го века математиков , которые под этим псевдонимом написали серию книг, представляющих изложение современной высшей математики, начиная с 1935 года. Французское слово sur означает сверх « » и связано с тем фактом, образ что область определения сюръективной функции полностью покрывает кодобласть функции.

Любая функция вызывает сюръекцию, ограничивая свою кодомен образом своей области. Каждая сюръективная функция имеет правую обратную, если принять аксиому выбора , и каждая функция с правой обратной обязательно является сюръекцией. Композиция . сюръективных функций всегда сюръективна Любую функцию можно разложить на сюръекцию и инъекцию.

Определение [ править ]

Сюръективная функция — это функция которой , образ равен ее кодомену . Эквивалентно, функция $f$ с доменом $X$ и кодомен $Y$ сюръективно, если для каждого $y$ в $Y$ существует хотя бы один $x$ в $X$ с $f(x)=y$ . ^[1] Сюръекции иногда обозначаются двунаправленной стрелкой вправо ( U+ 21A0 ↠ ДВУГОЛОВОЧНАЯ СТРЕЛКА ВПРАВО ), ^[5] как в $f\colon X\twoheadrightarrow Y$ .

Символически,

Если

f\colon X\rightarrow Y

, затем

f

называется сюръективным, если

\forall y\in Y,\,\exists x\in X,\;\;f(x)=y

. ^[2]^[6]

Примеры [ править ]

**Несюръективная функция** из области X в кодобласть Y . Меньший желтый овал внутри Y — это изображение (также называемое диапазоном ) f . Эта функция не является сюръективной, поскольку изображение не заполняет всю кодомен. Другими словами, Y окрашивается в два этапа: во-первых, для каждого x в X точка f ( x ) окрашивается в желтый цвет; Во-вторых, все остальные точки Y , не желтые, окрашены в синий цвет. Функция f была бы сюръективной только в том случае, если бы не было синих точек.

Для любого множества X id тождественная функция X _на X сюръективна .
Функция $f : Z \to {0, 1},$ определяемая формулой f ( n ) = n mod 2 (т. е. четные целые числа отображаются в 0, а нечетные целые числа в 1), является сюръективной.
Функция $f : R \to R$ , определенная формулой f ( x ) = 2 x + 1, является сюръективной (и даже биективной ), поскольку для каждого действительного числа y у нас есть x такой, что f ( x ) = y : такой подходящий x есть ( у - 1)/2.
Функция $f : R \to R,$ определенная формулой f ( x ) = x ³ − 3 x сюръективно, поскольку прообраз любого действительного числа y является множеством решений кубического полиномиального уравнения x ³ − 3 x − y = 0, и каждый кубический многочлен с вещественными коэффициентами имеет хотя бы один вещественный корень. Однако эта функция не является инъективной (и, следовательно, не биективной ), поскольку, например, прообразом y = 2 является { x = −1, x = 2}. (Фактически, прообраз этой функции для каждого y , −2 ≤ y ≤ 2 имеет более одного элемента.)
Функция $g : R \to R$ , определенная формулой g ( x ) = x ² является не сюръективным, поскольку не существует вещественного числа x такого, что x ² = −1 . Однако функция $g : R \to R \geq0$ , определенная формулой $g (x) = x 2$ (с ограниченной кодообластью) является сюръективным, поскольку для каждого y в неотрицательной вещественной кодомене Y существует хотя бы один x в вещественной области X такой, что x ² = и .
Функция натурального логарифма . $ln : (0, +\infty) \to R$ является сюръективной и даже биективной (отображение множества положительных действительных чисел во множество всех действительных чисел) Ее обратная экспоненциальная функция , если она определена с набором действительных чисел в качестве домена и кодомена, не является сюръективной (поскольку ее диапазон представляет собой набор положительных действительных чисел).
Матричная экспонента не является сюръективной, если рассматривать ее как отображение пространства всех n × n матриц размера в себя. Однако его обычно определяют как отображение пространства всех матриц размера n × n в общую линейную группу степени n (то есть группу всех размера n × n обратимых матриц ). Согласно этому определению, матричная экспонента сюръективна для комплексных матриц, но все же не сюръективна для вещественных матриц.
Проекция на один из его декартова произведения $A \times B$ факторов сюръективна, если только другой фактор не пуст.
В 3D-видеоигре векторы проецируются на плоский 2D-экран с помощью сюръективной функции.

Свойства [ править ]

Функция биективна тогда и только тогда, когда она одновременно сюръективна и инъективна .

Если (как это часто делается) функция отождествляется со своим графиком , то сюръективность является не свойством самой функции, а скорее свойством отображения . ^[7] Это функция вместе с ее кодоменом. В отличие от инъективности, сюръективность нельзя считать только по графику функции.

Сюръекции как обратимые вправо функции [ править ]

Функция g : Y → X называется правой обратной функцией f : X → Y , если f ( g ( y )) = y для каждого y из Y ( g может быть отменено с помощью f ). Другими словами, g является правой обратной функцией f, композиция f o g g и g f в этом порядке является функцией в области Y если тождественной . Функция g не обязательно должна быть полной обратной функцией f , поскольку композиция в другом порядке, g f , может не быть тождественной функцией в области X функции f . Другими словами, f может отменить или « перевернуть » g , но не обязательно может быть отменено с его помощью.

Любая функция, имеющая правую обратную, обязательно является сюръекцией. Утверждение о том, что каждая сюръективная функция имеет правую обратную, эквивалентно аксиоме выбора .

Если f : X → Y сюръективно и является подмножеством Y , B то f ( f ⁻¹( Б )) знак равно Б . Таким образом, B можно восстановить по его прообразу f ⁻¹( Б ) .

Например, на первой иллюстрации в галерее есть некоторая функция g такая, что g ( C Также существует некоторая функция f такая, что f (4) = C. )=4 . Не имеет значения, что g не уникален (это также будет работать, если g ( C ) равно 3); имеет значение только то, что f «переворачивает» g .

как эпиморфизмы Сюръекции

Функция f : X → Y сюръективна тогда и только тогда, когда она правосократима : ^[8] для любых функций g , h : Y → Z , если g o f = h o f , то g = h . Это свойство формулируется в терминах функций и их композиции может быть обобщено на более общее понятие морфизмов категории и и их композиции. Правосократительные морфизмы называются эпиморфизмами . В частности, сюръективные функции — это в точности эпиморфизмы в категории множеств . Префикс эпи происходит от греческого предлога ἐπί, означающего «над » , «над» , «на» .

Любой морфизм с правым обратным является эпиморфизмом, но обратное, вообще говоря, неверно. Правый g морфизма f называется сечением f . обратный Морфизм с правым обратным называется расщепляемым эпиморфизмом .

как бинарные Сюръекции отношения

Любую функцию с доменом X и кодоменом Y можно рассматривать как полное слева и уникальное справа бинарное отношение между X и Y , отождествив его с графиком функции . Сюръективная функция с областью определения X и кодоменом Y тогда представляет собой бинарное отношение между X и Y , уникальное справа и полное как слева, так и справа .

Мощность области сюръекции [ править ]

Мощность — сюръективная области определения сюръективной функции больше или равна мощности ее кодомена: Если f : X → Y функция, то X имеет по крайней мере столько же элементов, сколько Y , в смысле кардинальных чисел . (Доказательство апеллирует к аксиоме выбора, чтобы показать, что функция g : Y → X, удовлетворяющее условиям f ( g ( y )) = y для всех y в Y, существует. g Легко видеть, что инъективен, поэтому формальное определение | Ю | ≤ | Х | доволен.)

В частности, если и X, и Y конечны с одинаковым количеством элементов, то f : X → Y сюръективен тогда и только тогда, f инъективен когда .

Для двух наборов X и Y обозначение X ≤ ^* Y используется, чтобы сказать, что либо пуст , либо существует сюръекция из Y на X. X Используя аксиому выбора, можно показать, что X ≤ ^* Y и Y ≤ ^* X вместе подразумевают, что | Ю | = | X |, вариант теоремы Шрёдера–Бернштейна .

Состав и разложение [ править ]

Композиция оба сюръективны , сюръективных функций всегда сюръективна: если f и g а кодобласть g равна области определения f , то f o g сюръективен. И наоборот, если f o g сюръективна, то f сюръективна (но g , функция, применяемая первой, не обязательно). Эти свойства обобщаются от сюръекций в категории множеств на любые эпиморфизмы в любой категории .

Любую функцию можно разложить на сюръекцию и инъекцию : для любой функции h : X → Z существуют сюръекция f : X → Y и инъекция g : Y → Z такие, что h = g o f . Чтобы убедиться в этом, определим Y как набор прообразов h ⁻¹( z ) где z находится в час ( X ) . Эти прообразы не пересекаются и разбивают X . Затем f переносит каждый элемент x элемент Y в содержащий его , а g переносит каждый элемент Y в точку Z, в которую h отправляет свои точки. Тогда f сюръективно, поскольку это отображение проекции, а g инъективен по определению.

Индуцированная сюръекция индуцированная и биекция

Любая функция вызывает сюръекцию, ограничивая свою кодомен своим диапазоном. Любая сюръективная функция порождает биекцию, определенную на факторе ее области определения, путем свертывания всех аргументов, отображаемых на данное фиксированное изображение. Точнее, каждую сюръекцию f : A → B можно факторизовать как проекцию, за которой следует биекция следующим образом. Пусть A /~ — эквивалентности A классы при следующем отношении эквивалентности : x ~ y тогда и только тогда, когда f ( x ) = f ( y ). Эквивалентно, A /~ — это множество всех прообразов при отображении f . Пусть P (~) : A → A /~ — отображение проекции , которое переводит каждый x в A в его класс эквивалентности [ x ] _~ , и пусть f _P : A /~ → B — четко определенная функция, заданная f _P ([ Икс ] _~ ) знак равно ж ( Икс ). Тогда f = f _P o P (~).

Набор сюръекций [ править ]

Учитывая фиксированные $A$ и $B$ можно сформировать набор сюръекций $A ↠ B.$ , Мощность и этого набора является одним из двенадцати аспектов Двенадцатеричного пути Роты определяется выражением ${\textstyle |B|!{\begin{Bmatrix}|A|\\|B|\end{Bmatrix}}}$ , где ${\textstyle {\begin{Bmatrix}|A|\\|B|\end{Bmatrix}}}$ обозначает число Стирлинга второго рода .

Галерея [ править ]

Неинъективная сюръективная функция (сюръекция, а не биекция)
Инъективная сюръективная функция (биекция)
Инъективная несюръективная функция (инъекция, а не биекция)
Неинъективная несюръективная функция (не биекция)

Сюръективная композиция: первая функция не обязательно должна быть сюръективной.
Несюръективные функции в декартовой плоскости. Хотя некоторые части функции являются сюръективными, когда элементы y в Y имеют значение x в X такое, что y = f ( x ), некоторые части таковыми не являются. Слева: существует y ₀ в Y , но не существует x ₀ в X такого, что y ₀ = f ( x ₀ ). Справа: есть y ₁ , y ₂ и y ₃ в Y не существует таких x ₁ , x ₂ и x ₃ , но в X , что y ₁ = f ( x ₁ ), y ₂ = f ( x ₂ ), и y ₃ знак равно ж ( Икс ₃ ).
Интерпретация сюръективных функций в декартовой плоскости, определяемых отображением f : X → Y , где y = f ( x ), X = область определения функции, Y = диапазон функции. Каждый элемент диапазона сопоставляется с элементом домена по правилу f . Может существовать несколько элементов домена, которые сопоставляются с одним и тем же элементом диапазона. То есть каждый y в Y отображается из элемента x в X , более одного x может отображаться в один и тот же y . Слева: показан только один домен, что делает f сюръективным. Справа: два возможных домена X ₁ и X _{2 .} показаны

См. также [ править ]

Ссылки [ править ]

↑ Перейти обратно: Перейти обратно: ^а ^б «Инъективное, сюръективное и биективное» . www.mathsisfun.com . Проверено 7 декабря 2019 г.
↑ Перейти обратно: Перейти обратно: ^а ^б «Биекция, инъекция и сюръекция | Блестящая математическая и научная вики» . блестящий.орг . Проверено 7 декабря 2019 г.
^ Миллер, Джефф, «Инъекция, сюръекция и биекция», «Ранние варианты использования некоторых математических слов» , «Трипод» .
^ Машаал, Морис (2006). Бурбаки . Американское математическое соц. п. 106. ИСБН 978-0-8218-3967-6 .
^ «Стрелки – Юникод» (PDF) . Проверено 11 мая 2013 г.
^ Фарлоу, С. Дж. «Инъекции, сюръекции и биекции» (PDF) . math.umaine.edu . Проверено 6 декабря 2019 г.
^ ТМ Апостол (1981). Математический анализ . Аддисон-Уэсли. п. 35.
^ Голдблатт, Роберт (2006) [1984]. Топои, Категориальный анализ логики (пересмотренная ред.). Дуврские публикации . ISBN 978-0-486-45026-1 . Проверено 25 ноября 2009 г.

Дальнейшее чтение [ править ]

Бурбаки, Н. (2004) [1968]. Теория множеств . Элементы математики . Том. 1. Спрингер. дои : 10.1007/978-3-642-59309-3 . ISBN 978-3-540-22525-6 . LCCN 2004110815 .

[:0-1] Перейти обратно: Перейти обратно: ^а ^б «Инъективное, сюръективное и биективное» . www.mathsisfun.com . Проверено 7 декабря 2019 г.

[:1-2] Перейти обратно: Перейти обратно: ^а ^б «Биекция, инъекция и сюръекция | Блестящая математическая и научная вики» . блестящий.орг . Проверено 7 декабря 2019 г.

[3] Миллер, Джефф, «Инъекция, сюръекция и биекция», «Ранние варианты использования некоторых математических слов» , «Трипод» .

[4] Машаал, Морис (2006). Бурбаки . Американское математическое соц. п. 106. ИСБН 978-0-8218-3967-6 .

[Unicode_Arrows-5] «Стрелки – Юникод» (PDF) . Проверено 11 мая 2013 г.

[6] Фарлоу, С. Дж. «Инъекции, сюръекции и биекции» (PDF) . math.umaine.edu . Проверено 6 декабря 2019 г.

[7] ТМ Апостол (1981). Математический анализ . Аддисон-Уэсли. п. 35.

[8] Голдблатт, Роберт (2006) [1984]. Топои, Категориальный анализ логики (пересмотренная ред.). Дуврские публикации . ISBN 978-0-486-45026-1 . Проверено 25 ноября 2009 г.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]