процентиль

В статистике k процентиль -й , также известный как процентиль или центиль , представляет собой балл , ниже которого падает заданный процент k баллов в его частотном распределении (« исключительное » определение), или балл, на котором или ниже падает данный процент. (« инклюзивное » определение). Процентили выражаются в тех же единицах измерения, что и входные оценки, а не в процентах ; например, если баллы относятся к весу человека , соответствующие процентили будут выражены в килограммах или фунтах.В пределе бесконечного размера выборки процентиль аппроксимирует функцию процентиля , обратную кумулятивной функции распределения .

Процентили — это разновидность квантилей , получаемых путем разделения на 100 групп.25-й процентиль также известен как первый квартиль ( Q ₁ ), 50-й процентиль как медиана или второй квартиль ( Q ₂ ), а 75-й процентиль как третий квартиль ( Q ₃ ).Например, 50-й процентиль (медиана) — это оценка ниже (или на уровне или ниже , в зависимости от определения), которой соответствует 50% оценок в распределении.

Соответствующей величиной является процентильный ранг оценки, выраженный в процентах , который представляет собой долю оценок в его распределении, меньших ее (исключительное определение).Процентильные оценки и процентильные ранги часто используются при составлении отчетов о результатах тестов , соответствующих нормам , но, как только что отмечалось, они не одно и то же. Для процентильных рангов дается балл и вычисляется процент. Процентильные ранги являются исключительными: если процентильный ранг для определенного балла составляет 90%, то 90% баллов были ниже. Напротив, для процентилей указывается процент и определяется соответствующая оценка, которая может быть как исключающей, так и инклюзивной. Оценка для определенного процента (например, 90-е место) указывает оценку, ниже которой (исключительное определение) или на уровне или ниже которого (инклюзивное определение) находятся другие оценки в распределении.

Определения

Стандартного определения процентиля не существует; ^[1]^[2]^[3]однако все определения дают схожие результаты, когда количество наблюдений очень велико и распределение вероятностей непрерывно. ^[4] В пределе, когда размер выборки приближается к бесконечности, 100 p ^й процентиль (0< p <1) аппроксимирует обратную величину сформированной таким образом кумулятивной функции распределения (CDF), оцениваемой при p , поскольку p аппроксимирует CDF. Это можно рассматривать как следствие теоремы Гливенко – Кантелли . Некоторые методы расчета процентилей приведены ниже.

Нормальное распределение и процентили

Методы, приведенные в разделе «Методы расчета» (ниже), представляют собой приближения для использования в статистике малой выборки. В общих чертах, для очень больших групп населения, имеющих нормальное распределение , процентили часто могут быть представлены с помощью графика нормальной кривой. Нормальное распределение строится вдоль оси, масштабированной до стандартных отклонений или сигмы ( $\sigma$ ) единицы. Математически нормальное распределение простирается до отрицательной бесконечности слева и положительной бесконечности справа. Однако обратите внимание, что лишь очень небольшая часть особей в популяции выйдет за пределы диапазона от -3 σ до +3 σ . Например, при росте человека очень немногие люди имеют выше +3 σ высоту .

Процентили представляют собой площадь под нормальной кривой, увеличивающуюся слева направо. Каждое стандартное отклонение представляет собой фиксированный процентиль. Таким образом, округляя до двух десятичных знаков, −3 σ — 0,13-й процентиль, −2 σ — 2,28-й процентиль, −1 σ — 15,87-й процентиль, 0 σ — 50-й процентиль (как среднее, так и медиана распределения), + 1 σ — 84,13-й процентиль, +2 σ — 97,72-й процентиль и +3 σ — 99,87-й процентиль. Это связано с правилом 68–95–99,7 или правилом трех сигм. Обратите внимание, что теоретически 0-й процентиль приходится на отрицательную бесконечность, а 100-й процентиль на положительную бесконечность, хотя во многих практических приложениях, таких как результаты испытаний, применяются естественные нижние и/или верхние пределы.

Приложения

Когда интернет-провайдеры выставляют счета за «повышенную» пропускную способность Интернета , 95-й или 98-й процентиль обычно отсекают верхние 5% или 2% пиковой пропускной способности каждого месяца, а затем выставляют счета по ближайшему тарифу. Таким образом, нечастые пики игнорируются, и с клиента взимается более справедливая плата. Причина, по которой эта статистика настолько полезна при измерении пропускной способности данных, заключается в том, что она дает очень точную картину стоимости полосы пропускания. 95-й процентиль говорит, что в 95 % случаев использование ниже этого значения: следовательно, в оставшиеся 5 % времени использование превышает это значение.

Врачи часто используют вес и рост младенцев и детей для оценки их роста по сравнению со средними показателями по стране и процентилями, которые можно найти в диаграммах роста .

Скорость движения на дороге, составляющая 85-й процентиль, часто используется в качестве ориентира при установлении ограничений скорости и оценке того, является ли такой предел слишком высоким или низким. ^[5]^[6]

В финансах стоимость под риском — это стандартная мера для оценки (в зависимости от модели) величины, ниже которой ожидается, что стоимость портфеля не упадет в течение заданного периода времени и с учетом доверительного значения.

Методы расчета

Interpolated and nearest-rank, exclusive and inclusive, percentiles for 10-score distribution

Интерполированные и ближайшего ранга, исключительные и инклюзивные, процентили для распределения по 10 баллам

Существует множество формул и алгоритмов. ^[7] для процентильного балла. Гайндман и Фан ^[1] идентифицировано девять, и большинство статистических программ и программ для работы с электронными таблицами используют один из описанных ими методов. ^[8] Алгоритмы либо возвращают значение оценки, которая существует в наборе оценок (методы ближайшего ранга), либо интерполируют между существующими оценками и являются либо исключающими, либо инклюзивными.

Методы ближайшего ранга (исключающий/включающий)
ПК: указан процентиль	0.10	0.25	0.50	0.75	0.90
N: количество баллов	10	10	10	10	10
ИЛИ: порядковый номер = PC × N	1	2.5	5	7.5	9
Ранг: >ИЛИ / ≥ИЛИ	2/1	3/3	6/5	8/8	10/9
Оценка по рангу (искл./вкл.)	2/1	3/3	4/3	5/5	7/5

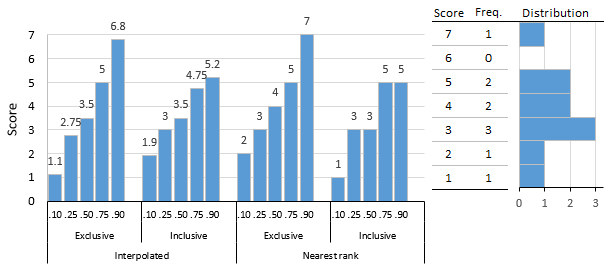
На рисунке показано распределение по 10 баллам, иллюстрируются процентильные оценки, полученные в результате этих различных алгоритмов, и служит введением к примерам, приведенным далее. Самыми простыми являются методы ближайшего ранга, которые возвращают оценку из распределения, хотя по сравнению с методами интерполяции результаты могут быть немного грубыми. В таблице «Методы ближайшего ранга» показаны этапы вычислений для исключающих и инклюзивных методов.

Интерполированные методы (исключающие/инклюзивные)
ПК: указан процентиль	0.10	0.25	0.50	0.75	0.90
N: количество баллов	10	10	10	10	10
ИЛИ: ПК×(N+1) / ПК×(N-1)+1	1.1/1.9	2.75/3.25	5.5/5.5	8.25/7.75	9.9/9.1
LoRank: ИЛИ усечено	1/1	2/3	5/5	8/7	9/9
HIRank: ИЛИ округляется в большую сторону	2/2	3/4	6/6	9/8	10/10
LoScore: оценка на LoRank	1/1	2/3	3/3	5/4	5/5
HiScore: оценка на HiRank	2/2	3/3	4/4	5/5	7/7
Разница: HiScore − LoScore	1/1	1/0	1/1	0/1	2/2
Мод: дробная часть OR	0.1/0.9	0.75/0.25	0.5/0.5	0.25/0.75	0.9/0.1
Интерполированный балл (искл./вкл.) = LoScore + Mod × Разница	1.1/1.9	2.75/3	3.5/3.5	5/4.75	6.8/5.2

Методы интерполяции, как следует из названия, могут возвращать оценку, находящуюся между оценками в распределении. Алгоритмы, используемые статистическими программами, обычно используют методы интерполяции, например функции Percentile.exc и Percentile.inc в Microsoft Excel. В таблице «Интерполированные методы» показаны этапы вычислений.

Метод ближайшего ранга

Значения процентиля для упорядоченного списка {15, 20, 35, 40, 50}

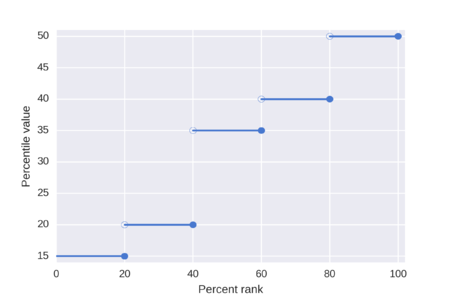
Одно из определений процентиля, часто даваемое в текстах, состоит в том, что P -й процентиль $(0<P\leq 100)$ списка из N упорядоченных значений (отсортированных от наименьшего к наибольшему) — это наименьшее значение в списке, такое, что не более P процентов данных строго меньше значения и по крайней мере P процентов данных меньше или равно до этого значения. Это получается путем сначала вычисления порядкового ранга, а затем взятия значения из упорядоченного списка, соответствующего этому рангу. Порядковый n ранг формуле рассчитывается по этой

n=\left\lceil {\frac {P}{100}}\times N\right\rceil .

Использование метода ближайшего ранга в списках, содержащих менее 100 различных значений, может привести к тому, что одно и то же значение будет использоваться более чем для одного процентиля.
Процентиль, рассчитанный с использованием метода ближайшего ранга, всегда будет членом исходного упорядоченного списка.
100-й процентиль определяется как наибольшее значение в упорядоченном списке.

Метод линейной интерполяции между ближайшими рангами

Альтернативой округлению, используемому во многих приложениях, является использование линейной интерполяции между соседними рангами.

Все следующие варианты имеют следующее общее. Учитывая статистику заказов

\{v_{i},i=1,2,\ldots ,N:v_{i+1}\geq v_{i},\forall i=1,2,\ldots ,N-1\},

мы ищем линейную интерполяционную функцию, проходящую через точки $(v_{i},i)$ . Это достигается просто

v(x)=v_{\lfloor x\rfloor }+(x{\bmod {1}})(v_{\lfloor x\rfloor +1}-v_{\lfloor x\rfloor }),\forall x\in [1,N]:v(i)=v_{i}{\text{, for }}i=1,2,\ldots ,N,

где $\lfloor x\rfloor$ использует функцию пола для представления целой части положительного $x$ , тогда как $x{\bmod {1}}$ использует функцию mod для представления своей дробной части (остатка после деления на 1). (Обратите внимание, что хотя в конечной точке $x=N$ , $v_{\lfloor x\rfloor +1}$ не определено, это не обязательно, потому что оно умножается на $x{\bmod {1}}=0$ .) Как мы видим, $x$ — это непрерывная версия индекса $i$ , линейно интерполирующая $v$ между соседними узлами.

Вариантные подходы различаются двумя способами. Первый заключается в линейной зависимости между рангом $x$ и процентным рангом. $P=100p$ и константа, которая является функцией размера выборки $N$ :

x=f(p,N)=(N+c_{1})p+c_{2}.

Существует дополнительное требование, чтобы средняя точка диапазона $(1,N)$ , соответствующие медиане , происходят при $p=0.5$ :

{\begin{aligned}f(0.5,N)&={\frac {N+c_{1}}{2}}+c_{2}={\frac {N+1}{2}}\\\therefore 2c_{2}+c_{1}&=1\end{aligned}},

и наша пересмотренная функция теперь имеет только одну степень свободы и выглядит так:

x=f(p,N)=(N+1-2C)p+C.

Второе различие между вариантами заключается в определении функции вблизи границ $[0,1]$ диапазон $р$ : $f(p,N)$ должен производить или быть вынужден производить результат в диапазоне $[1,N]$ , что может означать отсутствие взаимно однозначного соответствия в более широком регионе. Один автор предложил выбрать $C={\tfrac {1}{2}}(1+\xi )$ где $ξ$ — форма обобщенного распределения экстремальных значений , которое является пределом экстремальных значений выборочного распределения.

Первый вариант, С = 1/2

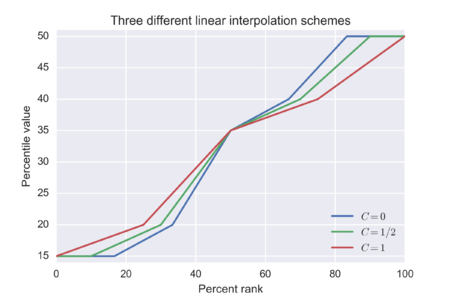
(Источники: функция «prctile» Matlab, ^[9]^[10])

x=f(p)={\begin{cases}Np+{\frac {1}{2}},\forall p\in \left[p_{1},p_{N}\right],\\1,\forall p\in \left[0,p_{1}\right],\\N,\forall p\in \left[p_{N},1\right].\end{cases}}

где

p_{i}={\frac {1}{N}}\left(i-{\frac {1}{2}}\right),i\in [1,N]\cap \mathbb {N}

\therefore p_{1}={\frac {1}{2N}},p_{N}={\frac {2N-1}{2N}}.

Кроме того, пусть

P_{i}=100p_{i}.

Обратная зависимость ограничена более узкой областью:

p={\frac {1}{N}}\left(x-{\frac {1}{2}}\right),x\in (1,N)\cap \mathbb {R} .

Второй вариант, C = 1

[Источник: некоторые пакеты программного обеспечения, включая NumPy. ^[11] и Microsoft Excel ^[3] (до версии 2013 включительно с помощью функции ПРОЦЕНТИЛЬ.ВКЛ). Отмечен как альтернатива NIST . ^[8]]

x=f(p,N)=p(N-1)+1{\text{, }}p\in [0,1]

\therefore p={\frac {x-1}{N-1}}{\text{, }}x\in [1,N].

Обратите внимание, что $x\leftrightarrow p$ отношения один к одному для $p\in [0,1]$ , единственный из трех вариантов с этим свойством; отсюда и суффикс «INC», обозначающий «включительно» , в функции Excel.

Третий вариант, С = 0

(Основной вариант, рекомендованный NIST . ^[8] Принято Microsoft Excel с 2010 года с помощью функции PERCENTIL.EXC. Однако, как указывает суффикс «EXC», версия Excel исключает обе конечные точки диапазона p , т.е. $p\in (0,1)$ , тогда как версия «INC», второй вариант, этого не делает; фактически, любое число меньше ${\frac {1}{N+1}}$ также исключено и приведет к ошибке.)

x=f(p,N)={\begin{cases}1{\text{, }}p\in \left[0,{\frac {1}{N+1}}\right]\\p(N+1){\text{, }}p\in \left({\frac {1}{N+1}},{\frac {N}{N+1}}\right)\\N{\text{, }}p\in \left[{\frac {N}{N+1}},1\right]\end{cases}}.

Обратное ограничено более узкой областью:

p={\frac {x}{N+1}}{\text{, }}x\in (0,N).

Метод взвешенного процентиля

Помимо функции процентиля, существует еще взвешенный процентиль , где вместо общего числа подсчитывается процент от общего веса. Стандартной функции для взвешенного процентиля не существует. Один метод естественным образом расширяет описанный выше подход.

Предположим, у нас есть положительные веса $w_{1},w_{2},w_{3},\dots ,w_{N}$ связаны, соответственно, с нашими N отсортированными значениями выборки. Позволять

S_{N}=\sum _{k=1}^{N}w_{k},

сумма весов. Тогда приведенные выше формулы обобщаются, взяв

p_{n}={\frac {1}{S_{N}}}\left(S_{n}-{\frac {w_{n}}{2}}\right)

когда

C=1/2

,

или

p_{n}={\frac {S_{n}-Cw_{n}}{S_{N}+(1-2C)w_{n}}}

для общего

C

,

и

v=v_{k}+{\frac {P-p_{k}}{p_{k+1}-p_{k}}}(v_{k+1}-v_{k}).

Взвешенный процентиль 50% известен как взвешенная медиана .

См. также

Ссылки

^ Jump up to: ^а ^б Гайндман, Роб Дж .; Фан, Янан (ноябрь 1996 г.). «Выборочные квантили в статистических пакетах» . Американский статистик . 50 (4). Американская статистическая ассоциация: 361–365. дои : 10.2307/2684934 . JSTOR 2684934 .
^ Лейн, Дэвид. «Процентили» . Проверено 15 сентября 2007 г.
^ Jump up to: ^а ^б Поттель, Ганс. «Статистические ошибки в Excel» (PDF) . Архивировано из оригинала (PDF) 4 июня 2013 г. Проверено 25 марта 2013 г.
^ Шунджанс Ф., Де Баккер Д., Шмид П. (2011). «Оценка процентилей населения» . Эпидемиология . 22 (5): 750–751. дои : 10.1097/EDE.0b013e318225c1de . ПМК 3171208 . ПМИД 21811118 .
^ Джонсон, Роберт; Куби, Патриция (2007), «Прикладной пример 2.15, Ограничение скорости 85-го процентиля: движение с 85% потока», Элементарная статистика (10-е изд.), Cengage Learning, стр. 102, ISBN 9781111802493 .
^ «Рациональные ограничения скорости и скорость 85-го процентиля» (PDF) . lsp.org . Полиция штата Луизиана. Архивировано из оригинала (PDF) 23 сентября 2018 года . Проверено 28 октября 2018 г.
^ Весса, П. (2021). «Процентили в бесплатном статистическом программном обеспечении» . Управление по развитию исследований и образования . Проверено 13 ноября 2021 г.
^ Jump up to: ^а ^б ^с «Справочник по инженерной статистике: процентиль» . НИСТ . Проверено 18 февраля 2009 г.
^ «Пакет инструментов статистики Matlab – процентили» . Проверено 15 сентября 2006 г. , Это эквивалентно методу 5, обсуждаемому здесь.
^ Лэнгфорд, Э. (2006). «Квартили в элементарной статистике» . Журнал статистического образования . 14 (3). дои : 10.1080/10691898.2006.11910589 .
^ «Документация NumPy 1.12» . SciPy . Проверено 19 марта 2017 г.

[hyndman-1] Jump up to: ^а ^б Гайндман, Роб Дж .; Фан, Янан (ноябрь 1996 г.). «Выборочные квантили в статистических пакетах» . Американский статистик . 50 (4). Американская статистическая ассоциация: 361–365. дои : 10.2307/2684934 . JSTOR 2684934 .

[2] Лейн, Дэвид. «Процентили» . Проверено 15 сентября 2007 г.

[pottel-3] Jump up to: ^а ^б Поттель, Ганс. «Статистические ошибки в Excel» (PDF) . Архивировано из оригинала (PDF) 4 июня 2013 г. Проверено 25 марта 2013 г.

[schoonjans-4] Шунджанс Ф., Де Баккер Д., Шмид П. (2011). «Оценка процентилей населения» . Эпидемиология . 22 (5): 750–751. дои : 10.1097/EDE.0b013e318225c1de . ПМК 3171208 . ПМИД 21811118 .

[5] Джонсон, Роберт; Куби, Патриция (2007), «Прикладной пример 2.15, Ограничение скорости 85-го процентиля: движение с 85% потока», Элементарная статистика (10-е изд.), Cengage Learning, стр. 102, ISBN 9781111802493 .

[6] «Рациональные ограничения скорости и скорость 85-го процентиля» (PDF) . lsp.org . Полиция штата Луизиана. Архивировано из оригинала (PDF) 23 сентября 2018 года . Проверено 28 октября 2018 г.

[7] Весса, П. (2021). «Процентили в бесплатном статистическом программном обеспечении» . Управление по развитию исследований и образования . Проверено 13 ноября 2021 г.

[nist-8] Jump up to: ^а ^б ^с «Справочник по инженерной статистике: процентиль» . НИСТ . Проверено 18 февраля 2009 г.

[9] «Пакет инструментов статистики Matlab – процентили» . Проверено 15 сентября 2006 г. , Это эквивалентно методу 5, обсуждаемому здесь.

[10] Лэнгфорд, Э. (2006). «Квартили в элементарной статистике» . Журнал статистического образования . 14 (3). дои : 10.1080/10691898.2006.11910589 .

[numpydocs-11] «Документация NumPy 1.12» . SciPy . Проверено 19 марта 2017 г.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]